北京市八年级数学下册 勾股定理专题讲解 (新版)新人教版(1)

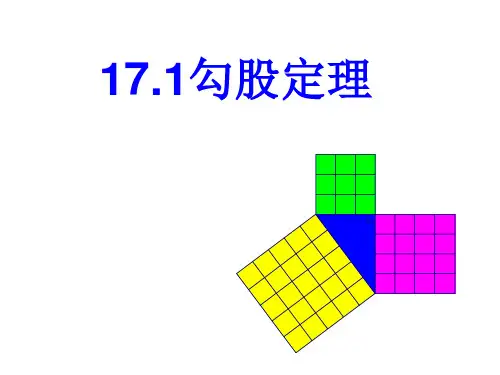
新人教版八年级下册勾股定理全章知识点和典型例习题一、基础知识点： １．勾股定理内容：直角三角形两直角边的平方和等于斜边的平方；表示方法：如果直角三角形的两直角边分别为a ，b ，斜边为c ，那么222a b c += 勾股定理的由来：勾股定理也叫商高定理，在西方称为毕达哥拉斯定理．我国古代把直角三角形中较短的直角边称为勾，较长的直角边称为股，斜边称为弦．早在三千多年前，周朝数学家商高就提出了“勾三，股四，弦五”形式的勾股定理，后来人们进一步发现并证明了直角三角形的三边关系为：两直角边的平方和等于斜边的平方 ２.勾股定理的证明勾股定理的证明方法很多，常见的是拼图的方法 用拼图的方法验证勾股定理的思路是 ①图形进过割补拼接后，只要没有重叠，没有空隙，面积不会改变②根据同一种图形的面积不同的表示方法，列出等式，推导出勾股定理常见方法如下： 方法一：4EFGHS S S ∆+=正方形正方形ABCD ，2214()2ab b a c ⨯+-=，化简可证．方法二：四个直角三角形的面积与小正方形面积的和等于大正方形的面积．四个直角三角形的面积与小正方形面积的和为221422S ab c ab c =⨯+=+ 大正方形面积为22()2S a b a a b b =+=++ 所以22a b c +=方法三：1()()2S a b a b =+⋅+梯形，2112S 222ADE ABE S S ab c ∆∆=+=⋅+梯形，化简得证３.勾股定理的适用范围勾股定理揭示了直角三角形三条边之间所存在的数量关系，它只适用于直角三角形，对于锐角三角形和钝角三角形的三边就不具有这一特征，因而在应用勾股定理时，必须明了所考察的对象是直角三角形 ４.勾股定理的应用①已知直角三角形的任意两边长，求第三边在ABC ∆中，90C ∠=︒，则22c a b =+，22b c a =-，22a c b =-②知道直角三角形一边，可得另外两边之间的数量关系③可运用勾股定理解决一些实际问题 ５.勾股定理的逆定理如果三角形三边长a ，b ，c 满足222a b c +=，那么这个三角形是直角三角形，其中c 为斜边 ①勾股定理的逆定理是判定一个三角形是否是直角三角形的一种重要方法，它通过“数转化为形”来确定三角形的可能形状，在运用这一定理时，可用两小边的平方和22a b +与较长cbaHG F ED CBAbacbac ca bcab a bc cbaED CB A边的平方2c 作比较，若它们相等时，以a ，b ，c 为三边的三角形是直角三角形；若222a b c +<，时，以a ，b ，c 为三边的三角形是钝角三角形；若222a b c +>，时，以a ，b ，c 为三边的三角形是锐角三角形；②定理中a ，b ，c 及222a b c +=只是一种表现形式，不可认为是唯一的，如若三角形三边长a ，b ，c 满足222a c b +=，那么以a ，b ，c 为三边的三角形是直角三角形，但是b 为斜边 ③勾股定理的逆定理在用问题描述时，不能说成：当斜边的平方等于两条直角边的平方和时，这个三角形是直角三角形 ６.勾股数①能够构成直角三角形的三边长的三个正整数称为勾股数，即222a b c +=中，a ，b ，c 为正整数时，称a ，b ，c 为一组勾股数 ②记住常见的勾股数可以提高解题速度，如3,4,5；6,8,10；5,12,13；7,24,25等 ③用含字母的代数式表示n 组勾股数： 221,2,1n n n -+（2,n ≥n 为正整数）；2221,22,221n n n n n ++++（n 为正整数）2222,2,m n mn m n -+（,m n >m ，n 为正整数）７．勾股定理的应用勾股定理能够帮助我们解决直角三角形中的边长的计算或直角三角形中线段之间的关系的证明问题．在使用勾股定理时，必须把握直角三角形的前提条件，了解直角三角形中，斜边和直角边各是什么，以便运用勾股定理进行计算，应设法添加辅助线（通常作垂线），构造直角三角形，以便正确使用勾股定理进行求解． ８.．勾股定理逆定理的应用勾股定理的逆定理能帮助我们通过三角形三边之间的数量关系判断一个三角形是否是直角三角形，在具体推算过程中，应用两短边的平方和与最长边的平方进行比较，切不可不加思考的用两边的平方和与第三边的平方比较而得到错误的结论． ９.勾股定理及其逆定理的应用勾股定理及其逆定理在解决一些实际问题或具体的几何问题中，是密不可分的一个整体．通常既要通过逆定理判定一个三角形是直角三角形，又要用勾股定理求出边的长度，二者相辅相成，完成对问题的解决．常见图形：AB C30°D C BA ADB C10、互逆命题的概念如果一个命题的题设和结论分别是另一个命题的结论和题设，这样的两个命题叫做互逆命题。

《勾股定理》教学解读主题解读：（1）课标比较2011版：探索勾股定理及其逆定理，并能运用它们解决一些简单的实际问题。

实验版：体验勾股定理的探索过程，会运用勾股定理解决简单问题；会用勾股定理的逆定理判定直角三角形。

新版更注重知识的生成过程，注重学生从无到有的体验。

（2）不同版本教材的比较人教版：北师大版：华师版：三个不同版本都突出了探索勾股定理的过程，人教版还原了几何勾股定理的历史原貌，体现了欧式几何的思想.华师版和北师版均从直角三角形三边的数量关系上寻找勾股定理，符合中国的数学思想与方法.（3）在数学史上的发展轨迹勾股定理是一个古老的数学问题，起源于实际测量和计算，只要有文明的地方，就有勾股定理的存在形式.从勾股定理的发现和证明的历史发展看，定理有其实际应用价值且蕴含了丰富的数学思想，如特殊到一般、归纳猜想、转化和数形结合的思想。

古代中国和古希腊人对定理的证明也彰显了东西方不同的数学文化和精神.不同的是，东方以中国为代表的称勾股定理，体现直角三角形三边数的运算规律，以西方希腊为代表的毕达哥拉斯定理，体现直角三角形三边的几何规律，这从他们的叙述就能看出来，并且从证明的角度，也体现了文化上的差异.但是，在中国，梅文鼎集东西方文化的大成，给予了融汇东西的证明方法.而随着数学的进一步发展，勾股定理成为了余弦定理的特殊形式，并在三维或n 维空间存在勾股定理的推广.并且随着非欧几何的产生，勾股定理在这些学科中具有相似的表现形式（4）课程内容的纵向发展轨迹勾股定理在小学阶段呈现的是数的计算以及特殊的直角三角形—等腰直角三角形的面积计算.进入中学以后，随着无理数及平方根的引入，以及欧式几何深入学习，学生可以逐渐理解代数下222a b c +=的运算以及演绎逻辑下的推理，开始进行系统的定理学习与简单应用.随后，学生还要在高中进行余弦定理的进一步学习，体会斜三角形转化为直角三角形的数学思想。

如果进入大学，还要体验三维空间或n 维空间的勾股定理的形式，甚至在数学系，还要学习非欧几何的勾股定理形式.（5）课程内容的横向联系勾股定理作为一个阶段性知识点的载体，可以作为代数形式的发展，一是从元的个数形式的发展，如2222a b c d ++=等等四元二次等式的研究；二是从次数增加的形式的发展，如n n n a b c +=的整数解.教学目标（1）结合阅读材料，通过课前查找资料，课本自学，了解勾股定理的表述与证明；（2）通过网络平台交流学习心得、提出问题，掌握勾股定理的证明方法；（3）通过与历史对话，体会数学大家的数学智慧.教学重点与难点教学重点：勾股定理的不同证明教学难点：从历史与文化的背后，理解勾股定理，并提出问题.教学内容：请同学们带着以下几个问题，认真阅读所给资料，并查阅其它相关资料，尝试回答这些问题和提出你的问题。