初二物理下册阿基米德原理
- 格式:doc
- 大小:135.00 KB
- 文档页数:6







阿基米德原理是指在液体中浸没的物体所受的浮力等于其排开液体的重力,即物体在液体中所受的浮力等于物体排开的液体的重量。
阿基米德原理是由古希腊数学家阿基米德在公元前三世纪提出的。
他通过一系列的实验发现,当一个物体浸没在液体中时,它所受的浮力等于排开的液体的重量。
这个原理在物理学中被广泛应用,对于理解物体的浮沉和浮力的作用具有重要意义。
根据阿基米德原理,一个物体在液体中浸没时受到的浮力等于物体排开的液体的重量。
浮力的大小等于液体的密度乘以排开液体的体积,公式为F=γVg,其中F代表浮力,γ代表液体的密度,V代表排开液体的体积,g代表重力加速度。
根据这个原理,我们可以解释物体浮力的大小和物体的浮沉现象。
当一个物体的密度大于液体的密度时,物体所受的浮力小于物体的重力,物体将下沉;当物体的密度小于液体的密度时,物体所受的浮力大于物体的重力,物体将浮起。
利用阿基米德原理,我们可以解释为什么物体在水中浮起,以及为什么一些物体可以漂浮在水上。
比如一艘船,在浸没在水中时,船体受到的浮力等于船体排开的水的重量,这个浮力正好抵消了船体的重力,所以船体就能够浮在水面上。
而一块密度小于水的木块也能浮在水上,是因为木块所受的浮力大于木块的重力,所以木块会浮起。
阿基米德原理的应用不仅仅局限于液体中,对于气体中的物体也是适用的。
在气体中,物体所受的浮力等于物体排开的气体的重力。
这个原理解释了为什么气球能够漂浮在空中。
除了浮力的应用,阿基米德原理还可以解释物体的测重现象。
当一个物体浸没在液体中时,液体会对物体施加一个向上的浮力,这个浮力的大小等于物体的重量。
所以,我们可以利用一个浸没在液体中的物体所受的浮力来测量物体的重量。
总之,阿基米德原理是物理学中一条重要的原理,它描述了浸没在液体中的物体所受的浮力等于物体排开的液体的重量。
这个原理对于解释浮沉现象、测重和理解物体的浮力起着重要作用。
我们在日常生活中可以通过阿基米德原理来理解许多现象,如船的浮力、气球的漂浮等。


20242025学年沪粤版八年级物理下册教案9.2 阿基米德原理教案设计意图:本节课的设计意图是让学生通过实验和观察,理解阿基米德原理,并能够运用该原理解决实际问题。
我希望通过生动有趣的实验和实际情境,激发学生的学习兴趣,培养他们的观察能力、思考能力和动手能力。
教学目标:1. 让学生理解阿基米德原理,知道浮力大小与排开液体体积的关系。
2. 培养学生通过实验观察、分析问题、解决问题的能力。
3. 培养学生的团队合作意识和动手操作能力。
教学重点与难点:重点:阿基米德原理的内容及应用。
难点:浮力大小与排开液体体积的关系的实验设计和数据分析。
教具与学具准备:教具:实验器材(浮力计、物体、液体)、多媒体设备。
学具:实验记录表、笔。
活动过程:一、导入(5分钟)通过一个有趣的实验引入本节课的内容。
我会演示一个物体在液体中浮起来的实验,让学生观察并思考:为什么物体能够浮起来?浮力的大小与什么有关?二、新课讲解(15分钟)1. 讲解阿基米德原理的概念和内容,通过PPT展示相关的图片和实例,让学生理解阿基米德原理的应用。
2. 讲解浮力大小与排开液体体积的关系,通过实验和数据分析,让学生掌握浮力的大小与排开液体体积的关系。
三、实验与观察(15分钟)1. 学生分组进行实验,每组有一个浮力计、一个物体和不同体积的液体。
2. 学生通过实验记录表记录实验数据,观察浮力大小与排开液体体积的关系。
3. 学生分享实验结果,讨论浮力大小与排开液体体积的关系。
四、巩固与拓展(10分钟)1. 通过随堂练习,让学生运用阿基米德原理解决实际问题,如计算物体的浮力。
2. 学生分组讨论,思考阿基米德原理在生活中的应用,如船舶的浮力原理。
2. 教师进行课堂小结,强调阿基米德原理的重要性和应用。
课后反思及拓展延伸:本节课通过有趣的实验和实际情境,让学生掌握了阿基米德原理,并能够运用该原理解决实际问题。
在活动中,学生积极参与,动手操作,培养了他们的观察能力、思考能力和动手能力。

二、 知识点归纳
阿基米德原理重要知识点归纳
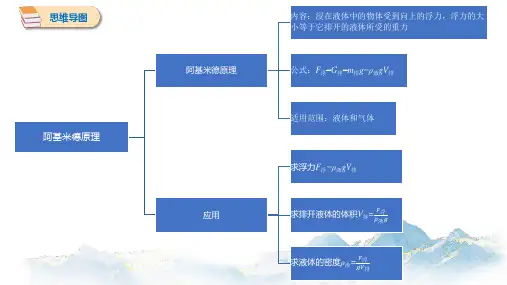
阿基米德原理:浸在液体里的物体受到的浮力的大小,等于物体排开液体所受的重力.
数学表达式:F 浮
=ρ液 g V 排 ( F 浮=G 排 )
影响浮力大小的因素: (1)液体的密度 (2)物体排开液体的体积
探究浮力大小跟那些因素有关的基本结论: (1) 在液体密度和物体排开液体体积相同时,物体所受的浮力与其浸没的深度无关. (2) 在液体密度相同时,物体排开液体的体积越大,所受的浮力越大. (3) 在物体排开液体的体积相同时, 液体密度越大,所受的浮力越大.
计算浮力的基本方法: (1) 用漂浮或悬浮条件求浮力: F 浮=G 物 (2) 用浮力产生的原因求浮力: F 浮=F 向上-F 向下 (3)
用弹簧测力计测浮力的方法求浮力:F 浮=G 物-F
(4) 用阿基米德原理求浮力:F 浮=ρ液g V 排
物体在液体中的浮沉状态
三、典型例题精炼
一、选择题
1.将挂在弹簧秤下的物体放入酒精中,弹簧秤的示数等于().
A.物体受到的重力 B.物体受到的重力减去它受到的浮力
C.物体受到的浮力 D.物体受到的浮力减去它受到的重力
2.把一个密度为10.2×103kg/m3的实心合金块投入水银中,这时合金块浸入水银中的体积和总体积之比为()(已知水银的密度为13.6×103kg/m3)
3.一木块浮在水面上时,总体积的1/5露出水面,把它放在另一种液体中,总体积的1/3露出液面,则水与这种液体的密度之比为()
A.5∶6 B.15∶8 C.6∶5 D.3∶5 4.质量相同的甲、乙两球,它们的密度之比是3∶2,甲球浸没在水中,乙球浸没在酒精中,则甲、乙两球所受浮力之比是()
A.6∶5 B.5∶6 C.5∶4 D.2∶3 5.浮在水面上的一正方体木块,若木块的水上部分是a,水下部分是b,则木块的密度为()
6.下面有关浮力的说法不正确的是()
A.漂浮的物体受到的浮力的大小等于物体的体积、液体的密度和g的乘积
B.浮力的方向总是竖直向上的
C.正在上浮的物体,在露出水面之前,它所受到的浮力大小不变
D.浸没在液体中的物体,如果浮力小于重力,物体就下沉
二、填空题
1.体积是100 的石块浸没在煤油中,它排开煤油的体积是_ _ ,它排开的煤油重_0.784_N,它受到的浮力是_ _N.
2.如图所示,三个质量相同的物体A、B、C放在水中保持静止状态,则它们所受
浮力的大小_ _ __ ,它们排开水的体积__ __ _ .(填
“>”、”=“或“<”).
3.将重是2.5N的物体A放进水中,它有一半体积露出水面,如图甲,
在A上面再放一个体积与A相同的物体B,恰好A、B两物体全部浸
入水中,且B上表面与水面相平,如图乙,求B物体的物重是
多少_ __N.
4.要打捞沉在水底的一个铁件,当铁件未露出水面时,起重机在匀速起吊的过程中,吊绳上承受的拉力是N.当铁件吊出水面后,匀速起吊时吊绳上承受的拉力是__ __N。
(铁的密度为7.8x103kg/m3.)
5.如图所示是某个实验的三个实验过程.这个实验的目的是____ __
__ _,把石块浸入盛满液体的溢水杯里,弹簧秤的示数减小,见图
乙,这说明石块__ _ _ _ _ _ _.把烧杯里接到的液体全部倒入
小筒内,见图丙.弹簧秤示数又回到了图甲的位置.这说明__ __ __
__ __ __ __ __ __ __ __ __ __ __ _。
6.给你一个实心铅锤,一个弹簧秤,密度表和一杯待测的油,请利用阿基米德原理,测出油的密度,简要写出你的实验步骤及计算公式.
三、计算题
1.体积是100cm3的实心小球放入水中,静止后有1/4体积露出水面.
求:(1)该小球受到的浮力(2)该小球的密度
2.一个木块用细绳拴着,固定在水里,(如图所示),这时绳的拉力是19.6N,用刀将绳子切断后,木块漂浮在水面上,求木块静止时露出液面部分的体积是多少?
3.有一空心铝球,重4.5N,体积为0.5dm3,如果把这个铝球浸没在水中.
①结合计算,说明它们为什么上浮?②漂浮的空心铝球露出水面的体积是多少?
4.重9.8N的木块,放在水中,有2/5体积露出水面,由此可求出哪些物理量?
四、课后作业
1.一木块浮在煤油中,露出体积的1/4,当它浮在另一种液体中时,露出体积的1/2,则木块在这两种液体中受到的浮力之比和煤油与这种液体密度之比分别是( B )
A.1∶1,1∶2 B.1∶1,2∶3 C.1∶3,1∶2 D.3∶1,3∶2
2.有一冰块漂浮在水面上,已知露出水面的体积是100dm3,求冰块的总体积?(冰的密度为0.9×103kg/m3)
3.一个实心金属球在空气中用弹簧秤称得读数为7.8N。
求:
(1)当这个金属球浸没在水中时,称得的读数6.8N,金属球在水中所受的浮力是多少?
(2)当这个金属球完全浸没在煤油中时,(煤油的密度ρ铁=0.8×103kg/m3)它受到的浮力是多少?(3)这个金属球的密度是多少?。