信号完整性透彻分析方宇杰
- 格式:pptx
- 大小:945.07 KB
- 文档页数:75


基于柔性压电薄膜的可穿戴脉搏传感器设计目录1. 内容综述 (2)1.1 研究背景及意义 (3)1.2 现有脉搏监测技术现状及不足 (4)1.3 本文研究目标及创新点 (5)2. 基于柔性压电薄膜的脉搏传感器工作原理 (6)2.1 压电材料的特性及应用 (7)2.2 传感器结构设计 (9)2.2.1 传感器组成部分 (10)2.2.2 柔性压电薄膜的特性与选择 (12)2.2.3 信号采集和处理电路设计 (13)2.3 脉搏信号获取及分析 (15)3. 材料及器件 (16)3.1 主流柔性压电薄膜材料研究 (17)3.2 器件加工工艺 (18)4. 实验设计与结果分析 (19)4.1 实验平台搭建 (21)4.2 传感器性能测试及分析 (22)4.3 压力感知特性研究 (24)4.3.1 传感器响应曲线 (25)4.3.2 传感器线性度分析 (27)4.4 脉搏信号采集与分析 (29)4.4.1 实验数据采集 (31)4.4.2 脉搏信号处理与提取 (31)4.4.3 信号分析与结果展示 (33)5. 讨论与结论 (34)5.1 研究成果总结和分析 (36)5.2 存在问题及未来展望 (37)1. 内容综述随着物联网与智能穿戴技术的不断进步,健康监测与远程医疗系统的发展需求日益显现。
在这个背景下,基于柔性压电薄膜的可穿戴脉搏传感器设计成为了研究热点。
该设计旨在实现实时、连续、非侵入式的生理信号监测,特别是针对心血管健康的监测。
该设计以人体脉搏信号的精准检测为目标,结合了柔性压电薄膜技术与现代传感技术,为用户提供一种舒适且可靠的新型穿戴监测方式。
柔性压电薄膜作为一种新兴材料,具有灵敏度高、响应速度快、可弯曲等特点,适用于可穿戴设备的制造。
基于柔性压电薄膜的可穿戴脉搏传感器不仅可用于医疗领域的心率失常预警、心血管疾病诊断,还可在运动健身领域用于运动效果评估和运动损伤预防等方面。
其设计理念的革新性在于将传统的医疗检测手段与现代可穿戴技术相结合,为用户提供个性化的健康监测服务。

第45卷第6期2023年11月沈 阳 工 业 大 学 学 报JournalofShenyangUniversityofTechnologyVol 45No 6Nov 2023收稿日期:2021-07-05基金项目:广东省自然科学基金项目(2018A030307033);南方电网科技基金项目(GDKJXM20200473)。
作者简介:杨翠茹(1980—),女,河北鹿泉人,教授级高级工程师,博士,主要从事高电压试验技术及外绝缘技术等方面的研究。
檪檪檪檪檪檪檪檪檪檪殏殏殏殏电气工程 DOI:10.7688/j.issn.1000-1646.2023.06.04结合小波变换与数学形态学的电缆局放信号识别与降噪方法杨翠茹,彭向阳,余 欣(广东电力公司科学研究院,广东广州510062)摘 要:针对大部分电缆局放(PD)信号识别方法在噪声影响下的识别准确率低、波形失真等问题,提出了一种基于小波变换与数学形态学的电缆PD信号识别及降噪方法。
该方法利用最大重叠离散小波变换提取PD信号的高频和低频特征,结合重构和数学形态法滤除噪声。
利用自适应神经网络学习小波变换后的特征,最终完成PD信号的识别分类。
基于某变电站实测PD信号波形对所提方法进行实验分析结果表明,信号降噪处理后的信噪比与均方误差分别为5 439dB、0 251,且整体的识别准确率超过了88%,均优于其他对比方法,具有良好的应用前景。
关 键 词:电缆局放信号;信号识别;信号降噪;最大重叠离散小波变换;数学形态学;自适应神经网络;白噪声;脉冲噪声中图分类号:TM247 文献标志码:A 文章编号:1000-1646(2023)06-0619-06RecognitionanddenoisingmethodofcablepartialdischargesignalbasedonwavelettransformandmathematicalmorphologyYANGCuiru,PENGXiangyang,YUXin(ScientificResearchInstitute,GuangdongElectricPowerCo.,Ltd.,Guangzhou510062,Guangdong,China)Abstract:Aimingattheproblemsoflowrecognitionaccuracyandwaveformdistortionofmostpartialdischarge(PD)signalrecognitionmethodsundertheinfluenceofnoise,aPDsignalrecognitionanddenoisingmethodbasedonwavelettransformandmathematicalmorphologywasproposed.Themaximumoverlapdiscretewavelettransformwasusedtoextractthehigh frequencyandlow frequencyfeaturesofPDsignals.Thereconstructionandmathematicalmorphologywerecombinedtofilteroutthenoise.Inaddition,theadaptiveneuralnetworkwasusedtolearnthefeaturesofwavelettransformforthefinalrecognitionandclassificationofPDsignal.TheexperimentalresultsshowthattheSNRandMSEoftheas proposedmethodare5 439dBand0 251,respectively,andtheoverallrecognitionaccuracyismorethan88%,outperformingothersimilarmethodsforcertainapplicationprospect.Keywords:cablepartialdischargesignal;signalrecognition;signalnoisereduction;maximumoverlapdiscretewavelettransform;mathematicalmorphology;adaptiveneuralnetwork;whitenoise;impulsenoise 随着对城市美化和环境保护要求的逐步提高,城市架空线路的电力电缆作为电力系统的骨架正在被逐步取代,但是例如局部放电(partialdischarge,PD)等影响电缆安全稳定的问题也日益凸显[1-2]。

于博士信号完整性分析入门于争 博士for more information,please refer to 电设计网欢迎您什么是信号完整性?如果你发现,以前低速时代积累的设计经验现在似乎都不灵了,同样的设计,以前没问题,可是现在却无法工作,那么恭喜你,你碰到了硬件设计中最核心的问题:信号完整性。
早一天遇到,对你来说是好事。
在过去的低速时代,电平跳变时信号上升时间较长,通常几个ns。
器件间的互连线不至于影响电路的功能,没必要关心信号完整性问题。
但在今天的高速时代,随着IC输出开关速度的提高,很多都在皮秒级,不管信号周期如何,几乎所有设计都遇到了信号完整性问题。
另外,对低功耗追求使得内核电压越来越低,1.2v内核电压已经很常见了。
因此系统能容忍的噪声余量越来越小,这也使得信号完整性问题更加突出。
广义上讲,信号完整性是指在电路设计中互连线引起的所有问题,它主要研究互连线的电气特性参数与数字信号的电压电流波形相互作用后,如何影响到产品性能的问题。
主要表现在对时序的影响、信号振铃、信号反射、近端串扰、远端串扰、开关噪声、非单调性、地弹、电源反弹、衰减、容性负载、电磁辐射、电磁干扰等。
信号完整性问题的根源在于信号上升时间的减小。
即使布线拓扑结构没有变化,如果采用了信号上升时间很小的IC芯片,现有设计也将处于临界状态或者停止工作。
下面谈谈几种常见的信号完整性问题。
反射:图1显示了信号反射引起的波形畸变。
看起来就像振铃,拿出你制作的电路板,测一测各种信号,比如时钟输出或是高速数据线输出,看看是不是存在这种波形。
如果有,那么你该对信号完整性问题有个感性的认识了,对,这就是一种信号完整性问题。
很多硬件工程师都会在时钟输出信号上串接一个小电阻,至于为什么,他们中很多人都说不清楚,他们会说,很多成熟设计上都有,照着做的。
或许你知道,可是确实很多人说不清这个小小电阻的作用,包括很多有了三四年经验的硬件工程师,很惊讶么?可这确实是事实,我碰到过很多。
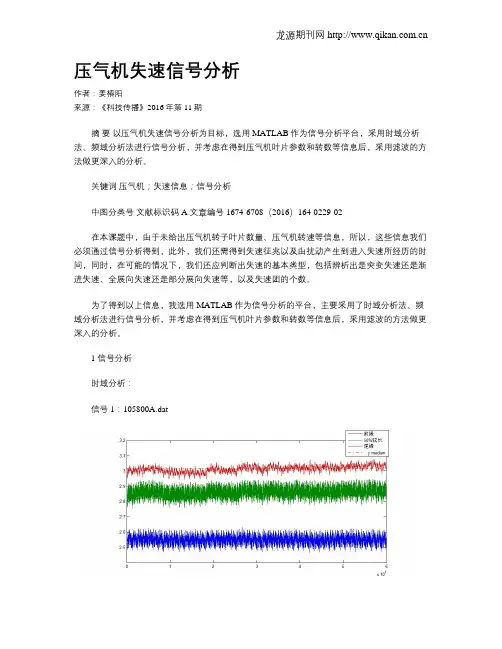
压气机失速信号分析作者:姜椿阳来源:《科技传播》2016年第11期摘要以压气机失速信号分析为目标,选用MATLAB作为信号分析平台,采用时域分析法、频域分析法进行信号分析,并考虑在得到压气机叶片参数和转数等信息后,采用滤波的方法做更深入的分析。
关键词压气机;失速信息;信号分析中图分类号文献标识码 A 文章编号 1674-6708(2016)164-0229-02在本课题中,由于未给出压气机转子叶片数量、压气机转速等信息,所以,这些信息我们必须通过信号分析得到,此外,我们还需得到失速征兆以及由扰动产生到进入失速所经历的时间,同时,在可能的情况下,我们还应判断出失速的基本类型,包括辨析出是突变失速还是渐进失速、全展向失速还是部分展向失速等,以及失速团的个数。
为了得到以上信息,我选用MATLAB作为信号分析的平台,主要采用了时域分析法、频域分析法进行信号分析,并考虑在得到压气机叶片参数和转数等信息后,采用滤波的方法做更深入的分析。
1 信号分析时域分析:信号1:105800A.dat如图1所示,即为近设计点工况时域图,横坐标按采集点个数均分,由于采样频率恒定为12K,采样时间为5s,所以采集点个数也就表征了时间。
由上图可以看出,近工况状态下,前缘、50%弦长和尾缘的压强信号基本保持稳定,只是在小范围内有脉动,将测得参数按按时间平均,并设前缘静压平均量为P1,50%弦长处P2,尾缘P3,则有P1=2.544,P3=3.013,于是得近设计点工况增压比n1=P1/P3=1.184。
如图2所示,压气机的近失速点实际即为压气机叶片气流分离点位于50%弦长处时,此时,微小扰动即可导致压气机进入失速状态。
按上一数据的处理方法,我们得到近失速点压比为n2=1.156,较近设计点工况略小,这是由于流动的分离导致压气机效率降低造成的/但是当进入失速状态时(近失速状态),我们可以定性的分析出尾缘处静压与前缘处静压在数值上呈现近似的负相关关系,这是由失速团的性质决定的,并且,节流阀开启后,压气机增压绝对值突然上升又剧烈下降,最后,成周期性变化,由此可以初步判定该失速类型为突变型失速。

《战略推演:获取竞争优势的思维与方法》读书随笔目录一、内容概括 (2)1.1 背景介绍 (3)1.2 研究意义 (4)1.3 研究目的和方法 (5)二、战略推演概述 (6)2.1 战略推演的定义 (7)2.2 战略推演的特点 (8)2.3 战略推演的重要性 (9)三、战略推演的核心要素 (10)3.1 情景设定 (12)3.2 目标设定 (13)3.3 推演过程 (14)3.4 结果分析与反馈 (15)四、战略推演的方法与技术 (17)4.1 定性分析方法 (18)4.2 定量分析方法 (20)4.2.1 数据包络分析 (21)4.2.2 博弈论 (22)4.2.3 实验设计法 (23)4.3 技术支持 (24)4.3.1 计算机模拟 (26)4.3.2 大数据分析 (27)4.3.3 人工智能辅助 (28)五、战略推演在实践中的应用 (29)5.1 企业战略规划 (31)5.2 项目管理 (33)5.3 军事战略 (34)5.4 其他领域的应用 (36)六、战略推演的挑战与未来展望 (37)七、结论 (39)7.1 主要研究发现 (40)7.2 对实践的启示 (41)7.3 研究不足与展望 (42)一、内容概括《战略推演:获取竞争优势的思维与方法》是一本深入探讨如何在竞争激烈的市场环境中获取竞争优势的书籍。
书中主要介绍了战略推演的概念、思维方式和方法论,帮助读者理解并应用战略推演来指导企业或个人的发展。
本书首先阐述了战略推演的重要性,指出在当今快速变化的时代,企业和个人都需要通过战略推演来明确自身的目标和发展方向。
书中详细介绍了战略推演的基本框架和步骤,包括环境分析、竞争态势分析、资源与能力分析等方面。
这些步骤为进行战略推演提供了系统的指导。
在内容方面,本书强调了竞争优势的来源和创造方式。
作者通过案例分析,展示了如何通过战略推演发现潜在的竞争优势,并将其转化为实际竞争力。
书中还探讨了如何利用创新思维、团队协作等关键能力来强化竞争优势,提升企业和个人的市场地位。



高速数字电路设计中信号完整性分析与思考作者:魏红艳来源:《西部论丛》2017年第01期摘要:提高信号的完整性,是提高高速数字电路设计水平及性能的主要途径。
本文简要分析了与高速数字电路信号完整性有关的因素,强调了控制各因素的重要性。
基于此,主要从反射、串扰、噪声三方面出发,详细探讨了各因素的控制方法。
并通过建立仿真模型、观察仿真效果的方式,证实了本课题所提出的设计方案的有效性。
关键词:高速数字;电路设计;信号完整性1高速数字电路的概念分析高速数字电路指的是信号在高速变化和电路模拟特性的情况下发生变化的电路,其模拟特征主要包括电容、电感等。
高速数字电路主要包括总参数系统和分布参数系统两部分,其中总参数系统中的电流与电压都不会受到其它因素影响,因此在信号日常传输的过程中不会出现畸形问题。
现阶段,分布参数系统已经在数字电路设计过程中得到了广泛应用,同时取得了很好的应用效果,该系统的主要优势是:设计与其实际运行情况接近,并充分考虑了信号传输过程的影响因素。
2信号的完整性简单来说,信号的完整性实质上指的就是信号在电路中传输的质量,信号的传输路径可以是金属线、光学器件,或者其他媒介物质等。
当信号完整性良好时,信号在需要的时候具备其需要达到的电压电平均值。
但在实际中,信号往往会受到各种因素影响,从而造成信号完整性变差。
其中最为常见的信号完整性问题便是信号反射噪音问题。
3数据的高速采集与处理技术要点分析如图1所述的数据采样与处理过程示意图,要想实现数据的高速采集与处理,就必须使检测装置、信号线、数据处理单元都能够满足相应速度的工作条件。
以常用的电流或电压传感器为例,其响应时间就代表着它能够多快的响应外部激励,也就决定着其多能实现的最高采样速度。
所以要想获得有效的高速数据首先要从检测装置选型做起。
图1数据采样与处理过程示意图信号线对信号质量有着重要的影响,尤其在高频以及恶劣的电磁环境下。
所以要选满足对应频率、屏蔽条件、阻抗特性的信号线,以保证信号质量,确保数据的正确性。


JournalofMechanicalStrength2023,45(3):633⁃639DOI:10 16579/j.issn.1001 9669 2023 03 018∗20210830收到初稿,20211017收到修改稿㊂军队军内科研项目资助㊂∗∗薛光明,男,1990年生,山东菏泽人,汉族,中国人民解放军63969部队工程师,博士,主要研究方向为车辆动力系统优化及试验㊂∗∗∗宁㊀鹏,男,1994年生,山东烟台人,汉族,中国人民解放军63969部队工程师,学士,主要研究方向为车辆试验理论㊂基于修正枢轴量方法的威布尔分布区间估计∗INTERVALESTIMATIONOFWEIBULLDISTRIBUTIONBASEDONMODIFIEDPIVOTALVARIABLEMETHOD薛光明∗∗㊀宁㊀鹏∗∗∗㊀傅耀宇㊀㊀何弘瑞㊀㊀周㊀军(中国人民解放军63969部队,南京211113)XUEGuangMing㊀NINGPeng㊀FUYaoYu㊀HEHongRui㊀ZHOUJun(PLATroop63969,Nanjing211113,China)摘要㊀针对威布尔分布传统区间估计方法计算复杂且不同参数下适用性不强的问题,提出一种多参数适用的简单区间估计方法㊂基于威布尔分布表达式得到卡方分布枢轴量,并对其自由度进行修正;然后结合最大似然法的点估计值以及形状参数的经验估计结果,确定威布尔分布双参数的区间估计方法;同时通过蒙特卡罗仿真对区间估计置信度进行验证,分析不同参数下估计方法的适用性,并与传统的最小二乘法和极大似然区间估计结果进行对比㊂结果表明,提出的修正枢轴量方法计算简单,在不同参数下的计算置信度与名义置信度差距较小,且较传统方法更加有效㊂关键词㊀威布尔分布㊀区间估计㊀置信度㊀蒙特卡罗仿真㊀修正枢轴量中图分类号㊀TB114 3Abstract㊀TosolvetheproblemsofcomplexcalculationandweakapplicabilityofthetraditionalintervalestimationmethodssuchasWeibulldistributionwiththedifferentparameters,asimpleintervalestimationmethodsuitabletotheconditionsofmulti⁃parameterswasproposed.ThroughtheexpressionofWeibulldistribution,thepivotal⁃variableobeyingchi⁃squaredistributionwasobtainedandthedegreesoffreedomweremodified.CombinedwiththepointestimationresultsfrommaximumlikelihoodestimationandtheempiricalestimationshapeparameterintheWeibulldistribution,theintervalestimationmethodoftwoparametersinWeibulldistributionwasestablished.TheconfidenceofproposedintervalestimationmethodwasverifiedbyMonteCarlosimulation,andtheapplicabilityofthemethodondifferentparameterswasalsoanalyzed.Furthermore,comparisonswiththeresultscomputedfromtraditionalleastsquareandmaximumlikelihoodestimationmethodswerecarriedoutbyusingsimulation.Simulationresultsindicatedthatthemodifiedpivotal⁃variablemethodhassimplecalculationprocessandsmalldeviationfrompredefinednominalconfidencewiththedifferentparameters.Therefore,itcanbeconcludedthatproposedmethodexecutesthemoreeffectiveestimationthanthetraditionalmethods.Keywords㊀Weibulldistribution;Intervalestimation;Confidence;MonteCarlosimulation;Modifiedpivotal⁃variableCorrespondingauthor:XUEGuangMing,E⁃mail:yy0youxia@163.comTheprojectsupportedbytheInternalScientificResearchProjectsofChineseArmy.Manuscriptreceived20210830,inrevisedform20211017.0㊀引言㊀㊀二参数威布尔分布是机械产品可靠性试验中常用的分布模型之一,在可靠性试验方案设计和统计分析中占据非常重要的位置[1]㊂二参数威布尔模型是一个适用性很强的模型,包含尺度和形状两个参数,当调整形状参数数值时,可描述失效率快增㊁失效率慢增㊁失效率递减和失效率恒定等多种情况㊂因此,威布尔分布在机电产品㊁磨损类零部件㊁无线通信㊁自然状况等多个工程领域的可靠性分析中均有应用实例[2]1⁃8[3]217⁃240[4][5]191⁃194㊂威布尔分布的抽样特性较为复杂,其参数的区间估计比较困难,由于形状参数点估计值的偏差是两个参数的函数,导致其区间估计尤其困难[2]1⁃8[6]㊂针对威布尔分布的区间估计及在各个领域的应用非常重要,常用的方法有枢轴量法㊁极大似然法㊁最小二乘法㊁贝叶斯法等,众多学者开展了研究并取得了较好的成㊀634㊀机㊀㊀械㊀㊀强㊀㊀度2023年㊀效㊂GUIDAM基于极大似然估计结果,直接给出了小样本截尾数据的威布尔区间估计表格,但并未指出计算过程和估计偏差[3]217⁃240㊂LEEJB等提出威布尔分布的近似区间估计结果,他们认为大量截尾或无截尾时,形状参数估计值大致服从特定自由度的卡方分布,并给出了可方便使用的经验公式㊂该结果的工程实用性很强,被国际标准采用,我国的威布尔分析标准也是基于该方法进行区间估计计算[7][8]6⁃10㊂经验公式使用简单,但是对近似环节以及误差情况不够清楚㊂比较容易理解的是基于中心极限定理的Fisher矩阵方法,该方法适用于样本量较大的情况,当样本量较小时效果不如极大似然类方法㊂曾国桓对比了Fisher矩阵方法㊁极大似然比方法的计算效果,同时通过枢轴量法和贝叶斯方法计算了下限,通过了小范围的计算,结果表明,在合理先验的前提下,贝叶斯方法在小样本情况下的点估计和区间估计具有更优的效果[9];贝叶斯方法依赖先验分布信息,分布方面依据依赖性较弱㊂李慧亮等直接采用卡方分位点计算了数控机床平均故障间隔时间的区间估计结果,实际上采用了指数分布的区间估计格式[5]191⁃194㊂贾祥等提出一种改进配分布曲线法,得到一种同时包含点估计和区间估计结果的少/零失效样本的参数估计方法,并验证了方法的合理性[10]㊂最小二乘计算方面,一般情况下,最小二乘计算结果均是偏窄的,对应的置信水平比名义值要低[8]6⁃10,YASUDAK指出当双参数的相关系数不小于0 90时,作图法 一种特殊的最小二乘拟合可取得较好的估计效果[11]㊂上述方法在一定程度上取得了较优的计算效果,但是计算过程复杂,部分还需要给定的先验信息,对于全新产品来说并不完全适用,因而在部分领域的使用并不方便[12];同时对特定参数下的计算示例展示较多,对不同参数下计算效果的评价较少,难以判断计算偏差㊂本文提出一种较为简单的威布尔分布区间估计方法,基于极大似然点估计值和部分卡方分位点即可得到有效的区间估计结果,同时设计蒙特卡罗仿真方案,验证了估计方法在不同的形状参数㊁不同样本量和不同置信水平下的适用性㊂1㊀威布尔分布区间估计1 1㊀极大似然点估计㊀㊀二参数威布尔分布在可靠性寿命分布中十分常用,其概率密度函数和累积分布函数描述为f(t)=βλ(tλ)β-1e-(tλ)βF(t)=1-e-(tλ)βìîíïïïï(1)式中,λ为尺度参数,大致决定均值幅度;β为形状参数,决定曲线走向㊂对于产品寿命或平均故障间隔里程分析,一般有λ>0,β>0,t>0㊂区间估计依赖点估计值,考虑极大似然法处理截尾样本的方便性,同时本文区间估计要用到极大似然求解格式,本文方法需基于极大似然的点估计结果㊂对于可靠性试验数据,若获得了1 r个完全样本 明确得到r个样本的失效时间,1 n-r个非完全样本 得到n-r个样本的非失效时间,基于式(1),可得到完全样本数据和非完全样本数据的似然函数L(β,λ)为L(β,λ)= ri=1βλ(tviλ)β-1e-(tviλ)β n-ri=1e-(tτiλ)β(2)式中,tvi㊁tτi分别为完全样本和非完全样本数据㊂式(2)包含了两部分:前部分为完全样本数据发生故障的似然函数,该部分由概率密度函数给出;后半部分为非完全样本数据未发生故障的似然函数,该部分由可靠度函数给定㊂这也展现了极大似然估计的方便性㊂对式(2)取对数后并对两个变量取偏导可得点估计方程组为∂lnLβ^,λ^()∂λ=-rβ^λ^+β^λ^-β^-1ðni=1tβ^i=0∂lnLβ^,λ^()∂β=rβ^-rlnλ^+ðri=1lntvi-㊀㊀㊀㊀㊀ðni=1tiλ^æèçöø÷β^lntiλ^=0ìîíïïïïïïïïïï(3)㊀㊀消除变量可得到极大似然点估计格式为-rλ^β^+ðni=1tβ^i=0rβ^+ðri=1lntvi-rðni=1tβ^ilntiðni=1tβ^i=0ìîíïïïï(4)式中,λ^㊁β^分别为尺度参数极大似然点估计和形状参数极大似然点估计值㊂先通过式(4)第二式求得β^㊂β^方程为非线性方程,目标是求解rβ^+ðri=1lntvi-rðni=1tβ^ilntiðni=1tβ^i的零点,可采用插值或最优化求解,最优化计算式为minrβ^+ðri=1lntvi-rðni=1tβ^ilntiðni=1tβ^i(5)㊀㊀通过一维搜索即可完成对β^的求解,再代入第一式求解得到λ^㊂1 2㊀基于修正枢轴量的区间估计㊀㊀对式(1)中的累积分函数进行变量代换,令te=㊀第45卷第3期薛光明等:基于修正枢轴量方法的威布尔分布区间估计635㊀㊀tβ,θe=λβ,可得Fe(te)=1-e-teθe(6)㊀㊀由式(6)可知,对于威布尔分布样本t,通过变量代换,形成新的随机变量te=tβ服从参数为θe=λβ的指数分布,那么定数试验前提下的求和ðtβ服从参数为(r,1/λβ)的Gamma分布㊂对应的枢轴量2ðtβ/λβ服从自由度为2r的卡方分布,即2ðtβλβχ2(2r)(7)㊀㊀执行风险为α或置信水平为1-α的区间估计,其形式为Pχ2α/2(2r)ɤ2ðtβλβɤχ21-α/2(2r)æèççöø÷÷=1-α(8)式中,P(∗)表示∗事件发生的概率;χ2α(2r)表示自由度为2r的下α卡方分位点,同时等于自由度为2r的上1-α卡方分位点㊂因此,枢轴量在1-α下的置信区间为χ2α/2(2r)ɤ2ðtβλβɤχ21-α/2(2r),一般地,形状参数作为自变量λ作为β的函数进行处理,当代入β的点估计值β^,即可求得λ的区间估计结果为2ðtβ^χ21-α/2(2r)éëêêùûúú1β^ɤλɤ2ðtβ^χ2α/2(2r)éëêêùûúú1β^(9)㊀㊀考虑极大似然估计第一式可知rλ^β^=ðni=1tβ^i,将该等式代入式(9)中,可得尺度参数λ的区间估计结果为λ^2rχ21-α/2(2r)éëêêùûúú1β^ɤλɤλ^2rχ2α/2(2r)éëêêùûúú1β^,同时根据定时截尾试验的自由度修正,一般将区间估计下限自由度增加2,最终确定1-α置信水平下尺度参数λ的区间估计结果为λ^2rχ21-α/2(2r+2)éëêêùûúú1β^ɤλɤλ^2rχ2α/2(2r)éëêêùûúú1β^(10)㊀㊀结合式(4)给出的极大似然点估计公式,ðtβ^/r()1β^为λ点估计值λ^,代入式(10)即可得到对应的区间估计结果㊂该公式计算简单,同时能够保证区间估计计算结果能够包围点估计值㊂为求解β的区间估计,可直接采用分布及近似经验公式,标准[8]6⁃10中也给出这些公式:β^χ2α/2[C(r-1)]rCæèçöø÷11+q2ɤβɤβ^χ21-α/2[C(r-1)]rCæèçöø÷11+q2(11)式中,q为故障比,q=r/n;C为经验数,C=2 14628-1 361119q㊂上述计算执行的是双侧对称估计,卡方数对应的置信度为1-α/2,若进行单侧下限或单侧上限估计,卡方数采用1-α置信度即可,如风险为α下λ㊁β的单侧区间估计下限分别为λ^2rχ21-α(2r+2)éëêêùûúú1β^㊁β^χ2α[C(r-1)]rCæèçöø÷11+q2㊂因此,单侧估计可从对应的双侧区间估计结果中得到,不需单独验证㊂依据式(10)和式(11),同时结合式(4)和式(5)给出的极大似然点估计方法,即可得到威布尔分布参数的区间估计结果㊂2㊀蒙特卡罗仿真验证2 1㊀计算方法㊀㊀为验证算法有效性,需对不同威布尔参数β㊁不同置信水平1-α㊁不同样本个数n的情况进行分析㊂1)不同形状参数β下的威布尔分布代表了不同失效状态,为验证不同分布下的区间估计效果,设定形状参数β的取值分别为0 8㊁1㊁2㊁3 44,既能覆盖β<1㊁β=1㊁β>1的情况,也是工程可靠性分析中常用的取值(后三种也分别表示指数分布㊁瑞利分布和近似正态分布);尺度参数λ不影响分布类型,也不影响各种方法下的区间估计效果,此处设为定值5,仿真结果表明取其他值时的估计效果与取5时相同㊂2)针对风险α和置信水平1-α,令风险分别为工程中常用的0 1㊁0 2㊁0 4㊁0 6,对应置信水平为90%㊁80%㊁60%和40%的双侧区间估计结果,同时可拆分为置信水平分别为95%㊁90%㊁80%㊁70%的单侧区间估计上限和下限结果㊂3)需要对不同样本量尤其是小样本量情况下的估计效果进行计算,重点进行样本量n不高于40的对比,从n=4间隔4计算至40,共计10种样本情况㊂因此,共计在4ˑ4ˑ10种情况下进行计算㊂依据约定的参数生成随机数,约定的λ㊁β参数值则为理论/实际解,根据生成的随机样本进行区间估计㊂任一种参数情况下生成N=5000次随机数,进行N次计算,得到N个区间估计结果,统计区间估计结果包含约定参数值的次数为Ne,则Ne/N为区间估计结果的置信度㊂与名义上的置信度进行对比,越接近名义置信度则表明估计方法越有效㊂同时与最小二乘拟合和极大似然法估计结果进行对比,考虑到小样本适用性,最小二乘法基于Bernard中位秩作为累积分布函数F进行拟合计算㊂㊀636㊀机㊀㊀械㊀㊀强㊀㊀度2023年㊀2 2㊀计算示例(部分计算结果展示)㊀㊀以形状参数β=0 8㊁样本量n=8㊁置信水平1-α=90%为例给出计算过程,图1展示了三种方法的计算效果对比㊂由于计算次数N过大影响显示效果,仅截取400次计算结果予以展示㊂图1㊀区间估计散点图截取(β=0 8㊁n=8㊁1-α=90%)Fig.1㊀Interceptedintervalestimationscatterdiagram(β=0 8,n=8,1-α=90%)㊀㊀由图1可以看出,在置信度1-α=90%的情况下,极大似然法和本文提出的修正枢轴量方法的计算上限和计算下限大致包含实际值曲线,说明大部分计算区间包含了实际值,因而置信度较高;而最小二乘拟合方法计算的上限和下限大致均匀分布在实际值曲线两边,意味着估计的区间结果较少地包含了理论值,因而置信度较低㊂从图1也能大致看出计算的区间宽度,最小二乘法估计下限和上限结果距离较近,说明估计的区间宽度较小,而极大似然法和修正枢轴量方法得到的区间宽度较大,其效果如图2所示㊂依据结果计算得到三种估计方法的置信度如图3所示㊂由图3可知,与名义置信度90%对比,无论是尺度参数λ还是形状参数β,最小二乘拟合的置信度远低于名义值,说明估计效果较差,而极大似然估计和本文提出的修正枢轴量估计与名义值相差不大,说明计算效果较好㊂结合图2给出的区间宽度,最小二乘拟合方法在计算尺度参数λ时小得多,这与该方法的置信度较低是对应的,而在计算形状参数β时会散落地出现大宽度噪点;对比极大似然法,本文提出的用修正枢轴量方法计算的λ区间较大,而β区间较小,同时置信水平图2㊀区间估计宽度(β=0 8㊁n=8㊁1-α=90%)Fig.2㊀Intervalestimationwidth(β=0 8,n=8,1-α=90%)更接近名义值,说明计算β方面,本文采用的方法更加有效(在β=0 8㊁n=8㊁1-α=90%情况下)㊂㊀第45卷第3期薛光明等:基于修正枢轴量方法的威布尔分布区间估计637㊀㊀图3㊀三种估计方法的置信水平(β=0 8㊁n=8㊁1-α=90%)Fig.3㊀Calculatedconfidenceslevelofthreeestimationmethods(β=0 8,n=8,1-α=90%)对于区间估计,计算置信度更接近名义置信度,同时区间估计宽度越小,说明估计方法以较小的偏差获得了较高的精度,估计效果越好㊂但总体来看,对于最小二乘拟合㊁极大似然和本文提出的修正枢轴量方法,若要获得更高的置信度,对应的计算区间宽度需更大㊂图4㊀不同名义置信水平下三种估计方法计算结果(β=0 8㊁n=8)Fig.4㊀Calculatedresultsofthreeestimationmethodswithdifferentnominalconfidenceslevel(β=0 8,n=8)图4给出了不同名义置信度下三种估计方法的实际置信度㊂由计算结果可知,最小二乘拟合估计得到的实际置信度偏低,不建议选用;本文提出的修正枢轴量方法较极大似然法大致上更趋近于名义置信度,计算效果最好㊂3 误差分析㊀㊀第2节对β=0 8㊁n=8的某种情况进行了分析,下面对约定的所有情况(威布尔形状参数βɪ[0 8,3 44],名义置信度度1-αɪ[40%,90%],抽取样本量nɪ[4,40])下的区间估计计算的置信度进行对比分析,评估三种方法在不同情况下的估计效果,以抽取样本量n为横轴,其结果如图5所示㊂由图5可知,极大似然估计法和本文提出的修正枢轴量方法估算置信度比较接近名义值1-α,尤其是置信度1-α不低于60%㊁样本量n不小于12时,两种方法置信度曲线与名义值曲线几乎重合,说明取得了㊀㊀较好的效果㊂从曲线形式上看,这两种估计方法计算的置信度曲线受威布尔分布形状参数的影响不大,但估计效果随样本的增大而有所提升,随置信水平1-α的增大也有所提升㊂最小二乘拟合的估计效果偏差较大,同时随样本量的增大估计效果也未变好,整体计算置信水平偏低,大致意味着估计区间偏窄㊂因而在执行威布尔分布的最小二乘区间估计时,应注意得到的估计结果偏窄,可采用合理的方法予以修正㊂图6给出了极大似然法和修正枢轴量方法的计算误差,分图由左至右表达置信风险α变化,由上至下表达形状参数β变化㊂同时,列举不同β下相对误差最大值如表1所示㊂由相对误差计算结果可知,对于置信度1-α不低于60%的常见情况,当样本量n不小于12时,极大似然法对尺度参数λ和形状参数β的估计误差小于7 9%,本文提出的修正枢轴量法的估计误差不高于3 7%,展现了较好的计算效果㊂当样本量不高于8时,极大似然法和指数估计方法偏差较大,但本文提出的修正枢轴量法明显误差较小:极大似然法相对误差高达20%以上,修正枢轴量法相对误差控制在15%以内㊂置信度1-α=40%情况下,极大似然法在样本量n不小于12时的估计偏差小于10%,同时能够随样本量的增大而迅速减小,取得了较好的效果;本文提出的修正枢轴量法在计算形状参数β时效果尚可,但计算尺度参数λ时相对误差约为10%,且相对误差并不随样本量增大而明显下降,意味着计算精度并未有效提升㊂因而低置信度情况下的威布尔分布尺度参数λ的推荐采用极大似然法估计㊂如分图标记自左向右,随名义置信风险α的增加,修正枢轴量法估计渐优;如分图标记自上向下,区间估计精度受威布尔分布参数β的影响很小,说明本文提出的修正枢轴量法适用于不同参数下的威布尔分布㊂㊀638㊀机㊀㊀械㊀㊀强㊀㊀度2023年㊀图5㊀不同情况下的估计效果对比Fig.5㊀Comparisonofestimationeffectsunderdifferentconditions图6㊀极大似然法和修正枢轴量法的计算误差Fig.6㊀Relativeerrorsofmaximumlikelihoodestimationandmodifiedpivotmethods㊀第45卷第3期薛光明等:基于修正枢轴量方法的威布尔分布区间估计639㊀㊀表1㊀极大似然法和修正枢轴量法的计算误差对比Tab.1㊀ComparisonofcalculationerrorsofmaximumlikelihoodestimationandmodifiedpivotmethodsNote: ML and MP respectivelyrepresentmaximumlikelihoodestimationmethodandmodifiedpivotalvariablemethod.4㊀结论㊀㊀本文提出一种基于修正枢轴量的威布尔分布区间估计方法,该方法基于极大似然点估计值,结合卡方数即可得到区间估计结果,计算十分简便,同时通过蒙特卡罗仿真与最小二乘拟合和极大似然法进行对比,验证了区间估计方法的有效性㊂1)对于不同参数下的分布㊁不同样本量和不同置信度等多种情况,本文提出的修正枢轴量方法的计算效果均可接受,估计置信度趋近于名义置信度㊂2)对于一般置信度情形,样本量不小于12时,本文提出修正枢轴量方法的估计相对误差不高于6%,当样本量不高于8时,相对误差可控制在15%以内㊂3)除偏低置信度情况下对尺度参数估计效果一般,本文提出的参数区间估计方法优于传统最小二乘拟合和极大似然估计方法㊂参考文献(References)[1]㊀WEIBULLW.Astatisticaldistributionfunctionofwideapplicability[J].JournalofAppliedMechanics,1951,18(3):293⁃297.[2]㊀MAKINOT.MeanhazardrateanditsapplicationtothenormalapproximationoftheWeibulldistribution[J].NavalResearchLogisticsQuarterly,2010,31(1):1⁃8.[3]㊀GUIDAM.OntheconfidencelimitsforWeibullreliabilityandquantiles:thecaseofmaximumlikelihoodestimationfromsmallsizecensoredsamples[J].ReliabilityEngineering,1985,12(4):217⁃240.[4]㊀付㊀涛,王德成,程㊀鹏.基于威布尔分布的圆柱螺旋压缩弹簧疲劳寿命分析[J].机械强度,2020,42(1):81⁃86.FUTao,WANGDeCheng,CHENGPeng.FatiguelifeanalysisofcylindricalhelicalcompressionspringbasedonWeibulldistribution[J].JournalofMechanicalStrength,2020,42(1):81⁃86(InChinese).[5]㊀李慧亮,贾现召,张㊀涛.基于威布尔分布的数控机床可靠性分析[J].机床与液压,2014,42(19):191⁃194.LIHuiLiang,JIAXianZhao,ZHANGTao.ReliabilityanalysisofNCmachinetoolsbasedonWeibulldistribution[J].MachineTool&Hydraulics,2014,42(19):191⁃194(InChinese).[6]㊀于晓红,张来斌,王朝晖,等.基于新的威布尔分布参数估计法的设备寿命可靠性分析[J].机械强度,2007,134(6):932⁃936.YUXiaoHong,ZHANGLaiBin,WANGChaoHui,etal.ReliabilitylifeanalysisoftheequipmentbasedonnewWeibulldistributionparameterestimationmethod[J].JournalofMechanicalStrength,2007,134(6):932⁃936(InChinese).[7]㊀LEEJB,MAXE.Statisticalanalysisofreliabilityandlife⁃testingmodels:theoryandmethods[M].2nded.BocaRaton:Routledge,1991:302⁃340.[8]㊀全国电工电子产品可靠性与维修性标准化技术委员会.威布尔分析:GB/T34987 2017[S].北京:中国标准出版社,2017:6⁃10.NationalTechnicalCommitteeforStandardizationofReliabilityandMaintainabilityofElectricalandElectronicProduct.Weibullanalysis:GB/T34987 2017[S].Beijing:StandardsPressofChina,2017:6⁃10(InChinese).[9]㊀曾国桓.两参数威布尔分布下定时截尾试验的参数评估方法研究[D].成都:电子科技大学,2018:18⁃31.ZENGGuoHuan.Methodsofparameterestimationoftwo⁃parameterWeibulldistributionfortype⁃icensoringtest[D].Chengdu:UniversityofElectronicScienceandTechnologyofChina,2018:18⁃31(InChinese).[10]㊀贾㊀祥,王小林,郭㊀波.极少失效数据和无失效数据的可靠性评估[J].机械工程学报,2016,52(2):182⁃188.JIAXiang,WANGXiaoLin,GUOBo.Reliabilityassessmentforveryfewfailuredataandzero⁃failuredata[J].JournalofMechanicalEngineering,2016,52(2):182⁃188(InChinese).[11]㊀YASUDAK.InfluenceoflinearityinWeibullplotonaccuracyofparameterestimation[J].MaterialsToday:Proceedings,2019(16):124⁃129.[12]㊀ELSAYEDAE.Reliabilityengineering[M].3rded.USAHoboken:Wiley,2021:5⁃16.。
第一章互连设计的重要性光速已经太慢了,当前大规模生产的普通数字电路要求时序控制达到皮秒的范围。
光从人的鼻子传输到耳朵所需要的时间大概为100ps(在100ps的时间里,光将传输1.2英寸)。
这样级别的时序控制不但要维持在硅芯片里,而且还必须在级别更大的系统板上实现,比如一个计算机的主板。
在这些系统中,将器件互连的导体不应再被看作一根简单的导线,而是呈现了高频效应的传输线。
如果这些传输线没有被合理的设计,他们将在不经意间毁灭系统时序。
有些数字设计(并非全部)的复杂程度已经达到甚至超过了模拟电路设计。
数字技术经历了令人瞩目的空前发展。
确实,在技术公司的市场部存在着这样的信条:如果让市场来告诉你公众需要什么,那已经太迟了!本书将要解决由于数字电路的迅速发展而而带来的技术瓶颈。
这要求现代数字电路设计者们掌握以前不需要的知识,而很多人却没有。
相关知识的缺乏导致了大量的错误信息在工程师中流行起来,高速设计的概念经常成为了谬论,由于知识的缺乏,这些谬论一直没有得到解决。
事实上,许多相同的概念已经在电子工程的其他学科被用了几十年。
例如射频设计和微波设计。
问题是阐述相关主题的参考书都太抽象而不能立即的被电子工程师接受,又或者工程师们太注重实际而没有足够多的理论知识来完全理解相应的主题。
本书将直接针对数字设计领域,以一种让工程师或学生能够理解的方式来讲解一些必要的概念,以使他们能理解并解决目前及将来的问题。
值得注意的是,本书所讲的内容已经被成功的运用到了现代设计当中。
1.1 基础知识读者应该知道,数字设计的基本思想是进行信号通讯,这些信号以0s或1s来表达并传递信息。
典型的数字电路是发送或接受一系列的梯形电压波(如图1.1所示)来进行通讯,这里,高电平代表1,低电平代表0,数字电路之间用来传输信号的路径被称作互连。
互连是从发送信号的芯片到接收信号芯片间的完整的电子路径,它包括芯片封装、连接器,插座及许多其他的结构。
希尔伯特-黄变换(Hilbert-HuangTransform,HHT)0前言传统的数据分析方法都是基于线性和平稳信号的假设,然而对实际系统,无论是自然的还是人为建立的,数据最有可能是非线性、非平稳的。
希尔伯特-黄变换(Hilbert-HuangTransform,HHT)是一种经验数据分析方法,其扩展是自适应性的,所以它可以描述非线性、非平稳过程数据的物理意义。
1HHT简介[贺礼平.希尔伯特-黄变换在电力谐波分析中的应用研究口.湖南:中南大学,2009]HHT的发展。
1995年,NordenE.Huang为研究水表面波构思出一种所谓“EMD--HSA”的时间序列分析法,通过这种方法他发现水波的演化不是连续的,而是突变、离散、局部的。
1998年,NordenE.Huang等人提出了经验模态分解方法,并引入了Hilbert谱的概念和Hilbert谱分析的方法,美国国家航空和宇航局(NASA)将这一方法命名为Hilbert-HuangTransform,简称HHT,即希尔伯特-黄变换。
HHT是一种新的分析非线性非平稳信号的时频分析方法,由两部分组成:第一部分为经验模态分解(EmpiricalModeDecomposition,EMD)(thesiftingprocess,筛选过程),它是由Huang提出的,基于一个假设:任何复杂信号都可以分解为有限数目且具有一定物理定义的固有模态函数(IntrinsicModeFunction,IMF;也称作本征模态函数);EMD方法能根据信号的特点,自适应地将信号分解成从高到低不同频率的一系列IMF;该方法直接从信号本身获取基函数,因此具有自适应性,同时也存在计算量大和模态混叠的缺点。
第二部分为Hilbert谱分析(HilbertSpectrumAnalysis,HSA),利用Hilbert变换求解每一阶IMF 的瞬时频率,从而得到信号的时频表示,即Hilbert谱。
第45卷 第12期2023年12月系统工程与电子技术SystemsEngineeringandElectronicsVol.45 No.12December2023文章编号:1001 506X(2023)12 3726 08 网址:www.sys ele.com收稿日期:20220809;修回日期:20221119;网络优先出版日期:20221229。
网络优先出版地址:https:∥kns.cnki.net/kcms/detail/11.2422.TN.20221229.2014.016.html 通讯作者.引用格式:刘丹阳,吴 ,朱永锋,等.地面目标HRRP识别的稳健性特征选择方法[J].系统工程与电子技术,2023,45(12):3726 3733.犚犲犳犲狉犲狀犮犲犳狅狉犿犪狋:LIUDY,WUK,ZHUYF,etal.RobustfeatureselectionmethodforgroundtargetHRRPrecognition[J].SystemsEngineeringandElectronics,2023,45(12):3726 3733.地面目标犎犚犚犘识别的稳健性特征选择方法刘丹阳1, ,吴 2,朱永锋1,张永杰2,周剑雄1(1.国防科技大学电子科学学院,湖南长沙410073;2.北京遥感设备研究所,北京100854) 摘 要:特征选择是雷达高分辨一维距离像目标识别的关键步骤,可降低特征维度,提高特征稳健性。
提出一种基于散度的特征选择方法,采用该方法对适用于距离像地面目标识别的特征集合进行特征选择,得到优选的特征子集后再进入分类器网络进行识别。
采用地面目标仿真数据和实测数据进行神经网络分类器识别实验。
实验结果表明:在距离像信噪比、俯仰角和距离分辨力参数变化的情况下,基于散度的特征选择方法在基本保持或提升特征集的识别性能的前提下,能保持甚至提升识别的稳健性,具有较好的应用价值。