第11讲算符特点证明题

证明角动量算符是厄米算符要证明角动量算符是厄米算符，我们需要证明它的本征值是实数，以及它满足厄米算符的性质。

首先，我们考虑角动量算符的本征值问题。

设一个态函数$|\psi\rangle$是角动量算符$\hat{L}$的本征态，对应的本征值为$\lambda$，即$\hat{L}|\psi\rangle=\lambda|\psi\rangle$。

我们希望证明$\lambda$是实数。

首先我们将$|\psi\rangle$在坐标表象下展开：$|\psi\rangle = \int d^3x\psi(\mathbf{x})|\mathbf{x}\rangle$，其中$\psi(\mathbf{x})$是态函数的波函数表示，$|\mathbf{x}\rangle$是坐标算符的本征态。

那么角动量算符在坐标表象下的表示为$\langle\mathbf{x}|\hat{L}|\mathbf{x}'\rangle$。

我们来考虑$\hat{L}|\psi\rangle$在坐标表象下的表示：$$\hat{L}|\psi\rangle = \intd^3x'\langle\mathbf{x}|\hat{L}|\mathbf{x}'\rangle\intd^3x\psi(\mathbf{x})|\mathbf{x}'\rangle\\=\intd^3x'\langle\mathbf{x}|\hat{L}|\mathbf{x}'\rangle\psi(\mathbf{x}') $$然后我们来考察$|\psi\rangle$与$\hat{L}|\psi\rangle$的内积：$$\langle\psi|\hat{L}|\psi\rangle = \int d^3x\intd^3x'\psi^*(\mathbf{x})\langle\mathbf{x}|\hat{L}|\mathbf{x}'\rangle\psi(\mathbf{x}')\\=\int d^3x\intd^3x'\psi^*(\mathbf{x})\langle\mathbf{x}|\hat{L}|\mathbf{x}'\ran gle\psi(\mathbf{x}')\\=\int d^3x\intd^3x'\psi^*(\mathbf{x'})\langle\mathbf{x}'|\hat{L}|\mathbf{x}\ra ngle\psi(\mathbf{x})$$上述的两行等式中，我们可以交换积分顺序，因为积分是与算符无关的。

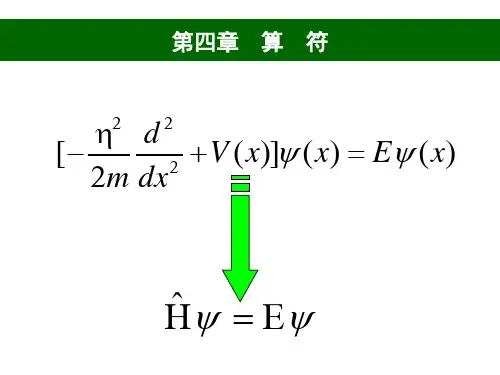
(壹x上) 量子力学基础第五节算符一、算符的定义和运算二、算符的本征方程、本征值、本征函数三、线性算符四、厄米算符小结作业思考题一、算符的定义和运算返回上页下页返回上页下页设符号代表某个运算规则，按此规则，由一个函数f 可唯一地确定另一个函数g ，记作符号称为算符.[算符的定义]Af g ˆ=AˆAˆ返回上页下页通常，算符记号上带有抑扬符“∧”.但是，对于单纯做乘法的算符，“∧”可省略.注可直接写做x ； ˆ()xx ⋅(5⋅)可直接写作5 .5ˆ例如，返回上页下页算符的等价性设和是两个算符，若对任意函数f 都有，则称和相等，记作.AˆB ˆf B f A ˆˆ=B A ˆˆ=[算符的运算]AˆB ˆ返回上页下页算符的加法(减法)AB f Af Bf ˆˆˆˆ()±=±Df x Df x f x ˆˆˆˆ(3)()()3()+=+例如，f x f x ()3()′=+规定：称为与的和(差).A ˆB ˆA Bˆˆ±运算规律：AB B A [交 换律 ]ˆˆˆˆ+=+AB C A B C 结合律] ˆˆˆˆˆˆ()()[++=++返回上页下页一般而言，(算符的乘法不满足交换律).ABBA ˆˆˆˆ≠对易子如果，即，则称和可对易；否则，就是不可对易的.A B ˆˆ[,]0=A BˆˆAB AB BA ˆˆˆˆˆˆ[,]=−规定：称为与的对易子.AB ˆˆ[,]A ˆB ˆAB BA ˆˆˆˆ=但不排除对某些特定的算符有.ABBA ˆˆˆˆ=返回上页下页对易子的恒等式(证明留作练习)：]ˆ,ˆ[]ˆ,ˆ[A B B A−=n A A ˆˆ[,]0=二、算符的本征方程、本征值、本征函数返回上页下页返回上页下页则⎯⎯常数a 称为的本征值;非零函数f 称为的属于(对应于)本征值a 的本征函数;ˆAaf f A =ˆ设：是算符，f 是非零函数，a 是常数.如果AˆˆA称为的本征方程.ˆA af f A=ˆ返回上页下页(3)本征函数总是和本征值联系在一起，一个本征函数不能同时属于两个不同的本征值；(4)对应于同一个本征值，可能有不止一个线性无关的本征函数.说明(1) 本征函数f 要求是非零函数(不恒等于零)；(2)一般而言，本征值(复数域)，相应的，本征函数f 是复函数.a ∈ 假设，则有.本征函数f 是非零函数，于是a =b ，矛盾., 其中ˆˆ()Afaf Af bf a b ==≠()0a b f −=三、线性算符返回上页下页返回上页下页线性算符有如下的对易子恒等式：]ˆ,ˆ[]ˆ,ˆ[]ˆ,ˆ[B A k B k A B Ak ==]ˆ,ˆ[]ˆ,ˆ[]ˆˆ,ˆ[C A B A C B A+=+]ˆ,ˆ[]ˆ,ˆ[]ˆ,ˆˆ[C B C A C B A+=+C B A C A B C B Aˆ]ˆ,ˆ[]ˆ,ˆ[ˆ]ˆˆ,ˆ[+=B C A C B A C B Aˆ]ˆ,ˆ[]ˆ,ˆ[ˆ]ˆ,ˆˆ[+=[线性算符的对易子]例6. 由，计算对易子和D xˆˆ[,]1=x i D ˆ[,]− x D 2ˆ[,]]ˆ,[2D x x i Dˆ[,]− i x D ˆ[,]=− i D x ˆ[,]= D ˆ2−=D D ˆˆ−−=D D x D x Dˆ]ˆ,[]ˆ,[ˆ+=i = 解返回上页下页112211221122ˆˆˆ()D c f c f c f c f c Df c Df ′′+=+=+都是线性算符，2ˆˆˆ,,xD D 222112211221122ˆˆˆ()D c f c f c f c f c D f c D f ′′′′+=+=+11221122()x c f c f c xf c xf ⋅+=⋅+⋅因此，返回上页下页[线性算符的性质]若f 1,f 2是线性算符的属于同一个本征值a 的本征函数，则它们的任意非零线性组合c 1f 1+c 2f 2(即c 1,c 2是任意常数但要保证c 1f 1+c 2f 2是非零函数)仍然是属于a 的本征函数.证2211ˆ ,ˆ af f A af f A==∵ 1122ˆ()A c f c f ∴+2211ˆˆf A c f A c +=注此性质对更多本征函数也成立.Aˆ2211af c af c +=)(2211f c f c a +=当c 1f 1+c 2f 2为非零函数时，是对应于a 的本征函数.四、厄米算符返回上页下页返回上页下页如果算符满足：则称算符是厄米算符.d d **ˆˆ()f Ag g Af ττ=∫∫AˆAˆ[厄米算符的定义](f ,g 是任意的品优函数)说明(1)一般来说，算符的本征值是复数域上的数.但是，厄米算符的本征值一定是实数.(2)一般来说，算符的本征函数不一定正交.但是，对于线性厄米算符，①非简并本征值：有且有一个线性无关的本征函数，任选一个；②简并本征值：能够选出一个两两正交的最大线性无关组[线性厄米算符的性质2(2)].所选的的这一系列本征函数必定是两两正交的[线性厄米算符的性质2(1)].返回上页下页四、小结作业思考题返回上页下页小结返回上页下页1算符的概念；算符的加法、乘法、幂及其运算规则.m n m n m n mn A A A A A； ˆˆˆˆˆ()+==[加法交换律] ˆˆˆˆAB B A +=+加法结律 合 ]ˆˆˆˆˆˆ()()[AB C A B C ++=++ [乘法结合律]ˆˆˆˆˆˆ()()ABC AB C =返回上页下页2对易子ˆˆˆˆˆˆ[,]AB AB BA =−如果(即)，则称和可对易.ˆA ˆB 重要的恒等式:ˆˆ[,]0AB =ˆˆˆˆAB BA =]ˆ,ˆ[]ˆ,ˆ[A B B A−=n A A ˆˆ[,]0=ˆˆ[,]AB返回上页下页3算符的本征方程、本征值、本征函数.af f A =ˆa 为常数，称为本征值；f 是非零函数，称为属于本征值a 的本征函数.的本征方程：ˆA4线性算符的概念和性质.()A c f c f c Af c Af 11221122ˆˆˆ+=+( f 1和f 2是任意函数；c 1和c 2是任意常数)返回上页下页线性算符的运算规律：线性算符的对易子恒等式：]ˆ,ˆ[]ˆ,ˆ[]ˆ,ˆ[B A k B k A B Ak ==ˆˆˆˆˆˆˆ[,][,][,]AB C A C B C +=+[左分配律] ˆˆˆˆˆˆˆ()AB C AB AC +=+[分 律] 右配ˆˆˆˆˆˆˆ()BC A BA CA +=+ˆˆˆˆˆˆˆ[,][,][,]AB C A B A C +=+C B A C A B C B Aˆ]ˆ,ˆ[]ˆ,ˆ[ˆ]ˆˆ,ˆ[+=B C A C B A C B Aˆ]ˆ,ˆ[]ˆ,ˆ[ˆ]ˆ,ˆˆ[+=返回上页下页(本征值的简并度：属于该本征值的全体本征函数中，最大线性无关组所含的函数个数)线性算符的性质：线性算符的属于同一个本征值的本征函数的任意非零线性组合，仍是属于同一个本征值的本征函数.返回上页下页5厄米算符的概念和性质. d d **ˆˆ()f Ag g Af ττ=∫∫(f ,g 是任意的品优函数)线性厄米算符的性质：1. 厄米算符的本征值必然是实数；2.(1)厄米算符属于不同本征值的本征函数必然是相互正交的;(2)线性算符的属于简并本征值的全体本征函数中，能够选出一个两两正交的最大线性无关组.作业p.145，第26，27，28题返回上页下页返回上页下页思考题下列哪些算符可对易⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅( )(A) ˆˆ,x y (B),x y ∂∂∂∂(C),x x ∂∂ (D),y x∂∂返回上页下页[提示]可对易⇔.将作用于二元函数f (x ,y )可得.[答案] (A)(B)(D)即 ˆˆˆˆˆˆ[,]00A B AB BA =−=ˆˆ,AB ˆˆˆˆABBA −ˆˆ[,]A B附录线性厄米算符性质的证明返回上页下页返回上页下页线性厄米算符的性质2(1)厄米算符的属于不同本征值的本征函数必然是相互正交的;(2)线性算符的属于同一个简并本征值的全体本征函数中，可选出两两正交的最大线性无关组.(1) 设是厄米算符，f , g 是分别属于两个不同特征值a , b 的本征函数，即ˆAd d **ˆˆ()f Ag g Af ττ=∫∫证； ()ˆˆAf af Agbg a b ==≠根据厄米算符的定义，有d d **()f bg g af ττ=∫∫d d ***b f g a gf ττ=∫∫返回上页下页上式中a *≠b (∵厄米算符的本征值是实数，a*=a ，而a ≠b )，从而有是相互正交的d 即*0,,g f g f τ=∫一般而言，{f 1,f 2,…,f n }不是两两正交的.但是，从最大线性无关组{f 1,f 2,…,f n }出发，利用施密特正交化方法，能够构造出一个等价的非零正交函数组{ϕ1,ϕ2,…,ϕn }.方法如下(参见数学复习)：(2)设是线性算符，f 1,f 2,…,f n 是属于简并本征值a 一个最大线性无关组.ˆA。

小学三年级上册数学奥数知识点讲解第11课《巧填算符1》试题附答案第十一讲巧填算符（一）所谓填算符，就是指在一些数之间的适当地方填上适当的运算符号（包括括号），从而使这些数和运算符号构成的算式成为一个等式。

在填算符的问题中，所填的算符包括+、-、X、+、0、口、{}O解决这类问题常用两种基本方法：一是凑数法，二是逆推法，有时两种方法并用。

凑数法是根据所给的数，凑出一个与结果比较接近的数，然后，再对算式中剩下的数字作适当的增加或减少，从而使等式成立。

逆推法常是从算式的最后一个数字开始，逐步向前推想，从而得到等式。

例1在下面算式适当的地方添上加号，使算式成立。

88888888=1000例2在下列算式中合适的地方添上+、二X使等式成立。

①987654321=1993②123456789=1993例3在下面算式合适的地方添上+、-、X号，使等式成立。

3333333333333333=1992例4在下面算式合适的地方添上+、=X,使等式成立。

12345678=195在下面算式中合适的地方，只添两个加号和两个减号使等式成立。

123456789=100例6在下列算式中合适的地方，添上0口，使等式成立。

①1+2X3+4X5+6X7+8X9=303②1+2X3+4X5+6X7+8X9=1395③1+2X3+4X5+6X7+8X9=4455答案笫十一讲巧填算符（一）所谓填算符，就是指在一些数之间的适当地方填上适当的运算符号（包括括号），从而使这些数和运算符号构成的算式成为一个等式。

在填算符的问题中，所填的算符包括+、-、X、+、O、口、。

解决这类问题常用两种基本方法：一是凑数法，二是逆推法，有时两种方法并用。

凑数法是根据所给的数，凑出一个与结果比较接近的数，然后，再对算式中剩下的数字作适当的增加或减少，从而使等式成立。

逆推法常是从算式的最后一个数字开始，逐步向前推想，从而得到等式。

例1在下面算式适当的地方添上加号，使算式成立。

（2）例子证明坐标算符和动量算符是线性厄密算符。

而对数算符不是线性算符。

证明：以一维情况为例。

坐标算符为x，动量算符为pˆ=-iћ∂/∂x。

i．因为rˆ=x，则有rˆ(c1ψ1+c2ψ2)=x(c1ψ1+c2ψ2)=c1xψ1+c2xψ2=c1rˆψ1+c2rˆψ2，所以坐标算符x是线性算符。

又因为x是实数，⎰ψ*xΦdx=⎰xψ*Φdx=⎰(xψ)*Φdx，因此坐标算符是厄密算符。

同理y、z分量的算符也是线性厄密算符。

ii．对于动量算符，有pˆ(c1ψ1+c2ψ2)=-iћ∂/∂x(c1ψ1+c2ψ2)=c1(-iћ∂ψ1/∂x)+c (-iћ∂ψ2/∂x)=c1pˆψ1+c2pˆψ2，2所以动量算符pˆ是线性算符。

又因为⎰ψ*pˆΦdx=-iћ⎰ψ*∂Φ/∂xdx=-iћ⎰ψ*dΦ=-iћψ*Φ|∞+iћ⎰Φdψ*=iћ⎰∂ψ*/∂xΦdx（该等号成立的条件是：ψ*(-∞)=ψ*(∞)和Φ(-∞)=Φ(∞)，讨论：当ψ、Φ表示束缚态时显然成立；都是自由态的平面波时，也有结论ψ(-∞)=ψ(+∞)和Φ(-∞)=Φ(+∞)；当表示不同本征值的本征态时，由于此时这两个函数必正交，故有：ψ*Φ|∞=⎰∞d(ψ*Φ)= ∂/∂x⎰∞ψ*Φdx=∂/∂x0=0，正交特点：⎰∞ψn*Φm dτ=δnm）=⎰(iћ∂/∂x)ψ*Φdx=⎰pˆ*ψ*Φdx=⎰(pˆψ)*Φdx因此动量算符是厄密算符。

同理p y、p z分量的算符也是线性厄密算符。

iii．设Â=log，则有Â(c1ψ1+c2ψ2)=log(c1ψ1+c2ψ2)≠c1logψ1+c2logψ2=c1Âψ1+c2Âψ2可见对数算符不是线性算符，不能作为表示量子力学中的力学量。

厄米算符的和仍为厄米算符证明我们得知道什么是厄米算符。

你可以把它想成一个神秘的宝箱，打开的时候里面的东西绝对不会乱。

比如说，如果你有一个厄米算符A，和另一个厄米算符B，它们各自的特性都很鲜明。

A的共轭就是A自己，B的共轭也是B自己，明白吗？这就像每个宝箱都有自己的钥匙，开了之后，里面的东西不会变。

好啦，现在咱们来加起来。

A+B是不是也应该有自己的宝箱？当然是的！这就像朋友聚会，大家一起嗨，不会有人突然变得奇怪。

嘿，数学也是如此。

我们要验证A+B的共轭。

咱们先来看A+B的共轭是什么。

根据公式，A+B的共轭其实是A的共轭加B的共轭。

没错，听上去简单吧？所以你把A和B的共轭加起来，结果依然是两个厄米算符，没啥好担心的。

它们的“身份”没有变化，依然是忠诚的守卫。

想想看，如果你有两只小狗，它们都是乖巧的狗狗，那么你把它们放在一起，它们肯定还是乖乖的，不会突然变成猫咪！再说了，算符的和是线性的。

这句话听起来好像有点抽象，但其实它就是告诉你，加法不会改变原有的特性。

你可以随意组合，只要是厄米算符，加起来的结果一定是厄米算符。

比如说，牛肉面和炸酱面，虽然风格不同，但只要都是面，放在一起还是能吃的！所以我们可以大胆地说，厄米算符们聚在一起，一定会组成一个新的大家庭。

再来看看一些实际例子，方便理解。

想象你在调音台上调节音量，A和B分别是两个音轨。

它们的声音都清脆动人，但你想把它们合成一首新曲子。

只要音轨没有变调，最后的音量和效果一定是和谐的，不会变得刺耳。

这就像物理学里的量子力学，多个厄米算符组合在一起，形成一个全新的状态，绝对不会破坏它们原本的特性。

所以说，厄米算符的和依然是厄米算符，这个道理不难理解。

可以说，这是数学中的“乐观主义”，无论怎么组合，结果总是充满希望的。

它告诉我们，合并的力量是巨大的，不管遇到什么问题，只要我们保持真诚和信任，就能得到理想的结果。

在生活中，我们也可以借鉴这个道理。

朋友之间，团队合作，只要每个人都贡献自己的力量，大家齐心协力，最后一定能达成目标。