黄金分割斐波那契数列--波浪理论的数学基础
- 格式:ppt
- 大小:3.61 MB
- 文档页数:42






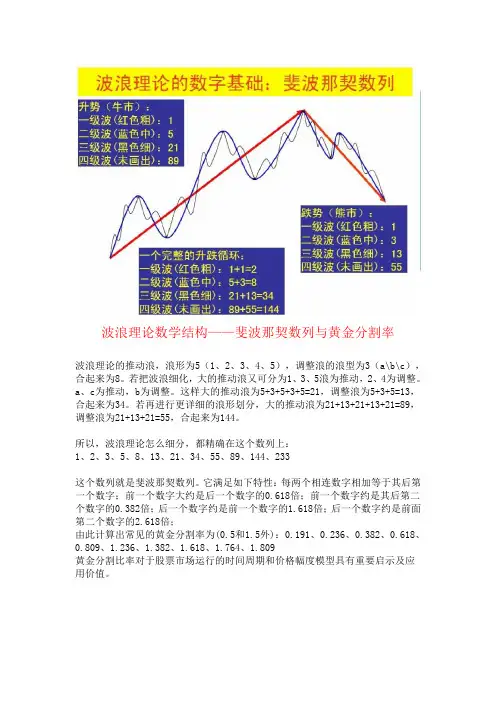
波浪理论数学结构——斐波那契数列与黄金分割率波浪理论的推动浪,浪形为5(1、2、3、4、5),调整浪的浪型为3(a\b\c),合起来为8。
若把波浪细化,大的推动浪又可分为1、3、5浪为推动,2、4为调整。
a、c为推动,b为调整。
这样大的推动浪为5+3+5+3+5=21,调整浪为5+3+5=13,合起来为34。
若再进行更详细的浪形划分,大的推动浪为21+13+21+13+21=89,调整浪为21+13+21=55,合起来为144。
所以,波浪理论怎么细分,都精确在这个数列上:1、2、3、5、8、13、21、34、55、89、144、233这个数列就是斐波那契数列。
它满足如下特性:每两个相连数字相加等于其后第一个数字;前一个数字大约是后一个数字的0.618倍;前一个数字约是其后第二个数字的0.382倍;后一个数字约是前一个数字的1.618倍;后一个数字约是前面第二个数字的2.618倍;由此计算出常见的黄金分割率为(0.5和1.5外):0.191、0.236、0.382、0.618、0.809、1.236、1.382、1.618、1.764、1.809黄金分割比率对于股票市场运行的时间周期和价格幅度模型具有重要启示及应用价值。
黄金分割比率在时间周期模型上的应用未来市场转折点=已知时间周期×分割比率已知时间周期有两种:(1)循环周期:最近两个顶之间的运行时间或两个底之间的运行时间(2)趋势周期:最近一段升势的运行时间或一段跌势的运行时间一般来讲,用循环周期可以计算出下一个反向趋势的终点,即用底部循环计算下一个升势的顶,或用顶部循环计算下一个跌势的底。
而用趋势周期可以计算下一个同方向趋势的终点或是下一个反方向趋势的终点。
用循环周期预测,可以用顶测底,用底测顶:已知点1、点3属于顶到顶的顶循环,运行6个时间周期,则点3到点4段跌势的底在6×0.5=3个时间周期出现;根据点2、点4的底循环6个时间周期,则点4到点5段升势的顶在6×0.809≈5个时间周期出现根据已知趋势周期预测未来同向或反向趋势终点:已知趋势A始于点1止于点2运行8个时间周期,则趋势B将运行8×0.618≈5个时间周期;B×1.618≈C运行的8个时间周期时间周期与波浪数浪的数学关系一个完整的趋势(推动浪5波或调整浪3波),运行时间最短为第一波(1浪或A浪)的1.618倍,最长为第一波的5.236倍。

艾略特波浪基础--黄金比率和费波纳奇数列本文来自:理想论坛作者:翘翘桥浏览:2545次一、斐波南希数列为波浪理论的结构基础艾略特,波浪理论的开山祖师,在1934年公开发表波浪理论,指出股市走势依据一定的模式发展,涨落之间,各种波浪有节奏地重复出现,艾略特创立的波浪理论,属于一整套精细的分析工具,包括下列三个课题:1、波浪运行的形态;2、浪与浪之间的比率;3、时间星期。
艾略特在1946年发表的第二本著作,索性就命名为《大自然的规律》(Nature's Law)。
波浪理论第二个重要课题,系浪与浪之间的比率,而该比率实际上跟随神奇数字系列发展。
艾略特在《大自然的规律》一书中谈到,其波浪理论的数字基础是一系列的数列,是斐波南希在13世纪时所发现的,因此,此数列一般却称之谓斐波南希数列。
神奇数字系列本身属于一个极为简单的数字系列,但其间展现的各种特点,令人对大自然奥秘,感叹玄妙之余,更多一份敬佩。
其实早在中国《道德经》第四十三章中就道出了神奇数字系列的真谛:“道生一,一生二,二生三,三生万物。
”神奇数字系列包括下列数字:1,2,3,5,8,13,21,34,55,89,144,233,377,610,987,1597……直至无限。
构成斐波南希神奇数字系列的基础非常简单,由1,2,3开始,产生无限数字系列,而3,实际上为1与2之和,以后出现的一系列数字,全部依照上述简单的原则,两个连续出现的相邻数字相加,等于一个后面的数字。
例如3加5等于8,5加8等于13,8加13等于21,……直至无限。
表面看来,此一数字系列很简单,但背后却隐藏着无穷的奥妙。
这个数列被称为费波纳奇数列。
这个数列有如下特性:(1)任何相列的两个数字之和都等于后一个数字,例如:1+1=2;2+3=5;5+8=13;144+233=377;……(2)除了最前面3个数(1,2,3),任何一个数与后一个数的比率接近0.618,而且越往后,其比率越接近0.618:3÷5=0.6;8÷13=0.618;21÷34=0.618;……(3)除了首3个数外,任何一个数与前一个数的比率,接近1.618。



波浪理论中神奇数字系列江恩理论中神秘的“七”波浪理论中神奇数字系列一、斐波南希数列为波浪理论的结构基础艾略特,波浪理论的开山祖师,在1934年公开发表波浪理论,指出股市走势依据一定的模式发展,涨落之间,各种波浪有节奏地重复出现,艾略特创立的波浪理论,属于一整套精细的分析工具,包括下列三个课题:1、波浪运行的形态;2、浪与浪之间的比率;3、时间星期。
艾略特在1946年发表的第二本著作,索性就命名为《大自然的规律》(Nature's Law)。
波浪理论第二个重要课题,系浪与浪之间的比率,而该比率实际上跟随神奇数字系列发展。
艾略特在《大自然的规律》一书中谈到,其波浪理论的数字基础是一系列的数列,是斐波南希在13世纪时所发现的,因此,此数列一般却称之谓斐波南希数列。
神奇数字系列本身属于一个极为简单的数字系列,但其间展现的各种特点,令人对大自然奥秘,感叹玄妙之余,更多一份敬佩。
其实早在中国《道德经》第四十三章中就道出了神奇数字系列的真谛:“道生一,一生二,二生三,三生万物。
”神奇数字系列包括下列数字:1,2,3,5,8,13,21,34,55,89,144,233,377,610,987,1597……直至无限。
构成斐波南希神奇数字系列的基础非常简单,由1,2,3开始,产生无限数字系列,而3,实际上为1与2之和,以后出现的一系列数字,全部依照上述简单的原则,两个连续出现的相邻数字相加,等于一个后面的数字。
例如3加5等于8,5加8等于13,8加13等于21,……直至无限。
表面看来,此一数字系列很简单,但背后却隐藏着无穷的奥妙。
二、平方的秘密俄罗斯著名数学家韦罗斯利夫,曾经发表的神奇数字研究论文报告中,提示许多有关斐波南希神奇数字的神秘性,其中之一就是神奇数字平方的秘密。
1、由1开始,可能随意选取连续出现的相邻两神奇数字,数目可不限,先将这些神奇数字进行平方,然后将平方所得数字进行相加,其和必定等于最后一个神奇数字与接着出现的下一个神奇数字相乘。
波浪理论的数学基础一、概述人们通常说,十个分析师有十一种数浪方法。
大部分人都觉得艾略特波浪理论过于玄奥,难以把握。
1946年,艾略特完成了关于波浪理论的集大成之作,《自然法则——宇宙的秘密》。
你瞧!他的气魄有多大。
艾略特坚信,他的波浪理论是制约人类一切活动的普遍自然法则的一部分。
波浪理论的优点是,对即将出现的顶部或底部却能提前发出警告信号,而传统的技术分析方法只有事后才能验证。
艾略特波浪理论对市场运作具备了全方位的透视能力,从而有助于解释特定的形态为什么要出现,在何处出现,以及它们为什么具备如此这般的预测意义等等问题。
另外,它也有助于我们判明当前的市场在其总体周期结构中所处的地位。
波浪理论的数学基础,就是菲波纳奇在13世纪发现的一组数列。
菲波纳奇数列还是黄金分割、黄金矩形、对数螺线的数学基础,在音乐、艺术、建筑中,都有它们的影子。
二、艾赂特波浪理论的基本原理波浪理论具有三个重要方面——形态、比例和时间,其重要性依上述次序等而下之。
所谓形态,指波浪的形态或构造,这是波浪理论最重要的部分。
而比例分析是指,通过测算各个波浪之间的相互关家,来确定回撤点和价格目标。
最后一方面是时间,各波浪之间在时间上也相互关联,我们可以利用这种关系来验证波浪形态和比例。
有些分析人士认为,时间关系在进行市场预测时较不可靠。
艾略特理论主要应用在股价指数,特别是道·琼斯工业股票指数的分析上的。
在波浪理论最基本的形式是,股票市场遵循着一种周而复始的节律,先是5浪上涨,随之有3浪下跌。
如图7.13所示的,是一个完整的周期。
数一数其中波浪的数目,那么,一个完整的周期包含8浪一5浪上升,3浪下降。
在周期的上升阶段,每一浪均以数字编号。
1浪、3浪和5浪是上升浪,称为主浪,而2浪和4浪的方向与上升趋势的方向相反,因为2浪和4浪分别是对1浪和3浪的调整,故称之为调整浪。
上述五浪完成后,出现了一个三浪形式的调整。
这三个波浪分别用字母a,b,c来表示。
波浪理论与黄金分割使用小心得1尽管埃及人很早就参透了0.618和1.618的神奇奥秘,并建立了金字塔。
但是,终究还是伟大的数学家里昂纳多-斐波拉奇将其发扬光大,并创造性的证明了斐波那契数列和黄金分割率。
至此,这个理论便应用在各行各业的个个领域。
这个接近自然个法则,当然也使用在资本市场的技术分析上。
经过,一段时间的验证、看书、思考以及求教,现记录下波浪理论以及黄金分割的一点小小使用方法。
一波浪理论艾略特也曾经表示,波浪理论的理论基础来源于斐波那契数列,波浪的浪序列服从斐波那契数列。
本人认为,波浪理论作为趋势理论的重要补充,对于预测行情走势以及验证趋势理论中的阻力支撑还是很有作用的。
波浪理论的主要心得是:①波浪理论的核心内容就是5浪和3浪。
任何的的波浪或形态都是由其组成的。
完整的浪是8浪(3浪+5浪),区别在于推动浪(主要趋势)用5浪,调整浪(次要趋势或短暂趋势)用3浪,当然也会有小小的例外。
因此,要按这个分发,浪中有浪,就可以从8浪中分出34个小浪,从34个小浪中分出144个小小浪,。
而8、34、144又恰好是斐波拉奇数列中重要的数字,而8是34的0.236,34是144的0.236,这又是何等的神奇。
此外,而且任何一个完整的大浪又可以看作是更大一个浪的开始,因此具备预测功能。
②有两种简单的调整形态:Ⅰ锯齿形(5-3-5)Ⅱ平台型(3-3-5)。
③在五浪结构中,其中一个浪出现了延伸浪,其余的朗格就不会在出现。
据说,股市中的延伸浪会出现在第三浪,而商品市场则会出现在第五浪。
④三角形通常会出现在第四浪,并且总是在最后一浪之前。
也可以出现在调整的b浪中。
⑤交替规则警示我们,不要指望同一类形态连续出现。
⑥4浪不可与1浪有重叠。
据说期货市场不这么严格,股市则需要。
⑦该理论在参与度高的市场,则越加准确。
⑧波浪理论中形态、比数、时间的重要性依次递减。
⑨以水平阻力支撑先来划分区域来看,但间隔变大时则进入了一个较大的波浪,这时候的阻力支撑更加可靠。
波浪理论数学结构——斐波那契数列与黄金分割率斐波那契数列(Fibonacci sequence),又称黄金分割数列、因数学家列昂纳多·斐波那契(Leonardoda Fibonacci)以兔子繁殖为例子而引入,故又称为“兔子数列”,指的是这样一个数列:1、1、2、3、5、8、13、21、34、……在数学上,斐波纳契数列以如下被以递推的方法定义:F(1)=1,F(2)=1, F(n)=F(n-1)+F(n-2)(n>=3,n∈N*)在现代物理、准晶体结构、化学等领域,斐波纳契数列都有直接的应用,为此,美国数学会从1963年起出版了以《斐波纳契数列季刊》为名的一份数学杂志,用于专门刊载这方面的研究成果。
黄金分割是指将整体一分为二,较大部分与整体部分的比值等于较小部分与较大部分的比值,其比值约为0.618。
这个比例被公认为是最能引起美感的比例,因此被称为黄金分割。
1、波浪理论的推动浪,浪形为5(1、2、3、4、5),调整浪的浪型为3(a\b\c),合起来为8。
若把波浪细化,大的推动浪又可分为1、3、5浪为推动,2、4为调整。
a、c为推动,b为调整。
这样大的推动浪为5+3+5+3+5=21,调整浪为5+3+5=13,合起来为34。
若再进行更详细的浪形划分,大的推动浪为21+13+21+13+21=89,调整浪为21+13+21=55,合起来为144。
所以,波浪理论怎么细分,都精确在这个数列上:1、2、3、5、8、13、21、34、55、89、144、2332、这个数列就是斐波那契数列。
它满足如下特性:每两个相连数字相加等于其后第一个数字;前一个数字大约是后一个数字的0.618倍;前一个数字约是其后第二个数字的0.382倍;后一个数字约是前一个数字的1.618倍;后一个数字约是前面第二个数字的2.618倍;3、由此计算出常见的黄金分割率为(0.5和1.5外):0.191、0.236、0.382、0.618、0.809、1.236、1.382、1.618、1.764、1.809 4、黄金分割比率对于股票市场运行的时间周期和价格幅度模型具有重要启示及应用价值。
斐波那契数列斐波那契数列斐波纳契数列,又称黄金分割数列,指的是这样一个数列:1、1、2、3、5、8、13、21、……在数学上,斐波纳契数列以如下被以递归的方法定义:F0=0,F1=1,Fn=F(n-1)+F(n-2)(n>=2,n∈N*)在现代物理、准晶体结构、化学等领域,斐波纳契数列都有直接的应用,为此,美国数学会从1960年代起出版了《斐波纳契数列》季刊,专门刊载这方面的研究成果。
定义斐波那契数列指的是这样一个数列:1、1、2、3、5、8、13、21、34……这个数列从第三项开始,每一项都等于前两项之和。
斐波那契数列的发明者,是意大利数学家列昂纳多〃斐波那契(Leonardo Fibonacci),自然中的斐波那契数列生于公元1170年,卒于1240年,籍贯是比萨。
他被人称作“比萨的列昂纳多”。
1202年,他撰写了《珠算原理》(Liber Abacci)一书。
他是第一个研究了印度和阿拉伯数学理论的欧洲人。
他的父亲被比萨的一家商业团体聘任为外交领事,派驻地点相当于今日的阿尔及利亚地区,列昂纳多因此得以在一个阿拉伯老师的指导下研究数学。
他还曾在埃及、叙利亚、希腊、西西里和普罗旺斯研究数学。
通项公式递推公式斐波那契数列:1、1、2、3、5、8、13、21、……如果设F(n)为该数列的第n项(n∈N+)。
那么这句话可以写成如下形式:F(1) = 1,F(2)=1,F(n)=F(n-1)+F(n-2) (n≥3),显然这是一个线性递推数列。
通项公式斐波那契数列通项公式(见上图)(又叫“比内公式”,是用无理数表示有理数的一个范例。
)注:此时a1=1,a2=1,an=a(n-1)+a(n-2)(n>=3,n∈N*)通项公式的推导方法一:利用特征方程(线性代数解法)线性递推数列的特征方程为:X^2=X+1解得X1=(1+√5)/2,,X2=(1-√5)/2。
则F(n)=C1*X1^n + C2*X2^n。