基于Fisher判别分析的贝叶斯分类器

F i s h e r准则线性分类器设计内部编号：（YUUT-TBBY-MMUT-URRUY-UOOY-DBUYI-0128）一 、基于F i s h e r 准则线性分类器设计1、 实验内容： 已知有两类数据1ω和2ω二者的概率已知1)(ωp =，2)(ωp =。

1ω中数据点的坐标对应一一如下：数据：x =y =z =2ω数据点的对应的三维坐标为x2 =y2 =z2 =数据的样本点分布如下图：1)请把数据作为样本，根据Fisher选择投影方向W的原则，使原样本向量在该方向上的投影能兼顾类间分布尽可能分开，类内样本投影尽可能密集的要求，求出评价投影方向W的函数，并在图形表示出来。

取极大值的*w。

用matlab完并在实验报告中表示出来，并求使)J(wF成Fisher线性分类器的设计，程序的语句要求有注释。

2)根据上述的结果并判断（1，，），，，，，，，，，（，，），属于哪个类别，并画出数据分类相应的结果图，要求画出其在W上的投影。

3)回答如下问题，分析一下W的比例因子对于Fisher判别函数没有影响的原因。

2、实验代码x1 =[];x2 =[];x3 =[];%将x1、x2、x3变为行向量x1=x1(:);x2=x2(:);x3=x3(:);%计算第一类的样本均值向量m1m1(1)=mean(x1);m1(2)=mean(x2);m1(3)=mean(x3);%计算第一类样本类内离散度矩阵S1S1=zeros(3,3);for i=1:36S1=S1+[-m1(1)+x1(i) -m1(2)+x2(i) -m1(3)+x3(i)]'*[-m1(1)+x1(i) -m1(2)+x2(i) -m1(3)+x3(i)];end%w2的数据点坐标x4 =[];x5 =[];x6 =[];x4=x4(:);x5=x5(:);x6=x6(:);%计算第二类的样本均值向量m2m2(1)=mean(x4);m2(2)=mean(x5);m2(3)=mean(x6);%计算第二类样本类内离散度矩阵S2S2=zeros(3,3);for i=1:36S2=S2+[-m2(1)+x4(i) -m2(2)+x5(i) -m2(3)+x6(i)]'*[-m2(1)+x4(i) -m2(2)+x5(i) -m2(3)+x6(i)];end%总类内离散度矩阵SwSw=zeros(3,3);Sw=S1+S2;%样本类间离散度矩阵SbSb=zeros(3,3);Sb=(m1-m2)'*(m1-m2);%最优解WW=Sw^-1*(m1-m2)'%将W变为单位向量以方便计算投影W=W/sqrt(sum(W.^2));%计算一维Y空间中的各类样本均值M1及M2for i=1:36y(i)=W'*[x1(i) x2(i) x3(i)]';endM1=mean(y);for i=1:36y(i)=W'*[x4(i) x5(i) x6(i)]';endM2=mean(y);%利用当P(w1)与P(w2)已知时的公式计算W0p1=;p2=;W0=-(M1+M2)/2+(log(p2/p1))/(36+36-2);%计算将样本投影到最佳方向上以后的新坐标X1=[x1*W(1)+x2*W(2)+x3*W(3)]';X2=[x4*W(1)+x5*W(2)+x6*W(3)]'; %得到投影长度XX1=[W(1)*X1;W(2)*X1;W(3)*X1];XX2=[W(1)*X2;W(2)*X2;W(3)*X2]; %得到新坐标%绘制样本点figure(1);plot3(x1,x2,x3,'r*'); %第一类hold onplot3(x4,x5,x6,'gp') ; %第二类legend('第一类点','第二类点');title('Fisher线性判别曲线');W1=5*W;%画出最佳方向line([-W1(1),W1(1)],[-W1(2),W1(2)],[-W1(3),W1(3)],'color','g'); %判别已给点的分类a1=[1,,]';a2=[,,]';a3=[,,]';a4=[,,]';a5=[,,]';A=[a1 a2 a3 a4 a5];n=size(A,2);%下面代码在改变样本时可不修改%绘制待测数据投影到最佳方向上的点for k=1:nA1=A(:,k)'*W;A11=W*A1;%得到待测数据投影y=W'*A(:,k)+W0; %计算后与0相比以判断类别，大于0为第一类，小于0为第二类if y>0plot3(A(1,k),A(2,k),A(3,k),'ro'); %点为"rp"对应第一类plot3(A11(1),A11(2),A11(3),'ro'); %投影为"r+"对应ro类elseplot3(A(1,k),A(2,k),A(3,k),'ch'); %点为"bh"对应ch类plot3(A11(1),A11(2),A11(3),'ch'); %投影为"b*"对应ch类endend%画出最佳方向line([-W1(1),W1(1)],[-W1(2),W1(2)],[-W1(3),W1(3)],'color','m');view([,30]);axis([-2,3,-1,3,,]);grid onhold off3、实验结果根据求出最佳投影方向，然后按照此方向，将待测数据进行投影。

一种基于加权核Fisher准则的朴素贝叶斯分类器
雷瑜;杨慧中
【期刊名称】《江南大学学报（自然科学版）》
【年(卷),期】2013(012)005
【摘要】利用加权核Fisher准则,给出一种朴素贝叶斯分类器的改进算法.该算法通过寻找使类与类最大分离的最优投影矩阵,将样本数据进行投影变换,再利用朴素贝叶斯分类器对新样本进行分类.将该方法应用于双酚A生产过程在线监测数据集的分类中,仿真结果表明,相比于单纯朴素贝叶斯分类器,该分类算法具有更好的分类性能.
【总页数】5页(P510-514)
【作者】雷瑜;杨慧中
【作者单位】江南大学教育部轻工过程先进控制重点实验室,江苏无锡214122;江南大学教育部轻工过程先进控制重点实验室,江苏无锡214122
【正文语种】中文
【中图分类】TP274
【相关文献】
1.一种基于粗糙集的特征加权朴素贝叶斯分类器 [J], 王国才;张聪
2.一种基于粗糙集的特征加权朴素贝叶斯分类器 [J], 王国才;张聪
3.基于加权Fisher准则的线性鉴别分析及人脸识别 [J], 郭娟;林冬;戚文芽
4.一种选择性的加权朴素贝叶斯分类器 [J], 王峻;刘淮生
5.基于加权核Fisher准则特征提取的多模型建模方法(英文) [J], 吕业;杨慧中
因版权原因，仅展示原文概要，查看原文内容请购买。

距离判别法和Bayes判别法[color=black][size=3]距离判别法和Bayes判别法是判别分析中常用的两类判别法。

多元统计书上一般都有介绍。

简单说就是[font=MS Shell Dlg]判别给定的样本属于哪一类的。

比方说一堆样本，分好几类，样本有n个属性。

把这堆样本输入程序训练好后，程序就可以判别新的样本属于哪一类了。

[/font]我把它们做成了一个简单的界面，大家可以按界面提示操作下。

为了方便我准备了一些数据，见附件。

[font=MS Shell Dlg]train是训练样本（判别准备前用的），test是测试样本，即新数据，用来判别新样本中每一个属于哪一类的。

这里属性个数n=3。

实际使用时，n可以不局限于3。

训练样本只要按照附件中的格式（即第一列为类名，其余列为属性）存为xls文件即可。

测试样本直接就是由属性列组成的，每一行表示一个样本。

[/font][/size][/color][font=MS Shell Dlg][size=3]下面是代码（注释比较详细，用nested function写回调函数可以供GUI 初学者借鉴）：[/size][/font][font=MS Shell Dlg][size=3][code]function DiscriminantMethodsfig=figure('defaultuicontrolunits','normalized','name','各类判别方法比较','numbertitle','off','menubar','none');%主界面，返回主界面句柄figUiButtonGroupH = uibuttongroup('Position',[0.55 0.08 0.40 0.85],'title','各判别方法','fontsize',12,'bordertype','etchedout');%群组对象，并返回句柄DistanceH = uicontrol('Style','Radio','String','距离判别法','fontsize',12,'pos',[0.05 0.73 0.9 0.15],'parent',UiButtonGroupH);%距离判别法的选项BayesH = uicontrol('Style','Radio','String','Bayes判别法','fontsize',12,'pos',[0.05 0.52 0.9 0.15],'parent',UiButtonGroupH);%Bayes判别法的选项FisherH = uicontrol('Style','Radio','String','Fisher判别法','fontsize',12,'pos',[0.05 0.31 0.9 0.15],'parent',UiButtonGroupH);%Fisher判别法的选项%下面几行建立相关按钮控件。

典则判别函数和fisher判别函数
典则判别函数和Fisher判别函数是模式分类中常用的两种算法。

它们都是通过选择合适的决策边界来对数据进行分类。

但是它们的实
现方式和应用场景有所不同。

典则判别函数是一种基于贝叶斯分类规则的判别函数。

它将数据
集分为多个类别，并计算每个类别的先验概率。

在观察到新的数据时，典则判别函数将计算各类别的后验概率并选择概率最大的类别作为分
类结果。

这种算法相对简单，但需要事先知道每个类别的先验概率。

Fisher判别函数则是一种基于判别分析的算法，它用于确定分类数据的最佳线性投影。

这个投影可以最大化类别之间的差异性，同时
最小化类别内部的差异性。

因此，Fisher判别函数在处理大量特征或
类别未知时效果更好。

它可以用于二分类和多分类问题，并且可以通
过聚类算法来确定类别数量。

总体而言，典则判别函数是一种简单而直接的方法，而Fisher
判别函数则更适合于处理高维数据和未知类别的情况。

但无论是哪种
算法，在实际应用中都需要根据具体的问题选择合适的算法，并根据
数据集进行调整。

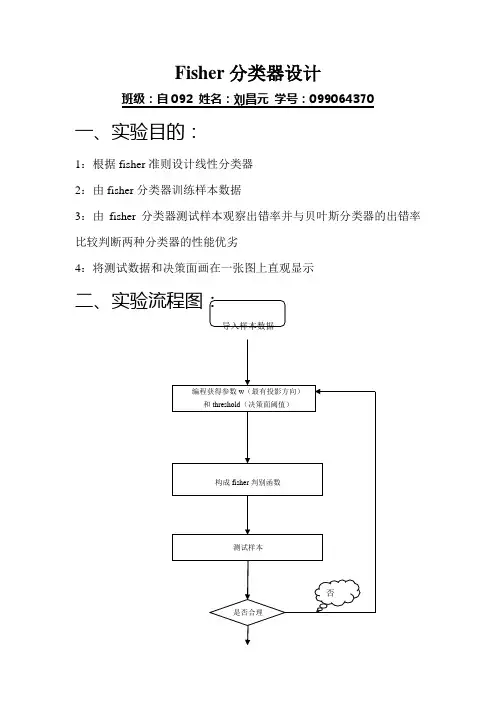
Fisher分类器设计班级：自092 姓名：刘昌元学号：099064370 一、实验目的：1：根据fisher准则设计线性分类器2：由fisher分类器训练样本数据3：由fisher分类器测试样本观察出错率并与贝叶斯分类器的出错率比较判断两种分类器的性能优劣4：将测试数据和决策面画在一张图上直观显示是三、实验所用函数：类均值向量：∑=∈ixj j i x N M χ1类内离散度矩阵：Ti j i ixj j iM x M x S ))((--∑∈=χ总类内离散度矩阵：21S S S w +=类间离散度矩阵：T b M M M M S ))((2121--= 最有投影方向：)(211*M M S W w -=-决策函数：0)(w x w x G T +=阈值：)(21210M w M w w T T+-= 四、实验结果：1：得到参数:最有投影向量和阈值2：利用分类器输入身高和体重数据得到性别分类（实验结果如下）w=[ 0.0012; 0.0003] threshold =0.2318classify(165,56) 结果为“女” classify(178,70) 结果为“男”3：fisher准则分类器的出错率统计：测试test1：实际个数分类个数出错率男生84.0000 31.0000 0.6310女生40.0000 93.0000 1.3250测试test2:4:bayes分类器测试出错统计：测试test1:测试test2:结论：很显然bayes分类器比fisher分类器准确率高的多。

4：分类面决策图：五、程序：程序1：求最有投影方向和阈值%程序功能：应用fisher分类方法，使用训练数据获得阈值和最佳变换向量(投影方向）% function fisher(boys,girls) %调用男生和女生的训练样本数据%A=boys.';B=girls.';[k1,l1]=size(A);[k2,l2]=size(B);M1=sum(boys);M1=M1.';M1=M1/l1; %求男生身高与体重的均值%M2=sum(girls);M2=M2.';M2=M2/l2; %求女生身高与体重的均值%S1=zeros(k1,k1);S2=zeros(k2,k2);for i=1:l1S1=S1+(A(:,i)-M1)*((A(:,i)-M1).'); %求类内离散度矩阵S1%endfor i=1:l2S2=S2+(B(:,i)-M2)*((B(:,i)-M2).'); %求类内离散度矩阵S2%endfor i=1:2for j=1:2Sw(i,j)=S1(i,j)+S2(i,j); %求总类内离散度矩阵Sw%endendw=inv(Sw)*(M1-M2) %求最有投影方向%wT=w.';for i=1:l1Y1(i)=wT(1,1)*A(1,i)+wT(1,2)*A(2,i); %由分类函数g(x)=wT*x求男生身高和体重的阈值%endfor i=1:l2Y2(i)=wT(1,1)*B(1,i)+wT(1,2)*B(2,i); %由分类函数g(x)=wT*x求女生身高和体重的阈值%endm1=sum(Y1)/l1; %阈值平均%m2=sum(Y2)/l2; %阈值平均%threshold=(l1*m1+l2*m2)/(l1+l2) %求fisher决策面的阈值%程序2：构成fisher判别器%函数功能：应用Fisher准则构成的分类器判断一个身高体重二维数据的性别%函数使用方法：输入classify(hight,weight)其中hight和weight分别是身高和体重的数据function value=classify(hight,weight)w=[0.0012;0.0003];threshold=0.2318;tem=[hight;weight]; %将输入的身高和体重数据构成列向量%result=(w.')*tem; %根据fisher判别式求判别值%if result>threshold %判别值和决策面阈值比较%value=1;elsevalue=0;end程序3：%功能：调用Fisher分类器统计出错率%开发者：安徽工业大学自动化092班刘昌元function result=Error(file)[m,n]=size(file);Boy=0;Girl=0;boy=0;girl=0;for i=1:mif(file(i,3)==0)Girl=Girl+1;elseBoy=Boy+1;endA(i,1)=file(i,1);A(i,2)=file(i,2);endw=[0.0012;0.0003];threshold =0.2318;for i=1:mclassify(A(i,1),A(i,2));if(ans==0)girl=girl+1;elseboy=boy+1;endendtem1=abs(Boy-boy)/Boy;tem2=abs(Girl-girl)/Girl;result(1,1)=Boy;result(1,2)=boy;result(1,3)=tem1;result(2,1)=Girl;result(2,2)=girl;result(2,3)=tem2;程序4：%程序：画图%功能：将训练样本boy.txt和girl.txt中的数据和线性决策面以及贝叶斯决策面画到一幅图上function graphics(boys,girls)w=[0.0012;0.0003];threshold =0.2318;A=boys.';B=girls.';[m1,n1]=size(A);[m2,n2]=size(B);for i=1:n1x=A(1,i);y=A(2,i);plot(x,y,'R.');hold onendfor i=1:n2x=B(1,i);y=B(2,i);plot(x,y,'G.');hold onenda1=min(A(1,:));a2=max(A(1,:));b1=min(B(1,:));b2=max(B(1,:));a3=min(A(2,:));a4=max(A(2,:));b3=min(B(2,:));b4=max(B(2,:));if a1<b1a=a1;elsea=b1;endif a2>b2b=a2;elseb=b2;endif a3<b3c=a3;elsec=b3;endif a4>b4。

距离判别法、贝叶斯判别法和费歇尔判别法的异同引言在模式识别领域，判别分析是一种常用的方法，用于将数据样本划分到不同的类别中。

距离判别法、贝叶斯判别法和费歇尔判别法是判别分析中常见的三种方法。

本文将对这三种方法进行比较，探讨它们的异同。

一、距离判别法距离判别法是一种基于距离度量的判别分析方法。

它的基本思想是通过计算样本点与各个类别中心的距离，将样本划分到距离最近的类别中。

常见的距离判别法有欧氏距离判别法和马氏距离判别法。

1. 欧氏距离判别法欧氏距离判别法是一种简单直观的距离判别方法。

它通过计算样本点与各个类别中心之间的欧氏距离，将样本划分到距离最近的类别中。

算法步骤如下： 1. 计算各个类别的中心点，即各个类别样本点的均值向量。

2. 对于给定的待判样本点，计算其与各个类别中心点的欧氏距离。

3. 将待判样本点划分到距离最近的类别中。

2. 马氏距离判别法马氏距离判别法考虑了各个类别的协方差矩阵，相比于欧氏距离判别法更加准确。

它通过计算样本点与各个类别中心之间的马氏距离，将样本划分到距离最近的类别中。

算法步骤如下： 1. 计算各个类别的中心点，即各个类别样本点的均值向量。

2. 计算各个类别的协方差矩阵。

3. 对于给定的待判样本点，计算其与各个类别中心点之间的马氏距离。

4. 将待判样本点划分到距离最近的类别中。

二、贝叶斯判别法贝叶斯判别法是一种基于贝叶斯理论的判别分析方法。

它的基本思想是通过计算后验概率，将样本划分到具有最高后验概率的类别中。

常见的贝叶斯判别法有贝叶斯最小错误率判别法和贝叶斯线性判别法。

1. 贝叶斯最小错误率判别法贝叶斯最小错误率判别法是一种理论上最优的判别方法。

它通过计算后验概率，将样本划分到具有最高后验概率的类别中。

算法步骤如下： 1. 计算各个类别的先验概率。

2. 计算给定样本点在各个类别下的条件概率。

3. 计算给定样本点在各个类别下的后验概率。

4. 将待判样本点划分到具有最高后验概率的类别中。

基于Fisher 线性判别的基因分类器的设计2000年6月人类基因组计划正式完成对人类分布在细胞核中的23条染色体的6万到10万个基因，大约30亿个碱基的测序工作，其中我国完成对3号染色体上的3000万个碱基的测序。

基因草图是由4个字符A 、T 、C 、G 按一定顺序排列组成的长约30亿的序列，其中没有断句，也没有标点。

除了知道这四个字符代表四种碱基之外，人类对基因知之甚少。

但众多的科研工作者发现，NDA 的序列中隐藏这重大的秘密，关系到人的生老病死，对基因的研究具有重大的意义。

本文对DNA 中的四种碱基：腺嘌呤（A ），鸟嘌呤（G ），胞嘧啶（C ）和胸腺嘧啶（T ）在基因链中出现的频率作为输入向量的四个特征成员，用Fisher 线性分类方法对已知类别的20个基因样本进行训练和测试，表明Fisher 线性分类方法能对这些已知类别的DNA 序列达到分类的目的。

本文采用的数据来自参考文献[1]，数据表1所示：显然表1中的样本共分为两类，其中0P >的为一类，在神经网络中以输出为“1”表示；0P <的为另一类，在神经网络中以输出为“0”表示。

Fisher 线性判别：Fisher 线性判别的基本思想是将d 维空间中的样本投射到一维空间中的一条直线上，将维度由多维压缩到一维。

在一维的直线上找到一个阈值点，大于该阈值点的样本分为一类，小于该阈值点的样本分为另一类。

基于以上思想，假设集合ψ包含N 个d 维样本123,,,......N x x x x 其中1N 个属于1ψ的样本，2N 个属于2ψ的样本。

若对n x 的分量做线性组合，可得到标量,1,2,3,......T n n y x n N ω==这样便得到N 个一维样本n y 的集合，可分为两个子集12,y y 。

从几何上，如果||||1ω=，则每个n y 就是对应于n x 到方向为ω的直线的投影。

ω方向的不同，将使样本投影后的可分程度不同，从而直接影响识别的效果。

基于贝叶斯算法的分类器设计与实现一、引言随着大数据时代的来临，数据分类和预测成为了各行各业中的重要任务。

其中，贝叶斯算法作为一种常用的机器学习算法，具有较好的分类效果和运算速度。

本文将探讨基于贝叶斯算法的分类器的设计与实现方法，旨在为研究者提供一种有效的分类解决方案。

二、贝叶斯分类器原理贝叶斯分类器是基于贝叶斯定理的一种分类算法。

其核心思想是通过计算后验概率，选取具有最大后验概率的类别作为分类结果。

贝叶斯分类器通过学习训练集中的样本数据，利用先验概率和条件概率来进行分类。

三、分类器设计1. 数据预处理在设计分类器之前，首先需要进行数据预处理。

数据预处理包括数据清洗、特征选择和数据转换等步骤。

其中，数据清洗可以去除异常数据和噪声数据，特征选择可以筛选出与分类任务相关的特征，数据转换可以将数据转换为分类器所需的输入格式。

2. 特征提取特征提取是分类器设计的关键步骤之一。

通过对原始数据进行特征提取，可以将数据转化为分类器所能理解的形式。

常用的特征提取方法包括词袋模型、TF-IDF权重和词嵌入等。

3. 训练模型在特征提取完成后，需要利用训练集来训练分类器模型。

贝叶斯分类器利用训练集中的样本数据计算先验概率和条件概率，并建立分类模型。

训练模型的过程包括计算类别先验概率、计算条件概率和选择最优特征等。

4. 分类预测分类预测是利用训练好的分类器模型对新样本进行分类的过程。

对于新的输入样本，分类器根据先验概率和条件概率计算后验概率，并将概率最大的类别作为分类结果输出。

四、分类器实现1. 贝叶斯公式实现贝叶斯算法的核心是贝叶斯公式。

在编程实现过程中，可以借助概率统计的库函数，计算样本的先验概率和条件概率。

同时，根据样本的特征提取结果，利用贝叶斯公式计算后验概率，并选择概率最大的类别作为分类结果。

2. 预测算法实现预测算法是分类器实现过程中的关键步骤。

贝叶斯分类器中常用的预测算法有朴素贝叶斯算法和多项式贝叶斯算法。

作业二 F i s h e r线性判别分类器一 实验目的 本实验旨在让同学进一步了解分类器的设计概念，能够根据自己的设计对线性分类器有更深刻地认识，理解Fisher 准则方法确定最佳线性分界面方法的原理，以及Lagrande 乘子求解的原理。

二 实验条件Matlab 软件三 实验原理线性判别函数的一般形式可表示成0)(w X W X g T += 其中根据Fisher 选择投影方向W 的原则，即使原样本向量在该方向上的投影能兼顾类间分布尽可能分开，类内样本投影尽可能密集的要求，用以评价投影方向W 的函数为：)(211*m m S W W -=-上面的公式是使用Fisher 准则求最佳法线向量的解，该式比较重要。

另外，该式这种形式的运算，我们称为线性变换，其中21m m -式一个向量，1-W S 是W S 的逆矩阵，如21m m -是d 维，W S 和1-W S 都是d ×d 维，得到的*W 也是一个d 维的向量。

向量*W 就是使Fisher 准则函数)(W J F 达极大值的解，也就是按Fisher 准则将d 维X 空间投影到一维Y 空间的最佳投影方向，该向量*W 的各分量值是对原d 维特征向量求加权和的权值。

以上讨论了线性判别函数加权向量W 的确定方法，并讨论了使Fisher 准则函数极大的d 维向量*W 的计算方法，但是判别函数中的另一项0W 尚未确定，一般可采用以下几种方法确定0W 如 或者 m N N m N m N W ~~~2122110=++-= 或当1)(ωp 与2)(ωp 已知时可用当W 0确定之后，则可按以下规则分类，2010ωω∈→-<∈→->X w X W X w X W T T四 实验程序及结果分析%w1中数据点的坐标x1 =[0.2331 1.5207 0.6499 0.7757 1.0524 1.19740.2908 0.2518 0.6682 0.5622 0.9023 0.1333-0.5431 0.9407 -0.2126 0.0507 -0.0810 0.73150.3345 1.0650 -0.0247 0.1043 0.3122 0.66550.5838 1.1653 1.2653 0.8137 -0.3399 0.51520.7226 -0.2015 0.4070 -0.1717 -1.0573 -0.2099];x2 =[2.3385 2.1946 1.6730 1.6365 1.7844 2.01552.0681 2.1213 2.4797 1.5118 1.9692 1.83401.87042.2948 1.7714 2.3939 1.5648 1.93292.2027 2.4568 1.7523 1.6991 2.4883 1.72592.0466 2.0226 2.3757 1.7987 2.0828 2.07981.94492.3801 2.2373 2.1614 1.9235 2.2604];x3 =[0.5338 0.8514 1.0831 0.4164 1.1176 0.55360.6071 0.4439 0.4928 0.5901 1.0927 1.07561.0072 0.4272 0.4353 0.9869 0.4841 1.09921.0299 0.7127 1.0124 0.4576 0.8544 1.12750.7705 0.4129 1.0085 0.7676 0.8418 0.87840.9751 0.7840 0.4158 1.0315 0.7533 0.9548];%将x1、x2、x3变为行向量x1=x1(:);x2=x2(:);x3=x3(:);%计算第一类的样本均值向量m1m1(1)=mean(x1);m1(2)=mean(x2);m1(3)=mean(x3);%计算第一类样本类内离散度矩阵S1S1=zeros(3,3);for i=1:36S1=S1+[-m1(1)+x1(i) -m1(2)+x2(i) -m1(3)+x3(i)]'*[-m1(1)+x1(i)-m1(2)+x2(i) -m1(3)+x3(i)];end%w2的数据点坐标x4 =[1.4010 1.2301 2.0814 1.1655 1.3740 1.18291.7632 1.97392.4152 2.5890 2.8472 1.95391.2500 1.2864 1.26142.0071 2.1831 1.79091.3322 1.1466 1.7087 1.59202.9353 1.46642.9313 1.8349 1.8340 2.5096 2.7198 2.31482.0353 2.6030 1.2327 2.1465 1.5673 2.9414];x5 =[1.0298 0.9611 0.9154 1.4901 0.8200 0.93991.1405 1.0678 0.8050 1.2889 1.4601 1.43340.7091 1.2942 1.3744 0.9387 1.2266 1.18330.8798 0.5592 0.5150 0.9983 0.9120 0.71261.2833 1.1029 1.2680 0.7140 1.2446 1.33921.1808 0.5503 1.4708 1.1435 0.7679 1.1288];x6 =[0.6210 1.3656 0.5498 0.6708 0.8932 1.43420.9508 0.7324 0.5784 1.4943 1.0915 0.76441.2159 1.3049 1.1408 0.9398 0.6197 0.66031.3928 1.4084 0.6909 0.8400 0.5381 1.37290.7731 0.7319 1.3439 0.8142 0.9586 0.73790.7548 0.7393 0.6739 0.8651 1.3699 1.1458];x4=x4(:);x5=x5(:);x6=x6(:);%计算第二类的样本均值向量m2m2(1)=mean(x4);m2(2)=mean(x5);m2(3)=mean(x6);%计算第二类样本类内离散度矩阵S2S2=zeros(3,3);for i=1:36S2=S2+[-m2(1)+x4(i) -m2(2)+x5(i) -m2(3)+x6(i)]'*[-m2(1)+x4(i) -m2(2)+x5(i) -m2(3)+x6(i)];end%总类内离散度矩阵SwSw=zeros(3,3);Sw=S1+S2;%样本类间离散度矩阵SbSb=zeros(3,3);Sb=(m1-m2)'*(m1-m2);%最优解WW=Sw^-1*(m1-m2)'%将W变为单位向量以方便计算投影W=W/sqrt(sum(W.^2));%计算一维Y空间中的各类样本均值M1及M2for i=1:36y(i)=W'*[x1(i) x2(i) x3(i)]';endM1=mean(y)for i=1:36y(i)=W'*[x4(i) x5(i) x6(i)]';endM2=mean(y)%利用当P(w1)与P(w2)已知时的公式计算W0p1=0.6;p2=0.4;W0=-(M1+M2)/2+(log(p2/p1))/(36+36-2);%计算将样本投影到最佳方向上以后的新坐标X1=[x1*W(1)+x2*W(2)+x3*W(3)]';X2=[x4*W(1)+x5*W(2)+x6*W(3)]';%得到投影长度XX1=[W(1)*X1;W(2)*X1;W(3)*X1];XX2=[W(1)*X2;W(2)*X2;W(3)*X2];%得到新坐标%绘制样本点figure(1)plot3(x1,x2,x3,'r*') %第一类hold onplot3(x4,x5,x6,'bp') %第二类legend('第一类点','第二类点')title('Fisher 线性判别曲线')W1=5*W;%画出最佳方向line([-W1(1),W1(1)],[-W1(2),W1(2)],[-W1(3),W1(3)],'color','b');%判别已给点的分类a1=[1,1.5,0.6]';a2=[1.2,1.0,0.55]';a3=[2.0,0.9,0.68]';a4=[1.2,1.5,0.89]';a5=[0.23,2.33,1.43]';A=[a1 a2 a3 a4 a5]n=size(A,2);%下面代码在改变样本时都不必修改%绘制待测数据投影到最佳方向上的点for k=1:nA1=A(:,k)'*W;A11=W*A1;%得到待测数据投影y=W'*A(:,k)+W0;%计算后与0相比以判断类别，大于0为第一类，小于0为第二类 if y>0plot3(A(1,k),A(2,k),A(3,k),'go'); %点为"rp"对应第一类plot3(A11(1),A11(2),A11(3),'go'); %投影为"r+"对应go 类elseplot3(A(1,k),A(2,k),A(3,k),'m+'); %点为"bh"对应m+类plot3(A11(1),A11(2),A11(3),'m+'); %投影为"b*"对应m+类endend%画出最佳方向line([-W1(1),W1(1)],[-W1(2),W1(2)],[-W1(3),W1(3)],'color','k');view([-37.5,30]);axis([-2,3,-1,3,-0.5,1.5]);grid onhold off实验结果和数据：首先根据求出最佳投影方向，然后按照此方向，将待测数据进行投影 。

一 、基于F i s h e r 准则线性分类器设计1、 实验内容：已知有两类数据1ω和2ω二者的概率已知1)(ωp =0.6，2)(ωp =0.4。

1ω中数据点的坐标对应一一如下：数据：x =0.2331 1.5207 0.6499 0.7757 1.0524 1.1974 0.2908 0.2518 0.6682 0.5622 0.9023 0.1333 -0.5431 0.9407 -0.2126 0.0507 -0.0810 0.7315 0.3345 1.0650 -0.0247 0.1043 0.3122 0.6655 0.5838 1.1653 1.2653 0.8137 -0.3399 0.5152 0.7226 -0.2015 0.4070 -0.1717 -1.0573 -0.2099 y =2.3385 2.1946 1.6730 1.6365 1.7844 2.0155 2.0681 2.1213 2.4797 1.5118 1.9692 1.8340 1.8704 2.2948 1.7714 2.3939 1.5648 1.9329 2.2027 2.4568 1.7523 1.6991 2.4883 1.7259 2.0466 2.0226 2.3757 1.7987 2.0828 2.0798 1.9449 2.3801 2.2373 2.1614 1.9235 2.2604 z =0.5338 0.8514 1.0831 0.4164 1.1176 0.5536 0.6071 0.4439 0.4928 0.5901 1.0927 1.0756 1.0072 0.4272 0.4353 0.9869 0.4841 1.09921.02990.71271.01240.45760.85441.12750.77050.41291.00850.76760.84180.87840.97510.78400.41581.03150.75330.9548数据点的对应的三维坐标为2x2 =1.40101.23012.08141.16551.37401.18291.76321.97392.41522.58902.84721.95391.25001.28641.26142.00712.18311.79091.33221.14661.70871.59202.93531.46642.93131.83491.83402.50962.71982.31482.03532.60301.23272.14651.56732.9414 y2 =1.02980.96110.91541.49010.82000.93991.14051.06780.80501.28891.46011.43340.70911.29421.37440.93871.22661.18330.87980.55920.51500.99830.91200.71261.28331.10291.26800.71401.24461.33921.18080.55031.47081.14350.76791.1288 z2 =0.62101.36560.54980.67080.89321.43420.95080.73240.57841.49431.09150.76441.21591.30491.14080.93980.61970.66031.39281.40840.69090.84000.53811.37290.77310.73191.34390.81420.95860.73790.75480.73930.67390.86511.36991.1458数据的样本点分布如下图：1)请把数据作为样本，根据Fisher选择投影方向W的原则，使原样本向量在该方向上的投影能兼顾类间分布尽可能分开，类内样本投影尽可能密集的要求，求出评价投影方向W的函数，并在图形表示出来。