公开课《平行四边形的面积》课件

苏教版五年级数学上册《平行四边形面积的计算》公开课说课稿一. 教材分析苏教版五年级数学上册《平行四边形面积的计算》这一节课，主要让学生掌握平行四边形的面积计算方法。

教材通过简单的实例和具体的操作，引导学生探究平行四边形面积的计算公式，并能够运用该公式解决实际问题。

教材还注重培养学生的空间观念和动手操作能力，提高他们解决实际问题的能力。

二. 学情分析五年级的学生已经掌握了四边形的性质，具备了一定的观察和操作能力。

他们对平行四边形的概念有一定的了解，但是对平行四边形面积的计算方法还不够熟悉。

因此，在教学过程中，我将以学生为主体，引导学生通过观察、操作、思考、交流等方式，自主探索平行四边形面积的计算方法。

三. 说教学目标1.知识与技能目标：让学生掌握平行四边形的面积计算方法，能够运用该公式解决实际问题。

2.过程与方法目标：通过观察、操作、思考、交流等过程，培养学生的空间观念和动手操作能力。

3.情感态度与价值观目标：激发学生对数学的兴趣，培养他们独立思考、合作交流的良好习惯。

四. 说教学重难点1.教学重点：平行四边形的面积计算方法。

2.教学难点：理解平行四边形面积计算的原理，能够灵活运用公式解决实际问题。

五. 说教学方法与手段1.教学方法：采用问题驱动法、启发式教学法、合作交流法等。

2.教学手段：利用多媒体课件、实物模型、操作卡片等辅助教学。

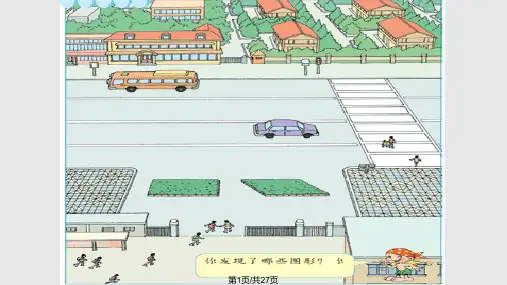
六. 说教学过程1.导入新课：通过展示平行四边形的图片，引导学生回顾平行四边形的性质，为新课的学习做好铺垫。

2.探究平行四边形面积计算方法：（1）观察实例：展示平行四边形的实物模型，引导学生观察并思考平行四边形的面积如何计算。

（2）小组讨论：让学生分组讨论，分享各自的思考和见解。

（3）总结公式：引导学生通过观察、操作、思考等过程，总结出平行四边形面积的计算公式。

3.实践操作：让学生利用操作卡片，亲自动手操作，验证平行四边形面积的计算公式。

4.解决问题：运用所学的平行四边形面积计算方法，解决实际问题。

平行四边形的面积第一课时教学目标1.使学生通过探索,理解和掌握平行四边形的面积计算公式,会计算平行四边形的面积。

2.使学生通过操作、观察、比较等活动,初步认识转化的方法,培养学生的观察、分析、概括、推导能力,发展学生的空间观念。

3.培养学生的合作意识和探究精神。

重点难点重点:推导平行四边形的面积计算公式。

难点:会计算平行四边形的面积。

教学过程一导入1.投影出示教材第86页的主题图,说说你发现了哪些图形,你会计算它们的面积吗?2.观察光明小学门前的两个花坛,分别是什么形状?哪个花坛的面积大?3.师:我们已经学过了长方形的面积计算方法,今天我们就来研究平行四边形的面积计算方法。

二教学实施1.用数方格的方法计算平行四边形的面积。

(1)我们在研究长方形面积的计算方法时用过数方格的方法来计算面积的大小。

现在请同学们也用这种方法算出这个平行四边形的面积。

(投影出示画着长方形和平行四边形的方格纸)说明:每一个方格表示1cm2,不满一格的都按半格计算。

请同学们数出数据,并填在教材第87页的表中。

(2)比较。

提问:观察表格中的数据,你发现了什么?平行四边形底高面积6424长方形长宽面积6424同桌相互讨论,得出结论:平行四边形和长方形的底与长、高与宽及面积分别相等,这个平行四边形的面积等于它的底乘高,这个长方形的面积等于它的长乘宽。

(3)小结。

从上面的研究我们知道,平行四边形的面积也可以用数方格的方法求出来,但数起来比较麻烦,而且不能算得精确。

特别是较大的平行四边形,像一块平行四边形菜地的面积,用数方格的方法就不好数了。

因此我们也要像求长方形面积那样,找出平行四边形的面积计算公式。

2.通过动手操作,推导平行四边形面积的计算公式。

(1)用数方格的方法我们已经发现平行四边形的面积等于底乘高。

那么,是不是所有的平行四边形都可以用这种方法求面积呢?下面就以小组为单位研究一下。

我们已经会计算长方形的面积了,能不能把一个平行四边形转化成一个长方形呢?想一想该怎么做。

平行四边形面积公开课一等奖平行四边形是一个非常基础的几何概念，它的面积公式的推导也相对简单。

在本次公开课中，我们将从基本概念开始，介绍平行四边形的性质，并推导出平行四边形的面积公式。

首先，让我们来回顾一下平行四边形的定义。

平行四边形是一个四边形，它的对边是平行的。

平行四边形的性质如下：性质1：平行四边形的对边长度相等。

这个性质可以通过平行四边形的定义直接推导出来。

因为平行四边形的对边是平行的，所以它们之间的距离是相等的，而对边的距离正好等于对边的长度。

性质2：平行四边形的对角线互相平分。

对角线是指连接平行四边形的两个非相邻顶点的线段。

由于平行四边形的对边是平行的，所以对角线所代表的两条线段是平行的，从而互相平分。

性质3：平行四边形的内角和为180度。

平行四边形的每条边都与它相邻的两条边之间夹一个内角，在平行四边形中我们可以通过交错内角相等和对内角求和等于180度来证明这个性质。

现在，让我们来推导平行四边形的面积公式。

首先，我们可以将平行四边形分割成两个三角形。

如图所示：A ______________ B/ \/ \D /_____________\C假设平行四边形的底边长度为b，高度为h。

我们可以看到两个三角形的高度都是h，并且它们的底边分别为a和c，其中a + c = b。

我们知道，三角形的面积等于底边长度乘以高度的一半。

所以，第一个三角形的面积为a * h / 2，第二个三角形的面积为c * h / 2。

因此，平行四边形的面积可以表示为：面积 = (a * h / 2) + (c * h / 2)现在，我们来寻找一个更简洁的表达式来表示平行四边形的面积。

通过观察可以发现，a和c分别是平行四边形的对边之一的长度，所以它们加起来等于对边的长度，即a + c = b。

由此，我们可以将公式进一步简化为：面积 = (a * h / 2) + ((b - a) * h / 2)= (a + b - a) * h / 2= b * h / 2因此，我们得出了平行四边形面积的最简形式。