九宫格的八种解法

九宫格的计算公式
九宫格的计算公式是指在一个3x3的矩阵中，通过对应位置的数字进行运算或排列，得到特定结果的方程式。

以下列举几种常见的九宫格计算公式：
1. 求解九宫格中每行、每列和对角线上数字之和相等的情况：
a +
b +
c =
d +
e +
f =
g +
h + i
a + d + g =
b + e + h =
c + f + i
a + e + i = c + e + g
2. 求解九宫格中每行、每列和对角线上数字乘积相等的情况：
a *
b *
c =
d *
e *
f =
g *
h * i
a * d * g =
b * e * h =
c * f * i
a * e * i = c * e * g
3. 九宫格的魔方阵：
2 7 6
9 5 1
4 3 8
在魔方阵中，任意一行、一列或对角线上数字之和均为15。

以上仅为九宫格计算公式的简单示例，实际上还存在很多其他类型的公式和规则，如数独等，具体应用取决于具体的问题和需求。

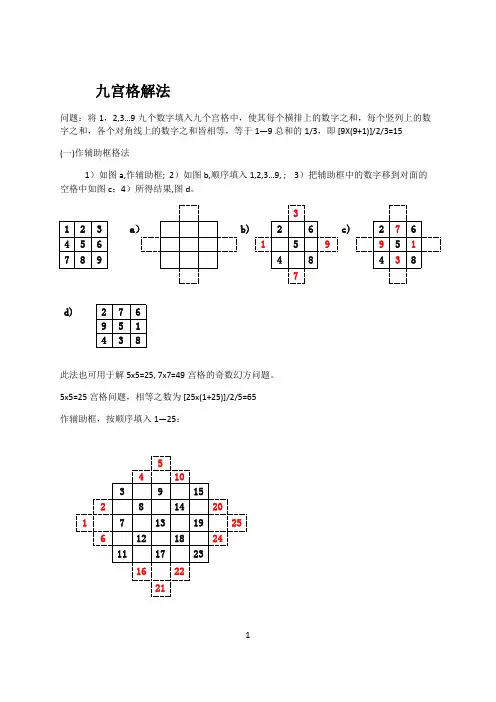
九宫格解法问题：将1，2,3…9九个数字填入九个宫格中，使其每个横排上的数字之和，每个竖列上的数字之和，各个对角线上的数字之和皆相等，等于1—9总和的1/3，即 [9X(9+1)]/2/3=15(一)作辅助框格法1）如图a,作辅助框; 2）如图b,顺序填入1,2,3…9, ; 3）把辅助框中的数字移到对面的空格中如图c；4）所得结果,图d。

a9 d)此法也可用于解5x5=25, 7x7=49宫格的奇数幻方问题。

5x5=25宫格问题，相等之数为 [25x(1+25)]/2/5=65作辅助框，按顺序填入1—25：1020252416 22211将框外的数字移到对面空框中，得结果，题解。

7x7=49宫格问题，相等之数为 [49x(1+49)]/2/7=17571413 21352 421 41 498 484729 37 4536 4443（二）移位挤压法2见下图，将对角上的数字对调图a; 将对角挤压成菱形图b; 归成方形即为解图c.a）b） 2 c）9 74 5 63 18（三）马步法按象棋的马步：向前两步再往右一步将1，2,3…数字顺序填入，图a,b,..；走不通（即此格已被占)时，往右走两步,图c,f；起点的位置，对于九宫格来说有九个，此法只有在右列中位起步才有解。

其余八个位置起步的结果有1或2列，1或2对角不成立。

5x5=25宫格起点在所有位置都有解。

37x7=49宫格起点在所有位置都有解。

4。

实际寻找解的过程为折叠：寻找九宫格摒除解：找到了某数在某一个九宫格可填入的位置只余一个的情形；意即找到了该数在该九宫格中的填入位置。

寻找列摒除解：找到了某数在某列可填入的位置只余一个的情形；意即找到了该数在该列中的填入位置。

基础摒除法的提升方法是区块摒除法，是直观法中使用频率最高的方法之一。

基础摒除法是直观法中最常用的方法，也是在平常解决数独谜题时使用最频繁的方法。

单元排除法使用得当的话，甚至可以单独处理中等难度的谜题。

使用单元排除法的目的就是要在某一单元（即行，列或区块）中找到能填入某一数字的唯一位置，换句话说，就是把单元中其他的空白位置都排除掉。

那么要如何排除其余的空格呢？当然还是不能忘了游戏规则，由于1-9的数字在每一行、每一列、每一个九宫格都要出现且只能出现一次，所以：如果某行中已经有了某一数字，则该行中的其他位置不可能再出现这一数字如果某列中已经有了某一数字，则该列中的其他位置不可能再出现这一数字如果某区块中已经有了某一数字，则该区块中的其他位置不可能再出现这一数字。

唯一解法折叠如果某行已填数字的单元格达到8个，那么该行剩余单元格能填的数字就只剩下那个还没出现过的数字；同理，如果某列已填数字的单元格达到8个，那么该列剩余单元格能填的数字就只剩下那个还没出现过的数字；如果某九宫格已填数字的单元格达到8个，那么该九宫格剩余单元格能填的数字就只剩下那个还没出现过的数字。

这应该算是直观法中最简单的方法了。

基本上只需要看谜题，推理分析一概都用不上，这是因为要使用它所需满足的条件十分明显。

同样，也正是因为它简单，所以只能处理很简单的谜题，或是在处理较复杂谜题的后期才用得上。

唯余解法折叠唯余解法就是某宫格可以添入的数已经排除了8个，那么这个宫格的数字就只能添入那个没有出现的数字.唯余解法是直观法中较不常用的方法。

虽然它很容易被理解，然而在实践中，却不易看出能够使用这个方法的条件是否得以满足，从而使这个方法的应用受到限制。

数独九宫格的解题方法和技巧高级
数独九宫格是一种以九个格子组成的方阵，每个格子可以填入1-9之间的数字，要求每行、每列、每个小九宫格中不能出现重复的数字，让人必须依据提供的部分已填数字，来推断和决定其他位置的数字。

这一般被认为是一种脑力游戏，有时有人用来培养逻辑思维能力、提升记忆力。

数独九宫格的解题方法和技巧高级，主要有以下几种：
1. 暴力解题法：对于一个数独九宫格，首先从每一行、每一列和每一个小九宫格中，找出空格填入的可能性，然后从中一个个尝试，直到找到正确的答案为止。

2. 分析法：在已有的数据基础上，运用一定的技巧，推算出空格填入的数字。

常用的技巧包括：排除法，省去法，对角线法，游戏者法等。

3. 回溯法：即将每一个可能的情况都尝试一遍，当出现不符合规则的情况时回溯，试探其他可能性，直到出现正确的解为止。

4. 高级技巧：比如双排技巧，这是指在某一行或某一列中，只有两个空格可以填入，此时可以把它们两个看作一个组，并根据其他已填的数字，来推断出它们可以填入
的数字。

还有X-Wing技巧，这是指当某一行中的两个空格可填入的数字，在其他行中也同时出现，而其他行中的两个空格又位于同一列时，就可以推断出这两个空格可以填入的数字。

5. 元素法：指将数独九宫格看作一个由81个元素组成的大矩阵，根据已有的数据来推断出其他空格可以填入的数字。

以上就是数独九宫格的解题方法和技巧高级，这些方法和技巧虽然看似复杂，但是只要熟练掌握，就可以很容易地解出数独九宫格。

数独题目九宫格的解法介绍数独题目九宫格的解法介绍1、逐个数填满法。

拿到题目的时候，先大致观察一下在九宫格中出现次数最多的数字，然后看看那一宫，那一行，那一列还缺这个数。

利用每个数在每一行，每一列，每一宫只能出现一次的规则来确定这个数的具体位置。

利用这个方法从1~9慢慢来尝试，减少空格。

2、再填满最少空格的每一宫，每一行，每一列。

当你每一个数都尝试填满之后，九宫格中，空格数就会减少，这时候再看看九宫格中的宫，行，列中，那个出现的空格数比较少，再看其还缺那个数，利用每个数在每一行，每一列，每一宫只能出现一次的规则来确定这个数的具体位置。

3、填满次少空格的宫，行，列。

当最少空格的宫，行，列都无法确定数，这时候，我们的注意力应该放在次少空格的宫，行，列中，看其缺什么数再利用每个数在每一行，每一列，每一宫只能出现一次的规则来确定这个数的具体位置。

4、注意事项知道解题方法后，要多运用，多练习才会有进步想要在数独方面有更大的突破，要多练，多总结自己的解题思路拓展：数独数独是源自18世纪瑞士的一种数学游戏。

是一种运用纸、笔进行演算的逻辑游戏。

玩家需要根据9某9盘面上的已知数字，推理出所有剩余空格的数字，并满足每一行、每一列、每一个粗线宫(3^3)内的数字均含1-9，不重复。

数独盘面是个九宫，每一宫又分为九个小格。

在这八十一格中给出一定的已知数字和解题条件，利用逻辑和推理，在其他的空格上填入1-9的数字。

使1-9每个数字在每一行、每一列和每一宫中都只出现一次，所以又称“九宫格”。

历史发展起源：既然“数独”有一个字是“数”，人们也往往会联想到数学，那就不妨从大家都知道的数学家欧拉说起，但凡想了解数独历史的玩家在网络、书籍中搜索时，共同会提到的就是欧拉的“拉丁方块(Latinsquare)”。

拉丁方块的规则：每一行(Row)、每一列(Column)均含1-N(N即盘面的规格)，不重复。

这与前面提到的标准数独非常相似，但少了一个宫的规则。

九宫格的八种解法如下：
1. 中心求法：首先在九宫格中心的数字开始，天平左右两边标有相同的数字。

即，若在左边的数字框里放一个1，那么右边的数字框中也必须放1。

2. 口诀法：戴九履一，左三右七，二四有肩，八六为足，五居中央。

3. 边线法：把纸上的九个格所有边线都剪出来，让走法线跟走日字有一定的规律（走不出的叫残棋）
4. 角线法：每行、每列以及对角线的各个数字相加等于15，不包括9。

5. 斜线法：斜线法是建立在“十”字的基础上，它适用于两个相对独立的部分。

6. 特殊数字法：九宫格有一些数字的组合是固定的，这些数字是：4、9、2；3、5、7；8、1、6。

7. 唯一解法：填唯一余数法对于小型的九宫格，我们可以把某几个指定数字的位置作为解，然后推导出其他数字的位置。

8. 联除法：在并排的三个九宫格中的两排寻找到相同数字，再利用九宫格得出另一排中该数字位置，该方法适用于只要找齐三宫格做代表。

以上就是九宫格的八种解法。

九宫格难题解法九宫格，也称数独，是一种独立于语言和文化的数学游戏。

它的规则很简单：在一个9×9的方格中填入数字1-9，使得每行、每列和每个3×3的小方格内都恰好包含1-9的数字，且不能重复。

虽然规则简单，但是九宫格的难度却是不小的，很多人在面对九宫格时都感到头疼。

本文将介绍一些九宫格难题的解法，希望能帮助读者提高九宫格的解题能力。

一、基本技巧首先，我们要讲一些基本的九宫格解题技巧。

这些技巧是解决九宫格问题的基础，掌握了这些技巧，对于初级和中级的九宫格难题都能迎刃而解。

1. 唯一候选数法唯一候选数法是指，在某个格子中只有一个数字是符合规则的，这个数字就是该格子的数字。

例如，在某个格子中只能填入数字6，那么这个格子的数字就是6。

这种方法在解决初级和中级的九宫格难题时非常有效。

2. 剪枝法剪枝法是指，在某个格子中填入一个数字后，根据规则来排除其他格子中的数字，从而减少待填数字的数量。

例如，在某个格子中填入数字6后，就可以排除该行、该列和该3×3小方格中所有的数字6，从而缩小了待填数字的范围。

3. 消除法消除法是指，在某行、某列或某个3×3小方格中，已经填入了8个数字，那么这一行、列或小方格中剩下的数字就只有一个，可以直接填入。

例如，在某行中已经填入了1、2、3、4、5、6、7和8，那么这一行中剩下的数字就只有9，可以直接填入。

二、高级技巧除了基本技巧之外，还有一些高级的九宫格解题技巧，这些技巧可以帮助我们解决那些难度较高的九宫格难题。

1. X-Wing法X-Wing法是指，在九宫格中，某两行或两列中只有两个格子可以填入某个数字，那么这两个格子就是该数字的唯一位置。

例如，在九宫格中，某两列中只有2个格子可以填入数字2，那么这两个格子就是数字2的唯一位置。

通过这种方法，我们可以排除其他行或列中的数字2，从而缩小待填数字的范围。

2. Swordfish法Swordfish法是指，在九宫格中，某三行或三列中只有三个格子可以填入某个数字，那么这三个格子就是该数字的唯一位置。

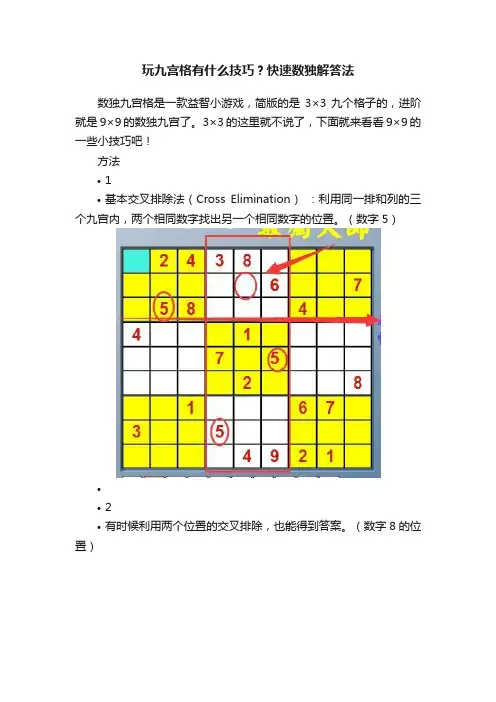
玩九宫格有什么技巧？快速数独解答法数独九宫格是一款益智小游戏，简版的是3×3九个格子的，进阶就是9×9的数独九宫了。

3×3的这里就不说了，下面就来看看9×9的一些小技巧吧！方法•1•基本交叉排除法（Cross Elimination）：利用同一排和列的三个九宫内，两个相同数字找出另一个相同数字的位置。

（数字5）••2•有时候利用两个位置的交叉排除，也能得到答案。

（数字8的位置）••3•三连数空格的利用(Blank Triples)：正中央的九宫内有一整排的三个空格，称为三连空格。

位在同一排其他两个九宫内的数字，应该会在本九宫内的其他位置。

（数字4与7）••4•正中央九宫内的其他数字，应该要出现在其他九宫内与三连空格同一排的位置。

（数字2与3应该在另外两个红筐位置，因而这三连空格的数字为4，6，9，蓝筐内为4。

）••5•三连数满格的利用（Full Triples）：中下位置的九宫内，上排已全有数字，针对右侧九宫的数字4，只能在本九宫的下排位置，以及左侧九宫的上排位置。

••6•单排数字的交叉排除（Straight Line）：中间横排数字2的位置只能在最右侧。

（由于没有相同两数的交叉，很容易被忽略）••7•双位交互排除法：这是很多难题的唯一破解方法(第3点定位)找寻数字7的位置。

上排的3个九宫，7的位置应该在A7或A9。

中排的3个九宫，7的位置应该在F7或F9。

那么右下角九宫的位置只能在H8。

••8•双位交互排除法----再试一次：找寻数字2的位置。

上排的3个九宫，2的位置应该在A2或A3。

下排的3个九宫，2的位置应该在G2或G3。

那么左中侧九宫2的位置只能在D1。

••9•双位交互排除法----双次的第3点定位：找寻数字的位置。

左排的3个九宫，4的位置应该在G1或I 1。

右排的3个九宫，4的位置应该在G8或I8。

再看中央九宫4的位置，只能在F4或F6，那么上排中央九宫4的位置只能在A5。

九宫格解题方法编者武晓鲁例 1. 将下面左边方格中的9 个数填入右边幻方中，使每一行、每一列、每条对角线中的三个数相加的和相等。

【解析】：解法一：先把这九个数按从小到大的顺序依次编号，1、2、3号为“6”，4、5、6 号为“8”，7、8、9号为“10”。

按口诀：九宫者，二四为肩，六八为足，左七右三，戴九履一，五居中央。

对号入座，如下图数字顺序可以填好表格。

解法二：先把这9个数从小到大排列，再算这9 个数的总和，总和÷ 9=中心数8。

每行每列的幻和为24，减8 后，另两数和为16。

利用对称性按下表排列即可。

:1. 在一个3列3行的9宫格中填入-1,+2,-3,+4,-5,+6,-7,+8,-9 使它满足(1) 每行每列每对角数的加起来为负数(2 )每行每列每对角的数的绝对值加起来一样2. 把1、-2、3、-4、5、-6 、7、-8 、9这九个数分别填在途中方框内，使每行，每一列和每条对角线上三个数的和都是正数。

3. 在九宫格里填上适当的数，使每行，每列及对角线上的各数的和都相等，中间那格是12。

4. 右表中有 9 个方格，要求每个方格中填入不相同的数， 使每行、每列及每条对角线上的三个方格中的数之和都相等（5.. 把-1 ，+2， -3 ，+4，-5 ，+6，-7 ，+8，-9 填入右图的方格内，使得每行，每 列，每一斜对角上的三个数都同时满足下列两个条件： 1）三个数的乘积为负数；2）三个数绝对值的和都相等．6、7、8 填入九宫格，把每行、每列及每条对角线上的得到8个和，把这 8个和再相加所得到的和的最大数是什5、3、三个方格中的数相Welcome 欢迎您的下载，资料仅供参考！。

九宫格破解方法介绍九宫格是一种常见的游戏，它要求玩家在一个3x3的格子中填入数字，使得每一行、每一列以及对角线数字的和都相等。

然而，有时候九宫格可能会变得很难解决，玩家需要一些破解方法来辅助他们完成游戏。

本文将探讨几种九宫格破解方法，帮助解决这个问题。

穷举法穷举法是一种基本的解决九宫格问题的方法，它通过尝试所有可能的数字组合，来找到解决方案。

穷举法的步骤如下： 1. 创建一个3x3的格子，并初始化所有的格子为空。

2. 从1到9的数字中选择一个数字。

3. 将选择的数字填入格子中的一个空位置。

4. 检查当前格局是否合法，即每一行、每一列以及对角线的数字和是否相等。

5. 如果当前格局合法，继续填写下一个空位置；如果不合法，则回溯到上一个空位置重新选择数字。

6. 重复步骤3-5，直到填满所有的格子或者找到一个合法的解决方案。

穷举法是一种可行的方法，但是由于要尝试所有可能的数字组合，它在处理复杂的九宫格问题时可能会非常耗时。

剪枝算法剪枝算法是一种优化穷举法的方法，它通过判断当前格局的合法性，来减少尝试的次数，从而提高解决问题的效率。

剪枝算法的步骤如下： 1. 创建一个3x3的格子，并初始化所有的格子为空。

2. 从1到9的数字中选择一个数字。

3. 将选择的数字填入格子中的一个空位置。

4. 如果当前格局合法，继续填写下一个空位置；如果不合法，则回溯到上一个空位置重新选择数字。

5. 重复步骤2-4，直到填满所有的格子或者找到一个合法的解决方案。

在每次选择数字填入格子之前，判断当前格局是否有可能获得合法解决方案。

如果没有可能，提前终止当前分支的搜索，减少不必要的尝试。

剪枝算法的关键在于如何判断当前格局是否有可能获得合法解决方案，这需要一些数学技巧和经验。

通过合理地剪枝，可以大大减少穷举法的尝试次数，提高解决问题的效率。

强化学习强化学习是一种机器学习的方法，可以用来解决九宫格问题。

它通过试错和奖励机制来学习并优化策略，逐步提高解决问题的效率。