2009年中考数学试题汇编之23-圆与圆的位置

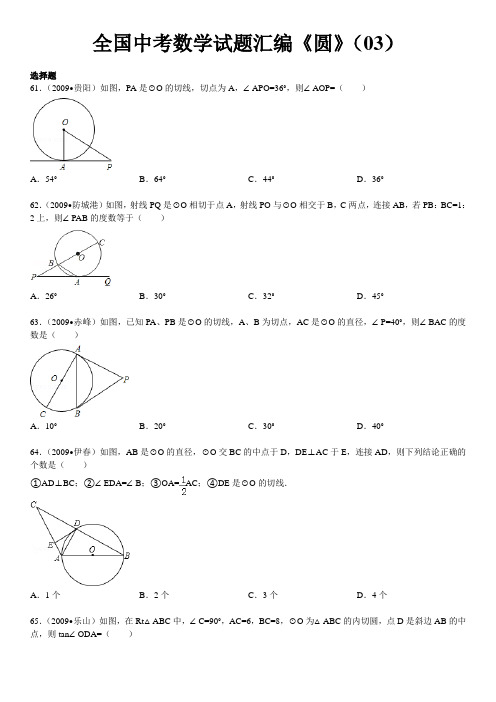
全国中考数学试题汇编《圆》（03）选择题61．（2009•贵阳）如图，PA是⊙O的切线，切点为A，∠APO=36°，则∠AOP=（）62．（2009•防城港）如图，射线PQ是⊙O相切于点A，射线PO与⊙O相交于B，C两点，连接AB，若PB：BC=1：2上，则∠PAB的度数等于（）63．（2009•赤峰）如图，已知PA、PB是⊙O的切线，A、B为切点，AC是⊙O的直径，∠P=40°，则∠BAC的度数是（）64．（2009•伊春）如图，AB是⊙O的直径，⊙O交BC的中点于D，DE⊥AC于E，连接AD，则下列结论正确的个数是（）①AD⊥BC；②∠EDA=∠B；③OA=AC；④DE是⊙O的切线．65．（2009•乐山）如图，在Rt△ABC中，∠C=90°，AC=6，BC=8，⊙O为△ABC的内切圆，点D是斜边AB的中点，则tan∠ODA=（）．C D66．（2009•安徽）△ABC中，AB=AC，∠A为锐角，CD为AB边上的高，I为△ACD的内切圆圆心，则∠AIB的67．（2010•黔南州）已知⊙O1和⊙O2的半径分别为1和4，如果两圆的位置关系为相交，那么圆心距O1O2的取值．C D．74．（2009•陕西）如图，圆与圆之间不同的位置关系有（）76．（2009•泸州）已知⊙O1的半径为5cm，⊙O2的半径为3cm，且圆心距O1O2=7cm，则⊙O1与⊙O2的位置关系是（）280．（2009•桂林）如图是一张卡通图，图中两圆的位置关系是（）81．（2009•佛山）将两枚同样大小的硬币放在桌上，固定其中一枚，而另一枚则沿着其边缘滚动一周，这时滚动的硬币滚动了（）86．（2009•内江）在校运动会上，三位同学用绳子将四根同样大小的接力棒分别按横截面如图（1），（2），（3）所示的方式进行捆绑，三个图中的四个圆心的连线（虚线）分别构成菱形、正方形、菱形，如果把三种方式所用绳子的长度分别用x，y，z来表示，则（）87．（2009•肇庆）如图，⊙O是正方形ABCD的外接圆，点P在⊙O上，则∠APB等于（）D．89．（2009•台州）如图，⊙O的内接多边形周长为3，⊙O的外切多边形周长为3.4，则下列各数中与此圆的周长最接近的是（）．C D．90．（2009•来宾）如图，正方形的四个顶点在直径为4的大圆圆周上，四条边与小圆都相切，AB，CD过圆心O，且AB⊥CD，则图中阴影部分的面积是（）．2009年全国中考数学试题汇编《圆》（03）参考答案与试题解析选择题61．（2009•贵阳）如图，PA是⊙O的切线，切点为A，∠APO=36°，则∠AOP=（）62．（2009•防城港）如图，射线PQ是⊙O相切于点A，射线PO与⊙O相交于B，C两点，连接AB，若PB：BC=1：2上，则∠PAB的度数等于（）x，63．（2009•赤峰）如图，已知PA、PB是⊙O的切线，A、B为切点，AC是⊙O的直径，∠P=40°，则∠BAC的度数是（）C=64．（2009•伊春）如图，AB是⊙O的直径，⊙O交BC的中点于D，DE⊥AC于E，连接AD，则下列结论正确的个数是（）①AD⊥BC；②∠EDA=∠B；③OA=AC；④DE是⊙O的切线．65．（2009•乐山）如图，在Rt△ABC中，∠C=90°，AC=6，BC=8，⊙O为△ABC的内切圆，点D是斜边AB的中点，则tan∠ODA=（）．C DODA=66．（2009•安徽）△ABC中，AB=AC，∠A为锐角，CD为AB边上的高，I为△ACD的内切圆圆心，则∠AIB的（∠=67．（2010•黔南州）已知⊙O1和⊙O2的半径分别为1和4，如果两圆的位置关系为相交，那么圆心距O1O2的取值．C D．74．（2009•陕西）如图，圆与圆之间不同的位置关系有（）76．（2009•泸州）已知⊙O1的半径为5cm，⊙O2的半径为3cm，且圆心距O1O2=7cm，则⊙O1与⊙O2的位置关系280．（2009•桂林）如图是一张卡通图，图中两圆的位置关系是（）81．（2009•佛山）将两枚同样大小的硬币放在桌上，固定其中一枚，而另一枚则沿着其边缘滚动一周，这时滚动的硬币滚动了（）86．（2009•内江）在校运动会上，三位同学用绳子将四根同样大小的接力棒分别按横截面如图（1），（2），（3）所示的方式进行捆绑，三个图中的四个圆心的连线（虚线）分别构成菱形、正方形、菱形，如果把三种方式所用绳子的长度分别用x，y，z来表示，则（）87．（2009•肇庆）如图，⊙O是正方形ABCD的外接圆，点P在⊙O上，则∠APB等于（）D．89．（2009•台州）如图，⊙O的内接多边形周长为3，⊙O的外切多边形周长为3.4，则下列各数中与此圆的周长最接近的是（）．C D．＜圆的周长＜90．（2009•来宾）如图，正方形的四个顶点在直径为4的大圆圆周上，四条边与小圆都相切，AB，CD过圆心O，且AB⊥CD，则图中阴影部分的面积是（）．。

50：圆与圆的位置关系一、选择题1.（天津3分）已知⊙1O 与⊙2O 的半径分别为3 cm 和4 cm ，若12O O =7 cm ，则⊙1O 与⊙2O 的位置关系是(A) 相交 (B) 相离 (C) 内切 (D) 外切 【答案】D 。

【考点】圆与圆位置关系的判定。

【分析】两圆半径之和3+4=7，等于两圆圆心距12O O =7，根据圆与圆位置关系的判定可知两圆外切。

2．（重庆潼南4分）已知⊙O 1与⊙O 2外切，⊙O 1的半径R=5cm ，⊙O 2的半径r=1cm ，则⊙O 1与⊙O 2的圆心距是A 、1cmB 、4cmC 、5cmD 、6cm【答案】D 。

【考点】圆与圆的位置关系。

【分析】根据两圆的位置关系的性质：相切（两圆圆心距离等于两圆半径之和或两圆半径之差），相离（两圆圆心距离大于两圆半径之和），相交（两圆圆心距离小于两圆半径之和大于两圆半径之差），内含（两圆圆心距离小于两圆半径之差）。

由于两圆外切，故两圆圆心距离等于两圆半径之和；5cm ＋1cm ＝6cm 。

故选D 。

3.（广西贺州3分）已知⊙O 1和⊙O 2的半径分别为2和5，如果两圆的位置关系为外离，那么圆心距O 1O 2的取值范围在数轴上表示正确的是【答案】C 。

【考点】两圆的位置关系，在数轴上表示不等式组的解集。

【分析】根据两圆的位置关系的判定：相切（两圆圆心距离等于两圆半径之和），相离（两圆圆心距离大于两圆半径之和），相交（两圆圆心距离小于两圆半径之和），由已知圆心距O 1O 2的取值范围为大于2＋5＝7。

从而根据在数轴上表示不等式组的解集的方法：把每个不等式的解集在数轴上表示出来（＞，≥向右画；＜，≤向左画），在表示解集时“≥”，“≤”要用实心圆点表示；“＜”，“＞”要用空心圆点表示。

故选C。

4..（浙江温州4分）已知线段AB=7cm，现以点A为圆心，2cm为半径画⊙A；再以点B为圆心，3cm为半径画⊙B，则⊙A和⊙B的位置关系A、内含B、相交C、外切D、外离【答案】D。

专题23圆的有关性质（30道）一、单选题1．（2023·辽宁鞍山·统考中考真题）如图，,AC BC 为O 的两条弦，D ，G 分别为,AC BC 的中点，O 的半径为2．若45C ∠=︒，则DG 的长为（）A ．2B ．3C ．32D ．22．（2023·辽宁阜新·统考中考真题）如图，A ，B ，C 是O 上的三点，若9025AOC ACB ∠=︒∠=︒，，则BOC ∠的度数是（）A ．20︒B ．25︒C ．40︒D ．50︒3．（2023·黑龙江哈尔滨·统考中考真题）如图，AB 是O 的切线，A 为切点，连接OA ﹐点C 在O 上，OC OA ⊥，连接BC 并延长，交O 于点D ，连接OD ．若65B ∠=︒，则DOC ∠的度数为（）A ．45︒B ．50︒C ．65︒D ．75︒4．（2023·陕西·统考中考真题）陕西饮食文化源远流长，“老碗面”是陕西地方特色美食之一．图②是从正面看到的一个“老碗”（图①）的形状示意图． AB 是O 的一部分，D 是 AB 的中点，连接OD ，与弦AB 交于点C ，连接OA ，OB ．已知24AB =cm ，碗深8cm CD =，则O 的半径OA 为（）A．13cm B．16cm C 5．（2023·辽宁锦州·统考中考真题）如图，点A 半径为3，则扇形AOC（阴影部分）的面积为（A．23πB．πC6．（2023·湖南娄底·统考中考真题）如图，正六边形线1l、2l的夹角为60︒，则图中的阴影部分的面积为（A．433π-B．4332π-C7．（2023·辽宁沈阳·统考中考真题）如图，四边形的长是（）A ．πB ．23πC ．2πD ．4π8．（2023·四川雅安·统考中考真题）如图，某小区要绿化一扇形OAB 空地，准备在小扇形OCD 内种花在其余区域内（阴影部分）种草，测得120AOB ∠=︒，15m OA =，10m OC =，则种草区域的面积为（）A ．225πm 3B ．2125πm 3C ．2250πm 3D ．2125m 39．（2023·山东泰安·统考中考真题）如图，O 是ABC 的外接圆，半径为4，连接OB ，OC ，OA ，若40CAO ∠=︒，70ACB ∠=︒，则阴影部分的面积是（）A ．4π3B ．8π3C ．16π3D ．32π310．（2023·山东泰安·统考中考真题）如图，AB 是O 的直径，D ，C 是O 上的点，115ADC ∠=︒，则BAC ∠的度数是（）A ．25︒B ．30︒C ．35︒D ．40︒11．（2023·黑龙江牡丹江·统考中考真题）如图，A ，B ，C 为O 上的三个点，4AOB BOC ∠=∠，若60ACB ∠=︒，则BAC ∠的度数是（）A．2πB．4 3π13．（2023·辽宁营口·统考中考真题）如图所示，30BAD∠=︒，则ACB∠的度数是（A．50︒B．40︒14．（2023·湖北鄂州·统考中考真题）如图，在的中点，以O为圆心，OB长为半径作半圆，交A．3533π-B．53-15．（2023·甘肃兰州·统考中考真题）我国古代天文学确定方向的方法中蕴藏了平行线的作图法．如《淮南子天文训》中记载：“正朝夕：先树一表东方；操一表却去前表十步，以参望日始出北廉．日直入，又树一表于东方，因西方之表，以参望日方入北康．则定东方两表之中与西方之表，则东西也．言叙述作图方法：已知直线a和直线外一定点径作圆，交直线a于点M，N；（取其中点C，过O，C两点确定直线A ．35︒B ．30︒C ．25︒D ．20︒16．（2023·内蒙古赤峰·统考中考真题）如图，圆内接四边形ABCD 中，105BCD ∠=︒，连接OB ，OC ，OD ，BD ，2BOC COD ∠=∠．则CBD ∠的度数是（）A ．25︒B ．30︒C ．35︒D ．40︒17．（2023·内蒙古·统考中考真题）如图，O 是锐角三角形ABC 的外接圆，,,OD AB OE BC OF AC ⊥⊥⊥，垂足分别为,,D E F ，连接,,DE EF FD ．若 6.5,DE DF ABC +=△的周长为21，则EF 的长为（）A ．8B ．4C ．3.5D ．318．（2023·湖南·统考中考真题）如图，圆锥底面圆的半径为4，则这个圆锥的侧面展开图中 AA '的长为（）A ．4πB ．6πC ．8πD ．16π19．（2023·吉林·统考中考真题）如图，AB ，AC 是O 的弦，OB ，OC 是O 的半径，点P 为OB 上任意A ．70︒20．（2023·内蒙古通辽点C 是半径OB 上一动点，若A ．26π+B 二、填空题21．（2023·江苏·统考中考真题）如图，4AC =，则O 的直径22．（2023·江苏南通·统考中考真题）如图，则ACD ∠=度．23．（2023·山东济南·统考中考真题）则阴影部分的面积为（结果保留π）．24．（2023·宁夏·统考中考真题）如图，四边形ABCD 内接于O ，延长AD 至点E ，已知140AOC ∠=︒，那么CDE ∠=︒．25．（2023·湖南·统考中考真题）如图，点A ，B ，C 在半径为2的O 上，60ACB ∠=︒，OD AB ⊥，垂足为E ，交O 于点D ，连接OA ，则OE 的长度为．26．（2023·江苏徐州·统考中考真题）如图，沿一条母线将圆锥侧面剪开并展平，得到一个扇形，若圆锥母线l =6，扇形的圆心角120θ=°，则该圆锥的底面圆的半径r 长为．27．（2023·山东东营·统考中考真题）“圆材埋壁”是我国古代数学名著《九章算术》中的一个问题：“今有圆材，埋在壁中，不知大小，以锯锯之，深一寸，锯道长一尺．问：径几何？”．用现在的几何语言表达即：如图，CD 为O 的直径，弦AB CD ⊥，垂足为点E ，1CE =寸，10AB =寸，则直径CD 的长度是寸．29．（2023·吉林·统考中考真题）如图是圆心，半径r 为15m 留π）30．（2023·广东深圳·统考中考真题）如图，交于点D ，若20ADC ∠=︒，则BAD ∠=。

一、选择题1. （2009年娄底）如图，AB是。

0的弦，ODLAB于D交于E,则下列说法错误的是（）A. AD=BD B ACB2 AOE C. AEBE D . OD=DE2. （2009恩施市）16.如图6, ©0的直径AB垂直弦CD于P，且P是半径OB 的中点，CD = 6cm，则直径AB的长是（）A. 2、3cm B . 3、、2cm C . 4.2cm D . 4,3cm3. （2009年甘肃白银）如图2，© O的弦AB=6，M是AB上任意一点，且OM 最小值为4，则© O的半径为（）4 . （2009年甘肃庆阳）如图5，© O的半径为5,弦AB=8，M是弦AB上的动点，贝U OM不可能为（）A . 2B . 3C . 4D . 5【关键词】圆周角和圆心角 【答案】D5. （ 2009年广西南宁）如图3, AB 是O O 的直径，弦CD _AB 于点E , CDB =30 °O O 的半径为■. 3cm ，则弦CD 的长为3cm 2B . 3cmC . 2、3cmD . 9cm6. （ 2009年孝感）如图，O O 是厶ABC 的外接圆，已知/ B=60° 的度数是（） A. 15° B . 30° C . 45° D . 60°7. （2009泰安）如图O 的半径为1，AB 是。

O 的一条弦，且 AB= . 3，则弦AB 所对圆周角的度数为60°（ C ） 8. （2009年天津市）如图, 为（ ） A . 28 ° B . 56°30°或 150°(D ) 60° 或 120°△ ABC 内接于 O O ,若.OAB=28°, C . 60° D . 62°则.C 的大小B9. （2009南宁）如图，AB 是O O 的直径，弦CD _AB 于点 E , CDB =30°O O 的半径为.Ecm , 则弦CD 的长为( )A . 3cmB . 3cmC . 2 . 3cmD . 9cm210. （2009年湘西自治州）14. O O 的半径为10cm ,弦AB = 12cm ,则圆心到 AB 的距离为（）A . 2cmB . 6cmC . 8cmD . 10cm【关键词】圆的计算，弦，点到直线的距离 【答案】C11. （2009白银市）8.如图2，O O 的弦AB=6，M 是AB 上任意一点，且 OM 最 小值为4，则O O 的半径为（ ） A . 5 B . 4 C . 3 D . 2【关键词】圆的相关概念、点到直线的距离 【答案】A12. （2009年清远）如图，AB 是O 0的直径，弦CD 一 AB 于点E ，连结OC ，若贝U tan COE=( C . 3D . 4 13 . （2009年长春）两圆的半径分别为2和5,圆心距为7,则这两圆的位置关 系为（ ） A .夕卜离 B .夕卜切 C .相交 D .内切OC =5,CD =8， B . 45【关键词】圆周角和圆心角 【答案】B14. （2009年安徽）如图，弦CD 垂直于O O 的直径AB ,垂足为H ，且CD = 2 2 ,15.（ 2009年安徽）△ ABC 中，AB = AC ,/ A 为锐角，CD 为AB 边上的高，IACD 的内切圆圆心，则/ AIB 的度数是【 】 A . 120° B . 125° C . 135° D . 150° 【关键词】与圆有关的综合题 【答案】C16. （2009年福州）如图，弧 AD 是以等边三角形 ABC 一边AB 为半径的四分之一圆周， P为弧AD 上任意一点，若 AC=5则四边形ACBP 周长的最大值是（ ）A. 15 B . 20 C . 15+5、2D . 15+5,5【关键词】圆周角和圆心角【关键词】等边三角形，勾股定理，同圆的半径相等17. （2009年重庆）如图，O O 是厶ABC 的外接圆, 则• A 等于（ ） AB 是直径.若 BOC = 80°， C. 40° D. 30 B. 50【答案】C.18. （2009年甘肃定西）如图2,00的弦AB=6, M 是AB 上任意一点，且 OM 最 小值为4，则。

中考模拟分类汇编圆一、选择题： 1、（2009·浙江温州·模拟1） 图①、图②、图③是三种方法将6根钢管用钢丝捆扎的截面图，三种方法所用的钢丝长分别为a,b,c, （不记接头部分），则a, b, c,的大小关系为（ ）。

A 、a=b >c B. a=b=c C. a<b<c D. a>b>c 答案：B2、（2009·浙江温州·模拟2）如图，A 、B 是⊙O 上的两点，AC 是⊙O 的切线，∠OBA ＝70°，则∠BAC 等于（ ）A ．20°B ．10°C ．70°D ．35° 答案：A3、（2009·浙江温州·模拟3）一个圆锥的底面半径为3㎝，它的侧面积为15π㎝2，那么这个圆锥的高线长为A 、6㎝B 、8㎝C 、4㎝D 、4π㎝ 答案：C4、（2009·浙江温州·模拟4）如图，AB 是O 的直径，20C ∠=，则BOC ∠的度数是（ ） A ．10B ． 20C ． 30D ． 40答案：D5、（2009·浙江温州·模拟5）在半径为18的圆中，120°的圆心角所对的弧长是（ ） A ．12π B ．10π C ．6π D ．3π答案：A 6、（2009·浙江温州·模拟6）如果圆锥的母线长为6cm ，底面圆半径为3cm ，则这个圆锥的侧面积为（ ）A. 29cm π B. 218cm πC. 227cm πD. 236cm π答案：B7、（2009·浙江温州·模拟6）如图，已知⊙O 的弦AB 、CD 相交于点E ，的度数为60°，的度数为100°，则∠AEC 等于 （ ）（A ）60° （B ）100° （C ）80° （D ）130°答案：C图① 图②O A BC （第2题）第4题图8、（2009·浙江温州·模拟7）如图，在⊙Ｏ中，弦ＡＢ，ＣＤ相交于点Ｅ。

第六章圆第二十三讲圆的有关概念及性质【基础知识回顾】一、圆的定义及性质：1、圆的定义：⑴形成性定义：在一个平面内，线段OA绕它固定的一个端点O旋转一周，另一个端点A随之旋转形成的图形叫做圆，固定的端点叫线段OA叫做⑵描述性定义：圆是到定点的距离等于的点的集合2、弦与弧：弦：连接圆上任意两点的叫做弦弧：圆上任意两点间的叫做弧，弧可分为、、三类3、圆的对称性：⑴轴对称性：圆是轴对称图形，有条对称轴，的直线都是它的对称轴⑵中心对称性：圆是中心对称图形，对称中心是【名师提醒：1、在一个圆中，圆心决定圆的半径决定圆的2、直径是圆中的弦，弦不一定是直径；3、圆不仅是中心对称图形，而且具有旋转性，即绕圆心旋转任意角度都被与原来的图形重合】二、垂径定理及推论：1、垂径定理：垂直于弦的直径，并且平分弦所对的。

2、推论：平分弦（）的直径，并且平分弦所对的。

【名师提醒：1、垂径定理及其推论实质是指一条直线满足：⑴过圆心⑵垂直于弦⑶平分弦⑷平分弦所对的优弧⑸平分弦所对的劣弧五个条件中的两个，那么可推出其余三个，注意解题过程中的灵活运用2、圆中常作的辅助线是过圆心作弦的线（即弦心距）。

3、垂径定理常用作计算，在半径r、弦a、弦心d和弓高h中已知其中两个量可求另外两个量。

】三、圆心角、弧、弦之间的关系：1、圆心角定义：顶点在的角叫做圆心角2、定理：在中，两个圆心角、两条弧、两条弦中有一组量它们所对应的其余各组量也分别【名师提醒：注意：该定理的前提条件是“在同圆或等圆中”】四、圆周角定理及其推论：1、圆周角定义：顶点在并且两边都和圆的角叫圆周角2、圆周角定理：在同圆或等圆中，圆弧或等弧所对的圆周角都等于这条弧所对的圆心角的推论1、在同圆或等圆中，如果两个圆周角那么它们所对的弧推论2、半圆（或直弦）所对的圆周角是，900的圆周角所对的弦是【名师提醒：1、在圆中，一条弦所对的圆心角只有一个，而它所对的圆周角有个，是类，它们的关系是，2、作直径所对的圆周角是圆中常作的辅助线】五、圆内接四边形：定义：如果一个多边形的所有顶点都在圆上，这个多边形叫做，这个圆叫做。

九年级数学同步练习：与圆有关的位置关系例1、：⊙A、⊙B、⊙C的半径区分为2、3、5，且两两相切，求AB、BC、CA的长解：分类讨论：(1)当⊙A与⊙B外切时，分4种状况：①如图1，AB=5，BC=8，CA=7;②如图2，AB=5，BC=2，CA=3;③如图3，AB=5，BC=8，CA=3;④如图4，AB=5，BC=2，CA=7;(2)当⊙A与⊙B内切时，分2种状况：①如图5，AB=1，BC=2，CA=3;②如图6，AB=1，BC=8，CA=7.说明：此题需求两次分类，但关键是以什么为规范停止分类，才干不重不漏.例2、两个等圆⊙Ol和⊙O2相交于A，B两点，⊙Ol经O2。

求OlAB的度数.剖析：由所学定理可知，O1O2是AB的垂直平分线，又⊙O1与⊙O2是两个等圆，因此连结O1O2和AO2，AO1，△O1AO2构成等边三角形，同时可以推证⊙Ol和⊙O2构成的图形不只是以O1O2为对称轴的轴对称图形，同时还是以AB为对称轴的轴对称图形.从而可由OlAO2=60，推得OlAB=30.解：⊙O1经过O2，⊙O1与⊙O2是两个等圆OlA= O1O2= AO2O1AO2=60，又ABO1O2OlAB =30.例3、R1、R2为两圆半径，圆心距d=5，且R1，R2，R1-R2是方程x3-6x2+11x-6=0的三个根，试判别以R1，R2为半径的两圆的位置关系。

剖析：经过解方程，把R1，R2，R1-R2都求出来以后，依据两圆位置关系的判定方法，即可作出结论。

解：将方程x3-6x2+11x-6=0变形得：(x-1)(x-2)(x-3)=0解得：x1=1，x2=2，x3=3∵R1，R2，R1-R2是方程的根(1)当R1=3，R2=2，R1-R2=1时，两圆外切。

(2)当R1=3，R2=1，R1-R2=2时，两圆外离。

故由(1)(2)可得：两圆的位置关系是外切或外离。

例4、：如图，⊙O1和⊙O2外切于P，直线APC交⊙O1于点A，交⊙O2于C，AB切⊙O2于B，设⊙O1的半径为r1，⊙O2的半径为r2。