浙江省重点中学2014-2015学年高二下期末考试数学(文理)试题及答案

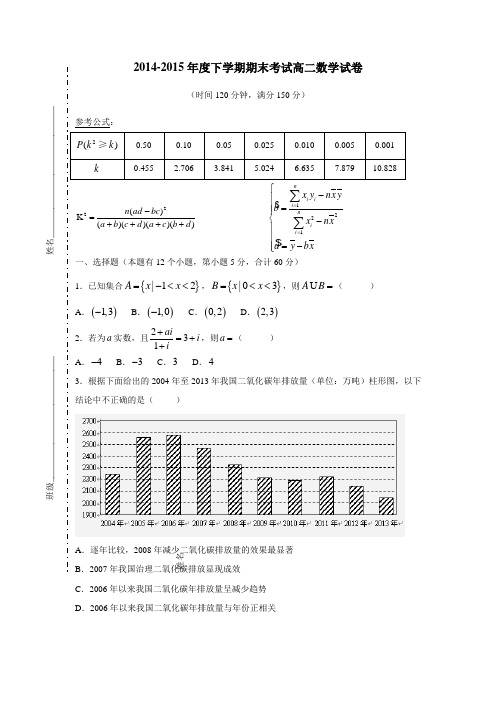
12i nb ==∑B =（ C ．2006年以来我国二氧化碳年排放量呈减少趋势 D ．2006年以来我国二氧化碳年排放量与年份正相关班级__________________________ 姓名___________________________4．一个正方体被一个平面截去一部分后，剩余部分的三视图如右图，则截去部分体积与剩余部分体积的比值为（ ）1.8A 1.7B 1.6C 1.5D 5．设n S 是等差数列{}n a 的前n 项和，若1353a a a ++=，则5S =（ ）A ．5B ．7C ．9D ．11 6．已知()0,1a =-，()1,2b =-，则(2)a b a +=（ ）A ．1-B ．0C ．1D ．2 7．右边程序框图的算法思路来源于我国古代数学名著《九章算术》中的“更相减损术”，执行该程序框图，若输入的,a b 分别为14,18,则输出的a 为（ ）.0A .2B .4C .14D8．已知等比数列{}n a 满足114a =，()35441a a a =-，则2a =（ ）.2A .1B 1.2C 1.8D9.已知长方形ABCD 的边AB=2，BC=1，O 是AB 的中点，点P 沿着边BC ，CD 与DA 运动，∠BOP=x 。

将动点P 到AB 两点距离之和表示为x 的函数f （x ），则f （x ）的图像大致为( )10. 在回归直线方程表示回归系数中b bx a y,ˆ+= （ ）A ．当0x =时，y 的平均值B ．当x 变动一个单位时，y 的实际变动量A B C DC ．当y 变动一个单位时，x 的平均变动量D ．当x 变动一个单位时，y 的平均变动量11. 在对分类变量X, Y 进行独立性检验时,算得2k =7有以下四种判断(1) 有99﹪的把握认为X 与Y 有关; (2)有99﹪的把握认为X 与Y 无关;(3)在假设H 0:X 与Y 无关的前提下有99﹪的把握认为X 与Y 有关; (4)在假设H 1: X 与Y 有关的前提下有99﹪的把握认为X 与Y 无关 .以上4个判断正确的是 （ ）A ． (1)、(4)B ． (2)、(3)C ． (3)D ． (4)12. 下面几种推理是类比推理的是( )A ．两条直线平行，同旁内角互补，如果A ∠和B ∠是两条平行直线的同旁内角，则180=∠+∠B AB ．由平面向量的运算性质，推测空间向量的运算性质C ．某校高二级有20个班，1班有51位团员，2班有53位团员，3班有52位团员，由此可以推测各班都超过50位团员D ．一切偶数都能被2整除，1002是偶数，所以1002能被2整除二、填空题（本题共4个小题，第个小题5分，合计20分） 13. 已知函数()32f x ax x =-的图像过点（-1,4）,则a = ．14. 某大学的信息中心A 与大学各部门、各院系B ，C ，D ，E ，F ，G ，H ，I 之间拟建立信息联网工程，实际测算的费用如图所示（单位：万元）.请观察图形，可以不建部分网线，而使得中心与各部门、院系彼此都能连通（直接或中转），则最少的建网费用（万元）是_____________________.15. 若x ,y 满足约束条件50210210x y x y x y +-≤⎧⎪--≥⎨⎪-+≤⎩,则z =2x +y 的最大值为 ．16. 如图,用与底面成30︒角的平面截圆柱得一椭圆截线,则该椭圆的离心率为_______.三、解答题（17题10分，其他的题12分，合计70分）17．（本小题满分12分）△ABC 中D 是BC 上的点,AD 平分∠BAC 且BD =2DC .（I ）求sin sin BC∠∠ ；（II ）若60BAC ∠=,求B ∠.18．（本小题满分12分）某公司为了了解用户对其产品的满意度,从A ,B 两地区分别随机调查了40个用户,根据用户对其产品的满意度的评分,得到A 地区用户满意度评分的频率分布直方图和B 地区用户满意度评分的频率分布表.（I ）在答题卡上作出B 地区用户满意度评分的频率分布直方图,并通过此图比较两地区满意度评分的平均值及分散程度,（不要求计算出具体值,给出结论即可）5060809010070满意度评分频率/组距0.0050.010 0.015 0.020 0.025 0.0350.030 B 地区满意度调查频率分布直方图（II）根据用户满意度评分,将用户的满意度评分分为三个等级：估计那个地区的用户的满意度等级为不满意的概率大,说明理由.19．（本小题满分12分）一台机器使用的时间较长，但还可以使用，它按不同的转速生产出来的某机械零件有一些会有缺点，每小时生产有缺点零件的多少，随机器的运转的速度而变化，下表为抽样试验的结果：（（2）如果y对x有线性相关关系，求回归直线方程；20．（本小题满分12分）在对人们休闲的一次调查中，共调查了124人，其中女性70人，男性54人。

2014-2015学年浙江省杭州市高二（下）期末数学试卷一、选择题（共24小题，每小题2分，满分52分）1．设集合M={1，3}，N={1，2，3}，则M∪N=（）A．{2} B．{1，2} C．{1，3} D．{1，2，3}2．函数f（x）=的定义域是（）A．[0，+∞）B．[0，1）∪（1，+∞）C．（0，1）D．（0，1）∪（1，+∞）3．向量=（m，2），=（n，﹣1），若⊥，则mn=（）A．B．﹣C． 2 D．﹣24．设数列是{a n}（n∈N*）是等差数列，若a1+a5=4，则a3=（）A．1 B．C．2 D． 45．若直线y=2x﹣b在x轴上的截距为1，则b=（）A．1 B．﹣1 C．D．26．命题P：“对于任意的x∈R，cosx≥1”，则命题P的否定是（）A．存在x0∈R，cosx0≥1 B．对于任意的x∈R，cosx＜1C．存在x0∈R，cosx0＜1 D．对于任意的x∈R，cosx＞17．计算：log225•log52=（）A．3 B． 4 C． 5 D． 68．cos690°=（）A．B．C．D．9．设正实数a，b满足a+2b=ab，则a+b的最小值为（）A．B．4C．3+2D．610．设O为坐标原点，直线l经过点P（1，1）且与OP垂直，则直线l的方程为（）A．x+y+2=0 B．x+y﹣1=0 C．x+y=0 D．x+y﹣2=011．下面各命题中，正确的是（）A．过平面外一点作与这个平面垂直的平面有且只有一个B．若两条直线与一个平面所成的角相等，则这两条直线平行C ． 若一个平面内有无数条直线与另一个平面平行，则这两个平面平行D ． 若两个平面平行，则其中一个平面内的所有直线都与另一个平面平行12．设函数f （x ）=sin2x+cos2x ，x ∈R ，则函数f （x ）的最小正周期为（ ）A ． 2πB ．C ． πD ．13．已知a ∈R ，则“a 2＜a ”是“a ＜1”的（ ）A ． 充分而不必要条件B ． 必要而不充分条件C ． 充要条件D ． 既不充分也不必要条件14．θ∈R ，则方程x 2+=4表示的曲线不可能是（ ）A ． 圆B ． 椭圆C ． 双曲线D ． 抛物线15．若某空间几何体的三视图如图所示，则该几何体的体积为（ ）A ．B ． 8C ． 4D ．16．若函数f （x ）是定义在R 上的奇函数，则函数F （x ）=|f （x ）|+f （|x|）的图象一定关于（ ）A ． x 轴对称B ． y 轴对称C ． 原点对称D ． 直线y=x 对称17．若实数x ，y 满足不等式组，则z=x+3y 的最大值是（ ）A ． ﹣3B ．C ． 11D ． 918．已知正四面体ABCD 中，E 是AB 的中点，则异面直线CE 与BD 所成角的余弦值为（ ）A ．B ．C ．D ．19．设函数f （x ）=1﹣|x|，g （x ）=﹣1+|x|，则函数F （x ）=f[g （x ）]的图象是（ ）A．B．C．D．20．某转弯路段为四分之一圆环，圆环道路外侧均匀栽种了10棵树（如图所示），小李在半径OA的延长线上一点C处观察到第四棵树（P点），第七棵树（Q点）与点C在同一条直线上，并测得AC=100米，则此弧形道路的大圆半径OA的长为（）A．100米B．100（+1）米C．200米D．100（+）米21．设函数f（x）=sinωπx（ω＞0）的图象在区间[0，]上有两个最高点和一个最低点，则（）A．3≤ω＜5 B．4≤ω＜6 C．5≤ω＜7 D．6≤ω＜822．设点F为双曲线C：﹣=1（a＞0，b＞0）的右焦点，直线l过原点且与双曲线C 相交于A，B两点，若双曲线C的右顶点M恰为△ABF的重心，则双曲线C的离心率为（）A．B．C．2 D．323．设P是曲线y=上的点，若对曲线y=x+（a＞0，x＞0）上的任意一点Q，恒有|PQ|≥1，则a的取值范围是（）A．[﹣1，+∞）B．[2﹣2，+∞）C．[，+∞）D．（0，2﹣2]24．已知正方体ABCD﹣A1B1C1D1的棱长为3，点O在棱AA1上，且OA1=2OA，平面α过点O且垂直于AA1，点P在平面α内，PQ⊥A1C1于点Q．若PA=PQ，则P点的轨迹是（）A．圆B．椭圆C．抛物线D．两条直线二、填空题（共6小题，每小题3分，满分18分）25．设函数f（x）=，则f[f（﹣2）]=．26．已知等差数列{a n}前n项和为S n，且满足=3，则数列{a n}的公差为．27．若是奇函数，则a=．28．设向量⊥，=+3．若向量与+的夹角为θ，则cosθ的最小值等于．29．若圆心在x轴上的圆C同时经过椭圆Γ：+=1（a＞b＞0）的左焦点F，上顶点B 和右顶点A，则椭圆Γ的离心率为．30．设x，y∈R，集合A={（x，y）|ax+by+1=0}，B={（x，y）|x2+y2=1}，且A∩B是一个单元素集合，若对所有的（a，b）∈{（a，b）|a＜0，b＜0}，则集合C={（x，y）|（x﹣a）2+（y﹣b）2≤1}所表示的图形的面积等于．三、解答题（共4小题，满分30分）31．若{a n}是等比数列，a2=2，a5=．（Ⅰ）求数列{a n}的通项公式；（Ⅱ）求和：a1a2+a2a3+…+a n a n+1（n∈N*）．32．在正三棱柱ABC﹣A1B1C1中，AB=4，AA1=3，点D是AC的中点，点E在棱BC上（不含端点），且DE⊥B1E．（Ⅰ）求证：平面B1DE⊥平面BCC1B1；（Ⅱ）求直线BD与平面B1DE所成角的正弦值．33．设抛物线C：y2=x与直线l交于A，B两点（异于原点O），以AB为直径的圆恰好经过原点O．（Ⅰ）求证：直线l过定点．（Ⅱ）求△OAB面积的最小值．34．设x1，x2是函数f（x）=ax2+（b﹣1）x+1（a＞0，b∈R）的两个不同零点．（Ⅰ）若x1=1，对任意x∈R，都有f（2﹣x）=f（x+2），求f（x）；（Ⅱ）若a≥2，x1﹣x2=﹣2，当x∈（x1，x2）时，g（x）=﹣f（x）+2（x2﹣x）的最大值为h（a），求h（a）的最小值．2014-2015学年浙江省杭州市高二（下）期末数学试卷参考答案与试题解析一、选择题（共24小题，每小题2分，满分52分）1．设集合M={1，3}，N={1，2，3}，则M∪N=（）A．{2} B．{1，2} C．{1，3} D．{1，2，3}考点：并集及其运算．专题：集合．分析：直接利用并集的定义求解即可．解答：解：集合M={1，3}，N={1，2，3}，则M∪N={1，2，3}．故选：D．点评：本题考查并集的运算，基本知识的考查．2．函数f（x）=的定义域是（）A．[0，+∞）B．[0，1）∪（1，+∞）C．（0，1）D．（0，1）∪（1，+∞）考点：函数的定义域及其求法．专题：函数的性质及应用．分析：根据函数成立的条件进行求解即可．解答：解：要使函数有意义，则，即，即函数的定义域为[0，1）∪（1，+∞），故选：B．点评：本题主要考查函数的定义域的求解，要求熟练掌握常见函数成立的条件．3．向量=（m，2），=（n，﹣1），若⊥，则mn=（）A．B．﹣C． 2 D．﹣2考点：平面向量数量积的运算．专题：平面向量及应用．分析：由向量垂直数量积为0 得到关于mn的等式．解答：解：因为向量=（m，2），=（n，﹣1），若⊥，所以=0，即mn﹣2=0，所以mn=2；故选：C．点评：本题考查了向量垂直，数量积为0．属于基础题．4．设数列是{a n}（n∈N*）是等差数列，若a1+a5=4，则a3=（）A．1 B．C．2 D． 4考点：等差数列的通项公式．专题：等差数列与等比数列．分析：根据题意和等差数列的性质即可求出a3的值．解答：解：∵数列是{a n}（n∈N*）是等差数列，a1+a5=4，∴由等差数列的性质得，2a3=a1+a5=4，解得a3=2，故选：C．点评：本题考查了等差数列的性质的灵活应用，属于基础题．5．若直线y=2x﹣b在x轴上的截距为1，则b=（）A．1 B．﹣1 C．D．2考点：直线的斜截式方程．专题：直线与圆．分析：根据直线y=2x﹣b在x轴上的截距为1，得到y=0时x=1，由此得到b．解答：解：因为直线y=2x﹣b在x轴上的截距为1，所以0=2×1﹣b，所以b=2；故选：D．点评：本题考查了直线在坐标轴上的截距；属于基础题．6．命题P：“对于任意的x∈R，cosx≥1”，则命题P的否定是（）A．存在x0∈R，cosx0≥1 B．对于任意的x∈R，cosx＜1C．存在x0∈R，cosx0＜1 D．对于任意的x∈R，cosx＞1考点：命题的否定．专题：简易逻辑．分析：直接利用全称命题的否定是特称命题，写出经过即可．解答：解：因为全称命题的否定是特称命题，所以，命题P：“对于任意的x∈R，cosx≥1”，则命题P的否定是：存在x0∈R，cosx0＜1．故选：C．点评：本题考查命题的否定全称命题与特称命题的否定关系，基本知识的考查．7．计算：log225•log52=（）A．3 B． 4 C． 5 D． 6考点：对数的运算性质．专题：函数的性质及应用．分析：根据换底公式，化简计算即可．解答：解：log225•log52=•=3．故选：A．点评：本题考查了对数的运算性质，属于基础题．8．cos690°=（）A．B．C．D．考点：运用诱导公式化简求值．专题：三角函数的求值．分析：利用利用诱导公式把要求的式子化为cos（﹣30°），从而求得结果．解答：解：cos690°=cos（720°﹣30°）=cos（﹣30°）=，故选C．点评：本题主要考查利用诱导公式进行化简求值，属于基础题．9．设正实数a，b满足a+2b=ab，则a+b的最小值为（）A．B．4C．3+2D．6考点：基本不等式在最值问题中的应用．专题：不等式的解法及应用．分析：化简已知条件，利用基本不等式求解最小值即可．解答：解：a+2b=ab，可得：，a+b=（a+b）（）=3+≥3+2，当且仅当a==2+时取等号．a+b的最小值：3+2．故选：C．点评：本题考查基本不等式的应用，考查计算能力，注意等号成立的条件．10．设O为坐标原点，直线l经过点P（1，1）且与OP垂直，则直线l的方程为（）A．x+y+2=0 B．x+y﹣1=0 C．x+y=0 D．x+y﹣2=0考点：直线的一般式方程与直线的垂直关系．专题：直线与圆．分析：求出直线的斜率，然后求解直线方程即可．解答：解：O为坐标原点，直线l经过点P（1，1）且与OP垂直，则直线l的斜率为：﹣1，直线l的方程为：y﹣1=﹣（x﹣1），即x+y﹣2=0．故选：D．点评：本题考查直线方程的求法，基本知识的考查．11．下面各命题中，正确的是（）A．过平面外一点作与这个平面垂直的平面有且只有一个B．若两条直线与一个平面所成的角相等，则这两条直线平行C．若一个平面内有无数条直线与另一个平面平行，则这两个平面平行D．若两个平面平行，则其中一个平面内的所有直线都与另一个平面平行考点：命题的真假判断与应用．专题：空间位置关系与距离．分析：A，B，C列举所有情况，D考虑线面平行的性质定理及平行公理即可．解答：解：A、过平面外一点作与这个平面垂直的平面有无数个，故A错误；B、若两条直线和同一个平面所成的角相等，则这两条直线平行、相交或异面，故A错误；C、若一个平面内有无数条直线与另一个平面平行，则这两个平面可能相交或平行，故C错误；D、若两个平面平行，则其中一个平面内的所有直线都与另一个平面平行，故D正确；故选：D．点评：本题主要考查了空间线面、面面位置关系，要求熟练掌握相应的定义和定理，注意定理成立的条件．12．设函数f（x）=sin2x+cos2x，x∈R，则函数f（x）的最小正周期为（）A．2π B．C．π D．考点：两角和与差的正弦函数；三角函数的周期性及其求法．专题：三角函数的图像与性质．分析：利用两角和的正弦函数化简已知条件，利用正弦函数的周期求解即可．解答：解：函数f（x）=sin2x+cos2x=2sin（2x+），函数f（x）的最小正周期为：．故选：C．点评：本题考查两角和与差的三角函数，三角函数的周期的求法，考查计算能力．13．已知a∈R，则“a2＜a”是“a＜1”的（）A．充分而不必要条件B．必要而不充分条件C．充要条件D．既不充分也不必要条件考点：必要条件、充分条件与充要条件的判断．专题：简易逻辑．分析：根据充分条件和必要条件的定义结合不等式的性质，进行判断即可．解答：解：由a2＜a得0＜a＜1，则“a2＜a”是“a＜1”的充分不必要条件，故选：A点评：本题主要考查充分条件和必要条件的判断，根据不等式的性质是解决本题的关键．14．θ∈R，则方程x2+=4表示的曲线不可能是（）A．圆B．椭圆C．双曲线D．抛物线考点：曲线与方程．专题：计算题．分析：先确定sinθ的范围，进而可判断方程可表示圆，双曲线，椭圆，由于不含一次项，故方程不表示抛物线．解答：解：由题意，sinθ∈[﹣1，0）∪（0，1]∴sinθ=1时，方程表示圆；sinθ∈[﹣1，0）时，方程表示双曲线；sinθ∈（0，1]，方程表示椭圆．由于不含一次项，曲线对应的方程至少有两条对称轴，而抛物线只有一条对称轴，故方程不表示抛物线故选D．点评：本题以方程为载体，考查方程与曲线的关系，解题的关键是判断sinθ的范围15．若某空间几何体的三视图如图所示，则该几何体的体积为（）A．B．8 C．4 D．考点：由三视图求面积、体积．专题：空间位置关系与距离．分析：利用三视图判断几何体的形状，然后求解几何体的体积．解答：解：由题意可知几何体是正方体的一半，也是放倒的三棱柱，底面直角三角形的直角边为2，高为2的直三棱柱，该几何体的体积为：=4．故选：C．点评：本题考查三视图与直观图的关系，判断几何体的形状是解题的关键，考查三棱柱的体积的求法．16．若函数f（x）是定义在R上的奇函数，则函数F（x）=|f（x）|+f（|x|）的图象一定关于（）A．x轴对称B．y轴对称C．原点对称D．直线y=x对称考点：函数奇偶性的判断．专题：函数的性质及应用．分析：根据函数奇偶性的定义和性质进行判断即可．解答：解：∵函数f（x）是定义在R上的奇函数，∴F（﹣x）=|f（﹣x）|+f（|﹣x|）=|﹣f（x）|+f（|x|）=|f（x）|+f（|x|）=F（x），即函数F（x）是偶函数，则图象关于y轴对称，故选：B点评：本题主要考查函数图象的判断，根据函数奇偶性的性质是解决本题的关键．17．若实数x，y满足不等式组，则z=x+3y的最大值是（）A．﹣3 B．C．11 D．9考点：简单线性规划．专题：不等式的解法及应用．分析：作出不等式组对于的平面区域，利用数形结合即可得到结论．解答：解：作出不等式组对于的平面区域如图：由z=x+3y，则y=，平移直线y=，由图象可知当直线y=经过点A时，直线y=的截距最大，此时z最大，由，解得，即A（2，3），此时z max=2+3×3=11，故选：C．点评：本题主要考查线性规划的应用，利用z的几何意义，利用数形结合是解决本题的关键．18．已知正四面体ABCD中，E是AB的中点，则异面直线CE与BD所成角的余弦值为（）A．B．C．D．考点：异面直线及其所成的角．专题：空间角．分析：由E为AB的中点，可取AD中点F，连接EF，则∠CEF为异面直线CE与BD所成角，设出正四面体的棱长，求出△CEF的三边长，然后利用余弦定理求解异面直线CE与BD所成角的余弦值．解答：解：如图，取AD中点F，连接EF，CF，∵E为AB的中点，∴EF∥DB，则∠CEF为异面直线BD与CE所成的角，∵ABCD为正四面体，E，F分别为AB，AD的中点，∴CE=CF．设正四面体的棱长为2a，则EF=a，CE=CF=．在△CEF中，由余弦定理得：=．故选：B．点评：本题考查异面直线及其所成的角，关键是找角，考查了余弦定理的应用，是中档题．19．设函数f（x）=1﹣|x|，g（x）=﹣1+|x|，则函数F（x）=f[g（x）]的图象是（）A．B．C．D．考点：函数的图象．专题：函数的性质及应用．分析：先根据绝对值函数，去掉绝对值，得到F（x）=根据每段函数的性质即可得到答案．解答：解：∵f（x）=1﹣|x|，g（x）=﹣1+|x|，∴F（x）=f[g（x）]=1﹣|﹣1+|x||==即当x＞1和﹣1≤x＜0时，函数为增函数，故选：C．点评：本题考查了绝对值函数的图象问题，关键是化为分段函数，属于中档题．20．某转弯路段为四分之一圆环，圆环道路外侧均匀栽种了10棵树（如图所示），小李在半径OA的延长线上一点C处观察到第四棵树（P点），第七棵树（Q点）与点C在同一条直线上，并测得AC=100米，则此弧形道路的大圆半径OA的长为（）A．100米B．100（+1）米C．200米D．100（+）米考点：正弦定理的应用．专题：计算题；解三角形．分析：求出∠AOP=×90°=30°，∠OPC=∠POQ+∠OQP=30°+75°=105°，∠C=45°，利用正弦定理，即可求出弧形道路的大圆半径OA的长．解答：解：由题意，∠AOP=×90°=30°，∠OPC=∠POQ+∠OQP=30°+75°=105°，∠C=45°，设半径为r，则，∴r=100（+1）米，故选：B．点评：本题考查求弧形道路的大圆半径OA的长，考查正弦定理的运用，考查学生分析解决问题的能力，属于中档题．21．设函数f（x）=sinωπx（ω＞0）的图象在区间[0，]上有两个最高点和一个最低点，则（）A．3≤ω＜5 B．4≤ω＜6 C．5≤ω＜7 D．6≤ω＜8考点：三角函数的周期性及其求法．专题：三角函数的图像与性质．分析：先求出函数的周期，结合三角函数的图象和性质进行求解即可．解答：解：f（x）=sinωπx，则函数的周期T==，∵f（0）=0，ω＞0，若图象在区间[0，]上至少有两个最高点和一个最低点，∴则区间[0，]上至少包含个周期，T≤，即，解得7＞ω≥5．故选：C．点评：本题主要考查三角函数的图象和性质，结合函数的周期关系是解决本题的关键，属于基本知识的考查．22．设点F为双曲线C：﹣=1（a＞0，b＞0）的右焦点，直线l过原点且与双曲线C 相交于A，B两点，若双曲线C的右顶点M恰为△ABF的重心，则双曲线C的离心率为（）A．B．C．2 D．3考点：双曲线的简单性质．专题：圆锥曲线的定义、性质与方程．分析：通过数形结合，利用重心性质即得结论．解答：解：如图，根据题意可得：OM=OF，又∵OM=a，OF=c，∴c=3a，即e==3，故选：D．点评：本题考查求双曲线的离心率，利用重心的性质是解决本题的关键，注意解题方法的积累，属于中档题．23．设P是曲线y=上的点，若对曲线y=x+（a＞0，x＞0）上的任意一点Q，恒有|PQ|≥1，则a的取值范围是（）A．[﹣1，+∞）B．[2﹣2，+∞）C．[，+∞）D．（0，2﹣2]考点：曲线与方程．专题：综合题；函数的性质及应用．分析：由题意，曲线y=x+（a＞0，x＞0）上的任意一点Q，恒有|OQ|≥2，可得2x4+（2a﹣2）x2+a2≥0，换元，利用判别式，即可得出结论．解答：解：由题意，曲线y=x+（a＞0，x＞0）上的任意一点Q，恒有|OQ|≥2，∴≥2，∴2x4+（2a﹣2）x2+a2≥0，令t=x2，则2t2+（2a﹣2）t+a2≥0在（0，+∞）上恒成立，∴△=（2a﹣2）2﹣8a2≤0或1﹣a＜0，∵a＞0，∴a≥﹣1，故选：A．点评：本题考查直线与圆的位置关系，考查学生分析解决问题的能力，正确转化是关键．24．已知正方体ABCD﹣A1B1C1D1的棱长为3，点O在棱AA1上，且OA1=2OA，平面α过点O且垂直于AA1，点P在平面α内，PQ⊥A1C1于点Q．若PA=PQ，则P点的轨迹是（）A．圆B．椭圆C．抛物线D．两条直线考点：轨迹方程．专题：综合题；空间位置关系与距离．分析：在对角面A1C1中，利用PQ⊥A1C1于点Q，PA=PQ，可得P到定点A的距离等于P 到定直线A1C1的距离，利用抛物线的定义，即可得出P点的轨迹．解答：解：由题意，在对角面A1C1中，∵PQ⊥A1C1于点Q，PA=PQ，∴P到定点A的距离等于P到定直线A1C1的距离，∴P点的轨迹是抛物线．故选：C．点评：本题考查轨迹方程，考查抛物线的定义，正确运用抛物线的定义是关键．二、填空题（共6小题，每小题3分，满分18分）25．设函数f（x）=，则f[f（﹣2）]=4．考点：函数的值．专题：函数的性质及应用．分析：根据函数的解析式求出f（﹣2），再求出f[f（﹣2）]的值即可．解答：解：由题意得，f（x）=，∴f（﹣2）=﹣2+4=2，∴f[f（﹣2）]=f（2）=4，故答案为：4．点评：本题考查分段函数的函数值，对于多层函数值应从内向外依次求值，属于基础题．26．已知等差数列{a n}前n项和为S n，且满足=3，则数列{a n}的公差为2．考点：等差数列的前n项和．专题：等差数列与等比数列．分析：=3，由此能求出数列{a n}的公差．解答：解：∵，∴，又，∴d=2．点评：本题考查等差数列的公差的求法，是基础题，解题时要认真审题，注意等差数列的性质的合理运用．27．若是奇函数，则a=﹣1．考点：对数函数图象与性质的综合应用；函数奇偶性的性质．专题：计算题；函数的性质及应用．分析：根据奇函数的定义：在定义域内任意一个x，都有f（﹣x）=﹣f（x）．可以用这一个定义，采用比较系数的方法，求得实数m的值．解答：解：∵∴∵是奇函数∴f（﹣x）=﹣f（x）=∴恒成立即恒成立∴2+a=1⇒a=﹣1故答案为：﹣1点评：本题着重考查了函数奇偶性的定义、基本初等函数的性质等知识点，属于基础题．请同学们注意比较系数的解题方法，在本题中的应用．28．设向量⊥，=+3．若向量与+的夹角为θ，则cosθ的最小值等于．考点：数量积表示两个向量的夹角．专题：平面向量及应用．分析：设||=x||，（x＞0），利用向量垂直以及向量的夹角公式，结合基本不等式进行求解即可得到结论．解答：解：设||=x||，（x＞0），∴•=0，||=|+3|===||，|+|===||，•（+）=（+3）•（+）=+3=||2+3x2||2=（1+3x2）||2，则cosθ======≥====，故cosθ的最小值等于，故答案为：点评：本题主要考查向量的数量积的应用以及基本不等式求最值，考查学生的运算能力．29．若圆心在x轴上的圆C同时经过椭圆Γ：+=1（a＞b＞0）的左焦点F，上顶点B和右顶点A，则椭圆Γ的离心率为．考点：椭圆的简单性质．专题：圆锥曲线的定义、性质与方程．分析：求出圆的圆心与椭圆的上顶点的距离等于圆的半径，然后求出椭圆的离心率即可．解答：解：由题意可知圆的圆心坐标为（，0），椭圆的上顶点（0，b），所以（）2+b2=（）2，即b2=ac，又b2=a2﹣c2，所以a2﹣c2﹣ac=0，即e2+e﹣1=0，解得e=，故答案为：．点评：本题考查椭圆的基本性质的应用，椭圆的离心率的求法，圆与椭圆的位置关系，考查计算能力．30．设x，y∈R，集合A={（x，y）|ax+by+1=0}，B={（x，y）|x2+y2=1}，且A∩B是一个单元素集合，若对所有的（a，b）∈{（a，b）|a＜0，b＜0}，则集合C={（x，y）|（x﹣a）2+（y﹣b）2≤1}所表示的图形的面积等于2π．考点：集合的表示法．专题：集合．分析：先根据A∩B是一个单元素集合，得到直线和圆相切，即a2+b2=1，结合图象得到集合C的面积=半径为1小圆的面积+半径为2大圆的面积的，问题得以解决．解答：解：集合A={（x，y）|ax+by+1=0}，B={（x，y）|x2+y2=1}，且A∩B是一个单元素集合，∴直线和圆相切，∴=1，即a2+b2=1，∵（a，b）∈{（a，b）|a＜0，b＜0}，C={（x，y）|（x﹣a）2+（y﹣b）2≤1}，∴圆心在以原点为圆心，以1为半径的圆上的一部分（第三象限）∴如图所示，集合C中圆的边界的移动是半径的为1的圆的边界的移动就是沿着那个半径为2的那个圆弧上，∴集合C的面积=半径为1小圆的面积+半径为2大圆的面积的，∴集合C的面积=π+π=2π，故答案为：2π．点评：本题考查了直线和圆的位置关系，以及集合与集合的关系，关键是画出图形，属于难题．三、解答题（共4小题，满分30分）31．若{a n}是等比数列，a2=2，a5=．（Ⅰ）求数列{a n}的通项公式；（Ⅱ）求和：a1a2+a2a3+…+a n a n+1（n∈N*）．考点：数列的求和；等比数列的通项公式．专题：等差数列与等比数列．分析：（Ⅰ）通过q3=及题意，可得公比和首项，进而可得结论；（Ⅱ）通过（Ⅰ）可知a n a n+1=，进而可得数列{a n a n+1}是以8为首项，为公比的等比数列，计算即得结论．解答：解：（Ⅰ）根据题意可得q3==，∴q=，a1==4，∴数列{a n}的通项为：a n=4•=；（Ⅱ）由（Ⅰ）可知a n a n+1=•=，又∵a1a2==8，∴数列{a n a n+1}是以8为首项，为公比的等比数列，∴a1a2+a2a3+…+a n a n+1=8•=（1﹣）．点评：本题考查求等比数列的通项及求和，注意解题方法的积累，属于中档题．32．在正三棱柱ABC﹣A1B1C1中，AB=4，AA1=3，点D是AC的中点，点E在棱BC上（不含端点），且DE⊥B1E．（Ⅰ）求证：平面B1DE⊥平面BCC1B1；（Ⅱ）求直线BD与平面B1DE所成角的正弦值．考点：直线与平面所成的角；平面与平面垂直的判定．专题：空间位置关系与距离；空间角．分析：（Ⅰ）通过证明DE⊥平面BCC1B1，利用平面与平面垂直的判定定理证明平面B1DE⊥平面BCC1B1；（Ⅱ）作BH⊥B1E于H，连结DH，说明∠BDH是直线BD与平面B1DE所成角，在Rt△BDH 中，求解直线与平面所成角的正弦函数值．解答：解：（Ⅰ）证明：由三棱柱ABC﹣A1B1C1的性质可知CC1⊥平面ABC，又DE⊂平面ABC，故CC1⊥DE，又DE⊥B1E，所以DE⊥平面BCC1B1，又因为DE⊂平面B1DE，所以平面B1DE⊥平面BCC1B1；（Ⅱ）作BH⊥B1E于H，连结DH，由（Ⅰ）得平面B1DE⊥平面BCC1B1；故BH⊥平面B1DE，故∠BDH是直线BD与平面B1DE所成角，又因为△BDH为边长为4的正三角形，点D是AC的中点，得CD=2，又由于BB1=AA1=3，所以△EBB1为等腰三角形，HB=．又BD=2，在Rt△BDH中，．点评：本题考查直线与平面所成角的求法，平面与平面垂直的判定定理的应用，考查空间想象能力以及计算能力．33．设抛物线C：y2=x与直线l交于A，B两点（异于原点O），以AB为直径的圆恰好经过原点O．（Ⅰ）求证：直线l过定点．（Ⅱ）求△OAB面积的最小值．考点：抛物线的简单性质．专题：计算题；圆锥曲线的定义、性质与方程．分析：（Ⅰ）设l方程为x=ty+m与抛物线方程联立得y2﹣ty﹣m=0，利用以AB为直径的圆过原点，即x1x2+y1y2=0，从而求出直线l过定点．（Ⅱ）△OAB面积为|y1﹣y2|，即可求△OAB面积的最小值．解答：（Ⅰ）证明：设l方程为x=ty+m联立y2=x得y2﹣ty﹣m=0，设A（x1，y1）、B（x2，y2）则y1+y2=t，y1y2=﹣m∴x1x2=m2∵以AB为直径的圆过原点，∴x1x2+y1y2=0，∴m2﹣m=0，∴m=1，∴直线l过定点（1，0）．（Ⅱ）解：设C（1，0），则△OAB面积为|y1﹣y2|=，∴t=0时，△OAB面积的最小值为1．点评：本题主要考查抛物线的简单性质，考查恒过定点问题，考查三角形面积的计算，注意挖掘题目隐含，将问题等价转化．34．设x1，x2是函数f（x）=ax2+（b﹣1）x+1（a＞0，b∈R）的两个不同零点．（Ⅰ）若x1=1，对任意x∈R，都有f（2﹣x）=f（x+2），求f（x）；（Ⅱ）若a≥2，x1﹣x2=﹣2，当x∈（x1，x2）时，g（x）=﹣f（x）+2（x2﹣x）的最大值为h（a），求h（a）的最小值．考点：二次函数的性质；函数的最值及其几何意义．专题：函数的性质及应用．分析：（Ⅰ）根据f（2﹣x）=f（x+2）得出x=2是f（x）的对称轴，从而得出函数的零点，求出a、b的值；（Ⅱ）设出函数f（x）的解析式，表示出g（x），求出g（x）的最大值h（a），再求h（a）的最小值．解答：解：（Ⅰ）∵对任意x∈R，都有f（2﹣x）=f（x+2），∴x=2是f（x）的对称轴，∴1，3为函数的两个零点，∴，解得a=，b=﹣；∴f（x）=x2﹣x+1；（Ⅱ）设函数f（x）=a（x﹣x1）（x﹣x2），则g（x）=﹣a（x﹣x1）（x﹣x2）+2（x2﹣x1）=a（x2﹣x）（x﹣x1+），当x∈（x1，x2），a≥2时，x2﹣x＞0，x﹣x1+＞0，∴g（x）≤a•=a++2，当x=﹣时“=”成立；∴h（a）=a++2，（a≥2）∴h（a）是单调递增的函数，∴h（a）的最小值是h（a）min=h（2）=．点评：本题考查了二次函数的图象与性质的应用问题，也考查了求函数的最值问题，是综合性题目．。

嵊州市2014学年第二学期期末教学质量检测试卷高二 数学(理科A 卷) 第Ⅰ卷（共40分）一、选择题:本大题共8个小题,每小题5分，共40分。

在每小题给出的四个选项中，只有一项 是符合题目要求的.1。

已知集合{}{}1,2,3,14M N x x ==∈<<Z ,则A ．N M ⊆B ．N M =C ．}3,2{=N MD ．)4,1(=N M 【答案】C 【解析】试题分析：根据题意可以求得集合{}2,3N =，所以有N M ⊆,所以A 错，显然两集合是不相等的,所以B 错，根据集合并集的定义，可知{}1,2,3MN =,故D 错，根据集合的交集的定义，可知{}2,3M N =，故C对,所以选C.考点：集合的运算。

2。

若0a b <<，则 A ．22ab <B ．2ab b <C ．1122a b⎛⎫⎛⎫< ⎪ ⎪⎝⎭⎝⎭D ．2b a ab+>【答案】D考点：不等式的性质。

3。

命题 “(),x f x ∀∈>0R ”的否定为 A ．()00,0xf x ∃∈>R B ．()0,0x f x ∃∈≤RC ．()0,0xf x ∀∈≤R D ．()0,0x f x ∀∈>R【答案】B 【解析】试题分析：根据全程命题的否定形式，可知 “(),x f x ∀∈>0R ”的否定为()00,0xf x ∃∈≤R ，故选B 。

考点:全称命题的否定。

4.已知,,,a b c d 为非零向量,且+=a b c ， -=a b d，则下列命题正确．．的个数为（1）若=a b ,则0⋅=c d （2）若0⋅=c d ,则=a b （3）若=c d ,则0⋅=a b （4)若0⋅=a b ，则=c dA ．1B ．2C ．3D ．4 【答案】D 【解析】试题分析：根据题意，有22()()c d a b a b ab⋅=+⋅-=-,从而可以得到a b =是0c d ⋅=的充要条件,故（1)（2）正确，根据c d=的等价条件为22()()a b a b +=-，整理可得0a b ⋅=,所以c d =成了的充要条件为0a b ⋅=，故(3）（4）正确,所以正确的命题的个数为4个，故选D 。

XX 中学2014—2015学年度第二学期高 二 级期末考试文科数学科试卷本试卷共 3 页，满分 150 分，考试时间 120 分钟一、选择题（本大题共12小题，每小题5分，共60分，在每小题给出的四个选项中，有且只有一项符合题目要求．）（1）设集合{}{}21,0,1,|M N x x x =-==,则M N ⋂=( )（A ）{}1,0,1-（B ）{}0,1（C ）{}1 （D ）{}0（2）复数z ＝1－3i1＋2i，则( )（A ）|z |＝2 （B ）z 的实部为1 （C ）z 的虚部为－i （D ）z 的共轭复数为－1＋i（3）已知函数()f x 是偶函数，当0x ≥时，()22f x x x =-，则()3f -=（ ）A ．15-B ．15C ．3-D ．3 （4）执行右面的程序框图，若输出的k ＝2，则输入x 的取值范围是( )（A ）(21，41) （B ）[21，41] （C ）(21，41] （D ）[21，41) （5）已知p ： ∀x ∈R ，ax 2－ax ＋1≥0，q ：(a －1)2≤1；则p 是q 成立的( )（A ）充分不必要条件 （B ）必要不充分条件 （C ）充要条件 （D ）既不充分也不必要条件 （6）函数f (x )＝(x ＋2)3－(1 2)x的零点所在区间是( )（A ）(－2，－1) （B ）(－1，0) （C ）(0，1) （D ）(1，2)（7）已知向量a=（1, 2），b=（2,3）若（c +a ）∥b ，c ⊥（b +a ），则c=( )（A ）（ 79 ， 73） （B ）（ 73 ， 79 ） （C ）（ 73 ， 79） （D ）（－ 79 ，－ 73）开始 是x ≤81？否 输入x x ＝2x －1结束k ＝0输出k k ＝k ＋1（8）空间几何体的三视图如图所示，则该几何体的表面积为( )（A ）8＋2 5 （B ）6＋2 5 （C ）8＋2 3（D ）6＋2 3（9）等比数列}{n a 的前321,2,4,a a a S n n 且项和为成等差数列，若a 1=1，则S 4为( )（A ）15 （B ）8 （C ）7 （D ）16（10）已知函数f (x )＝cos (2x ＋π 3)，g (x )＝sin (2x ＋2π3)，将f (x )的图象经过下列哪种变换可以与g (x )的图象重合( ) （A ）向右平移 π12（B ）向左平移 π6（C ）向左平移 π12（D ）向右平移 π6（11）过双曲线x 2a 2－y 2b2＝1的一个焦点F 作一条渐近线的垂线，若垂足恰在线段OF （O 为原点）的垂直平分线上，则双曲线的离心率为( )（A ） 2（B ）2（C ） 5（D ） 3（12）给出下列命题:○110.230.51log 32()3<<; ○2函数()lg sin f x x x =-有3个零点; ○3函数1()112++-=ln x xf x x 的图像以原点为对称中心; ○4已知a 、b 、m 、n 、x 、y 均为正数，且a ≠b ，若a 、m 、b 、x 成等差数列，a 、n 、b 、y 成等比数列，则有m> n ，x< y ．其中正确命题的个数是( ) （A ）4个（B ）3个（C ）2个（D ）1个二、填空题：（本大题共4小题，每小题5分，共20分，把答案填写在题中横线上．）（13）某城区有大学生3500人、中学生4000人，小学生4500人，为掌握各类学生的消费情况，现按分层抽样方法抽取一个容量为300的样本，应抽取中学生 人.（14） 若x ，y ∈R ，且⎩⎪⎨⎪⎧x≥1，x －2y ＋3≥0，y≥x ，则z =x ＋2y 的最小值等于__________.（15）已知双曲线过点，且渐近线方程为12y x=±，则该双曲线的标准方程为_____。

2014-2015学年浙江省杭州市（含周边）重点中学高二（下）期中数学试卷（文科）一、选择题1．（4分）i是虚数单位，复数=（）A．2+i B．1﹣2i C．1+2i D．2﹣i2．（4分）“a＞b”是“a2＞b2”的（）A．充分不必要条件B．必要不充分条件C．充要条件D．既不充分也不必要条件3．（4分）命题“对于任意的x∈R，x2+1＞0”的否定是（）A．对于任意的x∈R，x2+1≤0B．存在x∈R，x2+1≤0C．存在x∈R，x2+1＜0D．存在x∈R，x2+1＞04．（4分）下列四组函数中，表示同一函数的是（）A．y=与y=x B．y=x0与y=1C．y=2与y=D．y=x与y=（25．（4分）已知a=log30.7，b=30.7，c=（）﹣0.5，则a、b、c的大小关系是（）A．a＜b＜c B．c＜b＜a C．b＜c＜a D．a＜c＜b 6．（4分）已知函数f（x）满足：f（x）﹣3f（）=4x2，则f（x）的最大值是（）A．﹣2B．﹣3C．﹣2D．﹣7．（4分）已知函数y=f（﹣|x|）的图象如左图所示，则函数y=f（x）的图象不可能是（）A．（1）B．（2）C．（3）D．（4）8．（4分）设函数f（x）的定义域为D，若函数f（x）满足条件：存在[a，b]⊆D，使得f（x）在区间[a，b]上的值域为[]（n∈N*），则称g（x）为“n倍缩函数”，若函数f（x）=log3（3x+t）为“3倍缩函数”，则t的取值范围为（）A．（0，）B．（0，）C．（0，）D．（0，1）二、填空题：共7小题，9-12小题每题6分，13-15小题每题4分，共16分。

9．（6分）已知集合M={x|﹣2＜x＜4}，N={x|3x＞}，则M∩N=，M∪N=，M∪∁R N=．10．（6分）已知幂函数f（x）=kx a（k∈R，a∈R）的图象经过点（），则k+a=；函数y=的定义域为．11．（6分）已知函数f（x）=，则f（f（9））=，若f（a），则实数a的取值范围是．12．（6分）函数f（x）=+a为奇函数，则实数a=；若函数y=f（x）﹣m存在零点，则实数m的取值范围．13．（4分）（lg25﹣lg）÷100=．14．（4分）定义为R上的函数f（x）满足f（x）f（x+2）=7，f（1）=3，则f（2015）=．15．（4分）已知函数f（x）=2﹣x2﹣log2x，正实数a、b、c满足f（a）＜f（b）＜0＜f（c），若实数m是方程f（x）=0的一个根，那么下列四个结论：①m ＞a；②m＜b；③m＞c；④．其中成立的是．三、解答题：共4小题，16、17小题每题12分，18、19小题每题14分，共52分。

第Ⅰ卷（共40分）一、选择题：本大题共8个小题,每小题5分,共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.1.已知集合{}{}1,2,3,14M N x x ==∈<<Z ，则A ．N M ⊆B ．N M =C ．}3,2{=N MD ．)4,1(=N M 【答案】C 【解析】试题分析：根据题意可以求得集合{}2,3N =，所以有N M ⊆，所以A 错，显然两集合是不相等的，所以B 错，根据集合并集的定义，可知{}1,2,3M N =,故D 错，根据集合的交集的定义，可知{}2,3MN =,故C 对，所以选C.考点：集合的运算.2.已知向量()()2,1,3,4==-a b ，则+=a bA ．()1,5-B ．()1,5C ．()1,3--D ．()1,3【答案】A 【解析】试题分析：根据向量的加法运算法则，可知(23,14)(1,5)a b +=-+=-，故选A. 考点：向量的加法运算. 3.若0a b >>，则 A ． 2ab b <B ． 1122a b⎛⎫⎛⎫> ⎪ ⎪⎝⎭⎝⎭ C ． 1122log log a b >D ． 22a b >【答案】D试题分析：结合二次函数的性质，可知函数2y x =在区间(0,)+∞上是增函数，故有22a b >，所以D 正确，根据不等式的性质，不等式两边同时乘以一个大于零的数或式子，不等号的方向不改变，所以有2ab b >，所以A 不正确，根据底数是大于零小于一的指数函数是减函数，有11()()22a b <，所以B 不正确，根据底数是大于零小于一的对数函数是减函数，所以1122log log a b <，所以C 不正确，故选D.考点：不等式的性质.4.命题 “(),x f x ∀∈>0R ”的否定为 A ．()00,0x f x ∃∈>RB ．()00,0x f x ∃∈≤RC ．()00,0x f x ∀∈≤RD ．()00,0x f x ∀∈>R【答案】B 【解析】试题分析：根据全程命题的否定形式，可知 “(),x f x ∀∈>0R ”的否定为()00,0x f x ∃∈≤R ，故选B.考点：全称命题的否定.5.若数列{}n a 是首项为1，公比为4a 等于A ．8-B ．-C ．D ．8【答案】B 【解析】试题分析：根据等比数列的通项公式，可知33411(a a q =⋅=⋅=- B. 考点：等比数列的通项公式.6.已知()2,4P 在双曲线()222210,0x y a b a b-=>>的渐近线上，则该双曲线的离心率为A ． 2 C ．． 【答案】A试题分析：根据点()2,4P 在双曲线的渐近线上，所以双曲线的一条渐近线方程为2y x =，所以有2ba=，即2b a =，根据双曲线中,,a b c 的关系，可以得c =，所以有e =故选A.考点：双曲线的渐近线，双曲线的离心率.7.已知,,,a b c d 为非零向量，且+=a b c ， -=a b d ，则下列命题正确．．的个数为 （1）若=a b ，则0⋅=c d （2）若0⋅=c d ，则=a b （3）若=c d ，则0⋅=a b （4）若0⋅=a b ，则=c d A ．1 B ．2 C ．3 D ．4 【答案】D考点：向量的模，向量垂直的条件.8.如图，四边形OABC ，ODEF ，OGHI 是三个全等的菱形，60COD FOG AOI ∠=∠=∠=，P 为各菱形边上的动点，设OP xOD yOH =+，则x y+的最大值为A ．3B ．4C ．5D ．6【答案】B 【解析】试题分析：根据图形的特点，可知x y +取最大值时，应该在菱形的顶点处，经过检验，可以发现当点P 落在点E 处时取到最大值，此时OP xOD yOH xOD yOG yOI =+=++()x y OD yOG =-+，根据向量的运算，可知2OH OD OG =+，所以有2,1x y y -==，所以3,1x y ==，故4x y +=，故选B.考点：向量的运算.第Ⅱ卷（共90分）二、填空题（本大题共7小题，其中第9、10、11、12题每格3分，13、14、15题每格4分，共36分，将答案填在答题纸上）9.已知函数1,(1)()3,(1)x x x f x x -⎧=⎨>⎩≤，()9f a =，则()()0ff = ，a = ．【答案】2,2- 【解析】试题分析：根据题意有(0)1f =-，(1)112f -=--=-，所以有((0))2f f =-，根据所给的解析式，只可能39a=，解得2a =. 考点：分段函数求值问题.10.已知平面向量(1,2),(2,)y ==-a b ，且a ⊥b ，则||=a ，y = ．【解析】试题分析：根据向量的模的坐标公式，可知212a =+=1(2)20a b y ⋅=⋅-+=，解得1y =.考点：向量的模，向量垂直的条件.11.已知实数,x y 满足50,0,3.x y x y x -+≥⎧⎪+≥⎨⎪≤⎩则2x y -的最小值为 ，该不等式组所围成的区域的面积为 ． 【答案】12113,4- 【解析】试题分析：画出约束条件对应的可行域，可知2x y -的最小值在直线3x =与直线50x y -+=的交点(3,8)处取得，所以其最小值为31613-=-，该不等式组所围成的区域为一个直角三角形，直角顶点为55(,)22-，底边长为11，直角顶点到底边的距离为511322+=，所以所求的面积为11112111224S =⋅⋅=.考点：线性规划.12.若直线l ：30x -+=与圆C ：()22200x ax y a -+=>相切，则直线l 的斜率为 ，实数a 的值为 ． 【答案】3,3 【解析】3=，根据直线与圆的位置关系，可知圆心到直线的距离等于半径，所以有32a d a +==，结合0a >的条件，解得3a =. 考点：直线与圆的位置关系.13.设O 为原点，P 是抛物线24x y =上一点，F 为焦点， 5PF =，则OP = ．【答案】 【解析】试题分析：根据题意设(,)P m n ，则根据5PF =，可知点P 到抛物线的准线的距离为5，结合抛物线的准线方程为1y =-，所以有n =4，从而有216m =，故OP=4=考点：抛物线的几何性质.14.已知等差数列{}n a 的前n 项和为n S ，且满足36S =，63S =．则9S = ． 【答案】9- 【解析】试题分析：根据等差数列的性质36396,,S S S S S --成等差数列，即96,36,3S --成等差数列，解得99S =-.考点：等差数列的性质. 15.定义{},min ,,a a ba b b a b≤⎧=⎨>⎩，若关于x的方程{}()min 2x m m -=∈R 恰有二个不同的实根，则m 的值为 ．【答案】)21或0【解析】试题分析：根据题意可知{}44min 22,44x x x x ⎧≤≤-≥+⎪-=⎨--<+⎪⎩该题相当于曲线y={}44min 22,44x x x x ⎧≤≤-≥+⎪-=⎨--<+⎪⎩y m =有两个交点，当0m =时满足条件，当4x =-21)m ==，所以结合着函数图像得到m的值为)21或0.考点：分段函数，数形结合.三、解答题 （本大题共5小题，共74分.解答应写出文字说明、证明过程或演算步骤.） 16.（本小题满分15分）等差数列{}n a 中，13a =，422a a =． （Ⅰ）求数列{}n a 的通项公式；（Ⅱ）设13n n n b a n-=⋅，求数列{}n b 的前n 项和n S ．【答案】（Ⅰ）3n a n =（Ⅱ）()3312nn S =⋅- 【解析】试题分析：第一问根据题中的条件，找出等差数列的首项和公差所满足的等量关系式，从而求得其首项和公差，借助于等差数列的通项公式求得结果，第二问可得数列{}n b 为等比数列，应用等比数列的求和公式即可得结果.试题解析：（Ⅰ）设{}n a 的公差为d ，则422a a =得13d a == ………………5分 故3n a n =． ………………10分 （Ⅱ）()23333312n n n S =+++=⋅-． ………………15分考点：等差数列的通项公式，等比数列的求和公式. 17.（本小题满分15分）已知椭圆Γ：2214x y +=． （Ⅰ）求椭圆Γ的离心率；（Ⅱ）设直线y x m =+与椭圆Γ交于不同两点,A B ，若点()0,1P 满足=PA PB ，求实数m 的值．【答案】 （Ⅱ）53m =- 【解析】试题分析：第一问根据题中所给的椭圆的方程，确定出,,a b c 的值，利用离心率的公式，求得离心率的值，第二问将直线与椭圆的方程联立，消元，根据直线与椭圆有两个交点，从而得出其判别式大于零，根据韦达定理，结合中点坐标公式，确定出弦AB 的中点坐标，结合条件，可知点P 在弦AB 的中垂线上，利用两直线垂直时斜率的条件，可求得m 的值，经验值满足条件.试题解析：（Ⅰ）2a =，1b =，所以c =………………6分. ………………8分 （Ⅱ）设()()1122,,,A x y B x y ，由22,440y x m x y =+⎧⎨+-=⎩得()2258410x mx m ++-=， 由0∆>得(m ∈.1285m x x +=-，得1225my y +=， 故AB 的中点4,55m m M ⎛⎫-⎪⎝⎭. ………………12分 因为PM AB ⊥，所以15145mm -=--，得53m =-满足条件. ………………15分考点：直线与椭圆的综合问题. 18.（本小题满分15分）对于函数)(x f ，若存在R x ∈0，使00)(x x f =成立，则称0x 为)(x f 的一个不动点．设函数1)(2++=bx ax x f （0>a ）．（Ⅰ）当2=a ，2-=b 时，求)(x f 的不动点；（Ⅱ）设函数)(x f 的对称轴为直线m x =，21,x x 为)(x f 的不动点，当211x x <<时，求证：21>m ． 【答案】（Ⅰ）21和1 （Ⅱ）证明略. 【解析】试题分析：第一问注意题中对不动点的要求，转化为相应的方程的根的问题，解一元二次方程即可求得结果，第二问注意令()()()211,0g x f x x ax b x a =-=+-+>，根据不动点满足的条件211x x <<，由一元二次方程根的分布，可知(1)0g <，可得0a b +<，从而得出122b a ->，根据函数解析式可知2b m a=-，所以得到21>m .试题解析：（Ⅰ）依题意：x x x x f =+-=122)(2，即22310x x -+=，………………3分解得21=x 或1，即)(x f 的不动点为21和1 ………………7分 （Ⅱ）由()f x 表达式得2bm a=-，∵()()()211,0g x f x x ax b x a =-=+-+>由211x x <<得()10g <， ………………11分 得1b a->，即证21>m ………………15分 考点：新定义，函数的零点，一元二次方程根的分布，二次函数图像的对称轴.19.设数列{}n a 满足21*123222,2n n na a a a n -+++⋅⋅⋅+=∈N ． （Ⅰ）求n a ； （Ⅱ）设1lgn nb a =，1122n n n T a b a b a b =+++，求证：数列{}n T 中1T 最小．【答案】（Ⅰ）12n na = （Ⅱ）证明略. 【解析】试题分析：第一问根据题中所给的式子是一个和式，所以类比着写出将n 写成1n -时对应的式子，将两式子相减，得到当2n ≥时n a 关于n 的关系式，令1n =，求出1a 的值，验证上式成立，从而求得12n na =，第二问根据1lg n nb a =，得出lg 2lg 2nn b n ==，从而得出1()lg 22n n n a b n ⋅=⋅，利用错位相减法对数列求和，证明是递增的，从而求得数列{}n T 中1T 最小，也可以应用数列{}n n a b ⋅中的项都是正的，也可以证明. 试题解析：（Ⅰ）当1n =时，112a =． ………………2分 当2n ≥时，22123112222n n n a a a a ---+++⋅⋅⋅+=，相减得1112222n n n n a --=-=．所以，当2≥n 时，12n na =． ……………………4分 当1n =时，211=a 也满足上式，所求通项公式12n n a =……………5分．（Ⅱ）lg 2n b n =， ………………7分21122111lg 212222nn n n T a b a b a b n ⎡⎤⎛⎫⎛⎫⎛⎫=+++=⋅+⋅++⋅⎢⎥ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎢⎥⎣⎦， 2311111lg 2122222n n T n +⎡⎤⎛⎫⎛⎫⎛⎫=⋅+⋅++⋅⎢⎥ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎢⎥⎣⎦， ………………9分 相减得2111111lg 222222nn n T n +⎡⎤⎛⎫⎛⎫⎛⎫=+++-⎢⎥ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎢⎥⎣⎦， 所以122lg 212n n n T ++⎛⎫=-⎪⎝⎭．………………11分 设()122n n f n ++=，则()2312n n f n +++=，显然()()13124f n n f n n ++=<+，………………13分 即()f n 为减，从而n T 随着n 的增大而增大，故1T 最小． ………………15分 考点：数列的通项公式，错位相减法求和. 20.（本小题满分14分）设抛物线C ：px y 22=)0(>p 的焦点为F ，过F 且斜率为k 的直线l 交抛物线C 于),(11y x A ，),(22y x B 两点，且421-=y y ．（Ⅰ）求抛物线C 的标准方程；（Ⅱ）已知点()1,P k -，且PAB ∆的面积为，求k 的值．【答案】（Ⅰ）x y 42=（Ⅱ）k =【解析】试题分析：第一问将直线的方程与抛物线的方程联立，消去x ，得到关于y 的方程，利用韦达定理，可知212y y p ⋅=-，从而求得p 的值，进而确定出抛物线C 的标准方程，第二问在第一问的基础上，确定出焦点的坐标，直线的方程可以确定，联立方程组，应用弦长公式求得弦长，应用点到直线的距离公式，求得点P 到直线AB 的距离，根据三角形的面积公式，从而求得k 的值．试题解析：（Ⅰ）)0,2(p F ，设直线AB 的方程为)2(p x k y -=， …………2分 联立⎪⎩⎪⎨⎧=-=px y p x k y 2)2(2，消x ，得：0222=--kp py ky ， …………4分4221-=-=∴p y y ，从而2=p ，抛物线C 的方程为x y 42=．…………6分 （Ⅱ）由已知，)0,1(F ，直线AB 的方程为(1)y k x =-，联立24y kx k y x =-⎧⎨=⎩，消x ，得2440ky y k --=，所以12124,4.y y k y y ⎧+=⎪⎨⎪=-⎩…………8分21||41AB k ⎛⎫==+ ⎪⎝⎭． …………10分 又 P 到直线AB的距离d = …………12分故12OAB S AB d ∆=⨯⨯= …………14分故得2k =± ． …………15分 考点：抛物线的方程，直线与抛物线的综合问题.。

第Ⅰ卷（共40分）一、选择题：本大题共8个小题,每小题5分,共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.1.已知集合{}{}1,2,3,14M N x x ==∈<<Z ，错误！未找到引用源。

错误！未找到引用源。

则A ．N M ⊆B ．N M =C ．}3,2{=N MD ．)4,1(=N M 【答案】C 【解析】试题分析：根据题意可以求得集合{}2,3N =，所以有N M ⊆，所以A 错，显然两集合是不相等的，所以B 错，根据集合并集的定义，可知{}1,2,3M N =,故D 错，根据集合的交集的定义，可知{}2,3MN =,故C 对，所以选C.考点：集合的运算.2.已知向量()()2,1,3,4==-a b ，则+=a bA ．()1,5-B ．()1,5C ．()1,3--D ．()1,3【答案】A 【解析】试题分析：根据向量的加法运算法则，可知(23,14)(1,5)a b +=-+=-，故选A. 考点：向量的加法运算. 3.若0a b >>，则 A ． 2ab b <B ． 1122a b⎛⎫⎛⎫> ⎪ ⎪⎝⎭⎝⎭ C ． 1122log log a b >D ． 22a b >【解析】试题分析：结合二次函数的性质，可知函数2y x =在区间(0,)+∞上是增函数，故有22a b >，所以D 正确，根据不等式的性质，不等式两边同时乘以一个大于零的数或式子，不等号的方向不改变，所以有2ab b >，所以A 不正确，根据底数是大于零小于一的指数函数是减函数，有11()()22ab <，所以B 不正确，根据底数是大于零小于一的对数函数是减函数，所以1122log log a b <，所以C 不正确，故选D.考点：不等式的性质.4.命题 “(),x f x ∀∈>0R ”的否定为 A ．()00,0x f x ∃∈>RB ．()00,0x f x ∃∈≤RC ．()00,0x f x ∀∈≤RD ．()00,0x f x ∀∈>R【答案】B 【解析】试题分析：根据全程命题的否定形式，可知 “(),x f x ∀∈>0R ”的否定为()00,0x f x ∃∈≤R ，故选B.考点：全称命题的否定.5.若数列{}n a 是首项为1，公比为4a 等于A ．8-B ．-C ．D ．8【答案】B 【解析】试题分析：根据等比数列的通项公式，可知33411(a a q =⋅=⋅=- B. 考点：等比数列的通项公式.6.已知()2,4P 在双曲线()222210,0x y a b a b-=>>的渐近线上，则该双曲线的离心率为A ． 2 C ．．【解析】试题分析：根据点()2,4P 在双曲线的渐近线上，所以双曲线的一条渐近线方程为2y x =，所以有2ba=，即2b a =，根据双曲线中,,a b c 的关系，可以得c =，所以有e =故选A.考点：双曲线的渐近线，双曲线的离心率.7.已知,,,a b c d 为非零向量，且+=a b c ， -=a b d ，则下列命题正确．．的个数为 （1）若=a b ，则0⋅=c d （2）若0⋅=c d ，则=a b （3）若=c d ，则0⋅=a b （4）若0⋅=a b ，则=c d A ．1 B ．2 C ．3 D ．4 【答案】D 【解析】试题分析：根据题意，有22()()c d a b a b a b ⋅=+⋅-=-，从而可以得到a b =是0c d ⋅=的充要条件，故（1）（2）正确，根据c d =的等价条件为22()()a b a b +=-，整理可得0a b ⋅=，所以c d =成了的充要条件为0a b ⋅=，故（3）（4）正确，所以正确的命题的个数为4个，故选D.考点：向量的模，向量垂直的条件.8.如图，四边形OABC ，ODEF ，OGHI 是三个全等的菱形，60COD FOG AOI ∠=∠=∠=，P 为各菱形边上的动点，设OP xOD yOH =+，则x y+的最大值为A ．3B ．4C ．5D ．6【答案】B 【解析】试题分析：根据图形的特点，可知x y +取最大值时，应该 在菱形的顶点处，经过检验，可以发现当点P 落在点E 处 时取到最大值，此时OP xOD yOH xOD yOG yOI =+=++()x y OD yOG =-+，根据向量的运算，可知2OH OD OG =+，所以有2,1x y y -==，所以3,1x y ==，故4x y +=. 考点：向量的运算.第Ⅱ卷（共110分）二、填空题（本大题共7小题，其中第9、10、11、12题每格3分，13、14、15题每格4分，共36分，将答案填在答题纸上）9.已知函数|1|(1)()3(1)x x x f x x -⎧=⎨>⎩≤，()2f a =，则()()1ff -= ，a = ．【答案】9,1- 【解析】试题分析：根据题意可知，(1)112f -=--=，2(2)39f ==，所以有()()1ff -=9，根据题意，只能是12a -=，解得3a =（舍去）或1a =-，故有1a =-. 考点：函数值求值问题，已知函数值求自变量，分段函数.10.已知平面向量(1,2),(2,)y ==-a b ，且a ⊥b ，则||=a ，y = ．【解析】试题分析：根据向量的模的坐标公式，可知212a =+=1(2)20a b y ⋅=⋅-+=，解得1y =.考点：向量的模，向量垂直的条件.11.已知实数,x y 满足50,0,3.x y x y x -+≥⎧⎪+≥⎨⎪≤⎩则2x y -的最小值为 ，该不等式组所围成的区域的面积为 ． 【答案】12113,4- 【解析】试题分析：画出约束条件对应的可行域，可知2x y -的最小值在直线3x =与直线50x y -+=的交点(3,8)处取得，所以其最小值为31613-=-，该不等式组所围成的区域为一个直角三角形，直角顶点为55(,)22-，底边长为11，直角顶点到底边的距离为511322+=，所以所求的面积为11112111224S =⋅⋅=.考点：线性规划.12.若直线l ：30x +=与圆C ：()22200x ax y a -+=>相切，则直线l 的斜率为 ，实数a 的值为 ． 【答案】3,3 【解析】=，根据直线与圆的位置关系，可知圆心到直线的距离等于半径，所以有32a d a +==，结合0a >的条件，解得3a =. 考点：直线与圆的位置关系.13.设O 为原点，P 是抛物线24x y =上一点，F 为焦点， 5PF =，则OP = ．【答案】考点：抛物线的几何性质.14.已知等差数列{}n a 的前n 项和为n S ，且满足36S =，63S =．则9S = ． 【答案】9- 【解析】试题分析：根据等差数列的性质36396,,S S S S S --成等差数列，即96,36,3S --成等差数列，解得99S =-.考点：等差数列的性质. 15.定义{},min ,,a a ba b b a b≤⎧=⎨>⎩，若关于x的方程{}()min 2x m m -=∈R 恰有二个不同的实根，则m 的值为 ．【答案】)21或0【解析】试题分析：根据题意可知{}44min 22,44x x x x ⎧≤≤-≥+⎪-=⎨--<+⎪⎩该题相当于曲线y={}44min 22,44x x x x ⎧≤≤-≥+⎪-=⎨--+⎪⎩y m =有两个交点，当0m =时满足条件，当4x =-21)m ==，所以结合着函数图像得到m的值为)21或0.考点：分段函数，数形结合.三、解答题 （本大题共5小题，共74分.解答应写出文字说明、证明过程或演算步骤.） 16.等差数列{}n a 中，13a =，422a a =．（Ⅰ）求数列{}n a 的通项公式；（Ⅱ）设13n n n b a n-=⋅，求数列{}n b 的前n 项和n S ．【答案】（Ⅰ）3n a n =（Ⅱ）()3312nn S =⋅-考点：等差数列的通项公式，等比数列的求和公式. 17.（本小题满分15分）已知抛物线C ：px y 22=)0(>p 的焦点为()1,0F ，过F 且斜率为1的直线l 交抛物线C 于),(11y x A ，),(22y x B 两点．（Ⅰ）求抛物线C 的标准方程； （Ⅱ）求OAB ∆的面积．【答案】（Ⅰ）24y x =【解析】试题分析：第一问根据抛物线的焦点坐标可以确定12p=，从而得到2p =，进一步得到抛物线的标准方程，第二问根据直线的斜率为1，过抛物线的焦点，从而确定出直线的方程，将直线方程和抛物线方程联立，应用弦长公式，求得弦AB 的长，应用点到直线的距离，求得三角形的高，利用三角形的面积公式求得结果.试题解析：（Ⅰ）2p =． ………………3分 抛物线方程为24y x =． ………………5分 （Ⅱ）直线方程为1y x =-， ………………7分 联立抛物线得2610x x -+=， 故12126,1x x x x +==，12AB x =-= ………………10分又原点到直线距离为2d =． ………………13分故OAB ∆ ………………15分考点：抛物线的方程，直线与抛物线的综合问题. 18.（本小题满分15分）已知椭圆Γ：12222=+by a x （0>>b a ）的一个焦点为)，且Γ上一点到其两焦点的距离之和为4．（Ⅰ）求椭圆Γ的标准方程；（Ⅱ）设直线y x m =+与椭圆Γ交于不同两点,A B ，若点()0,1P 满足=PA PB ，求实数m 的值．【答案】（Ⅰ）2214x y += （Ⅱ）53m =- 【解析】试题分析：第一问根据椭圆的定义可知24a =，c =,,a b c 的关系，从而求得1b =，进一步求得椭圆的方程，第二问利用直线与椭圆的位置关系，联立方程组，根据韦达定理，求得弦的中点，根据=PA PB 可以确定出点P 在线段AB 的中垂线上，利用斜率乘积等于1-，确定出m 的值.试题解析：（Ⅰ）c =2a =． ………………2分 故1b = ………………4分故椭圆方程为2214x y +=． ………………5分 （Ⅱ）设()()1122,,,A x y B x y ，由22,440y x m x y =+⎧⎨+-=⎩得()2258410x mx m ++-=，由0∆>得(m ∈． ………………7分1285m x x +=-，得1225m y y +=， 故AB 的中点4,55m m M ⎛⎫-⎪⎝⎭． ………………10分因为PM AB ⊥，所以1515m -=--， ………………13分得53m =-满足条件． ………………15分考点：椭圆的标准方程，直线与椭圆的综合问题. 19.（本小题满分15分）设数列{}n a 满足21*123222,2n n na a a a n -+++⋅⋅⋅+=∈N ．（Ⅰ）求n a ； （Ⅱ）设1lgn nb a =，1122n n n T a b a b a b =+++，求证：数列{}n T 中1T 最小．【答案】（Ⅰ）12n na = （Ⅱ）证明略. 【解析】试题分析：第一问根据题中所给的式子是一个和式，所以类比着写出将n 写成1n -时对应的式子，将两式子相减，得到当2n ≥时n a 关于n 的关系式，令1n =，求出1a 的值，验证上式成立，从而求得12n na =，第二问根据1lg n n b a =，得出lg2lg2n n b n ==，从而得出1()lg 22n n n a b n ⋅=⋅，利用错位相减法对数列求和，证明是递增的，从而求得数列{}n T 中1T 最小，也可以应用数列{}n n a b ⋅中的项都是正的，也可以证明. 试题解析：（Ⅰ）当1n =时，112a =． ………………2分 当2n ≥时，22123112222n n n a a a a ---+++⋅⋅⋅+=，相减得1112222n n n n a --=-=． 所以，当2≥n 时，12n na =． ……………………4分 当1n =时，211=a 也满足上式，所求通项公式12n n a =……………5分．（Ⅱ）lg 2n b n =， ………………7分21122111lg 212222nn n n T a b a b a b n ⎡⎤⎛⎫⎛⎫⎛⎫=+++=⋅+⋅++⋅⎢⎥ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎢⎥⎣⎦，2311111lg 2122222n n T n +⎡⎤⎛⎫⎛⎫⎛⎫=⋅+⋅++⋅⎢⎥ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎢⎥⎣⎦， ………………9分 相减得2111111lg 222222n n n T n +⎡⎤⎛⎫⎛⎫⎛⎫=+++-⎢⎥ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎢⎥⎣⎦， 所以122lg 212n n n T ++⎛⎫=- ⎪⎝⎭． ………………11分 设()122n n f n ++=，则()2312n n f n +++=，显然()()13124f n n f n n ++=<+，………………13分 即()f n 为减，从而n T 随着n 的增大而增大，故1T 最小．………………15分 考点：数列的通项公式，错位相减法求和.20.（本小题满分14分）对于函数)(x f ，若存在R x ∈0，使00)(x x f =成立，则称0x 为)(x f 的一个不动点． 设函数1)(2++=bx ax x f （0>a ）．（Ⅰ）当2=a ，2-=b 时，求)(x f 的不动点；（Ⅱ）若)(x f 有两个相异的不动点21,x x ．（i ）当211x x <<时，设)(x f 的对称轴为直线m x =，求证：21>m ； （ii ）若2||1<x ，且2||21=-x x ，求实数b 的取值范围．【答案】（Ⅰ）21和1 （Ⅱ）（ⅰ）证明略，(ⅱ）14b <或74b >解得21=x 或1，即)(x f 的不动点为21和1． ………………4分（Ⅱ）（ⅰ）由()f x 表达式得2bm a =-，∵()()()211,0g x f x x ax b x a =-=+-+>． 由211x x <<得()10g < ， ………………6分 得1ba ->，即证21>m ． ………………8分(ⅱ）△()2140b a =-->，121211,bx x x x a a -+==， 又2124x x -=，∴ ()22144b a a -=+． ………………10分 又1x ，2x 到()g x 对称轴12bx a -=的距离都为1，要使()0g x =有一根属于)2,2(-，则()g x 对称轴12bx a -=∈)3,3(-，∴ 16b a ->． ………………12分 故()()222111139b b b ->-+-，解得14b <或74b >．………………14分考点：函数的零点，一元二次方程根的分布，韦达定理.。

嵊州市2014学年第二学期期末教学质量检测试卷高二 数学（理科A 卷） 第Ⅰ卷（共40分）一、选择题：本大题共8个小题,每小题5分,共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.1.已知集合{}{}1,2,3,14M N x x ==∈<<Z ，则A ．N M ⊆B ．N M =C ．}3,2{=N MD ．)4,1(=N M 【答案】C 【解析】试题分析：根据题意可以求得集合{}2,3N =，所以有N M ⊆，所以A 错，显然两集合是不相等的，所以B 错，根据集合并集的定义，可知{}1,2,3M N =,故D 错，根据集合的交集的定义，可知{}2,3MN =,故C 对，所以选C.考点：集合的运算.2.若0a b <<，则 A ．22a b < B ．2ab b < C ．1122a b⎛⎫⎛⎫< ⎪ ⎪⎝⎭⎝⎭D ．2b aa b+> 【答案】D考点：不等式的性质.3.命题 “(),x f x ∀∈>0R ”的否定为A ．()00,0x f x ∃∈>RB ．()00,0x f x ∃∈≤RC ．()00,0x f x ∀∈≤RD ．()00,0x f x ∀∈>R【答案】B 【解析】试题分析：根据全程命题的否定形式，可知 “(),x f x ∀∈>0R ”的否定为()00,0x f x ∃∈≤R ，故选B.考点：全称命题的否定.4.已知,,,a b c d 为非零向量，且+=a b c ， -=a b d ，则下列命题正确．．的个数为 （1）若=a b ，则0⋅=c d （2）若0⋅=c d ，则=a b （3）若=c d ，则0⋅=a b （4）若0⋅=a b ，则=c d A ．1 B ．2 C ．3 D ．4 【答案】D 【解析】试题分析：根据题意，有22()()c d a b a b a b ⋅=+⋅-=-，从而可以得到a b =是0c d ⋅=的充要条件，故（1）（2）正确，根据c d =的等价条件为22()()a b a b +=-，整理可得0a b ⋅=，所以c d =成了的充要条件为0a b ⋅=，故（3）（4）正确，所以正确的命题的个数为4个，故选D.考点：向量的模，向量垂直的条件.5.对于函数()y f x =图象上任意一点11(,)P x y ，存在22(,)Q x y ，使得12120x x y y +=， 则函数()y f x =可以为A ．22x y =-B ．2log y x =C ．2+1y x =D ．1y x =+ 【答案】A 【解析】试题分析：根据题意，结合图像，对于D 项，当取(0,0)P 时，没有满足条件的Q 存在，故D 不正确，对于C 项，过原点的抛物线的两条切线对应的切点为(1,2),(1,2)A B -，而此时30OA OB ⋅=>,不满足条件，所以当P 点定在(1,2)-时，满足条件的Q 不存在，故C 不正确，对于B 项，将P 点定在(1,0)时，满足条件的Q 不存在，故C 不正确，对于A 项，图像上的点与坐标原点的连线的斜率的取值范围为(,)-∞+∞，所以图像上的点与坐标原点的连线的倾斜角的取值范围为[0,)π，所以肯定图象上任意一点11(,)P x y ，存在22(,)Q x y ，使得12120x x y y +=，所以只有A 项满足，故选A.考点：函数的性质，向量垂直.6.设双曲线C ：()222210,0x y a b a b-=>>的离心率为e ，右顶点为A ，点()3,0Q a ，若C 上存在一点P ，使得AP PQ ⊥，则A ．(e ∈ B ． e ∈ C ． (e ∈ D ． )e ∈+∞【答案】A考点：双曲线的离心率.7.已知等差数列{}n a 的公差为d ，前n 项和为n S ，若675S S S >>，则下列命题错误．．的是A ．0d <B ．110S >C ．{}n S 中的最大项为11SD ． 67a a >【答案】C 【解析】试题分析：根据题意有67670,0,0a a a a ><+>，所以有0d <，67111212()02a a S S +>=>，67a a >，所以A,B,D 都是正确的，而{}n S 中的最大项为6S ，所以C 不正确，故选C.考点：等差数列的性质.8.定义{},min ,,a a ba b b a b≤⎧=⎨>⎩，若关于x的方程{}min 2x m -= ()m ∈R 有三个不同的实根123,,x x x ，则A ． 123x x x ++有最小值，123x x x 无最大值B ． 123x x x ++无最小值，123x x x 有最大值C ． 123x x x ++有最小值，123x x x 有最大值D ． 123x x x ++无最小值，123x x x 无最大值 【答案】B 【解析】试题分析：根据题意可知{}44min 22,44x x x x ⎧≤≤-≥+⎪-=⎨--<+⎪⎩通过图像可以断定方程有三个不同的实根，则(0,2)m ∈)，对于234x x +=，104x <<-2322,24x x <<<<+所以123x x x ++无最小值，而m 在增大的过程中1x 在逐渐增大，23x x ⋅逐渐减小，所以123x x x 有最大值，故选B. 考点：分段函数的问题.第Ⅱ卷（共110分）二、填空题（本大题共7小题，其中第9、10、11、12题每格3分，13、14、15题每格4分，共36分，将答案填在答题纸上）9.已知函数|1|(1)()3(1)x x x f x x -⎧=⎨>⎩≤，()2f a =，则()()1ff -= ，a = ．【答案】9,1- 【解析】试题分析：根据题意可知，(1)112f -=--=，2(2)39f ==，所以有()()1ff -=9，根据题意，只能是12a -=，解得3a =（舍去）或1a =-，故有1a =-. 考点：函数值求值问题，已知函数值求自变量，分段函数.10.已知平面向量(1,2),(2,)y ==-a b ，且a ⊥b ，则||=a ，y = ．【解析】试题分析：根据向量的模的坐标公式，可知212a =+=1(2)20a b y ⋅=⋅-+=，解得1y =.考点：向量的模，向量垂直的条件.11.已知实数,x y 满足50,0,3.x y x y x -+≥⎧⎪+≥⎨⎪≤⎩则2x y -的最小值为 ，该不等式组所围成的区域的面积为 ． 【答案】12113,4- 【解析】试题分析：画出约束条件对应的可行域，可知2x y -的最小值在直线3x =与直线50x y -+=的交点(3,8)处取得，所以其最小值为31613-=-，该不等式组所围成的区域为一个直角三角形，直角顶点为55(,)22-，底边长为11，直角顶点到底边的距离为511322+=，所以所求的面积为11112111224S =⋅⋅=.考点：线性规划.12.若直线l ：30x +=与圆C ：2220x ax y -+=有交点，则直线l 的斜率为 ，实数a 的取值范围为 ．(][),13,-∞-+∞【解析】3=，根据直线与圆有公共点，可知圆心到直线的距离小于等于半径，可知32a a +≤，解得实数a 的取值范围为(][),13,-∞-+∞.考点：直线的斜率，直线与圆的位置关系.13.设O 为原点，P 是抛物线24x y =上一点，F 为焦点， 5PF =，则OP = ．【答案】 【解析】试题分析：根据题意设(,)P m n ，则根据5PF =，可知点P 到抛物线的准线的距离为5，结合抛物线的准线方程为1y =-，所以有n =4，从而有216m =，故OP =4=考点：抛物线的几何性质.14.如图，四边形OABC ，ODEF ，OGHI 是三个全等的菱形，60COD FOG AOI ∠=∠=∠=，P 为各菱形边上的动点，设OP xOD yOH =+，则x y+的最大值为 ．【答案】4 【解析】试题分析：根据图形的特点，可知x y +取最大值时，应该在 菱形的顶点处，经过检验，可以发现当点P 落在点E 处时 取到最大值，此时OP xOD yOH xOD yOG yOI =+=++()x y OD yOG =-+，根据向量的运算，可知2OH OD OG =+，所以有2,1x y y -==，所以3,1x y ==，故4x y +=. 考点：向量的运算.15.已知数列{}n a 满足()1121nn n a a n ++-=-，则数列{}n a 的前12项的和为 ．【答案】78 【解析】试题分析：根据题意，可知2132431,3,5a a a a a a -=+=-=，对式子进行变形，可以得到31422,8a a a a +=+=，从而得到123410a a a a +++=，同理可得567826a a a a +++=，910111242a a a a +++=，所以有数列{}n a 的前12项的和为78.考点：数列的求和问题.三、解答题 （本大题共5小题，共74分.解答应写出文字说明、证明过程或演算步骤.） 16.（本小题满分15分）等差数列{}n a 中，26a =，314312a a a =++． （Ⅰ）求数列{}n a 的通项公式； （Ⅱ）设13n n b -=，求1122n n a b a b a b +++．【答案】（Ⅰ）3n a n =（Ⅱ）()1333124n nn n T +=⋅--考点：等差数列的通项公式，应用错位相减法对数列求和.17.（本小题满分15分）对于函数)(x f ，若存在0x ∈R ，使00)(x x f =成立，则称0x 为)(x f 的一个不动点．设函数1)(2++=bx ax x f （0>a ）．（Ⅰ）当2=a ，2-=b 时，求)(x f 的不动点；（Ⅱ）设函数)(x f 的对称轴为直线m x =，若21,x x 为)(x f 的不动点，且211x x <<，求证：21>m ． 【答案】（Ⅰ）21和1 （Ⅱ）证明略. 【解析】试题分析：第一问注意题中对不动点的要求，转化为相应的方程的根的问题，解一元二次方程即可求得结果，第二问注意令()()()211,0g x f x x ax b x a =-=+-+>，根据不动点满足的条件211x x <<，由一元二次方程根的分布，可知(1)0g <，可得0a b +<，从而得出122b a ->，根据函数解析式可知2b m a=-，所以得到21>m .试题解析：（Ⅰ）依题意：x x x x f =+-=122)(2，即22310x x -+=，………………3分解得21=x 或1，即)(x f 的不动点为21和1 ………………7分 （Ⅱ）由()f x 表达式得2bm a=-，∵()()()211,0g x f x x ax b x a =-=+-+>由211x x <<得()10g <， ………………11分 得1b a->，即证21>m ………………15分 考点：新定义，函数的零点，一元二次方程根的分布，二次函数图像的对称轴.18.（本小题满分15分）设抛物线C ：px y 22=)0(>p 的焦点为F ，过F 且斜率为k 的直线l 交抛物线C 于),(11y x A ，),(22y x B 两点，且421-=y y ．（Ⅰ）求抛物线C 的标准方程；（Ⅱ）若1=k ，O 为坐标原点，求OAB ∆的面积．【答案】（Ⅰ）x y 42=（Ⅱ）【解析】试题分析：第一问将直线的方程与抛物线的方程联立，消去x ，得到关于y 的方程，利用韦达定理，可知212y y p ⋅=-，从而求得p 的值，进而确定出抛物线C 的标准方程，第二问在第一问的基础上，求得抛物线的焦点坐标，斜率也是已知的，所以直线的方程和抛物线的方程都已知，从而应用弦长公式可以求得弦AB 的长度，应用点到直线的距离公式，可以求得原点到直线的距离，应用三角形的面积公式，从而求得三角形的面积. 试题解析：（Ⅰ）)0,2(p F ，设直线AB 的方程为)2(px k y -=， ………………2分 联立⎪⎩⎪⎨⎧=-=px y p x k y 2)2(2，消x ，得：0222=--kp py ky ， ………………4分4221-=-=∴p y y ，从而2=p ，抛物线C 的方程为x y 42=．………………6分 （Ⅱ）由已知，)0,1(F ，直线AB 的方程为1-=x y ， ………………7分联立⎩⎨⎧=-=xy x y 412，消x ，得0442=--y y ，所以⎩⎨⎧-==+442121y y y y ， 8)4(442||2=-⨯-⋅=∴AB ………………10分又 O 到直线AB 的距离2221==d ， ………………13分故1822OAB S ∆=⨯=． ………………15分 考点：抛物线的方程，直线与抛物线的综合问题.19.（本小题满分15分）已知椭圆Γ：12222=+by a x （0>>b a ）的右焦点为)0,22(，且椭圆Γ上一点M 到其两焦点12,F F 的距离之和为．（Ⅰ）求椭圆Γ的标准方程；（Ⅱ）设直线:(l y x m m =+∈R)与椭圆Γ交于不同两点,A B ，且AB =．若点0(,2)P x 满足=PA PB ，求0x 的值．【答案】（Ⅰ）141222=+y x（Ⅱ）3-或1-【解析】试题分析：第一问根据椭圆的定义可知2a =c =,,a b c 的关系，从而求得2b =，进一步求得椭圆的方程，第二问利用直线与椭圆的位置关系，利用弦长公式，求得m 的值，根据=PA PB 可以确定出点P 在线段AB 的中垂线上，即为线段的中垂线与椭圆的交点，解方程组即可得结果.试题解析：（Ⅰ）由已知2=a 得=a ，又=c ………………2分∴2224=-=b a c ． ………………4分∴椭圆Γ的方程为141222=+y x ． ………………5分 （Ⅱ）由⎪⎩⎪⎨⎧=++=,1412,22y x m x y 得01236422=-++m mx x ① ∵直线l 与椭圆Γ交于不同两点A 、B ，∴△0)123(163622>--=m m ，得216<m ． ………………6分设),(11y x A ，),(22y x B ，则1x ，2x 是方程①的两根， 则2321m x x -=+， 2123124-⋅=m x x ．∴2=-==AB x ．…………8分又由AB =，得231294-+=m ，解之2m =±． ………………10分 据题意知，点P 为线段AB 的中垂线与直线2=y 的交点．设AB 的中点为),(00y x E ，则432210m x x x -=+=，400m m x y =+=， 当2m =时，31(,)22E - ∴此时，线段AB 的中垂线方程为13()22y x -=-+，即1y x =--． 令2=y ，得03x =-． ………………12分 当2m =-时，31(,)22E -∴此时，线段AB 的中垂线方程为13()22y x +=--，即1y x =-+． 令2=y ，得01x =-． ………………14分 综上所述，0x 的值为3-或1-．………………15分科网考点：椭圆的方程，直线与椭圆的综合问题.20.（本小题满分14分）设数列{}n a 满足21*123222,2n n n a a a a n -+++⋅⋅⋅+=∈N ． （Ⅰ）求n a ； （Ⅱ）设11111n n n b a a +=++-，数列{}n b 的前n 项和为n T ．求证：122n T n >-． 【答案】（Ⅰ）12n na =（Ⅱ）证明略.【解析】 试题分析：第一问根据题中所给的式子是一个和式，所以类比着写出将n 写成1n -时对应的式子，将两式子相减，得到当2n ≥时n a 关于n 的关系式，令1n =，求出1a 的值，验证上式成立，从而求得12n n a =，第二问对n b 的关系式进行转化，进行适当的放缩，转化为比较容易求和的式子，从而得结果. 试题解析：（Ⅰ）当1n =时，112a =． ………………2分 当2n ≥时，22123112222n n n a a a a ---+++⋅⋅⋅+=，相减得1112222n n n n a --=-= 所以，当2≥n 时，.21n n a = ………………4分 当1n =时，211=a 也满足上式，所求通项公式12n n a =……………6分． （Ⅱ）11111221121211()1()22n n n n n n n b +++=+=++-+- 21121n n +-=++1121121n n ++-+-1121n =-+1++1121n +- 12(21n =--+1121n +-) ． ………………8分 由11212n n <+，1111212n n ++>-， 得121n -+1121n +-12n <-112n +．所以n b 12(21n =--+1121n +-)12(2n >--112n +)． ………………12分 从而122231111111[2()][2()][2()]222222n n n n T b b b +=+++>--+--++-- 22311111112[()()]()]222222n n n +=--+-++-11112()2222n n n +=-->-，即n T >122n -．………………14分 考点：数列的通项公式，数列求和，放缩法.。

浙江省杭州地区（含周边）重点中学 2014—2015学年度上学期期末考试高二数学文试题考生须知：1．本卷满分120分，考试时间100分钟；2．答题前，在答题卷密封区内填写班级、学号和姓名；座位号写在指定位置； 3．所有答案必须写在答题卷上，写在试卷上无效； 4．考试结束后，只需上交答题卷。

一、选择题（本大题共10小题，每小题4分，共40分，每小题给出的四个选项中，只有一项是符合题目要求的）1．半径为2cm 的球的体积是（ ▲ ） A ． cm 3 B ． cm 3 C ． cm 3 D ． cm 3 2．直线x ＝－的倾斜角和斜率分别是（ ▲ ） A ．45°，1 B ．135°，－1 C ．90°，不存在 D ．180°，不存在 3.已知实数，则是且的（ ▲ ）条件A 充分不必要B 必要不充分C 充要D 既不充分也不必要4.设是两个不同的平面，是一条直线，以下命题正确的是（ ▲ ）A ．若，则 B ．若，则C ．若，则 D ．若，则5．六个棱长为1的正方体在桌面上堆叠成一个几何体，该几何体的正视图与俯视图如下图所示，则其左视图不可能为（ ▲ ）A. B. C. D.6．若直线与圆2240x y kx my +++-=交于M ，N 两点，且M ，N 关于直线对称，则的值是（ ▲ ） A ． B ．0 C ． D ． 3 7.已知双曲线与椭圆共顶点，且焦距是6，此双曲线的渐近线是（ ▲ ） A ． B ． C ． D ．8．已知椭圆的左、右焦点分别为、，过且斜率为2的直线交椭圆于、两点，若△为直角三角形，则椭圆的离心率为（ ▲ ）A ．53B ．23C ．23D ．139.三棱柱中，与、所成角均为，，且，则与所成角的余弦值为（ ▲ ）A ．1B ．－1C ．D ．－10．已知ABCD-ABCD 是边长为1的正方体，P 为线段AB 上的动点，Q 为底面ABCD 上的动点，则最小值为（ ▲ ） A ． B ． C ．2 D ． 二．填空题（共7小题，每小题4分，共28分）11.在空间直角坐标系中，是点关于轴的对称点，则= ___▲___． 12.两平行直线与之间的距离为___▲___．13.设抛物线的准线为，为抛物线上的动点，定点，则与点到准线的距离之和的最小值为___▲___． 14. 某几何体的三视图如图所示，该几何体的体积为___▲___．15.如图四边形是边长为1的正方形，平面，平面，且,为中点，则下列结论中正确的是___▲___．①； ②//平面； ③平面平面； ④平面//平面.16.已知分别是双曲线的左右焦点，A 是双曲线在第一象限内的点，若且，延长交双曲线右支于点B ，则的面积等于___▲___．17.已知动点在椭圆上，若A 点的坐标为(6,0)，，且，则的最小值为___▲___．三、解答题：（共4小题，共52分，解题应写出文字说明，证明过程或演算步骤.） 18.（本题满分12分）已知命题13102:22=-+-m y m x p 方程表示焦点在轴上的椭圆； 已知命题125:22=+-my m x q 方程表示双曲线； 若为真，为假，求实数的取值范围。