多元统计分析课程设计题目知识分享
- 格式:pdf
- 大小:1.27 MB
- 文档页数:13

多元统计分析学习笔记——概论及数据描述知识点回顾这个系列的笔记是疫情期间在家听的⽹络课程——多元统计分析,由经院刘婧媛、钟威两位⽼师主讲,从中国⼤学mooc上可以搜到。
笔记将对课程的主要知识点进⾏总结和整理,记录⼀些课程截图,也会从⽹上搜集⼀些相关的资料,⽬的是加深认识,防⽌遗忘。
今后如果对相关内容有了更深的理解和认识,可能会对内容进⾏更正和补充。
本⽂为前两章的总结多元统计分析是同时考量多个变量,从多元数据集中获取信息的统计⽅法。
⼀个经典的例⼦就是鸢尾花数据集,其中的每个样本包含了四个特征和⼀个对应的标签,如下图所⽰,通过统计分析,⼈们可以找到鸢尾花类型(标签)与四个特征之间的关系,从⽽实现未来利⽤新数据已知的特征变量对未知的花类型进⾏预测的⽬标。
多元统计分析在市场营销、⾦融⾏业、医疗及学术研究等各个领域都有着⼴泛的应⽤。
1 随机变量数据描述样本就是通过采样获得的部分数据点。
随机采样的样本均值可以⽤来估计总体均值。
样本⽅差是对总体⽅差的⽆偏估计。
对于多元随机向量,样本的期望是由各个分量的期望组成的向量随机向量:由多个随机变量组成的向量。
⼀般⽤来代表整个数据集对应的样本向量Y = (y1,……,y n)。
随机样本:是指总体中的每个个体都有同等的机会被选中。
⼀般代表数据集中任意⼀个样本对应的特征向量。
y n = (y n1,……,y np)对于⼆元随机变量,协⽅差等于变量乘积的均值减去变量均值的乘积。
变量间正相关则协⽅差cov(x,y) > 0,负相关cov(x,y) < 0,不相关则cov(x,y) = 0,此处所谓正相关负相关皆属于线性相关关系。
相关系数实际上是消除了量纲的协⽅差,将度量尺度标准化为[1,-1]区间,其中σ=0时说明X与Y不相关(线性独⽴)。
值得注意的是,σ=0时只能说明X与Y线性独⽴,⽽仍有可能以某种⾮线性的⽅式关联,但如果X和Y服从⼆元正态分布,并满⾜σ=0,则可认为是相互独⽴的。

多元统计分析复习题一、填空题1、设有n 个一维数据:12,,...,n x x x ,则均值x -=________,方差2_____________s =。
若将它们从小到大记为(1)(2)(),,...,n x x x ,中位数M=______________________,极差R=______________。
2、请指出下面SPSS 软件操作分别代表多元统计分析中什么分析: (1)Analysis→Classify→Discriminant (2)Analysis→Data Reduction →Factor3、系统聚类法是在聚类分析的开始,每个样本自成 ________ ;然后 ,按照某种方法度量所有样本之间的亲疏程度,并把最相似的样本首先聚成一小类;接下来,度量剩余的样本和小类间的___________,并将当前最接近的样本或小类再聚成一类;如此反复,直到所有样本聚成一类为止。
4、设12(0,1),,,...,in N ξξξξ且相互独立,则n21n212_______;________ii ii ξξξ==∑∑。
5、在线性回归模型中,设因变量Y 与自变量121,,...,p XX X -的n 组观测数据为1,1(;,...,)(1,2,...,i i i p y x x i n -=),记11nii y y n ==∑,线性拟合值0111,1ˆˆˆˆ...i i p i p y x x βββ--=+++,则总离差平方和___________SST =,残差平方和___________SSE =,回归平方和__________SSR =,三者之间关系为___________________。
6、设x,y 是来自均值向量为μ,协方差矩阵为∑的总体G 的两个样品,则x,y之间的马氏平方距离2(,)______________d x y =;x 与总体G 的马氏平方距离2(,)______________d x G =。

填空题:1、费希尔(Fisher)判别法是1936年提出来的,该方法的主要思想是通过将多维数据投影到某个方向上。
2、因子分析的内容非常丰富,常用的因子分析类型是R型因子分析和Q型因子分析。
3、K均值聚类分析的基本思想是将每一个样品分配给最接近业壶些直的类中。
4、对应分析是将R型因子分析Q型因子分析结合起来进行的统计分析方法。
5、总体方差未知的情况下,采用样本方差代替总体方差的方法进行计算。
6、主成分分析数学模型中的正交变换,在几何上就是作一个坐标旋转7、设X、N2 ( U , N),其中X=(》1,》2),号),则CovQq +》2,*1 - *2)= _0__8、判别分析是判别样品所属类型的一种统计方法,常用的判别方法有距离判别法、Fisher 判另U法、Bayes判另U法、逐步判另U法9 多元正态分布的任何边缘分布为正态分布10、应用多元统计分析方法用于解决多指标问题,聚类分析就是分析如何对样品(或变量)进行量化分类的问题。
通常聚类分析分为Q型聚类和R型聚类。
11、总离差平方和可以分解为回归离差平方和和剩余离差平方和两个部分,各自的自由度为(P )和(n-p-1),其中回归离差平方和在总离差平方和中所占比重越大,则线性回归效果越显著。
12、系统聚类分析方法有最短距离法、最长距离法、中间距离法、重心法、类平均统和可变类平均法。
13、典型相关分析是研究两组变量之间相关关系的一种多元统计方法14、因子分析中因子载荷系数叫,•的统计意义是:(第i个变量与第j个公因子的相关系数)15、相应分析的特点是研究的变量是定性的16、公共因子方差与特殊因子方差之和为o17、设Z 是总体X=(X”…,乂皿)的协方差阵,X 的特征根人。
=1,2,..・田)与对应的单位正交化特征向量% =(%,%2,,则第一主成分的表达式=% ]X| + %2、2 + ・•• + /mX"],方差为2]18、相应分析的主要目的是寻求列联表行因素A和列因素B的基本分析特征和它们的最优联立表示19聚类分析一是分析如何对样品或变量进行量化分类的问题。

一、什么是多元统计分析❖多元统计分析是运用数理统计的方法来研究多变量(多指标)问题的理论和方法,是一元统计学的推广。
❖多元统计分析是研究多个随机变量之间相互依赖关系以及内在统计规律的一门统计学科。
二、多元统计分析的内容和方法❖1、简化数据结构(降维问题)将具有错综复杂关系的多个变量综合成数量较少且互不相关的变量,使研究问题得到简化但损失的信息又不太多。
(1)主成分分析(2)因子分析(3)对应分析等❖2、分类与判别(归类问题)对所考察的变量按相似程度进行分类。
(1)聚类分析:根据分析样本的各研究变量,将性质相似的样本归为一类的方法。
(2)判别分析:判别样本应属何种类型的统计方法。
例5:根据信息基础设施的发展状况,对世界20个国家和地区进行分类。
考察指标有6个:1、X1:每千居民拥有固定电话数目2、X2:每千人拥有移动电话数目3、X3:高峰时期每三分钟国际电话的成本4、X4:每千人拥有电脑的数目5、X5:每千人中电脑使用率6、X6:每千人中开通互联网的人数❖3、变量间的相互联系一是:分析一个或几个变量的变化是否依赖另一些变量的变化。
(回归分析)二是:两组变量间的相互关系(典型相关分析)❖4、多元数据的统计推断点估计参数估计区间估计统 u检验计参数 t检验推 F检验断假设相关与回归检验卡方检验非参秩和检验秩相关检验❖1、假设检验的基本原理小概率事件原理❖ 小概率思想是指小概率事件(P<0.01或P<0.05等)在一次试验中基本上不会发生。
反证法思想是先提出假设(检验假设H0),再用适当的统计方法确定假设成立的可能性大小,如可能性小,则认为假设不成立;反之,则认为假设成立。
❖ 2、假设检验的步骤 (1)提出一个原假设和备择假设❖ 例如:要对妇女的平均身高进行检验,可以先假设妇女身高的均值等于 160 cm (u=160cm )。
这种原假设也称为零假设( null hypothesis ),记为 H 0 。

多元统计分析(1)题目:多元统计分析知识点研究生专业指导教师完成日期 2013年 12月目录第一章绪论 (1)§1.1什么是多元统计分析 ....................................................................................................... 1 §1.2多元统计分析能解决哪些实际问题 ............................................................................... 2 §1.3主要内容安排 ................................................................................................................... 2 第二章多元正态分布 .. (2)§2.1基本概念 ........................................................................................................................... 2 §2.2多元正态分布的定义及基本性质 .. (8)1.(多元正态分布)定义 ................................................................................................ 9 2.多元正态变量的基本性质 (10)§2.3多元正态分布的参数估计12(,,,)p X X X X '= (11)1.多元样本的概念及表示法 (12)2. 多元样本的数值特征 ................................................................................................ 123.μ和∑的最大似然估计及基本性质 (15)4.Wishart 分布 (17)第五章 聚类分析 (18)§5.1什么是聚类分析 ............................................................................................................. 18 §5.2距离和相似系数 . (19)1.Q —型聚类分析常用的距离和相似系数 ................................................................ 20 2.R 型聚类分析常用的距离和相似系数 ...................................................................... 25 §5.3八种系统聚类方法 (26)1.最短距离法 .................................................................................................................. 27 2.最长距离法 .................................................................................................................. 30 3.中间距离法 .................................................................................................................. 32 4.重心法 .......................................................................................................................... 35 5.类平均法 ...................................................................................................................... 37 6.可变类平均法 .............................................................................................................. 38 7.可变法 .......................................................................................................................... 38 8.离差平方和法(Word 方法) (38)第六章判别分析 (39)§6.1什么是判别分析 ............................................................................................................. 39 §6.2距离判别法 (40)1、两个总体的距离判别法 (40)2.多总体的距离判别法 (45)§6.3费歇(Fisher)判别法 (46)1.不等协方差矩阵两总体Fisher判别法 (46)2.多总体费歇(Fisher)判别法 (51)§6.4贝叶斯(Bayes)判别法 (58)1.基本思想 (58)2.多元正态总体的Bayes判别法 (59)§6.5逐步判别法 (61)1.基本思想 (61)2.引入和剔除变量所用的检验统计量 (62)3.Bartlett近似公式 (63)第一章绪论§1.1什么是多元统计分析在自然科学、社会科学以及经济领域中,常常需要同时观察多个指标。

实用多元统计分析相关习题练习题一、填空题1.人们通过各种实践,发现变量之间的相互关系可以分成(相关)和(不相关)两种类型。
多元统计中常用的统计量有:样本均值、样本方差、样本协方差和样本相关系数。
2.总离差平方和可以分解为(回归离差平方和)和(剩余离差平方和)两个部分,其中(回归离差平方和)在总离差平方和中所占比重越大,则线性回归效果越显著。
3.回归方程显著性检验时通常采用的统计量是(S R/p)/[S E/(n-p-1)]。
4.偏相关系数是指多元回归分析中,(当其他变量固定时,给定的两个变量之间的)的相关系数。
5.Spss中回归方程的建模方法有(一元线性回归、多元线性回归、岭回归、多对多线性回归)等。
6.主成分分析是通过适当的变量替换,使新变量成为原变量的(线性组合),并寻求(降维)的一种方法。
7.主成分分析的基本思想是(设法将原来众多具有一定相关性(比如P个指标),重新组合成一组新的互相无关的综合指标来替代原来的指标)。
8.主成分表达式的系数向量是(相关系数矩阵)的特征向量。
9.样本主成分的总方差等于(1)。
10.在经济指标综合评价中,应用主成分分析法,则评价函数中的权数为(方差贡献度)。
主成分的协方差矩阵为(对称)矩阵。
主成分表达式的系数向量是(相关矩阵特征值)的特征向量。
11.SPSS中主成分分析采用(analyze—data reduction—facyor)命令过程。
12.因子分析是把每个原始变量分解为两部分因素,一部分是(公共因子),另一部分为(特殊因子)。
13.变量共同度是指因子载荷矩阵中(第i行元素的平方和)。
14.公共因子方差与特殊因子方差之和为(1)。
15.聚类分析是建立一种分类方法,它将一批样品或变量按照它们在性质上的(亲疏程度)进行科学的分类。
16.Q型聚类法是按(样品)进行聚类,R型聚类法是按(变量)进行聚类。
17.Q型聚类统计量是(距离),而R型聚类统计量通常采用(相关系数)。

《多元统计分析》复习一、填空题1、设k 是常数,x 是随机变量,则()E kx = ;设x ,y 是随机变量,且两者独立,则()V x y +=2、多元正态分布是 在多元情形下的直接推广;最简单的多元正态分布是3、聚类分析可分为 聚类分析和 聚类分析4、在判别分析中,通常用 距离来度量样品到组的距离5、需考虑先验概率和 是贝叶斯判别不同于其他判别法的关键之处6、用于大数据集的一种聚类方法是7、在主成分分析中,第一主成分包含的信息量 ;本质上,主成分分析是一种 方法8、在因子分析中,因子载荷是 的;模型不受 的影响9、在SAS 中,判别分析运用的是 过程10、典型相关分析能够有效地揭示两组变量之间的 关系1、设k 是常数,则()E k = ;设x ,y 是随机变量,则()V x y +=2、一元正态分布在多元情形下的直接推广是 ;最简单的多元正态分布是3、聚类分析可分为 聚类分析和 聚类分析4、在判别分析中,通常用 距离来度量样品到组的距离5、需考虑先验概率和 是贝叶斯判别不同于其他判别法的关键之处6、用于大数据集的一种聚类方法是7、在主成分分析中,第一主成分包含的信息量 ;本质上,主成分分析是一种 方法8、对于典型相关分析,可运用SAS 软件中的 过程进行计算;对于聚类分析,可运用SAS 软件中的 过程进行计算9、在SAS 中,判别分析运用的是 过程10、典型相关分析是研究两组变量之间 关系的统计分析方法1、设k 是常数,x 是随机变量,则()V kx = 。
2、设A 为常数矩阵,b 是常数向量,则()V Ax b += 。
3、设随机向量(0,)q u N I ,μ为p 维常数向量,A 为p q ⨯常数矩阵,若x Au μ=+,则x 。
4、常用的判别分析方法有 、 和 。
5、通常测量变量有三种尺度:间隔尺度、有序尺度和 。
6、因子分析是主成分分析的推广,它也是一种 技术。
7、主成分分析的目的是:(1)变量的降维;(2) 。

1.什么是单变量(一元)分析?什么是多元分析?对多变量资料为什么不能用一元分析代替多元分析?答案:应变量(因变量/反应变量)即分析指标仅一个时:称一元分析或单变量分析。
应变量(因变量/反应变量)即分析指标有多个时:称多元分析/多变量分析。
◆对多变量资料分别进行单变量分析,可能导致①增大犯第Ⅰ类错误的概率②当单变量分析结果不一致时,很难得到一个综合的结论③忽略变量间的相互关系。
◆因此,多元分析与一元分析在使用时是相辅相成的。
◆多元统计分析具有概括和全面考虑的综合能力和特点◆一元分析(单指标)容易分析各指标各组间的关系和差异◆两种结合起来所得结论更丰富2.某研究者对当地40岁以上人群进行调查,收集性别、、年龄与患冠状动脉疾病数据,并进行回归分析,数据的编码及软件分析结果如下,写出回归模型的一般形式,并解释各回归系数(结合值)。
因素性别赋值说明1=男性,0=女性1=段压低<0.1,2=段压低范围在0.1~0.23=段压低范围≥0.2年龄(岁)冠状动脉疾是=1否=0病Y软件分析结果因素常数回归系数-20.207标准误4.562卡方18.666P值0.000值项性别年龄0.2631.6340.0850.6360.6820.0360.1715.7445.5210.6790.0720.017 5.1240.019 1.089答案:20.207+0.263性别+1.6340.085年龄根据软件结果可知,影响冠状动脉疾病患病的因素有和年龄;偏回归系数解释实际是对的解释:的值为5.124,即每增加一个等级,患冠状动脉疾病的风险增加4.124倍(5.124-1))并且的影响大于年龄的影响;年龄值1.089,年龄增大一岁患冠状动脉疾病的风险是原来的1.089倍。
3、测定n例糖尿病人的血糖(Y,),胰岛素(X1)以及生长素(X2,)的数值,均为定量资料。
并建立了血糖对于胰岛素及生长素的多重线性回归方程,Y=17.0018-0.4059X1+0.0977X2.假定经过检验方程有意义,且两个偏回归系数都有统计学意义,请回答:1)多重线性回归对应变量和自变量有哪些要求?答案:Y(应变量)变量服从正态分布的连续性随机变量;自变量x大多数应为连续性变量,可以有少部分的分类变量(两分类、无序多分类和有许多分类)2)请解释两个偏回归系数的含义。

多元统计分析习题与答案多元统计分析是一种在社会科学研究中广泛应用的方法,它通过同时考虑多个变量之间的关系,帮助研究者更全面地理解和解释现象。
在本文中,我将分享一些多元统计分析的习题和答案,希望能够帮助读者更好地掌握这一方法。
习题一:相关分析假设你正在研究一个学生的学习成绩和他们每天花在学习上的时间之间的关系。
你收集了100个学生的数据,学习成绩用分数表示,学习时间用小时表示。
以下是你的数据:学习成绩(X):75, 80, 85, 90, 95, 70, 65, 60, 55, 50学习时间(Y):5, 6, 7, 8, 9, 4, 3, 2, 1, 0请计算学习成绩和学习时间之间的相关系数,并解释其含义。
答案一:首先,我们需要计算学习成绩和学习时间之间的协方差和标准差。
根据公式,协方差可以通过以下公式计算:协方差= Σ((X - X平均) * (Y - Y平均)) / (n - 1)其中,X和Y分别表示学习成绩和学习时间,X平均和Y平均表示它们的平均值,n表示样本数量。
标准差可以通过以下公式计算:标准差= √(Σ(X - X平均)² / (n - 1))根据以上公式,我们可以得出学习成绩和学习时间之间的协方差为-22.5,标准差分别为18.03和2.87。
然后,我们可以通过以下公式计算相关系数:相关系数 = 协方差 / (X标准差 * Y标准差)根据以上公式,我们可以得出相关系数为-0.93。
由于相关系数接近于-1,可以得出结论:学习成绩和学习时间之间存在强烈的负相关关系,即学习时间越长,学习成绩越低。
习题二:多元线性回归假设你正在研究一个人的身高(X1)、体重(X2)和年龄(X3)对其收入(Y)的影响。
你收集了50个人的数据,以下是你的数据:身高(X1):160, 165, 170, 175, 180, 185, 190, 195, 200, 205体重(X2):50, 55, 60, 65, 70, 75, 80, 85, 90, 95年龄(X3):20, 25, 30, 35, 40, 45, 50, 55, 60, 65收入(Y):5000, 5500, 6000, 6500, 7000, 7500, 8000, 8500, 9000, 9500请利用多元线性回归分析,建立一个预测人的收入的模型,并解释模型的结果。
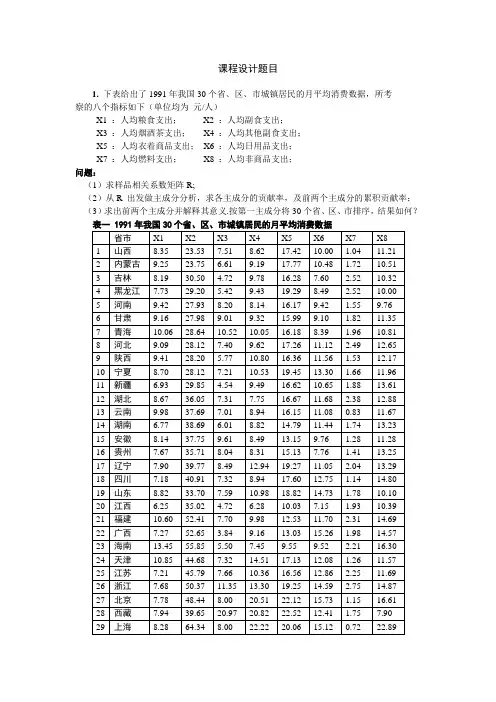
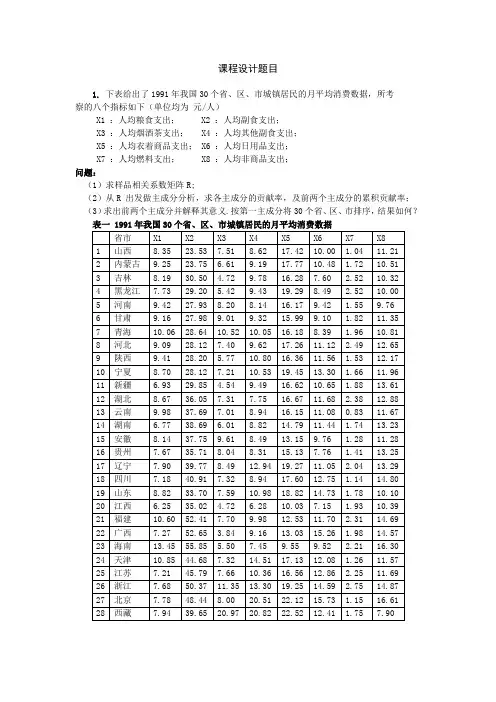
课程设计题目1. 下表给出了1991年我国30个省、区、市城镇居民的月平均消费数据,所考察的八个指标如下(单位均为元/人)X1 :人均粮食支出;X2 :人均副食支出;X3 :人均烟酒茶支出;X4 :人均其他副食支出;X5 :人均衣着商品支出;X6 :人均日用品支出;X7 :人均燃料支出;X8 :人均非商品支出;问题:(1)求样品相关系数矩阵R;(2)从R 出发做主成分分析,求各主成分的贡献率,及前两个主成分的累积贡献率;(3)求出前两个主成分并解释其意义.按第一主成分将30个省、区、市排序,结果如何?2. 下表是49位女性在空腹情况下三个不同时刻的血糖含量(用X1 ,X2 ,X3表示)和摄入等量食糖一小时后的三个时刻的血糖含量(用小X4 ,X5 ,X6表示)的观测值(单位:mg/100ml).问题:分别从样本协方差阵S和样本相关系数矩阵R出发做主成分分析,求主成分的贡献率和各个主成分. 在两种情况下,你认为应保留几个主成分?其意义如何解释?就此而言,你认为基于S和R的分析那个结果更为合理?3. 考察1985年至2000年全国如下各价格指数:X1 :商品零售价格指数;X2 :居民消费价格指数;X3 :城市居民消费价格指数;X4 :农村居民消费价格指数;X5 :农产品收购价格指数;X6 :农村工业品零售价格指数;观测数据见下表.问题:按年份用下列方法进行系统聚类分析,画出谱系聚类图,并给出聚为3类的结果.(a)最短距离法;(b)最长距离法;(c)类平均距离法;4. 考察1985年至2000年全国如下各价格指数:X1 :商品零售价格指数;X2 :居民消费价格指数;X3 :城市居民消费价格指数;X4 :农村居民消费价格指数;X5 :农产品收购价格指数;X6 :农村工业品零售价格指数;观测数据见下表.问题:先将数据标准化,再按年份用下列方法进行系统聚类分析,画出谱系聚类图,并给出聚为3类的结果.(a)最短距离法;(b)最长距离法;(c)重心距离法.5. 研究货运总量y(万吨)与工业总产值x1(亿元)、农业总产值x2(亿元)。
多元统计复习题答案一、单项选择题1. 多元统计分析中,用于描述多个变量之间关系的统计方法是()。
A. 相关分析B. 聚类分析C. 因子分析D. 主成分分析答案:C2. 以下哪个不是多元统计分析中常用的降维方法?()A. 主成分分析B. 因子分析C. 聚类分析D. 典型相关分析答案:C3. 在多元统计分析中,用于识别数据集中的异常值或离群点的统计方法是()。
A. 马氏距离B. 箱线图C. 相关系数D. 卡方检验答案:B二、多项选择题1. 多元统计分析中,以下哪些方法可以用来进行变量选择?()A. 逐步回归B. 岭回归C. 偏最小二乘回归D. 主成分分析答案:A|B|C2. 多元统计分析中,以下哪些方法可以用来进行数据的分类?()A. 判别分析B. 聚类分析C. 因子分析D. 典型相关分析答案:A|B三、判断题1. 多元统计分析中的因子分析可以用于变量的降维。
(对)2. 多元统计分析中的主成分分析和因子分析是完全相同的方法。
(错)3. 多元统计分析中的聚类分析可以用于识别数据集中的异常值。
(错)四、简答题1. 简述多元统计分析中主成分分析(PCA)的主要步骤。
答:主成分分析的主要步骤包括:数据标准化、计算协方差矩阵、求解特征值和特征向量、选择主成分、构造主成分得分。
2. 描述多元统计分析中判别分析的应用场景。
答:判别分析在多元统计分析中主要应用于根据已有的分类变量来预测新样本的分类,例如在医学诊断、市场细分、信用评分等领域。
五、计算题1. 给定一组数据,计算其主成分得分。
答:首先需要对数据进行标准化处理,然后计算协方差矩阵,接着求解特征值和特征向量,最后根据特征值的大小选择前几个主成分,并计算对应的得分。
2. 利用判别分析对一组数据进行分类,并给出分类结果。
答:首先需要确定分类的依据,然后计算各类别的判别函数,接着对新样本进行判别分析,最后根据判别得分将样本分类到相应的类别中。
一、填空题:1、多元统计分析是运用数理统计方法来研究解决多指标问题的理论和方法.2、回归参数显著性检验是检验解释变量对被解释变量的影响是否著.3、聚类分析就是分析如何对样品(或变量)进行量化分类的问题。
通常聚类分析分为 Q型聚类和R型聚类。
4、相应分析的主要目的是寻求列联表行因素A 和列因素B 的基本分析特征和它们的最优联立表示。
5、因子分析把每个原始变量分解为两部分因素:一部分为公共因子,另一部分为特殊因子。
6、若()(,), Px N αμα∑=1,2,3….n且相互独立,则样本均值向量x服从的分布为_x~N(μ,Σ/n)_。
二、简答1、简述典型变量与典型相关系数的概念,并说明典型相关分析的基本思想。
在每组变量中找出变量的线性组合,使得两组的线性组合之间具有最大的相关系数。
选取和最初挑选的这对线性组合不相关的线性组合,使其配对,并选取相关系数最大的一对,如此下去直到两组之间的相关性被提取完毕为止。
被选出的线性组合配对称为典型变量,它们的相关系数称为典型相关系数。
2、简述相应分析的基本思想。
相应分析,是指对两个定性变量的多种水平进行分析。
设有两组因素A和B,其中因素A包含r个水平,因素B包含c个水平。
对这两组因素作随机抽样调查,得到一个rc的二维列联表,记为。
要寻求列联表列因素A和行因素B 的基本分析特征和最优列联表示。
相应分析即是通过列联表的转换,使得因素A 和因素B具有对等性,从而用相同的因子轴同时描述两个因素各个水平的情况。
把两个因素的各个水平的状况同时反映到具有相同坐标轴的因子平面上,从而得到因素A 、B 的联系。
3、简述费希尔判别法的基本思想。
从k 个总体中抽取具有p 个指标的样品观测数据,借助方差分析的思想构造一个线性判别函数 系数:确定的原则是使得总体之间区别最大,而使每个总体内部的离差最小。
将新样品的p 个指标值代入线性判别函数式中求出 值,然后根据判别一定的规则,就可以判别新的样品属于哪个总体。
题目:研究不同温度与不同湿度对粘虫发育历期的影响,得试验数据如表。
分析不同温度和湿度对粘虫发育历期的影响是否存在着显著性差异。
(注:要对方差齐性进行检验)不同温度与不同湿度粘虫发育历期表根据上述题目,分析结果如下。
一、相关理论概述F 检验与方差齐性检验在方差分析的F 检验中,是以各个实验组内总体方差齐性为前提的,因此,按理应该在方差分析之前,要对各个实验组内的总体方差先进行齐性检验。
如果各个实验组内总体方差为齐性,而且经过F 检验所得多个样本所属总体平均数差异显著,这时才可以将多个样本所属总体平均数的差异归因于各种实验处理的不同所致;如果各个总体方差不齐,那么经过F 检验所得多个样本所属总体平均数差异显著的结果,可能有一部分归因于各个实验组内总体方差不同所致。
但是,方差齐性检验也可以在F 检验结果为多个样本所属总体平均数差异显著的情况下进行,因为F 检验之后,如果多个样本所属总体平均数差异不显著,就不必再进行方差齐性检验。
本文分析数据采用后一种方法,即先F 检验再方差齐次性检验。
相对湿度(%) 温度℃ 重复1 2 3 4 10025 91.2 95.0 93.8 93.0 2787.6 84.7 81.2 82.4 29 79.2 67.0 75.7 70.6 31 65.2 63.3 63.6 63.3 8025 93.2 89.3 95.1 95.5 2785.8 81.6 81.0 84.4 29 79.0 70.8 67.7 78.8 31 70.7 86.5 66.9 64.9 4025 100.2 103.3 98.3 103.8 2790.6 91.7 94.5 92.2 29 77.2 85.8 81.7 79.7 3173.673.276.472.5二、从单因子方差角度分析(一)在假定相对湿度不变的情况下分析1、假定相对湿度恒为40%,分析不同温度对粘虫发育历期的影响。
如下表: 温度℃重复252729311100.2 90.6 77.2 73.6 2 103.3 91.7 85.8 73.2 3 98.3 94.5 81.7 76.4 4 103.8 92.2 79.7 72.5 Ti 405.6 369324.4295.7T 2i164511.36136161105235.36 87438.49在本例中,r=4,m=4, n=16 ,=1394.7,= 123413.4696T 2/n=(1394.7)2/16=121574.2556 (式1)( 式2)(式3)S E =S T -S A =1839.214-1762.297=76.917 (式4)数据的方差分析表见表1.表1 粘虫发育历期方差分析表粘虫发育历期 (相对湿度40%)来源平方和 df 均方 F 显著性 组间 1762.297 3 587.432 91.646.000组内 76.917 12 6.410总数1839.21415分析表1可知,F 0.05(3,12)=3.49,F 值=,91.646,F>F 0.05,P=0.000<0.05,说明在相对湿度为40%时,不同温度对粘虫发育历期有显著影响。
(完整版)多元统计分析试题及答案试题:1. 试解释多元统计分析的含义及其与单变量和双变量统计分析的区别。
2. 简述卡方检验方法及适用场景。
3. 请解释回归分析中的回归系数及其p值的含义及作用,简单说明如何进行回归模型的选择和评估。
4. 试解释主成分分析的原理及目的,如何进行主成分分析及如何解释因子载荷矩阵。
5. 请列举和简要解释聚类分析和判别分析的适用场景,并说明两种方法的区别。
答案:1. 多元统计分析是一种将多个变量进行综合分析的方法。
与单变量和双变量统计分析不同的是,多元统计分析可以处理多个自变量和因变量的组合关系,从而探究它们之间的综合关系。
该方法通常适用于探究多种变量在某个问题中的关系、探究影响某一结果变量的因素、探究各个变量相互作用的影响等。
2. 卡方检验是根据样本数据与期望值的差异来判断观察值与理论预期是否相符,以此来验证假设是否成立的方法。
它通常用于对某个现象进行分类的相关度检验。
适用场景包括:样本的数量大于等于40,且至少有一个期望值小于5;变量为分类变量,且分类类别数不超过10个。
卡方检验的原理是将观察值和期望值进行比较,并计算卡方值,然后根据卡方值与自由度的乘积查找p值,从而得出结论。
3. 回归系数是回归方程中自变量与因变量之间的关系,在线性回归中,回归系数表示每一个自变量单位变化与因变量单位变化的关系。
p值是评估回归系数是否具有显著性的指标。
回归模型的选择有两种方法:一种是逐步回归分析,根据不同的准则进行多个回归模型的比较,选择最优的模型;另一种是正则化回归,通过加入惩罚项来保证回归模型具有良好的泛化性能。
回归模型的评估有多种方法,包括:残差分析、R方值、方差齐性检验、变量的共线性检验等。
4. 主成分分析是一种将多维数据降维处理的方法,它的目的是通过数据的变换,将多个变量转化为一些综合指标,这些指标是原始变量的线性组合。
主成分分析的步骤包括:数据标准化、计算协方差矩阵或相关系数矩阵、计算特征值和特征向量、选取主成分。
多元统计分析思考题第一章 回归分析1、回归分析是怎样的一种统计方法,用来解决什么问题答:回归分析作为统计学的一个重要分支,基于观测数据建立变量之间的某种依赖关系,用来分析数据的内在规律,解决预报、控制方面的问题;2、线性回归模型中线性关系指的是什么变量之间的关系自变量与因变量之间一定是线性关系形式才能做线性回归吗为什么答:线性关系是用来描述自变量x 与因变量y 的关系;但是反过来如果自变量与因变量不一定要满足线性关系才能做回归,原因是回归方程只是一种拟合方法,如果自变量和因变量存在近似线性关系也可以做线性回归分析;3、实际应用中,如何设定回归方程的形式答:通常分为一元线性回归和多元线性回归,随机变量y 受到p 个非随机因素x1、x2、x3……xp 和随机因素的影响,形式为:01p βββ⋅⋅⋅是p+1个未知参数,ε是随机误差,这就是回归方程的设定形式;4、多元线性回归理论模型中,每个系数偏回归系数的含义是什么答:偏回归系数01p βββ⋅⋅⋅是p+1个未知参数,反映的是各个自变量对随机变量的影响程度;5、经验回归模型中,参数是如何确定的有哪些评判参数估计的统计标准最小二乘估计法有哪些统计性质要想获得理想的参数估计值,需要注意一些什么问题答:经验回归方程中参数是由最小二乘法来来估计的;评判标准有:普通最小二乘法、岭回归、主成分分析、偏最小二乘法等;最小二乘法估计的统计性质:其选择参数满足正规方程组,1选择参数01ˆˆββ分别是模型参数01ββ的无偏估计,期望等于模型参数; 2选择参数是随机变量y 的线性函数要想获得理想的参数估计,必须注意由于方差的大小表示随机变量取值的波动性大小,因此自变量的波动性能够影响回归系数的波动性,要想使参数估计稳定性好,必须尽量分散地取自变量并使样本个数尽可能大;6、理论回归模型中的随机误差项的实际意义是什么为什么要在回归模型中加入随机误差项建立回归模型时,对随机误差项作了哪些假定这些假定的实际意义是什么答:随机误差项的引入使得变量之间的关系描述为一个随机方程,由于因变量y 很难用有限个因素进行准确描述说明,故其代表了人们的认识局限而没有考虑到的偶然因素;7、建立自变量与因变量的回归模型,是否意味着他们之间存在因果关系为什么答:不是,因果关系是由变量之间的内在联系决定的,回归模型的建立只是一种定量分析手段,无法判断变量之间的内在联系,更不能判断变量之间的因果关系;8、回归分析中,为什么要作假设检验检验依据的统计原理是什么检验的过程是怎样的答:因为即使我们已经建立起了模型,但是尚且不知这个回归方程是否能够比较好地反映所描述的变量之间的影响关系,必须进行统计学上的假设检验;假设性检验原理可以用小概率原理解释,通常认为小概率事件在一次试验中几乎不可能发生的,即对总体的某个假设是真实的,那么不支持这一个假设事件在一次试验中是几乎不可能发生的,要是这个事件发生了,我们就有理由怀疑这一假设的真实性,拒绝原假设;检验过程:1提出统计假设H0和H1;2构造一个与H相关的统计量,称其为检验统计量;3根据其显着性水平 的值,确定一个拒绝域;4作出统计决断;9、回归诊断可以大致确定哪些问题回归分析有哪些基本假定如果实际应用中不满足这些假定,将可能引起怎样的后果如何检验实际应用问题是否满足这些假定对于各种不满足假定的情形,分别采用哪些改进方法答:回归诊断解决:1回归方程的线性假定;2是否存在多重共线性;3误差项的正态性假定;4误差项的独立性假设;5误差项同方差假定;6是否存在数据异常;原基本假定H:1假设回归方程不显着;2假设回归系数不显着;引起后果:与模型误差相比,自变量对因变量的影响是不重要的模型误差太大、自变量对y的影响确实太小;如何检验:用F统计量或者P值法来检验方程的显着性;改进方法:1对于模型的误差太大,我们要想办法缩小误差,检查是否漏掉了重要的自变量,或检查自变量与y的非线性关系;2对于自变量对y影响较小,此时应该放弃回归分析方法;10、回归分析中的R2有何意义它能用来衡量模型优劣吗答:R2是回归平方和与总离差平方和之比,作为评判一个模型拟合度的标准,称为样本决定系数,其值越接近1,意味着模型的拟合优度越高;但是其不是衡量模型优劣唯一标准,增加自变量会使得自由度减少,因此需要引入自由度修正的复相关系数;这些都需要视具体的情况而定;11、如何确定回归分析中变量之间的交互作用存在交互作用时,偏回归系数的意义与不存在交互作用的情形下是否相同为什么答:交互作用是指因素之间联合搭配对试验指标的影响作用,存在交互作用是,偏回归系数肯定与不存在是的系数不同,毕竟变量之间有相互影响的关系;12、有哪些确定最优回归模型的准则如何选择回归变量答:1修正的复相关系数2aR达到最大;2预测平方和达到最小;3定义Cp 统计量值小,选择pC p小的回归方程;4赤池信息量达到最小;按照以上准则进行回归变量的选择;13、在怎样的情况下需要建立标准化的回归模型标准化回归模型与非标准化模型有何关系形式有否不同答:在多元线性回归分析中,由于涉及到的变量量纲不同,差别很大,需要对变量进行中心化和标准化,数据中心化处理相当于将坐标原点移至样本中心坐标系的平移不改变直线的斜率;标准化处理后建立的回归方程模型比非标准化的回归方程少一个常数项,系数存在关系;14、利用回归方法解决实际问题的大致步骤是怎样的答:1根据预测目标,确定自变量和因变量;2建立回归预测模型;3进行相关分析;4检验回归预测模型,计算预测误差;5计算并确定预测值;15、你能够利用哪些软件实现进行回归分析能否解释全部的软件输出结果答:目前会用的软件是SPSS和matlab,关于地球物理的软件如grapher也可以进行回归分析;对于SPSS的一些输出结果,还是不太理解;第二章判别分析1、判别分析的目的是什么答:在自然科学和社会科学研究中,研究对象用某种方法已经划分为若干类别,当得到一个新的样本数据时,要确定该样本属于已知的哪一类;2、有哪些常用的判别分析方法这些方法的基本原理或步骤是怎样的它们各有什么特点或优劣之处答:1距离判别法:根据已知分类数据,分别计算各类的重心,即是分类的均值;判别方法是—对于任意一个样品,若它与第i类的重心距离最近,就认为它来自第i类;特点是对各类数据分布并无特定的要求2Fisher判别法:其基本思想是投影,将k组m元数据投影到某一个方向,使得投影后组与组之间尽可能分开,其中利用了一元方差分析的思想导出判别函数;其特点是对总体的分布没有特殊要求,是处理概率分布未知的一种方法;3逐步判别法:逐步引入一个“最重要”的变量进入判别式,同时对先引入判别式的一些变量进行检验,如果判别能力随着引入新变量而变得不显着,则将它从判别式中剔除,直到没有新的变量能够进入,依然没有旧变量需要剔除为止;3、判别分析与回归分析有何异同之处答:1相同点:这两种方法都有关于数据预测的功能;不同点:这个估计太多了,一般来讲判别分析功能是将样品归类,回归分析是探究样品对因变量的变动影响;4、判别分析对变量与样本规模有何要求答:判别分析对总体分布没有要求,但是判别分析的假设之一是要求每一个变量不能是其他判别变量的线性组合,即不能存在多重共线性;5、如何度量判别效果有哪些影响判别效果的因素答:通过评价判别准则来度量判别效果,常用方法:1误判率回代法;2误判率交叉确认估计;影响因素是个总体之间的差异程度,各个总体之间差异越大,就越有可能建立有效的判别准则,如果差异太小,则判别分析的意义不大;当各个总体服从多元正态分布,我们可以根据各总体的均值向量是否相等进行统计检验;当然也可以检验各总体的协方差矩阵是否相等来采用判别函数;6、逐步判别是如何选择判别变量的基本思想或步骤是什么答:在判别分析中,并不是观测变量越多越好,而是选择主要变量进行判别分析,将各个变量在分析中起的不同作用,将影响力比较低的变量保留在判别式中,会增加干扰,影响效果;因此选择显着判别力的变量来建立判别式就是逐步判别法;基本思想:其与逐步回归法类似,都是采用“有进有出”的算法,即逐步引入一个“最重要”的变量进入判别式,同时对先引入的判别式进行检验,如果其判别能力随着新引入的变量显着性降低,则该因素应该被剔除,直到变量全部进入为止;7、判别分析有哪些现实应用举例说明;答:判别分析在实际中的应用无处不在;例如我们根据各种经济指标把各个国家分为发达国家和发展中国家,通过这些指标成功的判定了一个国家的经济发展水平;第三章聚类分析1、聚类分析的目的是什么与判别分析有何异同这种方法有哪些局限或欠缺答:把某些方面相似的东西进行归类,以便从中发现规律性,达到认识客观事物规律的目的;其与判别分析相同的地方是都是研究分组的问题;不同的是各自对于预先分组对象不一样,聚类分析是未知类别,判别分析是已知类别;2、有哪些常用的聚类统计量答:1Q型统计量:对样本进行聚类,用“距离”来描述样本之间的接近程度;R型统计量:对变量进行聚类,用“相似系数”来度量变量之间的近视程度;3、系统谱系聚类法的基本思想是怎样的它包含哪些具体方法答:先将待聚类的n个样品或变量各自看成一类,共有n类,然后按照事先选定的聚类方法计算每两类之间的聚类统计量,即某种距离或者相似系数,将关系最密切的两类并为一类,其余不变,即的n-1类,再按照前面的计算方法计算新类与其他类之间的距离或者相似系数,再将关系最密切的两类归为一类,其余不变,即得n-2类,继续下去,每次重复都减少一类,直到所有样品或者变量都归于一类;4、聚类分析对变量与样本规模有何要求有哪些因素影响分类效果要想减少不利因素的影响,可以采取哪些改进方法答:聚类分析要求其样本规模较大,需要变量之间相关性较弱,变量个数小于样本数;5、实际应用问题,如何确定分类数目答:按理来说聚类分析的分类数目是事先不知道的,但是在实际应用中,应该根据相关专业知识确定分类数目,结合聚类统计量参考确定,并使用误判定理具体分析;6、快速聚类法K—均值法的基本思想或步骤是怎样的答:如果待分类样品比较多,应先给出一个大概的分类,然后不断对其进行修正,一直到分类结果比较合理为止;7、有序样品的最优分别法的基本思想或步骤是怎样的答:将n个样品看成一类,然后根据分类的误差函数逐渐增加分类,寻求最优分割,用分段的方法找出使组内离差平方和最小的分割点;8、应用聚类分析解决实际问题的基本步骤是怎样的应该注意哪些方面的问题答:1n个变量样品各自成一类,一共有n类,计算两两之间的距离,构成一个对称矩阵;2选择这个对称矩阵中主对角元素以外的上或者下三角部分中的最小元素,合成的新类,并计算其与其他类之间的距离;3划去与新类有关的行和列,将新类与其余类别的距离组成新的n-1阶对称矩阵;4再重复以上步骤,直到n个样品聚为一个大类;5记录下合并类别的编号以及所对应的距离,绘制聚类图;6决定类的个数和聚类结果;第四章主成分分析与典型相关分析1、主成分分析的基本思想是什么在低维情况下,如何利用几何图形解释主成分的意义答:构造原始变量的适当线性组合,使其产生一系列互不相关的新变量,从中选出少量的几个新变量并使它们含有足够多的原始变量的信息,从而使这几个新变量代替原始变量分析问题和解决问题提供了可能;几何解释,可以借用平面上旋转坐标系方法来达到降维的目的;2、什么是主成分的贡献率与累计贡献率实际应用时,如何确定主成分的个数答:主成分中,描述第k个主成分提取的信息占据原来变量总信息的比重,称为第k个主成分的贡献率;若将前m个主成分提取的总信息的比重相加,称为主成分的累计贡献率;实际应用中,通常选取前m个主成分的累积贡献率达到一定的比列来确定主成分的个数;3、主成分有哪些基本性质答:1每一个主成分都是原始变量的线性组合;2主成分的数目大大小于原始变量的数目;3主成分保留了原始变量所包含的绝大部分信息;4各个主成分之间互不相关;4、对于任何情形的多个变量,都可以采取主成分方法降维吗为什么答:肯定不是,必须要满足适合主成分分析的要求才可以降维;举个简单的例子,其适用范围是各个变量之间应该具有比较强的相关性,如果多个变量均为各项同性,则主成分分析效果不明显;5、怎样的情况下需要计算标准化的主成分答:因为实际问题的变量有很多量纲,不同的量纲会引起各个变量的取值的分散程度差异较大,总体方差将主要受到方差较大的变量的控制;如果用协方差矩阵 求主成分,则优先照顾方差大的变量,可能会得到不合理的结果,因此为了消除量纲的影响,需要计算标准化的主成分;6、主成分有哪些应用答:它的主要作用是降维,因此应用范围比较广泛,举个例子,衡量一个城市的综合发展指数涉及到的变量参数相当多,但是如果运用主成分的思想,只需要考虑较少的变量样品就好,一般选择GDP指数、环境指数、人口、面积等;7、如何解释主成分的实际含义答:主成分的实际意义需要结合到实际应用中,其往往不是最终目的,重要的是利用降维的思想来综合分析原始信息,利用有限的主成分来解释规律,从而进行相关研究;8、典型相关分析的基本思想是什么有何实际用途答:是研究两组变量间的相互依赖关系,把两组变量之间的关系变为研究两个新变量的相关,而又不抛弃原来变量的信息;因为这两组变量所代表的内容不同,可以直接考虑其相关关系来反映两组变量之间的整体相关性;例如工厂考察使用原料质量对生产产品质量的影响,需要对产品各种各样质量指标与所使用的原料指标之间的相关关系进行评判;9、典型相关分析与回归分析、判别分析、主成分分析、因子分析有何关联试比较这些方法的异同之处;答:这是一个涉及面很大的问题,总的来讲这些方法的存在能够帮助我们对于客观数据现象的相关关系有一个更加深刻的了解,有的是对另外一种方向的优化与推广,有的本质思想与另外一种分析方法很接近,异同点可以根据教科书进行两两比对;10、典型相关分析有哪些基本假定答:线性假定影响典型相关分析的两个方面,首先任意两个变量间的相关系数是基于线性关系的;如果这个关系不是线性的,一个或者两个变量需要变换;其次,典型相关是变量间的相关,如果关系不是线性的,典型相关分析将不能测量到这种关系;11、如何解释典型相关函数的实际意义答:1典型权重标准化系数;2典型荷载结构系数;3典型交叉载荷;用以上三种参数来使多个变量与多个变量的相关性转化为两个变量的相关性;12、典型相关方法中冗余度分析的意义是什么答:冗余度主要说明典型变量对各组观测变量总方差的代表比例和解释比例;第五章因子分析与对应分析1、因子分析是怎样的一种统计方法它的基本目的和用途是什么答:其根据相关性大小将变量分组,使得同组内的变量之间相关性较高,不同组的相关性较低,每组变量代表一个基本结构,用一个不可观测的综合变量表示,这个基本结构成为公共因子,对所研究的问题就可以用最少的个数的不可观测的所谓公共因子的线性函数与特殊因子之和来描述原来观测的每一个分量;目的:利用降维的思想,从研究原始变量相关矩阵内部结构出发,把一些具有错综复杂关系的变量归结为少数几个综合因子;用途:对变量进行分类,根据因子得分值在其轴所构成的空间中吧变量点画出来,从而分类;2、因子分子中的KMO统计量与巴特莱特球形性检验的目的是什么答:KMO统计量:通过比较各个变量之间简单相关系数和偏相关系数的大小判断变量间的相关性,相关性强时,偏相关系数远小于简单相关系数,KMO值接近1.一般KMO>非常适合做因子分析;而大于都可以,但是一下不适合;巴特莱特球形检验:用于检验相关矩阵是否是单位矩阵,及各个变量是否是独立的;它以变量的相关系数矩阵为出发地点,如果统计量数值较大,且相伴随的概率值小于用户给定的显着性水平,则应该拒绝原假设;反之,则认为相关系数矩阵可能是一个单位阵,不适合做因子分析;3、因子分析有哪些类型它们有何区别Q型因子分析与聚类分析有何异同答:Q型和R型两种;Q型:对样本进行因子分析,R型:对变量进行因子分析;Q型因子分析可以认为是考虑指标的重要性,保留哪些去掉哪些;Q型聚类分析考虑的是指标的相关性,哪几类指标可能组成一类,使得组内距离尽可能小,组间距离尽可能大; 4、因子分析中的变量类型是怎样的因子分析对变量数目有没有要求对样本规模有没有要求答:被描述的变量一般来讲都是可观测的随机变量;变量必须是标准化的;样品的数目大于变量的数目;5、因子分析有怎样的基本假定对样本特点或性质有何要求答:各个共同因子之间不相关,特殊因子之间也不相关,共同因子与特殊因子之间也不相关;样本之间相关性越强越好;6、因子分析模型中,因子载荷、变量共同度、方差贡献等统计量的统计意义是什么答:1因子载荷:指综合因子与公共因子的相关关系,表示其依赖公共因子的程度,反映了第i个变量对第j个公共因子的相对重要性,也是其间的密切程度,也是其公共因子的权;2变量共同度:指因子载荷矩阵中各行元素的平方和,表示x的第i个分量对于公共因子的每一个分量的共同依赖程度;3方差贡献:指因子载荷矩阵第j列各个元素的平方和,是衡量公共因子相对重要性的指标;7、因子分析与主成分分析有何区别与联系它们分别适用于怎样的情况答:联系:均是降维的处理变量样品的方法;区别:因子分析是把变量表示成各个因子的线性组合,而主成分分析是把主成分表示成变量的线性组合;因子分析重点是解释各个变量之间的协方差,主成分分析是解释变量的总方差;因子分析需要一些假定,共同因子之间不相关,特殊因子之间不相关,以上两者也不相关,而主成分分析不需要假设;因子分析中因子不是独特的,可以旋转得到不同的因子,主成分分析中对于给定的协方差和相关矩阵特殊值,成分是独特的;因子个数需要分析者指定,而主成分中成分的数量是一定的;8、如何确定公共因子数目如何解释公共因子的实际意义答:用方差累计贡献率,一般只要前几个达到80%即可,或者碎石图也可以确定;公共因子的含义,与实际问题相关,表示变量之间内部错综复杂的关联性;9、怎样的情况下,需要作因子旋转答:如果求出主因子解,但是主因子代表的变量不是很突出,容易使因子的含义模糊不清,需要做旋转;10、有哪些估计因子得分的方法因子得分的估计是普通意义下的参数估计吗为什么答:回归估计法、巴特莱特估计法、汤姆逊估计法;不是普通意义下的参数估计,需要用公共因子F用变量的线性组合来表示;11、对应分析的基本思想或原理是什么试举例说明它的应用;答:为了克服因子分析的不足之处,寻求R型和Q型变量的内在联系,将两者统一起来,将样品和变量反映到相同的坐标轴上进行解释;比如对某一行业的经济效益进行综合性评价,要研究企业与企业的信息,指标与指标的内部结构、企业与指标的内在联系,这三个方面是一个密不可分的整体;12、对应分析中总惯量的意义是什么答:代表总体两个变量相互联系的总信息量,可以反映某种变量特征属性的接近程度,及时对数据组分进行约束;。
1、简述多元统计分析中协差阵检验的步骤 第一,提出待检验的假设H0和H1; 第二,给出检验的统计量及其服从的分布;第三,给定检验水平,查统计量的分布表,确定相应的临界值,从而得到否定域; 第四,根据样本观测值计算出统计量的值,看是否落入否定域中,以便对待判假设做出决策(拒绝或接受)。
协差阵的检验检验0=ΣΣ0p H =ΣI : /2/21exp 2np n e tr n λ⎧⎫⎛⎫=-⎨⎬ ⎪⎩⎭⎝⎭S S00p H =≠ΣΣI : /2/2**1exp 2np n e tr n λ⎧⎫⎛⎫=-⎨⎬ ⎪⎩⎭⎝⎭S S检验12k ===ΣΣΣ012k H ===ΣΣΣ:统计量/2/2/2/211i i kkn n pn np k iii i nnλ===∏∏SS2. 针对一个总体均值向量的检验而言,在协差阵已知和未知的两种情形下,如何分别构造的统计量?3. 作多元线性回归分析时,自变量与因变量之间的影响关系一定是线性形式的吗?多元线性回归分析中的线性关系是指什么变量之间存在线性关系? 答:作多元线性回归分析时,自变量与因变量之间的影响关系不一定是线性形式。
当自变量与因变量是非线性关系时可以通过某种变量代换,将其变为线性关系,然后再做回归分析。
多元线性回归分析的线性关系指的是随机变量间的关系,因变量y 与回归系数βi 间存在线性关系。
多元线性回归的条件是:(1)各自变量间不存在多重共线性; (2)各自变量与残差独立;(3)各残差间相互独立并服从正态分布; (4)Y 与每一自变量X 有线性关系。
4.回归分析的基本思想与步骤 基本思想:所谓回归分析,是在掌握大量观察数据的基础上,利用数理统计方法建立因变量与自变量之间的回归关系函数表达式(称回归方程式)。
回归分析中,当研究的因果关系只涉及因变量和一个自变量时,叫做一元回归分析;当研究的因果关系涉及因变量和两个或两个以上自变量时,叫做多元回归分析。
此外,回归分析中,又依据描述自变量与因变量之间因果关系的函数表达式是线性的还是非线性的,分为线性回归分析和非线性回归分析。
多元统计分析课程设计题目课程设计题目1. 下表给出了1991年我国30个省、区、市城镇居民的月平均消费数据,所考察的八个指标如下(单位均为元/人)X1 :人均粮食支出; X2 :人均副食支出;X3 :人均烟酒茶支出; X4 :人均其他副食支出;X5 :人均衣着商品支出; X6 :人均日用品支出;X7 :人均燃料支出; X8 :人均非商品支出;问题:(1)求样品相关系数矩阵R;(2)从R 出发做主成分分析,求各主成分的贡献率,及前两个主成分的累积贡献率;(3)求出前两个主成分并解释其意义.按第一主成分将30个省、区、市排序,结果如何?表一 1991年我国30个省、区、市城镇居民的月平均消费数据省市X1 X2 X3 X4 X5 X6 X7 X81 山西8.35 23.53 7.51 8.62 17.42 10.00 1.04 11.212 内蒙古9.25 23.75 6.61 9.19 17.77 10.48 1.72 10.513 吉林8.19 30.50 4.72 9.78 16.28 7.60 2.52 10.324 黑龙江7.73 29.20 5.42 9.43 19.29 8.49 2.52 10.005 河南9.42 27.93 8.20 8.14 16.17 9.42 1.55 9.766 甘肃9.16 27.98 9.01 9.32 15.99 9.10 1.82 11.357 青海10.06 28.64 10.52 10.05 16.18 8.39 1.96 10.818 河北9.09 28.12 7.40 9.62 17.26 11.12 2.49 12.659 陕西9.41 28.20 5.77 10.80 16.36 11.56 1.53 12.1710 宁夏8.70 28.12 7.21 10.53 19.45 13.30 1.66 11.9611 新疆 6.93 29.85 4.54 9.49 16.62 10.65 1.88 13.6112 湖北8.67 36.05 7.31 7.75 16.67 11.68 2.38 12.8813 云南9.98 37.69 7.01 8.94 16.15 11.08 0.83 11.6714 湖南 6.77 38.69 6.01 8.82 14.79 11.44 1.74 13.2315 安徽8.14 37.75 9.61 8.49 13.15 9.76 1.28 11.2816 贵州7.67 35.71 8.04 8.31 15.13 7.76 1.41 13.2517 辽宁7.90 39.77 8.49 12.94 19.27 11.05 2.04 13.2918 四川7.18 40.91 7.32 8.94 17.60 12.75 1.14 14.8019 山东8.82 33.70 7.59 10.98 18.82 14.73 1.78 10.1020 江西 6.25 35.02 4.72 6.28 10.03 7.15 1.93 10.3921 福建10.60 52.41 7.70 9.98 12.53 11.70 2.31 14.6922 广西7.27 52.65 3.84 9.16 13.03 15.26 1.98 14.5723 海南13.45 55.85 5.50 7.45 9.55 9.52 2.21 16.3024 天津10.85 44.68 7.32 14.51 17.13 12.08 1.26 11.5725 江苏7.21 45.79 7.66 10.36 16.56 12.86 2.25 11.6926 浙江7.68 50.37 11.35 13.30 19.25 14.59 2.75 14.8727 北京7.78 48.44 8.00 20.51 22.12 15.73 1.15 16.6128 西藏7.94 39.65 20.97 20.82 22.52 12.41 1.75 7.9029 上海8.28 64.34 8.00 22.22 20.06 15.12 0.72 22.8930 广东12.47 76.39 5.52 11.24 14.52 22.00 5.46 25.502. 下表是49位女性在空腹情况下三个不同时刻的血糖含量(用X1 ,X2 ,X3表示)和摄入等量食糖一小时后的三个时刻的血糖含量(用小X4 ,X5 ,X6表示)的观测值(单位:mg/100ml).问题:分别从样本协方差阵S和样本相关系数矩阵R出发做主成分分析,求主成分的贡献率和各个主成分. 在两种情况下,你认为应保留几个主成分?其意义如何解释?就此而言,你认为基于S和R的分析那个结果更为合理?表二 49位女性在空腹和摄入食糖后三个不同时刻的血糖含量编号空腹摄入食糖X1 X2 X3 X4 X5 X61 60 69 62 97 69 982 56 53 84 103 78 1073 80 69 76 66 99 1304 55 80 90 80 85 1145 62 75 68 116 130 916 74 64 70 109 101 1037 64 71 66 77 102 1308 73 70 64 115 110 1099 68 67 75 76 85 11910 69 82 74 72 133 12711 60 67 61 130 134 12112 70 74 78 150 158 10013 66 74 78 150 131 14214 83 70 74 99 98 10515 68 66 90 119 85 10916 78 63 75 164 98 13817 103 77 77 160 117 12118 77 68 74 144 71 15319 66 77 68 77 82 8920 70 70 72 114 93 12221 75 65 71 77 70 10922 91 74 93 118 115 15023 66 75 73 170 147 12124 75 82 76 153 132 11525 74 71 66 143 105 10026 76 70 64 114 113 12927 74 90 86 73 106 11628 74 77 80 116 81 7729 67 71 69 63 87 7030 78 75 80 105 132 8031 64 66 71 83 94 13332 71 80 76 81 87 8633 63 75 73 120 89 5934 90 103 74 107 109 10135 60 76 61 99 111 9836 48 77 75 113 124 9737 66 93 97 136 112 12238 74 70 76 109 88 10539 60 74 71 72 90 7140 63 75 66 130 101 9041 66 80 86 130 117 14442 77 67 74 83 92 10743 70 67 100 150 142 14644 73 76 81 119 120 11945 78 90 77 122 155 14946 73 68 80 102 90 12247 72 83 68 104 69 9648 65 60 70 119 94 8949 52 70 76 92 94 100 3. 考察1985年至2000年全国如下各价格指数:X1 :商品零售价格指数;X2 :居民消费价格指数;X3 :城市居民消费价格指数;X4 :农村居民消费价格指数;X5 :农产品收购价格指数;X6 :农村工业品零售价格指数;观测数据见下表.问题:按年份用下列方法进行系统聚类分析,画出谱系聚类图,并给出聚为3类的结果.(a)最短距离法;(b)最长距离法;(c)类平均距离法;表三全国各年度各种价格指数年份X1 X2 X3 X4 X5 X6 1985 128.1 100.0 134.2 100.0 166.8 111.1 1986 135.8 106.5 143.6 106.1 177.5 114.7 1987 145.7 114.3 156.2 112.7 198.8 120.2 1988 172.7 135.8 188.5 132.4 244.5 138.5 1989 203.4 160.2 219.2 157.9 281.2 164.4 1990 207.7 162.2 222.0 165.1 273.9 172.0 1991 213.7 170.8 233.3 168.9 268.4 177.2 1992 225.7 181.7 253.4 176.8 277.5 182.7 1993 254.9 208.4 294.2 201.0 314.7 204.3 1994 310.2 258.6 367.8 248.0 440.3 239.4 1995 356.1 302.8 429.6 291.4 527.9 274.6 1996 377.8 327.9 467.4 314.4 550.1 291.6 1997 380.8 337.1 481.9 322.3 525.3 294.8 1998 370.9 334.4 479.0 319.1 483.3 288.3 1999 359.8 329.7 472.8 314.3 424.3 280.5 2000 354.4 331.0 476.6 314.0 409.0 277.14. 考察1985年至2000年全国如下各价格指数:X1 :商品零售价格指数;X2 :居民消费价格指数;X3 :城市居民消费价格指数;X4 :农村居民消费价格指数;X5 :农产品收购价格指数;X6 :农村工业品零售价格指数;观测数据见下表.问题:先将数据标准化,再按年份用下列方法进行系统聚类分析,画出谱系聚类图,并给出聚为3类的结果.(a)最短距离法;(b)最长距离法;(c)重心距离法.表四全国各年度各种价格指数年份X1 X2 X3 X4 X5 X6 1985 128.1 100.0 134.2 100.0 166.8 111.1 1986 135.8 106.5 143.6 106.1 177.5 114.7 1987 145.7 114.3 156.2 112.7 198.8 120.2 1988 172.7 135.8 188.5 132.4 244.5 138.5 1989 203.4 160.2 219.2 157.9 281.2 164.4 1990 207.7 162.2 222.0 165.1 273.9 172.0 1991 213.7 170.8 233.3 168.9 268.4 177.2 1992 225.7 181.7 253.4 176.8 277.5 182.7 1993 254.9 208.4 294.2 201.0 314.7 204.3 1994 310.2 258.6 367.8 248.0 440.3 239.4 1995 356.1 302.8 429.6 291.4 527.9 274.6 1996 377.8 327.9 467.4 314.4 550.1 291.6 1997 380.8 337.1 481.9 322.3 525.3 294.8 1998 370.9 334.4 479.0 319.1 483.3 288.3 1999 359.8 329.7 472.8 314.3 424.3 280.5 2000 354.4 331.0 476.6 314.0 409.0 277.15. 研究货运总量y(万吨)与工业总产值x1(亿元)、农业总产值x2(亿元)。