第三章回归测法

第三章 一元线性回归模型一、预备知识（一）相关概念对于一个双变量总体,若由基础理论，变量和变量之间存在因果),(i i x y x y 关系，或的变异可用来解释的变异。

为检验两变量间因果关系是否存在、x y 度量自变量对因变量影响的强弱与显著性以及利用解释变量去预测因变量x y x ，引入一元回归分析这一工具。

y 将给定条件下的均值i x i yi i i x x y E 10)|(ββ+=（3.1）定义为总体回归函数（PopulationRegressionFunction,PRF ）。

定义为误差项（errorterm ）,记为，即，这样)|(i i i x y E y -i μ)|(i i i i x y E y -=μ，或i i i i x y E y μ+=)|(i i i x y μββ++=10（3.2）（3.2）式称为总体回归模型或者随机总体回归函数。

其中，称为解释变量x （explanatory variable ）或自变量（independent variable ）；称为被解释y 变量（explained variable ）或因变量（dependent variable ）；误差项解释μ了因变量的变动中不能完全被自变量所解释的部分。

误差项的构成包括以下四个部分：（1）未纳入模型变量的影响（2）数据的测量误差（3）基础理论方程具有与回归方程不同的函数形式，比如自变量与因变量之间可能是非线性关系（4）纯随机和不可预料的事件。

在总体回归模型（3.2）中参数是未知的，是不可观察的，统计计10,ββi μ量分析的目标之一就是估计模型的未知参数。

给定一组随机样本，对（3.1）式进行估计，若的估计量分别记n i y x i i ,,2,1),,( =10,),|(ββi i x y E 为，则定义3.3式为样本回归函数^1^0^,,ββi y （）i i x y ^1^0^ββ+=n i ,,2,1 =（3.3）注意，样本回归函数随着样本的不同而不同，也就是说是随机变量，^1^0,ββ它们的随机性是由于的随机性（同一个可能对应不同的）与的变异共i y i x i y x 同引起的。

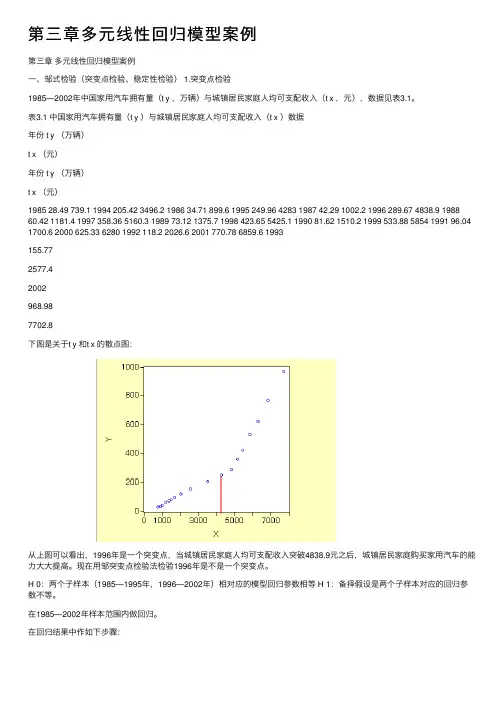
第三章多元线性回归模型案例第三章多元线性回归模型案例⼀、邹式检验（突变点检验、稳定性检验） 1.突变点检验1985—2002年中国家⽤汽车拥有量（t y ，万辆）与城镇居民家庭⼈均可⽀配收⼊（t x ，元），数据见表3.1。

表3.1 中国家⽤汽车拥有量（t y ）与城镇居民家庭⼈均可⽀配收⼊（t x ）数据年份 t y （万辆）t x （元）年份 t y （万辆）t x （元）1985 28.49 739.1 1994 205.42 3496.2 1986 34.71 899.6 1995 249.96 4283 1987 42.29 1002.2 1996 289.67 4838.9 1988 60.42 1181.4 1997 358.36 5160.3 1989 73.12 1375.7 1998 423.65 5425.1 1990 81.62 1510.2 1999 533.88 5854 1991 96.04 1700.6 2000 625.33 6280 1992 118.2 2026.6 2001 770.78 6859.6 1993155.772577.42002968.987702.8下图是关于t y 和t x 的散点图：从上图可以看出，1996年是⼀个突变点，当城镇居民家庭⼈均可⽀配收⼊突破4838.9元之后，城镇居民家庭购买家⽤汽车的能⼒⼤⼤提⾼。

现在⽤邹突变点检验法检验1996年是不是⼀个突变点。

H 0：两个⼦样本（1985—1995年，1996—2002年）相对应的模型回归参数相等 H 1：备择假设是两个⼦样本对应的回归参数不等。

在1985—2002年样本范围内做回归。

在回归结果中作如下步骤：输⼊突变点：得到如下验证结果：由相伴概率可以知道，拒绝原假设，即两个样本（1985—1995年，1996—2002年）的回归参数不相等。

所以，1996年是突变点。

2.稳定性检验以表3.1为例，在⽤1985—1999年数据建⽴的模型基础上，检验当把2000—2002年数据加⼊样本后，模型的回归参数时候出现显著性变化。

第三章 回歸分析 §1 一元線性回歸 一、回歸模型設隨機變數y 與引數x 之間存在線性關係，它們的第i 次觀測數據是：(xi,yi)(i=1,2,…,n)那麼這組數據可以假設具有如下的數學結構式：i i i x y εββ++=0（i=1,…,n ）,其中β0, β為待估參數，),0(~2σεN i ，且n εεε,,,21 相互獨立，這就是一元線性回歸的數學模型。

二、參數估計 1.回歸係數設b0和b 分別是參數β0, β的最小二乘估計，於是一元線性回歸方程為：i i bx b y+=0ˆ （i=1,2,…,n ） b0,b 叫做回歸係數，它使偏差平方和∑∑==--=-=ni i i ni i i bx b y yy Q 12012)()ˆ(取最小值。

由 ⎝⎛=---=∂∂=---=∂∂∑∑==0)(20)(210100ni i i i ni i i x bx b y b Q bx b y b Q整理得正規方程組： 020()()()i ii i i inb x b y x b x b x y +∑=∑⎛∑+∑=∑⎝解得 xx xy S S b x b y b /,0=-= 其中 222)(x n x x x S i i xx -∑=-∑=y x n y x y y x x S i i i i xy -∑=--∑=))((另外 y n y y y S i i yy -∑=-∑=22)( 2.最小二乘估計b0,b 的統計性質 (1)E(b)= β,E(b0)= β0即b0,b 分別是β0，β的無偏估計 (2)22()/()i D b x x σ=∑-22201()[/()]i D b x x x nσ=+∑-即回歸係數b0,b 與σ2，x 的波動大小有關，b0還與n 有關，這就是說，x 值越分散，數據越多，估計b0,b 越精確。

三、假設檢驗 1.回歸方程顯著性檢驗欲檢驗y 與x 之間是否有線性關係，即檢驗假設H0：β＝0。

第三章回归分析基本方法最小二乘法回归分析是统计学中一种常用的方法，主要用于研究一个或多个自变量与因变量之间关系的强度和方向。

在回归分析中，最常用的方法是最小二乘法。

最小二乘法是一种通过最小化观测值与拟合值之间的平方误差来估计参数的方法。

其基本思想是通过找到使得平方误差最小的参数值来拟合数据。

最小二乘法可以应用于各种类型的回归模型，包括简单线性回归和多元线性回归。

在简单线性回归中，我们研究一个自变量与一个因变量之间的关系。

假设我们有一组观测数据(x_i,y_i)，其中x_i为自变量的取值，y_i为相应的因变量的取值。

我们想要找到一条直线来拟合这些数据点，使得误差最小化。

最小二乘法的目标是找到最合适的斜率和截距来拟合数据，最小化残差平方和。

具体而言，假设我们的模型为y=β_0+β_1*x，其中β_0为截距，β_1为斜率。

我们的目标是找到最合适的β_0和β_1来最小化残差平方和，即最小化∑(y_i-(β_0+β_1*x_i))^2最小二乘法的求解过程是通过对残差平方和关于β_0和β_1求偏导数，令偏导数为0，得到关于β_0和β_1的方程组。

通过求解这个方程组，我们可以得到最佳的β_0和β_1的估计值。

在多元线性回归中，我们考虑多个自变量与一个因变量之间的关系。

假设我们有p个自变量，我们的模型可以表示为y=β_0+β_1*x_1+β_2*x_2+...+β_p*x_p。

最小二乘法的求解过程与简单线性回归类似，只是需要求解一个更复杂的方程组。

最小二乘法在回归分析中的应用非常广泛。

它可以用于预测和建模，也可以用于建立因果关系的推断。

此外，最小二乘法还可以用于进行参数估计和统计检验。

总结起来，最小二乘法是一种基本的回归分析方法，通过最小化观测值与拟合值之间的平方误差来估计参数。

它在简单线性回归和多元线性回归中都有广泛应用，是统计学中重要的工具之一。