典型件结合知识点问答
- 格式:doc
- 大小:47.50 KB
- 文档页数:6
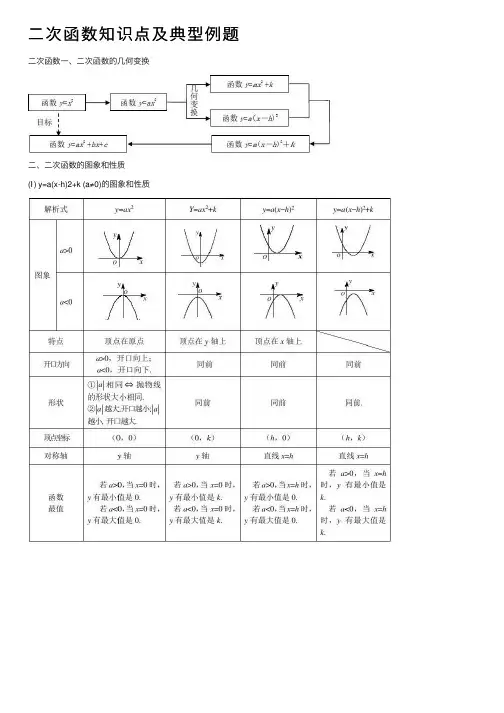
⼆次函数知识点及典型例题⼆次函数⼀、⼆次函数的⼏何变换⼆、⼆次函数的图象和性质(Ⅰ) y=a(x-h)2+k (a≠0)的图象和性质(Ⅱ) y=ax2+bx+c (a≠0)的图象和性质(Ⅲ) a 、b 、c 的符号对抛物线形状位置的影响三、待定系数法求⼆次函数的解析式1、⼀般式:c bx ax y ++=2.已知图像上三点或三对x 、y 的值,通常选择⼀般式。
2、顶点式:()k h x a y +-=2.已知图像的顶点或对称轴,通常选择顶点式。
3、交点式:已知图像与x 轴的交点横坐标1x 、2x ,通常选⽤交点式:()()21x x x x a y --=。
4、顶点在原点,可设解析式为y=ax 2。
5、对称轴是y 轴(或者顶点在y 轴上),可设解析式为y= ax 2+c 。
6、顶点在x 轴上,可设解析式为()2h x a y -=。
7、抛物线过原点,可设解析式为y=ax2+bx 。
四、抛物线的对称性1、抛物线与x 轴有两个交点(x 1,0)(x 2,0),则对称轴为x=2x x 21+。
2、抛物线上有不同的两个交点(m ,a )(n,a ),则对称轴为x=2nm +。
3、抛物线c bx ax y ++=2(a ≠0)与y 轴交点关于对称轴的对称点为(ab-, c)。
五、⼆次函数与⼀元⼆次⽅程的关系对于抛物线c bx ax y ++=2(a ≠0),令y=0,即为⼀元⼆次⽅程02=++c bx ax ,⼀元⼆次⽅程的解就是⼆次函数与x 轴交点的横坐标。
要分三种情况:1、判别式△=b 2-4ac >0?抛物线与x 轴有两个不同的交点(ab 24acb -2+,0)(a b 24ac b --2,0)。
有韦达定理可知x 1+x 2=a b - ,x 1·x 2=ac 。
2、判别式△=b 2-4ac=0?抛物线与x 轴有⼀个交点(ab 2-,0)。
3、判别式△=b 2-4ac=0?抛物线与x 轴⽆交点。


学习-----好资料二次函数分类知识点、考点、典型例题及对应练习题型 1 二次函数的概念例1(基础).二次函数2365y x x =--+的图像的顶点坐标是( ) A .(-1,8) B.(1,8) C (-1,2) D (1,-4) 点拨:本题主要考察二次函数的顶点坐标公式 例2.(拓展,2008年武汉市中考题,12) 下列命题中正确的是○1若b 2-4ac >0,则二次函数y=ax 2+bx+c 的图象与坐标轴的公共点的个数是2或3 ○2若b 2-4ac=0,则二次函数y=ax 2+bx+c 的图象与x 轴只有一个交点,且这个交点就是抛物线顶点。
○3当c=-5时,不论b 为何值,抛物线y=ax 2+bx+c 一定过y 轴上一定点。
○4若抛物线y=ax 2+bx+c 与x 轴有唯一公共点,则方程ax 2+bx+c=0有两个相等的实数根。
○5若抛物线y=ax 2+bx+c 与x 轴有两个交点A 、B ,与y 轴交于c 点,c=4,S △ABC=6,则抛物线解析式为y=x 2-5x+4。
○6若抛物线y=ax 2+bx+c (a ≠0)的顶点在x 轴下方,则一元二次方程ax 2+bx+c=0有两个不相等的实数根。
○7若抛物线y=ax 2+bx+c (a ≠0)经过原点,则一元二次方程ax 2+bx+c=0必有一根为0。
○8若a -b+c=2,则抛物线y=ax 2+bx+c (a ≠0)必过一定点。
○9若b 2<3ac ,则抛物线y=ax 2+bx+c 与x 轴一定没有交点。
○10若一元二次方程ax 2+bx+c=0有两个不相等的实数根,则函数y=cx 2+bx+a 的图象与x 轴必有两个交点。
○11若b=0,则抛物线y=ax 2+bx+c 与x 轴的两个交点一个在原点左边,一个在原点右边。
点拨:本题主要考查二次函数图象及其性质,一元二次方程根与系数的关系,及二次函数和一元二次方程二者之间的联系。

政治问答题九大题型及举例——骆芷洋2012.071、“体现类”【题型特点】:体现型的设问中有“体现了什么”“怎样体现”“如何体现”等字眼。
【解题技巧】:1.涉及的知识点2.材料与所学知识联系3.梳理对照,两者结合作答【举例分析】:杭州市政府发放消费券,主要是为了拉动本地的消费,同时也为了改善民生。
目前已发放消费券2.2亿元,产生了l至5倍的放大效应,同时也明显带动了相关企业的生产。
杭州市还将准备再发放6亿元消费券,主要面向外地的旅游消费券,还有面向本地企业职工、大学生和农民工的教育培训券。
请问——杭州市政府发行消费券行为体现了《政治生活》中的哪些道理?答:①杭州市政府发放消费券,主要是为了拉动本地消费,面向本地企业职工、大学生和农民工的教育培训券,体现杭州市政府履行了组织社会主义经济建设与文化建设的职能,一定程度上推动了杭州经济文化事业的发展。
②为了改善民生,杭州市政府发放消费券,这表明我们的政府是人民利益的捍卫者,体现了政府坚持了为人民服务的宗旨和对人民负责的原则,把人民根本利益作为政府行使权力的出发点和落脚点,做到了权为民所用、情为民所系、利为民所谋。
2、“反映类”【题型特点】:文字式或图表式:反映了什么问题或现象,上述材料反映了什么变化.【解题技巧】:把材料所提供的信息用教材中所学的知识加以表明。
【举例分析】:阿布哈兹和南奥塞梯分别是格鲁吉亚的自治共和国和自治州,8月8日晨,格军进入南奥塞梯控制区,炮击了南奥塞梯首府茨欣瓦利市。
8月9日,俄军坦克向爆发冲突的格鲁吉亚南奥塞梯地区行进,俄58军占据了这个几乎被摧毁的城市。
26日,梅德韦杰夫宣布俄承认南奥塞梯和阿布哈兹独立。
美国、法国、德国等北约国家对此表示反对。
中方则希望有关各方通过对话协商和平解决在南奥塞梯冲突地区的有关争端。
上述材料共同反映了什么政治现象?答:①说明和平与发展是当今时代的主题。
但世界的和平局面又是不稳定的。
地区冲突和局部战争时有发生,威胁世界和平的隐患仍然存在。

二次函数各知识点、考点、典型例题及对应练习(超全)【典型例题】题型 1 二次函数的概念例1(基础).二次函数2365y x x =--+的图像的顶点坐标是( ) A .(-1,8) B.(1,8) C (-1,2) D (1,-4) 点拨:本题主要考察二次函数的顶点坐标公式例2.(拓展,2008年武汉市中考题,12)下列命题中正确的是○1若b 2-4ac >0,则二次函数y=ax 2+bx+c 的图象与坐标轴的公共点的个数是2或3 ○2若b 2-4ac=0,则二次函数y=ax 2+bx+c 的图象与x 轴只有一个交点,且这个交点就是抛物线顶点。
○3当c=-5时,不论b 为何值,抛物线y=ax 2+bx+c 一定过y 轴上一定点。
○4若抛物线y=ax 2+bx+c 与x 轴有唯一公共点,则方程ax 2+bx+c=0有两个相等的实数根。
○5若抛物线y=ax 2+bx+c 与x 轴有两个交点A 、B ,与y 轴交于c 点,c=4,S △ABC=6,则抛物线解析式为y=x 2-5x+4。
○6若抛物线y=ax 2+bx+c (a ≠0)的顶点在x 轴下方,则一元二次方程ax 2+bx+c=0有两个不相等的实数根。
○7若抛物线y=ax 2+bx+c (a ≠0)经过原点,则一元二次方程ax 2+bx+c=0必有一根为0。
○8若a -b+c=2,则抛物线y=ax 2+bx+c (a ≠0)必过一定点。
○9若b 2<3ac ,则抛物线y=ax 2+bx+c 与x 轴一定没有交点。
○10若一元二次方程ax 2+bx+c=0有两个不相等的实数根,则函数y=cx 2+bx+a 的图象与x 轴必有两个交点。
○11若b=0,则抛物线y=ax 2+bx+c 与x 轴的两个交点一个在原点左边,一个在原点右边。
点拨:本题主要考查二次函数图象及其性质,一元二次方程根与系数的关系,及二次函数和一元二次方程二者之间的联系。

排列组合知识点总结+典型例题及答案解析一.基本原理1.加法原理:做一件事有n 类办法,则完成这件事的方法数等于各类方法数相加. 2.乘法原理:做一件事分n 步完成,则完成这件事的方法数等于各步方法数相乘。
注:做一件事时,元素或位置允许重复使用,求方法数时常用基本原理求解。
二.排列:从n 个不同元素中,任取m (m ≤n )个元素,按照一定的顺序排成一.m n mn A 有排列的个数记为个元素的一个排列,所个不同元素中取出列,叫做从1。
公式:1。
()()()()!!121m n n m n n n n A m n -=+---=……2.规定:0!1=(1)!(1)!,(1)!(1)!n n n n n n =⨯-+⨯=+ (2) ![(1)1]!(1)!!(1)!!n n n n n n n n n ⨯=+-⨯=+⨯-=+-; (3)111111(1)!(1)!(1)!(1)!!(1)!n n n n n n n n n +-+==-=-+++++ 三.组合:从n 个不同元素中任取m(m ≤n )个元素并组成一组,叫做从n 个不同的m 元素中任取 m 个元素的组合数,记作 Cn .1. 公式: ()()()C A A n n n m m n m n m nmn m mm ==--+=-11……!!!! 10=n C 规定:组合数性质:.2 n n n n n m n m n m n m n n m n C C C C C C C C 21011=+++=+=+--……,, ①;②;③;④11112111212211r r r r r r r rr r r rr r r r r r n n r r r n n r r n n n C C C C C C C C C C C C C C C +++++-+++-++-+++++=++++=+++=注:若12m m 1212m =m m +m n n n C C ==则或四.处理排列组合应用题 1。

第三章概率3.1随机事件的概率3.1.1基本概念:(1)必然事件:在条件S下,一定会发生的事件,叫相对于条件S的必然事件;(2)不可能事件:在条件S下,一定不会发生的事件,叫相对于条件S的不可能事件;(3)确定事件:必然事件和不可能事件统称为相对于条件S的确定事件;(4)随机事件:在条件S下可能发生也可能不发生的事件,叫相对于条件S的随机事件;(5)频数与频率:在相同的条件S下重复n次试验,观察某一事件A是否出现,称n次试验中事件A出现的次数为事件A出现的频数;称事件A出现的比例为事件A出现的概率:对于给定的随机事件A,如果随着试验次数的增加,事件A发生的频率稳定在某个常数上,把这个常数记作P(A),称为事件A的概率。
3.1.2 概率的基本性质3.1.2.1基本概念:(1)事件的包含、并事件、交事件、相等事件(2)若A∩B为不可能事件,即A∩B=,那么称事件A与事件B互斥;(3)若A∩B为不可能事件,A∪B为必然事件,那么称事件A与事件B互为对立事件;(4)当事件A与B互斥时,满足加法公式:P(A∪B)= P(A)+ P(B);若事件A与B为对立事件,则A∪B为必然事件,所以P(A∪B)= P(A)+ P(B)=1,于是有P(A)=1—P(B)3.1.2.2概率的基本性质:1)必然事件概率为1,不可能事件概率为0,因此0≤P(A)≤1;2)当事件A 与B 互斥时,满足加法公式:P(A ∪B)= P(A)+ P(B);3)若事件A 与B 为对立事件,则A ∪B 为必然事件,所以P(A ∪B)= P(A)+ P(B)=1,于是有P(A)=1—P(B);【典型例题】已知同种血型的人可以输血,O 型血可以输给任一种血型的人,任何人的血都可以输给AB 型血的人,其他不同血型的人不能互相输血.小明是B 型血,若小明因病需要输血,问:(1)任找一个人,其血可以输给小明的概率是多少?(2)任找一个人,其血不能输给小明的概率是多少?[基础巩固]1.下列叙述错误的是( )A . 频率是随机的,在试验前不能确定,随着试验次数的增加,频率一般会越来越接近概率B . 若随机事件A 发生的概率为()A p ,则()10≤≤A pC . 互斥事件不一定是对立事件,但是对立事件一定是互斥事件D .5张奖券中有一张有奖,甲先抽,乙后抽,那么乙与甲抽到有奖奖券的可能性相同2.从装有5只红球、5只白球的袋中任意取出3只球,有事件:① “取出2只红球和1只白球”与“取出1只红球和2只白球”;② “取出2只红球和1只白球”与“取出3只红球”;③ “取出3只红球”与“取出3只球中至少有1只白球”;④ “取出3只红球”与“取出3只白球”.其中是对立事件的有( )A .①、④B .②、③C .③、④D .③3.下列说法中正确的是( )A .事件A 、B 中至少有一个发生的概率一定比A 、B 中恰有一个发生的概率大B .事件A 、B 同时发生的概率一定比事件A 、B 恰有一个发生的概率小C .互斥事件一定是对立事件,对立事件不一定是互斥事件D .互斥事件不一定是对立事件,对立事件一定是互斥事件[综合提高]4.某人在打靶中,连续射击2次,事件“至少有一次中靶”的互斥事件是( )A .至多有一次中靶B .两次都中靶C .两次都不中靶D .只有一次中靶5.在一对事件A 、B 中,若事件A 是必然事件,事件B 是不可能事件,那么事件A 和B ( )A .是互斥事件,但不是对立事件B .是对立事件,但不是互斥事件C .是互斥事件,也是对立事件D .既不是是互斥事件,也不是对立事件6.从5名礼仪小姐、4名翻译中任意选5人参加一次经贸洽谈活动,其中礼仪小姐、翻译均不少于2人的概率是( )A .B .C .D .7.若()1P A B +=,则事件A 与B 的关系是( )A .A 、B 是互斥事件 B .A 、B 是对立事件C .A 、B 不是互斥事件D .以上都不对8.某市派出甲、乙两支球队参加全省足球冠军赛.甲乙两队夺取冠军的概率分别是37和14. 试求该市足球队夺得全省足球冠军的概率为_____________ .9.某产品分甲、乙、丙三级,其中乙、丙两级均属次品.在正常生产情况下出现乙级品和丙级品的概率分别为3%和1%.求抽验一只是正品(甲级)的概率_____________ .10.一个口袋装有3个红球和n 个绿球,从中任意取出3个球中至少有1个是绿球的概率是,则n=______________ .[能力提高]11.圆周上有2n 个等分点(n >1),以其中任三点为顶点作三角形,其中可构成直角三角形的概率为 ____________ .12.某高校有5名学生报名参加义务献血活动,这5人中血型为A 型、O 型的学生各2名,血型为B 型的学生1 名,已知这5名学生中每人符合献血条件的概率均是23.(1)若从这5名学生中选出2名学生,求 所选2人的血型为O 型或A 型的概率;(2)求这5名学生中至少有2名学生符合献血条件的概率.(注:答案均用分数表示).13.在一只袋子中装有7个红玻璃球,3个绿玻璃球.从中无放回地任意抽取两次,每次只取一个.试求:(1)取得两个红球的概率; (2)取得两个绿球的概率; (3)取得两个同颜色的球的概率;(4)至少取得一个红球的概率.14.在放有5个红球、4个黑球、3个白球的袋中,任意取出3个球,分别求出3个全是同色球的概率及全是异色球的概率.15.从男女学生共有36名的班级中,任意选出2名委员,任何人都有同样的当选机会.如果 选得同性委员的概率等于,求男女生相差几名?3.2古典概率3.2.1 —3.2.2古典概型及随机数的产生(1)古典概型的使用条件:试验结果的有限性和所有结果的等可能性。
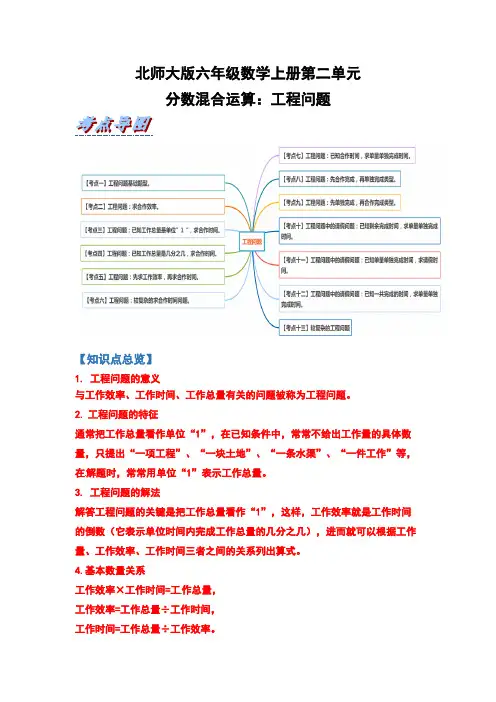
北师大版六年级数学上册第二单元分数混合运算:工程问题【知识点总览】1. 工程问题的意义与工作效率、工作时间、工作总量有关的问题被称为工程问题。
2.工程问题的特征通常把工作总量看作单位“1”,在已知条件中,常常不给出工作量的具体数量,只提出“一项工程”、“一块土地”、“一条水渠”、“一件工作”等,在解题时,常常用单位“1”表示工作总量。
3. 工程问题的解法解答工程问题的关键是把工作总量看作“1”,这样,工作效率就是工作时间的倒数(它表示单位时间内完成工作总量的几分之几),进而就可以根据工作量、工作效率、工作时间三者之间的关系列出算式。
4.基本数量关系工作效率×工作时间=工作总量,工作效率=工作总量÷工作时间,工作时间=工作总量÷工作效率。
【考点一】工程问题基础题型。
【方法点拨】工程问题的基础题型是主要根据工作总量、工作时间、工作效率三者之间基本数量关系列出算式:工作效率×工作时间=工作总量, 工作效率=工作总量÷工作时间, 工作时间=工作总量÷工作效率。
【典型例题】一项工程,甲队需要20天完成,甲队每天完成这项工程的几分之几?【对应练习1】 乙队完成一项工程的32需要12天,求乙队的工作效率。
【对应练习2】一项工程,甲队的工作效率是101,甲队完成这项工程需要几天?【对应练习3】 乙队的工作效率是151,乙队完成这项工程的54需要多少天?【对应练习4】一项工程,甲队的工作效率是121,甲队工作5天可以完成这项工程的几分之几?工作9天可以完成这项工程的几分之几?【对应练习5】砌一道墙,甲单独7小时完成,这道墙已由别人砌了41,还要多少小时能完成?【考点二】工程问题:求合作效率。
【方法点拨】合作效率=工作效率1+工作效率2 【典型例题】一项工作,甲单独做12天完成,乙单独做20天完成。
(1)甲的工作效率是几分之几?乙的工作效率是几分之几?(2)甲、乙合做1天完成全工程的几分之几?(3)甲、乙合作3天完成完成全工程的几分之几?还剩几分之几没完成?【对应练习1】一项工程,甲队单独做10天完成,乙队单独做15天完成。


语文七年级上册名著阅读知识点-+典型题及解析一、名著阅读1.阅读下面语段,回答问题。
我笑着跳着,催他们要搬得快。
忽然,工人的脸色很谨肃了,我知道有些蹊跷,四面一看,父亲就站在我背后。
“去拿你的书来。
”他慢慢地说。
这所谓“书”,是指我开蒙时候所读的《鉴略》,因为我再没有第二本了。
我们那里上学的岁数是多拣单数的,所以这使我记住我其时是七岁。
我忐忑着,拿了书来了。
他使我同坐在堂中央的桌子前,教我一句一句地读下去。
我担着心,一句一句地读下去。
两句一行,大约读了二三十行罢,他说:“给我读熟。
背不出,就不准去看会。
”他说完,便站起来,走进房里去了。
我似乎从头上浇了一盆冷水,但是,有什么法子呢?自然是读着,读着,强记着,——而且要背出来。
(1)本选段节选自《朝花夕拾》中________。
(2)请简要回答文章刻画了一个怎样的父亲形象。
2.鲁迅在《朝花夕拾》序文中这样写道:“我有一时,曾经屡次忆起儿时在故乡所吃的蔬果:菱角、罗汉豆、茭白、香瓜。
凡这些,都是极其鲜美可口的;都曾是使我思乡的蛊惑。
后来,我在久别之后尝到了,也不过如此;惟独在记忆上,还有旧来的意味留存。
他们也许要哄骗我一生,使我时时反顾。
”鲁迅在“时时反顾”什么?结合《朝花夕拾》中的内容,写出两点并分析。
3.名著阅读阅读下面的文字,要求作答。
在百静中,我似乎头里要伸出许多铁钳,将什么“生于太荒”之流夹住;也听到自己急急诵读的声音发着抖,仿佛深秋的蟋蟀,在夜中鸣叫似的。
(1)文段出自鲁迅的散文集《朝花夕拾》中的《________》一文。
(2)文中记叙了作者儿时与父亲之间一场微妙的冲突:“我”热切盼望__________,父亲却要“我”__________,文章表现了父亲对儿童心理的无知,含蓄地批判了_____________的不合理。
4.新华中学新学校落成后,打算设计走廊和雕塑。
聪明的你,一起来参与吧。
(项目一:恩师长廊)(1)学校打算在过道两边设计一条“恩师长廊”。
复习资料问答题(15至18分,一题)1、公共安全法的调整对象是什么?并简单说明。
参考答案:(第14页)法律的调整对象是致法律所调整的社会关系。
经过法律调整后所产出的权利和义务关系就是法律关系。
从公共安全法的调整对象看,它是一部调整公共安全方面社会关系的专门法律。
公共安全法律关系是基于公共安全法律规范所确定和调整的当事人之间在参与公共安全事务、从事公共安全法律行为过程中产出的具有公共安全权利义务的关系。
它是公共安全法律规范对社会关系的调整而形成的法律关系,具体包括公共安全财产关系、公共安全人身关系及公共安全行政关系。
2、我国公共安全事件应急处理法律制度建设存在的主要问题是什么?参考答案:(第56页)我国公共安全事件应急处理法律制度建设存在的主要问题有:(1)、是现行宪法没有确立统一的应急状态制度。
现行宪法仅对戒严、动员和战争状态等几个问题分别做了原则规定,缺乏适用于各类突发事件引起的应急状态的统一规定。
(2)、是缺乏统一的紧急状态立法。
紧急状态立法的核心是哟啊解决给予政府特别授权和对公民权利以适当保护与救济的界限问题。
我国没有统一的紧急状态法,对各种紧急状态所带来的共性问题缺乏统一规定。
在出现紧急状态后,容易产生政府与社会成员。
中央与地方责任不清,行使权利与履行职责程序不明,应急措施不到位等问题,影响及时有效应对突发事件。
(3)、现有应急制度不够完善。
宪法和有关法律未就紧急状态做出明确的实体规定和程序规定,对政府在紧急状态下可以采取的紧急措施规定得不够具体,对公民权利的限制规定得不够明确,现行法律、法规之间存在有的问题上衔接不够。
(4)、是有些突发事件的应急制度还缺少法律规定。
一方面,与突发事件应急制度比较健全的其他国家相比,我国的应急制度还不够完善,还有一些急需建立、但尚未通过法律、法规、规章甚至规范性文件建立的应急制度。
另一方面,在已经确立的突发事件应急制度中,有的是有部门规章或者规范性文件确立的,其规范性不强、效力不高,给及时有效应对突发事件带来了困难,不利于有关部门之间的协调与配合。
《西游记》《西游记》是中国古代第一部浪漫主义小说、长篇神魔小说。
作者是明代(朝代)的吴承恩。
主要写孙悟空、猪八戒、沙僧三人保护唐僧西行取经,沿途遇到八十一难,一路降妖伏魔,化险为夷,最后到达西天、取得真经的故事。
主要由等三大部分组成。
其中的大闹天宫、三打白骨精、车迟国斗法、女儿国遇难、真假美猴王、(智取红孩儿、三调芭蕉扇)等情节扣人心弦,引人入胜。
1.《西游记》,长篇章回体神话小说,有着历史真实的影子,即唐贞观年间玄奘远出西域取经的事件。
2.《西游记》的作者是吴承恩,明代人。
3.全书共100回,基本由两个故事组成,第1至7回,写孙悟空出世至大闹天宫,表现的是孙悟空对自由的无限追求和斗争最终失败的悲剧,体现出了人性的自由本质与现实生活的约束的矛盾处境。
第8至100回总写唐僧师徒历经八十一难,去西天大雷音寺取经,蕴含着人必须经历艰难才能最终获得幸福成功的人生真谛。
4.全书共分三大部分:前7回写大闹天宫的故事,是全书的精华部分,表现孙悟空的反抗精神;8—12回写唐僧的来历、魏征斩蛇、唐太宗入冥府,交待取经的缘起;第13回—100回写唐僧师徒取经途中历经81难和师徒终成正果,带经回东土大唐5.孙悟空的第一个师傅是菩提祖师,它的兵器原是大禹治水的定海神针,又唤如意金箍棒,大闹天宫后被如来佛祖压在五行山,后受观世音菩萨规劝皈依佛门,唐僧为他取名孙行者。
为西天取经立下汗马功劳,后被封为斗战胜佛。
6.猪八戒又叫猪悟能,原为管理天河水兵的天蓬元帅,获罪下凡,误投猪胎,曾占福陵山、云栈洞为妖,后经菩萨点化,保唐僧取经,得成正果,封为净坛使者。
7.沙僧也叫沙悟净,原为天宫中的卷帘大将,被贬下界,在流沙河为妖,后保唐僧取经,得成正果,封为金身罗汉。
8.白龙马原是西海龙王之三太子小白龙,因违逆父命被囚鹰愁涧,后化作白马驮负唐僧取经,被封为八部天龙广力菩萨。
后在化龙池中得复原身,盘绕在大雷音寺的擎天华表柱上。
910.《西游记》中孙悟空从菩提祖师处学到__七十二变__、_筋斗云__等神通,又从龙宫索取如意金箍棒作为兵器,因大闹天宫而被__如来佛祖__压在五行山下,受苦五百年,后受_观世音菩萨规劝,皈依佛门,给唐僧做了大徒弟,取名孙行者。
【精选】人教版七年级上册数学第三章《一元一次方程》知识点+典型例题知识点、概念总结1.一元一次方程:只含有一个未知数,并且未知数的次数是1,并且含未知数项的系数不是零的整式方程是一元一次方程。
2.一元一次方程的标准形式:ax+b=0(x是未知数,a、b是已知数,且a≠0)。
3.条件:一元一次方程必须同时满足4个条件:(1)它是等式;(2)分母中不含有未知数;(3)未知数最高次项为1;(4)含未知数的项的系数不为0.4.等式的性质:等式的性质一:等式两边同时加一个数或减去同一个数或同一个整式,等式仍然成立。
等式的性质二:等式两边同时扩大或缩小相同的倍数(0除外),等式仍然成立。
等式的性质三:等式两边同时乘方(或开方),等式仍然成立。
解方程都是依据等式的这三个性质等式的性质一:等式两边同时加一个数或减同一个数,等式仍然成立。
5.合并同类项(1)依据:乘法分配律(2)把未知数相同且其次数也相同的相合并成一项;常数计算后合并成一项(3)合并时次数不变,只是系数相加减。
6.移项(1)含有未知数的项变号后都移到方程左边,把不含未知数的项移到右边。
(2)依据:等式的性质(3)把方程一边某项移到另一边时,一定要变号。
7.一元一次方程解法的一般步骤:使方程左右两边相等的未知数的值叫做方程的解。
一般解法:(1)去分母:在方程两边都乘以各分母的最小公倍数;(2)去括号:先去小括号,再去中括号,最后去大括号;(记住如括号外有减号的话一定要变号)(3)移项:把含有未知数的项都移到方程的一边,其他项都移到方程的另一边;移项要变号(4)合并同类项:把方程化成ax=b(a≠0)的形式;(5)系数化成1:在方程两边都除以未知数的系数a,得到方程的解x=b/a.8.同解方程如果两个方程的解相同,那么这两个方程叫做同解方程。
9.方程的同解原理:(1)方程的两边都加或减同一个数或同一个等式所得的方程与原方程是同解方程。
(2)方程的两边同乘或同除同一个不为0的数所得的方程与原方程是同解方程。
9月18事知识问答-回复标题:[9月18事知识问答] 解答一系列有趣问题引言:每天我们都会面临各种问题,有时候这些问题或许会令我们感到困惑,甚至困扰。
为了解答并增加我们对世界的认识,下面将回答一系列有趣问题,希望能够帮助大家更好地了解一些知识。
一、为什么天空是蓝色的?天空之所以呈现蓝色,是由于太阳光中的可见光光谱中蓝色光的波长较短。
当太阳光进入大气中时,其中的蓝色光波长更容易散射。
这种散射会使得我们看到的天空呈现出蓝色。
二、为什么海水是咸的?海水中的盐分主要来自于河流的冲刷,将地壳中的盐矿物带入海洋。
随着时间的推移,这些盐分逐渐积累。
同时,海洋中的蒸发也会增加盐度。
虽然大量岩石的矿物成分是含盐的,但淡水河流的冲刷会将这些盐分带走,使得地球上的淡水资源保持平衡。
三、为什么狗可以闻出癌症?狗拥有非常灵敏的嗅觉系统,其鼻子上的嗅觉受体比人类多很多倍。
研究表明,癌症患者体内会产生一种特殊的化合物,这种化合物会通过呼吸、尿液、汗液等形式释放出来。
狗可以通过嗅觉感知到这种变化,从而能够闻出癌症。
四、为什么吃辣会觉得口里火辣辣的?辣椒中的辣素(辣椒碱)是口中感受辣味的主要化合物。
当我们食用辣椒时,辣素会结合辣椒受体,触发神经传递信号到大脑,产生辣的感觉。
事实上,辣味并不会增加口腔温度,而是与我们的热感受受体相互作用,产生了一种类似被烧灼的感觉。
五、为什么我们会打哈欠?打哈欠是机体一种自然反应,它可以使我们的大脑和身体重新充氧。
哈欠时,我们的口腔会张开,胸腔会扩张,从而吸入更多的氧气。
打哈欠还可以清醒大脑并帮助保持警觉。
六、为什么在接收到噩耗时我们会感到心碎?当我们遭受到噩耗,如失去亲友或遭受挫折,我们会感到心碎。
这是因为我们的身体和心理都会对这些创伤性事件产生重大影响。
身体上,这些情绪通过激活身体的应激反应系统,如血压上升、心率加快等,从而导致我们感到身心俱疲。
心理上,失去亲友等重要人物会引发强烈的哀伤和悲痛情绪,使我们感到心碎。
第二章 一元二次方程第一节 一元二次方程 第二节 一元二次方程的解法 第三节 一元二次方程的应用 第四节 一元二次方程根与系数的关系 五大知识点:1、一元二次方程的定义、一元二次方程的一般形式、一元二次方程的解的概念及应用2、一元二次方程的四种解法(因式分解法、开平方法和配方法、配方法的拓展运用、公式法)3、根的判别式4、一元二次方程的应用(销售问题和增长率问题、面积问题和动态问题)5、一元二次方程根与系数的关系(韦达定理)【课本相关知识点】1、一元二次方程:只含有 未知数,并且未和数的 是2,这样的整式方程叫做一元二次方程。
2、能使一元二次方程 的未知数的值叫做一元二次方程的解(或根)3、一元二次方程的一般形式:任何一个一元二次方程经过化简、整理都可以转化为 的形式,这个形式叫做一元二次方程的一般形式。
其中ax 2是 ,a 是 ,bx 是 ,b 是 ,c是常数项【典型例题】【题型一】应用一元二次方程的定义,求字母的值例1、当a 为何值时,关于x 的方程(a-1)x |a|+1+2x-7=0是一元二次方程?【题型二】一元二次方程解的应用例1、关于x 的一元二次方程(a-1)x 2+x+|a|-1=0的一个根是0,则实数a 的值为( )A .-1B .0C .-1D .-1或1例2、已知多项式ax 2-bx+c ,当x=1时,它的值是0;当x=-2时,它的值是1(1)试求a+b 的值(2)直接写出关于x 的一元二次方程ax 2+bx+c=0的一个根【题型三】一元二次方程拓展开放型题例1、已知关于x 的方程(k 2-1)x 2-(k+1)x-2=0(1)当k 取何值时,此方程为一元一次方程?并求出此方程的根(2)当k 取何值时,此方程为一元二次方程?并写出这个一元二次方程的二次项系数、一次项系数、常数项。
巩 固 练 习1、下列方程中,是一元二次方程的为( )A. x 2= -1B. 2x (x-1)+1=2x 2C. x 2+3x=2x D. ax 2+bx+c-0 2、已知关于x 的方程mx 2+(m-1)x-1=2x 2-x ,当m 取什么值时,这个方程是一元二次方程?3、若关于x 的一元二次方程(a-2)x 2是一元二次方程,则a 的取值范围是4、把方程 (x-1)2-3x (x-2)=2(x+2)+1化成一般形式,并写出它的二次项系数、一次项系数和常数项5、若a 是方程x 2-3x+1=0的一个根,求2a 2-5a-2+231a +的值 6、若关于x 的方程ax 2+bx+c=0(a ≠0)中,abc 满足a+b+c=0和a-b+c=0,则方程的根是( )A. 1,0B. -1,0C. 1,-1D. 1,27、已知x=1是一元二次方程ax 2+bx-40=0的一个解,且a ≠b ,求2222a b a b --的值【课本相关知识点】(一)1、利用因式分解的方法实现“降次”,把解一元二次方程转化为解一元一次方程的方法,叫做因式分解法。
二次函数知识点、考点、典型试题集锦(带详细解析答案)考点1:二次函数的图象和性质一、考点讲解:1.二次函数的定义:形如c bx ax y ++=2(a ≠0,a ,b ,c 为常数)的函数为二次函数.2.二次函数的图象及性质:⑴ 二次函数y=ax 2 (a ≠0)的图象是一条抛物线,其顶点是原点,对称轴是y 轴;当a >0时,抛物线开口向上,顶点是最低点;当a <0时,抛物线开口向下,顶点是最高点;a 越小,抛物线开口越大.y=a(x -h)2+k 的对称轴是x=h ,顶点坐标是(h ,k )。
⑵ 二次函数c bx ax y ++=2的图象是一条抛物线.顶点为(-2b a ,244ac b a -),对称轴x=-2b a;当a >0时,抛物线开口向上,图象有最低点,且x >-2b a ,y 随x 的增大而增大,x <-2b a,y 随x 的增大而减小;当a <0时,抛物线开口向下,图象有最高点,且x >-2b a ,y 随x 的增大而减小,x <-2b a,y 随x 的增大而增大. ⑶ 当a >0时,当x=-2b a 时,函数有最小值244ac b a -;当a <0时,当 x=-2b a时,函数有最大值244ac b a-。
3.图象的平移:将二次函数y=ax 2 (a ≠0)的图象进行平移,可得到y=ax 2+c ,y=a(x -h)2,y=a(x -h)2+k 的图象.⑴ 将y=ax 2的图象向上(c >0)或向下(c< 0)平移|c|个单位,即可得到y=ax 2+c 的图象.其顶点是(0,c ),形状、对称轴、开口方向与抛物线y=ax 2相同.⑵ 将y=ax 2的图象向左(h<0)或向右(h >0)平移|h|个单位,即可得到y=a(x -h)2的图象.其顶点是(h ,0),对称轴是直线x=h ,形状、开口方向与抛物线y=ax 2相同.⑶ 将y=ax 2的图象向左(h<0)或向右(h >0)平移|h|个单位,再向上(k>0)或向下(k<0)平移|k|个单位,即可得到y=a(x -h)2 +k 的图象,其顶点是(h ,k ),对称轴是直线x=h ,形状、开口方向与抛物线y=ax 2相同.注意:二次函数y=ax 2 与y =-ax 2 的图像关于x 轴对称。
典型件结合知识点问答1、光滑圆柱结合精度设计应从哪几方面开始?答:圆柱结合的精度设计实际上就是公差与配合的选用,圆柱结合的精度设计包括配合制、公差等级及配合的选用。
1)配合制的选择基孔制和基轴制是两种平行的配合制。
基孔制配合能满足要求的,用同一偏差代号按基轴制形成的配合,也能满足使用要求。
所以,配合制的选择与功能要求无关,主要是考虑加工的经济性和结构的合理性。
从制造加工方面考虑,两种基准制适用的场合不同;从加工工艺的角度来看,对应用最广泛的中小直径尺寸的孔,通常采用定尺寸刀具(如钻头、铰刀、拉刀等)加工和定尺寸量具(如塞规、心轴等)检验。
而一种规格的定尺寸刀具和量具,只能满足一种孔公差带的需要。
对于轴的加工和检验,一种通用的外尺寸量具,也能方便地对多种轴的公差带进行检验。
由此可见:对于中小尺寸的配合,应尽量采用基孔制配合。
当孔的尺寸增大到一定的程度,采用定尺寸的刀具和量具来制造,将逐渐变得不方便也不经济。
这时如都用通用工具制造孔和轴,则选择哪种基准制都一样。
标准规定:应优先选用基孔制。
下列特殊情况下,由于结构和工艺的影响,采用基轴制更为合理:(1)用冷拉光轴作轴时。
冷拉圆型材,其尺寸公差可达IT7~IT9,能够满足农业机械、纺织机械上的轴颈精度要求,在这种情况下采用基轴制,可免去轴的加工。
(2)采用标准件时。
例:滚动轴承为标准件,它的内圈与轴颈配合无疑应是基孔制,而外圈与外壳孔的配合应是基轴制。
(3)一轴与多孔相配合,且配合性质要求不同时。
2)公差等级的选择公差等级选择的基本原则是:在满足使用性能的前提下,尽量选择较低的精度等级。
(1)应遵循工艺等价的原则,即相互结合的零件,其加工的难易程度应基本相当。
(2)相配合的零、部件的精度应相匹配。
如:与齿轮孔相配合的轴的精度就受齿轮精度的制约;与滚动轴承相配合的外壳孔和轴的精度应当与滚动轴承的精度相匹配。
(3)过盈、过渡和较紧的间隙配合,精度等级不能太低。
一般孔的公差等级应不低于IT8级,轴的不低于IT7级。
这是因为公差等级过低,使过盈配合的最大过盈过大,材料容易受到损坏;使过渡配合不能保证相配的孔、轴既装卸方便又能实现定心的要求;使间隙配合产生较大的间隙,不能满足较紧配合的要求。
(4)在非配合制的配合中,当配合精度要求不高,为降低成本,允许相配合零件的公差等级相差2~3级,。
3)配合种类的选择配合种类的选择主要就是根据零件的功能要求,确定配合的类型及非配合制的基本偏差代号。
选择的基本方法还是类比法、计算法和试验法三种。
类比法是选择配合种类的主要方法。
应用类比法选择时,要考虑以下因素:(1)配合件的工作情况选择配合的类型时,应考虑配合件间有无相对运动、定心精度高低、配合件受力情况、装配情况等。
(2)各种基本偏差形成配合的特点间隙配合有A~H(a~h)共十一种,其特点是利用间隙贮存润滑油及补偿温度变形、安装误差、弹性变形等所引起的误差。
生产中应用广泛,不仅用于运动配合,加紧固件后也可用于传递力矩。
不同基本偏差代号与基准孔(或基准轴)分别形成不同间隙的配合。
主要依据变形、误差需要补偿间隙的大小、相对运动速度、是否要求定心或拆卸来选定。
过渡配合有JS~N(js~n)四种基本偏差,其主要特点是定心精度高且可拆卸。
也可加键、销紧固件后用于传递力矩,主要根据机构受力情况、定心精度和要求装拆次数来考虑基本偏差的选择。
定心要求高、受冲击负荷、不常拆卸的,可选较紧的基本偏差,如N(n),反之应选较松的配合,如:K(k)或JS(js)。
过盈配合有P~ZC(p~zc)13种基本偏差,其特点是由于有过盈,装配后孔的尺寸被胀大而轴的尺寸被压小,产生弹性变形,在结合面上产生一定的正压力和摩擦力,用以传递力矩和紧固零件。
选择过盈配合时,如不加键、销等紧固件,则最小过盈应能保证传递所需的力矩,最大过盈应不使材料破坏,故配合公差不能太大,所以公差等级一般为IT5~IT7。
基本偏差根据最小过盈量及结合件的标准来选取。
(3)配合件的生产情况按大批大量生产时,加工后所得的尺寸通常呈下态分布;而单件小批量生产时,加工所得的孔的尺寸多偏向最小极限尺寸,轴的尺寸多偏向最大极限尺寸,即呈偏态分布。
所以,对于同一使用要求,单件小批生产时采用的配合应比大批大量生产时要松一些。
如大批量生产时的φ50H7/js6的要求,在单件小批生产时应选择φ50H7/h6。
同样,受其它工作条件的影响,配合的间隙或过盈也应随之变化。
2、滚动轴承的精度根据什么分?共有几级?代号是什么?根据国家标准的规定,向心滚动轴承按其尺寸公差和旋转精度分为五个公差等级,用0,6,5,4,2表示。
精度依次提高,0级公差轴承精度最低,2级公差精度最高,3、滚动轴承内圈与外壳孔的配合分别采用何种基准制?有什么特点?答:由于轴承是标准部件,为便于互换和大量生产,轴承外圈外径和外壳孔的配合采用基轴制,内圈内径与轴颈的配合采用基孔制。
所以,外圈外径是基准轴,内圈内径是基准孔。
但基准孔的公差带与一般基准孔H不同,其上偏差ES=0,下偏差EI为负值,轴承内圈通常与轴一起旋转,为防止结合面间相对滑动而产生磨损,应选用小过盈的配合。
为此,滚动轴承国家标准将内圈内径的公差带规定在零线的下方,使它与形成标准过渡配合的公差带(j、is、k、m、n)相配时,得到较紧的配合。
轴承外圈安装在外壳孔中,通常不旋转。
考虑到工作时温度升高会使轴热胀伸长而产生轴向移动,因此两端轴承中有一端应是浮动支承,配合应较松;不然,轴会弯曲使轴承内部有可能卡死。
为此,标准将外圈外径公差带规定在零线的下方,它与基本偏差h的公差带位置相同,但公差值是根据轴承特别需要,依其公差等级另行规定的。
4、圆锥公差的给定方法有哪几?各适用于什么场合?怎样标注?对于一个具体给定的圆锥,并不需要将所规定的四项公差全部给出,而应根据零件的功能要求给出所需的公差项目。
(1)给定圆锥直径公差T D和圆锥角α(或锥度C)此时由T D确定了两个极限圆锥,圆锥角误差、圆锥直径误差和形状误差都应控制在此两极限圆锥所限定的区域内——即圆锥直径公差带内。
其实质是包容要求,标注时应在直径公差值后加注○T。
当对圆锥角公差和圆锥形状公差有更高要求时,可再加注圆锥角公差AT和圆锥形状公差T F,但AT a和T F只能占T D的一部分。
这种给定方法是设计中常用的一种方法,适用于有配合要求的内、外圆锥。
(2)给定圆锥角公差AT和给定截面内的圆锥直径公差T DS此时,AT 只用来控制截面的实际直径,AT 只用来控制圆锥角误差,它们各自分别满足要求,其关系相当于独立原则。
当对圆锥形状精度有较高要求时,再单独给出形状公差T F 。
它适用于对圆锥的某给定截面有较高要求的情况。
5、 什么是普通螺纹的作用尺寸?如何判断中径的合格性?答:螺纹的加工过程中,螺距偏差和牙型半角偏差同时存在的,由于螺距偏差和牙型半角偏差可以折算成中径当量,因而可以不单独规定螺距公差和牙型半角公差,而仅规定中径总公差,用它来控制中径本身的尺寸偏差、螺距偏差和牙型车角偏差的综合影响。
当实际外螺纹存在螺距偏差和牙型半角偏差时,该实际外螺纹只可能与一个中径较大而具有设计牙型的理想内螺纹旋合。
在规定的旋合长度内,恰好包容实际外螺纹的一个假想内螺纹的中径称为外螺纹的作用中径。
它等于外螺纹的实际中径与螺距偏差对中径补偿值和牙型半角偏差对中径补偿值之和,即)(2/22αf f d d p s m ++=内螺纹的作用中径D 等于内螺纹的单一中径D 与螺距偏差对中径的补偿值F P 和牙型半角偏差F a /2对中径的补偿值之差,即:)(2/22αF F D D p s m +-=判断中径的合格性的原则是泰勒原则泰勒原则的要求是:实际螺纹的作用中径不允许超越其最大实体牙型的中径,任何部位的单一中径不允许超越其最小实体牙型的中径。
因此,螺纹中径合格的条件是:外螺纹: d 2m ≤d 2max , d 2a ≥d 2min内螺纹: D 2m ≥D 2min , D 2a ≤D 2max6、 什么是螺纹的旋合长度与精度等级,其关系如何?该如何选用?螺纹中径公差包含实际中径公差、补偿螺距偏差影响的公差、以及补偿牙型半角偏差影响的公差三部分。
而螺距偏差与螺纹的旋合长度有关,在同等制造条件下,旋合长度愈长,螺距偏差越大。
为了满足普通螺纹不同使用性能的要求,按螺纹公称直径和螺距基本尺寸规定了三组旋合长度,即短旋合长度(S )、中等旋合长度(N )和旋合长度长(L )。
在精度设计时,一般采用中等旋合长度。
对于一些有特殊需要的螺纹如:调整用的螺纹,为满足调整量大小的需要;铝、锌合金上的螺纹,为保证其机械强度;一些不通孔紧固螺纹等,均可选用长旋合长度。
当受力不大,或受空间位置限制的螺纹。
如锁紧用的特薄螺母,则可用短旋合长度。
螺纹精度不仅取决于螺纹直径的公差等级,而且与旋合长度有关。
当公差等级一定时,旋合长度越长,则加工时产生的螺距累积偏差和牙型半角偏差就可能越大,加工就越困难。
因此公差等级相同而旋合长度不同时,螺纹精度就有所不同。
为此,按螺纹公差等级和旋合长度规定了三种精度级,分别称为精密级,中等级和粗糙级,其中精密级的精度最高,粗糙级的精度最低。
精密级用于精密螺纹以及要求配合性质稳定和保证定位精度的螺纹,如航空宇航机械中的螺纹连接常用4H 、4h 和5H 等。
中等级广泛用于一般用途的螺纹,如机床和汽车上的螺纹,常用6H ,6h 和6g 。
粗糙级用于要求不高或制造上比较困难的螺纹,如热轧棒料加工的螺纹或较深的不通孔螺纹常用7H 和8g 等7、平键联结的特点和要求有哪些?平键联结的特点是通过健的侧面与轮毂槽和轴槽的侧面相接触来传递扭矩,键的上表面与轮毂槽间留有一定的间隙(0.2~0.5mm)。
键和槽侧面的配合性质决定键联结的可靠性。
在平键联结中键宽、轴槽宽和轮毂槽宽b为配合尺寸,其它为非配合尺寸。
平键联结的主要尺寸如图3-30,其中t 与t1分别为轴槽和轮毂槽的深度,h为键高,d为轴和轮毂槽直径。
考虑到在键联结中,键是标准件,键的侧面同时与轮毂槽及轴槽联结,且往往要求不同的配合性质。
为便于对它进行专门化生产,所以键结合采用基轴制配合,即规定键宽的公差带不变,平键联结方式及主要尺寸通过改变轴槽宽,轮毂槽宽的公差带达到不同的配合要求。
键宽b规定了一种公差带h9,以利于采用精拉钢大量制造。
8、为什么矩形花键规定小径定心一种定心方式?其优点何在?矩形花键除规定尺寸公差外,还规定了哪些位置公差?在矩形花键结合中,要使内、外花键的大径D、小径d、键宽B相应的结合面都同时耦合得很好是相当困难的。
因为这3个尺寸都会有制造误差,而且即使这3个尺寸都做得很准,但其相应的表面之间还会有位置误差,为了保证使用性能,改善加工工艺,只选择一个结合面作为主要配合面,对其规定较高的精度,以保证配合性质和定心精度,该表面称为定心表面。