9 + 3m − n = 0 ∴ ∆ = m 2 + 4n = 0
解得:m = -6,n = -9, ∴B = {3,-3}.
例6 :已知集合A = x | ax 2 − 3x + 2 = 0, x ∈ R, a ∈ R}.
(1 ) 若 A 是空集 , 求 a 的取值范围 ;
(2)若A中只含有一个元素求a的值, 并求出这个元素;
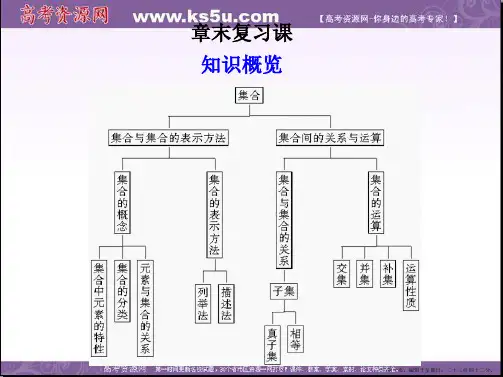
高 一 数 学
∉ 例1:用符号“ ∈”或“
⑴、0 2
∉ ∅, 0 ∈ N, π Q; ∉ Z, ∉ { ⑵ 2 3∉ {x|x< 11 }, 2 + 5 ∈ x | x ≤ 2 + 3}; ⑶、3 ∉{x | x = n + 1, n ∈ N }, 5 ∈{x | x = n + 1, n ∈ N }; ⑷、(-1,1) ∉ { y | y = x }, (−1,1) ∈ {( x, y ) | y = x }.
(2) x1 ∈ S , x2 ∈ S , 不妨设x2 = m + n 2 , x2 = p + q 2 , m, n, p, q ∈ Z .
∴ x1 + x2 = (m + p ) + (n + q ) 2 , 且(m + p ), (n + q) ∈ Z ,.
∴ ( x1 + x2 ) ∈ S .
{
9 (1) A = {x | ∈ N , x ∈ N }; 9− x
9 9 解 : 当x = 0时, = 1; x = 6时, = 3; 9− x 9− x 9 x = 8时, = 9, 9− x ∴ A = {0,6,8}
9 9 (2) B = { | x ∈ N且 ∈ N }; 9− x 9− x