第四章 索洛增长模型

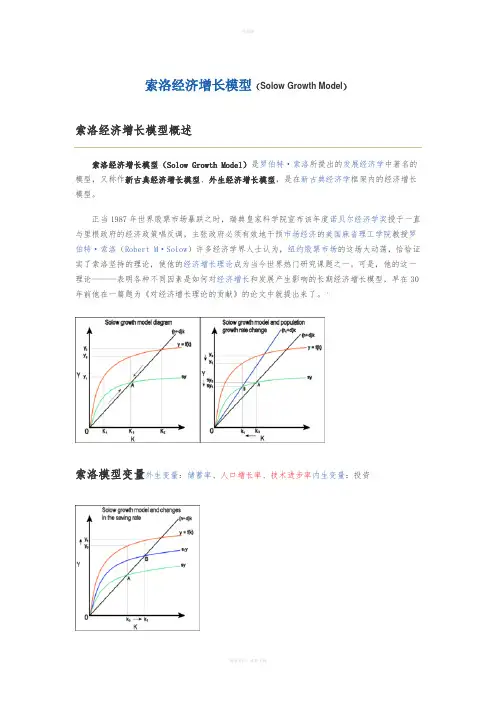
索洛经济增长模型（Solow Growth Model）索洛经济增长模型概述索洛经济增长模型（Solow Growth Model）是罗伯特·索洛所提出的发展经济学中著名的模型，又称作新古典经济增长模型、外生经济增长模型，是在新古典经济学框架内的经济增长模型。

正当1987年世界股票市场暴跌之时，瑞典皇家科学院宣布该年度诺贝尔经济学奖授于一直与里根政府的经济政策唱反调，主张政府必须有效地干预市场经济的美国麻省理工学院教授罗伯特·索洛（Robert M·Solow）许多经济学界人士认为，纽约股票市场的这场大动荡，恰恰证实了索洛坚持的理论，使他的经济增长理论成为当今世界热门研究课题之一。

可是，他的这一理论———表明各种不同因素是如何对经济增长和发展产生影响的长期经济增长模型，早在30年前他在一篇题为《对经济增长理论的贡献》的论文中就提出来了。

[1]索洛模型变量外生变量：储蓄率、人口增长率、技术进步率内生变量：投资索洛模型的数学公式模型的基本假定[1]索洛在构建他的经济增长模型时，既汲取了哈罗德—多马经济增长模型的优点，又屏弃了后者的那些令人疑惑的假设条件。

索洛认为，哈罗德—多马模型只不过是一种长期经济体系中的“刀刃平衡”，其中，储蓄率、资本—产出比率和劳动力增长率是主要参数。

这些参数值若稍有偏离，其结果不是增加失业，就是导致长期通货彭胀。

用哈罗德的话来说，这种“刀刃平衡”是以保证增长率（用Gw表示，它取决于家庭和企业的储蓄与投资的习惯）和自然增长率（用Gn表示，在技术不变的情况下，它取决于劳动力的增加）的相等来支撑的。

索洛指出，Gw和Gn之间的这种脆弱的平衡，关健在于哈罗德—多马模型的劳动力不能取代资本，生产中的劳动力与资本比例是固定的假设。

倘若放弃这种假设，Gw和Gn之间的“刀刃平衡”也就随之消失。

基于这一思路，索洛建立了一种没有固定生产比例假设的长期增长模型。

该模型的假设条件包括：1.只生产一种产品，此产品既可用于消费也可用于投资。

索洛增长模型名词解释
一、概念
索洛增长模型，又称作新古典经济增长模型或外生经济增长模型，是 Solow 于 1956 年首次创立的经济增长模型。

该模型旨在说明储蓄、资本积累和经济增长之间的关系，是分析以上三个变量关系的主要理论框架。

二、原理
索洛模型对经济总体的增长贡献被设定为由劳动、资本和技术进步三者组成。

该模型假设边际生产递减的一次齐次的总生产函数，满足稻田条件，储蓄率一定，技术进步为外生等条件。

在此基础上，得出了政府政策对于经济增长的作用是无效的结论。

三、应用
索洛模型的应用十分广泛，可以用于分析国家和地区的经济增长情况，为企业和政府制定经济政策提供理论依据。

例如，通过索洛模型可以分析资本积累、技术进步、劳动力等因素对经济增长的贡献，以及各种政策对经济增长的影响。

四、影响
索洛模型的创立对经济增长理论产生了深远的影响。

一方面，该模型提出了储蓄、资本积累和技术进步是经济增长的重要因素，为经济增长理论研究提供了新的视角和思路。

另一方面，该模型得出的政府政策无效论使人们意识到，政府政策并非万能，经济增长还需要依靠市场机制和内在动力。

然而，需要注意的是，索洛模型存在诸多假设条件，如边际生产递减、储蓄率一定等，这些假设条件在现实经济中并不完全符合。

因此，在应用索洛模型进行分析时，需要结合实际情况进行调整和改进，以更好地解释和预测经济增长。

总之，索洛增长模型作为一种重要的经济增长理论框架，对于分析和理解经济增长的基本原理和机制具有重要意义。

模型假设模型假设:1、该模型假设储蓄全部转化为投资，即储蓄-投资转化率假设为1;2、该模型假设投资的边际收益率递减，即投资的规模收益是常数;3、该模型修正了哈罗德-多马模型的生产技术假设，采用了资本和劳动可替代的新古典科布-道格拉斯生产函数，从而解决了哈罗德-多马模型中经济增长率与人口增长率不能自发相等的问题。

该模型假设储蓄全部转化为投资，即储蓄-投资转化率假设为1; 该模型假设投资的边际收益率递减，即投资的规模收益是常数; 该模型修正了哈罗德-多马模型的生产技术假设，采用了资本和劳动可替代的新古典科布-道格拉斯生产函数，从而解决了哈罗德-多马模型中经济增长率与人口增长率不能自发相等的问题。

因为在科布-道格拉斯生产函数中，劳动数量既定，随资本存量的增加，资本的边际收益递减规律确保经济增长稳定在一个特定值上。

该模型没有投资的预期，因此回避了有保证的经济增长率与实际经济增长率之间的不稳定，就此可得出结论:经济稳定增长。

编辑本段模型变量外生变量:储蓄率、人口增长率、技术进步率内生变量:投资模型的数学表达其中，K--资本;L--劳动;A--技术发展水平;I--毛投资;S--储蓄;k--有效劳动投入之上的资本密度;s--边际储蓄率;n--人口增长率;g--技术进步率;δ--资本折旧率;y--有效劳动投入之上的人均国内生产总值。

索洛增长模型的假设{①生产和供给方面:Y=F(K，L)，劳动和资本可以平滑替代，规模报酬不变，稻田条件(公式)，在生产函数两边同除以L--y=F(k,1)=f(k)，所有符号均代表人均产量;需求方面:y=c+i，c=(1-s)y，y=(1-s)y+i，i=sy=s f(k)}，资本存量的变化{△k=i-δk= s f(k)-δk}，投资、折旧和资本存量的"稳态"(图，储蓄率对稳态的影响，资本积累能提高产出水平，但是无法实现经济持续增长，"黄金律水平"{c*=f(k*)-δk*，条件:MPK=δ}，一个经济肯定会自动收敛于一个稳定状态，但并不会自动收敛到一个"黄金律水平"的稳定状态编辑本段模型结论经济增长的路径是稳定的编辑本段模型评价在索罗模型中，较高的储蓄导致较快的经济增长，但是，这只是暂时的。

模型假设模型假设:1、该模型假设储蓄全部转化为投资，即储蓄-投资转化率假设为1;2、该模型假设投资的边际收益率递减，即投资的规模收益是常数;3、该模型修正了哈罗德-多马模型的生产技术假设，采用了资本和劳动可替代的新古典科布-道格拉斯生产函数，从而解决了哈罗德-多马模型中经济增长率与人口增长率不能自发相等的问题。

该模型假设储蓄全部转化为投资，即储蓄-投资转化率假设为1; 该模型假设投资的边际收益率递减，即投资的规模收益是常数; 该模型修正了哈罗德-多马模型的生产技术假设，采用了资本和劳动可替代的新古典科布-道格拉斯生产函数，从而解决了哈罗德-多马模型中经济增长率与人口增长率不能自发相等的问题。

因为在科布-道格拉斯生产函数中，劳动数量既定，随资本存量的增加，资本的边际收益递减规律确保经济增长稳定在一个特定值上。

该模型没有投资的预期，因此回避了有保证的经济增长率与实际经济增长率之间的不稳定，就此可得出结论:经济稳定增长。

编辑本段模型变量外生变量:储蓄率、人口增长率、技术进步率内生变量:投资模型的数学表达其中，K--资本;L--劳动;A--技术发展水平;I--毛投资;S--储蓄;k--有效劳动投入之上的资本密度;s--边际储蓄率;n--人口增长率;g--技术进步率;δ--资本折旧率;y--有效劳动投入之上的人均国内生产总值。

索洛增长模型的假设{①生产和供给方面:Y=F(K，L)，劳动和资本可以平滑替代，规模报酬不变，稻田条件(公式)，在生产函数两边同除以L--y=F(k,1)=f(k)，所有符号均代表人均产量;需求方面:y=c+i，c=(1-s)y，y=(1-s)y+i，i=sy=s f(k)}，资本存量的变化{△k=i-δk= s f(k)-δk}，投资、折旧和资本存量的"稳态"(图，储蓄率对稳态的影响，资本积累能提高产出水平，但是无法实现经济持续增长，"黄金律水平"{c*=f(k*)-δk*，条件:MPK=δ}，一个经济肯定会自动收敛于一个稳定状态，但并不会自动收敛到一个"黄金律水平"的稳定状态编辑本段模型结论经济增长的路径是稳定的编辑本段模型评价在索罗模型中，较高的储蓄导致较快的经济增长，但是，这只是暂时的。

索洛经济增长模型理论概述-最新年文档索洛经济增长模型理论概述一、模型的推导1.假设条件资本边际产品递减；规模报酬不变；劳动力参与率不变；忽略政府作用；封闭经济；家庭收入储蓄比例S，消费比例1-S；固定的人口增长率n；外生中性技术进步。

2.生产函数的推导1928年，美国经济学教授道格拉斯与数学家柯布提出了柯布-道格拉斯生产函数（简称CD模型），其基本形式为Y=At?KαLβ，其中α、β分别代表资本弹性和劳动弹性，At表示第t年的技术水平，这个参数在短期内是个常量。

1957年，索洛将技术进步引入生产函数，提出希克斯中性技术进步函数Y=A（t）?F（K，L），具体形式为：Y=A0eλt?Kα?Lβ，其中A0为基期的科技水平，λ为科技进步系数或技术进步率，α、β为资本弹性和劳动弹性。

对上述方程取对数再对时间t求导，得：1/Y?dY/dt=λ+α/K?dK/dt+β/L?dL/dt。

由于实际经济活动及统计数据的非连续性，所以用差分替代微分，且dt=1，得：ΔY/Y=λ+α?ΔK/K+β?ΔL/L （1）令y=ΔY/Y，k=ΔK/K，l=ΔL/L，即得索洛增长速度方程：y=λ+αk+βl （2）从上式可以看出，索洛模型中认为影响经济增长的因素有技术进步率、资本以及劳动。

通过测算出α和β的值，可以得出这三者对经济的贡献程度。

3.增长模型的推导在上文中，技术进步率可以用ΔA/A来表示，则方程（1）可以写为：ΔY/Y=ΔA/A+α?ΔK/K+β?ΔL/L （3）在模型推导过程中，暂定ΔA/A=0。

根据规模报酬不变，当ΔL/L=1，ΔK/K=1时，ΔY/Y=1，即α+β=1。

因此，公式（3）可写为：ΔY/Y=ΔA/A+α?ΔK/K+（1-α）?ΔL/L （4）定义y=Y/L，又Δy/y=ΔY/Y-ΔL/L，Δk/k=ΔK/K-ΔL/L 对公式（4）进行移项，得出ΔY/Y-ΔL/L=α?（ΔK/K-ΔL/L），最终得出：Δy/y=α?Δk/k。

第4章运用索洛增长模型4.1复习笔记1．索洛模型中的参数变化对稳态均衡的影响（1）储蓄率的变化储蓄率s 的上升意味着当期的消费必须下降，尽管长期内会带来更高的消费水平，但这是以牺牲当期消费为代价的。

总体上说，储蓄率的上升并不必然带来福利的增加，这涉及人们对当期和未来的权衡取舍。

在考虑是否采用政策方法来改变储蓄率时，政策制定者必须决定与下一代人的福利相比这一代人的福利有多大。

如图4-1所示，两条()/s y k ⋅曲线对应储蓄率分别是1s 和2s ，2s 大于1s 。

两条s n δ+水平线也对应储蓄率1s 和2s 。

当储蓄率较高时，在k 的任何水平上每个工人有更高的资本增长率/k k ∆。

也就是说，在短期内，当储蓄率s 上升时，储蓄率的增加提高了每个工人的资本增长率；此增长率在向稳态过渡期间仍保持较高的数值。

图4-1储蓄率提高的长期影响在长期内，每个工人的资本增长率对于任何储蓄率来说都为0；在长期或稳态情况下，更高的储蓄率导致每个工人有更高的稳态资本k *，而达到稳态时的增长率仍为0。

长期内，总体的实际GDP 增大到稳态值后以稳定的速度增长，这时候增长速度等于人口增长率n ，这是因为///Y yL Y Y y y L L =⇒∆=∆+∆，稳态时/0y y ∆=，所以就有//Y Y L L n ∆=∆=。

（2）技术水平的变化在索洛模型中，技术水平提高将导致更高的稳态均衡水平。

如图4-2所示，两条曲线()()/f k s y k sA k ⋅=对应于技术水平1A 和2A ，2A 大于1A 。

当技术水平提高时，在任何k 的水平上每个工人的资本增长率/k k ∆也会提高。

在稳态情况下，/k k ∆为0，不管技术水平如何。

更高的技术水平产生每个工人更高的稳态资本，即*2k 大于*1k 。

图4-2技术水平提高的长期影响数学证明如下：人均稳态资本应满足方程：()//A f k k n s δ**⋅=+。

技术水平A 的上升并不影响方程的右边。

模型假设模型假设:1、该模型假设储蓄全部转化为投资，即储蓄-投资转化率假设为1;2、该模型假设投资的边际收益率递减，即投资的规模收益是常数;3、该模型修正了哈罗德-多马模型的生产技术假设，采用了资本和劳动可替代的新古典科布-道格拉斯生产函数，从而解决了哈罗德-多马模型中经济增长率与人口增长率不能自发相等的问题。

该模型假设储蓄全部转化为投资，即储蓄-投资转化率假设为1; 该模型假设投资的边际收益率递减，即投资的规模收益是常数; 该模型修正了哈罗德-多马模型的生产技术假设，采用了资本和劳动可替代的新古典科布-道格拉斯生产函数，从而解决了哈罗德-多马模型中经济增长率与人口增长率不能自发相等的问题。

因为在科布-道格拉斯生产函数中，劳动数量既定，随资本存量的增加，资本的边际收益递减规律确保经济增长稳定在一个特定值上。

该模型没有投资的预期，因此回避了有保证的经济增长率与实际经济增长率之间的不稳定，就此可得出结论:经济稳定增长。

编辑本段模型变量外生变量:储蓄率、人口增长率、技术进步率内生变量:投资模型的数学表达其中，K--资本;L--劳动;A--技术发展水平;I--毛投资;S--储蓄;k--有效劳动投入之上的资本密度;s--边际储蓄率;n--人口增长率;g--技术进步率;δ--资本折旧率;y--有效劳动投入之上的人均国内生产总值。

索洛增长模型的假设{①生产和供给方面:Y=F(K，L)，劳动和资本可以平滑替代，规模报酬不变，稻田条件(公式)，在生产函数两边同除以L--y=F(k,1)=f(k)，所有符号均代表人均产量;需求方面:y=c+i，c=(1-s)y，y=(1-s)y+i，i=sy=s f(k)}，资本存量的变化{△k=i-δk= s f(k)-δk}，投资、折旧和资本存量的"稳态"(图，储蓄率对稳态的影响，资本积累能提高产出水平，但是无法实现经济持续增长，"黄金律水平"{c*=f(k*)-δk*，条件:MPK=δ}，一个经济肯定会自动收敛于一个稳定状态，但并不会自动收敛到一个"黄金律水平"的稳定状态编辑本段模型结论经济增长的路径是稳定的编辑本段模型评价在索罗模型中，较高的储蓄导致较快的经济增长，但是，这只是暂时的。

索洛增长模型公式索洛增长模型（Solow Growth Model）是经济学家罗伯特·索洛（Robert Solow）于1956年提出的一种经济增长理论模型，用来解释一个经济体系长期稳定增长的原因和机制。

该模型的核心是一个生产函数，描述了技术进步、资本积累和劳动力的变化对经济增长的影响。

1.短期内，劳动力和资本积累规模都是固定的。

2.技术进步是外生的，即与资本积累和劳动力变化无关。

3.经济系统的均衡水平由劳动力与资本的投入和产出之间的比率决定。

Y(t)=F(K(t),AL(t))其中，Y(t)表示在时间t的产出（GDP）、K(t)表示在时间t的资本积累（物质资本）、AL(t)表示在时间t的劳动力。

F(K(t),AL(t))表示生产函数，描述了资本积累和劳动力变化对产出的影响。

生产函数通常是一个Cobb-Douglas生产函数，具体形式为：Y(t)=A(t)*[K(t)^α]*[AL(t)^(1-α)]其中，A(t)表示技术水平，α表示资本积累在产出中的比重，1-α表示劳动力的比重。

根据索洛增长模型，经济体系的长期增长取决于资本积累和劳动力变化的影响。

资本积累的增加可以提升产出，但随着资本积累的增长，其对产出的边际贡献递减。

劳动力的增加也可以提高产出，但同样受到边际贡献递减的限制。

另外，技术进步对经济增长的影响也是索洛增长模型关注的重点。

技术进步可以提高生产效率，使得单位资本和劳动力的投入能够创造更多的产出。

索洛增长模型中，技术进步被引入为生产函数中的A(t)项，它是一个外生变量，不受资本积累和劳动力的影响。

除了基本的索洛增长模型，后续的研究还对其进行了扩展和改进。

例如，考虑到资本积累和劳动力变化并非都是固定的假设，一些改进的模型引入了动态变化和人口增长等因素。

此外，一些研究还结合了不完全竞争市场和新经济学等理论，对索洛增长模型进行了进一步的发展。

总结来说，索洛增长模型是一种解释经济增长机制的经济学模型。

第4章运用索洛增长模型一、概念题1．绝对趋同（absolute convergence）答：绝对趋同是指不论各国的其他特征如何，穷国的人均收入增长倾向于比富国更快，这样穷国就能在一段时间内赶上富裕国家的假说。

“绝对”指趋同是不受其他经济变量的制约。

从理论上说，经济趋同可分为“绝对趋同”和“条件趋同”两种，但实证研究证明绝对趋同并不存在，而无论是在理论上，还是在现实世界中，条件趋同都是客观存在的现象。

2．有条件趋同（conditional convergence）答：有条件的趋同是指实际人均GDP的起始水平相对于长期或稳态位置越低，则增长率越快的一种理论。

实际人均GDP的起始水平越低则增长率越快的这一性质是由于边际产品递减规律作用的结果。

而趋同之所以是有条件的，是由于各国的稳态增长水平不同。

稳态水平依赖于储蓄率、人口增长率、生产函数的性质以及政府政策和人力资本初始存量上的差异——正是这些差异导致各国经济增长巨大的差异，当这些差异被排除时，各国经济将趋于收敛到相同的稳态，这就是条件趋同理论，也称作“条件收敛”。

3．趋同（convergence）答：趋同是指不同的经济体向着同样或相同的方向发展的现象。

经济趋同是经济增长理论的一个重要假说。

新古典经济增长理论认为，实际人均GDP的起始水平相对于长期或稳态位置越低，则增长率越快，这一性质是由于报酬递减规律作用的结果。

在资本报酬递减、技术进步一致性的条件下，不发达地区的经济增长比发达地区快。

经济趋同可分为绝对趋同和条件趋同：绝对趋同考虑的是对于不同的经济体，初始的人均资本水平0k不同而其他的外生变量A、s、n、δ均相同的条件下，初始的人均资本水平较低的穷国将会以较快的速度增长追赶上初始人均资本水平较高的富国，达到趋同，即稳态的人均资本k*相等；有条件的趋同是指实际人均GDP的起始水平相对于长期或稳态位置越低，则增长率越快的一种理论。

4．维持生存的水平（subsistence level）答：维持生存的水平是指人们维持生命所需要的最起码的生活水平。

索洛增长模型公式
索洛增长模型（Solow growth model）是经济学家罗伯特·索洛（Robert Solow）在20世纪50年代提出的一种经济增长模型。

该模型旨在解释一个国家或地区的长期经济增长率是如何由劳动力、资本积累和技术进步共同决定的。

索洛增长模型的基本公式如下：
Y = A * F(K, L)
其中，Y代表国内生产总值（Gross Domestic Product，GDP），A代表全要素生产率（Total Factor Productivity，TFP），K代表资本存量，L代表劳动力。

公式中的F(K, L)代表生产函数，描述了劳动力和资本如何组合产生产出。

生产函数通常假设具有递增边际产出递减的性质，即增加资本或劳动力对产出的贡献越来越小。

索洛增长模型的核心假设是资本和劳动力的增长率均保持恒定。

在这种情况下，索洛模型分析了长期经济增长率随技术进步的变化情况。

模型还引入了储蓄率和资本边际产出率的概念。

储蓄率表示国家或地
区的储蓄行为，即将一部分收入用于储蓄或投资。

资本边际产出率则表示每新增一单位资本对产出的贡献。

通过对索洛增长模型进行数学推导和经济分析，经济学家可以研究技术进步、储蓄率和资本积累对经济增长的影响。

这个模型为经济政策提供了理论框架，帮助决策者制定增长战略和政策。

需要注意的是，索洛增长模型是一个简化的经济模型，假设非常理想化，忽略了很多现实经济中的复杂因素。

实际经济增长往往受到政治、制度、自然资源等多种因素的影响。

因此，在实际应用中，索洛增长模型仅作为一种参考工具使用，并不完全能够解释现实经济增长的复杂性。