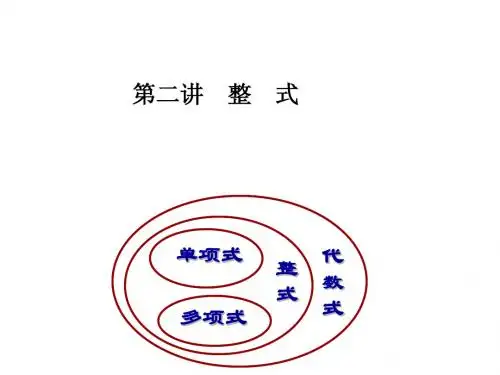
整式基本概念(含答案)

（2）分母中含有字母的式子一定不是整式．【典型例题】类型一、整式概念辨析1．指出下列各式中哪些是单项式？哪些是多项式？哪些是整式？ 22x y +，x -，3a b +，10，61xy +，1x ，217m n ，225x x --，22x x +，7a 【答案与解析】单项式有：x -，10，217m n ，7a ； 多项式有：22x y +，3a b +，61xy +，225x x --； 整式有：22x y +，x -，3a b +，10，61xy +，217m n ，225x x --，7a ． 【总结升华】22x x +不是整式，因为分母中含有字母； 212a a ++也不是多项式，因为1a 不是单项式．举一反三： 【变式】下列代数式：322332111;;;;2;-232a x y ab x x y x y y x+--++π①②③④⑤⑥，其中是单项式的是_______________，是多项式的是_______________.【答案】①②③，④⑥类型二、单项式2．指出下列代数式中的单项式，并写出各单项式的系数和次数．234a b -，a -，442x ，a mn ，223a y π，a -3，5-3，82-310tm ⨯，2x y 【答案与解析】234a b -，a -，442x ，223a y π，5-3，82-310tm ⨯，2x y 是单项式，其中 234a b -的系数是34-，次数是3；a -的系数是-1，次数是1；442x 的系数是42，次数是4；223a y π的系数是3π，次数是4；53-为非零常数，只有数字因式，系数是它本身，次数为0；82-310tm ⨯的系数仍按科学记数法表示为-3×108，次数是3；2x y 只含有字母因数，系数是l ，次数为字母指数之和为3．【总结升华】（1）要区分数字因数、字母因数；（2）不能见了指数就相加，如442x 中，42的指数4不能相加，次数为4；（3）有分数线的，分子、分母的数字都是系数；（4）π是常数，不能看作字母．举一反三：【变式1】单项式3x 2y 3的系数是 ． 【答案】3． 【变式2】下列结论正确的是( )．A ．没有加减运算的代数式叫做单项式．B ．单项式237xy 的系数是3，次数是2． C ．单项式m 既没有系数，也没有次数．D ．单项式2xy z -的系数是-1，次数是4．【答案】D 类型三、多项式3.多项式24242153x y x y x -+-+，这个多项式的最高次项是什么？一次项的系数是什么？常数项是什么？这是几次几项式? 【答案与解析】这个多项式中共有四项，分别为：24242,,,153x y x y x --，它们的次数分别为：3,6,1,0；其中4223x y 的次数是6，是最高次项，一次项x -的系数是-1，常数项是1，它是六次四项式．【总结升华】确定多项式的次数时，分两步：（1）先求多项式中每一项的次数；（2）取这些次数中的最大的数即为多项式的次数．4. 已知多项式32312246753m x xy x y y x y ---+--． (1)求多项式各项的系数和次数．(2)如果多项式是七次五项式，求m 的值．【答案与解析】(1)依题意知此多项式是五项式，第一项26xy -的系数是-6，次数是3；第二项3127m x y --的系数是-7，次数是3m+1；第三项343x y 的系数是43，次数是4；第四项2x y -系数是-l ，次数3；第五项-5系数是-5，次数是0． (2)由多项式是七次五项式，可得3127m xy --的次数是7，即3m -1+2＝7，解得m ＝2． 【总结升华】对于单项式3127m x y --的次数为3m+1的认识会不太习惯，通过适量的练习，会对用字母表示多项式的次数或系数有较深地认识．举一反三：【变式】多项式()34b a x x x b --+-是关于x 的二次三项式，求a 与b 的差的相反数．【答案】()()4042242 2.a ab b a b -==⎧⎧∴⎨⎨==⎩⎩∴--=--=-解：由题意得类型四、整式的应用5. 用整式填空：(1)某商场将一种商品A 按标价的9折出售(即优惠10%)仍可获利10%，若商场商品A 的标价为a 元，那么该商品的进价为________元(列出式子即可，不用化简)．(2)甲商品的进价为1400元，若标价为a 元，按标价的9折出售；乙商品的进价是400元，若标价为b 元，按标价的8折出售，列式表示两种商品的利润率分别为甲：________ 乙：________．【答案】(1)90%10%1a +；(2)甲商品的利润率为90%14001400a -×100%，乙商品的利润率为： 80%400400b -×100%． 【解析】本例属于实际生活问题，应分清“进价”、“标价”、“利润”、“利润率”、“打折”等问题，打几折就是标价的十分之几．【总结升华】解答本例需弄清以下两个数量关系：(1)利润＝售价－进价; (2)利润率＝-售价进价进价． 举一反三：【变式】（2014秋•栖霞市期末）对下列代数式作出解释，其中不正确的是（ ）A. a ﹣b ：今年小明b 岁，小明的爸爸a 岁，小明比他爸爸小（a ﹣b ）岁B. a ﹣b ：今年小明b 岁，小明的爸爸a 岁，则小明出生时，他爸爸为（a ﹣b ）岁C. ab ：长方形的长为acm ，宽为bcm ，长方形的面积为abcm2 D. ab ：三角形的一边长为acm ，这边上的高为bcm ，此三角形的面积为abcm2 【答案】D.6. （2015•重庆）下列图形都是由同样大小的小圆圈按一定规律组成的，其中第①个图形中一共有6个小圆圈，第②个图形中一共有9个小圆圈，第③个图形中一共有12个小圆圈，…，按此规律排列，则第⑦个图形中小圆圈的个数为（ ）A. 21B. 24C.27D. 30【答案】 B【解析】观察图形得：第1个图形有3+3×1=6个圆圈，第2个图形有3+3×2=9个圆圈，第3个图形有3+3×3=12个圆圈，…第n 个图形有3+3n=3（n+1）个圆圈，当n=7时，3×（7+1）=24，故选B ．【总结升华】找规律问题一般应经历四个阶级“特例引路”、“对比分析”、“总结规律”、“反思检验”等． 【巩固练习】一、选择题1．（2014秋•章丘市校级期末）下面的说法正确的是（ ）A. ﹣2不是代数式B. ﹣a 表示负数C. 的系数是3D. x+1是代数式2．已知单项式243x y -，下列说法正确的是( )． A ．系数是-4，次数是3B ．系数是43-，次数是3 C ．系数是43，次数是3 D ．系数是43-，次数是2 3．如果一个多项式的次数是3，那么这个多项式的任何一项的次数( )．A ．都小于3B ．都等于3C ．都不小于3D ．都不大于34．下列式子：a+2b ，2a b -，221()3x y -，2a，0中，整式的个数是( )． A ．2个 B ．3个 C ．4个 D ．5个 5.．关于单项式3222x y z -，下列结论正确的是( )．A ．系数是-2，次数是4B ．系数是-2，次数是5C ．系数是-2，次数是8D ．系数是-23，次数是56．一组按规律排列的多项式：a b +，23a b -，35a b +，47a b -，…，其中第10个式子是( )．A ．1019a b +B ．1019a b -C ．1017a b -D ．1021a b -二、填空题7．代数式23mn ，2353x y ，2x y -，23ab c -，0，31a a +-中是单项式的是________，是多项式的是________．8.关于x 的多项式3(1)23nm x x x --+的次数是2，那么______,______m n ==． 9．多项式2x 2-3x+5是_ 次______项式．10．（2015•长春模拟）今年五．一假期，张老师一家四口开着一辆轿车去长春市净月潭森林公园度假．若门票每人a 元，进入园区的轿车每辆收费20元，则张老师一家开车进入净月潭森林公园园区所需费用是 元（用含a 的代数式表示）． 11．有一组单项式：2a ，32a -，43a ，…，请观察它们的构成规律，用你发现的规律写出第10个单项式：________．12．关于x 的二次三项式的一次项的系数为5，二次项的系数为-3，常数项为-4，按照x 的次数逐渐降低排列，这个二次三项式为________．13．某校生物教师李老师在生物实验室做试验时，将水稻种子分组进行发芽试验：第1组取3粒，第2组取5粒，第3组取7粒，第4组取9粒……按此规律，请你推测第n 组应该取种子数是________粒．14. 如图所示，在一个三角点阵中，从上向下数有无数多行，其中各行点数依次为2，4，6，…，2n ，…，请你探究出前n 行的点数和所满足的规律．若前n 行点数和为930，则n ＝________．三、解答题15．（2015•宜宾）如图，以点O 为圆心的20个同心圆，它们的半径从小到大依次是1、2、3、4、…、20，阴影部分是由第1个圆和第2个圆，第3个圆和第4个圆，…，第19个圆和第20个圆形成的所有圆环，则阴影部分的面积为多少？16．已知单项式4312x y -的次数与多项式21228m a a b a b +++的次数相同，求m 的值． 17．某电影院有20排座位，已知第一排有18个座位，后面一排都比前一排多2个座位，试用代数式表示出第n 排的座位数，并求第19排的座位数．18．已知多项式12111021112a a b a b ab b -+-++-，(1)请你按照上述规律写出该多项式的第5项，并指出它的系数和次数；(2)这个多项式是几次几项式?【答案与解析】一、选择题1. 【答案】D【解析】A 、﹣2是代数式，故此选项错误；B 、﹣a 不一定是负数，故此选项错误；C 、的系数是，故此选项错误；D 、x+1是代数式，故此选项正确．2．【答案】B3．【答案】D【解析】多项式的次数是该多项式中各项次数最高项的次数。

1.1 整式一、选择题（让你算的少，要你想的多，只选一个可要认准啊！） 1、下面说法中正确的是（ ）A 、一个代数式不是单项式，就是多项式B 、单项式是整式C 、整式是单项式D 、以上说法都不对2、下列代数式中整式有( )x 1,2x +y ,31a 2b ,πy x -,xy 45,0.5,a A 、4个 B 、5个 C 、6个D 、7个3、制造一种产品，原来每件成本a 元，先提价5%，后降价5%，则此时该产品的成本价为( )A 、不变B 、a (1+5%)2C 、a (1+5%)(1－5%)D 、a (1－5%)24、随着计算机技术的迅猛发展，电脑价格不断降低，某品牌电脑按原售价降低m 元后，又降低20%，现售价为n 元，那么该电脑的原售价为( ) A 、(54n +m )元 B 、(45n +m )元 C 、(5m +n )元D 、(5n +m )元二、填空题（简洁的结果，表达的是你敏锐的思维，需要的是细心！） 5、_____和_____统称整式. 6、多项式a 2－21ab 2－b 2有_____项，其中－21ab 2的次数是_____. 7、整式21，3x －y 2,23x 2y ,a ,πx +21y ,522a π,x +1中_____是单项式，_____是多项式8、有一棵树苗，刚栽下去时，树高2.1米，以后每年长0.3米，则n 年后树高_____米.三、解答题（耐心计算，仔细观察，表露你萌动的智慧！） 9、某人买了50元的月票卡，乘车后的余额如下表求：(1)乘车m次时的余额为多少元？(2)乘车13次时的余额是多少？(3)最多能乘多少次？10、如图，长方形的ABCD的长是a，宽为b，在长方形内画两个扇形，大扇形的半径为b，求图中阴影部分的面积.参考答案一、1 C 2 B 3 C 4 B 二、5、单项式 多项式 6. 三 37、21 23x 2y a 522a ;3x －y 2 πx +21y x +1 8. 2.1+0.3n三、9、 (1)50－0.8m (2)50－0.8×13=39.6(元) (3)6210、【解题思路】 扇形面积我们目前可以没法用公式求出，但可知图中的扇形的面积等于对应半径圆的面积的41.分别求出图中的半径为a-b 、b 的扇形面积，再用长方形形面积减去两扇形面积即可.解：图中的扇形的面积等于对应半径圆的面积的.所以阴影部分的面积＝ab-41πb 2-41π（a-b ）2.附:整式的加减导航一、学习提要1．理解单项式、多项式以及整式的概念.2．理解同类项的概念，会判断同类项，并能熟练地合并同类项. 3．掌握去括号法则，能正确依据法则去括号4．会进行整式的加减运算，并能根据整式的加减解决一些实际问题； 二、重点、易考点提示1．重点：（1）单项式的概念、系数与次数的辨别；（2）同类项的概念、合并同类项法则的应用；（3）根据整式的加减解决实际问题.2．易考点：（1）辨别单项式的系数；（2）同类项的辨别；（3）整式的化简求值；（4）根据整式的加减解决实际问题.三、知识扫描 （一）有关概念1．整式：单项式和多项式统称为整式.友情提示：单独一个单项式是整式；单独一个多项式也是整式不能说整式是单项式，也不能说整式是多项式整式是代数式，但一个代数式不一定是整式2．单项式：数与字母的积的代数式单独一个数或一个字母也是单项式. （1）单项式的系数：单项式中的数字因数. （2）单项式的次数：单项式中所有字母的指数的和.友情提示：（1）判别一个代数式是否是单项式的依据是单项式的概念，如21mn 是单项式，因为它是数21与字母m 、n 的积；而m 2就不是单项式；因为m 2不是数与字母的积. （2）识别单项式的系数要注意将单项式写成数字与字母的积的形式，然后找数字因式；如确定单项式52ab -系数，应将单项式写成ab 52-，然后确定其系数为52-而不是-2. （3）单项式的次数是单项式中所有字母的指数和，而不包括系数的指数，如b a 232次数是3，而不是5.3．多项式；几个单项式的和.（1）常数项：多项式中不含有字母的项.（2）多项式的次数：多项式中，次数最高项的次数就是多项式的次数.友情提示：项的次数实际就是单项式的次数，也是这一项中所有字母的指数的和.4．同类项：在多项式中，所含字母相同，且各相同字母的指数也相同的项叫做同类项几个常数项也是同类项.友情提示：同类项应具备两个条件：（1）所含字母相同；（2）相同字母的指数相同同类项与系数无关，与字母的顺序无关.5．合并同类项：把多项式中几个同类项合并成一项的过程，叫做合并同类项.友情提示：合并同类项是整式加减的基础.（二）有关法则1．合并同类项法则：在合并同类项时，把同类项的系数相加，字母和字母的指数保持不变.友情提示：合并同类项的依据是加法交换律和结合律.2．去括号法则：（1）括号前是“+”时，把括号和它前面的“+”去掉，原括号里的各项都不改变符号.（2）括号前是“-”时，把括号和它前面的“-”去掉，原括号里的各项都改变符号.友情提示：去括号时首先要看清括号前是“+”还是“-”，然后再依据法则去括号注意改变符号时，改变是括号内的项的符号，而不是括号外的项的符号.3．整式的加减：整式加减的实质是先去括号，再合并同类项.友情提示：整式的加减一般分成以下几步：（1）写出算式；（2）去括号；（3）合并同类项在运算的过程中要保证每一步都要正确；求多项式的值实际上是整式的加减的应用，化简的过程就是整式加减运算的过程.四、几点说明1．单项式的系数包括它前面的符号.2．多项式的次数不是各项字母的指数的和，多项式没有系数的说法.3．同类项的识别应注意满足两个相同，即所含字母相同，相同字母的指数也分别相同.4．用分配律去括号时，一是不要漏乘括号中的项，二是括号前是“-”时，括号内各项都要变号.5．在整式的加减运算中，应注意整体思想是灵活应用.。

整式的概念知识总结归纳一. 提出问题：有了用字母表示数之后，就出现了形形色色的代数式。

为了便于研究，我们往往把代数式分成类，然后归类去讨论它的特征和运算。

二. 梳理知识：1. 单项式：因为它分母中含有字母，所以也就不是整式，故判断单项式的方法主要从两个角度出发，一是看运算中是否只含乘除法运算；二是看分母中含不含字母。

特别要注意的是，单独的一个数或一个字母也是单项式。

如－8，a，y也都是单项式。

在单项式中，有两个重要概念：（1）系数：单项式中的数字因数，叫做这个单项式的系数。

12单项式ab的系数是1，但省略不写，单项式－xy3的系数是－1，只保留一个“－”号，1字省略不写（2）次数：一个单项式中，所有字母的指数的和叫做这个单项式的次数。

例如232，y的指数是3，所以5x2y3的次数就是5，同样48单项式ab的次数是2学习单项式应注意的几点：单项式是初一代数中一个重要的基本概念，同学们在学习这一概念时，应注意以下几点。

1.式。

特别要强调的是：单独的一个数或一个字母也是单项式，如m，x，－2，0等都是单项式。

2.1或－1时，1通常省略不写。

如：mn2，－x3y4的系数分别是1与－1，而不是没有系数。

有的单项式含有多个字母，有时为了需要，往往把其中一个或几个字母作为主要字母，这时单项式中的数字因数和其它字母因数都被称为这个单项式的系数。

例如：单项式3mx2y，一般情况下，其系数是3，若以x2y为主要字母，则系数就是3m；若以y为主要字母，则其系数就是3mx2。

4b3c2的字母a，b，c的指数的和是4＋3＋2＝94b3c2是一个九次单项式。

单独一个非零的数，例如：3，－7都叫做零次单项式。

因数零与任何一个或几个字母的乘积还是零，所以可以把零看作与任何一个或几个字母的乘积，故零也可以看成是次数不能确定的单项式。

4. 2b3c，对于字母a，b，c来讲是六次单项式；对于字母a来讲是二次单项式；对于字母b来讲是三次单项式；对于字母c来讲是一次单项式。

人教版七年级数学（上）第一章《整式》经典例题及练习一. 教学内容：整式1. 单项式的有关概念，如何确定单项式的系数和次数；2. 多项式的有关概念，如何确定多项式的系数和次数；3. 什么是整式；4. 分析实际问题中的数量关系，培养用字母表示数量关系以及解决实际问题的能力.二. 知识要点：1. 用字母表示数时，应注意以下几点：（1）加、减、乘、除、乘方等运算符号将数和表示数的字母连接而成的式子是代数式.（2）代数式中出现的乘号一般用“·”或省略不写，例如4乘a写作4a.（3）在代数式中出现除法运算时，一般按分数的写法来写，例如a除以t写作.（4）代数式中大于1的分数系数一般写成假分数，例如2. 单项式（1）如3a，xy，－6m2，－k等，它们都是数与字母的积，像这样的式子叫做单项式. 对于单项式的理解有以下几点需要注意：①单项式反映的或者是数与字母，或者是字母与字母之间的运算关系，且这种运算只能是乘法，而不能含有加减运算，如代数式（x＋1）3不是单项式.②字母不能出现在分母里，如不是单项式，因为它是n与m的除法运算.③单独的一个数或一个字母也是单项式，如0，－2，a都是单项式.（2）单项式的系数：是指单项式中的数字因数，如果一个单项式只含有字母因数，它的系数就是1或－1，如m就是1·m，其系数是1；－a2b就是－1·a2b，其系数是－1.（3）单项式的次数：是指一个单项式中所有字母的指数的和. 掌握好这个概念要注意以下几点：①从本质上说，单项式的次数就是单项式中字母因数的个数，如5a3b就是5aaab，有4个字母因数，因此它的次数就是4.②确定单项式的次数时，不要漏掉“1”. 如单项式3x2yz3的次数是2＋1＋3＝6，字母因数的指数为1时，不能认为它没有指数.③单项式的次数只与单项式中的字母因数的指数有关，而不能误加入系数的指数，如单项式－2a3b4c5的次数是字母a、b、c的指数和，即3＋4＋5＝12，而不是2＋3＋4＋5＝14.④单独一个非零数字的次数是零.3. 多项式（1）多项式：是指几个单项式的和. 其含义有：①必须由单项式组成；②体现和的运算法则，如3a2＋b－5是多项式，（2）多项式的项：是指多项式中的每个单项式. 其中不含字母的项叫做常数项. 要特别注意，多项式的项包括它前面的性质符号（正号或负号）.另外，一个多项式化简后含有几项，就叫做几项式. 多项式中的某一项的次数是n，这一项就叫做n次项. 如多项式x3＋2xy＋x2－x＋y－1是六项式，x3的次数是3，叫三次项，2xy、x2的次数都是2，都叫二次项，－x、y的次数都是1，都叫一次项，后面的－1叫常数项.（3）多项式的次数：是指多项式里次数最高的项的次数. 应当注意的是：不要与单项式的次数混淆，而误认为多项式的次数是各项次数之和，如多项式3x4＋2y2＋1的次数是4，而不是4＋2＝6，故此多项式叫做四次三项式.4. 单项式与多项式统称为整式.三. 重点难点：1. 重点：单项式和多项式的有关概念.2. 难点：如何确定单项式的次数和系数，如何确定多项式的次数.【典型例题】例1. （1）（2008年宁夏）某市对一段全长1500米的道路进行改造. 原计划每天修x米，为了尽量减少施工对城市交通所造成的影响，实际施工时，每天修路比原计划的2倍还多35米，那么修这条路实际用了__________天.（2）（2008年全国数学竞赛广东初赛）某商店经销一批衬衣，每件进价为a元，零售价比进价高m%，后因市场变化，该商店把零售价调整为原来零售价的n%出售，那么调整后每件衬衣的零售价是（）A. a（1＋m%）（1－n%）元B. am%（1－n%）元C. a（1＋m%）n%元D. a（1＋m%·n％）元分析：（1）修这条路实际用的天数等于这条路的全长1500米除以实际每天的工作量，原计划每天修x米，实际施工时，每天比原计划的2倍还多35米，即（2x＋35）米. 用1500除以（2x＋35）就可以了. （2）每件衬衣进价为a元，零售价比进价高m%，那么零售价就是a（1＋m%），后来零售价调整为原来的n%，也就是a（1＋m%）n%.评析：用字母表示数时，要注意书写代数式的惯例（数字在前字母在后，乘号省略，如果是除法写成分数的形式，系数是代分数时写成假分数，数字和字母写在括号的前面等）例2. 找出下列代数式中的单项式，并写出各单项式的系数和次数.单独一个数字是单项式，它的次数是0.8a3x的系数是8，次数是4；－1的系数是－1，次数是0.评析：判定一个代数式是否是单项式，关键就是看式子中的数字与字母或字母与字母之间是不是纯粹的乘积关系，如果含有加、减、除的关系，那么它就不是单项式.例3. 请你用代数式表示如图所示的长方体形无盖的纸盒的容积（纸盒厚度忽略不计）和表面积，这些代数式是整式吗？如果是，请你分别指出它们是单项式还是多项式.分析：容积是长×宽×高，表面积（无盖）是五个面的面积，在分辨它们是不是整式，是单项式还是多项式时，牵牵把握住概念，根据概念判断.解：纸盒的容积为abc；表面积为ab＋2bc＋2ac（或ab＋ac＋bc＋ac＋bc）. 它们都是整式；abc是单项式，ab＋2bc＋2ac（或ab＋ac＋bc＋ac＋bc）是多项式.评析：①本题是综合考查本节知识的实际问题，作用有二：一是将本节所学知识直接应用到具体问题的分析和解答中，既巩固了知识，又强化了对知识的应用意识；二是将几何图形与代数有机结合起来，有利于综合解决问题能力的提高. ②本题解答关键：长方体的体积公式和表面积公式.故只剩下－2x2a＋1y2的次数是7，即2a＋1＋2＝7，则a＝2.解：2评析：本题考查对多项式的次数概念的理解. 多项式的次数是由次数最高的项的次数决定的.例5. 把代数式2a2c3和a3x2的共同点填写在下列横线上.例如：都是整式.（1）都是____________________；（2）都是____________________.分析：观察两式，共同点有：（1）都是五次式；（2）都含有字母a.解：（1）五次式；（2）都含有字母a.评析：主要观察单项式的特征.例6. 如果多项式x4－（a－1）x3＋5x2－（b＋3）x－1不含x3和x项，求a、b的值.分析：多项式不含x3和x项，则x3和x项的系数就是0. 根据这两项的系数等于0就可以求出a和b 的值了.解：因为多项式不含x3项，所以其系数－（a－1）＝0，所以a＝1.因为多项式也不含x项，所以其系数－（b＋3）＝0，所以b＝－3.答：a的值是1，b的值是－3.评析：多项式不含某项，则某项的系数为0.【方法总结】1. “用字母表示数”是代数学的基础，这种符号化的表示方法随着学习的深入会逐渐加深数学抽象化的程度，我们要体会这种抽象化，它更接近数学的本质，也是有效地解决数学问题的工具.2. 在学习多项式的时候，要注意和单项式的概念进行比较，通过比较两者之间的相同点和不同点，掌握两个概念之间的联系与区别，突出概念的本质，帮助我们理解多项式的概念.【模拟试题】（答题时间：40分钟）一. 选择题1. 在代数式中单项式共有（）A. 2个B. 4个C. 6个D. 8个*2. 下列说法不正确的是（）C. 6x2－3x＋1的项是6x2，－3x，1D. 2πR＋2πR2是三次二项式3. 下列整式中是多项式的是（）4. 下列说法正确的是（）A. 单项式a的指数是零B. 单项式a的系数是零C. 24x3是7次单项式D. －1是单项式5. 组成多项式2x2－x－3的单项式是下列几组中的（）A. 2x2，x，3B. 2x2，－x，－3C. 2x2，x，－3D. 2x2，－x，3*7. 下列说法正确的是（）B. 单项式a的系数为0，次数为2C. 单项式－5×102m2n2的系数为－5，次数为58. 下列单项式中的次数与其他三个单项式次数不同的是（）**9. （2007年华杯初赛）如果一个多项式的各项的次数都相同，则称该多项式为齐次多项式. 例如：x3＋2xy2＋2xyz＋y3是3次齐次多项式. 若x m＋2y2＋3xy3z2是齐次多项式，则m等于（）A. 1B. 2C. 3D. 4二. 填空题1. （2007年云南）一台电视机的原价为a元，降价4％后的价格为__________元.三. 解答题*1. 下列代数式中哪些是单项式，并指出其系数和次数.2. 说出下列多项式是几次几项式：（1）a3－ab＋b3（2）3a－3a2b＋b2a－1（3）3xy2－4x3y＋12（4）9x4－16x2y2＋25y2＋4xy－1四. 综合提高题**3. 一个关于字母a、b的多项式，除常数项外，其余各项的次数都是3，这个多项式最多有几项？试写出一个符合这种要求的多项式，若a、b满足︱a＋b︱＋（b－1）2＝0，求你写出的多项式的值.【试题答案】一. 选择题1. B2. D3. B4. D5. B6. C7. D8. B9. B二. 填空题三. 解答题2. （1）三次三项式（2）三次四项式（3）四次三项式（4）四次五项式四. 综合提高题1. 由题意可知m＋2＋1＝8，∴m＝52. （1）四次六项式，最高次项是－3x3y，最高次项系数是－3，常数项是1（2）三次三项式，最高次项是y3，最高次项系数是1，常数项是－0.53. 最多有5项（可以含有a3，b3，a2b，ab2），如a3+a2b＋ab2＋b3＋1（答案不唯一）. 因为︱a＋b ︱＋（b－1）2＝0，所以b＝1，a＝－1，所以原式＝－1＋1－1＋1＋1＝1。

第5讲 整式的基本概念【学习目标】整式的基本概念及合并同类项是在学生学习了有理数、用字母表示数和代数式等知识的基础上安排的．该章属于《义务教育数学课程标准》中的“数与代数”部分，其主要内容包括整式、单项式、多项式；合并同类项；等．这些内容既是对有理数的概括与抽象，又是后继学习整式加减运算的基础，还是学习物理、化学等学科及其他科学技术不可缺少的工具．【基础知识】一、整式的基本概念1、 单项式：由数字与字母的积或字母与字母的积所组成的代数式叫做单项式．也就是说单项式中不存在数字与字母或字母与字母的加、减、除关系，特别的单项式的分母中不含未知数．单独的一个字母或数也叫做单项式．（1）单项式的次数：是指单项式中所有字母的指数和．例如：单项式212ab c -，它的指数为1214++=，是四次单项式．单独的一个数(零除外)，它们的次数规定为零，叫做零次单项式223xy（2）单项式的系数：单项式中的数字因数叫做单项数的系数．2、多项式：由几个单项式的和组成的代数式叫做多项式．例如：27319x x -+是多项式．（1）多项式的项：其中每个单项式都是该多项式的一个项．多项式中的各项包括它前面 的符号．多项式中不含字母的项叫做常数项．（2）多项数的次数：多项式里，次数最高项的次数就是这个多项式的次数．（3）多项式的降（升）幂排列：按照同一个字母的指数从大到小（或从小到大）的顺序排列． 3、整式：单项式和多项式统称整式． 二：合并同类项 1、同类项的概念：所含的字母相同，且相同字母的指数也相同的单项式叫做同类项． 2、合并同类项：合并同类项的法则：在合并同类项时，把同类项的系数相加的结果作为合并后的系数，字母和字母的指数不变．【考点剖析】考点一：整式的基本概念例1．在代数式221135()63x x y m n a +-+，，，0，269y y ++中，整式共有（ ）个A 、5B 、6C 、7D 、8【难度】★【答案】B【解析】1()3x m n x a +和分母中含有字母，是分式的形式，不属于整式，单项式和多项式都 是整式，故本题中的整式共6个．【总结】本题主要考查整式的概念．例2．找出下列各代数式中的单项式，并写出各单项式的系数和次数．223xy ，a -，a bc ，32mn +，572t ，233a b c -，2，x π-． 【难度】★【答案】以上代数式是单项式的有：223xy ，a -，572t ，233a b c -，2，xπ-．223xy 的系数为23，次数为3； a -的系数为-1，次数为1；572t ，系数为52，次数为7；233a b c -，系数为-3，次数为6；2，系数为2，次数为0； xπ-，系数1π-，次数为1．【解析】此题主要考查单项式的相关概念，属于基础题目．例3．写出下列多项式的次数及最高次项的系数．（1）；（2）413xyx y π+--． 【难度】★【答案】（1）此多项式的次数是3次，最高次项的系数为34；（2）此多项式的次数是2次，最高次项的系数是43π-．【解析】这是一道基础题目，考查的是多项式的系数和次数的概念．例4．解答题：（1）把多项式323562a a a -+-按a 的降幂排列； （2）把多项式按y 的升幂排列；（3）求多项式223252x xy y --+的各项系数之和．【难度】★【答案】（1）325632a a a -++-；（2）3223543x x y xy y -+-+；（3）．【解析】（1）（2）升降幂的概念的考查，（3）多项式223252x xy y --+的各项系数分别为3，，，2，这四个数字之和为．【总结】本题一方面考查多项式的排列，另一方面考查多项式中每一项的系数．例5．多项式44222315352y x x y xy x y -+--是几次几项式？【难度】★★ 【答案】五次五项式【解析】多项式中所包含的单项式的次数最高的项是235x y -，是五次单项式，故此多项式 的次数为五次，共五项，所以是五次五项式． 【总结】本题主要考查几次几项式的概念．例6．多项式2262n n x x +--+是三次三项式，求代数式221n n -+的值．【难度】★★ 【答案】0或4．【解析】多项式2262n n x x +--+是二次三项式，则分两种情况： （1）当23n +=时，1n =，所以2211210n n -+=-+=；（2）当23n -=时，1n =-，所以2221(11)4n n -+=--=．【总结】本题一方面考查了几次几项式的概念，另外由于没有说最高次项是哪一项，因此要分类讨论．例7．多项式21231365m x y xy x +-+--是六次四项式，单项式352n m x y z -的次数与这个多项式次数相同，求m n ，的值． 【难度】★★【答案】31m n ==，．【解析】由题意知多项式是六次四项式，则可得：2163m m ++==，；又单项式的次数与 多项式的次数相同，所以可得3516n m +-+=，所以1n =．【总结】本题主要考查多项式的次数与单项式的次数，注意两个概念的不同之处．例8．设自然数m n 、满足1m n ≤<，求多项式222n m m n m n x y xy ++-的次数？【难度】★★ 【答案】2或者是n ．【解析】（1）当n ≤2时，次数为2；（2）当n >2时，次数为n ．【总结】本题主要考查多项式的次数，注意多项式的次数与系数的指数无关．例9．请各写出一个符合条件的整式：（1）系数是1-，次数是3的单项式； （2）系数是3，次数是1的单项式； （3）常数项为的二次三项式． 【难度】★★【答案】（1）3x -；（2）3x ；（3）22x x +-．【解析】这是一道开放性的题目，主要考查的是整式、单项式和多项式的基础概念，答案不唯一．考点二：合并同类项例1．下列各组单项式中属于同类项的是：①22m n 和22a b ；②312x y -和3yx ；③6xyz 和6xy ；④20.2x y 和20.2xy ；⑤xy 和yx -；⑥12-和2．【难度】★ 【答案】②⑤⑥【解析】①③两个单项式所含字母不相同；④相同字母的次数不相同．【总结】本题主要考查同类项的概念：所含字母相同，并且相同字母的指数也分别相同的单项式，注意同类项与字母的顺序无关．例2．合并下列同类项：（1）2215232x x x x -+-+-； （2）333332m n m n --+；（3）．【难度】★【答案】（1）211232x x --+；（2）332m n -+；（3）25037a a m --． 【解析】（1）原式222111(3)(2)(5)2322x x x x x x =-+--++=--+；（2）原式333333(3)22m m n n m n =-+-+=+（）-；（3）原式．师生总结1、单项式学习中主要注意哪几个方面？2、多项式学习中主要注意哪几个方面？【总结】本题主要考查合并同类项的概念，合并时只需要将同类项的系数相加减即可．例3．单项式449m x y -与223n x y 是同类项，求23m n +的值．【难度】★ 【答案】7【解析】由题意，可得：，解得：，所以12323272m n +=⨯+⨯=．【总结】本题主要考查同类项的概念．例4．合并下列同类项（1）2222210.120.150.12x y x y y x yx +-+； （2）122121342n n n n n x y x y y x y x +++---；（3）．【难度】★★【答案】（1）； （2）4n n x y -； （3）21.4a b ab --． 【解析】（1）原式2222222221(0.12)0.150.10.620.150.12x y yx x y y x x y x y xy =++-=+-； （2）原式121212(32)44n n n n n n n x y x y x y x y x y +++=---=-；（3）原式222(0.8 3.2)(65) 1.4a b a b ab ab a b ab =-++-+=--．【总结】本题主要考查的是合并同类项，若是同类项只需将相应的系数相加减即可．例5．单项式313a b a b x y +--与23x y 是同类项，求a b -的值．【难度】★★【答案】32【解析】由题意，可得：，解得：，所以713442a b -=-=． 【总结】本题主要考查同类项的概念．例6．如果322279m x y x y --+是五次多项式，求m 的值．【难度】★★ 【答案】6【解析】由题意得3256m m -+==，． 【总结】本题主要考查几次几项式的概念．【过关检测】一、单选题1．（2020·上海七年级期末）单项式324x y -的系数与次数依次是（ ） A ．4，5 B ．－4，5C ．4，6D ．－4，6【答案】B【分析】利用单项式中的数字因数叫做单项式的系数，一个单项式中所有字母的指数的和叫做单项式的次数，进而分析即可．【详解】解：单项式324x y -的系数与次数依次是-4和5， 故选：B ．【点睛】本题主要考查了单项式，正确把握单项式的次数与系数确定方法是解题关键． 2．（2020·上海市建平中学西校七年级期中）代数式；0；32x y ；12m ；732-a b；a -；2762--x x 中，单项式有（ ） A ．1个 B ．2个C ．3个D ．4个【答案】C【分析】直接利用单项式定义分析得出答案． 【详解】解：代数式；0；32x y ；12m ；732-a b；a -；2762--x x 中， 多项式为：；2762--x x ； 分式为：12m ；732-a b； 单项式有：0，32x y ，a -，共3个． 故选C ．【点睛】本题考查了单项式，正确把握单项式的定义是解题的关键．3．（2020·上海市进才中学北校七年级月考）在1，a ，+a b ，，22x y xy +，32>，1x x+，325+=中，整式共有（ ） A ．3个 B ．4个C ．5个D ．6个【答案】C【分析】根据整式的定义即可得出答案．【详解】解：根据整式的定义1，a ，+a b ，，22x y xy +这些都是整式 故选：C ．【点睛】本题考查整式的定义，属于基础题型．4．（2020·上海市进才中学北校七年级月考）多项式2244327x y x y x -+-的项数和次数分别是（ ） A ．4，9 B ．4，6C ．3，9D ．3，10【答案】B【分析】根据项数和次数的定义即可求解．【详解】解：多项式2244327x y x y x -+-的项数是4，次数是6， 故答案为：B ．【点睛】本题考查多项式的项数和次数，掌握多项式项数和次数的定义是解题的关键． 5．（2020·上海七年级期末）下列各组中的两个单项式，属于同类项的是（ ） A ．2a 与a B ．2a 与2bC ．2a b 与2abD ．0.2ab -与12ba 【答案】D【分析】根据同类项的概念，一是所含字母相同，二是相同字母的指数也相同，两者缺一不可进行求解． 【详解】解：A 、a 2与a ，所含字母相同，相同字母的指数不同，不是同类项； B 、2a 与2b ，所含字母不同，不是同类项；C 、2a b 与2ab ，所含字母相同，相同字母的指数不同，不是同类项；D 、0.2ab -与12ba ，所含字母相同，相同字母的指数相同，是同类项； 故选：D ．【点睛】本题考查了同类项的概念，熟练掌握概念是解题的关键． 6．（2020·上海文来实验学校）下列乘法中，不是同类项的是（ ） A ．8与18B ．xy 与12xy -C ．3x 与5yD ．42y x 与2412x y -【答案】C【分析】根据同类项可直接进行排除选项． 【详解】A 、8与18是同类项，故不符合题意；B 、xy 与12xy -是同类项，故不符合题意； C 、3x 与5y 不是同类项，因为不含有相同的字母，故符合题意； D 、42y x 与2412x y -是同类项，故不符合题意； 故选C ．【点睛】本题主要考查同类项，熟练掌握同类项的概念是解题的关键． 二、填空题7．（2021·上海七年级期末）多项式32324x x x -+-的二次项系数是________________． 【答案】-1【分析】先找出多项式中的二次项，根据系数的定义即可得出结论． 【详解】解：多项式32324x x x -+-的二次项为，其系数为-1 故答案为：-1．【点睛】此题考查的是求多项式中某项的系数，掌握多项式中的项的定义和系数的定义是解题关键． 8．（2020·上海七年级期末）将多项式23365x x x --+按字母x 降幂排列，结果为________． 【答案】32365x x x +--【分析】按x 的指数从大到小排列即可．【详解】解：将多项式23365x x x --+按字母x 降幂排列，结果为32365x x x +-- 故答案为：32365x x x +--．【点睛】此题考查的是将多项式降幂排列，掌握降幂的定义是解题关键．9．（2020·上海市建平中学西校七年级期中）单项式27π2-x y的系数是______，次数是______．【答案】7π2-3 【分析】直接利用单项式的次数与系数确定方法分析得出答案．【详解】解：单项式27π2-x y的系数是：7π2-，次数是：3．故答案为：7π2-，3． 【点睛】本题考查了单项式的系数和次数的定义，单项式中的数字因数叫做单项式的系数，一个单项式中所有字母的指数的和叫做单项式的次数．在判别单项式的系数时，要注意包括数字前面的符号，还要注意π不是字母．10．（2020·上海第二工业大学附属龚路中学七年级期中）多项式是_______次多项式，常数项是_______． 【答案】三 1-【分析】根据多项式的定义即可得．【详解】多项式是三次多项式，常数项是1-， 故答案为：三、1-．【点睛】本题考查了多项式，掌握理解多项式的概念是解题关键．11．（2020·上海市蒙山中学七年级期中）观察下列各单项式：按此规律写出第n 个单项式是_________（n 为正整数）【答案】21nx n + 【分析】根据题意，找出单项式的规律即可． 【详解】解：因为，所以第n 个单项式是21nx n +（n 为正整数） ，故答案为：21nx n +．【点睛】本题考查学生通过观察、归纳、抽象出规律的能力，要求学生首先分析题意，找到规律，并进行推导得出答案．12．（2020·上海市蒙山中学七年级期中）写出一个只含字母x 的二次三项式，如果它的二次项系数为2，常数项和一次项系数互为相反数，那么这个二次三项式可以为_________（只需写出一种情况） 【答案】2233x x -+（答案不唯一）【分析】根据二次三项式和多项式的系数、次数、常数项的有关概念，只含字母x 及相反数的概念，即可得出答案．【详解】解：∵这个只含字母x 的二次三项式常数项和一次项系数互为相反数， ∴常数项可以是3，则一次项系数为-3， ∵它的二次项系数为2，∴这个二次三项式可以是：2233x x -+．故答案为2233x x -+（答案不唯一）【点睛】本题考查了多项式及相反数．关键是能根据多项式的系数、次数、常数项的有关概念写出多项式．13．（2020·上海第二工业大学附属龚路中学七年级期中）单项式23x y-的系数是_______ ，次数是_______．【答案】13-3 【分析】根据单项式的系数与次数的定义即可得．【详解】单项式23x y-的系数是13-，次数是213+=，故答案为：13-，3． 【点睛】本题考查了单项式的系数与次数，熟记定义是解题关键．14．（2020·上海市进才中学北校七年级月考）把多项式按字母y 的降幂排列是__________． 【答案】42325232xy y x y x -++++【分析】根据题意，先计算多项式的每个项中字母y 的指数，再将每个项按字母y 指数的降幂重新排列即可．【详解】将多项式按字母y 的降幂排列：42325232xy y x y x -++++ 故答案为：42325232xy y x y x -++++．【点睛】本题考查多项式的降幂排列，是基础考点，难度容易，掌握相关知识是解题关键． 15．（2021·上海七年级期末）如果单项式24m a bc 为7次单项式，那么m 的值为_____． 【答案】4【分析】根据单项式次数的定义，算出m 的值． 【详解】解：∵单项式24m a bc 的次数为7， ∴，解得4m =． 故答案是：4．【点睛】本题考查单项式的次数，解题的关键是掌握单项式次数的定义． 16．（2020·上海市澧溪中学七年级月考）多项式的次数是__________． 【答案】3【分析】多项式中每个单项式叫做多项式的项，这些单项式中的最高次数，就是这个多项式的次数，根据这个定义即可判定．【详解】解：多项式的次数是1+2=3次．故答案为：3．【点睛】此题考查的是多项式的定义，多项式中每个单项式叫做多项式的项，这些单项式中的最高次数，就是这个多项式的次数．17．（2020·上海市浦东新区建平中学南校七年级月考）若3k 541a b-ab +353是五次多项式，则k=________． 【答案】4【分析】根据多项式次数的定义列方程即可求得k 的值． 【详解】解：3k 541a b-ab +353是五次多项式， 15k ∴+=，解得：4k =，故答案为：4．【点睛】本题考查了多项式的次数：多项式里次数最高项的次数，叫做这个多项式的次数．18．（2021·上海七年级期末）计算：________________．【答案】23a b【分析】根据合并同类项法则：同类项的系数相加，所得的结果作为系数，字母和字母的指数不变，即可求出结论．【详解】解：=23a b故答案为：23a b ．【点睛】此题考查的是整式的加法，掌握合并同类项法则是解题关键．19．（2020·上海七年级期末）已知单项式和单项式325m a b -是同类项，那么3n m -=__________．【答案】-2【分析】根据同类项的定义（所含字母相同，相同字母的指数相同）列出方程，求出n ，m 的值，再代入代数式计算即可．【详解】解：根据题意得：，解得：，则3n m -=-2．故答案为：-2．【点睛】本题考查同类项，解题的关键是掌握同类项定义中的两个“相同”：所含字母相同，且相同字母的指数相同．20．（2021·上海七年级期末）已知单项式33m x y 与单项式25n x y 的和仍然是单项式，那么m n +=________________．【答案】5【分析】根据题意可知：单项式33m x y 与单项式25n x y 是同类项，然后根据同类项的定义即可求出m 和n ，从而求出结论．【详解】解：∵单项式33m x y 与单项式25n x y 的和仍然是单项式，∴单项式33m x y 与单项式25n x y 是同类项，∴m=2，n=3∴m n +=5故答案为：5．【点睛】此题考查的是求同类项的指数中的参数，掌握合并同类项法则和同类项的定义是解题关键．三、解答题21．（2020·上海七年级月考）已知多项式23324212553x y x y xy x ++-- （1）把这个多项式按x 的降幕重新排列；（2）请指出该多项式的次数，并写出它的二次项和常数项．【答案】（1）43223215253x x y x y xy -+++-；（2）5，xy ，13- 【分析】（1）按x 的降幂排列：即按照x 的指数由高到低进行排列即可得到答案；（2）由多项式中的最高次项的次数是多项式的次数，结合二次项及常数项的概念可得答案．【详解】解：（1）按x 的降幂排列是：43223215253x x y x y xy -+++- （2）由最高次项为：32232,25x y x y ，所以多项式的次数是5， 它的二次项是xy ，常数项是13-. 【点睛】本题考查的是多项式的降幂排列，多项式的二次项，常数项，掌握以上知识是解题的关键．22．（2020·上海市南汇第四中学七年级月考）已知多项式23324212553x y x y xy x ++-- （1）把这个多项式按x 的降幂重新排列；（2）请指出该多项式的次数，并写出它的二次项和常数项．【答案】（1）43223215253x x y x y xy -+++-；（2）该多项式的次数是5，它的二次项是xy ，常数项是13- 【分析】（1）将多项式按x 的降幂重新排列即可．（2）多项式次数最高的项的次数即为该多项式的次数，再写出它的二次项和常数项即可．【详解】（1）按x 降幂排列为：43223215253x x y x y xy -+++-． （2）该多项式的次数是5，它的二次项是xy ，常数项是13-． 【点睛】本题主要考查多项式的次数的概念，熟记多项式的次数的概念是解题关键．23．（2020·上海市蒙山中学七年级期中）计算：22222344x xy y xy y x -++--．【答案】223x xy y +-【分析】通过合并同类项，即可完成计算．【详解】原式22=3x xy y +-．【点睛】本题考查了合并同类项的知识；解题的关键是熟练掌握合并同类项的性质，从而完成求解． 24．（2020·上海市静安区实验中学七年级课时练习）单项式2n 1m 13x y -+与单项式n 125x y +的和仍是单项式，求这两个单项式的和．【答案】328x y【分析】根据题意，可知2n 1m 13x y -+与单项式n 125x y +为同类项，列方程可求出m ，n 的值，然后求出两个单项式的和即可．【详解】解：由题意得，，解得：，则．【点睛】本题考查了合并同类项的知识，解答本题的关键是根据题意判断两个单项式为同类项，求出m ，n 的值．。

整式的加减专题知识点+常考题型+重难点题型（含详细答案）一、目录一、目录 (1)二、基础知识点 (2)1.单项式的概念 (2)2.多项式的概念 (3)3.整式的概念 (4)4.正确列代数式 (5)5.同类项的概念 (7)6.合并同类项 (8)7.去括号法则 (9)8.整式的加减（合并同类项） (10)三、重难点题型 (11)1.整式加法的应用 (11)2.待定系数法 (12)3.整式的代入思想 (13)4.整数的多项式表示 (14)5.与字母的取值无关的问题 (15)6.整式在生活中的应用 (16)二、基础知识点1.单项式的概念单项式：数或字母的积叫作单项式注：①分母中有字母，那就是字母的商，不是单项式②“或”单独的一个数字或单独一个字母也称为单项式例：5x；100；x；10ab等系数：单项式中的数字叫做单项式的系数单项式的次数：一个单项式中所有字母的指数的和例1.判断下列各式中那些是单项式，那些不是？如果是单项式，请指出它的系数和次数。

-13b；13xy2；2π；−ab；32a2b；13a−b；−5x2y33答案：单项式有：-13b，系数为－13，次数为11 3xy2，系数为13，次数为1+2=32π，系数为2π，次数为032a2b，系数为9，次数为2+1=3−5x2y33，系数为−53，次数为2+3=5例2.−xy2z3的系数是，次数是。

答案：系数为：－1，次数为1+2+3=62.多项式的概念多项式：几个单项式的和叫作多项式注：减单项式，实际是加该单项式的负数，也称作“和”项：每个单项式叫做多项式的项，有几项，就叫做几项式常数项：不含字母的项多项式的次数：所有项中，次数最高的项的次数就是多项式的次数（最高次数是n次，就叫做n次式）x2y2按字母y作升幂排列。

例1.将多项式3xy3−4x4+15x2y2+3xy3答案：−4x4+15−4x4中y的次数为01x2y2中y的次数为253xy3中y的次数为3例2.指出下列多项式的项和次数，并说明每个多项式是几次几项式。

整式的概念【学习目标】1．掌握单项式系数及次数的概念；2. 理解多项式的次数及多项式的项、常数项及次数的概念；3．掌握整式的概念，会判断一个代数式是否为整式；4. 能准确而熟练地列式子表示一些数量关系．【要点梳理】要点一、单项式1.单项式的概念：如22xy -，13mn ，-1，它们都是数与字母的积，像这样的式子叫单项式，单独的一个数或一个字母也是单项式．要点诠释：〔1〕单项式包括三种类型：①数字与字母相乘或字母与字母相乘组成的式子；②单独的一个数；③单独的一个字母．〔2〕单项式中不能含有加减运算，但可以含有除法运算．如：2st 可以写成12st 。

但假设分母中含有字母，如5m就不是单项式，因为它无法写成数字与字母的乘积． ：单项式中的数字因数叫做这个单项式的系数．要点诠释：〔1〕确定单项式的系数时，最好先将单项式写成数与字母的乘积的形式，再确定其系数；〔2〕圆周率π是常数．单项式中出现π时，应看作系数；〔3〕当一个单项式的系数是1或-1时，“1〞通常省略不写；〔4〕单项式的系数是带分数时，通常写成假分数，如：2114x y 写成254x y ． 3.单项式的次数：一个单项式中，所有字母的指数的和叫做这个单项式的次数．要点诠释：单项式的次数是计算单项式中所有字母的指数和得到的，计算时要注意以下两点： 〔1〕没有写指数的字母，实际上其指数是1，计算时不能将其遗漏；〔2〕不能将数字的指数一同计算．要点二、多项式1.多项式的概念：几个单项式的和叫做多项式．要点诠释：“几个〞是指两个或两个以上．2. 多项式的项：每个单项式叫做多项式的项，不含字母的项叫做常数项． 要点诠释：〔1〕多项式的每一项包括它前面的符号．〔2〕一个多项式含有几项，就叫几项式，如：2627x x --是一个三项式．3. 多项式的次数：多项式里次数最高项的次数，叫做这个多项式的次数．要点诠释：〔1〕多项式的次数不是所有项的次数之和，而是多项式中次数最高的单项式的次数．〔2〕一个多项式中的最高次项有时不止一个，在确定最高次项时，都应写出． 要点三、 整式单项式与多项式统称为整式．要点诠释：〔1〕单项式、多项式、整式这三者之间的关系如下图．即单项式、多项式必是整式，但反过来就不一定成立．〔2〕分母中含有字母的式子一定不是整式．【典型例题】类型一、整式概念辨析1．指出以下各式中哪些是单项式？哪些是多项式？哪些是整式？ 22x y +，x -，3a b +，10，61xy +，1x ，217m n ，225x x --，22x x+，7a 【答案与解析】单项式有：x -，10，217m n ，7a ； 多项式有：22x y +，3a b +，61xy +，225x x --； 整式有：22x y +，x -，3a b +，10，61xy +，217m n ，225x x --，7a ． 【总结升华】22x x +不是整式，因为分母中含有字母； 212a a ++也不是多项式，因为1a 不是单项式．举一反三： 【变式】以下代数式：322332111;;;;2;-232a x y ab x x y x y y x+--++π①②③④⑤⑥，其中是单项式的是_______________，是多项式的是_______________.【答案】①②③，④⑥类型二、单项式2．指出以下代数式中的单项式，并写出各单项式的系数和次数．234a b -，a -，442x ，a mn ，223a y π，a -3，5-3，82-310tm ⨯，2x y 【答案与解析】234a b -，a -，442x ，223a y π，5-3，82-310tm ⨯，2x y 是单项式，其中 234a b -的系数是34-，次数是3；a -的系数是-1，次数是1；442x 的系数是42，次数是4；223a y π的系数是3π，次数是4；53-为非零常数，只有数字因式，系数是它本身，次数为0；82-310tm ⨯的系数仍按科学记数法表示为-3×108，次数是3；2x y 只含有字母因数，系数是l ，次数为字母指数之和为3．【总结升华】〔1〕要区分数字因数、字母因数；〔2〕不能见了指数就相加，如442x 中，42的指数4不能相加，次数为4；〔3〕有分数线的，分子、分母的数字都是系数；〔4〕π是常数，不能看作字母．举一反三：【变式1】单项式3x 2y 3的系数是 ． 【答案】3． 【变式2】以下结论正确的选项是( )．A ．没有加减运算的代数式叫做单项式．B ．单项式237xy 的系数是3，次数是2． C ．单项式m 既没有系数，也没有次数．D ．单项式2xy z -的系数是-1，次数是4．【答案】D 类型三、多项式3.多项式24242153x y x y x -+-+，这个多项式的最高次项是什么？一次项的系数是什么？常数项是什么？这是几次几项式? 【答案与解析】这个多项式中共有四项，分别为：24242,,,153x y x y x --，它们的次数分别为：3,6,1,0；其中4223x y 的次数是6，是最高次项，一次项x -的系数是-1，常数项是1，它是六次四项式．【总结升华】确定多项式的次数时，分两步：〔1〕先求多项式中每一项的次数；〔2〕取这些次数中的最大的数即为多项式的次数．4. 多项式32312246753m x xy x y y x y ---+--． (1)求多项式各项的系数和次数．(2)如果多项式是七次五项式，求m 的值．【答案与解析】(1)依题意知此多项式是五项式，第一项26xy -的系数是-6，次数是3；第二项3127m x y --的系数是-7，次数是3m+1；第三项343x y 的系数是43，次数是4；第四项2x y -系数是-l ，次数3；第五项-5系数是-5，次数是0． (2)由多项式是七次五项式，可得3127m xy --的次数是7，即3m -1+2＝7，解得m ＝2． 【总结升华】对于单项式3127m x y --的次数为3m+1的认识会不太习惯，通过适量的练习，会对用字母表示多项式的次数或系数有较深地认识．举一反三：【变式】多项式()34b a x x x b --+-是关于x 的二次三项式，求a 与b 的差的相反数．【答案】()()4042242 2.a ab b a b -==⎧⎧∴⎨⎨==⎩⎩∴--=--=-解：由题意得类型四、整式的应用5. 用整式填空：(1)某商场将一种商品A 按标价的9折出售(即优惠10%)仍可获利10%，假设商场商品A 的标价为a 元，那么该商品的进价为________元(列出式子即可，不用化简)．(2)甲商品的进价为1400元，假设标价为a 元，按标价的9折出售；乙商品的进价是400元，假设标价为b 元，按标价的8折出售，列式表示两种商品的利润率分别为甲：________ 乙：________．【答案】(1)90%10%1a +；(2)甲商品的利润率为90%14001400a -×100%， 乙商品的利润率为： 80%400400b -×100%． 【解析】本例属于实际生活问题，应分清“进价〞、“标价〞、“利润〞、“利润率〞、“打折〞等问题，打几折就是标价的十分之几．【总结升华】解答本例需弄清以下两个数量关系：(1)利润＝售价－进价; (2)利润率＝-售价进价进价． 举一反三：【变式】〔2021秋•栖霞市期末〕对以下代数式作出解释，其中不正确的选项是〔 〕A. a ﹣b ：今年小明b 岁，小明的爸爸a 岁，小明比他爸爸小〔a ﹣b 〕岁B. a ﹣b ：今年小明b 岁，小明的爸爸a 岁，那么小明出生时，他爸爸为〔a ﹣b 〕岁C. ab ：长方形的长为acm ，宽为bcm ，长方形的面积为abcm2 D. ab ：三角形的一边长为acm ，这边上的高为bcm ，此三角形的面积为abcm2 【答案】D.6. 〔2021 •重庆〕以下图形都是由同样大小的小圆圈按一定规律组成的，其中第①个图形中一共有6个小圆圈，第②个图形中一共有9个小圆圈，第③个图形中一共有12个小圆圈，…，按此规律排列，那么第⑦个图形中小圆圈的个数为〔 〕A. 21B. 24C.27D. 30【答案】 B【解析】观察图形得：第1个图形有3+3×1=6个圆圈，第2个图形有3+3×2=9个圆圈，第3个图形有3+3×3=12个圆圈，…第n个图形有3+3n=3〔n+1〕个圆圈，当n=7时，3×〔7+1〕=24，应选B．【总结升华】找规律问题一般应经历四个阶级“特例引路〞、“比照分析〞、“总结规律〞、“反思检验〞等．【本文档内容可以自由复制内容或自由编辑修改内容期待你的好评和关注，我们将会做得更好】。

一、【原章基原观念】★☆▲之阳早格格创做1、单项式战多项式统称整式.①单项式：由数取字母的积或者字母取字母的积所组成的代数式称为单项式.单独一个数或者一个字母也是单项式，如a ，5.·单项式的系数：单式项里的数字果数喊搞单项式的系数.·单项式的次数：单项式中所有字母的指数的战喊搞单项式的次数.②多项式:几个单项式的战喊搞多项式.其中，每个单项式喊搞多项式的项，没有含字母的项喊搞常数项.·多项式的次数：多项式里次数最下项的次数，喊搞多项式的次数.·多项式的命名：一个多项式含有几项，便喊几项式.所以咱们便根据多项式的项数战次数去命名一个多项式.如：3n4－2n2＋1是一个四次三项式.2、共类项——必须共时具备的二个条件（缺一没有成）：①所含的字母相共；②相共字母的指数也相共.·合并共类项，便是把多项式中的共类项合并成一项. 要领：把共类项的系数相加，而字母战字母的指数没有变.3、去括号规则规则1.括号前里是“+”号,把括号战它前里的“+”号去掉,括号里各项皆没有变标记；规则2.括号前里是“－”号,把括号战它前里的“－”号去掉,括号里各项皆变标记.▲去括号规则的依据本质是乘法调配律.〖注意1〗要注意括号前里的标记,它是去括号后括号内各项是可变号的依据.〖注意2〗去括号时应将括号前的标记连共括号所有去掉.〖注意3〗括号前里是“－”时,去掉括号后,括号内的各项均要改变标记,没有克没有及只改变括号内第一项或者前几项的标记,而记记改变其余的标记.若括号前是数字果数时,可使用乘法调配律先将数取括号内的各项分别相乘再去括号,免得爆收过失.〖注意4〗逢到多层括号普遍由里到中,逐层去括号,也可由中到里.数“－”的个数.4、整式的加减整式的加减的历程便是去括号战合并共类项.如逢到括号，则先去括号，再合并共类项，合并到最简式为止.5、原单元需要注意的几个问题①整式（既单项式战多项式）中，分母一律没有克没有及含有字母.②π没有是字母，而是一个数字，③多项式相加（减）时，必须用括号把多项式括起去，才搞举止估计.④去括号时，要特地注意括号前里的果数.。

3 针对训练 2 1: 计算( 2x) ÷ x的结果正确的是(
)
( A) 8x2 ( B) 6x2 ( C) 8x3 ( D) 6x3 解析: 原式= 8x3÷ x= 8x2, 故选 A. 针对训练 2 2: ( 2011 年成都)下列计算正确的是( ( A) x+x=x2 ( B) x· x= 2x
• 例1，下列各式子中，是单项式的有___①、 ②、④、⑦ • ___________（填序号
多项式的项数与次数
• • • （1）多项式的次数不是所有项的次数的和，而是它的最高次项次数； （2）多项式的每一项都包含它前面的符号； （3）再强调一次， “π”当作数字，而不是字母
• （4）一个多项式的次数最高项的次数是几，就说这个多项式是几次多 项式。 • （5）.在多项式中，每个单项式都是这个多项式的项，每一项都有系 数，但对整个多项式来说，没有系数的概念，只有次数的概念。
• 【例1】若单项式-5x3ym的次数是9，求m 的值. • 【思路点拨】根据单项式次数的定义得到 关于m的一元一次方程，解方程得m的值. • 【自主解答】根据题意，得m+3=9, • 解得m=6.
• 3.(2010· 肇庆中考)观察下列单项式：a,2a2,4a3,-8a4, • 16a5,…按此规律第n个单项式是_____.(n 是正整数) • 【解析】由题意知第n项的系数为(1)n+12n-1, • 第n项a的次数为n, • 所以第n个单项式是(-1)n+12n-1an. • 答案：(-1)n+12n-1an
同类项
1，同类项的判定与合并同类项的法则： 例1 判断下列各式是否是同类项？
(1)2a b 与2 x y
2 3
2 3

上一页
下一页
宇轩图书
中考典例精析
首页
2.检查一个多项式分解是否彻底时，要注意以下几个方面：（1）每 一个多项式都不能再分解；（2）重因式的乘积写成幂的形式；（3）不能
含有多重括号.
另外，注意书写最后结果时，单项式要写在多项式的前面.可以用整 式乘法来检验因式分解的结果是否正确.
上一页
下一页
宇轩图书
B．(－2a)2＝－2a2
D．－2(a－1)＝－2a－1
上一页
下一页
宇轩图书
中考典例精析
(3)题均从四个方面考查整式的运算，解答此题需要逐项检验． 【解答】(1)B (2)C (3)A
首页
【点拨】(1)题考查幂的四种运算，正确掌握运算法则是关键；(2)、
(1)(2010·红河自治州)如果3x2n－1ym与－5xmy3是同类项，则m和
上一页
下一页
宇轩图书
中考典例精析
考查平方差公式和完全平方公式的特征．
首页
【点拨】(1)、(4)、(5)考查分解因式的一般步骤及检验；(2)、(3)
【解答】(1)D (2)C (3)D (4)2(2a＋1)(2a－1) (5)－3(x－y)2 方法总结 1.当多项式是二项式，且该二项式又可看作某两项平方的差时，可用
n的取值是(
)
A．3和－2
C．3和2
B．－3和2
D．－3和－2
(2)(2011·北京)已知a2＋2ab＋b2＝0，求代数式a(a＋4b)－(a＋ 2b)(a－2b)的值．
上一页
下一页
宇轩图书
中考典例精析
首页
【点拨】(1)题考查同类项概念和二元一次方程组的解法，由题意 2n－1＝m， m＝3， 得 解得 m＝3， n＝2. (2)①括号前是负号，去括号时要注意改变符号．如－(a －4b )应 2 2 2 2 等于－a ＋4b ，不能化成－a －4b . ②利用整体代入求值的方法求代数式的值，体现了整体思想．

学生做题前请先回答以下问题问题1：什么是同类项？问题2：合并同类项法则是什么？问题3：去括号法则是什么？以下是问题及答案，请对比参考:问题1：什么是同类项？答：所含字母相同，并且相同字母的指数也相同的项叫做同类项．问题2：合并同类项法则是什么？答：把同类项的系数相加，字母和字母的指数不变．问题3：去括号法则是什么？答：括号前面是“+”号，把括号和它前面的“+”号去掉后，原括号里各项的符号都不改变；括号前面是“-”号，把括号和它前面的“-”号去掉后，原括号里各项的符号都要改变．整式基本概念（二）（人教版）一、单选题(共11道，每道9分)1.下列各组代数式中，不是同类项的是( )A.与B.与C.和D.与解题思路：试题难度：三颗星知识点：同类项的定义2.下列各项中，合并同类项正确的是( )A. B.C. D.答案：A解题思路：试题难度：三颗星知识点：合并同类项3.去括号正确的是( )A. B.C. D.解题思路：试题难度：三颗星知识点：去括号法则4.若单项式与是同类项，则的值为( )A.32B.3C.6D.12答案：C解题思路：试题难度：三颗星知识点：同类项的定义5.若单项式与是同类项，则的值为( )A.81B.-64C.64D.-81答案：A解题思路：试题难度：三颗星知识点：同类项的定义6.若单项式与的和仍是单项式，则的值为( )A.21B.-21C.29D.-29答案：B解题思路：试题难度：三颗星知识点：同类项的定义7.若多项式是五次二项式，则的值为( )A.4B.±2C.-2D.2答案：D解题思路：试题难度：三颗星知识点：多项式的项数8.如果是关于的二次三项式，那么应满足的条件是( )A. B.C. D.答案：D解题思路：试题难度：三颗星知识点：多项式的次数与项数9.已知多项式是六次四项式，单项式的次数与这个多项式的次数相同，那么的值为( )A.13B.-5C. D.答案：A解题思路：试题难度：三颗星知识点：单项式的次数10.如果一个多项式的次数是6，则这个多项式的任何一项的次数都( )A.不小于6B.等于6C.不大于6D.小于6答案：C解题思路：试题难度：三颗星知识点：多项式的次数11.若将看作一个因式，则合并的结果是( )A. B.C. D.答案：B解题思路：试题难度：三颗星知识点：合并同类项。

7年级上册数学电子课本(带答案)7年级上册数学电子课本带答案第一章整式的基本概念1.1 整式的定义和性质整式的定义：由有限个同一变量的变量、常数和它们的积或商的有理数指数幂组成的代数式称为整式。

整式的性质：(1)整式的项有多项式项和常数项两种；(2)整式的次数是指所有单项式次数的最大值；(3)同次异项相加得同次项；(4)同底数指数幂相乘，指数相加；(5)整式可以化简成同类项相加的形式。

1.2 多项式的概念和运算多项式的定义：只含有同一个变量的各项代数和式称为多项式。

多项式的运算：(1)同类项之间可以相加减；(2)多项式和多项式相加减；(3)多项式和数相乘。

1.3 整式的因式分解因式分解的步骤：(1)提公因式；(2)区分平方差公式、立方差公式、两数平方差等特殊公式；(3)配方法；(4)求根公式。

第二章一元一次方程2.1 一元一次方程的概念一元一次方程的定义：形如ax+b=0(a≠0)的式子称为一元一次方程，其中x是未知数，a和b是已知数。

2.2 一元一次方程的解法(1)移项法；(2)等式两边乘以相同的数；(3)约分；(4)去分母。

2.3 较复杂的运算问题第三章图形的基本概念3.1 图形的基本概念和性质图形的基本概念和性质：(1)点、线、面的概念；(2)图形的相似和全等性质；(3)图形的投影和投影的性质。

3.2 平面几何问题的解法平面几何问题的解法：(1)全等三角形的性质；(2)相似三角形的性质；(3)平行四边形的性质。

第四章勾股定理4.1 勾股定理的概念勾股定理的定义：直角三角形的斜边的平方等于两条直角边的平方和。

4.2 勾股定理的应用(1)求一条直角边；(2)求斜边；(3)证明两个角是否为直角；(4)在平面直角坐标系中求距离和中点坐标等。

第五章平面向量5.1 平面向量的概念和性质平面向量的定义：既有大小又有方向的量称为向量。

平面向量的性质：(1)向量的加法和减法；(2)数与向量的乘法；(3)向量的数量积和向量积的概念和计算公式。

整式的基本概念（习题）1. 下列代数式中，书写规范的是（ ）A ．3a πB ．125xC ．6x 5D ．(2÷3)a2. 下列各式2xy 2，-3x +1，-π，243a bπ+，0，b 中，单项式的个数是（ ） A ．3个B ．4个C ．5个D ．6个3. 单项式323πx y 的系数是______，次数是______；单项式225πa b−的系数是________，次数是_______． 4. 填表：5. 多项式4a 2b -3ab -5是____次____项式，包含的项有_________________，常数项为________，二次项的系数为________．6. 一个关于x 的二次三项式的一次项系数和常数项都是1，二次项系数是12−，则这个二次三项式为__________．7. 若M 是关于x 的四次三项式，则M 的每一项的次数都（ ）A ．小于4B ．等于4C ．不大于4D ．不小于48. 如果多项式232(3)1kx k x −−+是关于x 的三次三项式，那么k 的值为__________．9. 下列各式中，不是同类项的是（ ）A ．2ab 2与-3b 2aB ．22πx −与213xC ．2212m n −与5n 2m 2D ．22xy −与6yx 210. （2020苏州）若单项式2x m -1y 2与单项式2113n x y +是同类项，则m +n =__________． 11. 化简：（1）23a a a −+； （2）23682x y x y −+−−；（3）22245233x xy x yx x −−+−； （4）-a 2+6ab -5b 2+a 2-4ab +b 2；复习巩固（5）2225634m mn m m nm m −−+++−；（6）3a 2b -2ab 2+5-2a 2b -5ab 2-2；（7）222223743xy x y x yx y x −−−−；（8）3222231533222m m n mn n m m n m −+−−−．1. 填空：（1）单项式27a bπ−的系数是________，次数是________；（2）多项式2x 2y +xy -4y 是______次_______项式． 2. 判断正误：（对的打“√”，错的打“×”）（1）π是一个单项式，它的系数是1，次数也是1（ ） （2）27a b+−是一个多项式（ ） （3）2a 2b 与-πab 2不是同类项（ ）思考小结参考答案1. C2. B3. 32535π−π，；，4.5. 三；三；24a b ，3ab −，-5；-5；-3．6. 2112x x −++ 7. C 8. -3 9. D 10.411. （1）2a ； （2）8112x y −−； （3）22x xy −−； （4）224ab b−；（5）222m mn m −−+；（6）2273a b ab −+；（7）22267xy x y x −−−； （8）323m m n −−．1. （1）7π−，3；（2）三，三． 2. （1）×；（2）√； （3）√．复习巩固 思考小结。

整式学习本节先复习单项式的系数和次数、多项式的项等概念，为学习同类项的概念及合并同类项法则做好准备.主要包括 单项式的系数和次数,多项式的项和每项的系数.一单项式、多项式的概念及它们各自对应的系数，项这是本节的重点；【典例引路】中例2，【当堂检测】中第2题，【课时作业】中第3题。

二.正确的判断所给代数式的系数或项这是本节的难点;【典例引路】中例2，【当堂检测】中第3题，【课时作业】中第10题。

三．易错题目单项式的次数,多项式的次数是同学们易错的地方. 【典例引路】中例2，【基础练习】中第2题,【当堂检测】中第4题，【课时作业】中第9题。

知识点击一:单项式的概念及其次数与系数（1）单项式的定义：像 1.5V ，28n π，h r 231π等，都是数与字母的乘积，这样的代数式叫做单项式．注：①单独一个数与一个字母也是单项式．②形如21＋x 形式的代数式不是单项式．（2）单项式的次数：一个单项式中，所有字母的指数和叫做这个单项式的次数．注：单独一个数的次数是0次．（3）单项式的系数：单项式中的数字因数叫做单项式的系数．注：①单个字母的系数为1；②单项式的系数包括符号．知识点击二:多项式的概念及其项数与次数（1）多项式的概念：几个单项式的和叫做多项式．注：①多项式概念中的和指代数和，即省略了加号的和的形式．②多项式中不含字母的项叫做常数项．（2）多项式的次数：一个多项式中，次数最高项的次数，叫做这个多项式的次数．（3）多项式的项数：多项式中单项式的个数叫做多项式的项数．知识点击三:整式的概念单项式和多项式统称为整式．区别是否整式：关键：分母中是否含有字母.针对性练习:一、判断题．（对的打“∨”，错的打“×”）1．x是单项式．（）2．6不是单项式．（）3．m的系数是0，次数也是0．（）【解答】1．∨ 2．× 3．× 4．∨类型之一:应用创新型例1.根据题意列出代数式，并判断是否为整式．3月12日是植树节，七年级一班和二班的同学参加了植树活动，一班种了a棵树，二班种的比一班的2倍多b棵，这两个班一共种了多少棵树？【解答】(2a+b+a) 棵, 是整式.类型之二:明辨是非型例2 判断下列各说法是否正确，错误的改正过来；（1）单项式的系数是，次数是2次．（）（2）单项式的次数是1次．（）（3）任何两个单项式的和是多项式．（）（4）是单项式．（）（5）不是单项式．（）（6）的系数是，次数是1次．（）（7）没有系数．（）（8）多项式是一次二项式．（）（9）是二次三项式．解：（1）错．的系数是－，次数是3次．（2）错．单项式的次数是3次．（3）错．任何两个单项式的和不一定是单项式；（4）错．是多项式．（5）错．是单项式．（6）对（7）错．的系数是1．（8）错．多项式是三次二项式．（9）对说明：单项式的次数是单项式中所有字母的指数和，如 的次数是次．任何两个单项式的和不一定是多项式，如单项1与单项式的和为 ，而 为单项式． 可写成 ，因此多项式 是二次三项式．1.下列代数式分别有几项？每一项的系数分别是多少？2x －3y 4a 2－4ab +b 2 －31x 2y +2y －x 【解答】 2x －3y 有2项，每一项的系数分别是2，－3；4a 2－4ab +b 2有3项，每一项的系数分别是：4,－4,1. －31x 2y +2y －x 有3项，每一项的系数分别是－31，2，－1. 2．若－2a m ＋2b 4是7次单项式，则m ＝_______；【解析】:m+2+4=7,m=1;3．多项式x 2－3x －4共有_____项，次数是________．【解析】3,2;4．x 2yz 的系数是________，次数是________．【解析】1, 4.5．如果单项式－2x 2y n 与单项式a 4b 的次数相同，则n=________．【解析】3.6．写出系数为5，含有x 、y 、z •三个字母且次数为4•的所有单项式，•它们分别是_______．【解析】5xy 3，5x 2y 2，5x 3y1.代数式ab －mn －81πn 2+1是哪几项的和？每项的系数分别是什么？ 【解析】式子中数与字母的积为一项，如ab ，－mn ，每一项应包含它前面的符号.单独一个数或一个字母也是一项，字母前的数字因数是它的系数，如ab 的系数是1，－mn 的系数是－1，－81πn 2的系数是－81π，因为π是常数. 【解答】ab －mn －81πn 2+1分别是ab ，－mn ，－81πn 2，1四项的和， 每项的系数分别是1，－1，－81π，1. 2.下列代数式中，哪些是整式？单项式？多项式？ab ＋c ，ax 2＋bx ＋c ，－5，π，2y x －，12－x x 【解析】整式: ab ＋c ，ax 2＋bx ＋c ，－5，2y x －; 单项式: －5; 多项式: ab ＋c ，ax 2＋bx ＋c ，2y x －; 3.求下列各单项式的系数及次数：73xy ，－ab 2c 【解析】73xy 的系数及次数:73,2; －ab 2c 的系数及次数:－1,4; 4.说出下列多项式为几次几项式？ －31x －x 2y ＋2π，6x 3y 2－5＋xy 3－x 2 【解析】－31x －x 2y ＋2π，6x 3y 2－5＋xy 3－x 2 5.根据题意列出代数式，并判断是否为整式．①ab 两数的积除以ab 两数的和；②ab 两数的积的一半的平方；【解析】:①ab÷(a+b)=b a ab +;（2）(ab 21)2=2241b a ;例1、将多项式3+6x 2y －2xy －5x 3y 2－4x 4y 先按字母x 升幂排列，再按x 降幂排列。

4．如果 a－3b＝－3，那么代数式 5－a＋3b 的值是( D ) A．0 B．2 C．5 D．8
5．如果代数式 4y2－2y＋5 的值为 7，那么代数式 2y2－y＋1 的值等于( A．2 B．3 C．－2 D．4
A )
6．若 m2－n2＝6，且 m－n＝3，则 m＋n＝2.
7．化简：(x＋3) 2－(x－1)(x－2)． 9x＋7
4.(2010·日照中考)由m(a+b+c)=ma+mb+mc，可得：(a+b)(a2 －ab+b2)=a3－a2b+ab2+a2b－ab2+b3=a3+b3，即(a+b)(a2－ ab+b2)=a3+b3． ① 我们把等式①叫做多项式乘法的立方公式. 下列应用这个立方公式进行的变形不正确的是( (A)(x+4y)(x2－4xy+16y2)=x3+64y3 (B)(2x+y)(4x2－2xy+y2)=8x3+y3 (C)(a+1)(a2＋a+1)=a3+1 )
)
(D)②④⑤
(C)③④⑤
【解析】选B.③(a+b)2=a2+2ab+b2，⑤3x2-4x≠-x.
二、填空题(每小题6分，共24分) 6.xa=4,xb=3,则xa-2b=_____.
【解析】xa-2b=xa÷x2b=xa÷(xb)2=4÷32=
4 答案： 9
4 . 9
7.(2010·青岛中考)如图，是用棋子摆成的图案，摆第1个图
【答案】D
4．(2010· 昆明)下列各式运算中，正确的是( A．(a＋b)2＝a2＋b2 C．a3· a4＝a12 B. －32＝3 3 6 D．( )2＝ 2(a≠0) a a )

中国教育培训领军品牌 一、整式 1、单项式和多项式统称为整式。

2、单项式或多项式都是整式。

3、整式不一定是单项式。

4、整式不一定是多项式。

5、分母中含有字母的代数式不是整式；而是今后将要学习的分式。

二、整式的加减 1、整式加减的理论根据是：去括号法则，合并同类项法则，以及乘法分配率。

去括号法则：如果括号前是“十”号，把括号和它前面的“+”号去掉，括号里各项都不变符号；如果括号前是 “一”号，把括号和它前面的“一”号去掉，括号里各项都改变符号。

2、同类项：所含字母相同，并且相同字母的指数也相同的项叫做同类项。

合并同类项： 1）.合并同类项的概念： 把多项式中的同类项合并成一项叫做合并同类项。

2）.合并同类项的法则： 同类项的系数相加，所得结果作为系数，字母和字母的指数不变。

3）.合并同类项步骤： a．准确的找出同类项。

b．逆用分配律，把同类项的系数加在一起（用小括号），字母和字母的指数不变。

c．写出合并后的结果。

4）.在掌握合并同类项时注意： a.如果两个同类项的系数互为相反数，合并同类项后，结果为 0. b.不要漏掉不能合并的项。

c.只要不再有同类项，就是结果（可能是单项式，也可能是多项式）。

说明：合并同类项的关键是正确判断同类项。

3、几个整式相加减的一般步骤： 1）列出代数式：用括号把每个整式括起来，再用加减号连接。

2）按去括号法则去括号。

3）合并同类项。

4、代数式求值的一般步骤： （1）代数式化简 （2）代入计算 （3）对于某些特殊的代数式，可采用“整体代入”进行计算。

【经典例题】【例 1】（2010•台湾）已知有一整式与（2x +5x-2）的和为（2x +5x+4），则此整式为（ A． 2 B． 6 C ． 10x+6 ） D ． 18x-3 D ． 4x +10x+22 2 2）【例 2】（2012•济南）化简 5（2x-3）+4（3-2x）结果为（ A ． 2x-3 B ． 2x+9 C ． 8x-31中国教育培训领军品牌 【例 3】（2011•恩施州）某校组织若干师生到恩施大峡谷进行社会实践活动．若学校租用 45 座的客车 x 辆，则余下 20 人无座位；若租用 60 座的客车则可少租用 2 辆，且最后一辆还没坐满，则乘坐最后一辆 60 座客车的人数是（ ） A ． 200-60x B ． 140-15x2C ． 200-15x ）D ． 140-60x【例 4】下列哪个式子的计算结果为 7a -7ab（ A ． （ 3a -ab+7 ） - （ 4a +6ab+7 ） C ． （ 3a -ab+7 ） - （ -4a -6ab-7 ） 【例 5】若单项式-2a A．2n-1 4 8m 4 2 2 2 2B ． （ 3a -ab+7 ） - （ -4a -6ab+7 ） D ． （ 3a -ab+7 ） - （ -4a +6ab+7 ）3 2 222b 与 7ab 的和为 5ab ，则（m-n） =（ B． -） D． ） D ． -2a1 61 6C． -1 81 8【例 6】如果 a＜0，ab＜0，那么|a-b|+3-（a-b+3）的值是（ A． 0 B ． 2b C ． -2a+2b ） C ． 123 2【例 7】若 x+y=3，xy=1，则-5x-5y+3xy 的值为（ A ． -123 2B ． -14D ． 18【例 8】若多项式 2x -8x +x-1 与多项式 3x +2mx -5x+3 相加后不含二次项，则 m 的值为 【例 9】（2012•峨边县模拟）在数轴上有示 a、b、c 三个实数的点的位置如图所示化简式子：|b-a|+|c-a|-|c-b|=【例 10】已知 a+b=-7，ab=10，则代数式（3ab+6a+4b）-（2a-2ab）的值为 2 2 2 2 2 2 【例 11】先化简，再求值：3x y -[5xy -（4xy -3）+2x y ]，其中 x=-3，y=2．【例 12】【例 13】【例 14】2中国教育培训领军品牌【例 15】【例 16】【课堂练习】1 （-4x+8）-3（4-5x），可得下列哪一个结果（ 4B ． -16x-4 ） B ． 2 （ a+2b ） =2a+2b D ． a +a =a2 2 2 3 2 51．（2011•台湾）化简）A ． -16x-10C ． 56x-40D ． 14x-102．（2013•江西模拟）下列计算正确的是（ A ． x y-2x y=-x y C ． 7ab- （ -3ab ） =102 2 2 23．一个多项式减去 x -2y 等于 x +y ，则这个多项式是（ A ． -2x +y2 2 2）2 2B ． 2x -y222C ． x -2y ） C ． 16D ． -x +2y224．整式 x -3x 的值是 4，则 3x -9x+8 的值是（ A ． 20 B． 4D ． -45．已知 a=−2 2 2 ，b=2，c=-3，则多项式 3a+abc-3c -3a+3c 的值是（ 3B ． -12 2）A ． -4C． 1D． 46．（2011•泰州）一个多项式与 m +m-2 的和是 m -2m．这个多项式是3中国教育培训领军品牌 7．（2007•中山）已知 a、b 互为相反数，并且 3a-2b=5，则 a +b = 8．当 x=-2 时，二次三项式 2x +mx+4 的值等于 18，那么当 x=2 时，该二次三项式的值等于 9．求代数式的值： 2 2 （1）（5x -3x）-2（2x-3）+7x ，其中 x=-2； （2）2a-[4a-7b-（2-6a-4b）]，其中 a=−2 2 2 2 2 2 21 2 ，b= ． 4 310．若 P=a +3ab+b ，Q=a -3ab+b ，则代数式 P-[Q-2P-（-P-Q）]= 11．已知 2x+3y=5，则 6x-4y-2（x-5y）= 12．先化简，再求值： 2 2 2 2 （1）5a b-2ab +3ab -4a b，其中 a=-1，b=2；（2）（2x -xyz）-2（x -y +xyz）-（xyz+2y ），其中 x=1，y=2，z=-3．333313.14.已知 A  x3  2x2  4x  3, B  x2  2x  6, C  x3  2x  3 ，求 A  ( B  C ) 的值，其中 x  2 .15.若 (a  2) 2  b  1 =0,求 5ab2  2a 2b  [3ab2  (4ab2  2a 2b)] 的值.16.某位同学做一道题： 已知两个多项式 A 、B ， 求 A  2 B 的值。

初一寒假 第三讲 整式（一）知识点1、代数式：（1）用基本的运算符号（加、减、乘、除、乘方等）把数或表示数的字母连结而成的式子叫做代数式。

（2）注意：单独的一个数或字母也是代数式。

2、整式：单项式和多项式统称为整式3、单项式：（1）单项式：像2a -，2πr ，213x y -，abc -，237x yz ，…，这些代数式中，都是数字与字母的积，这样的代数式称为单项式。

（2）单项式的次数：是指单项式中所有字母的指数和。

（3）单项式的系数：单项式中的数字因数叫做单项数的系数。

4、多项式：（1）多项式：几个单项式的和叫做多项式。

（2）多项式的项：其中每个单项式都是该多项式的一个项。

（3）多项式的次数：多项式里，次数最高项的次数就是这个多项式的次数。

（4）多项式的升幂和降幂排列：把一个多项式的各项按某个字母的指数从小到大（或从大到小）排列起来，叫做按这个字母的升幂排列（或降幂排列）.注意：多项式计算的最后结果一般应该进行升幂（或降幂）排列.5、同类项：所含字母相同，并且相同字母的指数也分别相同的单项式叫做同类项。

（二）例题类型一、整式例1、下列代数式：（1）mn，（2）m，（3），（4），（5）2m+1，（6），（7），（8）x2+2x+，（9）y3﹣5y+中，整式有（）A．3个B．4个C．6个D．7个类型二、单项式与多项式例2、下列关于单项式﹣的说法中，正确的是（）A．系数是﹣，次数是2 B．系数是，次数是2C．系数是﹣3，次数是3 D．系数是﹣，次数是3例3、多项式1+2xy﹣3xy2的次数为（）A．1 B．2 C．3 D．5例4、观察下列一串单项式的特点：xy，﹣2x2y，4x3y，﹣8x4y，16x5y，…（1）按此规律写出第9个单项式；（2）试猜想第n个单项式为多少？它的系数和次数分别是多少？例5、多项式x5y2+2x4y3﹣3x2y2﹣4xy是（）A．按x的升幂排列B．按x的降幂排列C．按y的升幂排列D．按y的降幂排列类型三、同类项例6、按某种标准把多项式进行分类时，3x3﹣4和a2b+ab2+1属于同一类，则下列哪一个多项式也属于此类（）A．abc﹣1 B．x2﹣2 C．3x2+2xy4D．m2+2mn+n2例7、已知关于x的多项式3x4﹣（m+5）x3+（n﹣1）x2﹣5x+3不含x3和x2，则（）A．m=﹣5，n=﹣1 B．m=5，n=1 C．m=﹣5，n=1 D．m=5，n=﹣1（三）练习题基础题1、下列代数式：（1）﹣mn，（2）m，（3），（4），（5）2m+1，（6），（7），（8）x2+2x+中，整式有（）A．3个B．4个C．6个D．7个2、下列各式﹣mn，m，8，，x2+2x+6，，，中，整式有（）A．3个B．4个C．6个D．7个3、如果单项式2a n b2c是六次单项式，那么n的值取（）A．6 B．5 C．4 D．34、一组按规律排列的式子：a2，，，，…，则第2016个式子是（）A．B．C．D．5、代数式3x2y﹣4x3y2﹣5xy3﹣1按x的升幂排列，正确的是（）A．﹣4x3y2+3x2y﹣5xy3﹣1 B．﹣5xy3+3x2y﹣4x3y2﹣1C．﹣1+3x2y﹣4x3y2﹣5xy3 D．﹣1﹣5xy3+3x2y﹣4x3y26、下列单项式中，与a2b是同类项的是（）A．2a2b B．a2b2C．ab2D．3ab7、若﹣x3y a与x b y是同类项，则a+b的值为（）A．2 B．3 C．4 D．58、已知单项式﹣2x2y的系数和次数分别是a，b．（1）求a b﹣ab的值；（2）若|m|+m=0，求|b﹣m|﹣|a+m|的值．9、观察下列各式：﹣a，a2，﹣a3，a4，﹣a5，a6，…（1）写出第2014个和2015个单项式；（2）写出第n个单项式．10、若关于x、y的多项式x2y﹣（a﹣4）x2+（8b﹣a+2）xy+3x﹣2y﹣7不含二次项，则a101•（﹣b）100的值为多少？11、已知多项式（3﹣b）x5+x a+x﹣6是关于x的二次三项式，求a2﹣b2的值．12、已知﹣4xy n+1与是同类项，求2m+n的值．13、将多项式2a3+a2b﹣b3﹣5ab2按字母b的降幂排列是（）A．2a3﹣b3﹣5ab2+a2b B．a2b﹣b3﹣5ab2+2a3C．﹣b3﹣5ab2+a2b+2a3D．﹣b3+a2b﹣5ab2+2a314、m，n都是正数，多项式x m+x n+3x m+n的次数是（）A．2m+2n B．m或nC．m+n D．m，n中的较大数15、若2x2m y3与﹣5xy2n是同类项，则|m﹣n|的值是（）A．0 B．1 C．7 D．﹣1提高题1．观察一列单项式：1x，3x2，5x2，7x，9x2，11x2，…，则第2013个单项式是．2．如图是有关x的代数式的方阵，若第10行第2项的值为1034，则此时x的值为．3．下列式子：x2+2，+4，0，，，中，整式有个．4．代数式﹣的系数是．5．已知：A=ax2+x﹣1，B=3x2﹣2x+1（a为常数）①若A与B的和中不含x2项，则a=；②在①的基础上化简：B﹣2A．6．已知﹣5x3y|a|﹣（a﹣4）x﹣6是关于x、y的七次三项式，求a2﹣2a+1的值．7．请你做评委：在一堂数学活动课上，同在一合作学习小组的小明、小丁、小彭对刚学过的知识发表了自己的一些感受：小明说：“绝对值不大于4的整数有7个．”小丁说：“若|a|=3，|b|=2，则a+b的值为5或1．”小彭说：“单项式的系数是﹣2，多项式﹣2x+x2y+y3是三次三项式．”你觉得他们的说法正确吗？如不正确，请帮他们修正，写出正确的说法．8．已知多项式（2mx2﹣x2+3x+1）﹣（5x2﹣4y2+3x），是否存在m，使此多项式与x无关？若不存在，说明理由；若存在，求出m的值．9．对于多项式（n﹣1）x m+2﹣3x2+2x（其中m是大于﹣2的整数）．（1）若n=2，且该多项式是关于x的三次三项式，求m的值；（2）若该多项式是关于x的二次单项式，求m，n的值；（3）若该多项式是关于x的二次二项式，则m，n要满足什么条件？10．已知单项式是同类项，求代数式2x﹣7y的值．11．如果﹣a|m﹣3|b与是同类项，且m、n互为负倒数．求：n﹣mn﹣m的值．12、已知关于x、y的多项式mx2+4xy﹣x﹣3x2+2nxy﹣4y合并后不含有二次项，求n﹣m的值．13、如果单项式5mx a y与﹣5nx2a﹣3y是关于x、y的单项式，且它们是同类项．求（1）（7a﹣22）2013的值；（2）若5mx a y﹣5nx2a﹣3y=0，且xy≠0，求（5m﹣5n）2014的值．（四）答案例题答案：例1、【解答】解：根据整式的概念可知，整式有：（1）mn；（2）m；（3）；（5）2m+1；（6）；（8）x2+2x+．共6个．故选C．例2、【解答】解：单项式﹣的系数是：﹣，次数是3．故选D．例3、【解答】解：多项式1+2xy﹣3xy2的次数为3，故选C例4、【解答】解：（1）∵当n=1时，xy，当n=2时，﹣2x2y，当n=3时，4x3y，当n=4时，﹣8x4y，当n=5时，16x5y，∴第9个单项式是29﹣1x9y，即256x9y．（2）∴n为偶数时，单项式为负数．x的指数为n时，2的指数为n﹣1，∴当n为奇数时的单项式为2n﹣1x n y，该单项式为（﹣1）n+12n﹣1x n y它的系数是（﹣1）n+12n﹣1，次数是n+1．例5、【解答】解：按某一个字母的升幂排列是指按此字母的指数从小到大依次排列，降幂正好相反，常数项应放在最前面．多项式x5y2+2x4y3﹣3x2y2﹣4xy中，x的指数依次5、4、2、1；因此A不正确；y的指数依次是2、3、2、1，因此C、D不正确．故选B．例6、【解答】解：3x3﹣4和a2b+ab2+1属于同一类，都是3次多项式，A、abc﹣1是3次多项式，故本选项正确；B、x2﹣2是2次多项式，故本选项错误；C、3x2+2xy4是5次多项式，故本选项错误；D、m2+2mn+n2是2次多项式，故本选项错误．故选A．例7、【解答】解：因为多项式3x4﹣（m+5）x3+（n﹣1）x2﹣5x+3不含x3和x2．所以含x3和x2的单项式的系数应为0，即m+5=0，n﹣1=0，求得m=﹣5，n=1．故选C．基础题答案：1、【解答】解：整式的有：（1）﹣mn，（2）m，（3），（5）2m+1，（6），（8）x2+2x+，故选：C．2、【解答】解：整式有﹣mn，m，8，x2+2x+6，，，故选C3、【解答】解：∵单项式2a n b2c是六次单项式，∴n+2+1=6，解得：n=3，故n的值取3．故选：D．4、【解答】解：∵一组按规律排列的式子：a2，，，，…，∴第2016个式子是：，故选C．5、【解答】解：3x2y﹣4x3y2﹣5xy3﹣1的项是3x2y、﹣4x3y2、﹣5xy3、﹣1，按x的升幂排列为﹣1﹣5xy3+3x2y﹣4x3y2，故D正确；故选：D．6、【解答】解：A、2a2b与a2b所含字母相同，且相同字母的指数也相同，是同类项，故本选项正确；B、a2b2与a2b所含字母相同，但相同字母b的指数不相同，不是同类项，故本选项错误；C、ab2与a2b所含字母相同，但相同字母a的指数不相同，不是同类项，本选项错误；D、3ab与a2b所含字母相同，但相同字母a的指数不相同，不是同类项，本选项错误．故选A．7、【解答】解：∵﹣x3y a与x b y是同类项，∴a=1，b=3，则a+b=1+3=4．故选C．8、【解答】解：由题意，得a=﹣2，b=2+1=3．a b﹣ab=（﹣2）3﹣（﹣2）×3=﹣8+8=0；（2）由|m|+m=0，得m≤0．m≤﹣2时，|b﹣m|﹣|a+m|=b﹣m﹣（a﹣m）=b﹣a=3﹣（﹣2）=5；﹣2＜m≤0时，|b﹣m|﹣|a+m|=b﹣m﹣（m﹣a）=﹣2m+b+a=﹣2m+1．9、【解答】解：（1）由﹣a，a2，﹣a3，a4，﹣a5，a6，…可得第n项的表达式为（﹣1）n，所以第2014个单项式为，第2015个单项式为﹣．（2）由单项式的特点可得第n个单项式为（﹣1）n．10、【解答】解：∵不含二次项，∴a﹣4=0，8b﹣a+2=0，∴a=4，b=，∴a101•（﹣b）100=a100•a•b100=（ab）100•a=×4=4．11、【解答】解：由题意可知：关于x的多项式不能有5次项，且最高次数项为2，∴3﹣b=0，a=2，∴a=2，b=3，∴a2﹣b2=﹣512、【解答】解：由题意得：m=1，n+1=4，解得：m=1，n=3．∴2m+n=5．13、【解答】解：将多项式2a3+a2b﹣b3﹣5ab2按字母b的降幂排列为﹣b3﹣5ab2+a2b+2a3，故选C．14、【解答】解：∵m，n都是正数，∴m+n＞m，m+n＞n，∴m+n最大，∴多项式x m+x n+3x m+n的次数是m+n，故选C15、【解答】解：∵2x2m y3与﹣5xy2n是同类项，∴2m=1，2n=3，解得：m=，n=，∴|m﹣n|=|﹣|=1．故选：B．提高题答案：1．【解答】解：系数依次为1，3，5，7，9，11，…2n﹣1；x的指数依次是1，2，2，1，2，2，1，2，2，可见三个单项式一个循环，故可得第2013个单项式的系数为4025；∵=671，∴第2013个单项式指数为2，故可得第2013个单项式是4025x2．故答案为：4025x2．2．【解答】解：∵每一个式子的第二项是2n﹣1x+n，∴第10行第2项的值为29x+10=1034，解得x=2，故答案为2．3．【解答】解：整式有：x2+2，0，，共3个，故答案为3．4．【解答】解：根据单项式系数的定义，单项式的系数为﹣π3．5．【解答】解：①A+B=ax2+x﹣1+3x2﹣2x+1=（a+3）x2﹣x∵A与B的和中不含x2项，∴a+3=0，解得a=﹣3．②B﹣2A=3x2﹣2x+1﹣2×（﹣3x2+x﹣1）=3x2﹣2x+1+6x2﹣2x+2=9x2﹣4x+3．6．【解答】解：∵﹣5x3y|a|﹣（a﹣4）x﹣6是关于x、y的七次三项式，∴3+|a|=7，a﹣4≠0，解得：a=﹣4，故a2﹣2a+1=（a﹣1）2=25．7．【解答】解：小明的说法不正确，理由是绝对值不大于4的整数有9个，故小明说法错误；小丁说法错误，理由是|a|=3，|b|=2，得a=3或a=﹣3，b=2或b=﹣2，a+b=±5或a+b=±1，故小丁说法错误；小鹏说的单项式错误，理由是单项式的系数是﹣，小鹏说的多项式正确．8．【解答】解：（2mx2﹣x2+3x+1）﹣（5x2﹣4y2+3x）=2mx2﹣x2+3x+1﹣5x2+4y2﹣3x=（2m﹣1﹣5）x2+4y2+1=（2m﹣6）x2+4y2+1，当2m﹣6=0，即m=3时，此多项式为4y2+1，与x无关．因此存在m，使多项式（2mx2﹣x2+3x+1）﹣（5x2﹣4y2+3x），与x无关，m的值为3．9．【解答】解：（1）当n=2，且该多项式是关于x的三次三项式，故原式=x m+2﹣3x2+2x，m+2=3，解得：m=1，故m的值为：1；（2）若该多项式是关于x的二次单项式，则m+2=1，n﹣1=﹣2，解得：m=﹣1，n=﹣1；（3）若该多项式是关于x的二次二项式，①n﹣1=0，m为任意实数．则m，n要满足的条件是：n=1，m为任意实数；②当m=﹣1时，n≠﹣1，③m=0时，n≠4．10．【解答】解：由同类项定义得：2x﹣1=5，得x=3，2y=4，得y=2，把x=3，y=2代入2x﹣7y得：2x﹣7y=2×3﹣7×2=﹣8．11．【解答】解：∵﹣a|m﹣3|b与是同类项，∴|m﹣3|=1，|4n|=1，解得：m=4或2，n=，又∵m、n互为负倒数，∴m=4，n=﹣∴n﹣mn﹣m=﹣﹣（﹣1）﹣4=．12、【解答】解：mx2+4xy﹣x﹣3x2+2nxy﹣4y=（m﹣3）x2+（4+2n）xy﹣x﹣4y，∵合并后不含二次项，∴m﹣3=0，4+2n=0，∴m=3，n=﹣2，∴n﹣m=﹣2﹣3=﹣5．13、【解答】解：（1）由单项式5mx a y与﹣5nx2a﹣3y是关于x、y的单项式，且它们是同类项，得a=2a﹣3，解得a=3，（7a﹣22）2013=（7×3﹣22）2013=（﹣1）2013=﹣1；（2）由5mx a y﹣5nx2a﹣3y=0，且xy≠0，得5m﹣5n=0，解得m=n，（5m﹣5n）2014=02014=0．11。