平面向量题型及方法

妙用等和线解决平面向量系数和、差、商、平方问题【题型归纳目录】题型一：x +y 问题(系数为1)题型二：mx +ny 问题(系数不为1)题型三：mx -ny 问题题型四：m x +ny 问题题型五：yx 问题题型六：x 2+y 2问题【方法技巧与总结】(1)平面向量共线定理已知OA =λOB +μOC ，若λ+μ=1，则A ,B ,C 三点共线；反之亦然。

(2)等和线平面内一组基底OA ,OB 及任一向量OP ，OP =λOA +μOB (λ,μ∈R )，若点P 在直线AB 上或者在平行于AB 的直线上，则λ+μ=k (定值)，反之也成立，我们把直线AB 以及与直线AB 平行的直线称为等和线。

①当等和线恰为直线AB 时，k =1；②当等和线在O 点和直线AB 之间时，k ∈(0,1)；③当直线AB 在点O 和等和线之间时，k ∈(1,+∞)；④当等和线过O 点时，k =0；⑤若两等和线关于O 点对称，则定值k 互为相反数；【典型例题】题型一：x +y 问题(系数为1)1(2024·山东滨州·统考一模)在△ABC 中，M 为BC 边上任意一点，N 为线段AM 上任意一点，若AN=λAB +μAC (λ，μ∈R )，则λ+μ的取值范围是()A.0,13 B.13,12C.[0,1]D.[1,2]【答案】C【解析】由题意，设AN =tAM，0≤t ≤1 ，当t =0时，AN =0 ，所以λAB +μAC =0 ，所以λ=μ=0，从而有λ+μ=0；当0<t ≤1时，因为AN =λAB +μAC(λ，μ∈R )，所以tAM =λAB +μAC ，即AM =λt AB +μt AC ，因为M 、B 、C 三点共线，所以λt +μt=1，即λ+μ=t ∈0,1 .综上，λ+μ的取值范围是[0,1].故选：C .2(2024·陕西西安·高一西北工业大学附属中学校考阶段练习)在ΔABC 中，M 为边BC 上的任意一点，点N 在线段AM 上，且满足AN =13NM ，若AN =λAB +μAC(λ,μ∈R )，则λ+μ的值为()A.14B.13C.1D.4【答案】A【解析】设BM =tBC ，将AN 用AB 、AC 表示出来，即可找到λ和μ的关系，从而求出λ+μ的值．设BM=tBC (0≤t ≤1)，AN =13NM ，所以AN =14AM =14(AB +BM )=14AB +14tBC =14AB+14t (AC -AB )=14-14t AB+14tAC ，又AN =λAB +μAC ，所以λ+μ=14-14t +14t =14．故选：A ．3(2024·重庆铜梁·高一统考期末)在△ABC 中，点D 是线段BC 上任意一点，点P 满足AD =3AP，若存在实数m 和n ，使得BP =mAB +nAC，则m +n =()A.23B.13C.-13D.-23【答案】D【解析】由题意，AD =λAB +1-λ AC ，且0<λ<1，而AD =3AP =3AB +BP ，所以3AB +3BP =λAB +1-λ AC ，即BP =λ-33AB +1-λ3AC ，由已知，m =λ-33,n =1-λ3,则m +n =-23，选项D 正确.故选：D题型二：mx +ny 问题(系数不为1)1(2024·山东潍坊·高一统考期末)已知O 是ΔABC 内一点，且OA +OB +OC =0，点M 在ΔOBC 内(不含边界)，若AM =λAB +μAC，则λ+2μ的取值范围是()A.1,52B.1,2C.23,1D.12,1【答案】B【解析】根据OA +OB +OC =0 可知O 为ΔABC 的重心；根据点M 在ΔOBC 内，判断出当M 与O 重合时，λ+2μ最小；当M 与C 重合时，λ+2μ的值最大，因不含边界，所以取开区间即可．因为O 是ΔABC 内一点，且OA +OB +OC =0所以O 为ΔABC 的重心M 在ΔOBC 内(不含边界)，且当M 与O 重合时，λ+2μ最小，此时AM =λAB +μAC =23×12AB +AC =13AB +13AC 所以λ=13,μ=13，即λ+2μ=1当M 与C 重合时，λ+2μ最大，此时AM =AC所以λ=0,μ=1，即λ+2μ=2因为M 在ΔOBC 内且不含边界所以取开区间，即λ+2μ∈1,2 所以选B2(2024·江苏南京·高一南京师大附中校考期末)在扇形OAB 中，∠AOB =60o，OA=1，C 为弧AB 上的一个动点，且OC =xOA +yOB．则x +4y 的取值范围为()A.[1,4)B.[1,4]C.[2,3)D.[2,3]【答案】B【解析】以O 为原点，OB 所在直线为x 轴建立平面直角坐标系，令∠COB =θ，则θ∈0°,60° ，因为OA =1，则B 1,0 ，A 12,32,C cos θ,sin θ ，又OC =xOA +yOB ，则cos θ=x 2+y sin θ=32x ，则y =cos θ-13sin θx =23sin θ ，则x +3y =-233sin θ+4cos θ，又θ∈0°,60° ，易知f θ =-233sin θ+4cos θ为减函数，由单调性易得其值域为1,4 .故选：B .3(2024·辽宁沈阳·高三统考期末)如图，在扇形OAB 中，∠AOB =30°，C 为弧AB 上且与A ,B 不重合的一个动点，且OC =xOA +yOB，若μ=x +λy (λ>0)存在最大值，则λ的取值范围是()A.34,33B.33,32C.34,32D.32,233【答案】D 【解析】设射线OB 上存在为B ，使OB =1λOB，AB 交OC 于C ，由于OC =xOA +yOB =xOA +λy 1λOB=xOA +λyOB ，设OC =tOC ，OC =x OA+λy OB ，由A ,B ,C 三点共线可知x +λy =1，所以u =x +λy =tx +t ∙λy =1，则μ=OC OC存在最大值1，即在弧AB (不包括端点)上存在与AB平行的切线，所以λ∈32,233．故答案为32,233题型三：mx -ny 问题1(2024·上海徐汇·高二位育中学校考阶段练习)如图，OM ⎳AB ，点P 在由射线OM 、线段OB 及AB 的延长线组成的区域内(不含边界)运动，且OP =xOA +yOB ，当x =-12时，y 的取值范围是【答案】12,32【解析】如图，OM ⎳AB ，点P 在由射线OM ，线段OB 及AB 的延长线围成的区域内(不含边界)运动，且OP =xOA +yOB ，由向量加法的平行四边形法则，OP 为平行四边形的对角线，该四边形应是以OB 和OA 的反向延长线为两邻边，∴x 的取值范围是(-∞,0)；当x =-12时，要使P 点落在指定区域内，即P 点应落在DE 上，CD =12OB ，CE =32OB ，∴y 的取值范围是12，32 ．故答案为：12，322(2024·河南平顶山·高一统考期末)如图所示，点P 在由线段AB ，AC 的延长线及线段BC 围成的阴影区域内(不含边界)，则下列说法中正确的是．(填写所有正确说法的序号)①存在点P ，使得AP =12AB +2AC ；②存在点P ，使得AP =-12AB+2AC ；③存在点P ，使得AP =12AB -2AC；④存在点P ，使得AP =12AB +32AC．【答案】①④【解析】设AP =λAB +μAC,λ,μ∈R ，由图可知：λ>0,μ>0,且λ+μ>1，∴①④正确，故答案为：①④3(2024·高一课时练习)已知△ABC 中，CD =-35BC,EC =12AC ,AF =13AB ，若点P 为四边形AEDF 内一点(不含边界)且DP =-13DC+xDE ，则实数x 的取值范围为.【答案】12,43【解析】如图所示，在线段BD 上取一点G ，使得DG =-13DC，设DC =3a ，则DG =a ，BC =5a ，BG =a ；过点G 作GH ∥DE ，分别交DF ､AE 于K ､H ，连接FH ，则点K ､H 为临界点；GH ∥DE ，所以HE =13EC ，AH =23EC ，HG =43DE ，AH HC=12=AFFB ，所以FH ∥BC ；所以FH =13BC ，所以FH DG =KH KG，所以KG =35HK ，KG =38HG =12DE .所以实数x 的取值范围是12，43.故答案为：12，43 .题型四：m x +ny问题1(2024·江苏·高三专题练习)在△ABC 中，点O 是BC 的三等分点，OC =2OB，过点O 的直线分别交直线AB ,AC 于点E ,F ，且AB =mAE ，AC =nAF (m >0,n >0)，若1m +t n 的最小值为83，则正数t的值为【答案】2【解析】因为点O 是BC 的三等分点，OC =2OB则AO =AB +BO =AB +13BC =AB +13AC -13AB=23AB +13AC =2m 3AE +n 3AF ，又由点E ,O ,F 三点共线，所以AO =AE +EO =AE +λEF =AE +λAF -AE =1-λ AE +λAF，所以2m3=1-λn3=λ，可得2m 3+n3=1，所以1m +t n =2m 3+n 3 1m +t n =23+t 3 +2mt 3n +n 3m ≥23+t3 +22mt 3n ×n 3m=23+t 3 +22t 9，当且仅当2tm 2=n 2时，等号成立，即1m +t n 的最小值为23+t 3 +22t 9，则有23+t 3 +22t 9=83，即t +22t -6=0，所以t +32 t -2 =0，因为t >0，所以t =2，故答案为：2.2(2024·江苏盐城·高一统考期末)在△ABC 中，点O 是BC 的三等分点，OC =2OB，过点O 的直线分别交直线AB ，AC 于点E ，F ，且AB =mAE ，AC =nAF (m >0，n >0)，若1m +t 2nt >0 的最小值为3，则正数t 的值为.【答案】3-2【解析】∵在△ABC 中，点O 是BC 的三等分点，|OC |=2|OB |，∴AO =AB +BO =AB +13BC =AB +13(AC -AB )=23AB+13AC ，∵AB =mAE ，AC =nAF ，∴AO =23mAE +13nAF ，∵O ，E ，F 三点共线，∴23m +13n =1，∴1m +t 2n =1m +t 2n 23m +13n =23+n 3m +2mt 23n +t 23≥22t 29+t 23+23=t 23+232t +23，当且仅当n 3m =2mt 23n ，即2m 2t 2=n 2时取等号，∴1m +t 2n 的最小值为t 23+232t +23，即t 23+232t +23=3，∵t >0，∴t =3-2．故答案为：3-2．3(2024·山东菏泽·高一统考期末)在△ABC 中，点O 是线段BC 上的点，且满足OC =3OB，过点O 的直线分别交直线AB ,AC 于点E ,F ，且AB =mAE ，AC =nAF ，其中m >0且n >0，若1m +2n的最小值为.【答案】5+264【解析】依题意，作出图形如下，因为OC =3OB ，AB =mAE ，AC =nAF ，则BO =14BC ，所以AO =AB +BO =AB +14BC =AB +14AC -AB =34AB +14AC =3m 4AE +n 4AF ，因为E ,O ,F 三点共线，所以3m 4+n4=1，因为m >0，n >0，所以1m +2n =1m +2n 3m 4+n 4 =54+n 4m +6m 4n ≥54+2n 4m ⋅6m 4n =54+264，当且仅当n 4m =6m4n ，即n =6m =46-2 时取等号，所以1m +2n 的最小值为5+264.故答案为：5+264.题型五：yx问题1(2024·山西·高一统考期末)已知在△ABC 中，点D 满足BD =34BC，点E 在线段AD (不含端点A ，D )上移动，若AE =λAB +μAC ，则μλ=.【答案】3【解析】如图，由题意得存在实数m ，使得AE =mAD0<m <1 .又AD =AB +BD =AB +34BC =AB +34AC -AB =14AB+34AC ，所以AE =m 14AB +34AC =m 4AB +3m 4AC ，又∵AE =λAB +μAC ，且AB ,AC 不共线，故由平面向量的分解的唯一性得λ=m 4,μ=3m4.所以μλ=3.故答案为：3.2(2024·山东潍坊·高三开学考试)在△ABC 中，点D 满足BD =34BC，当点E 在射线AD (不含点A )上移动时，若AE =λAB +μAC ，则λ+1μ的最小值为．【答案】233/233【解析】由BD =34BC ，得AD -AB =34(AC -AB )，即AD =14AB +34AC，因为点E 在射线AD (不含点A )上移动，所以AE =tAD =t 4AB+3t 4AC ，又因为AE =λAB +μAC ，所以λ=t 4,μ=3t4(t >0)，则λ+1μ=t 4+43t ≥213=233(当且仅当t 4=43t ，即t =433时取等号)，所以λ+1μ的最小值为233.故答案为：233．3(2024·黑龙江哈尔滨·高三哈师大附中校考期末)在ΔABC 中，点D 满足BD =34BC，当E 点在线段AD (不包含端点)上移动时，若AE =λAB +μAC ，则λ+3μ的取值范围是A.233,+∞B.[2,+∞)C.174,+∞D.(2,+∞)【答案】C【解析】如图所示，△ABC 中，BD =34BC，∴AD =AB +BD =AB +34BC =AB +34(AC -AB )=14AB+34AC ，又点E 在线段AD (不含端点)上移动，设AE =kAD ，0<k <1，∴AE =k 4AB +3k 4AC ，又AE =λAB +μAC ，∴λ=k4μ=3k 4，∴λ+3μ=k 4+4k ．∵k 4+4k在(0，1)上单调递减，∴λ+3μ的取值范围为174，+∞ ，故选C ．题型六：x 2+y 2问题1(2024·江苏泰州·高一泰州中学阶段练习)在ΔABC 中，点D 满足BD =34BC，当点E 在射线AD (不含点A )上移动时，若AE =λAB +μAC，则(λ+1)2+μ2的取值范围为．【答案】(1,+∞)【解析】因为点E 在射线AD (不含点A )上，设AE =kAD , 0<k ，又BD =34BC ，所以AE =k (AB +AD )=k AB +34(AC -AB ) =k 4AB+3k 4AC ，所以λ=k4μ=3k4 ，t =(λ+1)2+μ2=k 4+12+916k 2=58k +252+910>1，故(λ+1)2+μ2的取值范围1,+∞ .2(2024·天津·高三校联考阶段练习)如图，在△ABC 中，BD =13BC，点E 在线段AD 上移动(不含端点)，若AE =λAB +μAC ，则λμ=，λ2-μ的最小值为.【答案】 2-116【解析】因为在△ABC 中，BD =13BC，所以AD =AB +BD =AB +13BC =AB +13(AC -AB )=23AB+13AC ,即AD =23AB +13AC .因为点E 在线段AD 上移动(不含端点)，所以设AE =xAD(0<x <1).所以AE =2x 3AB +x 3AC ，对比AE =λAB +μAC 可得λ=2x 3,μ=x 3.代入λ=2x 3,μ=x 3，得λμ=2x3x 3=2；代入λ=2x 3,μ=x 3可得λ2-μ=2x 3 2-x 3=4x 29-x 3(0<x <1)，根据二次函数性质知当x =--132×49=38时，λ2-μ min =49×382-13×38=-116.故答案为：2;-1163(2024·全国·高三专题练习)在△ABC 中，点D 满足BD =DC ，当E 点在线段AD 上移动时，若AE=λAB +μAC ，则t =(λ-1)2+μ2的最小值为.【答案】12【解析】BD =DC；∴D 为边BC 的中点，如图，则：AD =12(AB +AC )；∵E 在线段AD 上；∴设AE =kAD =k 2AB +k 2AC ，0≤k ≤1；又AE =λAB +μAC ；∴λ=k2μ=k2；即λ=μ，且0≤μ≤12；∴t =(μ-1)2+μ2=μ2-2μ+1+μ2=2μ-12 2+12；∴μ=12时，t 取最小值12．故答案为：12．4(2024·山东德州·高三统考期末)在△ABC 中，M 为边BC 上任意一点，N 为AM 的中点，且满足AN=λAB +μAC ，则λ2+μ2的最小值为.【答案】18/0.125【解析】由M 为边BC 上任意一点，则BM =γBC,0≤γ≤1 ，AN =12AM =12AB +BM =12AB +γBC =12AB+γ2AC -AB =1-γ2AB +γ2AC ，可得λ=1-γ2μ=γ2，则λ+μ=12，即λ=12-μ，由0≤γ≤1，可得0≤γ2≤12，则μ∈0,12 ，故λ2+μ2=12-μ2+μ2=2μ2-μ+14=2μ-14 2+18，当μ=14时，λ2+μ2取得最小值为18.故答案为：18.【过关测试】一、单选题1(2024·高三课时练习)在△ABC 中，M 为边BC 上任意一点，N 为AM 中点，AN =λAB +μAC，则λ+μ的值为()A.12B.13C.14D.1【答案】A【解析】由题可设BM =tBC ，则AM =AB +BM =AB +tBC =AB +t AC -AB =1-t AB +tAC ，∵N 为AM 中点，∴AN =12AM =121-t AB +12tAC,又AN =λAB +μAC ，∴λ=121-t ,μ=12t ，∴λ+μ=12.故选：A .2(2024·安徽六安·高一六安一中校考期末)如图所示，在△ABC 中，点D 是边BC 上任意一点，M 是线段AD 的中点，若存在实数λ和μ，使得BM =λAB +μAC，则λ+μ=()A.-1B.-12C.-2D.-32【答案】B【解析】如图所示，因为点D 在线段BC 上，所以存在t ∈R ，使得BD =tBC =t AC -AB，因为M 是线段AD 的中点，所以：BM =12BA +BD =12-AB +tAC -tAB =-12t +1 AB +12tAC ，又BM =λAB +μAC ，所以λ=-12t +1 ，μ=12t ，所以λ+μ=-12.故选：B .3(2024·重庆·高三重庆南开中学校考阶段练习)已知点O 为ΔABC 所在平面内一点，满足OA +OB+OC =0 ，M 为AB 中点，点P 在ΔAOC 内(不含边界)，若BP =xBM +yBC ，则x +y 的取值范围是()A.1,2B.23,2C.12,1D.13,32【答案】A 【解析】如图：∵OA +OB +OC =0 ，∴点O 是ΔABC 的重心，点N 是BC 的中点，BO =BC +CO =BC +23CM =BC +23BM -BC =13BC+23BM ，BN =12BC ，BA =2BM当点P 在ΔAOC 内(不含边界)，BP =BO +OP =BO +λOQ =BO +λOA +AQ ，0<λ<1=BO +λ23NA +μAC =BO +λ23BA -BN +μBC -BA ，0<μ<1=BO +λ232BM -12BC +μBC -2BM =13BC+23BM +43λBM -13λBC +λμBC -2λμBM =13-13λ+λμ BC +23+43λ-2λμ BM∴x +y =13-13λ+λμ+23+43λ-2λμ=1+λ-λμ=1+λ1-μ ，∵0<λ<1，0<μ<1，∴0<1-μ<1，0<λ1-μ <1，∴1<1+λ1-μ <2.故选：A4(2024·广东惠州·高一校联考阶段练习)在△ABC 中，点O 是线段BC 上的点，且满足|OC |=3|OB|，过点O 的直线分别交直线AB 、AC 于点E 、F ，且AB =mAE ，AC =nAF ，其中m >0且n >0，若1m+tn的最小值为3，则正数t 的值为()A.2B.3C.83D.113【答案】B【解析】AO =AB +BO =AB +14BC =AB +14AC -AB =34AB+14AC =3m 4AE +n 4AF ，∵E 、O 、F 三点共线，∴3m 4+n4=1，∵m >0，n >0，t >0，∴1m +t n =1m +t n 3m 4+n 4 =34+n 4m +3mt 4n +t 4≥3+t 4+2n 4m ⋅3mt 4n =3+t 4+23t 4，当且仅当n 4m =3mt4n时取等号，∴3+t 4+23t 4=3⇒t +33 t -3 =0⇒t =3⇒t =3．故选：B ．5(2024·江西南昌·高三阶段练习)在△ABC 中，点O 是BC 的三等分点(靠近点B )，过点O 的直线分别交直线AB ，AC 于不同两点M ，N ，若AB =mAM ,AC =nAN ，m ,n 均为正数，则1m +1n的最小值为()A.2 B.1+23C.1+223D.1+233【答案】C【解析】由题意知AO =AB +13BC =AB +13AC -AB =23AB+13AC =2m 3AM +n 3AN ，由于M 、O 、N 三点共线，可知2m 3+n3=1，由于m ,n 均为正数，所以1m +1n =1m +1n 2m 3+n 3 =1+n 3m +2m 3n ≥1+229=1+223，当且仅当n 3m =2m3n ，即m =3(2-2)2,n =3(2-1)时取得等号，故选：C 二、多选题6(2024·江苏南京·高一南京市宁海中学校联考期末)在△ABC 中，点D 是线段BC 上任意一点，点M 是线段AD 的中点，若存在λ,μ∈R 使BM =λAB +μAC，则λ,μ的取值可能是()A.λ=-35,μ=110B.λ=1,μ=-32C.λ=-910,μ=25D.λ=-710,μ=35【答案】AC【解析】令BD =mBC 且m ∈[0,1]，而BM =12(BA +BD )=12(BA+mBC )，又BC =BA +AC ，则BM =12[BA +m (BA +AC )]=-1+m 2AB+m 2AC ，所以λ=-1+m2μ=m2，则λ∈-1,-12，μ∈0,12 且λ+μ=-12，故A 、C 满足，B 、D 不满足.故选：AC7(2024·浙江宁波·高一宁波市北仑中学校考期末)已知O 是△ABC 内一点，且OA +OB +OC =0，点M 在△OBC 内(不含边界)，若AM =λAB +μAC，则λ+2μ的值可能为()A.97B.117C.137D.157【答案】ABC【解析】因为O 是△ABC 内一点，且OA +OB +OC =0 所以O 为△ABC 的重心M 在△OBC 内(不含边界)，且当M 与O 重合时，λ+2μ最小，此时AM =λAB +μAC =23×12AB +AC =13AB +13AC 所以λ=13,μ=13，即λ+2μ=1当M 与C 重合时，λ+2μ最大，此时AM =AC所以λ=0,μ=1，即λ+2μ=2因为M 在△OBC 内且不含边界所以取开区间，即λ+2μ∈1,2 ，结合选项可知ABC 符合，D 不符合故选：ABC8(2024·重庆·高一校联考阶段练习)在ΔABC 中，点D 满足BD =DC，当点E 在线段AD 上(不含A 点)移动时，记AE =λAB +μAC，则()A.λ=2μB.λ=μC.14λ+μ的最小值为1D.4λ+μ的最小值为4【答案】BC【解析】∵BD =DC ，∴D 是BC 中点,则AD =12AB +AC,又点E 在线段AD 上,即A ,E ,D 三点共线,设AE =mAD 0<m ≤1 ,故AE =mAD =12m AB +AC ,λ=μ=12m .故B 对A 错.14λ+μ=14λ+λ≥214λ⋅λ=1,当且仅当14λ=λ时,即λ=12,故C 对.4λ+μ=4λ+λ在λ∈0,12上单调递减，当λ=12取最小值172，故D 错.故答案为：BC9(2024·湖北武汉·高三校联考期末)在△ABC 中，点D 满足BD =DC，当点E 在线段AD 上移动时，记AE =λAB +μAC ，则()A.λ=2μB.λ=μC.λ-2 2+μ2的最小值为2D.λ-2 2+μ2的最小值为52【答案】BD 【解析】由BD =DC 得AD =12AB +AC ，又点E 在线段AD 上移动，AE =kAD =12k AB +AC =12kAB+12kAC ,0≤k ≤1，∴λ=12k ,μ=12k ，故A 错误，B 正确；λ-2 2+μ2=12k -2 2+12k 2=12k 2-2k +4=12k -2 2+2，当k =1时，有最小值52，故C 错误，D 正确.故选：BD .三、填空题10(2024·全国·高三专题练习)如图，边长为2的等边三角形的外接圆为圆O ，P 为圆O 上任一点，若AP =xAB +yAC ，则2x +2y 的最大值为【答案】83【解析】作BC 的平行线与圆相交于点P ，与直线AB 相交于点E ，与直线AC 相交于点F ，设AP =λAE +μAF ，则λ+μ=1，等边三角形边长为2，则外接圆半径为233，当点P 为切点时, AE =AF =83，∵BC ⎳EF ，∴设AE AB =AF AC =k ，则k ∈0,43 ，当点P 为切点时, k 有最大值43,AE =kAB ，AF =kAC ，AP =λAE +μAF =λkAB +μkAC∴x =λk ，y =μk ，∴2x +2y =2λ+μ k =2k ≤83.即2x +2y 的最大值为83.故答案为：8311(2024·福建三明·高二三明一中校考开学考试)如图，在扇形OAB 中，∠AOB =π3，C 为弧AB 上的一个动点，若OC=xOA +yOB，则x +4y 的取值范围是.【答案】1,4【解析】如图所示，以O 为原点，OB 所在直线为x 轴，建立平面直角坐标系，则根据题意可知B (1,0)，A 12，32，设C (cos θ,sin θ)，0°≤θ≤60°．由OC =xOA +yOB ，得cos θ=y +12x sin θ=32x ，∴x =23sin θy =cos θ-sin θ3，∴x +4y =4cos θ-233sin θ，点C 在弧AB 上由B →A 运动，θ在0，π3 上逐渐变大，cos θ变小，sin θ逐渐变大，∴当θ=0°时x +4y 取得最大值4，当θ=60°时x +4y 取得最小值1．∴x +4y 的取值范围是[1，4]．故答案为：1,4 ．12(2024·四川绵阳·高一统考期末)在扇形OAB 中，∠AOB =60°，C 为弧AB 上的一动点，若OC=xOA +yOB ，则3x +y 的取值范围是．【答案】1,3【解析】以O 为原点，OA ,OB 分别为x ，y 轴正方向建立平面直角坐标系.则OA =1,0 ,OB =12,32 .不妨设OC =cos θ,sin θ ,0≤θ≤π3.因为OC =xOA +yOB，所以cos θ=x +12y sin θ=32y ，解得：x =cos θ-33sin θy =233sin θ，所以3x +y =3cos θ-33sin θ.因为y =cos θ在θ∈0,π3 上单调递减，y =-sin θ在θ∈0,π3上单调递减，所以3x +y =3cos θ-33sin θ在θ∈0,π3 上单调递减.所以当θ=0时3x +y =3最大；当θ=π3时3x +y =3cos π3-33sin π3=32-33⋅32=1最小.所以3x +y 的取值范围是1,3 .故答案为：1,3 .13(2024·全国·高三专题练习)在扇形OAB 中，OA =1，∠AOB =π3，C 为弧AB 上的一个动点，若OC =xOA +yOB ，则x +3y 的取值范围是.【答案】[1,3]【解析】如图所示，建立平面直角坐标系以O 为坐标原点，OA 所在直线为x 轴建立平面直角坐标系，则A(1,0)，B 12,32，设∠AOC =θ，则C (cos θ,sin θ)0≤θ≤π3 ，由OC =xOA +yOB 得cos θ=x +12y ,sin θ=32y , 从而x =cos θ-13sin θ,y =23sin θ, 则x +3y =cos θ+533sin θ=283sin (θ+φ)，易知0<φ<π6，故y =f (θ)=cos θ+533sin θ=283sin (θ+φ)在0,π3上单调递增，∴y min =f (0)=1，y max =f π3 =cos π3+533sin π3=12+52=3.故x +3y ∈[1,3].故答案为：[1,3]14(2024·全国·高三专题练习)扇形OAB 中，∠AOB =120°，C 为AB 上的一个动点，且OC =xOA+yOB ，其中x ,y ∈R .(1)x +y 的取值范围为；(2)2x +y 的取值范围为.【答案】1,21,2213【解析】(1)解法一：(等和线)设OC 与AB 相交于点D ，OD =λOC =λxOA +λyOB，λx +λy =1，x +y =1λ=OC OD ∈[1,2].解法二：(坐标法)C (cos α,sin α)，α∈0,2π3，cos α=x -12y ，sin α=32y ，x =cos α+33sin α，y =233sin α，x +y =cos α+3sin α=2sin α+π6∈[1,2].解法三：设∠AOC =α∈0,2π3，OC ⋅OA =xOA ⋅OA +yOB ⋅OA ,OC ⋅OB =xOA ⋅OB +yOB ⋅OB , ，即cos α=x -12y cos (1200-α)=-12x +y∴x +y =2[cos α+cos (1200-α)]=cos α+3sin α=2sin α+π6∈[1,2].(2)解法一：(等和线)解法二：2x +y =2cos α+433sin α=2213sin (α+θ)∈1,2213，其中sin (α+θ)先增后减.15(2024·吉林·高一阶段练习)如图，在ΔABC 中，D ,E ,F 分别为BC ,CA ,AB 上的点，且CD =35BC ，EC =12AC ，AF =13AB .设P 为四边形AEDF 内一点(P 点不在边界上)，若DP =-13DC+λDE ，则实数λ的取值范围为【答案】12,43【解析】取BD 中点M ,过M 作MH ⎳DE 交DF ,AC 分别为G ,H ,如图：则由DP =-13DC+λDE =DM +λDE 可知,P 点在线段GH 上运动(不包括端点)当P 与G 重合时，根据DP =tDF =-89tDC +43tDE =-13DC +λDE ,可知λ=12，当P 与H 重合时,由P ,C ,E 共线可知-13+λ=1，即λ=43，结合图形可知λ∈12,43.16(2024·重庆万州·高一万州外国语学校天子湖校区校考期末)如图，在△ABC 中，BD =13BC，点E 在线段AD 上移动(不含端点)，若AE =λAB +μAC ，则λ2+1μ的取值范围是．【答案】103,+∞【解析】由题可知，BD =13BC ，设AE =mAD0<m <1 ，则AE =m AB +13BC =m AB +13BA +AC，所以AE =23mAB +13mAC ，而AE =λAB +μAC ，可得：λ=23m ,μ=13m ，所以λ2+1μ=m 3+3m0<m <1 ，设f m =m 3+3m0<m <1 ，由双钩函数性质可知，f x 在0,1 上单调递减，则f x >f 1 =13+3=103，所以λ2+1μ的取值范围是103,+∞ .故答案为：103,+∞ .四、解答题17(2024·高一课时练习)在学习向量三点共线定理时，我们知道当P 、A 、B 三点共线，O 为直线外一点，且OP =xOA +yOB 时，x +y =1(如图1)，小明同学提出了如下两个问题，请同学们帮助小明解答．(1)当x +y >1或x +y <1时，O 、P 两点的位置与AB 所在直线之间存在什么关系？写出你的结论，并说明理由；(2)如图2，射线OM ⎳AB ，点P 在由射线OM 、线段OA 及BA 的延长线围成的区域内(不含边界)运动，且OP =xOA +yOB ，求实数x 的取值范围，并求当x =12时，实数y 的取值范围．【解析】(1)若x +y >1，则O ，P 在直线AB 异侧；若x +y <1，则O ，P 在直线AB 同侧．理由如下：设x +y =t ，则由OP =xOA +yOB ，得：OP =xOA +(t -x )OB =xOA +1-x OB +t -1 OB ，则在直线AB 上有一点Q ，使得OQ =xOA +1-x OB ，如下图所示：则OP =OQ +t -1 OB ，即QP =t -1 OB ，∴当t >1时，则OB =t -1 OB 与OB 同向，且QP =OB ，由平面共线定理可得，O ，P 在直线AB 异侧；当t <1时，OB =t -1 OB 与OB 反向，如下图所示，且QP =OB ，由平面共线定理可得，O ，P 在直线AB 同侧．(2)射线OM ⎳AB ，点P 在由射线OM 、线段OA 及BA 的延长线围成的区域内(不含边界)运动如图所示，阴影部分为点P 的运动区域(不含边界)，由(1)可知，O ，P 在直线AB 同侧，由于OP =xOA +yOB ，则x +y <1．过点P 作PE ⎳OB 交射线OA 于E ，过点P 作PF ⎳OB 交射线BO 的延长线OB 于F ,由平行四边形法则可得OP =OE +OF ，又OE 与OA 方向相同，则OE =mOA ，且m >0，OF 与OB 方向相反，则OF =nOB ，且n <0，则OP =mOA +nOB =xOA +yOB ，故x =m >0,y =n <0，即实数x 的取值范围是(0,+∞)，当x =12时，此时E 为OA 中点，过E 作直线平行与OB 交AB 于M ，交射线OM 于M ，则点P 运动轨迹为线段EM (不含端点E ,M )，如下图：当点P 运动到E 时，OP =OE =12OA +0⋅OB ，此时y =0；当点P 运动到M 时，OP =OE +EM =12OA +M E =12OA +12BO =12OA -12OB ，此时y =-12；且由平面向量加法的平行四边形法则得y ∈-12,0 .18(2024·高一课时练习)如图，OM ⎳AB ，点P 在由射线OM ，线段OB 及AB 的延长线围成的区域内(不含边界)运动，且OP =xOA +yOB ．(1)求x 的取值范围；(2)当x =-12时，求y 的取值范围．【解析】(1)如图，作PE ⎳BA 交OB 于E ，则OP =OE +EP =mOB +nAB =-nOA +(m +n )OB ．由P 点的位置容易知道0<m <1，n >0．因此，x =-n <0，即x 的取值范围是(-∞,0)．(2)当x =-12时，y =m +n =m +12，所以此时y 的取值范围是12,32．19(2024·上海浦东新·高二华师大二附中校考阶段练习)小郭是一位热爱临睡前探究数学问题的同学，在学习向量三点共线定理时，我们知道当P 、A 、B 三点共线，O 为直线外一点，且OP =xOA +yOB 时，x +y =1(如图1)第二天，小郭提出了如下三个问题，请同学帮助小郭解答.(1)当x +y >1或x +y <1时，O 、P 两点的位置与AB 所在直线之间存在什么关系？写出你的结论，并说明理由(2)如图2，射线OM ∥AB ，点P 在由射线OM 、线段OA 及BA 的延长线围成的区域内(不含边界)运动，且OP =xOA +yOB ，求实数x 的取值范围，并求当x =12时，实数y 的取值范围.(3)过O 作AB 的平行线，延长AO 、BO ，将平面分成如图3所示的六个区域，且OP =xOA +yOB ，请分别写出点P 在每个区域内运动(不含边界)时，实数x ，y 应满足的条件.(不必证明)【解析】(1)若x +y >1，则O 、P 异侧，若x +y <1，则O 、P 同侧；理由如下：设x +y =t ，则由OP =xOA +yOB 得，OP =xOA +t -x OB =xOA -xOB +tOB =xBA +tOB ，当t >1时，tOB 与OB 同向，由平面向量加法的平行四边形法则可知，O 、P 异侧；当t <1时，tOB 与OB 反向，由平面向量加法的平行四边形法则可知，O 、P 同侧；(2)由图及平面向量基本定理可知，x >0，即实数x 的取值范围是0,+∞ ，当x =12时，由平面向量加法的平行四边形法则可知，y ∈-12,0 ；(3)Ⅰ：y <0x +y >0 ；Ⅱ：x >0y >0 ；Ⅲ：x <0x +y >0 ；Ⅳ：y >0x +y <0 ；Ⅴ：x <0y <0 ；Ⅵ：x >0x +y <0 ．。

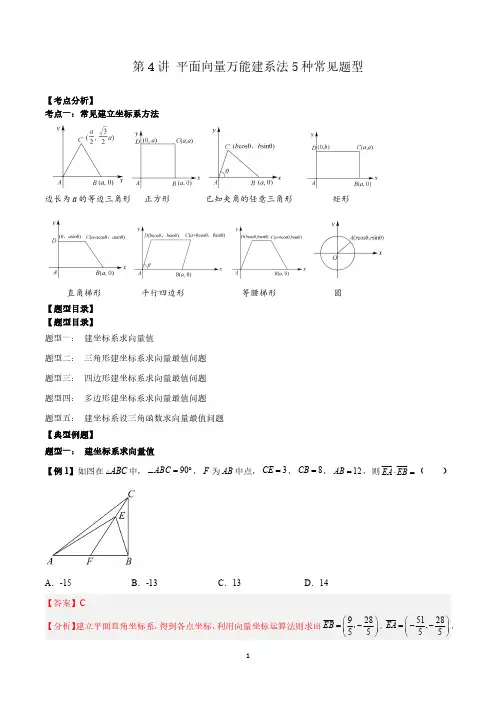
第4讲平面向量万能建系法5种常见题型【考点分析】考点一：常见建立坐标系方法边长为a 的等边三角形正方形已知夹角的任意三角形矩形直角梯形平行四边形等腰梯形圆【题型目录】【题型目录】题型一：建坐标系求向量值题型二：三角形建坐标系求向量最值问题题型三：四边形建坐标系求向量最值问题题型四：多边形建坐标系求向量最值问题题型五：建坐标系设三角函数求向量最值问题【典型例题】题型一：建坐标系求向量值【例1】如图在ABC 中，90ABC ∠=︒，F 为AB 中点，3CE =，8CB =，12AB =，则EA EB ⋅= （）A ．-15B ．-13C ．13D ．14则()120A -，，(00)B ，，(08)C ，，(60)F -，，又3CE =，8CB =，12AB =，则2210CF CB BF =+=，即310CE FC =，即710FE FC =，则()77601010BE BF FE BF FC +==+=-+ ，()(776,81010EA EF FA CF FA =+=+=--+- 【例2】已知正方形ABCD 的边长为2，以CD 为边作正三角形CDE ，使得,A E 位于直线CD 的两侧，则AC AE →→⋅的值为（）A ．6-B ．6-C ．6+D ．6+【答案】D 【分析】建立平面直角坐标系，利用向量的坐标运算求解.【详解】以A 为坐标原点，以,AB AD 为,x y 轴非负半轴，建立平面直角坐标系，如图，由正三角形CDE 及正方形ABCD ()()2,2,1,23C E +，所以()()2,21,23AC AE →→⋅=⋅+=故选：D【例3】如图甲所示，古代中国的太极八卦图是以同圆内的圆心为界，画出相等的两个阴阳鱼.其平面图形记为图乙中的正八边形ABCDEFGH ，其中2OA =，则以下结论错误的是（）A 0OE OG ++=B ．OA OD ⋅=-C ．4AG EH +=D ．AO 在OH 方向上的投影向量为2OH - 【答案】C【分析】选择合适的位置建立平面直角坐标系，写出相应点的坐标，逐项验证即可.【详解】由题意，分别以,HD BF 所在直线为,x y 轴，建立平面直角坐标系，如图所示：在正八边形ABCDEFGH 中，由AOB BOC COD DOE ∠=∠=∠=∠360458GOH HOA =∠=∠== 过A 作AM HD OM AM⊥⇒=因为2OA =，所以OM AM ==所以(2,2),(0,2),(2,A B E ---【例4】《九章算术》中有一个“引葭赴岸”问题：“今有池方一丈，葭生其中央，出水一尺．引葭赴岸，适与岸齐．问水深、葭长各几何？”其大意为现有水池1丈见方（即1CE =丈10=尺），芦苇生长在水池的中央，长出水面部分的长度为1尺．将芦苇向池岸牵引，牵引至恰巧与水岸齐接的位置（如图所示）．试问水深、芦苇的长度各是多少？若将芦苇,AB AC 均视为线段，在芦苇移动的过程中，设其长度不变，则AC DE ⋅=（）．A ．90平方尺B ．92平方尺C ．94平方尺D ．98平方尺【答案】C 【分析】设AB x =（尺），利用勾股定理可构造方程求得AB ，以A 为坐标原点可建立平面直角坐标系，利用平面向量数量积的坐标运算可求得结果.【详解】设AB x =（尺），则1AC x =+（尺），5AD = （尺），()22251x x ∴+=+，解得：12x =．以A 为坐标原点，建立如图所示的平面直角坐标系（单位：尺），则()0,0A ，()5,0D ，()5,12C ，()5,12E -，()5,12AC ∴= ，()10,12DE =- ，5014494AC DE ∴⋅=-+= （平方尺）．故选：C.【例5】已知正方形ABCD 的边长为2，点P 满足1()2AP AB AC =+ ，则||PD = _________；PB PD ⋅= _________．【答案】(1).(2).1-【解析】以点A 为坐标原点，AB 、AD 所在直线分别为x 、y 轴建立如下图所示的平面直角坐标系，则点()0,0A 、()2,0B 、()2,2C 、()0,2D ，()()()()1112,02,22,1222AP AB AC =+=+= ，则点()2,1P ，()2,1PD ∴=- ，()0,1PB =- ，因此，PD == ()021(1)1PB PD ⋅=⨯-+⨯-=- .【题型专练】1．已知矩形ABCD 中，4AB =uuu r ，2AD = ，3DM MC = ，BP PC = ，则AM AP ⋅= （）A ．6B ．10C ．14D ．38【答案】C 【分析】以B 为原点，,BA BC 分别为,x y 轴建立平面直角坐标系，由条件得出点,P M 的坐标，进而得出向量,AP AM uuu r uuur的坐标，从而得出向量的数量积.【详解】以B 为原点，,BA BC 分别为,x y 轴建立平面直角坐标系.则()0,4A ,()2,4,D ()2,0C 由BP PC = ，则()1,0P ,由3DM MC = ，则()2,1M 所以()1,4AP =-uuu r ,()2,3AM =-uuur 所以()()124314AM AP ⋅=⨯+-⨯-=uuur uuu r 故选：C。

高中数学第六章平面向量及其应用考点题型与解题方法单选题1、在△ABC 中，若AB⃗⃗⃗⃗⃗ ⋅AC ⃗⃗⃗⃗⃗ <0，则△ABC －定是（ ） A ．锐角三角形B ．直角三角形C ．钝角三角形D ．等边三角形 答案：C分析：根据向量的数量积的运算公式，求得cosA <0，得到A 为钝角，即可求解. 由向量的数量积的运算公式，可得AB ⃗⃗⃗⃗⃗ ⋅AC ⃗⃗⃗⃗⃗ =|AB ⃗⃗⃗⃗⃗ |⋅|AC ⃗⃗⃗⃗⃗ |cosA <0，即cosA <0， 因为A ∈(0,π)，所以A 为钝角，所以△ABC －定是钝角三角形. 故选：C.2、已知a ，b ⃗ 是不共线的向量，OA ⃗⃗⃗⃗⃗ =λa +μb ⃗ ，OB ⃗⃗⃗⃗⃗ =3a −2b ⃗ ，OC ⃗⃗⃗⃗⃗ =2a −3b ⃗ ，若A,B,C 三点共线，则实数λ，µ满足（ ）A ．λ=μ−5B ．λ=μ+5C ．λ=μ−1D ．λ=μ+1 答案：B解析：根据向量的线性运算方法，分别求得AB ⃗⃗⃗⃗⃗ =(3−λ)a −(2+μ)b ⃗ ，BC ⃗⃗⃗⃗⃗ =−a −b ⃗ ； 再由AB⃗⃗⃗⃗⃗ //BC ⃗⃗⃗⃗⃗ ，得到3−λ=−(2+μ)，即可求解. 由OA ⃗⃗⃗⃗⃗ =λa +μb ⃗ ，OB ⃗⃗⃗⃗⃗ =3a −2b ⃗ ，OC ⃗⃗⃗⃗⃗ =2a −3b⃗ ， 可得AB ⃗⃗⃗⃗⃗ =OB ⃗⃗⃗⃗⃗ −OA ⃗⃗⃗⃗⃗ =(3−λ)a −(2+μ)b ⃗ ，BC ⃗⃗⃗⃗⃗ =OC ⃗⃗⃗⃗⃗ −OB ⃗⃗⃗⃗⃗ =−a −b ⃗ ； 若A,B,C 三点共线，则AB ⃗⃗⃗⃗⃗ //BC ⃗⃗⃗⃗⃗ ，可得3−λ=−(2+μ)，化简得λ=μ+5. 故选：B.3、在△ABC 中，角A,B,C 的对边分别为a,b,c ，且B =π3，b =3，a =√3，则c =（ ）． A ．√3B ．2√3C ．3−√3D ．3 答案：B分析：利用余弦定理可构造方程直接求得结果.在△ABC 中，由余弦定理得：b 2=a 2+c 2−2accosB =3+c 2−√3c =9，即c 2−√3c −6=0，解得：c =−√3（舍），∴c =2√3.c故选：B.4、已知非零向量a →与b →共线，下列说法不正确的是（ ） A ．a →=b →或a →=−b →B ．a →与b →平行C ．a →与b →方向相同或相反D ．存在实数λ，使得a →=λb →答案：A分析：根据向量共线的概念，以及向量共线定理，逐项判断，即可得出结果． 非零向量a →与b →共线，对于A ，a →=λb →，λ≠0，故A 错误；对于B ，∵向量a →与b →共线，∴向量a →与b →平行，故B 正确； 对于C ，∵向量a →与b →共线，∴a →与b →方向相同或相反，故C 正确； 对于D ，∵a →与b →共线，∴存在实数λ，使得a →=λb →，故D 正确. 故选：A.5、已知向量a =(−1,m )，b ⃗ =(m +1,2)，且a ⊥b ⃗ ，则m =（ ） A ．2B ．−2C ．1D ．−1 答案：C分析：由向量垂直的坐标表示计算．由题意得a ⋅b ⃗ =−m −1+2m =0，解得m =1 故选：C ．6、已知f (x )=sin (ωx +π6)+cosωx （ω>0），将f (x )图象上的横坐标伸长到原来的2倍（纵坐标不变时），得到g (x )的图象．g (x )的部分图象如图所示（D 、C 分别为函数的最高点和最低点）：其中CA ⃗⃗⃗⃗⃗ ⋅CB ⃗⃗⃗⃗⃗ =|AD ⃗⃗⃗⃗⃗⃗ |22，则ω=（ ）A ．π4B ．π2C ．πD ．2π 答案：C分析：先求出g (x )的解析式，再利用CA ⃗⃗⃗⃗⃗ ⋅CB ⃗⃗⃗⃗⃗ =|AD ⃗⃗⃗⃗⃗⃗ |22得到cos∠ACB =12，进而求出|AB |=2，所以T =2×2=4，ω=π 由f (x )=√32sinωx +32cosωx =√3sin (ωx +π3)，∴g (x )=√3sin (12ωx +π3)，因为D 、C 分别为函数的最高点和最低点，所以DA =AC =CB ，由CA⃗⃗⃗⃗⃗ ⋅CB ⃗⃗⃗⃗⃗ =|AD ⃗⃗⃗⃗⃗⃗ |22，即|CA ⃗⃗⃗⃗⃗ |2⋅cos∠ACB =|AD |22∴cos∠ACB =12，∴△ACB 为正三角形，又△ABC 的高为√3， ∴|AB |=2 ∴T =2×2=4， ∴即2π12ω=4πω=4，∴ω=π， 故选：C ．7、某人先向东走3km ，位移记为a →，接着再向北走3km ，位移记为b →，则a →+b →表示（ ） A ．向东南走3√2km B ．向东北走3√2km C ．向东南走3√3km D ．向东北走3√3km 答案：B分析：由向量的加法进行求解.由题意和向量的加法，得a →+b →表示先向东走3km ，再向北走3km，即向东北走3√2km.故选：B.8、在锐角△ABC中，角A，B，C的对边分别为a，b，c，S为△ABC的面积，且2S=a2−(b−c)2，则2b2+c2bc 的取值范围为（）A．(4315,5915)B．[2√2,4315)C．[2√2,5915)D．[2√2,+∞)答案：C分析：根据余弦定理和△ABC的面积公式，结合题意求出sinA、cosA的值，再用C表示B，求出bc =sinBsinC的取值范围，即可求出2b2+c2bc的取值范围．解：在△ABC中，由余弦定理得a2=b2+c2−2bccosA，且△ABC的面积S=12bcsinA，由2S=a2−(b−c)2，得bcsinA=2bc−2bccosA，化简得sinA+2cosA=2，又A∈(0,π2)，sin2A+cos2A=1，联立得5sin2A−4sinA=0，解得或sinA=0（舍去），所以bc =sinBsinC=sin(A+C)sinC=sinAcosC+cosAsinCsinC=45tanC+35，因为△ABC为锐角三角形，所以0<C<π2，B=π−A−C<π2，所以π2−A<C<π2，所以tanC>tan(π2−A)=1tanA=34，所以1tanC∈(0,43)，所以bc∈(35,53)，设bc =t，其中t∈(35,53)，所以2b2+c2bc=2bc+cb=2t+1t=2(t+12t)，由对勾函数单调性知y=2t+1t 在(35,√22)上单调递减，在(√22,53)上单调递增，当t=√22时，y=2√2；当t=35时，y=4315；当t=53时，y=5915；所以y∈[2√2,5915)，即2b2+c2bc的取值范围是[2√2,5915)．故选：C.小提示：关键点点睛：由2b2+c2bc =2bc+cb，所以本题的解题关键点是根据已知及bc=sinBsinC=sin(A+C)sinC=4 sin5AsinAcosC+cosAsinCsinC=45tanC+35求出bc的取值范围.多选题9、等边三角形ABC 中，BD →=DC →,EC →=2AE →，AD 与BE 交于F ，则下列结论正确的是（ ） A ．AD →=12(AB →+AC →)B ．BE →=23BC →+13BA →C ．AF →=12AD →D ．BF →=12BA →+13BC →答案：AC分析：可画出图形，根据条件可得出D 为边BC 的中点，从而得出选项A 正确； 由EC →=2AE →可得出AE →=13AC →，进而可得出BE →=13BC →+23BA →，从而得出选择B 错误；可设AF →=12AD →，进而得出AF →=λ2AB →+3λ2AE →，从而得出λ=12，进而得出选项C 正确；由AF →=12AD →即可得出BF →=12BA →+14BC →，从而得出选项D 错误． 如图，∵BD →=DC →，∴D 为BC 的中点，∴AD →=12(AB →+AC →)，∴A 正确； ∵EC →=2AE →，∴AE →=13AC →=13(BC →−BA →)，∴BE →=BA →+AE →=BA →+13(BC →−BA →)=13BC →+23BA →，∴ B 错误；设AF →=λAD →=λ2AB →+λ2AC →=λ2AB →+3λ2AE →，且B ，F ，E 三点共线，∴λ2+3λ2=1，解得λ=12，∴AF →=12AD →，∴C 正确；BF →=BA →+AF →=BA →+12AD →=BA →+12(BD →−BA →)=BA →+14BC →−12BA →=12BA →+14BC →，∴D 错误. 故选：AC10、已知△ABC 是边长为2的等边三角形，D ，E 分别是AC,AB 上的点，且AE ⃗⃗⃗⃗⃗ =EB ⃗⃗⃗⃗⃗ ，AD ⃗⃗⃗⃗⃗ =2DC ⃗⃗⃗⃗⃗ ，BD 与CE 交于点O ，则（ ）A ．OC ⃗⃗⃗⃗⃗ +EO ⃗⃗⃗⃗⃗ =0⃗B ．AB⃗⃗⃗⃗⃗ ⋅CE ⃗⃗⃗⃗⃗ =0 C ．|OA ⃗⃗⃗⃗⃗ +OB ⃗⃗⃗⃗⃗ +OC ⃗⃗⃗⃗⃗ +OD ⃗⃗⃗⃗⃗⃗ |=√3D ．ED ⃗⃗⃗⃗⃗ 在BC ⃗⃗⃗⃗⃗ 方向上的投影为76 答案：BD解析：可证明EO =CE ，结合平面向量线性运算法则可判断A ；由AB⃗⃗⃗⃗⃗ ⊥CE ⃗⃗⃗⃗⃗ 结合平面向量数量积的定义可判断B ；建立直角坐标系，由平面向量线性运算及模的坐标表示可判断C ；由投影的计算公式可判断D. 因为△ABC 是边长为2的等边三角形，AE⃗⃗⃗⃗⃗ =EB ⃗⃗⃗⃗⃗ ， 所以E 为AB 的中点，且CE ⊥AB ，以E 为原点如图建立直角坐标系，则E (0,0)，A (−1,0)，B (1,0)，C(0,√3)，由AD ⃗⃗⃗⃗⃗ =2DC ⃗⃗⃗⃗⃗ 可得AD ⃗⃗⃗⃗⃗ =23AC ⃗⃗⃗⃗⃗ =(23,2√33)，则D (−13,2√33)， 取BD 的中点G ，连接GE ，易得GE//AD 且GE =12AD =DC ， 所以△CDO ≌△EGO ，EO =CO ，则O (0,√32)， 对于A ，OC⃗⃗⃗⃗⃗ +EO ⃗⃗⃗⃗⃗ =EC ⃗⃗⃗⃗⃗ ≠0⃗ ，故A 错误；对于B ，由AB ⃗⃗⃗⃗⃗ ⊥CE ⃗⃗⃗⃗⃗ 可得AB⃗⃗⃗⃗⃗ ⋅CE ⃗⃗⃗⃗⃗ =0，故B 正确； 对于C ，OA ⃗⃗⃗⃗⃗ =(−1,−√32)，OB ⃗⃗⃗⃗⃗ =(1,−√32)，OC ⃗⃗⃗⃗⃗ =(0,√32)，OD ⃗⃗⃗⃗⃗⃗ =(−13,√36)， 所以OA⃗⃗⃗⃗⃗ +OB ⃗⃗⃗⃗⃗ +OC ⃗⃗⃗⃗⃗ +OD ⃗⃗⃗⃗⃗⃗ =(−13,−√33)，所以|OA ⃗⃗⃗⃗⃗ +OB⃗⃗⃗⃗⃗ +OC ⃗⃗⃗⃗⃗ +OD ⃗⃗⃗⃗⃗⃗ |=23，故C 错误； 对于D ，BC⃗⃗⃗⃗⃗ =(−1,√3)，ED ⃗⃗⃗⃗⃗ =(−13,2√33)， 所以ED ⃗⃗⃗⃗⃗ 在BC ⃗⃗⃗⃗⃗ 方向上的投影为BC ⃗⃗⃗⃗⃗ ⋅ED ⃗⃗⃗⃗⃗⃗ |BC⃗⃗⃗⃗⃗ |=13+22=76，故D 正确.故选：BD.小提示：关键点点睛：建立合理的平面直角坐标系是解题关键. 11、下列说法中错误的是（ ）. A ．若a //b ⃗ ，b ⃗ //c ，c //d ，则a //d B ．若|a |=|b ⃗ |且a //b ⃗ ，则a =b⃗ C ．若a ，b ⃗ 非零向量且|a +b ⃗ |=|a −b ⃗ |，则a ⊥b ⃗ D ．若a //b ⃗ ，则有且只有一个实数λ，使得a =λb ⃗ 答案：ABD分析：对于题中所给的条件与结论需要考虑周全，可以得出结论. A 选项，当b ⃗ ，c 中至少有一个0⃗ 时，a 与d 可能不平行，故A 错误； B 选项，由|a |=|b ⃗ |且a //b ⃗ ，可得a =b ⃗ 或a =−b⃗ ，故B 错误； C 选项，|a +b ⃗ |=|a −b ⃗ |，根据数量积规则，则两边平方化简可得a ⋅b ⃗ =0， ∴a ⊥b⃗ ，故C 正确； D 选项，根据向量共线基本定理可知当a ,b⃗ 都为非零向量时成立， a 为零向量时也成立(λ=0) ，若b ⃗ =0⃗ 时，λ 不存在，但b ⃗ //a （零向量与所有的向量共线），故D 错误； 故选：ABD.12、下列说法错误的是（ ）A ．若a //b ⃗ ，则存在唯一实数λ使得a =λb⃗ B ．两个非零向量a ，b ⃗ ，若|a −b ⃗ |=|a |+|b ⃗ |，则a 与b⃗ 共线且反向C ．已知a =(1,2)，b ⃗ =(1,1)，且a 与a +λb ⃗ 的夹角为锐角，则实数λ的取值范围是(−53,+∞) D ．在△ABC 中，BC ⃗⃗⃗⃗⃗ ⋅CA ⃗⃗⃗⃗⃗ =CA ⃗⃗⃗⃗⃗ ⋅AB ⃗⃗⃗⃗⃗ ，则△ABC 为等腰三角形 答案：AC分析：若a =b ⃗ =0⃗ 可判断A ；将已知条件两边平方再进行数量积运算可判断B ；求出a +λb ⃗ 的坐标，根据a ⋅(a +λb ⃗ )>0且a 与a +λb ⃗ 不共线求出λ的取值范围可判断C ；取AC 的中点D ，根据向量的线性运算可得CA ⃗⃗⃗⃗⃗ ⋅BD⃗⃗⃗⃗⃗⃗ =0可判断D ，进而可得正确选项. 对于A ：若a =b ⃗ =0⃗ 满足a //b⃗ ，则实数λ不唯一，故选项A 错误； 对于B ：两个非零向量a ，b ⃗ ，若|a −b ⃗ |=|a |+|b ⃗ |，则(a −b ⃗ )2=(|a |+|b⃗ |)2， 所以a 2+b ⃗ 2−2a ⋅b ⃗ =|a |2+|b ⃗ |2+2|a ||b ⃗ |，可得2a ⋅b ⃗ =2|a ||b ⃗ |⋅cos 〈a ⋅b ⃗ 〉=−2|a ||b ⃗ |，cos 〈a ⋅b ⃗ 〉=−1，因为0≤〈a ⋅b ⃗ 〉≤π，所以〈a ⋅b ⃗ 〉=π，所以a 与b⃗ 共线且反向，故选项B 正确； 对于C ：已知a =(1,2)，b ⃗ =(1,1)，所以a +λb ⃗ =(1+λ,2+λ)，若a 与a +λb ⃗ 的夹角为锐角，则a ⋅(a +λb ⃗ )=1+λ+2(2+λ)>0，解得：λ>−53，当λ=0时，a +λb ⃗ =a ，此时a 与a +λb ⃗ 的夹角为0，不符合题意，所以λ≠0，所以λ的取值范围是(−53,0)∪(0,+∞)，故选项C 不正确；对于D ：在△ABC 中，取AC 的中点D ，由BC⃗⃗⃗⃗⃗ ⋅CA ⃗⃗⃗⃗⃗ =CA ⃗⃗⃗⃗⃗ ⋅AB ⃗⃗⃗⃗⃗ ，得CA ⃗⃗⃗⃗⃗ ⋅(BC ⃗⃗⃗⃗⃗ −AB ⃗⃗⃗⃗⃗ )=CA ⃗⃗⃗⃗⃗ ⋅(BC ⃗⃗⃗⃗⃗ +BA ⃗⃗⃗⃗⃗ )=CA ⃗⃗⃗⃗⃗ ⋅2BD ⃗⃗⃗⃗⃗⃗ =0，故BD 垂直平分AC ，所以△ABC 为等腰三角形，故选项D 正确． 故选：AC ．13、有下列说法，其中错误的说法为 A ．若a //b ⃗ ,b ⃗ //c ，则a //cB ．若2OA ⃗⃗⃗⃗⃗ +OB ⃗⃗⃗⃗⃗ +3OC ⃗⃗⃗⃗⃗ =0，S ΔAOC ，S ΔABC 分别表示ΔAOC ，ΔABC 的面积，则S ΔAOC :S ΔABC =1:6 C ．两个非零向量a ，b ⃗ ，若|a −b ⃗ |=|a |+|b ⃗ |，则a 与b ⃗ 共线且反向D ．若a //b ⃗ ，则存在唯一实数λ使得a =λb ⃗ 答案：AD分析：对每一个选项逐一分析判断得解.A. 若a //b ⃗ ,b ⃗ //c ，则a //c ，如果a ，c 都是非零向量，b ⃗ =0⃗ ，显然满足已知条件，但是结论不一定成立，所以该选项是错误的；B. 如图，D,E 分别是AC,BC 的中点，2OA ⃗⃗⃗⃗⃗ +OB ⃗⃗⃗⃗⃗ +3OC ⃗⃗⃗⃗⃗ =0⃗ ，∴2（OA ⃗⃗⃗⃗⃗ +OC ⃗⃗⃗⃗⃗ ）+（OB ⃗⃗⃗⃗⃗ +OC ⃗⃗⃗⃗⃗ ）=0⃗ ，∴4OD ⃗⃗⃗⃗⃗⃗ +2OE ⃗⃗⃗⃗⃗ =0⃗ ,∴OE ⃗⃗⃗⃗⃗ =−2OD ⃗⃗⃗⃗⃗⃗ ， 所以OD =16AB,则S ΔAOC :S ΔABC =1:6,所以该选项是正确的；C. 两个非零向量a ，b ⃗ ，若|a −b ⃗ |=|a |+|b ⃗ |，则a 与b ⃗ 共线且反向，所以该选项是正确的；D. 若a //b ⃗ ，如果a 是非零向量，b ⃗ =0⃗ ，则不存在实数λ使得a =λb ⃗ ，所以该选项是错误的. 故选A,D小提示：本题主要考查平面向量的运算，考查向量的平行及性质，意在考查学生对这些知识的理解掌握水平，属于基础题. 填空题14、已知P ，Q 分别是四边形ABCD 的对角线AC 与BD 的中点，BC ⃗⃗⃗⃗⃗ =a ,DA ⃗⃗⃗⃗⃗ =b ⃗ ，且a ,b ⃗ 是不共线的向量，则向量PQ⃗⃗⃗⃗⃗ =___________. 答案：−12a −12b⃗ 分析：取AB 的中点E ，连接PE,QE ，然后利用向量的加法法则和三角形中位线定理求解. 如图，取AB 的中点E ，连接PE,QE ，因为P ，Q 分别是四边形ABCD 的对角线AC 与BD 的中点，BC ⃗⃗⃗⃗⃗ =a ,DA ⃗⃗⃗⃗⃗ =b⃗ 所以PE ⃗⃗⃗⃗⃗ =12CB ⃗⃗⃗⃗⃗ =−12a ,EQ ⃗⃗⃗⃗⃗ =12AD ⃗⃗⃗⃗⃗ =−12b ⃗ ， 所以PQ ⃗⃗⃗⃗⃗ =PE ⃗⃗⃗⃗⃗ +EQ ⃗⃗⃗⃗⃗ =12CB ⃗⃗⃗⃗⃗ +12AD ⃗⃗⃗⃗⃗ =−12a −12b⃗ .所以答案是：−12a−12b⃗15、在△ABC中，若a=2，c=2√3,cosC=−12，M是BC的中点，则AM的长为____________．答案：√7分析：在△ABC中，由余弦定理求出b=2，进而，在△AMC中，由余弦定理可得AM.在△ABC中，由余弦定理c2=b2+a2−2abcosC得b2+2b−8=0，又b>0，所以b=2.在△AMC中，CA=b=2，CM=a2=1，由余弦定理得AM2=CA2+CM2−2CA⋅CM⋅cosC=22+12−2×2×1×(−12)=7，所以AM=√7.所以答案是：√7.16、在△ABC中，cos∠BAC=−13，AC＝2，D是边BC上的点，且BD＝2DC，AD＝DC，则AB等于 ___．答案：3分析：运用余弦定理，通过解方程组进行求解即可.设DC=x,AB=y，因为BD＝2DC，AD＝DC，所以BC=3x,AD=DC=x，在△ADC中，由余弦定理可知：cosC=AC2+CD2−AD22AC⋅DC =4+x2−x24x=1x，在△ABC中，由余弦定理可知：cosC=AC2+CB2−AB22AC⋅BC =4+9x2−y212x，于是有4+9x2−y212x =1x⇒9x2−y2=8(1)，在△ABC中，由余弦定理可知：cosA=AB2+CA2−CB22AB⋅AC =y2+4−9x24y=−13，⇒27x2−3y2−4y=12(2)，把(1)代入(2)中得，y=3，所以答案是：3解答题17、记△ABC的内角A，B，C的对边分别为a，b，c﹐已知sinCsin(A−B)=sinBsin(C−A)．(1)若A=2B，求C；(2)证明：2a2=b2+c2答案：(1)5π8；(2)证明见解析．分析：（1）根据题意可得，sinC=sin(C−A)，再结合三角形内角和定理即可解出；（2）由题意利用两角差的正弦公式展开得sinC(sinAcosB−cosAsinB)=sinB(sinCcosA−cosCsinA)，再根据正弦定理，余弦定理化简即可证出．（1）由A=2B，sinCsin(A−B)=sinBsin(C−A)可得，sinCsinB=sinBsin(C−A)，而0<B<π2，所以sinB∈(0,1)，即有sinC=sin(C−A)>0，而0<C<π,0<C−A<π，显然C≠C−A，所以，C+C−A=π，而A=2B，A+B+C=π，所以C=5π8．（2）由sinCsin(A−B)=sinBsin(C−A)可得，sinC(sinAcosB−cosAsinB)=sinB(sinCcosA−cosCsinA)，再由正弦定理可得，accosB−bccosA=bccosA−abcosC，然后根据余弦定理可知，1 2(a2+c2−b2)−12(b2+c2−a2)=12(b2+c2−a2)−12(a2+b2−c2)，化简得：2a2=b2+c2，故原等式成立．18、如图，有一景区的平面图是一个半圆形，其中O为圆心，直径AB的长为2km，C，D两点在半圆弧上，且BC=CD，设∠COB=θ；（1）当θ=π12时，求四边形ABCD的面积.（2）若要在景区内铺设一条由线段AB，BC，CD和DA组成的观光道路，则当θ为何值时，观光道路的总长l 最长，并求出l的最大值.答案：（1）√6−√24+14；（2）5分析：（1）把四边形ABCD分解为三个等腰三角形：△COB,△COD,△DOA，利用三角形的面积公式即得解；（2）利用θ表示（1）中三个等腰三角形的顶角，利用正弦定理分别表示BC，CD和DA，令t=sinθ2，转化为二次函数的最值问题，即得解.（1）连结，则∠COD=π12,∠AOD=5π6∴四边形ABCD的面积为2×12×1×1×sinπ12+12×1×1×sin5π6=√6−√24+14（2）由题意，在△BOC中，∠OBC=π−θ2，由正弦定理BC sinθ=OBsin(π−θ2)=1cosθ2∴BC=CD=sinθcosθ2=2sinθ2同理在△AOD中，∠OAD=θ,∠DOA=π−2θ，由正弦定理DAsin(π−2θ)=ODsinθ∴DA=sin2θsinθ=2cosθ∴l=2+4sin θ2+2cosθ=2+4sinθ2+2(1−2sin2θ2),0<θ<π2OD令t =sin θ2(0<t <√22) ∴l =2+4t +2(1−2t 2)=4+4t −4t 2=−4(t −12)2+5 ∴t =12时，即θ=π3，l 的最大值为5 小提示：本题考查了三角函数和解三角形综合实际应用问题，考查了学生综合分析，数学建模，转化划归，数学运算能力，属于较难题。

第13讲平面向量十大题型总结【题型目录】题型一：平面向量线性运算题型二：平面向量共线问题题型三：平面向量垂直问题题型四：平面向量的夹角问题题型五：平面向量数量积的计算题型六：平面向量的模问题题型七：平面向量的投影问题题型八：万能建系法解决向量问题题型九：平面向量中的最值范围问题题型十：平面向量中多选题【典型例题】题型一：平面向量线性运算【例1】在ABC △中，D 是AB 边上的中点，则CB =（）A ．2CD CA+ B ．2CD CA- C ．2CD CA- D ．2CD CA+ 【答案】C【解析】：CA CD AC CD CD AC CD AD CD DB CD CB -=+=++=+=+=22【例2】在△ABC 中，AD 为BC 边上的中线，E 为AD 的中点，则EB =A ．3144AB AC-B ．1344AB AC-C ．3144+AB AC D ．1344+AB AC 【答案】A【解析】根据向量的运算法则，可得()111111222424BE BA BD BA BC BA BA AC=+=+=++ 1113124444BA BA AC BA AC=++=+，所以3144EB AB AC =-，故选A.【例3】在ABC 中，点P 为AC 中点，点D 在BC 上，且3BD DC = ，则DP =()A ．1144AB AC+B ．1144AB AC--C ．1144AB AC-D ．1144AB AC-+【答案】B【解析】∵点P 为AC 中点，∴12AP AC = ,∵3BD DC =，()3AD AB AC AD ∴-=- ,∴1344AD AB AC =+ ,∴113244DP AP AD AC AB AC =-=-- =1144AB AC --,故选：B.【例4】在ABC 中，AD 为BC 边上的中线，E 为AD 的中点，且EB AB AC λμ=+，则λ=________，μ=_________．【答案】3414-【解析】如下图所示：D Q 为BC 的中点，则()()111222AD AB BD AB BC AB AC AB AB AC =+=+=+-=+，E 为AD 的中点，所以，()1124AE AD AB AC ==+，因此，()131444EB AB AE AB AB AC AB AC =-=-+=- ，即34λ=，14μ=-.故答案为：34；14-.【例5】如图，等腰梯形ABCD 中，3AB BC CD AD ===，点E 为线段CD 中点，点F 为线段BC 的中点，则FE =（）A ．2136AB AC+B ．2136AB AC-+C ．1263AB AC+D ．1263AB AC-+点F 为线段BC 的中点，13BD BA AD BA BC BA =+=+=+ 又2BD FE = ，2136FE AB AC ∴=-+.【题型专练】1.设,,D E F 分别为ABC 的三边BC,CA,AB 的中点，则EB FC +=()A ．ADB ．12ADC ．12BCD ．BC【答案】A【解析】111()()()222EB FC BA BC CA CB AB AC AD +=-+-+=+=，故选：A2.设D为△ABC所在平面内的一点,若3,AD BD CD CA CBλμ==+,则μλ=_____.【答案】3-【解析】如图所示：3CD CA AD CA BD=+=+，CA=+3(CD CB-)，即有CD=﹣1322CA CB+，因为CD CA CBλμ=+，所以λ=﹣12，μ=32，则μλ=﹣3，故答案为：﹣3.3.在ABC中，4AC AD=，P为BD上一点，若13AP AB ACλ=+，则实数λ的值（）A．18B．316C．16D．38【答案】C【解析】4AC AD=，14AD AC∴=，则14BD AD AB AC AB=-=-，1233BP AP AB AB AC AB AC ABλλ⎛⎫=-=+-=-⎪⎝⎭，由于P为BD上一点，则//BP BD，设BP k BD=，则21344kAC AB k AC AB AC k ABλ⎛⎫-=-=-⎪⎝⎭，所以423kkλ⎧=⎪⎪⎨⎪=⎪⎩，解得16λ=.4.在ABC 中，2AB =，4BC =，60ABC ∠=︒，AD 为BC 边上的高，O 为AD 的中点，若AO AB BC λμ=+，则λμ+=（）A ．13B ．23C ．38D ．58【答案】D【解析】AD 是BC 边上的高，∴90ADB ∠=︒，在ADB △中，1cos 22BD BD ABD AB ∠===，解得1BD =， 4BC =，∴14BD BC =，∴14AD AB BD AB BC =+=+， O 为AD 中点，∴1111122428AO AD AB BC AB BC ⎛⎫==+=+ ⎪⎝⎭ ， AO AB BC λμ=+ ，∴1128AB BC AB BC λμ+=+ ，∴12λ=，18μ=，∴115288λμ+=+=.5.已知O 是ABC 所在平面内一点，D 为BC 边中点，且20OA OB OC ++=，那么（）A ．AO OD =B ．2AO OD=C ．3AO OD=D ．4AO OD =【答案】A【解析】D 为BC 边中点，∴2OB OC OD +=，∵20OA OB OC ++=，∴0OA OD =+，即AO OD =.6．设D 为ABC 所在平面内一点，且满足3CD BD =，则（）A ．3122AD AB AC =-B ．3122=+AD AB ACC ．4133AD AB AC =-D ．4133AD AB AC=+ ∴2CB BD =，即12BD CB = .()12123122AD AB BD ABCBAB AB ACAB AC ∴=+=+=+-=- 故选：A.题型二：平面向量共线问题【例1】已知向量()1,2a =- ，()sin ,cos b αα= ，若//a b，则tan α=（）A ．12-B ．2-C ．12D ．2【例2】与模长为13的向量()12,5d =平行的单位向量为（）A ．1251313⎛⎫ ⎪⎝⎭，B ．1251313⎛⎫-- ⎪⎝⎭，C ．1251313⎛⎫ ⎪，或1251313⎛⎫-- ⎪，D ．1251313⎛⎫- ⎪，或1251313⎛⎫- ⎪，【例3】已知向量()1,2AB =，(),7BC m =，()3,1CD =-，若A ，B ，D 三点共线，则m =________．【例4】设向量,a b 不平行，向量λ+a b 与2+a b 平行，则实数λ=___．【答案】21【解析】因向量λ+a b 与2+a b 平行，所以()b a b a ba μμμλ22+=+=+，所以⎩⎨⎧==μμλ21，解得⎪⎩⎪⎨⎧==2121μλ【例5】在ABC ∆中，点P 满足3BP PC = ，过点P 的直线与AB 、AC 所在的直线分别交于点M 、N ，若AM AB λ= ，()0,0AN AC μλμ=>>，则λμ+的最小值为（）A ．212+B ．12+C ．32D ．52【答案】B【解析】如下图所示：3BP PC = ，即()3AP AB AC AP -=- ，1344AP AB AC∴=+ ，AM AB λ= ，()0,0AN AC μλμ=>> ，1AB AM λ∴=，1AC ANμ= ，1344AP AM ANλμ∴=+ ，M 、P 、N 三点共线，则13144λμ+=.()133********λμλμλμλμμλ⎛⎫∴+=++=++≥=+ ⎪⎝⎭，当且仅当μ=时，等号成立，因此，λμ+的最小值为312+，故选：B.【题型专练】1.已知非零向量a ，b ，c ，若(1)a x = ，，(41)b =- ，，且//a c ，//b c则x =（）A ．4B ．4-C ．14D ．14-【答案】D【解析】：因非零向量c b a ,,，且//a c ，//b c ，所以a 与b 共线，所以()x 411=-⨯，所以41-=x 2.已知向量的(7,6)AB =，(3,)BC m =- ，(1,2)AD m =- ，若A ，C ，D 三点共线，则m =______.3.已知向量a ，b 是两个不共线的向量，且35OA a b =+，47OB a b =+，OC a mb =+，若A ，B ，C 三点共线，则m =（）A ．1B ．1-C ．2D ．2-【答案】A【解析】法一：b a b a b a OB AO AB 27453+=++--=+=，()b m a b m a b a OC BO BC 7374-+-=++--=+=，因A ，B ，C 三点共线，所以AB 与BC 共线，所以()[]()b m a b m a b a 73732-+-=-+-=+λλλ，所以()⎩⎨⎧-=-=7231m λλ，解得⎪⎩⎪⎨⎧=-=131m λ法二：由,,A B C 三点共线，得(1)(4)(72)OC xOA x OB x a x b =+-=-+-，故41,72,x x m -=⎧⎨-=⎩解得1m =．4.设12e e，是两个不共线的向量，若向量12m e ke =-+（k ∈R ）与向量212n e e =-共线，则A ．0k =B ．1k =C ．2k =D ．12k =【答案】D【解析】因为向量12=-+ m e ke （k ∈R ）与向量212=-n e e 共线，所以存在实数λ，使得λ=m n ，所以有2211(2)λ-+=- e ke e e ，因此12k λλ=⎧⎨-=-⎩，解得12k =.5.如图，在ABC 中，点O 是BC 的中点，过点O 的直线分别交直线AB ，AC 于不同的两点M N ，，若AB mAM = ，AC nAN =，则m n +=（）A ．1B ．32C ．2D ．3【答案】C【解析】连接AO ，由O 为BC 中点可得，1()222m n AO AB AC AM AN =+=+，M 、O 、N 三点共线，122m n∴+=，2m n ∴+=.故选：C.6.已知M 为ABC 的边AB 的中点，N 为ABC 内一点，且13AN AM BC =+ ，则AMNBCNS S =△△（）A ．16B ．13C ．12D ．23【答案】B【解析】因为13AN AM BC =+，所以13MN BC = ，所以MN ∥BC ，又因为M 为边AB 的中点，所以点A 到MN 的距离等于点N 到BC 的距离，所以13AMNBCNMN S S BC== △△,题型三：平面向量垂直问题【例1】已知向量(1)(32)m =-，，=，a b ，且()+⊥a b b ，则m =（）A ．8-B ．6-C ．6D ．8【答案】D【解析】：()()()2,42,3,1-=-+=+m m b a ，因()b b a ⊥+，所以()0=⋅+b b a ，即()()()022122,32,4=--=--m m ，所以8=m 【例2】已知单位向量a ，b 的夹角为45°，ka –b 与a 垂直，则k =__________.【答案】22【解析】由题意可得：11cos 452a b →→⋅=⨯⨯=，由向量垂直的充分必要条件可得：0k a b a →→→⎛⎫-⋅= ⎪⎝⎭，即：202k a a b k →→→⨯-⋅=-=，解得：22k =.【例3】已知单位向量,a b 的夹角为60°，则在下列向量中，与b 垂直的是（）A ．b a 2+B ．ba +2C ．ba 2-D ．ba -2【答案】D【思路导引】根据平面向量数量积的定义、运算性质，结合两平面向量垂直数量积为零这一性质逐一判断即可．【解析】由已知可得：11cos 601122⋅=︒=⨯⨯=a b a b ．A ：∵215(2)221022+⋅=⋅+=+⨯=≠a b b a b b ，∴本选项不符合题意；B ：∵21(2)221202+⋅=⋅+=⨯+=≠a b b a b b ，∴本选项不符合题意；C ：∵213(2)221022-⋅=⋅-=-⨯=-≠a b b a b b ，∴本选项不符合题意；D ：∵21(2)22102-⋅=⋅-=⨯-=b b b a b b ，∴本选项符合题意．故选D ．【例4】已知向量(2,1),(3,)a b m →→=-=，且()a b a →→→+⊥，则实数m =___________.【答案】1【分析】先求出+=(1,1)a b m →→+，再解方程1(2)1(1)0m ⨯-+⨯+=即得解.【详解】解：由题得+=(1,1)a b m →→+，因为()a b a →→→+⊥，所以()=0a b a →→→+g ，所以1(2)1(1)0,1m m ⨯-+⨯+=∴=.故答案为：1【例5】已知非零向量m,n 满足4|3|=m |n |，1cos ,3<>=m n ．若()t ⊥+n m n ，则实数t 的值为（）A ．4B ．–4C ．94D ．–94【答案】B 【解析】由()t ⊥+n m n 可得()0t ⋅+=n m n ，即20t ⋅+=m n n ，所以2221|cos |3||t |||<,>|||=-=-=-⋅⋅⨯⨯n n n m n m n m n m n ||4334||3=-=-⨯=-n m ．故选B ．【例6】已知向量AB 与AC 的夹角120，且|AB |=3，|AC |=2，若AP AB AC λ=+ ，且AP BC ⊥ ，则实数λ的值为_____．【答案】712【解析】向量与的夹角为，且所以．由得，，即，所以，即，解得．【题型专练】1.ΑΒC ∆是边长为2的等边三角形，已知向量a ，b 满足2ΑΒ= a ，2ΑC =+a b ，则下列结论正确的是（）A ．1=b B ．⊥a bC ．1⋅=a b D ．()4ΒC-⊥a b 【答案】D【解析】如图由题意，(2)2BC AC AB a b a b =-=+-= ，故||2b = ，故A 错误；|2|2||2a a ==，所以||1a = ，又22(2)4||222cos 602AB AC a a b a ab ⋅=⋅+=+=⨯=，所以1a b ⋅=- ，故,B C 错误；设,B C 中点为D ，则2AB AC AD += ，且AD BC ⊥ ，所以()4C a b +⊥B ，故选D ．2.已知1e ，2e 12-e 与12λ+e e 的夹角为60 ，则实数λ的值是．【答案】33【解析】解法一：因1e ，2e 11==，021=⋅e e所以221212112122)()λλλ-⋅+=+⋅-⋅-=-e e e e e e e e ，12|2-=e ，12||λ+===e e ，2cos60λ==，解得：33λ=．解法二：建立坐标系，设()()1,0,0,121==e e ()()λλ,1,1,3212=+-=-e e e ，所以()()2221213λ+=+=-+=)()λλ-=+-3212e e e所以由数量积的定义得︒⨯+⨯=-60cos 1232λλ，解得：33λ=．3.已知向量()(),2,1,1a m b ==，若()a b b +⊥ ，则m =__________.【答案】4-【分析】根据向量的坐标运算即可求解.【详解】由题意可得()1,3a b m +=+，则130m ++=，解得4m =-.故答案为：4-4.已知向量(,2),(2,4)m a a n a =+=- ，且()n m n ⊥-，则实数=a _____________．【答案】2【分析】根据向量坐标运算及向量垂直的坐标表示即得.【详解】因为(,2)(2,4)(2,2)m n a a a a -=+--=-，又()n m n ⊥- ，所以2(2)(2)40a a ⨯-+-⨯=，解得2a =．故答案为：2.5.在ABC 中，()1,2,3A k -，()2,1,0B -，()2,3,1C -，若ABC 为直角三角形，则k 的值为（）A ．23B ．83C ．－1D ．325-题型四：平面向量的夹角问题【例1】已知平面向量a ，b满足||4,||1== a b ，()a b b -⊥ ，则cos ,a b 〈〉= （）A ．14B ．4C．4D ．4【例2】已知(2,0)a = ，1,22b ⎛= ⎝⎭r ，则a b - 与12a b + 的夹角等于（）A ．150°B ．90°C ．60°D ．30°【例3】已知向量a=（2，1），()3,1b =- ，则（）A．若c =-⎝⎭ ，则a c ⊥B ．向量a 在向量b 上的投影向量为12b-C ．a 与a b -D ．()//a b a+【例4】若向量a ，b 满足||a = ，(2,1)b =-，5a b ⋅=- ，则a 与b 的夹角为_________．【例5】已知向量a b ，满足566a b a b ==⋅=-，，，则cos ,a a b +=()A ．3135-B ．1935-C ．1735D ．1935【例6】若非零向量,a b 满足32a b a b ==+，则a 与b 夹角的余弦值为________．【例7】设向量(68)=-，a ，(34)=，b ，t =+c a b，t ∈R ，若c 平分a与b 的夹角，则t 的值为．【答案】2【解析】解法一：()t t b t a c 48,36++-=+=，所以()()t t t c a 14100488366+=+++--=⋅；()()1425484363+=+++-=⋅t t t c b 510==因c 平分a 与b 的夹角，所以=c b c a ==，所以()1425214100+=+t t ，解得2=t解法二：因c 平分a 与b的夹角，所以()()⎪⎭⎫⎝⎛=⎪⎭⎫ ⎝⎛+-=⎫⎛=58,054,3108,6λλλb a c ，又因()t t b t a c 48,36++-=+=，所以()()t t 3658480+-=+⨯，解得2=t 【例8】已知A B C △的三个顶点分别为(3(60)(5A B C ，，，，，求ACB ∠的大小．【答案】C【解析】()()3,1,0,2=-=CB CA()()()2312022222=+==+-=所以21223012cos -=⨯⨯+⨯-==∠CB CA ACB ，所以︒=∠120ACB 【题型专练】1.设非零向量、ab满足||2||,||||a b a b b =+= ，则向量a 与b的夹角为（）A ．30°B ．60︒C ．120︒D ．150︒2.已知(2,1)a =-，||b =，且()10a b a +⋅= ，则,a b 〈〉= ___________.3.已知向量,a b 满足||1a =，||a b =+1)b =- ，则,a b 的夹角等于___________.4.若两个非零向量a 、b 满足2a b a b a +=-=，则a b - 与b 的夹角___________.5.已知单位向量a ，b 满足0a b ⋅=，若向量c =+，则sin ,a c ＝（）A B C D6.已知向量,a b 满足()()3,4,·28a b a b a b ==+-=，则向量a 与b 所成的夹角为（）A ．π6B ．π3C ．π2D ．2π37.已知向量a ，b 满足||2||2b a == ，|2|2a b -= ，则向量a ，b 的夹角为（）A ．30°B ．45︒C ．60︒D ．90︒8.已知向量()PA =，(1,PB =，则APB ∠=A ．30︒B ．60︒C ．120︒D ．150︒【答案】D【解析】根据题意，可以求得2,2PA PB ===，所以333cos 222PA PB APB PA PB⋅∠===-⋅，结合向量所成角的范围，可以求得150APB ∠=︒，故选D ．9.非零向量a ，b 满足：-=a b a ，()0⋅-=a a b ，则-a b 与b 夹角的大小为A ．135︒B ．120︒C ．60︒D ．45︒【答案】A【解析】 非零向量a ，b 满足()0⋅-=a a b ，∴2=⋅a a b，由-=a b a 可得2222-⋅+=a a b b a，解得=b ，()22cos 2θ-⋅⋅-∴===--a b ba b b a b ba b，θ为-a b 与b 的夹角，135θ∴= ，故选A ．10.已知a ，b 为单位向量，且a ·b =0，若2=c a ，则cos,=a c ___________.【答案】23【解析】因为2=c a，0⋅=a b ，所以22⋅=⋅a c a b 2=，222||4||5||9=-⋅+=c a b b ，所以||3=c ，所以cos ,=a c 22133⋅==⨯⋅a c a c ．11.已知向量(4,3),(1,2)a b =-=-，,a b的夹角为θ，则sin θ=__________.【答案】55【解析】依题意[]0,πθ∈，所以255cos ,sin 55||||a b a b θθ⋅===-== .故答案为.12.已知向量,a b 满足5,6,6==⋅=-a b a b ，则cos ,+=a a b （）A ．3531-B ．3519-C ．3517D ．3519【答案】D【思路导引】计算出()a ab ⋅+ 、a b + 的值，利用平面向量数量积可计算出cos ,a a b <+>的值．【解析】5a = ，6b = ，6a b ⋅=- ，()225619a a b a a b ∴⋅+=+⋅=-= ．7a b +== ，因此()1919cos ,5735a ab a a b a a b ⋅+<+>===⨯⋅+ ．故选D ．题型五：平面向量数量积的计算【例1】（2021新高考2卷）已知向量0,||1,||||2,a b c a b c a b b c c a ++====⋅+⋅+⋅=_______．【答案】29-【解析】方法一：因为0=++c b a ，所以()02=++cb a ，即0222222=+++++c b c a b a c b a所以0222441=+++++c b c a b a ，所以9222-=++c b c a b a ，所以29-=++c b c a b a 方法二：因为0=++c b a ，所以c b a -=+，所以()()22c b a -=+，即2222cb a b a=++所以4241=++b a ，所以21-=b a ，同理b c a -=+，所以()()22b ca -=+，即2222b c a c a =++，所以4241=++c a ，所以21-=c a ，同理a c b -=+，所以()()22a c b -=+，即2222a c b c b =++，所以1244=++c b ，所以27-=⋅c b ，所以29-=++c b c a b a 【例2】在△ABC 中，6,AB O =为△ABC 的外心，则AO AB ⋅等于A B ．6C ．12D ．18【答案】D【解析】试题分析：如图，过点O 作OD AB ⊥于D ，则()36018AO AB AD DO AB AD AB DO AB ⋅=+⋅=⋅+⋅=⨯+=，应选D.【例3】已知边长为3的正2ABC BD DC = ，，则AB AD ⋅=（）A ．3B ．9C ．152D ．6【例4】已知ABC 为等边三角形，AB =2，设点P ，Q 满足AP AB λ=，(1)AQ AC λ=-，R λ∈，若2BQ CP ⋅=-，则λ=（）A ．12B ．12C ．12±D故选：A.【例5】在ABC 中，6A π=，||AB =||4AC =，3BD BC =，则AB AD ⋅=______．【答案】24-【分析】利用基底,AB AC 3AD AB BD AB BC =+=+ ,BC AC = 23AD AB AC ∴=-+ ,∴()232AB A AB AD AB AB C =⋅-+=-⋅ 【题型专练】1.如图，在△ABC 中，AD ⊥AB ，BC =，1AD = ，则AC AD ⋅=（）A ．B CD ．3-2.在ABC 中，3AB AC ==，DC BD 2=﹒若4AD BC ⋅=，则AB AC ⋅=______．3.ABC 中，90C ∠=︒，2AC =，P 为线段BC 上任一点，则AP AC ⋅=（）A ．8B ．4C ．2D ．64.已知ABC 为等边三角形，D 为BC 的中点，3AB AD ⋅=，则BC =（）A BC ．2D ．45.如图，在ABC 中，3BAC ∠=，2AD DB =，P 为CD 上一点，且满足2AP mAC AB =+，若||3AC =，||4AB =，则AP CD ⋅的值为（）A ．-3B ．1312-C ．1312D ．1126．在平行四边形ABCD 中，AC ＝6，AB AD ⋅＝5，则BD ＝____________.【详解】AC AB BC AB AD =+=+ ，则2AC AB = 236226AD AB AD +=-⋅=，AD AB - ，则222BD AD AB AD =-⋅+ 7．已知在ABC 中，90C ∠=︒，4CA =，3CB =，D 为BC 的中点，2AE EB =，CE 交AD 于F ，则CE AD ⋅=_______【答案】73-##123-题型六：平面向量的模问题【例1】已知(1)t =，a ，(6)t =-，b ，则|2|+a b 的最小值为________．【答案】52【解析】：()()()40205362444462262,2222222+-=+-+++=-++=-+=+t t t t t t t t t t a对称轴2=t ，所以当2=t 时，524040202=+-=a 【例2】（2021新高考1卷）已知O 为坐标原点，点1(cos ,sin )P αα，2(cos ,sin )P ββ-，3(cos(),sin())P αβαβ++，(1,0)A ，则：A ．12||||OP OP = B ．12||||AP AP =C ．312OA OP OP OP ⋅=⋅D ．123OA OP OP OP ⋅=⋅ 【答案】AC 【解析】【详解】A ：1(cos ,sin )OP αα=，2(cos ,sin )OP ββ=- ，所以1||1OP == ，2||1OP == ，故12||||OP OP = ，正确；B ：1(cos 1,sin )AP αα=- ，2(cos 1,sin )AP ββ=-- ，所以1||2|sin |2AP α===== ，同理2||2|sin |2AP β== ，故12||,||AP AP 不一定相等，错误；C ：由题意得：31cos()0sin()cos()OA OP αβαβαβ⋅=⨯++⨯+=+，12cos cos sin (sin )cos()OP OP αβαβαβ⋅=⋅+⋅-=+ ，正确；D ：由题意得：11cos 0sin cos OA OP ααα⋅=⨯+⨯= ，23cos cos()(sin )sin()OP OP βαββαβ⋅=⨯++-⨯+()()()cos βαβcos α2β=++=+，故一般来说123OA OP OP OP ⋅≠⋅故错误；故选：AC【例3】已知向量a ，b 的夹角为60°，||2=a ，||1=b ，则|2|+a b =．【答案】324211244+⨯⨯⨯+====+3212==【例4】已知a 与b 均为单位向量，其中夹角为θ，有下列四个命题1p ：||1+>a b ⇔θ∈[0，23π）2p ：||1+>a b ⇔θ∈(23π，π]3p ：||1->a b ⇔θ∈[0，3π）4p ：||1->a b ⇔θ∈(3π，π]其中真命题是（A ）1p ，4p (B)1p ，3p (C)2p ，3p (D)3p ，4p 【答案】A【解析】由||1+>a b 得，221∙>a +2a b +b ，即∙a b ＞12-，即cos θ=||||∙a b a b ＞12-，∵θ∈[0，π]，∴θ∈[0，23π），由||1->a b 得，22-1∙>a 2a b +b ，即∙a b ＜12，即cos θ=||||∙a b a b ＜12，∵θ∈[0，π]，∴θ∈(3π，π]，故选A ．【例5】设a ，b 是两个非零向量A ．若||||||+=-a b a b ，则⊥a bB ．若⊥a b ，则||||||+=-a b a b C ．若||||||+=-a b a b ，则存在实数λ，使得λ=b a D ．若存在实数λ，使得λ=b a ，则||||||+=-a b a b 【答案】C【解析】对于A b b a a2222-=⇒+-=+⋅+⇒=θ，所以1cos -=θ，所以︒=180θ，所以A 错，B 错；C 对，D 有可能为︒0【题型专练】1．设向量(10)，a =，22()22=-b ，若t =+c a b (t ∈R)，则||c 的最小值为A B ．1C ．2D ．12【答案】C【解析】()⎪⎪⎭⎫ ⎝⎛-+=⎪⎪⎭⎫ ⎝⎛-+=+=t t t b t a c 22,22122,220,12222221⎪⎪⎭⎫ ⎝⎛-+⎪⎪⎭⎫ ⎝⎛+=t t 222122122121212222≥+⎪⎪⎭⎫ ⎝⎛+=++=+++=t t t t t t 2.已知向量(1,2)a =- ，(21,1)b m =- ，且a b ⊥，则|2|a b -= （）A ．5B ．4C ．3D ．23.已知向量a ，b满足1a =，2b =，a b -=，则2a b +=（）A ．B ．C D4.已知[02π)αβ∈、，，(cos ,sin )a αα=r，(cos(),sin())b αβαβ=++，且23a b -=，则β可能为（）A ．π3B ．2π3C ．πD ．4π3【答案】BD【分析】根据向量模的运算列方程，化简求得cos β的值，进而求得正确答案.5.平面向量a 与b 的夹角为60︒，(3,4),||1==a b ，则|2|a b += _____________．6.已知向量,a b 满足||2,(2,2)a b == ，且|2|6a b += ，则||a b += __________．7.设,a b 为单位向量，且||1+=a b ，则||a b -=______________.【解析】因为,a b为单位向量，所以1a b ==r r所以1a b +==，解得：21a b ⋅=-所以a b -==8.设a ，b 均为单位向量，则“33-=+a b a b ”是“a ⊥b ”的A ．充分而不必要条件B ．必要而不充分条件C ．充分必要条件D ．既不充分也不必要条件【答案】C【解析】∵33-=+a b a b ，∴22(3)(3)-=+a b a b ，∴2269-⋅+=a ab b 2296+⋅+a a b b ，又||||1==a b ，∴0⋅=a b ，∴⊥a b ；反之也成立，故选C ．9.已知向量a ，b 夹角为045，且|a |=1，|2-a b |b |=．【答案】．【解析】∵|2-a b |=平方得224410-= a a b +b ，即260--=|b |b |，解得|b |=（舍）题型七：平面向量的投影问题【例1】已知向量(2,1),(1,1)a b =-= ，则a 在b上的投影向量的模为（）A B ．12C ．2D ．1【例2】已知6a =，3b =，向量a 在b 方向上投影向量是4e ，则a b ⋅ 为（）A ．12B ．8C ．-8D ．2【例3】已知平面向量a ，b ，满足2a =，1b =，a 与b 的夹角为23π，2b 在a 方向上的投影向量为（）A ．1-B ．12aC ．12a - D ．1【例4】已知平面向量a ，b 满足2=a ，()1,1b =，a b +=r r a 在b 上的投影向量的坐标为（）A ．22⎛ ⎝⎭B ．()1,1C ．()1,1--D ．⎛ ⎝⎭【例5】已知O 为正三角形ABC 的中心，则向量OA 在向量AB 上的投影向量为（）A ．ABB C ．12AB-D ．12AB故选：C【例6】设向量a 在向量b 上的投影向量为m ，则下列等式一定成立的是（）A ．||a b m bb ⋅=⋅ B ．2||a b m bb ⋅=⋅ C ．m b a b⋅=⋅ D ．ma b a⋅=⋅【题型专练】1．已知()1,2a = ，()1,2b =- ，则a 在b上的投影向量为（）A ．36,55⎛⎫- ⎪B ．36,55⎛⎫- ⎪C ．36,55⎛⎫-- ⎪D ．36,55⎛⎫ ⎪2．如图，在平面四边形ABCD 中，120ABC BCD ∠=∠= ，AB CD =，则向量CD 在向量AB 上的投影向量为（）A ．2AB -B ．12AB -C ．12AB D ．2AB 【答案】B【分析】根据图形求出向量AB 与CD的夹角，再根据投影向量的公式进行求解即可.【详解】延长AB ，DC 交于点E ，如图所示，3.已知向量()1,3a =，()2,4b =-，则下列结论正确的是（）A ．()a b a+⊥r r r B ．2a b +=C ．向量a 与向量b 的夹角为34πD ．b 在a的投影向量是()1,34.已知()3,1a =-，()1,2b =，下列结论正确的是（）A ．与b同向共线的单位向量是⎝⎭B ．a 与bC ．向量a在向量b 上的投影向量为12,55⎛⎫ ⎪⎝⎭D ．15a b b⎛⎫-⊥ ⎪ 5.关于平面向量，有下列四个命题，其中说法正确的是（）A ．若1,,120a b a b ===︒，则()2a b a+⊥r r r B ．点()()1,1,3,2M N --，与向量MN同方向的单位向量为43,55⎛⎫- ⎪⎝⎭C ．若20a b a b a +=-=≠ ，则+r r a b 与a b - 的夹角为60°D ．若向量()()2,1,6,2a b =-= ，则向量b 在向量a 上的投影向量为2a-同方向的单位向量为6．己知空间向量||3,||2a b ==，且2a b ⋅=，则b 在a 上的投影向量为________．【答案】29a ##29a7.已知1a =，2b =，且()a ab ⊥+，则a 在b 上的投影向量为（）A ．b -B ．bC ．14b- D ．14b【答案】C 【详解】因为()a a b ⊥+ ，所以()0a a b ⋅+= ，即220,0a a b a a b +⋅=+⋅= ，又因为1a = ，设,a b 的夹角为θ，所以1a b ⋅=-，a 在b 上的投影为：cos b a b a θ⋅=⋅ ，所以a 在b 上的投影向量为214cos b a b b b ba b θ⋅⋅=⋅=⋅- .故选：C8.已知点(1,1)A -、(1,2)B 、(2,1)C --、(3,4)D ，则向量AB 在CD 方向上的投影为ABC．D．【答案】A【解析】AB =（2，1），CD =（5，5），则向量AB 在向量CD方向上的射影为22325515255)5,5()1,2(cos 22=⨯+⨯=+⋅==CD AB AB θ9.若向量,a b满足22a a b =+= ，则a 在b 方向上投影的最大值是AB．CD．【答案】B【详解】由题意2,22a a b =+= ，所以2||4164b a b +⋅+=，设,a b 的夹角为θ，则2||8cos 120b b θ++= ，所以212cos 8b bθ+=- ，所以a 在b 方向上投影为2123cos 2()(48b b a bb θ+=⨯-=-+，因为3b b +≥cos a θ≤ ，故选B.题型八：万能建系法解决向量问题边长为a 的等边三角形已知夹角的任意三角形正方形矩形平行四边形直角梯形等腰梯形圆建系必备（1）三角函数知识cos ,sin x r y r q q ==；（2）向量三点共线知识(1)OC OB OAl l =+-（对面女孩看过来）．【例1】如图，在等腰梯形ABCD 中，2,3,4AB BC CD BC BE ==== ，则CA DE ⋅=（）A ．43B ．154-C ．558-D ．6516-3315,0,,0,1,D C A ⎛⎛⎫⎛⎫【例2】如图，正八边形ABCDEFGH 中，若AE AC AF λμ=+()R λμ∈，，则λμ+的值为________．正八边形的中心【详解】、HD BF 所在的直线分别为x y 、轴建立平面直角坐标系，正八边形的中心M 点，3608⎛∠=∠=∠=∠= ⎝AOB COB AOH EOD 18045135-= ，所以22.5∠= BAC ，13522.5112.5∠-∠=-= HAB CAB ，所以∠HAC y 轴，、AOM MOC 为等腰直角三角形，2，则2=====OD OF OE OA OC ，()0,2F ，2===OM MC ，所以()2,2--A ，(2,-C【点睛】本题主要考查了平面向量坐标法解决几何问题，建立坐标系是解题的关键，还考查了向量的加法运算，考查方程思想及转化思想，属于中档题．【题型专练】1.如图，在梯形ABCD 中，//AB DC ，10AB =，7BC =，2CD =，5AD =，则AC BD ⋅=___________.则5,02A ⎛⎫- ⎪⎝⎭，532,2C ⎛⎫ ⎪ ⎪⎝⎭，15,02B ⎛⎫ ⎪⎝⎭，530,2D ⎛ ⎝953,22AC ⎛⎫∴= ⎪ ⎪⎝⎭ ，1553,22BD ⎛⎫=- ⎪ ⎪⎝⎭，AC BD ∴⋅ 故答案为：15-.2.已知正方形ABCD 的边长为2，点P 满足1()2AP AB AC =+ ，则||PD = _________；PB PD ⋅=_________．【答案】(1).(2).1-【解析】以点A 为坐标原点，AB 、AD 所在直线分别为x 、y 轴建立如下图所示的平面直角坐标系，则点()0,0A 、()2,0B 、()2,2C 、()0,2D ，()()()()1112,02,22,1222AP AB AC =+=+= ，则点()2,1P ，()2,1PD ∴=-，()0,1PB =- ，因此，PD == ()021(1)1PB PD ⋅=⨯-+⨯-=-.题型九：平面向量中的最值范围问题【例1】如下图，在平面四边形ABCD 中，AB BC ⊥，AD CD ⊥，3BCD π∠=，CB CD ==M 为边BC 上的动点，则AM DM ⋅的最小值为（）A ．83B ．214C ．114-D ．133-【例2】ABC 是边长为4的等边三角形，点D 、E 分别在边AC 、BC 上，且DE BC ⊥，则DA DE ⋅的最小值为（）AB ．C ．3D ．－3则(0,0),(2,23),(4,0)C A B【例3】四边形ABCD 中，4AB =，60A B ∠=∠=︒，150D ∠=︒，则DA DC ⋅的最小值为（）AB ．C ．3D ．－3∴90,60DCB E ∠=︒∠= ，设CE x =，则3,DC x DA =∴()423cos150DA DC x x ⋅=-⋅⋅ 所以当1x =时，DA DC ⋅的最小值为【例4】如图，在梯形ABCD 中，//AD BC ，2AD =，9BC =，5AB =，cos 5B =，若M ，N 是线段BC上的动点，且1MN = ，则DM DN ⋅的最小值为（）A ．134B ．132C ．634D ．352//AD BC ，32AD =，9BC =，5AB =(9,0)C ∴，∴3cos 5A xB AB ==，3,4A A x y ==9(3,4),(,4)2A D ∴，【例5】已知边长为2的菱形ABCD 中，点F 为BD 上一动点，点E 满足2BE EC =，3AE BD ⋅=-，则AF BE⋅的最小值为（）A ．0B ．23C ．43D ．2【例6】已知向量a，b，c共面，且均为单位向量，0a b⋅=，则ab c++的最大值是（）A B C1D1【例7】骑自行车是一种能有效改善心肺功能的耐力性有氧运动，深受大众喜爱，如图是某一自行车的平面结构示意图，已知图中的圆A （前轮），圆DABE △，BEC △，ECD 均是边长为4的等边三角形．设点P 为后轮上的一点，则在骑动该自行车的过程中，AC BP ⋅的最小值为（）A ．12B ．24C ．36D ．18故选：A【例8】已知AB AC ⊥ ，1AB t = ，AC t = ，若点P 是ABC ∆所在平面内一点，且4AB AC AP AB AC=+ ，则PB PC ⋅的最大值等于（）A ．13B ．15C ．19D ．21【答案】A【解析】以题意，以点A 为坐标原点，以AB 所在的直线为x 轴，AC 所在的直线为y 轴建立如图所示的平面直角坐标系，所以点(1,4)P ，1(,0)B t，(0,)C t ，所以11(1,4)(1,4)(1)(1)4(4)PB PC t t t t ⋅=----=-⨯--⨯- =1174t t --17-≤=13（当且仅当14t t =，即12t =时取等号），所以PB PC ⋅ 的最大值为13．故选A ．【题型专练】1．已知梯形ABCD 中，3B π∠=，2AB =，4BC =，1AD =，点P ，Q 在线段BC 上移动，且1PQ =，则DP DQ ⋅的最小值为（）A ．1B ．112C ．132D ．1142．在ABC 中，902A AB AC ∠=== ，，点M 为边AB 的中点，点P 在边BC 上运动，则AP MP ⋅的最小值为___________.【答案】78【分析】建立平面直角坐标系，利用数量积的坐标运算求出3.ABC 为等边三角形，且边长为2，则AB 与BC 的夹角大小为120，若1BD =，CE EA =，则AD BE ⋅的。

平面向量一.向量的基本概念与基本运算 1向量的概念：①向量：既有大小又有方向的量向量一般用c b a,,……来表示,或用有向线段的起点与终点的大写字母表示,如：AB 几何表示法 AB ,a；坐标表示法),(y x yj xi a =+=向量的大小即向量的模长度,记作|AB |即向量的大小,记作｜a｜向量不能比较大小,但向量的模可以比较大小．②零向量：长度为0的向量,记为0 ,其方向是任意的,0 与任意向量平行零向量a＝0⇔｜a｜＝ 由于0的方向是任意的,且规定0平行于任何向量,故在有关向量平行共线的问题中务必看清楚是否有“非零向量”这个条件．注意与0的区别 ③单位向量：模为1个单位长度的向量向量0a 为单位向量⇔｜0a｜＝1④平行向量共线向量：方向相同或相反的非零向量任意一组平行向量都可以移到同一直线上方向相同或相反的向量,称为平行向量记作a ∥b行任意的平移即自由向量,平行向量总可以平移到同一直线上,故平行向量也称为共线向量⑤相等向量：长度相等且方向相同的向量相等向量经过平移后总可以重合,记为b a=大小相等,方向相同),(),(2211y x y x =⎩⎨⎧==⇔2121y y x x2向量加法求两个向量和的运算叫做向量的加法设,AB a BC b ==,则a+b =AB BC +=AC1a a a=+=+00；2向量加法满足交换律与结合律； 向量加法有“三角形法则”与“平行四边形法则”：1用平行四边形法则时,两个已知向量是要共始点的,和向量是始点与已知向量的始点重合的那条对角线,而差向量是另一条对角线,方向是从减向量指向被减向量2 三角形法则的特点是“首尾相接”,由第一个向量的起点指向最后一个向量的终点的有向线段就表示这些向量的和；差向量是从减向量的终点指向被减向量的终点当两个向量的起点公共时,用平行四边形法则；当两向量是首尾连接时,用三角形法则．向量加法的三角形法则可推广至多个向量相加：AB BC CD PQ QR AR +++++=,但这时必须“首尾相连”．3向量的减法① 相反向量：与a 长度相等、方向相反的向量,叫做a的相反向量记作a-,零向量的相反向量仍是零向量关于相反向量有： i )(a --=a； ii a +a -=a -+a =0 ； iii 若a 、b是互为相反向量,则a =b -,b =a -,a +b =0②向量减法：向量a 加上b 的相反向量叫做a 与b的差,记作：)(b a b a-+=-求两个向量差的运算,叫做向量的减法③作图法：b a -可以表示为从b 的终点指向a 的终点的向量a 、b有共同起点 4实数与向量的积：①实数λ与向量a 的积是一个向量,记作λa,它的长度与方向规定如下：Ⅰa a⋅=λλ；Ⅱ当0>λ时,λa 的方向与a 的方向相同；当0<λ时,λa 的方向与a的方向相反；当0=λ时,0=a λ,方向是任意的②数乘向量满足交换律、结合律与分配律 5两个向量共线定理：向量b 与非零向量a共线⇔有且只有一个实数λ,使得b =a λ 6平面向量的基本定理：如果21,e e 是一个平面内的两个不共线向量,那么对这一平面内的任一向量a ,有且只有一对实数21,λλ使：2211e e a λλ+=,其中不共线的向量21,e e叫做表示这一平面内所有向量的一组基底 7 特别注意:1向量的加法与减法是互逆运算2相等向量与平行向量有区别,向量平行是向量相等的必要条件3向量平行与直线平行有区别,直线平行不包括共线即重合,而向量平行则包括共线重合的情况4向量的坐标与表示该向量的有向线条的始点、终点的具体位置无关,只与其相对位置有关二.平面向量的坐标表示 1平面向量的坐标表示：在直角坐标系中,分别取与x 轴、y 轴方向相同的两个单位向量,i j 作为基底由平面向量的基本定理知,该平面内的任一向量a 可表示成a xi yj =+,由于a 与数对x,y 是一一对应的,因此把x,y 叫做向量a 的坐标,记作a =x,y,其中x 叫作a 在x 轴上的坐标,y 叫做在y 轴上的坐标1相等的向量坐标相同,坐标相同的向量是相等的向量2向量的坐标与表示该向量的有向线段的始点、终点的具体位置无关,只与其相对位置有关2平面向量的坐标运算：(1)若()()1122,,,a x y b x y ==,则()1212,a b x x y y ±=±± (2)若()()2211,,,y x B y x A ,则()2121,AB x x y y =-- (3)若a =x,y,则λa =λx, λy(4)若()()1122,,,a x y b x y ==,则1221//0a b x y x y ⇔-= (5)若()()1122,,,a x y b x y ==,则1212a b x x y y ⋅=⋅+⋅若a b ⊥,则02121=⋅+⋅y y x x3,数与向量的乘积,向量的数量内积及其各运算的坐标表示和性质12(a b x x +=+AB BC AC +=12(a b x x -=-)(b a b a-+=- AB BA =-OB OA AB -=a a)()(λμμλ=12a b x x •=+三．平面向量的数量积 1两个向量的数量积：已知两个非零向量a 与b ,它们的夹角为θ,则a ·b =︱a ︱·︱b ︱cos θ叫做a 与b 的数量积或内积 规定00a ⋅=2向量的投影：︱b ︱cos θ=||a ba ⋅∈R,称为向量b 在a 方向上的投影投影的绝对值称为射影3数量积的几何意义：a ·b 等于a 的长度与b 在a 方向上的投影的乘积 4向量的模与平方的关系：22||a a a a ⋅== 5乘法公式成立：()()2222a b a b a b a b +⋅-=-=-；()2222a ba ab b ±=±⋅+222a a b b =±⋅+6平面向量数量积的运算律： ①交换律成立：a b b a ⋅=⋅②对实数的结合律成立：()()()()a b a b a b R λλλλ⋅=⋅=⋅∈ ③分配律成立：()a b c a c b c ±⋅=⋅±⋅()c a b =⋅± 特别注意：1结合律不成立：()()a b c a b c ⋅⋅≠⋅⋅； 2消去律不成立a b a c⋅=⋅不能得到b c =⋅3a b ⋅=0不能得到a =0或b =0 7两个向量的数量积的坐标运算：已知两个向量1122(,),(,)a x y b x y ==,则a ·b =1212x x y y +8向量的夹角：已知两个非零向量a 与b ,作OA =a , OB =b ,则∠AOB=θ001800≤≤θ叫做向量a 与b 的夹角cos θ=cos ,a b a b a b•<>=•=222221212121y x y x y y x x +⋅++当且仅当两个非零向量a 与b 同方向时,θ=00,当且仅当a 与b 反方向时θ=1800,同时0与其它任何非零向量之间不谈夹角这一问题9垂直：如果a 与b 的夹角为900则称a 与b 垂直,记作a ⊥b 10两个非零向量垂直的充要条件：a ⊥b ⇔a ·b＝O ⇔2121=+y y x x 平面向量数量积的性质题型1.基本概念判断正误：1共线向量就是在同一条直线上的向量.2若两个向量不相等,则它们的终点不可能是同一点. 3与已知向量共线的单位向量是唯一的. 4四边形ABCD 是平行四边形的条件是AB CD =. 5若AB CD =,则A 、B 、C 、D 四点构成平行四边形. 6因为向量就是有向线段,所以数轴是向量. 7若a 与b 共线, b 与c 共线,则a 与c 共线. 8若ma mb =,则a b =. 9若ma na =,则m n =.10若a 与b 不共线,则a 与b 都不是零向量. 11若||||a b a b ⋅=⋅,则//a b . 12若||||a b a b +=-,则a b ⊥. 题型2.向量的加减运算1.设a 表示“向东走8km ”, b 表示“向北走6km ”,则||a b += .2.化简()()AB MB BO BC OM ++++= .3.已知||5OA =,||3OB =,则||AB 的最大值和最小值分别为 、 .4.已知AC AB AD为与的和向量,且,AC a BD b ==,则AB = ,AD = .5.已知点C 在线段AB 上,且35AC AB =,则AC = BC ,AB = BC . 题型3.向量的数乘运算1.计算：13()2()a b a b +-+= 22(253)3(232)a b c a b c +---+-=2.已知(1,4),(3,8)a b =-=-,则132a b -= .题型4.作图法球向量的和已知向量,a b ,如下图,请做出向量132a b +和322a b -.a b题型5.根据图形由已知向量求未知向量1.已知在ABC ∆中,D 是BC 的中点,请用向量AB AC ，表示AD . 2.在平行四边形ABCD 中,已知,AC a BD b ==,求AB AD 和.题型6.向量的坐标运算1.已知(4,5)AB =,(2,3)A ,则点B 的坐标是 .2.已知(3,5)PQ =--,(3,7)P ,则点Q 的坐标是 .3.若物体受三个力1(1,2)F =,2(2,3)F =-,3(1,4)F =--,则合力的坐标为 .4.已知(3,4)a =-,(5,2)b =,求a b +,a b -,32a b -.5.已知(1,2),(3,2)A B ,向量(2,32)a x x y =+--与AB 相等,求,x y 的值.6.已知(2,3)AB =,(,)BC m n =,(1,4)CD =-,则DA = .7.已知O 是坐标原点,(2,1),(4,8)A B --,且30AB BC +=,求OC 的坐标.题型7.判断两个向量能否作为一组基底1.已知12,e e 是平面内的一组基底,判断下列每组向量是否能构成一组基底： A.1212e e e e +-和 B.1221326e e e e --和4 C.122133e e e e +-和 D.221e e e -和2.已知(3,4)a =,能与a 构成基底的是A.34(,)55B.43(,)55C.34(,)55--D.4(1,)3--题型8.结合三角函数求向量坐标1.已知O 是坐标原点,点A 在第二象限,||2OA =,150xOA ∠=,求OA 的坐标.2.已知O 是原点,点A 在第一象限,||43OA =60xOA ∠=,求OA 的坐标.题型9.求数量积1.已知||3,||4a b ==,且a 与b 的夹角为60,求1a b ⋅,2()a a b ⋅+,31()2a b b -⋅,4(2)(3)a b a b -⋅+.2.已知(2,6),(8,10)a b =-=-,求1||,||a b ,2a b ⋅,3(2)a a b ⋅+, 4(2)(3)a b a b -⋅+.题型10.求向量的夹角1.已知||8,||3a b ==,12a b ⋅=,求a 与b 的夹角.2.已知(3,1),(23,2)a b ==-,求a 与b 的夹角.3.已知(1,0)A ,(0,1)B ,(2,5)C ,求cos BAC ∠. 题型11.求向量的模1.已知||3,||4a b ==,且a 与b 的夹角为60,求1||a b +,2|23|a b -.2.已知(2,6),(8,10)a b =-=-,求1||,||a b ,5||a b +,61||2a b -.3.已知||1||2a b ==，,|32|3a b -=,求|3|a b +.题型12.求单位向量 与a 平行的单位向量：||a e a =± 1.与(12,5)a =平行的单位向量是 .2.与1(1,)2m =-平行的单位向量是 . 题型13.向量的平行与垂直1.已知(6,2)a =,(3,)b m =-,当m 为何值时,1//a b 2a b ⊥2.已知(1,2)a =,(3,2)b =-,1k 为何值时,向量ka b +与3a b -垂直 2k 为何值时,向量ka b +与3a b -平行3.已知a 是非零向量,a b a c ⋅=⋅,且b c ≠,求证：()a b c ⊥-.题型14.三点共线问题1.已知(0,2)A -,(2,2)B ,(3,4)C ,求证：,,A B C 三点共线.2.设2(5),28,3()2AB a b BC a b CD a b =+=-+=-,求证：A B D 、、三点共线. 3.已知2,56,72AB a b BC a b CD a b =+=-+=-,则一定共线的三点是 .4.已知(1,3)A -,(8,1)B -,若点(21,2)C a a -+在直线AB 上,求a 的值.5.已知四个点的坐标(0,0)O ,(3,4)A ,(1,2)B -,(1,1)C ,是否存在常数t ,使OA tOB OC +=成立题型15.判断多边形的形状1.若3AB e =,5CD e =-,且||||AD BC =,则四边形的形状是 .2.已知(1,0)A ,(4,3)B ,(2,4)C ,(0,2)D ,证明四边形ABCD 是梯形.3.已知(2,1)A -,(6,3)B -,(0,5)C ,求证：ABC ∆是直角三角形.4.在平面直角坐标系内,(1,8),(4,1),(1,3)OA OB OC =-=-=,求证：ABC ∆是等腰直角三角形.题型16.平面向量的综合应用1.已知(1,0)a =,(2,1)b =,当k 为何值时,向量ka b -与3a b +平行2.已知(3,5)a =,且a b ⊥,||2b =,求b 的坐标.3.已知a b 与同向,(1,2)b =,则10a b ⋅=,求a 的坐标.3.已知(1,2)a =,(3,1)b =,(5,4)c =,则c = a + b .4.已知(5,10)a =,(3,4)b =--,(5,0)c =,请将用向量,a b 表示向量c .5.已知(,3)a m =,(2,1)b =-,1若a 与b 的夹角为钝角,求m 的范围； 2若a 与b 的夹角为锐角,求m 的范围.6.已知(6,2)a =,(3,)b m =-,当m 为何值时,1a 与b 的夹角为钝角 2a 与b 的夹角为锐角7.已知梯形ABCD 的顶点坐标分别为(1,2)A -,(3,4)B ,(2,1)D ,且//AB DC ,2AB CD =,求点C 的坐标.8.已知平行四边形ABCD 的三个顶点的坐标分别为(2,1)A ,(1,3)B -,(3,4)C ,求第四个顶点D 的坐标.9.一航船以5km/h 的速度向垂直于对岸方向行驶,航船实际航行方向与水流方向成30角,求水流速度与船的实际速度.10.已知ABC ∆三个顶点的坐标分别为(3,4)A ,(0,0)B ,(,0)C c ,1若0AB AC ⋅=,求c 的值；2若5c =,求sin A 的值.备用1.已知||3,||4,||5a b a b ==+=,求||a b -和向量,a b 的夹角.2.已知x a b =+,2y a b =+,且||||1a b ==,a b ⊥,求,x y 的夹角的余弦.1.已知(1,3),(2,1)a b ==--,则(32)(25)a b a b +⋅-= .4.已知两向量(3,4),(2,1)a b ==-,求当a xb a b +-与垂直时的x 的值.5.已知两向量(1,3),(2,)a b λ==,a b 与的夹角θ为锐角,求λ的范围. 变式：若(,2),(3,5)a b λ==-,a b 与的夹角θ为钝角,求λ的取值范围. 选择、填空题的特殊方法：1.代入验证法例：已知向量(1,1),(1,1),(1,2)a b c ==-=--,则c = A.1322a b -- B.1322a b -+ C.3122a b - D.3122a b -+ 2.排除法例：已知M 是ABC ∆的重心,则下列向量与AB 共线的是A.AM MB BC ++B.3AM AC +C.AB BC AC ++D.AM BM CM ++。

精选全文完整版（可编辑修改）向量题型归纳(全)平面向量部分常见的题型类型（一）：向量共线问题1.设向量a=(2,1)，b=(2,3)，若向量λa+b与向量c=(-4,-7)共线，则λ=?2.已知A(1,3)，B(-2,-3)，C(x,7)，设AB=a，BC=b且a∥b，则x=?3.已知a=(1,2)，c=25，且a∥c，求c的坐标。

4.n为何值时，向量a=(n,1)与向量b=(4,n)共线且方向相同？5.已知a,b不共线，c=ka+b，d=a-b，如果c∥d，那么k=？c与d的方向关系是？类型（二）：向量的垂直问题1.已知向量a=(1,n)，b=(-1,n)，若2a-b与b垂直，则a=?2.已知a=2,b=4，且a与b的夹角为π/3，若ka+2b与ka-2b垂直，求k的值。

3.已知单位向量m和n的夹角为π/3，求证：(2n-m)⊥m。

4.已知a=(4,2)，求与a垂直的单位向量的坐标。

5.已知a∥b，c⊥(a+b)，则c=？类型（三）：向量的夹角问题1.平面向量a,b，满足a=1,b=4且满足a·b=2，则a与b的夹角为？2.已知非零向量a,b满足a=b，(a-b)·(2a+b)=-4且a=2，b=4，则a与b的夹角为？3.已知平面向量a,b满足|a|=|b|，a+b=c，则⟨a,b⟩=？4.设非零向量a、b、c满足|a|=|b|=|c|，a+b=c，则⟨a,b⟩=？5.已知a=2,b=3,a+b=7，求a与b的夹角。

6.若非零向量a,b满足a=b，(2a+b)·b=0，则a与b的夹角为？类型（四）：求向量的模的问题1.已知零向量a=(2,1)，a·b=10，a+b=5，求b=？2.已知向量a=1,b=2，a-b=2，则a+b=？3.已知向量a=(1,3)，b=(-2,x)，则a+b=？4.已知向量a=(1,sinθ)，b=(1,cosθ)，则a-b的最大值为？5.设点M是线段BC的中点，点A在直线BC外，BC=16，AB+AC=AB-AC，则AM=？平面向量部分常见的题型类型（一）：向量共线问题1.已知向量a=(2,1)，b=(2,3)，若向量λa+b与向量c=(-4,-7)共线，则λ=？2.已知A(1,3)，B(-2,-3)，C(x,7)，设AB=a，BC=b且a∥b，则x=？3.已知a=(1,2)，c=25，且a∥c，求c的坐标。

《平面向量》热点题型探究题型一 向量的概念及线性运算 1．向量的有关概念(1)向量：既有大小又有方向的量．两个向量不能比较大小，但它的模可以比较大小． (2)零向量：模为0的向量，记作0，其方向为任意的，所以0与任意向量平行，其性质有0·a ＝0，0＋a ＝a .(3)单位向量：模为1个长度单位的向量，与a 方向相同的单位向量为a|a |.2．共线向量(1)概念：若两个非零向量a ，b 的方向相同或相反，则称a 与b 共线，也叫a 与b 平行，规定零向量与任意向量共线．两个向量共线，其所在的直线可能重合也可能平行．(2)共线向量定理：a ∥b (b ≠0)⇔存在唯一实数λ，使得a ＝λb . (3)若a ＝(x 1，y 1)，b ＝(x 2，y 2)，则a ∥b ⇔x 1y 2－x 2y 1＝0. (4)若A ，B ，C 三点共线且OA →＝λOB →＋μOC →，则λ＋μ＝1. 3．平面向量线性运算的两种技巧(1)对于平面向量的线性运算问题，要尽可能转化到三角形或平行四边形中，灵活运用三角形法则、平行四边形法则，紧密结合图形的几何性质进行运算．(2)在证明两向量平行时，若已知两向量的坐标形式，常利用坐标运算来判断；若两向量不是以坐标形式呈现的，常利用共线向量定理来判断.1．有下列命题： ①若|a|＝|b|，则a ＝b ；②若|AB →|＝|DC →|，则四边形ABCD 是平行四边形； ③若m ＝n ，n ＝k ，则m ＝k ； ④若a ∥b ，b ∥c ，则a ∥c . 其中假命题的个数是( ) A ．1 B ．2 C ．3D ．4C 解析 对于①，|a|＝|b|，a ，b 的方向不确定，则a ，b 不一定相等，所以①错误；对于②，若|AB →|＝|DC →|，则AB →，DC →的方向不一定相同，所以四边形ABCD 不一定是平行四边形，所以②错误；对于③，若m ＝n ，n ＝k ，则m ＝k ，③正确；对于④，若a ∥b ，b ∥c ，则b ＝0时，a ∥c 不一定成立，所以④错误．综上，假命题是①②④，共3个．故选C 项．2．如图所示，在正方形ABCD 中，E 为AB 的中点，F 为CE 的中点，则AF →＝( )A ．34AB →＋14AD →B ．14AB →＋34AD →C ．12AB →＋AD →D ．34AB →＋12AD →D 解析 根据题意得AF →＝12(AC →＋AE →)，又AC →＝AB →＋AD →，AE →＝12AB →，所以AF →＝12⎝⎛⎭⎫AB→＋AD →＋12AB →＝34AB →＋12AD →.故选D 项．3．设e 1与e 2是两个不共线向量，AB →＝3e 1＋2e 2，CB →＝k e 1＋e 2，CD →＝3e 1－2k e 2，若A ，B ，D 三点共线，则k 的值为________.解析 由题意，A ，B ，D 三点共线，故必存在一个实数λ，使得AB →＝λBD →.又AB →＝3e 1＋2e 2，CB →＝k e 1＋e 2，CD →＝3e 1－2k e 2，所以BD →＝CD →－CB →＝3e 1－2k e 2－(k e 1＋e 2)＝(3－k )e 1－(2k＋1)e 2，所以3e 1＋2e 2＝λ(3－k )e 1－λ(2k ＋1)e 2，又e 1与e 2不共线，所以⎩⎪⎨⎪⎧3＝λ(3－k )，2＝－λ(2k ＋1)，解得k ＝－94.答案 －944．已知点P 在△ABC 所在的平面内，若2P A →＋3PB →＋4PC →＝3AB →，则△P AB 与△PBC 的面积的比值为________.解析 由2P A →＋3PB →＋4PC →＝3AB →，得2P A →＋4PC →＝3AB →＋3BP →，所以2P A →＋4PC →＝3AP →，即4PC →＝5AP →.所以A ，C ，P 三点共线，且|AP →||PC →|＝45，所以S △P AB S △PBC ＝|AP →||PC →|＝45.答案 45题型二 平面向量基本定理平面向量基本定理：若a ，b 是平面内不共线的向量，向量c 是平面内任意一个向量，则存在唯一实数对x ，y ，使c ＝x a ＋y b .平面向量基本定理是定义向量坐标的基础，是将平面内任意向量用不共线的平面向量即基底表示出来的基础．5．已知平面直角坐标系内的两个向量a ＝(m,3m －4)，b ＝(1,2)，且平面内的任意向量c 都可以唯一地表示成c ＝λa ＋μb (λ，μ为实数)，则m 的取值范围是( )A ．(－∞，4)B ．(4，＋∞)C ．(－∞，4)∪(4，＋∞)D ．(－∞，＋∞)C 解析 平面内的任意向量c 都可以唯一地表示成c ＝λa ＋μb ，由平面向量基本定理可知，向量a ，b 可作为该平面所有向量的一组基底，即向量a ，b 是不共线向量．又因为a ＝(m,3m －4)，b ＝(1,2)，则m ×2－(3m －4)×1≠0，即m ≠4，所以m 的取值范围为(－∞，4)∪(4，＋∞)．故选C 项．6．如图所示，|OA →|＝|OB →|＝1，|OC →|＝3，∠AOB ＝60°，OB ⊥OC ，设OC →＝xOA →＋yOB →，则( )A ．x ＝－2，y ＝－1B ．x ＝－2，y ＝1C ．x ＝2，y ＝－1D ．x ＝2，y ＝1B 解析 过点C 作CD ∥OB 交AO 的延长线于点D ，连接BC ，如图所示．由|OB →|＝1，|OC →|＝3，∠AOB ＝60°，OB ⊥OC ，知∠COD ＝30°.在Rt △OCD 中，可得OD ＝2CD ＝2，则OC →＝OD →＋DC →＝OD →＋OB →＝－2OA →＋OB →.故x ＝－2，y ＝1.故选B 项．7．在△ABC 中，点P 是AB 上一点，且CP →＝23CA →＋13CB →，点Q 是BC 的中点，AQ 与CP 的交点为M ，又CM →＝tCP →，则实数t 的值为________.解析 因为CP →＝23CA →＋13CB →，所以3CP →＝2CA →＋CB →，即2CP →－2CA →＝CB →－CP →，所以2AP→＝PB →，即点P 为AB 的一个三等分点(靠近点A )．又由题意可知A ，M ，Q 三点共线，则可设AM →＝λAQ →，所以CM →＝AM →－AC →＝λAQ →－AC →＝λ⎝⎛⎭⎫12AB →＋12AC →－AC →＝λ2AB →＋λ－22AC →，又CM →＝tCP →＝t (AP →－AC →)＝t ⎝⎛⎭⎫13AB →－AC →＝t 3AB →－tAC →，故⎩⎪⎨⎪⎧ λ2＝t 3，λ－22＝－t ，解得⎩⎨⎧t ＝34，λ＝12.故t 的值是34.答案 34【变式】如图，平行四边形ABCD 的两条对角线相交于点O ，7AE →＝5AB →，AD →＝4AF →，EF 交AC 于点K ，AK →＝λOA →，则实数λ的值为____________.解析 因为AK →＝λOA →＝－λAO →＝－λ2(AB →＋AD →)，所以AK →＝－λ2⎝⎛⎭⎫75AE →＋4AF →.又E ，F ，K 三点共线，所以－λ2×⎝⎛⎭⎫75＋4＝1，解得λ＝－1027. 答案 －1027题型三 向量的数量积及应用)1．向量的数量积是一个实数，求向量数量积的三种方法：一是利用向量数量积的定义，a·b ＝|a||b|cos θ；二是根据向量数量积的几何意义，a·b 等于a 的模与b 在向量a 方向上的投影的乘积；三是建立坐标系，写出向量坐标a ＝(x 1，y 1)，b ＝(x 2，y 2)，a·b ＝x 1x 2＋y 1y 2.在解决与平面几何有关的数量积问题时，充分利用向量的线性运算，将所求向量用共同的基底表示出来，再利用平面向量的数量积运算法则求解．2．向量的投影：|b |cos θ叫向量b 在向量a 方向上的投影，|b |cos θ＝a·b|a|.3．若向量a 与b 的夹角为θ，则θ的范围为[0，π]，cos θ＝a·b|a||b|；若已知向量a ＝(x 1，y 1)，b ＝(x 2，y 2)，向量a 与b 的夹角为θ，则cos θ＝x 1x 2＋y 1y 2x 21＋y 21x 22＋y 22.4．已知非零向量a ，b ，则a ⊥b ⇔a·b ＝0；已知非零向量a ，b ，若a ＝(x 1，y 1)，b ＝(x 2，y 2)，则a ⊥b ⇔x 1x 2＋y 1y 2＝0.5．向量的模是非负数，|a|2＝a 2＝a·a ；若向量a ＝(x 1，y 1)，则|a |＝x 21＋y 21.8．已知非零向量a ，b 满足|a|＝2|b|，且(a －b )⊥b ，则a 与b 的夹角为( ) A ．π6B ．π3C ．2π3D ．5π6B 解析 因为(a －b )⊥b ，所以(a －b )·b ＝a·b －b 2＝0，所以a·b ＝b 2，所以cos θ＝a·b|a|·|b|＝|b|22|b|2＝12，所以a 与b 的夹角为π3.故选B 项． 9．已知AB →＝(2,3)，AC →＝(3，t )，|BC →|＝1，则AB →·BC →＝( ) A ．－3 B ．－2 C ．2D ．3C 解析 因为BC →＝AC →－AB →＝(1，t －3)，所以|BC →|＝12＋(t －3)2＝1，所以t ＝3，所以AB →·BC →＝(2,3)·(1，0)＝2.故选C 项．10．已知向量a ＝(－4,3)，b ＝(6，m )，且a ⊥b ，则m ＝________.解析 依题意向量a ＝(－4,3)，b ＝(6，m )，a ⊥b ，则a·b ＝0，即－4×6＋3m ＝0，即m ＝8.答案 811．在四边形ABCD 中，AD ∥BC ，AB ＝23，AD ＝5，∠A ＝30°，点E 在线段CB 的延长线上，且AE ＝BE ，则BD →·AE →＝________.解析 如图，因为E 在线段CB 的延长线上，所以EB ∥AD ．因为∠DAB ＝30°，所以∠ABE ＝30°.因为AE ＝BE ，所以∠EAB ＝30°.又因为AB ＝23，所以BE ＝2.因为AD ＝5，所以EB →＝25AD →.所以AE →＝AB →＋BE →＝AB →－25AD →.又因为BD →＝AD →－AB →，所以BD →·AE →＝(AD →－AB →)·⎝⎛⎭⎫AB →－25AD →＝AD →·AB →－25AD →2－AB →2＋25AD →·AB →＝75|AD →|·|AB →|·cos 30°－25×52－(23)2＝75×5×23×32－10－12＝21－22＝－1.答案 －1 【规范演练】1．下列各组向量中，可以作为基底的是( )A ．e 1＝(0,0)，e 2＝(1,2)B ．e 1＝(－1,2)，e 2＝(5,7)C ．e 1＝(3,5)，e 2＝(6,10)D ．e 1＝(2，－3)，e 2＝⎝⎛⎭⎫12，－34 B 解析 A 项中，零向量与任意向量都共线，故其不可以作为基底；B 项中，不存在实数λ，使得e 1＝λe 2，故两向量不共线，故其可以作为基底；C 项中，e 2＝2e 1，两向量共线，故其不可以作为基底；D 项中，e 1＝4e 2，两向量共线，故其不可以作为基底．故选B 项．2．设a ，b 均为单位向量，则“a 与b 夹角为2π3”是“|a ＋b |＝3”的( )A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件D 解析 因为a ，b 均为单位向量，若a 与b 夹角为2π3，则|a ＋b |＝|a |2＋|b |2＋2a·b ＝1＋1＋2×1×1×cos 2π3＝1，所以由“a 与b 夹角为2π3”不能推出“|a ＋b |＝3”；若|a ＋b |＝3，则|a ＋b |＝|a|2＋|b|2＋2a·b ＝1＋1＋2×1×1×cos 〈a ，b 〉＝3，解得cos 〈a ，b 〉＝12，即a 与b 夹角为π3，所以由“|a ＋b |＝3”不能推出“a 与b 夹角为2π3”．因此“a 与b 夹角为2π3”是“|a ＋b |＝3”的既不充分也不必要条件．故选D 项．3．已知向量a ＝(1,2)，b ＝(－2,3)，c ＝(4,5)，若(a ＋λb )⊥c ，则实数λ＝( ) A ．－12B ．12C ．－2D ．2C 解析 因为a ＝(1,2)，b ＝(－2,3)，所以a ＋λb ＝(1－2λ，2＋3λ)，又(a ＋λb )⊥c ，所以(a ＋λb )·c ＝0，即4(1－2λ)＋5(2＋3λ)＝0，解得λ＝－2.故选C 项．4．在△ABC 中，点D 在线段BC 的延长线上，且BC →＝3CD →，点O 在线段CD 上(与点C ，D 不重合)，若AO →＝xAB →＋(1－x )AC →，则x 的取值范围是( )A ．⎝⎛⎭⎫0，13 B ．⎝⎛⎭⎫0，12C ．⎝⎛⎭⎫－13，0 D ．⎝⎛⎭⎫－12，0 C 解析 由题意得AO →＝AC →＋CO →，O 在线段CD 上且不与端点重合，所以存在k (0<k <1)，使CO →＝kCD →，又BC →＝3CD →，所以CD →＝13BC →＝13(AC →－AB →)，所以AO →＝AC →＋k 3(AC →－AB →)＝－k 3AB→＋⎝⎛⎭⎫1＋k 3AC →，又AO →＝xAB →＋(1－x )AC →，所以x ＝－k 3，所以－13<x <0.故选C 项． 5．在矩形ABCD 中，|AB →|＝4，|AD →|＝2.若点M ，N 分别是CD ，BC 的中点，则AM →·MN →＝( )A ．4B ．3C ．2D ．1C 解析 由题意作出图形，如图所示．由图及题意，可得AM →＝AD →＋DM →＝AD →＋12AB →，MN →＝CN →－CM →＝12CB →－12CD →＝－12BC →＋12DC →＝－12AD →＋12AB →.所以AM →·MN →＝⎝⎛⎭⎫AD →＋12AB →·⎝⎛⎭⎫－12AD →＋12AB →＝－12·|AD →|2＋14·|AB →|2＝－12×4＋14×16＝2.故选C 项． 【跟踪检测】 基础热身1．已知向量BA →＝⎝⎛⎭⎫12，32，BC →＝⎝⎛⎭⎫32，12，则∠ABC ＝( )A ．30°B ．45°C ．60°D ．120°A 解析 |BA →|＝1，|BC →|＝1，cos ∠ABC ＝BA →·BC →|BA →|·|BC →|＝32.因为0°≤∠ABC ≤180°，所以∠ABC＝30°.故选A 项．2．向量a ，b ，c 在正方形网格中的位置如图所示．若向量c ＝λa ＋b ，则实数λ＝( )A ．－2B ．－1C ．1D ．2D 解析 由题中所给图象可得2a ＋b ＝c ，又c ＝λa ＋b ，所以λ＝2.故选D 项． 3．已知平面向量a ＝(－1,2)，b ＝(2，y )，且a ∥b ，则3a ＋2b ＝( ) A ．(－1,7) B ．(－1,2) C ．(1,2)D ．(1，－2)D 解析 因为a ＝(－1,2)，b ＝(2，y )，且a ∥b ，所以－1×y －2×2＝0，解得y ＝－4，故可得3a ＋2b ＝3(－1,2)＋2(2，－4)＝(1，－2)．故选D 项．4．设向量a ，b 满足|a ＋b|＝10，|a －b|＝6，则a·b ＝( ) A ．1 B ．2 C ．3D ．5A 解析 由|a ＋b |＝10得|a ＋b |2＝10， 即a 2＋2a·b ＋b 2＝10，①又|a －b |＝6，所以a 2－2a·b ＋b 2＝6，② 由①－②得4a·b ＝4，则a·b ＝1.故选A 项．5．已知向量a ＝(2，－4)，b ＝(－3，x )，c ＝(1，－1)，若(2a ＋b )⊥c ，则|b|＝( ) A ．9 B ．3 C ．109D ．310 D 解析 向量a ＝(2，－4)，b ＝(－3，x )，c ＝(1，－1)，所以2a ＋b ＝(1，x －8)，由(2a ＋b )⊥c ，可得1＋8－x ＝0，解得x ＝9，则|b |＝(－3)2＋92＝310.故选D 项．6．(2019·广东东莞统考)如图所示，△ABC 中，BD →＝2DC →，点E 是线段AD 的中点，则AC →＝( )A ．34AD →＋12BE →B ．34AB →＋BE →C ．54AD →＋12BE →D ．54AD →＋BE →C 解析 由题意和图可知，AC →＝AD →＋DC →，DC →＝12BD →，BD →＝BE →＋ED →，ED →＝12AD →，所以AC →＝54AD →＋12BE →.故选C 项．7．如图，已知|OA →|＝|OB →|＝1，|OC →|＝2，tan ∠AOB ＝－43，∠BOC ＝45°，OC →＝mOA →＋nOB →，则m n＝( )A ．57B ．75C ．37D ．73A 解析 以OA 所在的直线为x 轴，过O 作与OA 垂直的直线为y 轴，建立平面直角坐标系如图所示．因为|OA →|＝|OB →|＝1，且tan ∠AOB ＝－43，所以cos ∠AOB ＝－35，sin ∠AOB ＝45，所以A (1,0)，B ⎝⎛⎭⎫－35，45，又令∠AOC ＝θ，则θ＝∠AOB －∠BOC ，所以tan θ＝tan(∠AOB －∠BOC )＝－43－11－43＝7，又因为点C 在∠AOB 内，所以cos θ＝210，sin θ＝7210，又|OC →|＝2，所以C ⎝⎛⎭⎫15，75，因为OC →＝mOA →＋nOB →(m ，n ∈R )，所以⎝⎛⎭⎫15，75＝(m,0)＋⎝⎛⎭⎫－35n ，45n ＝⎝⎛⎭⎫m －35n ，45n ，即⎩⎨⎧15＝m －35n ，75＝45n ，解得⎩⎨⎧n ＝74，m ＝54，所以m n ＝57.故选A 项．8．已知e 1，e 2是互相垂直的单位向量，若3e 1－e 2与e 1＋λe 2的夹角为60°，则实数λ的值是________.解析 cos 60°＝(3e 1－e 2)·(e 1＋λe 2)|3e 1－e 2||e 1＋λe 2|＝3－λ3＋11＋λ2＝12，解得λ＝33. 答案339．已知向量a ，b 的夹角为120°，且|a|＝2，|b|＝4，则b 在a 方向上的投影等于________.解析 因为a·b ＝2×4cos 120°＝－4，所以b 在a 方向上的投影为a·b |a|＝－42＝－2.答案 －210．已知△ABC 和点M 满足MA →＋MB →＋MC →＝0.若存在实数m 使得AB →＋AC →＝mAM →成立，则m ＝________.解析 由条件知M 是△ABC 的重心，设D 是BC 边的中点，则AB →＋AC →＝2AD →，而AM →＝23AD →，所以2AD →＝m ·23AD →，所以m ＝3.答案 311．在△ABC 中，∠ACB 为钝角，AC ＝BC ＝1，CO →＝xCA →＋yCB →，且x ＋y ＝1，函数f (m )＝|CA →－mCB →|的最小值为32，则|CO →|的最小值为________.解析 如图，△ABC 中，∠ACB 为钝角，AC ＝BC ＝1，记NA →＝CA →－mCB →，则当N 在D 处，即AD ⊥BC 时，f (m )取得最小值32，因此|AD →|＝32，容易得到∠ACB ＝120°.因为CO →＝xCA →＋yCB →，且x ＋y ＝1，所以O 在边AB 上，所以当CO ⊥AB 时，|CO →|最小，|CO →|min ＝12.答案 1212．平行四边形ABCD 中，AB ＝4，AD ＝2，AB →·AD →＝4，点P 在边CD 上，则P A →·PC →的取值范围是________.解析 设|PD →|＝x ，x ∈[0,4]，则P A →·PC →＝(PD →＋DA →)·PC →＝⎝⎛⎭⎫－x 4AB →－AD →·4－x 4AB →＝－x 4×4－x 4AB →2－4－x 4AD →·AB →＝－x 4×4－x 4×16－4－x 4×4＝x 2－3x －4＝⎝⎛⎭⎫x －322－254，所以当x ＝32时，取最小值－254，当x ＝4时，取最大值0，即P A →·PC →的取值范围是⎣⎡⎦⎤－254，0. 答案 ⎣⎡⎦⎤－254，0 能力提升13．设平面向量a ＝(－2,1)，b ＝(1，λ)，若a 与b 的夹角为钝角，则λ的取值范围是____________.解析 因为a 与b 的夹角为钝角，所以a ·b <0，且a 与b 不平行，所以有⎩⎪⎨⎪⎧－2＋λ<0，－2λ≠1，即λ<2且λ≠－12，所以λ的取值范围为⎝⎛⎭⎫－∞，－12∪⎝⎛⎭⎫－12，2. 答案 ⎝⎛⎭⎫－∞，－12∪⎝⎛⎭⎫－12，2 14．已知A B →与A C →的夹角为90°，|A B →|＝2，|A C →|＝1，AM →＝λA B →＋μA C →(λ，μ∈R )，且AM →·B C →＝0，则λμ的值为________．解析 根据题意，建立如图所示的平面直角坐标系，则A (0,0)，B (0,2)，C (1,0)，所以AB→＝(0,2)，AC →＝(1,0)，BC →＝(1，－2)．设M (x ，y )，则AM →＝(x ，y )，所以AM →·BC →＝(x ，y )·(1，－2)＝x －2y ＝0，所以x ＝2y ，又AM →＝λAB →＋μAC →，即(x ，y )＝λ(0,2)＋μ(1,0)＝(μ，2λ)，所以x ＝μ，y ＝2λ，所以λμ＝12y x ＝14. 答案 1415．如图，△ABC 是边长为23的正三角形，P 是以C 为圆心，1为半径的圆上任意一点，则AP →·BP →的取值范围是________.解析 取AB 的中点D ，连接CD ，CP ，则CA →＋CB →＝2CD →，所以AP →·BP →＝(CP →－CA →)·(CP →－CB →)＝CP →2－CP →·(CA →＋CB →)＋CA →·CB →＝CP →2－2CD →·CP →＋CA →·CB →＝1－2×3×1×cos CD →，CP→＋(23)2cos π3＝7－6cos CD →，CP →，所以当cos CD →，CP →＝1时，AP →·BP →取得最小值为1；当cos CD →，CP →＝－1时，AP →·BP →取得最大值为13.因此AP →·BP →的取值范围是[1,13]．答案 [1,13]16．已知向量a ＝(cos α，sin α)，b ＝(cos β，sin β)，0＜β＜α＜π.(1)若|a －b |＝2，求向量a 在b 上的投影；(2)设c ＝(0,1)，若a ＋b ＝c ，求α，β的值．解析 (1)a －b ＝(cos α－cos β，sin α－sin β)，则|a －b |＝2－2cos (α－β)＝2，所以cos(α－β)＝0，而0＜β＜α＜π，所以0＜α－β＜π，所以α－β＝π2.所以向量a 在b 上的投影为|a |cos a ，b ＝a ·b |b |＝cos(α－β)＝0. (2)由a ＋b ＝c 得⎩⎪⎨⎪⎧ cos α＋cos β＝0， ①sin α＋sin β＝1， ②①2＋②2得cos(α－β)＝－12，而0＜α－β＜π，故α－β＝2π3，而由①得α＋β＝π，解得α＝5π6，β＝π6.。

平面向量重难点题型训练摘要：一、平面向量的基本概念二、平面向量的重难点题型三、平面向量的解题技巧四、总结与展望正文：一、平面向量的基本概念平面向量是平面内的有序线段，可以用来表示平面内的物理量，如速度、加速度、力等。

平面向量具有大小和方向两个属性，通常用有序实数对(a,b) 来表示，其中a 和b 分别表示向量的水平和垂直分量。

平面向量的基本运算包括加法、减法、数乘和向量积等。

二、平面向量的重难点题型1.向量加法与减法向量加法和减法是平面向量的基本运算之一，其难点在于处理不同方向的向量。

解决这类问题时，需要将向量分解为水平和垂直分量，然后进行相应的加减运算。

2.向量数乘向量数乘是平面向量的另一个基本运算，其难点在于理解数乘的物理意义和计算方法。

向量数乘的结果是一个向量，其大小等于原向量的大小与数乘因子的乘积，方向与原向量相同或相反。

3.向量积向量积是平面向量的高级运算，其难点在于理解向量积的物理意义和计算方法。

向量积的结果是一个向量，其大小等于原向量之积与夹角的余弦值的乘积，方向垂直于原向量所在的平面。

三、平面向量的解题技巧1.图形法图形法是解决平面向量问题的一种直观方法，通过画图可以直观地表示向量的大小和方向，以及向量之间的运算关系。

2.分解法分解法是解决平面向量问题的一种常用方法，通过将向量分解为水平和垂直分量，可以简化向量运算，尤其是处理不同方向的向量时。

3.数学建模法数学建模法是解决平面向量问题的一种高级方法，通过将实际问题抽象为数学模型，可以更好地理解向量的物理意义和计算方法。

四、总结与展望平面向量是物理学、工程学等领域中的重要概念，掌握平面向量的基本概念和解题技巧对于解决实际问题具有重要意义。

最全归纳平面向量中的范围与最值问题目录题型一：三角不等式题型二：定义法题型三：基底法题型四：几何意义法题型五：坐标法题型六：极化恒等式题型七：矩形大法题型八：等和线题型九：平行四边形大法题型十：向量对角线定理方法技巧总结技巧一．平面向量范围与最值问题常用方法：(1)定义法第一步：利用向量的概念及其基本运算将所求问题转化为相应的等式关系第二步：运用基木不等式求其最值问题第三步：得出结论(2)坐标法第一步：根据题意建立适当的直角坐标系并写出相应点的坐标第二步：将平面向量的运算坐标化第三步：运用适当的数学方法如二次函数的思想、基本不等式的思想、三角函数思想等求解(3)基底法第一步：利用其底转化向量第二步：根据向量运算律化简目标第三步：运用适当的数学方法如二次函数的思想、基本不等式的思想、三角函数思想等得出结论(4)几何意义法第一步：先确定向量所表达的点的轨迹第二步：根据直线与曲线位置关系列式第三步：解得结果技巧二．极化恒等式(1)平行四边形平行四边形对角线的平方和等于四边的平方和：|a +b |2+|a -b |2=2(|a|2+|b |2)证明：不妨设AB =a ,AD =b ，则AC =a +b ，DB =a -bAC 2=AC 2=a +b 2=a 2+2a ⋅b +b 2①DB 2=DB 2=a -b 2=a 2-2a ⋅b +b 2②①②两式相加得：AC 2+DB 2=2a 2+b 2=2AB 2+AD 2 (2)极化恒等式：上面两式相减，得：14a +b 2-a -b 2----极化恒等式①平行四边形模式：a ⋅b =14AC 2-DB 2几何意义：向量的数量积可以表示为以这组向量为邻边的平行四边形的“和对角线”与“差对角线”平方差的14．②三角形模式：a ⋅b =AM 2-14DB 2(M 为BD 的中点)技巧三．矩形大法矩形所在平面内任一点到其对角线端点距离的平方和相等已知点O 是矩形ABCD 与所在平面内任一点，证明：OA 2+OC 2=OB 2+OD 2．【证明】(坐标法)设AB =a ,AD =b ，以AB 所在直线为轴建立平面直角坐标系xoy ，则B (a ,0),D (0,b ),C (a ,b )，设O (x ,y )，则OA 2+OC 2=(x 2+y 2)+[(x -a )2+(y -b )2]OB 2+OD 2=[(x -a )2+y 2]+[x 2+(y -b )2]∴OA 2+OC 2=OB 2+OD 2技巧四．等和线(1)平面向量共线定理已知OA =λOB +μOC ，若λ+μ=1，则A ,B ,C 三点共线；反之亦然．(2)等和线平面内一组基底OA ,OB 及任一向量OP ，OP =λOA +μOB(λ,μ∈R )，若点P 在直线AB 上或者在平行于AB 的直线上，则λ+μ=k (定值)，反之也成立，我们把直线AB 以及与直线AB 平行的直线称为等和线．①当等和线恰为直线AB 时，k =1；②当等和线在O 点和直线AB 之间时，k ∈(0,1)；③当直线AB 在点O 和等和线之间时，k ∈(1,+∞)；④当等和线过O 点时，k =0；⑤若两等和线关于O 点对称，则定值k 互为相反数；技巧五．平行四边形大法1.中线长定理2AO 2=AB 2+AD 2-12DB 22.P 为空间中任意一点，由中线长定理得：2PO 2=PA 2+PC 2-12AC 22PO 2=PD 2+PB 2-12DB 2两式相减：PA 2+PC 2-PD 2+PB 2=AC2-BD 22=2AB ⋅AD技巧六．向量对角线定理AC ⋅BD =(AD 2+BC 2)-(AB 2+CD2)2必考题型归纳题型一:三角不等式1(2023·全国·高三专题练习)已知向量a ,b ,c 满足|a |=2,|b |=1,|c -a -b |=1，若对任意c ，(c -a )2+(c-b )2≤11恒成立，则a ⋅b 的取值范围是.2(2023·全国·高三专题练习)已知平面向量a ,b ,c 满足：|a|=1,b ⋅a =-1，若对满足条件的任意向量b ，|c -b |≥|c -a |恒成立，则cos c +a ,a 的最小值是．3已知向量a ,b ,c 满足a =b =c =2，a ⋅b =0，若关于t 的方程ta +b2-c=12有解，记向量a ,c 的夹角为θ，则sin θ的取值范围是.1.已知e 1 ,e 2 ,e 3 是平面向量，且e 1 ,e 2 是互相垂直的单位向量，若对任意λ∈R 均有e 3 +λe 1的最小值为e 3 -e 2 ，则e 1 +3e 2 -e 3 +e 3-e 2 的最小值为．2.已知平面向量e 1 ,e 2 满足2e 2 -e 1 =2，设a =e 1 +4e 2 ,b =e 1 +e 2 ，若1≤a ⋅b ≤2，则|a|的取值范围为．3.(2023·浙江金华·统考一模)已知平面向量a ，b ，c 满足a ⋅b =74，|a -b|=3，(a -c )(b -c )=-2，则c的取值范围是．1已知向量a ，b 的夹角为π3，且a ⋅b =3，向量c 满足c =λa +1-λ b 0<λ<1 ，且a ⋅c =b ⋅c ，记x =c ⋅aa ，y =c ⋅b b，则x 2+y 2-xy 的最大值为.2(2023·四川成都·高二校联考期中)已知向量a ，b ，c 满足a =1，b=2，a ⋅b=-1，向量c -a 与向量c -b 的夹角为π4，则c 的最大值为．3(2023·浙江绍兴·高二校考学业考试)已知向量a ，b 满足a =1，b=3，且a ⊥b ，若向量c 满足c -a -b =2a -b ，则c的最大值是．1.已知向量a ，b 满足a =1，b =3，且a ⋅b =-32，若向量a -c 与b -c 的夹角为30°，则|c |的最大值是. 2.已知向量a ，b ，满足a =2b =3c =6，若以向量a ，b 为基底，将向量c 表示成c =λa+μb (λ，μ为实数)，都有λ+μ ≤1，则a ⋅b的最小值为 3.已知向量a 、b 满足：a -b=4，a =2b .设a -b 与a +b 的夹角为θ，则sin θ的最大值为.1.已知菱形ABCD 的边长为2，∠BAD =120°，点E ，F 分在边BC ，CD 上，BE =λBC ，DF=μDC ．若λ+μ=23，则AE ⋅AF 的最小值为．2.(2023·天津·高三校联考阶段练习)已知菱形ABCD 的边长为2，∠BAD =120°，点E 、F 分别在边BC ，CD 上，BE =λBC ，DF =μDC ，若2λ+μ=52，则AE ⋅AF 的最小值．3.如图，菱形ABCD 的边长为4，∠BAD =30°，M 为DC 的中点，若N 为菱形内任意一点(含边界)，则AM ⋅AN的最大值为．4.菱形ABCD 的边长为4，∠BAD =30°，若N 为菱形内任意一点(含边界)，则AB ⋅AN的最大值为．5.如图，菱形ABCD 的边长为4,∠BAD =60°,M 为DC 的中点，若N 为菱形内任意一点(含边界)，则AM ⋅AN的最大值为.6.平面四边形ABCD 是边长为2的菱形，且∠A =120°，点N 是DC 边上的点，且DN =3NC，点M 是四边形ABCD 内或边界上的一个动点，则AM ⋅AN的最大值为.7.(2023·全国·高三专题练习)已知向量a ，b 满足a +b =3，a ⋅b =0．若c =λa+1-λ b ，且c ⋅a =c ⋅b，则c 的最大值为．8.已知平面向量a ，b ，c 满足a =2，b =1，a ⋅b =-1，且a -c 与b -c 的夹角为π4，则c 的最大值为．9.已知平面向量a 、b 、c 满足a=4，b =3，c =2，b ⋅c =3，则a -b 2a -c 2-a -b⋅a -c 2最大值为.10.在△ABC 中，M 为边BC 上任意一点，N 为AM 的中点，且满足AN =λAB +μAC，则λ2+μ2的最小值为.题型四:几何意义法1(2023·全国·模拟预测)已知a ，b ，c 是平面向量，满足a -b =a +b ，a =2b =2，c +a -b=5，则向量c 在向量a上的投影的数量的最小值是.2(2023·上海浦东新·上海市建平中学校考三模)已知非零平面向量a ，b ，c 满足：a ，b 的夹角为π4，c -a与c -b 的夹角为3π4，a -b=2，c -b =1，则b ⋅c 的取值范围是.3(2023·全国·高三专题练习)已知平面向量a ,b 夹角为π3，且平面向量c 满足c -a =c -b =1,c -a ⋅c -b =-12,记m 为f t =ta +1-t b (t ∈R )的最小值，则m 的最大值是． 1.(2023·全国·高三专题练习)已知平面向量a ，b ，c 满足a ⋅b =-3，a -b=4，c -a 与c -b 的夹角为π3，则c -a -b 的最大值为． 2.(2023·四川内江·高二四川省内江市第六中学校考开学考试)已知非零平面向量a ，b ，c 满足：a ，b 的夹角为π3，c -a 与c -b的夹角为2π3，a -b =23，c -b =2，则b ⋅c 的取值范围是．3.已知非零平面向量a ，b ，c 满足a -b =2，且(c -a )⋅(c -b )=0，若a 与b 的夹角为θ，且θ∈π6,π3，则|c |的最大值是.4.(2023·全国·高三专题练习)平面向量a ,b ,c 满足：a ,b 的夹角为π3，|a -b|=|b -c |=|a -c |=23，则b ⋅c的最大值为. 5.(2023·广东阳江·高二统考期中)已知非零平面向量a ，b ，c 满足a -b =4，且a -c⋅b -c =-1，若a 与b 的夹角为θ，且θ∈π3,π2，则c 的模取值范围是. 6.(2023·浙江·高三专题练习)已知平面向量a ，b ，c ，若a =b =a -b =1，且2a -c+2b +c =23，则a -c的取值范围是.7.(2023·安徽阜阳·高三安徽省临泉第一中学校考期末)已知向量a ，b 满足a =b =1，且a ⋅b=0，若向量c 满足c +a +b=1，则c 的最大值为.8.(2023·浙江·模拟预测)已知向量a ，b ，c 满足a -b +c=2b =2，b -a 与a 的夹角为3π4，则c 的最大值为．9.(2023·全国·高三专题练习)已知平面向量a ,b ,c 满足：a -b =5，向量a与向量b 的夹角为π3，a -c=23，向量a -c 与向量b -c 的夹角为2π3，则a 2+c 2的最大值为.题型五:坐标法1(2023·全国·高三专题练习)已知向量a ，b 满足2a +b=3，b =1，则a +2a +b 的最大值为.2(2023·江苏常州·高三统考期中)已知平面向量a ,b ,c 满足|a |=2，|b |=4，a ，b 的夹角为π3，且(a -c )⋅(b -c )=2，则|c |的最大值是.3设平面向量a ，b ，c 满足a =b =2，a 与b 的夹角为2π3，a -c ⋅b -c =0则c 的最大值为．1.(2023·安徽滁州·校考三模)已知平面向量a ，b ，c 满足|a|=1，|b |=3，a ⋅b =0，c -a 与c -b 的夹角是π6，则c ⋅b -a 的最大值为.2.(2023·河北·统考模拟预测)如图，在边长为2的正方形ABCD 中．以C 为圆心，1为半径的圆分别交CD ，BC 于点E ，F ．当点P 在劣弧EF 上运动时，BP ⋅DP的最小值为．3.(2023·山东·山东省实验中学校考一模)若平面向量a ，b ，c 满足a =1，b ⋅c =0，a ⋅b =1，a⋅c=-1，则b +c 的最小值为．4.(2023·四川眉山·仁寿一中校考一模)如图，在平面四边形ABCD 中，∠CDA =∠CBA =90°，∠BAD =120°，AB =AD =1，若点E 为CD 边上的动点，则AE ⋅BE的最小值为．5.(2023·安徽滁州·校考模拟预测)已知a=1，b +a +b -a =4，则b -14a 的最小值是.6.(2023·浙江·模拟预测)已知向量a ，b 满足a=3，且b -λa 的最小值为1(λ为实数)，记a,b =α，a ,a -b=β，则b ⋅b -a cos α+β最大值为.7.在矩形ABCD 中，AB =4，AD =3，M ，N 分别是AB ，AD 上的动点，且满足2AM +AN =1，设AC =xAM +yAN ，则2x +3y 的最小值为()A.48B.49C.50D.51题型六:极化恒等式1(2023·山东师范大学附中模拟预测)边长为1的正方形内有一内切圆，MN 是内切圆的一条弦，点P 为正方形四条边上的动点，当弦MN 的长度最大时，PM ⋅PN的取值范围是．2(2023·湖北省仙桃中学模拟预测)如图直角梯形ABCD 中，EF 是CD 边上长为6的可移动的线段，AD =4，AB =83，BC =12，则BE ⋅BF的取值范围为． 3(2023·陕西榆林·三模)四边形ABCD 为菱形，∠BAC =30°，AB =6，P 是菱形ABCD 所在平面的任意一点，则PA ⋅PC的最小值为． 1.(2023·福建莆田·模拟预测)已知P 是边长为4的正三角形ABC 所在平面内一点，且AP=λAB +(2-2λ)AC (λ∈R )，则PA ⋅PC 的最小值为()A.16B.12C.5D.42.(2023·重庆八中模拟预测)△ABC 中，AB =3，BC =4，AC =5，PQ 为△ABC 内切圆的一条直径，M 为△ABC 边上的动点，则MP ⋅MQ的取值范围为()A.0,4B.1,4C.0,9D.1,9题型七:矩形大法1已知圆C 1:x 2+y 2=9与C 2:x 2+y 2=36，定点P (2,0)，A 、B 分别在圆C 1和圆C 2上，满足PA ⊥PB ，则线段AB 的取值范围是．2在平面内，已知AB 1 ⊥AB 2 ，OB 1 =OB 2 =1，AP =AB 1 +AB 2 ，若|OP |<12，则|OA |的取值范围是()A.0,52B.52,72C.52,2D.72,23(2023·全国·高三专题练习)已知圆Q :x 2+y 2=16，点P 1,2 ，M 、N 为圆O 上两个不同的点，且PM⋅PN =0若PQ =PM +PN ，则PQ的最小值为．1.设向量a ，b ，c满足|a |=|b |=1，a ⋅b =12，(a -c )⋅(b -c )=0，则|c |的最小值是()A.3+12B.3-12C.3D.1题型八:等和线1如图，边长为2的等边三角形的外接圆为圆O ，P 为圆O 上任一点，若AP =xAB +yAC，则2x +2y 的最大值为()A.83B.2C.43D.12在△ABC 中，M 为BC 边上任意一点，N 为线段AM 上任意一点，若AN =λAB +μAC(λ，μ∈R )，则λ+μ的取值范围是()A.0,13B.13,12C.[0,1]D.[1,2]3(2023·全国·高三专题练习)如图,OM ∥AB ，点P 在由射线OM 、线段OB 及AB 的延长线围成的区域内(不含边界)运动,且OP =xOA +yOB .当x =-12时，y 的取值范围是()A.0，+∞ B.12，32C.12，+∞ D.-12，321.(2023·全国·高三专题练习)在扇形OAB 中，∠AOB =60°，C 为弧AB 上的一动点，若OC=xOA +yOB，则3x +y 的取值范围是．2.(2023·江西上饶·统考三模)在扇形OAB 中，∠AOB =60°，C 为弧AB 上的一个动点.若OC=xOA +yOB ，则2x +y 的取值范围是.3.(2023·全国·高三专题练习)在扇形OAB 中，OA =1，∠AOB =π3，C 为弧AB 上的一个动点，若OC =xOA +yOB ，则x +3y 的取值范围是.4.(2023·福建三明·高二三明一中校考开学考试)如图，在扇形OAB 中，∠AOB =π3，C 为弧AB 上的一个动点，若OC =xOA +yOB，则x +4y 的取值范围是.5.(2023·全国·高三专题练习)如图，OM ⎳AB ，点P 由射线OM 、线段OB 及AB 的延长线围成的阴影区域内(不含边界).且OP =xOA +yOB，则实数对x ,y 可以是()A.-14,34B.-15,75C.14,-12D.-23,236.如图，B 是AC 的中点，BE =2OB ，P 是平行四边形BCDE 内(含边界)的一点，且OP=xOA +yOBx ,y ∈R ，则下列结论正确的个数为()①当x =0时，y ∈2,3②当P 是线段CE 的中点时，x =-12，y =52③若x +y 为定值1，则在平面直角坐标系中，点P 的轨迹是一条线段④x -y 的最大值为-1A.1B.2C.3D.47.(2023·全国·高三专题练习)在△ABC 中，AB =AC=AB ⋅AC=2，点Q 在线段BC (含端点)上运动，点P 是以Q 为圆心，1为半径的圆及内部一动点，若AP =λAB +μAC，则λ+μ的最大值为()A.1B.33C.3+33D.328.在△ABC 中，AD 为BC 上的中线，G 为AD 的中点，M ，N 分别为线段AB ，AC 上的动点(不包括端点A ，B ，C )，且M ，N ，G 三点共线，若AM =λAB ，AN =μAC，则λ+4μ的最小值为()A.32 B.52C.2D.949.(2023·全国·高三专题练习)在ΔABC 中，AC =2,AB =2,∠BAC =120°,AE =λAB ,AF=μAC ，M 为线段EF 的中点，若AM=1，则λ+μ的最大值为()A.73B.273C.2D.21310.在扇形OAB 中，∠AOB =60o ，OA =1，C 为弧AB 上的一个动点，且OC =xOA +yOB．则x +4y 的取值范围为()A.[1,4)B.[1,4]C.[2,3)D.[2,3]11.(2023·全国·高三专题练习)如图，在扇形OAB 中，∠AOB =600，C 为弧AB 上且与A ,B 不重合的一个动点，且OC =xOA +yOB，若u =x +λy (λ>0)存在最大值，则λ的取值范围为()A.(1,3)B.13,3C.12,1D.12,2题型九:平行四边形大法1如图，圆O 是半径为1的圆，OA =12，设B ，C 为圆上的任意2个点，则AC ⋅BC 的取值范围是.2如图，C ，D 在半径为1的⊙O 上，线段AB 是⊙O 的直径，则AC ⋅BD的取值范围是.3(2023·浙江·模拟预测)已知e 为单位向量，平面向量a ，b 满足|a +e |=|b -e |=1，a ⋅b的取值范围是.1.(2023·江西宜春·校联考模拟预测)半径为1的两圆M 和圆O 外切于点P ，点C 是圆M 上一点，点B 是圆O 上一点，则PC ⋅PB的取值范围为.2.(2023·福建·高三福建师大附中校考阶段练习)设圆M ，圆N 的半径分别为1，2，且两圆外切于点P ，点A ，B 分别是圆M ，圆N 上的两动点，则PA ⋅PB的取值范围是()A.-8,12B.-16,34C.-8,1D.-16,1题型十:向量对角线定理1已知平行四边形ABCD ，AB ⊥BC ，AB =BC =AD =2，CD =3，AC 与BD 交于点O ，若记a =OA⋅OB ，b =OB ⋅OC ，c =OC ⋅OD ，则()A.a <b <cB ．a <c <bC ．c <a <bD ．b <a <c2如图，在圆O 中，若弦AB =3，弦AC =5，则AO ⋅BC的值是()A.-8B ．-1C ．1D ．83如图，在四边形ABCD 中，AB ⊥BC ，AD ⊥BC 若，AB =a ，AD =b ，则AC ⋅BD 等于()A.b 2-a 2B.a 2-b 2C.a 2+b 2D.a 2⋅b 2。

高考平面向量题型归纳总结在高考数学考试中，平面向量是一个常见的考点，也是学生普遍认为较为困难的部分之一。

平面向量题型包括向量的加减、数量积、向量方向等。

本文将对高考平面向量题型进行归纳总结，帮助学生更好地掌握此类题型。

一、向量的加减1. 向量的加法向量的加法满足交换律和结合律，即a + b = b + a，(a + b) + c = a + (b + c)。

在解题过程中，可以利用向量的平移性质，将向量平移至同一起点，再连接终点得到新的向量。

2. 向量的减法向量的减法可以转化为加法进行处理，即a - b = a + (-b)。

其中，-b表示b的反向量，即方向相反的向量，模长相等。

二、数量积数量积又称为内积或点积，记作a·b。

1. 定义对于两个向量a(x₁, y₁)和b(x₂, y₂)，它们的数量积a·b = x₁x₂ +y₁y₂。

另外，数量积还可以表示为向量模长和夹角的乘积，即a·b =|a| · |b| · cosθ，其中θ为a与b的夹角。

2. 性质(1) 交换律：a·b = b·a(2) 分配律：a·(b + c) = a·b + a·c(3) 结合律：k(a·b) = (ka)·b = a·(kb)，其中k为实数(4) 若a·b = 0，则a与b垂直或其中一个为零向量(5) 若a·b > 0，则夹角θ为锐角；若a·b < 0，则夹角θ为钝角。

三、向量方向向量的方向可以用两种方式来表示：1. 向量的方向角：向量a(x, y)的方向角为与x轴正方向之间的夹角α，其中-π < α ≤ π。

2. 方向余弦：向量a(x, y)的方向余弦为与x轴的夹角的余弦值cosα，与y轴的夹角的余弦值cosβ。

在解决平面向量题型时，可以利用这两种方式来确定向量的方向。

专题平面向量常见题型与解题指导Standardization of sany group #QS8QHH-HHGX8Q8-GNHHJ8-HHMHGN#平面向量常见题型与解题指导一、考点回顾1、本章框图2、高考要求1、理解向量的概念，掌握向量的几何表示，了解共线向量的概念。

2、掌握向量的加法和减法的运算法则及运算律。

3、掌握实数与向量的积的运算法则及运算律，理解两个向量共线的充要条件。

4、了解平面向量基本定理，理解平面向量的坐标的概念，掌握平面向量的坐标运算。

5、掌握平面向量的数量积及其几何意义，了解用平面向量的数量积可以处理有关长度、角度和垂直的问题，掌握向量垂直的条件。

6、掌握线段的定比分点和中点坐标公式，并且能熟练运用；掌握平移公式。

7、掌握正、余弦定理，并能初步运用它们解斜三角形。

8、通过解三角形的应用的教学，继续提高运用所学知识解决实际问题的能力。

3、热点分析对本章内容的考查主要分以下三类：1.以选择、填空题型考查本章的基本概念和性质.此类题一般难度不大，用以解决有关长度、夹角、垂直、判断多边形形状等问题.2.以解答题考查圆锥曲线中的典型问题.此类题综合性比较强，难度大，以解析几何中的常规题为主.3.向量在空间中的应用（在B类教材中）.在空间坐标系下，通过向量的坐标的表示，运用计算的方法研究三维空间几何图形的性质.在复习过程中，抓住源于课本，高于课本的指导方针.本章考题大多数是课本的变式题，即源于课本.因此，掌握双基、精通课本是本章关键.分析近几年来的高考试题，有关平面向量部分突出考查了向量的基本运算。

对于和解析几何相关的线段的定比分点和平移等交叉内容，作为学习解析几何的基本工具，在相关内容中会进行考查。

本章的另一部分是解斜三角形，它是考查的重点。

总而言之，平面向量这一章的学习应立足基础，强化运算，重视应用。

考查的重点是基础知识和基本技能。

4、复习建议由于本章知识分向量与解斜三角形两部分，所以应用本章知识解决的问题也分为两类：一类是根据向量的概念、定理、法则、公式对向量进行运算，并能运用向量知识解决平面几何中的一些计算和证明问题；另一类是运用正、余弦定理正确地解斜三角形，并能应用解斜三角形知识解决测量不可到达的两点间的距离问题。

考点30平面向量的概念及线性运算（3种核心题型+基础保分练+综合提升练+拓展冲刺练）【考试提醒】1.理解平面向量的意义、几何表示及向量相等的含义.2.掌握向量的加法、减法运算，并理解其几何意义及向量共线的含义.3.了解向量线性运算的性质及其几何意义．【知识点】1．向量的有关概念(1)向量：既有大小又有 的量叫做向量，向量的大小称为向量的．(2)零向量：长度为的向量，记作．(3)单位向量：长度等于 长度的向量．(4)平行向量：方向相同或 的非零向量，也叫做共线向量，规定：零向量与任意向量．(5)相等向量：长度相等且方向 的向量．(6)相反向量：长度相等且方向 的向量．2．向量的线性运算向量运算法则(或几何意义)运算律加法交换律：a ＋b ＝ ；结合律：(a ＋b )＋c ＝________减法a －b ＝a ＋(－b )数乘|λa |＝，当λ>0时，λa 的方向与a 的方向；当λ<0时，λa 的方向与a 的方向 ；当λ＝0时，λa ＝λ(μa )＝ ；(λ＋μ)a ＝ ；λ(a ＋b )＝3.向量共线定理向量a (a ≠0)与b 共线的充要条件是：存在唯一一个实数λ，使 .常用结论1．一般地，首尾顺次相接的多个向量的和等于从第一个向量起点指向最后一个向量终点的向量，即A 1A 2—→ ＋A 2A 3—→ ＋A 3A 4—→ ＋…＋A n －1A n ———→ ＝A 1A n —→，特别地，一个封闭图形，首尾连接而成的向量和为零向量．2．若F 为线段AB 的中点，O 为平面内任意一点，则OF → ＝12(OA → ＋OB → )．3．若A ，B ，C 是平面内不共线的三点，则PA → ＋PB → ＋PC → ＝0⇔P 为△ABC 的重心，AP → ＝13(AB → ＋AC → )．4．对于任意两个向量a ，b ，都有||a |－|b ||≤|a ±b |≤|a |＋|b |.【核心题型】题型一　平面向量的基本概念平行向量有关概念的四个关注点(1)非零向量的平行具有传递性．(2)共线向量即为平行向量，它们均与起点无关．(3)向量可以平移，平移后的向量与原向量是相等向量．(4)a|a |是与a 同方向的单位向量．【例题1】（2024·湖南永州·三模）在ABC V 中，120ACB Ð=o，3AC uuu r =，4BC =uuu r，0DC DB ×=uuu r uuu r，则AB AD +uuu r uuu r 的最小值为（ ）A ．2B ．4C ．1D 2【变式1】（2023·北京大兴·三模）设a r ，b r 是非零向量，“a a bb =r r rr ”是“a b =r r”的（ ）A ．充分而不必要条件B ．必要而不充分条件C ．充分必要条件D ．既不充分也不必要条件【变式2】（2022·江苏·三模）已知向量()6,2a =r ，与a r共线且方向相反的单位向量b =r.【变式3】（2022·上海虹口·二模）已知向量a r ，b r满足2a =r ，1b =r ，a +r ，则a b -=r r.题型二　平面向量的线性运算平面向量线性运算的常见类型及解题策略(1)向量求和用平行四边形法则或三角形法则；求差用向量减法的几何意义．(2)求参数问题可以通过向量的运算将向量表示出来，进行比较，求参数的值．命题点1　向量加、减法的几何意义【例题2】（2024·福建福州·三模）已知线段AB 是圆O 的一条长为2的弦，则AO AB ×=uuu r uuu r（ ）A ．1B ．2C ．3D ．4【变式1】（2024·河南三门峡·模拟预测）在ABC V 中，3,4AN NC BP PN ==uuu r uuu r uuu r uuu r ，则AP =uuu r （ ）A ．1355AB CA+uuur uuu r B ．3455AB CA-uuur uuu r C ．3155AB CA-uuur uuu r D ．1355AB CA-uuur uuu r 【变式2】（2023·四川乐山·一模）已知正六边形ABCDEF 边长为2，MN 是正六边形ABCDEF 的外接圆的一条动弦，2MN =，P 为正六边形ABCDEF 边上的动点，则PM PN ×uuuu r uuu r的最小值为 .【变式3】（2023·上海金山·二模）已知a r 、b r 、c r 、d ur 都是平面向量，且|||2||5|1a a b a c =-=-=r r r r r ，若,4a d p =r u r ，则||||b dcd -+-r u r r u r的最小值为．命题点2　向量的线性运算【例题3】（2023·河北·模拟预测）在平行四边形ABCD 中，已知24==A D A B ，且4AB BC ×=-uuu r uuu r ，则向量AB uuu r与AC uuu r 的夹角的余弦值为（ ）A ．12-B ．0C ．12D 【变式1】（2024·安徽·模拟预测）已知O 为等边ABC V 的中心，若3,2OA a AB b ==uuu r uuu r r r，则AC =uuu r．（用,a b r r 表示）【变式2】（2024·黑龙江哈尔滨·二模）已知不共线的三个单位向量,,a b c r r r 满足0,a b c a l ++=r r r r r 与b r 的夹角为π3，则实数l =.【变式3】（2024·江苏扬州·模拟预测）记ABC V 的内角,,A B C 的对边分别为,,a b c ，若()()3a b c a b c +++-=，且ABC V (1)求角C ；(2)若2AD DB =uuu r uuu r，求CD 的最小值.命题点3　根据向量线性运算求参数【例题4】（2024·江苏·二模）已知非零向量π(cos 2,sin())4a a a =+r ，π(sin(4b a =+r ，若//a b r r ，则sin 2a =（ ）A ．1-B C ．45D ．35【变式1】（2024·浙江杭州·三模）已知不共线的平面向量a r ，b r满足()()2a b a b l l ++∥r r r r ，则正数l =（ ）A ．1B C D ．2【变式2】（2024·上海·三模）设平面向量()sin ,1a q =r ，(cos b q =r ，若a r ，b r 不能组成平面上的一个基底，则tan q = ．【变式3】（2023·四川南充·一模）在ABC V 中，设角A ，B ，C 的对边分别为a ，b ，c ．已知向量),sin m A A =r，()1,1n =-r ，且m n ∥r r．(1)求角A 的大小；(2)若a =sin sin 0a B c A -=，求ABC V 的面积．题型三　共线定理及其应用利用共线向量定理解题的策略(1)a ∥b ⇔a ＝λb (b ≠0)是判断两个向量共线的主要依据．(2)若a 与b 不共线且λa ＝μb ，则λ＝μ＝0.(3)若OA → ＝λOB → ＋μOC → (λ，μ为常数)，则A ，B ，C 三点共线的充要条件是λ＋μ＝1.【例题5】（2024·全国·模拟预测）已知平面上点O ，A ，B 满足2OA OB ==uuu r uuu r ，且||OA OB OA +=uuu r uuu r uuu r ，点C 满足OC OB -=uuu r uuu rP 满足()1OP tOA t OC =+-uuu r uuu r uuu r ，则OP uuu r 的最小值为（ ）A B C ．1D ．1【变式1】（2024·浙江·模拟预测）已知向量1e u r ，2e u ur 是平面上两个不共线的单位向量，且122AB e e =+u r uuu r u u r ，1232BC e e =-+uuur u r u u r ，1236DA e e =-uuu r u r u u r ，则（ ）A ．、、ABC 三点共线B ．A BD 、、三点共线C ．A C D 、、三点共线D ．B C D 、、三点共线【变式2】（2024·上海松江·二模）已知正三角形ABC 的边长为2，点D 满足CD mCA nCB =+uuu r uuu r uuu r，且0m >，0n >，21m n +=，则||CD uuu r 的取值范围是 .【变式3】（2022·江苏盐城·模拟预测）如图，已知正方形ABCD 的边长为2，过中心O 的直线l 与两边AB ，CD 分别交于点M ，N ．(1)若Q 是BC 的中点，求QM QN ×uuuu r uuu r的取值范围；(2)若P 是平面上一点，且满足2(1)OP OB OC l l =+-uuu r uuu r uuu r ，求PM PN ×uuuu r uuu r的最小值．【课后强化】【基础保分练】一、单选题1．（2024·全国·模拟预测）已知平面向量a r ，b r ，则“//a b rr ”是“存在R l Î，使得a b l =r r ”的（ ）A ．必要不充分条件B ．充分不必要条件C ．充要条件D ．既不充分也不必要条件2．（2023·贵州黔东南·三模）在△ABC 中，已知4AB =，M 为线段AB 的中点，3CM =，若2CN NM=uuu r uuuu r，则NA NB ×=uuu r uuu r （ ）A ．92-B ．3-C ．D ．3．（2024·广东深圳·模拟预测）已知点()2,6A ，()2,3B --，()0,1C ，7,62D æöç÷èø，则与向量2AB CD +uuu r uuu r同方向的单位向量为（ ）A ．B ．C ．D ．43,55æö-ç÷èø4．（2024·山西朔州·一模）已知)2,a b ==r r，且a b ^r r ，则2a b -=r r （ ）A ．B ．C ．4D ．二、多选题5．（2024·辽宁·二模）ABC V 的重心为点G ，点O ，P 是ABC V 所在平面内两个不同的点，满足OP OA OB OC =++uuu r uuu r uuu r uuu r，则（ ）A ．,,O P G 三点共线B ．2OP OG =uuu r uuu rC ．2OP AP BP CP =++uuu r uuu r uuu r uuu rD ．点P 在ABC V 的内部6．（2024·浙江宁波·二模）若平面向量,,a b c r r r 满足1,1,3a b c ===r r r 且a c b c ×=×r r r r ，则（ ）A ．a b c ++r r r的最小值为2B ．a b c ++r r r的最大值为5C ．a b c -+r r r 的最小值为2D ．a b c -+r r r的最大值为三、填空题7．（2023·重庆·一模）在PAB V 中，4,3AB APB p=Ð=，点Q 满足2()QP AQ BQ =+uuu r uuu r uuu r ，则QA QB×uuu r uuu r的最大值为.8．（2023·云南大理·模拟预测）若a b =r r ，8a b +=r r ，6a b -=r r ，则a r 在b r上投影向量的模为．9．（2023·陕西西安·模拟预测）若平面四边形ABCD 满足0AB CD +=uuu r uuu r r，()0AB AD AC -×=uuu r uuu r uuu r ，则该四边形一定是 .四、解答题10．（2024·山西朔州·一模）已知ABC V 的内角,,A B C 的对边分别为,,a b c ，向量()(),,sin sin ,sin sin m a b c n A C A B =+=--r r ，且//m n r r ．(1)求B ；(2)求222b a c+的最小值．11．（2024·四川·模拟预测）已知ABC V 的内角,,A B C 的对边分别为,,a b c ，且cos 2cos B a bC c-=．(1)求角C ；(2)若4AB AC +=uuu r uuu r，求ABC V 面积的最大值．【综合提升练】一、单选题1．（2023·四川南充·一模）已知正方形ABCD 的边长为1，则AB BC CA +-=uuu r uuu r uuu r （ ）A ．0B C ．D ．42．（2024·全国·模拟预测）已知向量()4,a m =r ，()2,2b m =-r ，则“4m =”是“a r 与b r共线”的（ ）A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件3．（2024·安徽马鞍山·三模）已知平面向量1e u r ，2e u u r 不共线，12(21)2a k e e =-+r u r u u r ，12b e e =-r u r ur ，且//a b r r，则k =（ ）A ．12-B ．0C ．1D ．324．（2024·四川遂宁·模拟预测）在ABC V 中，点F 为线段BC 上任一点（不含端点），若()20,0AF xAB y AC x y =+>>uuu r uuu r uuu r ，则12x y+的最小值为（ ）A ．3B ．4C ．8D ．95．（2023·四川南充·一模）已知正方形ABCD 的边长为1，则AB BC CA +-=uuu r uuu r uuu r （ ）A ．0B C ．2D ．6．（23-24高三下·山东菏泽·阶段练习）已知向量a r ，b r，满足a b a b ==-r r r r ，则()·a a b +=r r r （ ）A ．212a r B ．212b rC ．()212a b +r r D ．()212a b -r r7．（23-24高三上·全国·阶段练习）设平面向量(1,3)a =r ，||2b =r ，且||a b -=rr ，则()()2·a b a b +-r rr r =（ ）A ．1B ．14C D8．（2024·上海杨浦·二模）平面上的向量a r 、b r 满足：3a =r，4b =r ，a b ^r r .定义该平面上的向量集合{|||||,}A x x a x b x a x b =+<+×>×r rr r r r r r r .给出如下两个结论：①对任意c A Îr ，存在该平面的向量d A Îu r ，满足0.5c d -=rr ②对任意c A Îr ，存在该平面向量d A Ïu r ，满足0.5c d -=rr 则下面判断正确的为（ ）A ．①正确，②错误B ．①错误，②正确C ．①正确，②正确D ．①错误，②错误二、多选题9．（2023·海南海口·模拟预测）下列命题为真命题的是（ ）A ．一组数据22 ，20 ，17 ，15，13，11，9，8，8，7 的第90百分位数是21B ．若等差数列{}n a 满足x y p q a a a a +=+(x 、y 、p 、*N )q Î，则x y p q +=+C ．非零平面向量a r 、b r 、c r 满足//a b r r ，//b c r r，则//a cr r D ．在ABC V 中，“AB AC >”与“cos cos C B <”互为充要条件10．（2024·全国·模拟预测）设,a b r r是两个非零向量，下列命题正确的是（ ）A ．若0a b ×=r r，则//a b r r B ．若a b a b ×=×r r r r ，则//a br r C ．若a b ^r r，则()2a b a b×=×r r r r D ．若a b a b +=-r r r r ，则a b^r r11．（2022·辽宁·模拟预测）“圆幂定理”是平面几何中关于圆的一个重要定理，它包含三个结论，其中一个是相交弦定理：圆内的两条相交弦，被交点分成的两条线段长的积相等.如图，已知圆O 的半径为2，点P 是圆O 内的定点，且OP =，弦AC 、BD 均过点P ，则下列说法正确的是（ ）A ．PA PC ×uu u r uuu r为定值B ．OA OC ×uuu r uuu r的取值范围是[]2,0-C ．当AC BD ^时，AB CD ×uuu r uuu r为定值D ．AC BD ×uuu r uuu r 的最大值为12三、填空题12．（2024·天津·一模）已知平行四边形ABCD 的面积为23πBAD Ð=，且2BE EC =uuu r uuu r .若F 为线段DE 上的动点，且56AF AB AD l =+uuu r uuu r uuu r，则实数l 的值为 ；AF uuu r 的最小值为 .13．（2023·河南·模拟预测）已知向量()1cos ,sin e a a =u r ，()2cos ,sin e b b =u u r ，()0,1m =u r ，若12e e m +=u r u u r u r ，则12e e ×=u r u u r．14．（2024·青海西宁·二模）若向量,a b r r 不共线，且()()//xa b a yb ++r r r r，则xy 的值为 ．四、解答题15．（2024·吉林延边·一模）已知ABC V 的内角A ，B ，C 所对的边分别为a ，b ，c ，sin sin sin A B c aC b a +-=-．(1)求B ；(2)若点D 在AC 上，且2AD BD DC ==，求ac．16．（2024·浙江温州·模拟预测）ABC V 的角,,A B C 对应边是 a ，b ，c ，三角形的重心是 O .已知3,4,5OA OB OC ===.(1)求 a 的长.(2)求ABC V 的面积.17．（2023·湖南·模拟预测）在ABC V 中，角,,A B C 所对的边分别为,,,a b c ABC V 的面积为πsin 3A A æö-ç÷èø.(1)求C 的大小.(2)点D 满足AD CA =uuu r uuu r.若c =,a b .18．（2023·四川成都·三模）在锐角ABC V 中，内角A ，B ，C 的对边分别为a ，b ，c ，且6a =，()2sin 2sin()A C b B C +++=(1)求角B 的大小；(2)若3AC DC =uuu r uuu r ，BD =c 的值．19．（2024·山东青岛·一模）已知O 为坐标原点，点W 为O e ：224x y +=和M e 的公共点，0OM OW ×=uuuu r uuuu r ，M e 与直线20x +=相切，记动点M 的轨迹为C ．(1)求C 的方程；(2)若0n m >>，直线1:0l x y m --=与C 交于点A ，B ，直线2:0l x y n --=与C 交于点A ¢，B ¢，点A ，A ¢在第一象限，记直线AA ¢与BB ¢的交点为G ，直线AB ¢与BA ¢的交点为H ，线段AB 的中点为E ．①证明：G ，E ，H 三点共线；②若()217m n ++=，过点H 作1l 的平行线，分别交线段AA ¢，BB ¢于点T ，T ¢，求四边形GTET ¢面积的最大值．【拓展冲刺练】一、单选题1．（2024·黑龙江·模拟预测）已知在梯形ABCD 中，//AB CD 且满足2AB DC =uuu r uuur，E 为AC 中点，F 为线段AB 上靠近点B 的三等分点，设AB a =uuu r r ，AD b uuu r r =，则EF =uuu r （ ）．A ．2132a b -r r B ．3146a b -r r C ．51122a b -r r D ．1126a b -r r 2．（2024·北京西城·二模）已知向量a r ，b r 满足()4,3a =r ，()210,5a b -=-r r ，则（ ）A ．0a b +=r r r B ．0a b ×=r r C ．a b >r r D ．a br r ∥3．（2024·全国·二模）点,O P 是ABC V 所在平面内两个不同的点，满足OP OA OB OC =++uuu r uuu r uuu r uuu r ，则直线OP 经过ABC V 的（ ）A ．重心B ．外心C ．内心D ．垂心4．（2024·浙江宁波·模拟预测）已知ABC V 是边长为1的正三角形，1,3AN NC P =uuu r uuu r 是BN 上一点且29AP mAB AC =+uuu r uuu r uuu r ，则AP AB ×=uuu r uuu r （ ）A ．29B ．19C ．23D ．1二、多选题5．（2024·福建厦门·三模）已知等边ABC V 的边长为4，点D ，E 满足2BD DA =uuu r uuu r ，BE EC =uuu r uuu r ，AE 与CD 交于点O ，则（ ）A ．2133CD CA CB =+uuu r uuu r uuu r B ．8BO BC ×=uuu r uuu rC ．2CO OD =uuu r uuu r D ．||OA OB OC ++=uuu r uuu r uuu r 6．（2024·安徽淮北·一模）如图，边长为2的正六边形ABCDEF ，点P 是DEF V 内部（包括边界）的动点，AP xAB y AD =+uuu r uuu r uuu r ，x ，y ÎR .（ ）A ．0AD BE CF -+=uuu r uuu r uuu r rB ．存在点P ，使x y=C ．若34y =，则点P 的轨迹长度为2D ．AP AB ×uuu r uuu r 的最小值为2-三、填空题7．（2024·山西太原·三模）赵爽是我国古代数学家、天文学家，大约在公元222年，赵爽为《周髀算经》一书作序时，介绍了 “勾股圆方图”，亦称“赵爽弦图” (以直角三角形的斜边为边得到的正方形). 类比 “赵爽弦图”，构造如图所示的图形，它是由三个全等的三角形与中间的一个小等边三角形拼成的一个大等边三角形，且DF AF =，点P 在AB 上，2BP AP =，点Q 在DEF V 内 (含边界)一点，若PQ PD PA l =+uuu r uuu r uuu r ，则l 的最大值为 .8．（2022·辽宁鞍山·模拟预测）点P 在椭圆2214x y +=上，P 不在坐标轴上，()2,0A ，()2,1C ，()10,1B ，()20,1B -，直线1B P 与2x =交于点T ，直线2B P 与x 轴交于点S ，设OS OA l ®®=，AT AC m ®®=，则l m +的值为 ．9．（2023·四川乐山·一模）已知正方形ABCD 边长为MN 是正方形ABCD 的外接圆的一条动弦，2MN =，P 为正方形ABCD 边上的动点，则MP PN ×uuu r uuu r 的最大值为 .四、解答题10．（2023·江西·模拟预测）在ABC V 中，内角A ，B ，C 的对边分别为a ，b ，c ，已知M为BC 边的中点，()2a ab AM CB -×=uuuu r uuu r ．(1)求角C 的大小；(2)若ABC V 的面积为ABC V 周长的最小值．11．（2023·河北·模拟预测）如图，D 为ABC V 内部一点，DE BC ^于E ，AB AD =.请从下面①②③中选取两个作为条件，证明另一个成立.①3CE EB =uuu r uuu r ；②())sin sin sin B C B C +=-；③2AD DE AE DE AD AD DE +=×.。

平面向量方法、题型、及应试技巧总结一．向量有关概念：1．向量的概念：既有大小又有方向的量，注意向量和数量的区别。

向量常用有向线段来表示，注意不能说向量就是有向线段，为什么?（向量可以平移)。

如：已知A （1，2），B （4，2），则把向量AB 按向量a ＝（－1，3）平移后得到的向量是_____（答：（3,0））2．零向量：长度为0的向量叫零向量,记作：0，注意零向量的方向是任意的；3．单位向量：长度为一个单位长度的向量叫做单位向量(与AB 共线的单位向量是||AB AB ±)； 4．相等向量:长度相等且方向相同的两个向量叫相等向量，相等向量有传递性;5．平行向量（也叫共线向量）:方向相同或相反的非零向量a 、b 叫做平行向量，记作：a ∥b ，规定零向量和任何向量平行. 提醒：①相等向量一定是共线向量，但共线向量不一定相等；②两个向量平行与与两条直线平行是不同的两个概念：两个向量平行包含两个向量共线， 但两条直线平行不包含两条直线重合;③平行向量无传递性!（因为有0）； ④三点A B C 、、共线⇔ AB AC 、共线；6．相反向量：长度相等方向相反的向量叫做相反向量。

a 的相反向量是－a 。

如下列命题:(1）若a b =，则a b =.（2)两个向量相等的充要条件是它们的起点相同，终点相同。

（3）若AB DC =,则ABCD 是平行四边形。

（4）若ABCD 是平行四边形，则AB DC =。

（5）若,a b b c ==，则a c =。

（6）若//,//a b b c ，则//a c 。

其中正确的是_______（答：（4）（5））二．向量的表示方法：1．几何表示法：用带箭头的有向线段表示，如AB ,注意起点在前,终点在后； 2．符号表示法：用一个小写的英文字母来表示，如a ，b ，c 等；3．坐标表示法：在平面内建立直角坐标系，以与x 轴、y 轴方向相同的两个单位向量i ，j 为基底,则平面内的任一向量a 可表示为(),a xi y j x y =+=，称(),x y 为向量a 的坐标，a ＝(),x y 叫做向量a 的坐标表示。

第1讲 平面向量的概念及线性运算4种题型【考点分析】考点一：向量的基本概念①定义：既有大小又有方向的量叫做向量．②向量的模：向量AB 的大小，也就是向量AB 的长度，叫做向量的模，记作||AB ． ③零向量：长度为0的向量，其方向是任意的． ④单位向量：长度等于1个单位的向量．⑤平行向量：方向相同或相反的非零向量．平行向量又叫共线向量．规定：0与任一向量平行． ⑥相等向量：长度相等且方向相同的向量． ⑦相反向量：长度相等且方向相反的向量． 考点二：向量的线性运算和向量共线定理 ①向量的线性运算考点三：向量共线定理①如果λ=a b 且0≠b ，则a b ∥；反之a b ∥且0≠b ，则一定存在唯一一个实数λ，使λ=a b ． 推论：①三点A ，B ，C 共线⇔AB ，AC 共线（功能：证明三点共线）；①向量PA ，PB ，PC 中三个向量的终点A ，B ，C 共线⇔存在实数λ，μ使得PA PB PC λμ=+，且1.λμ+=①BD DC λ=，111AD AC AC λλλ=+++． 【题型目录】题型一： 平面向量的概念 题型二： 平面向量的加法、减法 题型三： 平面向量的线性运算与共线定理 题型四： 由平面向量的性质判断图形的形状 【典型例题】题型一： 平面向量的概念【例1】给出下列说法：①零向量是没有方向的；①零向量的长度为0；①零向量的方向是任意的；①单位向量的模都相等.其中正确的有（ ） A ．1个 B ．2个C ．3个D ．4个【答案】C【分析】根据零向量及单位向量的概念即可求解. 【详解】解：对①：零向量的方向是任意的，故①错误； 对①：零向量的长度为0，故①正确； 对①：零向量的方向是任意的，故①正确； 对①：单位向量的模都等于1，故①正确. 故选：C.【例2】下列命题中正确的是（ ）A ．两个有共同起点且相等的向量，其终点必相同B ．两个有公共终点的向量，一定是共线向量C ．两个有共同起点且共线的向量，其终点必相同D ．若AB 与CD 是共线向量，则点A ，B ，C ，D 必在同一条直线上 【答案】A【分析】根据向量相等与共线的概念即可解决.【详解】两个相等的向量方向相同且长度相等，因此起点相同时终点必相同，故A 正确； 两个有公共终点的向量，可能方向不同，也可能模长不同，故B 错误；两个有共同起点且共线的向量可能方向不同，也可能模长不同，终点未必相同，故C 错误；AB 与CD 是共线向量，也可能是AB 平行于CD ，故D 错误.故选：A【例3】有下列结论：①表示两个相等向量的有向线段，若它们的起点相同，则终点也相同； ①若a b ≠，则a ，b 不是共线向量；①若AB DC =，则四边形ABCD 是平行四边形； ①若m n =，n k =，则m k =；①有向线段就是向量，向量就是有向线段. 其中，错误的个数是（ ） A ．2 B ．3C ．4D ．5，若a b ≠也有可能a ，b 长度不等，但方向相同或相反，即共线，AB DC =，则AB ，DC 不一定相等，所以四边形，若m n =，n k =，则m k =，①正确；，有向线段不是向量，向量可以用有向线段表示，综上，错误的是①①①，共3个. 【例4】设0a 为单位向量，①若a 为平面内的某个向量，则a ＝|a |0a ；②若a 与0a 平行，则a ＝|a |0a ；③若a 与0a 平行且|a |＝1，则a ＝0a ．上述命题中，假命题的个数是A ．0B ．1C ．2D ．3 【答案】D【详解】单位向量的模为1，方向可以是不同方向，所以①错 ；若a 与0a 平行，则两个向量可以同向，也可以反向，方向不一定相同，所以①错；①错因此选D 【例5】下列命题中，正确的个数是（ ）①单位向量都相等；①模相等的两个平行向量是相等向量； ①若,a b 满足||||a b >，且a 与b 同向，则a b >①若两个向量相等，则它们的起点和终点分别重合； ①若,a b b c ∥∥，则a c ∥ A ．0个 B ．1个C ．2个D ．3个【答案】A【分析】根据平面向量的基本概念，对选项中的命题进行分析、判断正误即可. 【详解】单位向量的大小相等，但方向不一定相同，故①错误； 模相等的两个平行向量是相等向量或相反向量，故①错误； 向量有方向，不能比较大小，故①错误；向量是可以自由平移的矢量，当两个向量相等时，它们的起点与终点不一定相同，故①错误； 当0b =时，可满足,a b b c ∥∥，但a 与c 不一定平行，故①错误； 综上，正确的个数是0， 故选：A ．【例6】下面关于向量的说法正确的是（ ） A ．单位向量：模为1的向量B ．零向量：模为0的向量，零向量没有方向C ．平行（共线）向量：方向相同或相反的向量D ．相等向量：模相等，方向相同的向量 【答案】ACD【分析】根据平面向量的基本定义逐个辨析即可.【详解】根据向量的定义可得，模为1的向量为单位向量，模为0的向量为零向量，零向量的方向是任意的，方向相同或相反的向量为共线向量，模相等，方向相同的向量为相等向量，ABCD 均正确， 故选：ACD ．【例7】下列叙述中错误的是（ ） A ．若a b =，则32a b > B ．若a b ∥，则a 与b 的方向相同或相反 C ．若a b ∥，b c ∥，则a c ∥ D ．对任一非零向量a ，||aa 是一个单位向量 【答案】ABC【分析】对于A ，根据向量的概念判断，对于BCD ，举例判断.【详解】因为是既有大小又有方向的量，所以向量不能比较大小，故A 错误；由于零向量与任意向量共线，且零向量的方向是任意的，故，若b 为零向量，则a 与c 可能不是共线向量，故，对任一非零向量a ，||aa 表示与a ABC 【题型专练】1.下列命题正确的是（ ）A ．向量AB 与BA 是相等向量 B ．共线的单位向量是相等向量C ．零向量与任一向量共线D ．两平行向量所在直线平行 【答案】C【详解】A 选项方向不同，所以错 ；B 选项共线向量是方向相同或者相反，所以错；C 选项，规定零向量的方向是任意的，所以C 对；D 选项向量共线可以在一条直线上，直线平行不能共线，所以D 错 2.下列命题中正确的个数是（ ）①若向量AB 与CD 是共线向量，则A 、B 、C 、D 必在同一直线上； ①若向量a 与向量b 平行，则a ，b 方向相同或相反；①若非零向量AB 与CD 是共线向量，则它们的夹角是0°或180°； ①若a b =，则a ，b 是相等向量或相反向量. A ．0 B ．1C ．2D ．3，根据模长的定义，可知方向不确定，可得答案.【详解】①错误，平行向量又叫共线向量，向量AB 与CD 是共线向量，则AB 与CD 平行或共线；错误，a 与b 至少有一个为零向量时，结论不成立；由向量的夹角可知正确； 错误，由a b =，只能说明a ，b 的长度相等，确定不了方向.3.给出下列命题:①共线向量一定在同一条直线上;①若A ,B ,C ,D 是不共线的四点,则AB DC =是四边形ABCD 为平行四边形的充要条件;①a b =的充要条件是||a b |=|且//a b .其中正确命题的序号是_______.【答案】①【详解】①不正确,共线向量不一定在同一条直线上,也可能在两条平行直线上; ①正确 ①AB DC =,①||||AB DC =且//AB DC , 又A ,B ,C ,D 是不共线的四点, ①四边形ABCD 为平行四边形.反之,若四边形ABCD 为平行四边形,则//AB DC 且||||AB DC =,①AB DC =;①不正确,当//a b 且方向相反时,||||a b =,但不能得到a b =,故||||a b =且//a b 不是a b =的充要条件,而是必要不充分条件. 故答案为：①4.把所有单位向量的起点平移到一点O ,则其终点构成的图形是_____________. 【答案】以O 为圆心的单位圆设终点为A ，则1AO =，则终点构成的图形是以O 为圆心的单位圆. 故答案为：以O 为圆心的单位圆. 5.下列说法中正确的是（ ） A ．若12,e e 为单位向量，则12e e = B ．若a 与b 共线，则a b =或a b =-C ．若0a =，则0a =D ．a a是与非零向量a 共线的单位向量中，向量12,e e 的方向不一定相同，所以中，向量a 与b 的长度不一定相等，所以0a =，根据零向量的定义，可得0a =，所以C 1a a a a =⋅，可得a a与向量a 同向，a a的模等于a a是与非零向量a 共线的单位向量，所以故选：CD.6．下列说法中正确的是（ ）A ．力是既有大小，又有方向的量，所以是向量B ．若向量//AB CD ，则//AB CDC ．在四边形ABCD 中，若向量//AB CD ，则该四边形为平行四边形 D ．速度、加速度与位移的合成与分解，实质上就是向量的加减法运算 【答案】AD【分析】根据向量的定义，共线向量的定义，逐项判定，即可求解.【详解】对于A 中，根据向量的定义，力是既有大小，又有方向的量，所以是向量，所以A 正确； 对于B 中，向量//AB CD ，则//AB CD 或AB 与CD 共线，所以B 错误；对于C 中，在四边形ABCD 中，若向量//AB CD 、则只有一组对边平行，不一定是平行四边形，所以C 错误；对于D 中，根据向量的运算法则，可得速度、加速度与位移的合成与分解，实质上就是向量的加减法运算，所以D 正确. 故选：AD.7．下列结论中正确的是（ ） A ．若a b =，则a b = B ．若,a b b c ==，则a c =C ．若A ，B ，C ，D 是不共线的四点，则“AB DC =”是“四边形ABCD 为平行四边形”的充要条件 D ．“a b =”的充要条件是“a b =且a b ∥” 是不共线的四点，则当AB DC =时，，故且,AB DC 同向，故AB DC =，故C ，当a b 且方向相反时，即使a b =，也不能得到a b =，故D 错误；8．下列结论中正确的是（ ） A ．a 与b 是否相等与a ，b 的方向无关 B ．零向量相等，零向量的相反向量是零向量 C ．若a ，b 都是单位向量，则a b = D ．向量AB 与BA 相等【答案】AB【分析】由向量的模、零向量、单位向量、相等向量的定义判断各选项．【详解】对于C ，单位向量的模相等，但方向不一定相同，故两个单位向量不一定相等；对于D ，向量AB 与BA 互为相反向量，由向量模的定义，零向量的定义AB 正确． 故选：AB ．题型二： 平面向量的加法、减法【例1】AO OB OC CA BO ++++等于（ ）A ．AB B ．0C ．BCD ．AC【答案】B【分析】根据平面向量加法的运算律计算可得； 【详解】解：AO OB OC CA BO ++++ ()()AO OC CA BO OB =++++000=+=故选：B【例2】化简下列各式： (1)AO OB CA CB ++-； (2)MN MD NQ DQ -+-.【答案】(1)0；(2)0【分析】（1）由向量的加法法则与减法法则求解即可； （2）由向量的加法法则与减法法则求解即可；（1）()()AO OB CA CB AO OB CA CB ++-=++-0AB BA =+=；（2）()()MN MD NQ DQ MN MD NQ QD -+-=-++0DN ND =+= 【例3】正方形ABCD 的边长为1，则AB AD +为（ ） A．1 BC ．3D ．根据向量加法的平行四边形法则，AB AD AC +=, 212AB A AD C +==，故选：B.【例4】在ABC 中，M 是BC 的中点，则AB AC +等于（ ） A ．12AM B ．AM C ．2AM D ．MA【答案】C【分析】根据向量的加法法则计算．【详解】如图，作平行四边形ABEC ，因为M 是BC 的中点，所以M 也是AE 的中点，则2AB AC AE AM +==. 故选：C.【例5】如图为正八边形ABCDEFGH ，其中O 为正八边形的中心，则OC HG FH ++=（ ）A ．OB B ．ODC ．OFD ．OH【答案】A【分析】根据平面向量的概念及加法的运算法则，准确运算，即可求解.【详解】由平面向量的运算法则，可得OC HG FH OC FG OC CB OB ++=+=+=. 故选：A.【例6】设M 是平行四边形ABCD 的对角线的交点，O 为平面上任意一点，则OA OB OC OD +++=（ ） A ．4OM B ．3OM C ．2OM D ．OM【分析】分别在OAC 和OBD 【详解】解：在OAC 所以1()2OM OA OC =+，即2OA OC OM +=．在OBD 中，因为M 是平行四边形ABCD 的对角线的交点，所以1()2OM OB OD =+，即2OB OD OM +=． 所以4OA OB OC OD OM +++=． 故选：A ．【例7】若74AB AC ==，，则BC 的取值范围是（ ）A ．[3，7]B ．()37，C ．[]311， D ．(311)， 【分析】根据向量的减法的几何意义，确定向量,AC AB 共线时取得最值，即可求得答案74AB AC ==，，且||BC AC AB -=,当,AC AB 同向时，BC 取得最小值，|||||||4||BC AC AB AC AB ===---当,AC AB 反向时，BC 取得最大值，|||||||||4BC AC AB AC AB -+===+当,AC AB 不共线时，BC 取得最小值，3||||||||||1||||1AC AB BC AC AB =<-<+=，BC 的取值范围是[]311，， 故选：C【例8】已知ABC 为正三角形，则下列各式中成立的是___________.（填序号）AC AB =-①AB CA BC AB -=-；①AB CA CA BC -=-；①CA BC AB AC -=-. AB AC CB BC -==，故①分别为,,AB BC AC 的中点，32AB ， 23AB CA AB AC AE AB -=+==， 23BC AB BC BA BF BA -=+==，所以AB CA BC AB -=-，故①成立；对于①，23CA BC CA CB CD AB -=+==， 所以AB CA CA BC -=-，故①正确；①，AB AC CB AB CA BC -==≠-，故①不成立故答案为：①①①.【题型专练】1.32AB BC AC +-=（ ） A ．AB AC + B ．AB AC - C ．AB D ．BA【答案】A【分析】根据向量的运算法则，准确化简，即可求解.【详解】由向量的运算法则，可得3222AB BC AC AB BC AB AC +-=++- 2AC CB AB AC =+=+．故选：A.2．下列能化简为PQ 的是（ ） A ．QC QP CQ -+ B ．()AB PA BQ ++C ．()()AB PC BA QC ++- D ．PA AB BQ +-【答案】ABC【分析】根据向量运算对选项进行分析，从而确定正确答案. 【详解】A 选项，QC QP CQ PC CQ PQ -+=+=，A 选项正确. B 选项，()AB PA BQ AB AQ BQ PA PA PQ ++=+=+=+，B 选项正确.C 选项，()()AB PC BA QC AB BA PC QC CQ CP PQ ++-=++-=-=，C 选项正确. D 选项，()PA AB BQ PB BQ BP BQ BP BQ PQ +-=-=--=-+≠，D 选项错误. 故选：ABC3. 在四边形ABCD 中，若CA CB CD =+，则（ ） A ．四边形ABCD 是矩形 B ．四边形ABCD 是菱形 C ．四边形ABCD 是正方形 D ．四边形ABCD 是平行四边形【答案】D【分析】根据平面向量加法的运算法则及向量相等的充要条件判断即可；【详解】解：CA CB CD =+，CA CB BA =+，∴CB BA CB CD +=+∴BA CD =，//AB DC ∴且AB DC =，∴四边形ABCD 是平行四边形．故选：D ．4. 在平面四边形ABCD 中，E ，F 分别为AD ，BC 的中点，则下列向量与AB DC +不相等的是（ ） A ．2EF B ．AC DB + C ．EB EC + D ．FA FD +所以11,22AE ED AD BF FC BC ====， 因为EF EA AB BF =++，EF ED DC CF =++ 2EF ED DC CF EA AB BF AB DC =+++++=+, A 正确，因为,DC DA AC AB AD DB =+=+，所以DC AB DA AC AD DB AC DB +=+++=+，所以B 正确，因为,DC DE EC AB AE EB =+=+，所以DC AB DE EC AE EB EC EB +=+++=+，所以因为()FA FD FB BA FC CD BA CD AB DC +=+++=+=-+， D 错误， 故选：D5．在四边形ABCD 中，给出下列四个结论，其中一定正确的是（ ） A ．AB BC CA +=B ．AB AD BD -=C．AB AD AC+=D．BC CD BD+=【答案】D【分析】由向量加法的三角形法则可判断AD，由向量减法的运算法则可判断B，由向量加法的平行四边形法则可判断C.【详解】根据三角形法则可得AB BC AC+=，所以A错误；根据向量减法的运算法则可得AB AD DB-=，所以B错误；四边形ABCD不一定是平行四边形，所以不一定有AB AD AC+=，C错误；根据三角形法则可得BC CD BD+=正确，所以D正确.故选：D.6．在四边形ABCD中，AB DC=，若AD AB BC BA-=-，则四边形ABCD是（）A．菱形B．矩形C．正方形D．不确定【分析】由AB DC=，可得四边形为平行四边形，又BD AC=，从而即可求解【详解】解：在四边形ABCD因为AB DC=，所以四边形AD AB BC BA-=-，即BD AC=，所以平行四边形ABCD为矩形，故选：B.7．在ABC中，D，E，F分别是边BC,CA,AB的中点，点G为ABC的重心，则下列结论中正确的是（）A．AB BC CA-=B．1()3AG AB AC=+C．0AF BD CE++=D．0GA GB GC++=【答案】BCD【分析】由向量的线性运算结合三角形的重心的性质求解即可．【详解】解：如图：，2AB BC AB CB EB AC-=+=≠，即选项为ABC的重心，则2211()()3323AG AD AB AC AB AC==⨯+=+，即选项，1()02AF BD CE AB BC CA++=++=，即选项C正确；，122()2GA GD GB GC=-=-⨯+，即0GA GB GC++=，即选项D正确，8．如图，E，F，G，H分别是梯形ABCD的边AB，BC，CD，DA的中点，化简下列各式：(1)DG EA CB++；(2)EG CG DA EB+++.【答案】(1)GE；(2)0.【分析】（1）（2）根据图形中相关线段的位置关系，结合向量加法的几何意义化简目标式.（1）DG EA CB GC BE CB GB BE GE+++++===；（2）EG CG DA EB EG GD DA AE ED DE==+=++++++.题型三：平面向量的线性运算与共线定理【例1】[多选题]下列命题是真命题的是（）．A．若A，B，C，D在一条直线上，则AB与CD是共线向量B．若A，B，C，D不在一条直线上，则AB与CD不是共线向量C．若向量AB与CD是共线向量，则A，B，C，D四点必在一条直线上D．若向量AB与AC是共线向量，则A，B，C三点必在一条直线上【答案】AD【分析】向量平行与共线是同一个概念，对四个命题依次判断即可．【详解】A 项为真命题，A，B，C，D在一条直线上，则向量AB，CD的方向相同或相反，因此AB与CD是共线向量；B 项为假命题，A ，B ，C ，D 不在一条直线上，则AB ，CD 的方向不确定，不能判断AB 与CD 是否共线；C 项为假命题，因为AB ，CD 两个向量所在的直线可能没有公共点， 所以A ，B ，C ，D 四点不一定在一条直线上；D 项为真命题，因为AB ，AC 两个向量所在的直线有公共点A ， 且AB 与AC 是共线向量，所以A ，B ，C 三点共线． 故选：AD ．【例2】已知向量a ，b ，且2AB a b =+，56BC a b =-+，72CD a b =-，则一定共线的三点是（ ） A ．A ，B ，D B ．A ，B ，CC ．B ，C ，DD ．A ，C ，D【分析】由已知，分别表示出选项对应的向量，然后利用平面向量共线定理进行判断即可完成求解【详解】因为2AB a b =+，BC 56a b =-+，72CD a b =-，，2AB a b =+，(56)(72)24B a b D B D b C a C b a ++-+==-+=，若A ，B 则AB BD λ=，即2(24)a b a b λ+=+，解得12λ=，故该选项正确； 选项B ，2AB a b =+，BC 56a b =-+，若A ，B ，C 三点共线，则AB BC λ=，即2(56)a b a b λ+=-+，解得不存在，故该选项错误；选项C ，BC 56a b =-+，72CD a b =-，若B ，三点共线，则BC BD λ=，即56(72)a b a b λ-+=-，不存在，故该选项错误；，(2)(56)48a b a A b AB BC a b C ++=+=+-=-+，72CD a b =-，若A ，C ，D 三点共线，则AC CD λ=，48(72)a b a b λ+=-，解得λ不存在，故该选项错误； 故选：A.【例3】下列说法正确的是（ ）A ．a 与b 是非零向量，则a 与b 同向是a b =的必要不充分条件B ．,,A BC 是互不重合的三点，若AB 与BC 共线，则,,A B C 三点在同一条直线上 C ．a 与b 是非零向量，若a 与b 同向，则a 与b -反向D ．设,λμ为实数，若a b λμ=，则a 与b 共线 【答案】ABC选项：根据向量共线的性质，可知A 、选项：a 与b 同向，则a 与b -反向，显然正确; 选项：如果0λμ==，则无法得知a 与b 共线.【详解】a 与b 同向，但a 不一定与b 相等，∴a b ≠，若a b =，则a 与b 同向， a =b ，∴a 与b 同向是a b =的必要不充分条件，A 正确.AB 与BC 共线，则有AB =BC λ，故一定有,,A B C 三点在同一条直线上，B 正确.a 与b 同向，则a 与b -反向，C 正确.0λμ==时，a 与b 不一定共线，D 错误.故选：ABC【例4】“AB CD ∥”是“A ，B ，C ，D 四点共线”的________条件． 【答案】必要不充分【分析】根据向量平行的定义结合充分性、必要性的定义判断即可. 【详解】当AB CD ∥时，直线AB 与CD 的位置关系有可能是平行或共线， 当二者平行时A ，B ，C ，D 四个点分别位于两条平行线上而不是四点共线， 则“AB CD ∥”无法推出“A ，B ，C ，D 四点共线”；当A ，B ，C ，D 四点共线时，直线AB 与CD 的位置关系为重合，此时，AB CD ∥， 则“A ，B ，C ，D 四点共线”可以推出“AB CD ∥”，因此“AB CD ∥”是“A ，B ，C ，D 四点共线”的必要不充分条件． 故答案为：必要不充分.【例5】设向量,a b 不平行，向量λ+a b 与2+a b 平行，则实数λ= ___． 【答案】21 【解析】因向量λ+a b 与2+a b 平行，所以()b a b a b a μμμλ22+=+=+，所以⎩⎨⎧==μμλ21，解得⎪⎩⎪⎨⎧==2121μλ 【例6】已知P 是①ABC 所在平面内的一点，若CB PB PA λ-=，其中λ①R ，则点P 一定在（ ） A ．AC 边所在的直线上 B ．BC 边所在的直线上 C ．AB 边所在的直线上D ．①ABC 的内部【答案】A【分析】根据向量的线性运算整理可得，再结合向量共线分析即可. 【详解】①CB PB PA λ-=，PB PC CB =+①()CB PC CB PA λ-+=，则PC -=λPA ，则CP PA λ= ①CP PA ∥①P 点在AC 边所在直线上． 故选：A ．【例7】在①ABC 中，AD 为BC 边上的中线，E 为AD 的中点，则EB =A ．3144AB AC - B ．1344AB AC - C ．3144+AB ACD ．1344+AB AC【答案】A【解析】根据向量的运算法则，可得()111111222424BE BA BD BA BC BA BA AC =+=+=++ 1113124444BA BA AC BA AC =++=+① 所以3144EB AB AC =-①故选A.【例8】在ABC 中，AD 为BC 边上的中线，E 为AD 的中点，且EB AB AC λμ=+，则λ=________，μ=_________．【答案】3414-【解析】如下图所示：D 为BC 的中点，则()()111222AD AB BD AB BC AB AC AB AB AC =+=+=+-=+，E 为AD 的中点，所以，()1124AE AD AB AC ==+，因此，()131444EB AB AE AB AB AC AB AC =-=-+=-，即34λ=，14μ=-. 故答案为：34；14-.【例9】在ABC 中，4AC AD =，P 为BD 上一点，若13AP AB AC λ=+，则实数λ的值（ ） A ．18B ．316C ．16D ．38【答案】C 【解析】4AC AD =，14AD AC ∴=，则14BD AD AB AC AB =-=-， 1233BP AP AB AB AC AB AC AB λλ⎛⎫=-=+-=- ⎪⎝⎭，由于P 为BD 上一点，则//BP BD ，设BP k BD =，则21344kAC AB k AC AB AC k AB λ⎛⎫-=-=- ⎪⎝⎭， 所以423k k λ⎧=⎪⎪⎨⎪=⎪⎩，解得16λ=.【例10】在ABC ∆中，点P 满足3BP PC =，过点P 的直线与AB 、AC 所在的直线分别交于点M 、N ，若AM AB λ=，()0,0AN AC μλμ=>>，则λμ+的最小值为（ ）A．12+ B1 C ．32D ．52【答案】B【解析】如下图所示：3BP PC =，即()3AP AB AC AP -=-，1344AP AB AC∴=+， AM AB λ=，()0,0AN AC μλμ=>>，1AB AM λ∴=，1AC ANμ=， 1344AP AM ANλμ∴=+，M 、P 、N 三点共线，则13144λμ+=. ()133********λμλμλμλμμλ⎛⎫∴+=++=++≥=+ ⎪⎝⎭，当且仅当μ=时，等号成立，因此，λμ+1+，故选：B. 【例11】已知M 为ABC 的边AB 的中点，N 为ABC 内一点，且13AN AM BC =+，则AMN BCNS S =△△（ ） A ．16B ．13C ．12D ．23【答案】B【解析】因为13AN AM BC =+，所以13MN BC =， 所以MN ①BC ，又因为 M 为边AB 的中点，所以点A 到MN 的距离等于点N 到BC 的距离， 所以13AMN BCN MN S S BC==△△,【题型专练】1.已知()1221123,,2AB e e CB e e CD e e =+=-=+，则下列结论中成立的是（ ）A ．A ，B ，C 三点共线B ．A ，B ，D 三点共线C ．A ，D ，C 三点共线D ．D ，B ，C 三点共线 【答案】C【分析】根据平面向量的线性运算可得2AC CD =，从而可求解.【详解】解：()()1221123422AC AB CB e e e e e e CD -=-=+-=+=,所以A ，D ，C 三点共线.故选:C.2.已知向量a ，b 是两个不共线的向量，且35OA a b =+，47OB a b =+，OC a mb =+，若A ，B ，C 三点共线，则m =（ ）A ．1B ．1-C ．2D ．2- 【答案】A【解析】法一：b a b a b a OB AO AB 27453+=++--=+=，()b m a b m a b a OC BO BC 7374-+-=++--=+=，因A ，B ，C 三点共线，所以AB 与BC 共线，所以()[]()b m a b m a b a 73732-+-=-+-=+λλλ，所以()⎩⎨⎧-=-=7231m λλ，解得⎪⎩⎪⎨⎧=-=131m λ 法二：由,,A B C 三点共线，得(1)(4)(72)OC xOA x OB x a x b =+-=-+-，故41,72,x x m -=⎧⎨-=⎩解得1m =． 3.设12e e ，是两个不共线的向量，若向量12m e ke =-+（k ∈R ）与向量212n e e =-共线，则 A ．0k =B ．1k =C ．2k =D ．12k = 【答案】D【解析】因为向量12=-+m e ke （k ∈R ）与向量212=-n e e 共线，所以存在实数λ，使得λ=m n ， 所以有2211(2)λ-+=-e ke e e ，因此12k λλ=⎧⎨-=-⎩，解得12k =. 4.在ABC △中，D 是AB 边上的中点，则CB =（ ）A ．2CD CA +B ．2CD CA -C ．2CD CA - D ．2CD CA +【答案】C【解析】：CA CD AC CD CD AC CD AD CD DB CD CB -=+=++=+=+=225.在ABC 中，点P 为AC 中点，点D 在BC 上，且3BD DC =，则DP =( )A ．1144AB AC + B ．1144AB AC -- C ．1144AB AC - D ．1144AB AC-+ 【答案】B【解析】①点P 为AC 中点，①12AP AC =,①3BD DC =，()3AD AB AC AD ∴-=-, ①1344AD AB AC =+,①113244DP AP AD AC AB AC =-=--=1144AB AC --,故选：B. 6.设,,D E F 分别为ABC 的三边BC,CA,AB 的中点，则EB FC +=( ) A ．ADB ．12ADC ．12BCD ．BC 【答案】A【解析】111()()()222EB FC BA BC CA CB AB AC AD +=-+-+=+=，故选：A7.设D 为①ABC 所在平面内的一点,若3,AD BD CD CA CB λμ==+,则μλ=_____. 【答案】3-【解析】如图所示：3CD CA AD CA BD =+=+，CA =+3(CD CB -)，即有CD =﹣1322CA CB +， 因为CD CA CB λμ=+，所以λ=﹣12，μ=32，则μλ=﹣3，故答案为：﹣3. 8.如图，在ABC 中，点O 是BC 的中点，过点O 的直线分别交直线AB ，AC 于不同的两点M N ，，若AB mAM =，AC nAN =，则m n +=（ ）A ．1B ．32C ．2D ．3【答案】C 【解析】连接AO ，由O 为BC 中点可得，1()222m n AO AB AC AM AN =+=+， M 、O 、N 三点共线，122m n ∴+=，2m n ∴+=.故选：C.9.在ABC 中，2AB =，4BC =，60ABC ∠=︒，AD 为BC 边上的高，O 为AD 的中点，若AO AB BC λμ=+，则λμ+=（ ）A ．13B ．23C ．38 D ．58【答案】D【解析】AD 是BC 边上的高，∴90ADB ∠=︒，在ADB △中，1cos 22BD BD ABD AB ∠===，解得1BD =，4BC =，∴14BD BC =， ∴14AD AB BD AB BC =+=+，O 为AD 中点， ∴1111122428AO AD AB BC AB BC ⎛⎫==+=+ ⎪⎝⎭，AO AB BC λμ=+， ∴1128AB BC AB BC λμ+=+，∴12λ=，18μ=， ∴115288λμ+=+=. 10.已知O 是ABC 所在平面内一点，D 为BC 边中点，且20OA OB OC ++=，那么（ ） A ．AO OD = B ．2AO OD = C ．3AO OD = D ．4?AO OD【答案】A【解析】D 为BC 边中点，①2OB OC OD +=，①20OA OB OC ++=，①0OA OD =+，即AO OD =.11．设,,D E F 分别是ABC 的三边BC,CA,AB 上的点，且2,2,2DC BD CE EA AF FB ===，则AD BE CF ++与BC （ ）A ．反向平行B ．同向平行C ．互相垂直D ．既不平行也不垂直 首先根据平面向量基本定理表示2133AD AB BD AB AC =+=+，2133BE BA BC =+，2133CF CB CA =+，【详解】()11213333AD AB BD AB BC AB AC AB AB AC =+=+=+-=+ 同理：2133BE BA BC =+，2133CF CB CA =+， 所以212121333333AD BE CF AB AC BA BC CB CA ⎛⎫⎛⎫⎛⎫++=+++++ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭13CB , 所以AD BE CF ++与BC 反向平行.故选：A【点睛】本题主要考查向量共线定理和平面向量基本定理，重点考查向量的表示，属于基础题型题型四：由平面向量的性质判断图形的形状【例1】若O 是ABC ∆所在平面内一点，且满足2OB OC OB OC OA -=+-，则ABC ∆的形状为____【答案】直角三角形=OC OA OC +=+=-+，+= 所以ABC ∆的形状为直角三角形【例2】若113e ,5e AB CD ===，则四边形ABCD 是（ ）A ．平行四边形B ．菱形C ．等腰梯形D ．不等腰的梯形 ，结合AD BC =，即可判断四边形【详解】解：因为113e ,5e AB CD ==，所以35AB CD =-，所以//AB CD AB CD ≠，AD BC =，所以四边形ABCD 为等腰梯形.故选：C.【题型专练】1．在四边形ABCD 中，对角线AC 与BD 交于点O ，若2323OA OC OD OB +=+，则四边形ABCD 一定是（ ）A ．矩形B ．梯形C ．平行四边形D ．菱形 【答案】B【分析】由2323OA OC OD OB +=+化简可得23DA CB =，结合向量共线定理判断四边形ABCD 的形状.【详解】① 2323OA OC OD OB +=+，① 2()3()OA OD OB OC -=-，① 23DA CB =，① 四边形ABCD 一定是梯形． 故选：B.2．四边形ABCD 中，2AB a b =+，4BC a b =--，53CD a b =--，若a 、b 不共线，则四边形ABCD 为（ ）A ．平行四边形B ．矩形C ．梯形D ．菱形 【分析】由向量知识可知//AD BC ，AD BC ≠可得答案【详解】由已知得，2453822AD AB BC CD a b a b a b a b BC =++=+----=--= ， 故//AD BC ，由AD BC ≠，所以四边形ABCD 是梯形.故选：C.3．在四边形ABCD 中，若CA CB CD =+，则（ ）A ．四边形ABCD 是矩形B ．四边形ABCD 是菱形C ．四边形ABCD 是正方形D ．四边形ABCD 是平行四边形 【答案】D 【分析】根据平面向量加法的运算法则及向量相等的充要条件判断即可；【详解】解：CA CB CD =+，CA CB BA =+，∴CB BA CB CD +=+ ∴BA CD =，//AB DC ∴且AB DC =，∴四边形ABCD 是平行四边形． 故选：D ．4．下列有关四边形ABCD 的形状判断正确的是（ ）A ．若AD BC =，则四边形ABCD 为平行四边形B ．若13AD BC =，则四边形ABCD 为梯形 C ．若AB DC =，且AB AD =，则四边形ABCD 为菱形D ．若AB DC =，且AC BD ⊥，则四边形ABCD 为正方形 【分析】由向量平行与相等的关系确定四边形的边的关系得结论．【详解】AD BC =，则AD 13AD BC =，则//AD BC 若AB DC =，四边形ABCD AB AD =，即AB 若AB DC =，四边形ABCD 是平行四边形，AC BD ⊥，即AC 故选：ABC ．。

平面向量常见题型与解题方法归纳1常见题型分类题型一：向量的有关概念与运算例1：已知a 是以点A 3;－1为起点;且与向量b = －3;4平行的单位向量;则向量a 的终点坐标是 .例2：已知| a |=1;| b |=1;a 与b 的夹角为60°; x =2a －b ;y =3b －a ;则x 与y 的夹角的余弦是多少题型二：向量共线与垂直条件的考查例11,a b 为非零向量..“a b ⊥”是“函数()()()f x xa b xb a =+⋅-为一次函数”的A 充分而不必要条件B 必要不充分条件C 充要条件D 既不充分也不必要条件2已知O;N;P 在ABC ∆所在平面内;且,0OA OB OC NA NB NC ==++=;且PA PB PB PC PC PA •=•=•;则点O;N;P 依次是ABC ∆的A.重心 外心 垂心B.重心 外心 内心C.外心 重心 垂心D.外心 重心 内心 例2．已知平面向量a ＝3;－1;b ＝21; 23.1 若存在实数k 和t ;便得x ＝a ＋t 2－3b ; y ＝－k a ＋t b ;且x ⊥y ;试求函数的关系式k ＝ft ；2 根据1的结论;确定k ＝ft 的单调区间.例3： 已知平面向量a ＝3;－1;b ＝21;23;若存在不为零的实数k 和角α;使向量c ＝a ＋sin α－3b ; d ＝－k a ＋sin αb ;且c ⊥d ;试求实数k 的取值范围.例4：已知向量)1,2(),2,1(-==b a ;若正数k 和t 使得向量 b t a k y b t a x 1)1(2+-=++=与垂直;求k 的最小值.题型三：向量的坐标运算与三角函数的考查向量与三角函数结合;题目新颖而又精巧;既符合在知识的“交汇处”构题;又加强了对双基的考查.例7．设函数f x ＝a · b ;其中向量a ＝2cos x ; 1; b ＝cos x ;3sin2x ; x ∈R.1若f x ＝1－3且x ∈－3π;3π;求x ；2若函数y ＝2sin2x 的图象按向量c ＝m ; n m ﹤2π平移后得到函数y ＝f x 的图象;求实数m 、n 的值.例8：已知a =cosα;sin α;b =cosβ;sinβ0<α<β<π;1求证： a +b 与a -b 互相垂直； 2若k a +b 与a -k b 的模大小相等k ∈R 且k ≠0;求β－α巩固练习1.函数cos(2)26y x π=+-的图象F 按向量a 平移到'F ;'F 的函数解析式为(),y f x =当()y f x =为奇函数时;向量a 可以等于.(,2)6A π-- .(,2)6B π- .(,2)6C π- .(,2)6D π 1. 2.给定两个长度为1的平面向量OA 和OB ;它们的夹角为120o .如图所示;点C 在以O 为圆心的圆弧AB 上变动.若,OC xOA yOB =+其中,x y R ∈;则x y +的最大值是________.3给出下列命题① 非零向量a 、b 满足|a |=|b |=|a -b |;则a 与a +b 的夹角为30°；② a ·b ＞0是a 、b 的夹角为锐角的充要条件；③ 将函数y =|x -1|的图象按向量a =-1;0平移;得到的图像对应的函数为y =|x |；④若AC AB +·AC AB -=0;则△ABC 为等腰三角形 以上命题正确的是 ..注：把你认为正确的命题的序号都填上。

“四大妙法”，剖析向量的秒杀体系目录一、重难点题型方法妙法一：奔驰定理与四心问题题型一：奔驰定理题型二：重心问题题型三：内心问题题型四：外心问题题型五：垂心问题妙法二：极化恒等式题型六：极化恒等式的应用妙法三：隐圆题型七：定点定长；定弦定角；对角互补；到两定点数量积(平方和)定值题型八：阿波罗尼斯圆妙法四：等和线题型九：等和线的应用二针对性巩固练习重难点题型方法妙法一：奔驰定理与四心问题题型一：奔驰定理【典例分析】例1.(2023·全国·高三专题练习)“奔驰定理”是平面向量中一个非常优美的结论，因为这个定理对应的图形与“奔驰”轿车(Mercedesbenz )的log o 很相似，故形象地称其为“奔驰定理”．奔驰定理：已知O 是△ABC 内的一点，△BOC ,△AOC ,△AOB 的面积分别为S A ,S B ,S C ，则有S A ⋅OA +S B ⋅OB +S C ⋅OC =0 ．设O 是锐角△ABC 内的一点，∠BAC ,∠ABC ,∠ACB 分别是△ABC 的三个内角，以下命题不正确的有( )A.若OA +OB +OC =0 ，则O 为△ABC 的重心B.若OA +2OB +3OC =0 ，则S A :S B :S C =1:2:3C.若OA =OB =2,∠AOB =5π6，2OA +3OB +4OC =0 ，则S △ABC =92D.若O 为△ABC 的垂心，则tan ∠BAC ⋅OA +tan ∠ABC ⋅OB +tan ∠ACB ⋅OC =0【答案】C【分析】对于A ，假设D 为AB 的中点，连接OD ，由已知得O 在中线CD 上，同理可得O 在其它中线上，即可判断；对于选项B ，利用奔驰定理可直接得出B 正确；对于C ，根据奔驰定理可得S A :S B :S C =2:3:4，再利用三角形面积公式可求得S C =1，即可计算出S △ABC =94，可得C 错误；选项D ，由垂心的性质、向量数量积的运算律OB ∙AC =OB ∙OC -OB ∙OA =0，得到OA :OB :OC =cos ∠BAC :cos ∠ABC :cos ∠BCA ，结合三角形面积公式及角的互补关系得结论.【详解】对于A ：如下图所示，假设D 为AB 的中点，连接OD ，则OA +OB =2OD =CO ，故C ,O ,D 共线，即O 在中线CD 上，同理可得O 在另外两边BC ,AC 的中线上，故O 为△ABC 的重心，即A 正确；对于B ：由奔驰定理O 是△ABC 内的一点，△BOC ,△AOC ,△AOB 的面积分别为S A ,S B ,S C ，则有S A ⋅OA +S B ⋅OB +S C ⋅OC =0 可知，若OA +2OB +3OC =0 ，可得SA :SB :SC =1:2:3，即B 正确；对于C ：由|OA |=|OB |=2,∠AOB =5π6可知，S C =12×2×2×sin 5π6=1，又2OA +3OB +4OC =0 ，所以S A :S B :S C =2:3:4由S C =1可得，S A =12,S B =34；所以S △ABC =S A +S B +S C =12+34+1=94，即C 错误；对于D ：由四边形内角和可知，∠BOC +∠BAC =π，则OB ∙OC =OB OC cos ∠BOC =-OB OC cos ∠BAC ，同理，OB ∙OA =OB OA cos ∠BOA =-OB OA cos ∠BCA ，因为O 为△ABC 的垂心，则OB ∙AC =OB ∙(OC -OA )=OB ∙OC -OB ∙OA =0，所以OC cos ∠BAC =OA cos ∠BCA ，同理得OC cos ∠ABC =OB cos ∠BCA ，OA cos ∠ABC =OB cos ∠BAC ，则OA :OB :OC =cos ∠BAC :cos ∠ABC :cos ∠BCA ，令OA =m cos ∠BAC ,OB =m cos ∠ABC ,OC =m cos ∠BCA ，由S A =12OB OC sin ∠BOC ，则S A =12OB OC sin ∠BAC =m 22cos ∠ABC cos ∠BCA sin ∠BAC ，同理：S B =12OA OC sin ∠ABC =m 22cos ∠BAC cos ∠BCA sin ∠ABC ，S C =12OA OB sin ∠BCA =m 22cos ∠BAC cos ∠ABC sin ∠BCA ，综上，S A :S B :S C =sin ∠BAC cos ∠BAC :sin ∠ABC cos ∠ABC :sin ∠BCA cos ∠BCA =tan ∠BAC :tan ∠ABC :tan ∠BCA ，根据奔驰定理得tan ∠BAC ⋅OA +tan ∠ABC ⋅OB +tan ∠ACB ⋅OC =0 ，即D 正确.故选：C【点睛】关键点点睛：利用向量数量积定义、运算律和垂心性质得到向量模的比例，结合三角形面积公式和奔驰定理判断结论即可.例2.(2023·全国·高三专题练习)奔驰定理：已知O 是△ABC 内的一点，△BOC ，△AOC ，△AOB 的面积分别为S A ，S B ，S C ，则S A ⋅OA +S B ⋅OB +S C ⋅OC =0 .“奔驰定理”是平面向量中一个非常优美的结论，因为这个定理对应的图形与“奔驰”轿车的log o 很相似，故形象地称其为“奔驰定理”.设O 为三角形ABC 内一点，且满足：OA +2OB +3OC =3AB +2BC +CA ，则S △AOB S △ABC=( )A.25B.12C.16D.13【答案】D 【分析】直接根据向量的基本运算得到3OA +OB +2OC =0 ，再结合“奔驰定理”即可求解结论．【详解】解：∵O 为三角形ABC 内一点，且满足OA +2OB +3OC =3AB +2BC +CA ，∴OA +2OB +3OC =3(OB -OA )+2(OC -OB )+(OA -OC )⇒3OA +OB +2OC =0 ，∵S A ⋅OA +S B ⋅OB +S C ⋅OC =0 ．∴S △AOB S △ABC =S △AOB S △AOB +S △BOC +S △AOC =S C S A +S B +S C=13，故选：D ．【方法技巧总结】1. 奔驰定理：S A ⋅OA +S B ⋅OB +S C ⋅OC =0 ，则△AOB 、△AOC 、△BOC 的面积之比等于λ3:λ2:λ1【变式训练】1.(2023春·湖南常德·高一临澧县第一中学校考阶段练习)如图.P 为△ABC 内任意一点，角A ,B ,C 的对边分别为a ,b ,c ，总有优美等式S △PBC PA +S △PAC PB +S △PAB PC =0 成立，因该图形酯似奔驰汽车车标，故又称为奔驰定理.则以下命题是真命题的有()A.若P 是△ABC 的重心，则有PA +PB +PC =0B.若aPA +bPB +cPC =0 成立，则P 是△ABC 的内心C.若AP =25AB +15AC ，则S △ABP :S △ABC =2:5D.若P 是△ABC 的外心，A =π4，PA =mPB +nPC ，则m +n ∈-2,1 【答案】AB 【分析】对于A ：利用重心的性质S △PBC =S △PAC =S △PAB ，代入S △PBC PA +S △PAC PB +S △PAB PC =0 即可；对于B ：利用三角形的面积公式结合S △PBC PA +S △PAC PB +S △PAB PC =0 与aPA +bPB +cPC =0 可知点P 到AB 、BC 、CA 的距离相等.对于C ：利用AB 、AC 将PA 、PB 、PC 表示出来，代入S △PBC PA +S △PAC PB +S △PAB PC =0 ，化简即可表示出S △PBC 、S △PAC 、S △PAB 的关系式，用S △PAB 将S △ABP 、S △ABC 表示出来即可得处其比值.对于D ：利用三角形的圆心角为圆周角的两倍，再将PA =mPB +nPC 两边平方，化简可得m 2+n 2=1，结合m 、n 的取值范围可得出答案.【详解】对于A ：如图所示：因为D 、E 、F 分别为CA 、AB 、BC 的中点，所以CP =2PE ，S △AEC =12S △ABC ,S △APC =23S △AEC =13S △ABC ，同理可得S △APB =13S △ABC 、S △BPC =13S △ABC ，所以S △PBC =S △PAC =S △PAB ，又因为S △PBC PA +S △PAC PB +S △PAB PC =0 ，所以PA +PB +PC =0 .正确；对于B ：记点P 到AB 、BC 、CA 的距离分别为h 1、h 2、h 3，S △PBC =12a ⋅h 2,S △PAC =12b ⋅h 3,S △PAB =12c ⋅h 1，因为S △PBC PA +S △PAC PB +S △PAB PC =0 ，则12a ⋅h 2⋅PA +12b ⋅h 3⋅PB +12c ⋅h 1⋅PC =0 ，即a ⋅h 2PA +b ⋅h 3PB +c ⋅h 1PC =0 ，又因为aPA +bPB +cPC =0 ，所以h 1=h 2=h 3，所以点P 是△ABC 的内心，正确；对于C ：因为AP =25AB +15AC ，所以PA =-25AB -15AC ，所以PB =PA +AB =35AB -15AC ，所以PC =PA +AC =-25AB +45AC ，所以S △PBC -25AB -15AC +S △PAC 35AB -15AC +S △PAB -25AB +45AC =0 ，化简得：-25S △PBC +35S △PAC -25S △PAB AB +-15S △PBC -15S △PAC +45S △PAB AC =0 ，又因为AB 、AC 不共线，所以-25S △PBC +35S △PAC -25S △PAB=0-15S △PBC -15S △PAC +45S △PAB =0 ，所以S △PBC =2S △PAB S △PAC =2S △PAB ，所以S △ABP S △ABC =S △PAB S △PBC +S △PAC +S △PAB =15，错误；对于D ：因为P 是△ABC 的外心，A =π4，所以∠BPC =π2,PA =PB =PC ，所以PB ⋅PC =PB ×PC ×cos ∠BPC =0，因为PA =mPB +nPC ，则PA 2=m 2PB 2+2mnPB ⋅PC +n 2PC 2，化简得：m 2+n 2=1，由题意知m 、n 同时为负，记m =cos αn =sin α，π<α<3π2，则m +n =cos α+sin α=2sin α+π4，因为5π4<α+π4<7π4，所以-1≤sin α+π4 <-22，所以-2≤2sin α+π4<-1，所以m +n ∈-2,-1 ，错误.故答案为：AB .2.(2023春·浙江嘉兴·高一校考阶段练习)“奔驰定理”是平面向量中一个非常优美的结论，因为这个定理对应的图形与“奔驰”(Mercedesbenz )的log o 很相似，故形象地称其为“奔驰定理”.奔驰定理：已知O 是△ABC 内的一点，△BOC ，△AOC ，△AOB 的面积分别为S A ，S B ，S C ，则S A ⋅OA +S B ⋅OB +S C ⋅OC =0 .若O 是锐角△ABC 内的一点，A ，B ，C 是△ABC 的三个内角，且点O 满足OA ⋅OB =OB ⋅OC =OA ⋅OC .则()A.O 为△ABC 的外心B.∠BOC +A =πC.OA :OB :OC =cos A :cos B :cos CD.tan A ⋅OA +tan B ⋅OB +tan C ⋅OC =0 【答案】BCD 【分析】由根据数量积的运算律可得OB ⋅CA =0⇔OB ⊥CA ,可得O 为△ABC 的垂心；结合∠OBC +C +∠OCB +B =π与三角形内角和等于π可证明B 选项；结合B 选项结论证明cos A :cos B =OA :OB 即可证明C 选项，利用奔驰定理证明S A :S B =tan A :tan B 可证明D 选项．【详解】解：因为OA ⋅OB =OB ⋅OC ⇔OB ⋅(OA -OC )=0⇔OB ⋅CA =0⇔OB ⊥CA ，同理OA ⊥CB ，OC ⊥AB ，故O 为△ABC 的垂心，故A 错误；∠OBC +C =π2,∠OCB +B =π2，所以∠OBC +C +∠OCB +B =π，又∠OBC +∠OCB +∠BOC =π，所以∠BOC =C +B ，又A +B +C =π，所以∠BOC +A =π，故B 正确；故A =π-∠BOC ，同理B =π-∠AOC ，延长CO 交AB 与点P ，则cos A :cos B =cos (π-∠BOC ):cos (π-∠AOC )=cos ∠BOP :cos ∠AOP =OP OB :OP OA=OA :OB ，同理可得cos A :cos C =OA :OC ，所以cos A :cos B :cos C =OA :OB :OC ，故C 正确；S A :S B =12⋅OC ⋅BP :12⋅OC ⋅AP =BP :AP =OP tan ∠POB :OP tan ∠AOP =tan ∠BOC :tan ∠AOC =tan (π-A ):tan (π-B )=tan A :tan B ，同理可得S A :S C =tan A :tan C ，所以S A :S B :S C =tan A :tan B :tan C ，又S A ⋅OA +S B ⋅OB +S C ⋅OC =0 ，所以tan A ⋅OA +tan B ⋅OB +tan C ⋅OC =0 ，故D 正确．故选：BCD ．题型二：重心问题【典例分析】例1.(四川省达州市2023届高三二模数学(理科))如图，在△ABC 中，AB =3，∠ABC =π4，BA ⋅BC =18，平面ABC 内的点D 、E 在直线AB 两侧，△ABD 与△BCE 都是以B 为直角顶点的等腰直角三角形，O 1、O 2分别是△ABD 、△BCE 的重心.则O 1O 2=( )A.26B.33C.5D.6【答案】A【分析】利用平面向量数量积的定义可求得AB ，求出BO 1、BO 2、∠O 1BO 2，利用余弦定理可求得O 1O 2的长.【详解】由平面向量数量积的定义可得BA ⋅BC =BA ⋅BC cos π4=322BC =18，解得BC =62，延长BO 1交AD 于点G ，延长BO 2交CE 于点H ，则G 、H 分别为AD 、CE 的中点，因为△ABD 、△BCE 均是以点B 为直角顶点的等腰直角三角形，且AB =3，BC =62，所以，AD =2AB =32，CE =2BC =12，则BG =12AD =322，BH =12CE =6，因为O 1、O 2分别是△ABD 、△BCE 的重心，则BO 1=23BG =23×322=2，BO 2=23BH =4，又因为∠ABG =12∠ABD =π4，同理可得∠CBH =π4，所以，∠O 1BO 2=∠ABG +∠BAC +∠CBH =3π4，由余弦定理可得O 1O 22=BO 21+BO 22-2BO 1⋅BO 2cos 3π4=2+16-2×2×4×-22=26，因此，O 1O 2=26.故选：A .例2.(2023·全国·高三专题练习)如图所示，已知点G 是△ABC 的重心，过点G 作直线分别与AB ，AC 两边交于M ，N 两点，设xAB =AM ，yAC =AN ，则1x +1y的值为( )A.3B.4C.5D.6【答案】A 【分析】由向量共线的推论知AG =λAM +(1-λ)AN 且0≤λ≤1，结合已知有AG =xλAB +y (1-λ)AC ，再由重心的性质有AG =13(AB +AC )，根据平面向量基本定理列方程组即可求值.【详解】由题意AG =λAM +(1-λ)AN 且0≤λ≤1，而xAB =AM ，yAC =AN ，所以AG =xλAB +y (1-λ)AC ，又G 是△ABC 的重心，故AG =23×12(AB +AC )=13(AB +AC )，所以xλ=13y (1-λ)=13，可得13x +13y =1，即1x +1y =3.故选：A【方法技巧总结】1.O 是△ABC 的重心：S △BOC :S △COA :S △A 0B =1:1:1⇔OA +OB +OC =0 ．【变式训练】1.(2022春·浙江·高二统考学业考试)在△ABC 中，设AD =2DB ，BE =2EC ，CF =λFA ，其中λ∈R .若△DEF 和△ABC 的重心重合，则λ=()A.12 B.1 C.32 D.2【答案】D【分析】设O 为△DEF 和△ABC 的重心，连接DO 延长交EF 与N ，连接AO 延长交BC 与M ，分别在△ABC 、△DEF 中用向量AB 、AC 表示向量DO ，再根据向量相等可得答案.【详解】设O 为△DEF 和△ABC 的重心，连接DO 延长交EF 与N ，连接AO 延长交BC 与M ，所以N 是EF 的中点，M 是BC 的中点，所以AO =23AM =23×12AB +AC =13AB +13AC ，DO =DA +AO =-23AB +13AB +13AC =-13AB +13AC ，DO =23DN =23×12DE +DF =13DB +BE +DA +AF =1313AB +23BC -23AB +11+λAC =13-13AB +23AC -AB +11+λAC =-13AB +1323+11+λAC ，可得1=23+11+λ，解得λ=2.故选：D .2.(2022春·四川攀枝花·高一攀枝花七中校考阶段练习)已知△ABC 的三个内角分别为A ,B ,C ,O 为平面内任意一点，动点Р满足OP =OA +λAB AB sin B +AC AC sin C,λ∈0,+∞ 则动点P 的轨迹一定经过△ABC 的()A.重心B.垂心C.内心D.外心【答案】A【分析】利用正弦定理及向量的线性运算可判断.【详解】在△ABC 中，令线段BC 的中点为M ，由正弦定理AB sin C =AC sin B ，得AB sin B =AC sin C ，由OP =OA +λAB AB sin B +AC AC sin C ，得OP -OA =λAB AB sin B +AC AB sin B 即AP =λAB sin B AB +AC =2λAB sin B AM ，而sin B >0，λ∈(0，+∞)则2λAB sin B∈(0，+∞)，于是得AP 与AM 同向共线，而它们有公共起点，即动点Р的轨迹是射线AM (除点A 外),又重心在线段AM 上，∴动点Р的轨迹一定经过△ABC 的重心．故选：A .题型三：内心问题【典例分析】例1.(2003·江苏·高考真题)O 是平面上一定点，A 、B 、C 是平面上不共线的三个点，动点P 满足OP =OA +λAB |AB |+AC |AC | ，λ∈[0,+∞)，则P 的轨迹一定通过△ABC 的()A.外心B.内心C.重心D.垂心【答案】B 【分析】根据AB |AB |+AC |AC |是以A 为始点，向量AB |AB |与AC |AC |为邻边的菱形的对角线对应的向量，可知P 点轨迹，据此可求解.【详解】∵OP -OA =AP ，∴AP =λAB |AB |+AC |AC |令AB |AB |+AC |AC |=AM ，则AM 是以A 为始点，向量AB |AB |与AC |AC |为邻边的菱形的对角线对应的向量，即AM 在∠BAC 的平分线上，∵AP =λAM ，∴AP ,AM 共线，故点P 的轨迹一定通过△ABC 的内心，故选：B例2.(2023·全国·高三专题练习)在△ABC 中，cos A =34，O 为△ABC 的内心，若AO =xAB +yAC x ,y ∈R ，则x +y 的最大值为()A.23B.6-65C.7-76D.8-227【答案】D 【分析】设AD =λAO =λxAB +λyAC ，根据三点共线可得x +y =1λ=AO AD =AO AO +OD，结合图像分析运算．【详解】如图：圆O 在边AB ,BC 上的切点分别为E ,F ，连接OE ,OF ，延长AO 交BC 于点D设∠OAB =θ，则cos A =cos2θ=1-2sin 2θ=34，则sin θ=24设AD =λAO =λxAB +λyAC∵B ,D ,C 三点共线，则λx +λy =1，即x +y =1λ1λ=AO AD =AO AO +OD ≤AO AO +OF =11+OF AO =11+OE AO=11+sin θ=11+24=8-227即x +y ≤8-227故选：D ．【方法技巧总结】1.O 是△ABC 的内心：S △B 0C :S △COA :S △AOB =a :b :c ⇔aOA +bOB +cOC =0 ．2.内心在向量AB AB +AC AC所在的直线上；AB ⋅PC +BC ⋅PC +CA ⋅PB =0 ⇔P 为△ABC 的内心.【变式训练】1.(2022·全国·高三专题练习)平面上有△ABC 及其内一点O ，构成如图所示图形，若将△OAB ，△OBC ， △OCA 的面积分别记作S c ，S a ，S b ，则有关系式S a ⋅OA +S b ⋅OB +S c ⋅OC =0 ．因图形和奔驰车的log o 很相似，常把上述结论称为“奔驰定理”．已知△ABC 的内角A ，B ，C 的对边分别为a ，b ，c ，若满足a ⋅OA +b ⋅OB +c ⋅OC =0 ，则O 为△ABC 的()A.外心B.内心C.重心D.垂心【答案】B 【分析】根据平面向量基本定理可得S b S a =b a ，S c S a =c a ，延长CO 交AB 于E ，延长BO 交AC 于F ，根据面积比推出|AE ||BE |=|AC ||BC |，结合角平分线定理推出CE 为∠ACB 的平分线，同理推出BF 是∠ABC 的平分线，根据内心的定义可得答案.【详解】由S a ⋅OA +S b ⋅OB +S c ⋅OC =0 得OA =-S b S a OB -S c S a OC ，由a ⋅OA +b ⋅OB +c ⋅OC =0 得OA =-b a OB -c a OC ，根据平面向量基本定理可得-S bS a =-b a ，-S c S a =-c a ，所以S b S a=b a ，S c S a =c a ，延长CO 交AB 于E ，延长BO 交AC 于F ，则S b S a =|AE ||BE |，又S b S a =b a ，所以|AE ||BE |=b a =|AC ||BC |，所以CE 为∠ACB 的平分线，同理可得BF 是∠ABC 的平分线，所以O 为△ABC 的内心.故选：B2.(2023·全国·高一专题练习)已知在△ABC 中，AB =BC =3，AC =4，设O 是△ABC 的内心，若AO =mAB +nAC ，则m n=( )A.34 B.916 C.43 D.169【答案】C【分析】以AC 的中点D 为坐标原点，建立如下图所示的坐标系，由内切圆的性质得出r ，再由AO=mAB +nAC 得出m n.【详解】以AC 的中点D 为坐标原点，建立如下图所示的坐标系：设△ABC 的内切圆的半径为r ，则12×3+3+4 r =12×4×5，解得r =255故O 0,255 ,A (-2,0),C (2,0),B (0,5)，则AB =(2,5),AC =(4,0),AO =2,255 因为AO =mAB +nAC ，所以2,255=(2m +4n ,5m )，即2m +4n =25m =255，解得m =25,n =310，故m n =25×103=43.故选：C题型四：外心问题【典例分析】例1.(2023·全国·高一专题练习)已知O 是平面上的一定点，A ，B ，C 是平面上不共线的三个点，动点P 满足OP =OB +OC 2+λAB AB cos B +ACAC cos C ，λ∈(0，+∞)，则动点P 的轨迹一定通过△ABC 的()A.重心B.外心C.内心D.垂心【答案】B【分析】设BC 的中点为D ，DP =λAB AB cos B +ACACcos C 两端同时点乘BC ，由DP ⋅BC =0可得答案.【详解】设BC 的中点为D ，因为OP =OB +OC 2+λAB AB cos B +AC AC cos C，所以OP =OD +λAB AB cos B +ACAC cos C ，即DP =λAB AB cos B +ACAC cos C，两端同时点乘BC ，所以DP ⋅BC =λAB ⋅BC AB cos B +AC ⋅BCACcos C=λAB ⋅BC cos π-B AB cos B +AC ⋅BCcos C AC cos C=λ-BC +BC =0，所以DP ⊥BC ，所以点P 在BC 的垂直平分线上，即P 经过△ABC 的外心.故选：B .例2.(2023·重庆·统考二模)已知点O 是△ABC 的外心，AB =6，BC =8，B =2π3，若BO =xBA +yBC ，则3x +4y =()A.5B.6C.7D.8【答案】C【分析】如图，点O 在AB 、AC 上的射影是点D 、E ，根据数量积的几何意义求出BO ⋅BA 、BO ⋅BC ，再根据数量积的定义求出BC ⋅BA，最后根据数量积的运算律得到x 、y 的方程组，解得再代入计算可得.【详解】如图，点O 在AB 、AC 上的射影是点D 、E ，它们分别为AB 、AC 的中点．由数量积的几何意义，可得BO ⋅BA =BA ⋅BD =12AB2=18，BC⋅BO =BC⋅BE =12BC 2=32．又B =2π3，所以BA ⋅BC =BA ⋅BC cos B =6×8×-12 =-24，又BO =xBA +yBC ，所以BO ⋅BA =xBA +yBC ⋅BA =x BA 2+yBC ⋅BA=36x -24y =18，即12x -8y =6．同理BO ⋅BC =xBA +yBC ⋅BC =y BC 2+xBC ⋅BA=-24x +64y =32，即-3x +8y =4，解得x =109y =1112．所以3x +4y =3×109+4×1112=7．故选：C .【方法技巧总结】1.O 是△ABC 的外心：S △B 0C :S △COA :S △AOB =sin2A :sin2B :sin2C ⇔sin2AOA +sin2BOB +sin2COC=0 .2.PA =PB =PC⇔P 为△ABC 的外心.【变式训练】1.(2022·全国·高三专题练习)如图，△ABC 中，AB =2，AC =3，∠BAC =π3，O 为△ABC 外心，且AO =mAB +nAC ，则m +n 的值为()A.23B.1118C.79D.1318【答案】B【分析】根据题意，结合数量积的定义和性质，建立关于m ，n 的方程组，解出即可求得m +n 的值.【详解】∵AB =2，AC =3，∠BAC =π3，∴AB ⋅AC =AB AC cos ∠BAC =2×3×12=3，因为O 为ΔABC 外心，所以AO ⋅AB =AO AB cos ∠OAB =12 AB2=2，同理AO ⋅AC =12|AC |2=92，又AO =mAB +nAC ，∴AO ⋅AB =mAB 2+nAB ⋅AC =4m +3n =2AO ⋅AC =mAB ⋅AC +nAC 2=3m +9n =92 ，∴m =16n =49，∴m +n =16+49=1118.故选：B2.(2023·北京·北京市八一中学校考模拟预测)已知O 是△ABC 的外心，外接圆半径为2，且满足2AO=AB +AC ，若BA 在BC 上的投影向量为34BC ，则AO ⋅BC =( )A.-4B.-2C.0D.2【答案】A【分析】由已知可得∠BAC =90°且|BC |=4，根据已知投影向量可得BAcos B BC=34，进而有BA ⋅BC =12，再由AO ⋅BC =(BO -BA )⋅BC 即可得求结果.【详解】由2AO =AB +AC，故O 为BC 中点，又O 是△ABC 的外心，易知：∠BAC =90°，且|BC|=4，由BA 在BC 上的投影向量BA cos B ⋅BCBC =34BC ，即BA cos B BC=34，所以BA ⋅BC =BA BC cos B =34BC2=12，由图，AO ⋅BC =(BO -BA )⋅BC =BO ⋅BC -BA ⋅BC =8-12=-4.故选：A题型五：垂心问题【典例分析】例1.(2020春·天津和平·高一耀华中学校考阶段练习)已知点O 为△ABC 所在平面内一点，且OA 2+BC2=OB 2+CA 2=OC 2+AB 2，则O 一定为△ABC 的()A.外心B.内心C.垂心D.重心【答案】C【解析】利用向量的等式关系OA 2+BC 2=OB 2+CA 2，转化成OA 2-OB 2=CA 2-BC 2，利用向量加减法运算化简得到BA ⋅CO=0，即证CO ⊥AB ，再同理证得OB ⊥AC ,OA ⊥BC ，即得O 是△ABC 的垂心．【详解】由OA 2+BC 2=OB 2+CA 2得：OA |2- OB 2=CA |2- BC 2，即OA 2-OB 2=CA 2-BC 2，故(OA -OB )⋅(OA +OB )=(CA -BC )⋅(CA +BC )，故BA ⋅(OA +OB )=(CA +CB )⋅BA ，∴BA ⋅(OA +OB -CA -CB )=0，又CA =OA -OC ，CB =OB -OC ，∴BA ⋅(OA +OB +CO -OA +CO -OB )=0∴BA ⋅CO=0，即CO ⊥AB ，同理AC ⋅OB =0,BC ⋅OA=0，即OB ⊥AC ,OA ⊥BC ，所以O 是△ABC 的垂心．故选：C .【点睛】关键点点睛：本题的解题关键在于将模的平方转化成向量的平方，进行向量的灵活运算，才能证得垂直关系，突破难点.例2.(2023·全国·高三专题练习)设O 是△ABC 所在平面上一点，点H 是△ABC 的垂心，满足OA +OB+OC =OH ，且3⋅OA +OB +2⋅OC =0 ，则角A 的大小是()A.3π4B.π3C.π2D.π4【答案】D【分析】由向量的减法运算可得OA +OB =CH ，从而可得OA +OB ⋅AB =CH ⋅AB =0，设点D是边AB 的中点，即OD ⋅AB=0，进而点O 在边AB 的中垂线上，即点O 是△ABC 的外心，利用向量的数量积求出∠BOC 的值，从而可得角A 的大小.【详解】因为OA +OB +OC =OH ，所以OA +OB =OH -OC，即OA +OB =CH ，OA +OB ⋅AB =CH ⋅AB =0，即OD ⋅AB=0(点D 是边AB 的中点)，所以点O 在边AB 的中垂线上.同理点O 在边BC 的中垂线上.因此点O 是△ABC 的外心.设△ABC 外接圆的半径是R .3⋅OA +OB +2⋅OC =0⇒3⋅OA =-2OC -OB ⇒3R 2=2R 2+R 2+22OC ⋅OB ⇒OC ⋅OB =0⇒R 2cos ∠BOC =0⇒∠BOC =π2⇒A =π4.故选：D【点睛】本题考查了向量的减法、向量的加法以及向量数量积的定义，属于中档题.【方法技巧总结】1.O 是△ABC 的垂心：S △B 0C :S △COA :S △AOB =tan A :tan B :tan C ⇔tan AOA +tan BOB +tan COC =0 ．2.PA ⋅PB =PB ⋅PC =PC ⋅PA⇔P 为△ABC 的垂心.【变式训练】1.(2023春·重庆南岸·高一重庆市辅仁中学校校考阶段练习)已知O 是平面上一定点，A 、B 、C 是平面上不共线的三个点，动点P 满足OP =OA +λAB AB cos B +ACACcos C，λ∈0,+∞ ，则动点P 的轨迹一定通过△ABC 的()A.重心B.外心C.内心D.垂心【答案】D【分析】计算AP ⋅BC的值，可得出结论.【详解】因为AP =λAB AB cos B +ACAC cos C，∴AP ⋅BC =λAB ⋅BC AB cos B +AC ⋅BCAC cos C =λ-AB ⋅BC cos B AB cos B +AC ⋅BC cos C AC cos C =0，∴AP ⊥BC ，因此，点P 的轨迹经过△ABC 的垂心，故选：D .2.(2023·全国·高三专题练习)已知H 为△ABC 的垂心，若AH =13AB +25AC ，则sin ∠BAC =( )A.155B.105C.63D.33【答案】C【分析】BH =-23AB+25AC ，CH =13AB -35AC ，利用BH ⋅AC =0、CH ⋅AB =0得cos ∠BAC=3AC 5AB，cos ∠BAC =5AB 9AC ，解得cos 2∠BAC =13，再利用平方共线可得答案.【详解】依题意，BH =BA +AH =-23AB+25AC ，同理CH =CA +AH =13AB -35AC ．由H 为△ABC 的垂心，得BH ⋅AC =0，即-23AB+ 25AC ⋅AC =0，可知25AC 2=23AC AB cos ∠BAC ，即cos ∠BAC =3AC5AB ．同理有CH ⋅AB =0，即13AB - 35AC ⋅AB =0，可知13AB 2=35AC AB cos ∠BAC ，即cos ∠BAC =5AB 9AC ，解得cos 2∠BAC =13，sin 2∠BAC =1-cos 2∠BAC =1-13=23，又∠BAC ∈0,π ，所以sin ∠BAC =63．故选：C ．妙法二：极化恒等式题型六：极化恒等式的应用【典例分析】例1.(2023·全国·高三专题练习)已知正方形ABCD 的边长为2,MN 是它的外接圆的一条弦，点P 为正方形四条边上的动点，当弦MN 的长度最大时，PM ⋅PN的取值范围是()A.-1,0B.0,2C.1,2D.-1,1【答案】A【分析】作出图形，利用极化恒等式化简PM ⋅PN ，求PO 的范围可得PM ⋅PN 的取值范围.【详解】当弦MN 的长度最大时，弦MN 过正方形ABCD 的外接圆的圆心O ，因为正方形ABCD 的边长为2，所以圆O 的半径为2，如下图所示：则PM =PO +OM ，PN =PO +ON =PO -OM ，所以，PM ⋅PN =PO +OM ⋅PO -OM =PO 2-OM 2.因为点P 为正方形四条边上的动点，所以1≤PO≤2，又OM =2，所以PM ⋅PN ∈-1,0 ，故选：A .例2.(2023春·江苏南京·高一校考期中)如图所示，矩形ABCD 的边AB =2，AD =1，以点C 为圆心，CB 为半径的圆与CD 交于点E ，若点P 是圆弧EB (含端点B ､E )上的一点，则PA ⋅PB的取值范围是()A.0,2-1B.1-2,0C.0,2-22D.2-22,0【答案】D【分析】建立坐标系，表示出P 的坐标，利用数量积的运算结合三角函数的性质可得答案.【详解】法一：以点C 为原点，以直线EC 为x 轴，建立如图所示的平面直角坐标系，则A (-2,-1)，B (0,-1)，设P (cos θ,sin θ)，π≤θ≤3π2 ，∴PA =(-2-cos θ,-1-sin θ)，PB =(-cos θ,-1-sin θ)，∴PA ·PB =2cos θ+2sin θ+2=22sin θ+π4+2，∵π≤θ≤3π2 ，∴5π4≤θ+π4≤7π4，∴-1≤sin θ+π4 ≤-22，∴2-22≤PA ⋅PB≤0，∴PA ⋅PB的取值范围是[2-22,0].法二：极化恒等式。

第02讲 平面向量的线性运算（3个知识点+4种题型+强化训练）知识点一、向量加法1．向量加法的定义定义：求两个向量和的运算 叫做向量的加法． 对于零向量与任意向量a 规定0＋a ＝a ＋0＝a . 2．向量求和的法则三角形法则已知非零向量a b 在平面内任取一点A 作AB →＝a BC →＝b 则向量AC →叫做a 与b的和 记作a ＋b 即a ＋b ＝A B →＋BC →＝A C →.平行四边形法则已知两个不共线向量a b 作AB →＝a AD →＝b 以AB → AD →为邻边作▱ABCD 则对角线上的向量AC →＝a ＋b .思考：两个向量相加就是两个向量的模相加吗？[提示] 不是 向量的相加满足三角形法则 而模相加是数量的加法． 3．向量加法的运算律 (1)交换律：a ＋b ＝b ＋a .(2)结合律：(a ＋b )＋c ＝a ＋(b ＋c )． 知识点二、向量减法1．相反向量(1)定义：与向量a 长度相等 方向相反的向量 叫做a 的相反向量． (2)性质：①－(－a )＝a .②对于相反向量有：a ＋(－a )＝0. ③若a b 互为相反向量 则a ＝－b a ＋b ＝0. 2．向量的减法(1)定义：a －b ＝a ＋(－b ) 即减去一个向量相当于加上这个向量的相反向量． (2)作法：在平面内任取一点O 作OA →＝a OB →＝b 则向量BA →＝a －b 如图所示．思考：在什么条件下|a－b|＝|a|＋|b|?[提示]当a b至少有一者为0或a b非零且反向时成立．知识点三、向量的数乘运算(1)定义：规定实数λ与向量a的积是一个向量这种运算叫做向量的数乘记作：λa它的长度与方向规定如下：①|λa|＝|λ||a|；②当λ＞0时λa的方向与a的方向相同；当λ＜0时λa的方向与a的方向相反．(2)运算律：设λμ为任意实数则有：①λ(μ a)＝(λμ)a；②(λ＋μ)a＝λa＋μ a；③λ(a＋b)＝λa＋λb；特别地有(－λ)a＝λ(－a)＝－(λa)；λ(a－b)＝λa－λb.(3)线性运算：向量的加、减、数乘运算统称为向量的线性运算向量线性运算的结果仍是向量．对于任意向量a b以及任意实数λμ1μ2恒有λ(μ1a＋μ2b)＝λμ1a±λμ2b.(4) 共线向量定理向量a(a≠0)与b共线的充要条件是：存在唯一一个实数λ使b＝λa.思考：定理中把“a≠0”去掉可以吗？[提示]定理中a≠0不能漏掉．若a＝b＝0则实数λ可以是任意实数；若a＝0b≠0则不存在实数λ使得b＝λa.知识复习题型一、向量的加法一、单选题1．在平面四边形ABCD中下列表达式化简结果与AB相等的是（）A．AC CD+B．AD DC CB++C．CA CB+--D．CB DA DC【答案】B【分析】根据平面的线性运算求得正确答案.【详解】AC C AD+=不符合题意.D++=+=符合题意.AD DC CB AC CB ABCA CB BA-=不符合题意.=+-+≠不符合题意.CB DA DC CB CA AB故选：B2．（2024下·全国·高一专题练习）下列等式不正确的是()①()()++=++；a b c a c b②0+=；AB BA③AC DC AB BD=++.A．②③B．②C．①D．③【答案】B【分析】根据向量加法的运算律判断即可.【详解】对于① ()()++=++正确；a b c a c b对于② 0+=错误；AB BA对于③ DC AB BD AB BD DC AC++=++=正确.故选：B3．（2024下·全国·高一专题练习）如图所示的方格纸中有定点O P Q E F G H则OP OQ+=（）A．OE B．OF C．OG D．OH【答案】B【分析】根据平行四边形法则即可求.【详解】以OP OQ 为邻边作平行四边形 可知OF 为所作平行四边形的对角线故由平行四边形法则可知OF 对应的向量OF 即所求向量． 故选：B4．（2024下·全国·高一专题练习）已知四边形ABCD 为菱形 则下列等式中成立的是（ ） A ．AB BC CA += B ．AB AC BC += C ．AC BA AD += D ．AC AD DC +=【答案】C【分析】根据菱形的性质 结合平面向量加法的运算性质进行判断即可. 【详解】对于A AB BC AC += 故A 错误；对于B 因为AB BC AC += 所以2AB AC AB BC +=+ 故B 错误； 对于C AC BA BA AC BC AD +=+== 故C 正确；对于D 因为AD DC AC += 所以2AC AD AD DC +=+ 故D 错误. 故选：C5．（2024上·河北石家庄·高一石家庄市第二十四中学校考期末）向量()AB OM BO MB +++= （ ） A ．BC B ．AB C ．AC D ．AM【答案】B【分析】利用向量加法的三角形法则及向量加法的运算律即可求解. 【详解】由()AB OM BO MB AB BO OM MB AB +++=+++= 故B 正确. 故选：B. 二、填空题6．（2024下·全国·高一专题练习）已知向量a 表示“向东航行3km” b 表示“向南航行3 km” 则a b +表示 .【答案】向东南航行32km. 【分析】根据向量加法法则分析即可.【详解】根据题意由于向量a 表示“向东航行3km” 向量b 表示“向南航行3km” 那么可知a b +表示向东南航行223332+=km. 故答案为：向东南航行32km 7．（2023·全国·高一随堂练习）化简：（1）AB BC CD ++= ； （2）AB BC CD DE EF ++++= ； （3）AB CB AC --= ； （4）12231n n A A A A A A -++⋅⋅⋅+= ． 【答案】 AD AF 0 1n A A 【分析】根据向量加减法的几何意义进行运算即可. 【详解】（1）AB BC CD AC CD AD ++=+=；（2）AB BC CD DE EF AC CD DE EF ++++=+++AD DE EF AE EF AF =++=+=； （3）0AB CB AC AB BC AC AC AC --=+-=-=； （4）122311311111n n n n n n n n A A A A A A A A A A A A A A A A ----++⋅⋅⋅+=+⋅⋅⋅+==+=.故答案为：AD ；AF ；0；1n A A . 三、解答题8．（2023·全国·高一随堂练习）如果0AB BC CA ++= 那么A B C 三点是否一定是一个三角形的三个顶点？ 【答案】不一定【分析】考虑A B C 三点是否共线即可回答.【详解】当A B C 三点共线也有0AB BC CA ++= 所以A B C 三点不一定是一个三角形的三个顶点.9．（2024下·全国·高一专题练习）如图 已知a 、b 、c 求作向量a b c ++．【答案】作图见解析【分析】在平面内任取一点O 作OA a = AB b = BC c = 利用平面向量加法的三角形法则可作出向量a b c ++.【详解】作法：如图所示 在平面内任取一点O 作OA a = AB b = BC c = 则OC OA AB BC a b c =++=++．题型二、向量的减法 一、单选题1．（2022上·江西·高三校联考阶段练习）对于非零向量a b “0a b +=”是“a b ∥”的（ ） A ．充分不必要条件 B ．必要不充分条件 C ．充要条件 D ．既不充分也不必要条件【答案】A【分析】根据相反向量一定是共线向量 共线向量不一定是相反向量可求解. 【详解】由0a b +=得0a b += 所以a b =- 则a b ∥； 由a b ∥得a 与b 方向相同或相反 模长不一定相等 所以0a b +=不一定成立所以“0a b +=”是“a b ∥”的充分不必要条件. 故选:A.2．（2023下·河北张家口·高一河北省尚义县第一中学校考阶段练习）向量AB CB DA -+=（ ） A ．BD B ．CDC ．DCD ．0【答案】C【分析】根据向量的概念 以及向量加减法的运算律 即可得出答案. 【详解】由AB CB DA AB BC DA AC AD DC -+=++=-=. 故选：C.3．（2024下·全国·高一专题练习）已知,a b 为非零向量 则下列说法错误的是（ ） A ．若||||||a b a b +=+ 则a 与b 方向相同B ．若||||||a b a b +=- 则a 与b 方向相反C ．若||||||a b a b +=- 则a 与b 有相等的模D ．若||||||a b a b -=- 则a 与b 方向相同 【答案】C【分析】运用向量三角不等式的取等条件求解即可.【详解】由向量三角不等式可知 只有当非零向量,a b 同向时 有||||||a b a b +=+||||||a b a b -=- 故A D 正确；只有当非零向量,a b 反向时 有||||||||b b a a +=- ||||||a b a b +=- 故B 正确 C 错误．故选：C ． 二、多选题4．（2023下·湖南怀化·高一校考期中）下列各式中结果一定为零向量的是（ ） A ．BO OM MB ++ B ．AB BC +C ．C BO OB O CO +++D ．AB AC BD CD -+-【答案】ACD【分析】利用向量的加法运算 结合零向量的意义逐项计算判断作答. 【详解】对于A 0O M BO M B MO OM ++=+= A 是； 对于B AB BC AC += AC 不一定是零向量 B 不是；对于C ()()000BO O OB OC CO B O C BO C O +++=+++=+= C 是； 对于D ()0AB AC BD CD AB AD AD BD AC CD -+-=+-+=-= D 是. 故选：ACD 5．若a 、b 为相反向量 且1a = 1b = 则a b += a b -= . 【答案】 0 2【分析】利用相反向量的定义结合平面向量的加、减法可求得结果. 【详解】因为a 、b 为相反向量 且1a = 1b = 则0a b += 2a b a -= 因此 0a b += 22a b a -==. 故答案为：0；2.6．（2022下·上海闵行·高一上海市七宝中学校考阶段练习）若向量a 与b 共线 且1==a b 则+=a b ． 【答案】0或2【分析】由题可知a 与b 相等或互为相反向量 据此即可求a b + 【详解】向量a 与b 共线 且a b = ∴a 与b 相等或互为相反向量 当a 与b 相等时 22a a b ==+ 当a 与b 互为相反向量时 0=0a b =+． 故答案为：0或2．7．（2022·高一课时练习）如图所示 中心为O 的正八边形1278A A A A 中()11,2,,7i i i a A A i +== ()1,2,,8j j b OA j == 则25257a a b b b ++++= ．（结果用i a ib 表示）【答案】6b【分析】根据向量的加减运算即可求得答案. 【详解】由题图可知 25257a a b b b ++++2356257A A A A OA OA OA =++++()()2235567OA A A OA A A OA =++++367OA OA OA =++36366OA OA OA OA b =+-==,故答案为：6b8．已知长度相等的三个非零向量,,OA OB OC 满足OA OB OC ++=0,则由A ,B ,C 三点构成的∴ABC 的形状是 三角形. 【答案】等边【详解】如图,以OA ,OB 为邻边作菱形OAFB ,则OA OB OF +=,∴OF OC +=0,∴OF =-OC . ∴O ,F ,C 三点共线. ∴四边形OAFB 是菱形, ∴CE 垂直平分AB.∴CA=CB. 同理,AB=AC.∴△ABC 为等边三角形. 四、解答题9．（2022下·河南周口·高一校考阶段练习）化简下列各式： (1)()()BA BC ED EC ---； (2)()()AC BO OA DC DO OB ++--- 【答案】(1)DA(2)0【分析】（1）根据平面向量加法和减法的运算法则化简即可得出结果； （2）首先化简出两个向量的结果 再与第三个向量进行加减运算即可求得结果. 【详解】（1）利用平面向量的加减运算法则可得()()()BA BC ED EC BA CB ED CE CA CD CA DC DA ---=+-+=-=+=（2）由平面向量的加减运算法则可得()()()()AC BO OA DC DO OB AC BA DC OD BO ++---=+-++()0BC DC BD BC BC =-+=-=题型三 、向量的数乘运算 一、单选题1．（2023·湖南岳阳·校联考模拟预测）已知向量,a b 则()()2a b a b +--=（ ） A ．a b + B ．a b - C ．3a b + D ．3ab【答案】D【分析】直接由向量的线性运算即可求解.【详解】由题意()()2223a b a b a b a b a b +--=+-+=+. 故选：D.2．（2024上·河南焦作·高三统考期末）已知ABC 所在平面内一点D 满足102DA DB DC ++=则ABC 的面积是ABD △的面积的（ ） A ．5倍 B ．4倍C ．3倍D ．2倍【答案】A【分析】利用平面向量的线性运算计算即可．【详解】设AB 的中点为M 因为102DA DB DC ++=所以2()CD DA DB =+ 所以4CD DM = 所以点D 是线段CM 的五等分点所以5ABC ABDCM S SDM==,所以ABC 的面积是ABD △的面积的5倍． 故选：A.3．（2023下·河南洛阳·高一河南省偃师高级中学校考阶段练习）在ABC 中 点M 是AB 的中点 N 点分AC 的比为:1:2,AN NC BN =与CM 相交于E 设,AB a AC b == 则向量AE =（ ）A．1132a b+B．1223a b+C．2155a b+D．3455a b+【答案】C【分析】由三点共线性质以及平面向量基本定理解方程组即可得解.【详解】由题意,,B E N三点共线所以存在Rλ∈使得()113AE AB AN AB ACλλλλ-=+-=+同理,,C E M三点共线所以存在Rμ∈使得()112AE AC AM AC ABμμμμ-=+-=+由平面向量基本定理可得1213μλλμ-⎧=⎪⎪⎨-⎪=⎪⎩解得21,55λμ==所以2155AE a b=+.故选：C.4．（2023·湖南永州·统考二模）在ABC中若1,2AB AC CA CB+=+=则ABC的面积的最大值为（）A．16B．15C．14D．13【答案】D【分析】设,E F分别为,BC AB的中点结合三角形相似推出43ABC ACEFS S=四边形由题意可得1||,||12AE CF==确定四边形ACEF面积的最大值即可得答案.【详解】设,E F分别为,BC AB的中点连接EF则EF AC∥则BEF△∴BCA故14BEF ABCS S=,则34ABC ACEF S S =四边形 故43ABCACEFSS =四边形 又1,2AB AC CA CB +=+= 则21,22AB AC AE CA CB CF +==+== 故1||,||12AE CF ==当AE CF ⊥时 四边形ACEF 面积最大 最大值为1111224⨯⨯=故ABC 的面积的最大值为411343⨯=故选：D 5．（2024下·全国·高一专题练习）在ABC 中 D 为AC 上一点且满足 12AD DC =，若P 为BD 的中点 且满足 AP AB AC λμ=+，则λμ+的值是 . 【答案】23【分析】根据平面向量的线性运算计算即可. 【详解】如图因为12AD DC = 所以13AD AC =则11111112222326AP AB AD AB AC AB AC =+=+⨯=+ 所以12λ=16μ= 23λμ+=.故答案为：23.6．（2024下·全国·高一专题练习）已知矩形ABCD 中 对角线交于点O 若125,3BC e DC e == 则OC = . 【答案】12 5322e e +【分析】利用向量的线性运算可得OC 的表达形式.【详解】因为ABCD 是矩形 所以1111122222OC AC AB BC DC BC ==+=+ 所以125322OC e e =+.故答案为：125322e e +7．（2022·全国·模拟预测）在平行四边形ABCD 中 点G 在AC 上 且满足3AC AG = 若DG mAB nAD =+ 则m n -= .【答案】1【分析】利用向量线性运算求得1233DG AB AD =- 与题干对照即可求解. 【详解】()11123333DG AG AD AC AD AB AD AD AB AD =-=-=+-=- 则13m = 23n =-所以1m n -=. 故答案为：1 三、解答题8．（2024下·全国·高一专题练习）若向量x y 满足23x y a += 32x y b -= a 、b 为已知向量 求向量x y ． 【答案】231313=+x a b 321313=-y a b 【分析】根据23x y a += 32x y b -= 列方程组求解. 【详解】解：由方程组2332x y ax y b +=⎧⎪⎨-=⎪⎩解得231313=+x a b 321313=-y a b .题型四、平面向量共线定理及应用一、单选题1．（2024·陕西安康·陕西省安康中学校联考模拟预测）已知平面向量a 与b 不共线 向量(),32m xa b n a x b =+=+- 若//m n 则实数x 的值为（ ）A ．1B ．13-C ．1或13-D ．1-或13【答案】C【分析】根据平面共线定理 由向量平行 求得x 满足满足的方程 求解即可. 【详解】由//m n 且,m n 均不为零向量 则()32,m n a x b λλλλ==+-∈R可得()132x x λλ=⎧⎨=-⎩ 则()3210x x --= 整理得23210x x 解得1x =或13x ． 故选：C ．2．（2024上·辽宁·高一校联考期末）已知a 与b 为非零向量,2,OA a b OB a b OC a b λμ=+=-=+ 若,,A B C 三点共线 则2λμ+=（ ）A ．0B ．1C ．2D ．3【答案】D【分析】根据三点共线可得向量共线 由此结合向量的相等列式求解 即得答案. 【详解】由题意知 ,,A B C 三点共线 故2,(2)(1)AB a b BC a b λμ=-=-++, 且,AB BC 共线故不妨设,(0)A k B k BC =≠ 则1(2)2(1)k k λμ=-⎧⎨-=+⎩ 所以122μλ+-=- 解得23λμ+=故选：D3．（2024下·全国·高一专题练习）已知21,e e 为两个不共线的向量 若向量12122,23a e e b e e =+=-+ 则下列向量中与向量2a b +共线的是（ ） A ．1252e e -+ B ．12410e e +C ．12104e e +D ．122e e +【答案】B【分析】根据向量线性运算表示12225a b e e +=+ 然后利用共线向量基本定理求解即可. 【详解】因为向量122a e e =+ 1223b e e =-+ 所以12225a b e e +=+．又()1212410225e e e e +=+ 所以12410e e +与2a b +共线． 故选：B ． 二、填空题4．（2024·全国·高三专题练习）在ABC 中 O 是边BC 的中点 AP t AO = 过点P 的直线l 交直线,AB AC 分别于,M N 两点 且,AM mAB AN nAC == 则11m n+= . 【答案】2t【分析】由三点共线的性质列式求值. 【详解】由题意：().222t t tAP t AO AB AC AB AC ==+=+ 由,,M P N 三点共线知 ()()11AP AM AN mAB nAC λλλλ=+-=+-. ()212t m t n λλ⎧=⎪⎪⎨⎪-=⎪⎩⇒ 212t m t n λλ⎧=⎪⎪⎨⎪-=⎪⎩消去λ 得112m n t+=. 故答案为：2t5．（2022上·河南·高二校联考期末）已知ABC 中 点D 在线段AB （不含端点）上 且满足()R CD xCA yCB x y =+∈, 则12x y+的最小值为 .【答案】322+/223+【分析】根据向量共线可得1x y += 即可利用基本不等式的乘“1”法求解. 【详解】∴(),R CD xCA yCB x y =+∈ 由于D 在线段AB （不含端点）上 故,,A D B 三点共线 所以1x y +=且00，x y >>则()121223322y xx y x y x y x y ⎛⎫+=++=++≥+ ⎪⎝⎭ 当且仅当2y x xy=时 即21,22x y =-=-时取等号 故12x y+有最小值322+. 故答案为：322+.6．（2024下·全国·高一专题练习）如图所示 在ABC 中 14AN NC =P 是BN 上的一点 若611AP AB mAC =+ 则实数m 的值为 ．【答案】111【分析】借助共线定理的推论即可得. 【详解】因为14AN NC = 所以5AC AN = 所以6651111AP AB mAC AB mAN =+=+ 因为P B N 三点共线 所以65111m += 解得111m =.故答案为：111. 7．（2023·吉林长春·东北师大附中校考模拟预测）在ABC 中 M N 分别是边AB AC 上的点 且23AN AC =13AM AB = 点O 是线段MN 上异于端点的一点 且满足340(0)OA OB OC λλ++=≠ 则λ= ．【答案】8【分析】用OA 、AN 表示出OC 、OB 从而得到6977AO AN AM λλ=+++ 再根据M O N 三点共线 得到69177λλ+=++ 解得即可. 【详解】解：因为23AN AC =13AM AB =所以()23AN OC OA =- ()13AM OB OA =- 即32OC AN OA =+ 3OB AM OA =+因为340OA OB OC λ++= 所以()333402OA AM OA AN OA λ⎛⎫++++= ⎪⎝⎭即()769AO AN AM λ+=+ 即6977AO AN AM λλ=+++ 因为M O N 三点共线 故69177λλ+=++ 解得8λ=． 故答案为：8 8．（2022下·陕西西安·高一统考期中）设,a b 是不共线的两个向量. (1)若2OA a b =- 3OB a b =+ 3OC a b =- 求证：A B C 三点共线； (2)若8a kb +与2ka b +共线 求实数k 的值. 【答案】(1)证明见解析； (2)±4.【分析】（1）要证明三点共线 即证明三点组成的两个向量共线即可. （2）由共线性质求出参数即可.【详解】（1）由2OA a b =- 3OB a b =+ 3OC a b =- 得3(2)2AB OB OA a b a b a b =-=+--=+ 3(3)242BC OC OB a b a b a b AB =-=--+=--=-因此//AB BC 且有公共点B 所以A B C 三点共线.（2）由于8a kb +与2ka b +共线 则存在实数λ 使得8(2)a kb ka b λ+=+ 即(8)(2)0k a k b λλ-+-= 而,a b 是不共线因此8020k k λλ-=⎧⎨-=⎩解得2,4k λ==或2,4k λ=-=- 所以实数k 的值是4±.9．（2024上·辽宁·高一校联考期末）如图 在ABC 中 D 是BC 上一点 G 是AD 上一点 且2AG BD DG CD== 过点G 作直线分别交,AB AC 于点,E F .(1)用向量AB 与AC 表示AD ； (2)若54AB AE = 求ACAF 和EG EF的值.【答案】(1)1233AD AB AC =+ (2)138AC AF = 1318EG EF =.【分析】（1）利用向量的线性运算求解；（2）设AC AF μ= 利用向量的线性运算和平面向量基本定理求解. 【详解】（1）2221233333AD AB BD AB BC AB BA AC AB AC =+=+=++=+.（2）因为54AB AE = 所以54AB AE =．设AC AF μ= 22122454333399189AG AD AB AC AB AC AE AF μ⎛⎫==+=+=+ ⎪⎝⎭ 因为,,G E F 三点共线 所以541189μ+= 解得138μ= 所以138AC AF =.因为48513EF EA AF AB AC =+=-+424264134859945918513EG EA AG AB AB AC AB AC AB AC ⎛⎫=+=-++=-+=-+ ⎪⎝⎭所以1318EG EF =即1318EG EF =. 10．（2024下·全国·高一专题练习）如图 在平行四边形ABCD 中 ,,AB a AD b M ==为AB 中点 N 为BD 上靠近点B 的三等分点 求证：,,M N C 三点共线．【答案】证明见解析【分析】根据三点共线要求证明//CM CN即可.【详解】∴,AB a AD b==∴BD AD AB b a=-=-．∴N是BD上靠近点B的三等分点∴11()33BN BD b a==-．∴在平行四边形中BC AD b==∴112()333CN BN BC b a b a b =-=--=--．①∴M为AB的中点∴111,()222MB a CM MC MB BC a b a b⎛⎫=∴=-=-+=-+=--⎪⎝⎭．②由①②可得32CM CN=．由向量共线定理知//CM CN．又∴CM与CN有公共点C ∴,,M N C三点共线．。