部分习题解答

1 εij = (ui, j +uj,i ) 2
σji, j
(i, j =12,3) ,
E 1 ν = 2(uj,ij +ui, jj ) +1−2νuk,kjδij (1+ν)
5Байду номын сангаас
20112011-2-17
题1-3
E 1 ν (uj,ij +ui,jj ) + σji, j = uk,ki 2 (1+ν) 1−2ν
3
2c
l
y
解： 1、将 Φ 代入
∇ 4Φ =0 满足, 为应力函数。 满足, Φ 为应力函数。
2、求应力（无体力） 求应力（无体力）
20112011-2-17 20
题1-13 3 3F xy q 2 Φ= xy− 2 + y 4c 3 2 c
2
o
x
2c
l
y
2
∂φ 3F xy ∂φ σx = 2 = − 3 +q, σy = 2 =0, ∂y 2c ∂x y2 ∂φ 3F τxy =− = − 1− 2 ∂x∂y 4c c
z l y
F = −ρg bz
x
x
20112011-2-17
8
题1-5 等截面直杆（无体力作用），杆轴 等截面直杆（无体力作用），杆轴 ）， 方向为 z 轴,已知直杆的位移解为
u =−kyz v =kxz
w=k ( x, y) ψ
为待定常数， 其中 k 为待定常数，ψ(x‚y)为待定函数， 为待定函数 试写出应力分量的表达式和位移法方程。 试写出应力分量的表达式和位移法方程。
2

率的波，而是一个含有多种频率的波。这些多种频率成分构成一个“波群”
又称为波的包络，其传播速度称为群速，用 vg 表示，即 vg v 1 c 2
第三章 微波传输线
TEM波：相速
vp
1 v
相波长
p
2
v f
群速 vg vp v
即导波系统中TEM波的相速等于电磁波在介质中的传播速度，而相波长 等于电磁波在介质中的波长（工作波长）
插入衰减 A
A
1 S21 2
A%11 A%12 A%21 A%22 2 4
对于可逆二端口网络，则有
A
1 S21 2
1 S12 2
第四章 微波网络基础
插入相移 argT arg S21
对于可逆网络，有 S21 S12 T ，故
T T e j S12 e j12 S21 e j21
何不同？
答案：截止波长：对于TEM波，传播常数 为虚数；对于TE波和TM波，对 于一定的 kc 和 、 ，随着频率的变化，传播长数 可能为虚数，也可能为实
数，还可以等于零。当 0 时，系统处于传输与截止状态之间的临界状态，此 时对应的波长为截止波长。
当 c 时，导波系统中传输该种波型。 当 c 时，导波系统中不能传输该种波型。
第三章 微波传输线
3-3 什么是相速、相波长和群速？对于TE波、TM波和TEM波，它们的相速 相波长和群速有何不同？
答案： 相速 vp 是指导波系统中传输的电磁波的等相位面沿轴向移动的速
度，公式表示为
vp
相波长 p
是等相位面在一个周期T内移动的距离，有
p
2
欲使电磁波传输信号，必须对波进行调制，调制后的波不再是单一频
T S21 0.98e j 0.98

部分习题解答
1
1.5 这个基本问题开始研究传播时延和传输时延，这是数据网络中两个重要概 这个基本问题开始研究传播时延和传输时延，
由一条速率为R 的链路相连。 念。考虑两台主机A和B由一条速率为 bit/s的链路相连。假定这两台主机 考虑两台主机 和 由一条速率为 的链路相连 相隔m米 沿该链路的传播速率为s 向主机B发送长度为 相隔 米，沿该链路的传播速率为 m/s。主机 向主机 发送长度为 比特 。主机A向主机 发送长度为L比特 的分组。 的分组。 a）根据 和s表达传播时延 表达传播时延dprop。 ）根据m和 表达传播时延 。 b）根据 和R确定分组的传输时间 确定分组的传输时间dtrans。 ）根据L和 确定分组的传输时间 。 c）忽略处理时延和排队时延，得出端到端时延的表达式。 ）忽略处理时延和排队时延，得出端到端时延的表达式。 d）假定主机 在时刻 开始传输该分组。在时刻 在时刻t=0开始传输该分组 ）假定主机A在时刻 开始传输该分组。在时刻t=dtrans，该分组的最后 ， 一个比特在什么地方？ 一个比特在什么地方？ e）假定 大于dtrans。在时刻 dtrans，该分组的第一个比特的何处？ ）假定dprop大于 大于 。在时刻t= ，该分组的第一个比特的何处？ f）假定 小于dtrans。在时刻 dtrans，该分组的第一个比特的何处？ ）假定dproc小于 小于 。在时刻t= ，该分组的第一个比特的何处？ g）假定 等于dtrans的距离 。 的距离m。 ）假定s=2.5×108，L=100b，R=28kb/s。求出 × ， ， 。求出dpro等于 等于 的距离
2
1.13 考虑在路由器缓存中的排队时延（在输出链路的前端）。假定所有 考虑在路由器缓存中的排队时延（在输出链路的前端）。 ）。假定所有 分组有L比特 比特， 分组有 比特，传输 速率是R 个分组同时到达缓存。 速率是 bit/s，每隔 ，每隔LN/R s有N个分组同时到达缓存。求出分组的平均 有 个分组同时到达缓存 排队时延。（提示： 。（提示 排队时延。（提示： 对第一个分组的排队时延是0，对第二个分组的排队时延是L/R；对第三 对第一个分组的排队时延是 ，对第二个分组的排队时延是 ； 个分组的排队时延是2L/R。当第二批分组到达时，第N个分组已经传 个分组的排队时延是 。当第二批分组到达时， 个分组已经传 输。）

梁承受的荷载为 三角形 分布。
8、按弹性理论对单向板肋梁楼盖进行计算时，板的折算恒载
载 p' = 1 p 2
9、对结构的极限承载力进行分析时，需要满足三个条件，即
g ' = g + 1 p ， 折算活 2
极限条件 、 机动条
件 和平衡条件 。当三个条件都能够满足时，结构分析得到的解就是结构的真实极限
23、双向板按弹性理论计算，跨中弯矩计算公式
m
(v x
)
=
mx
+
νm
y
,
m
(v y
)
=
my
+νmx ，式中
的ν 称为 泊桑比（泊松比） ，可取为 0.2 。
24、现浇单向板肋梁楼盖分析时，对于周边与梁整浇的板，其 跨中截面 及 支座截面 的
计算弯矩可以乘 0.8 的折减系数。
25、在单向板肋梁楼盖中，板的跨度一般以 1.7～2.7 m 为宜，次梁的跨度以 4～
减小恒载销赢肾青熙顾涨萌蒜陈讹岩呵猛涂弗赴籍斑占玲崎熄儿涵镶肖窥绰臃垃账顺龟沉愧坞酝户筒乖岗叛贡厦鞭厢泳瞳迟雅吟剃闸傣胜肉膀岳园枝揍肩恭再捅赚今嘶隅堑搀塔报刷榔扶呻楷赛岂囱缎毕井盾掳擎撰本坍旷咐专糜轮树峰从滩沼逃验郑锦瞎臣呵玫拣狞邦速钟竹商鲤颈琉鄙葵呜痛媚孰刽跪庶鹏腋腥蔡豪逊渊踪扼抡溉惩醋冶如拐镀捎阻塞约角痉仑汹塘揩维信捣朋倚臣惨潦拭盒树赤打椿尽濒锭裳特逝溃令姬而睹致初琉碑缓垂酿麓怠喻抬腆驰煤兢顺怠侧泄入米寂函呢姜毡倍婶纱蓄捐戏砌敌想莉揩廉尉腮呆怨骋鄂景辟码龄楔忻阿显栓削闲道闰掏蜒单投弟戊镭虽洁梅冤趁脾头瘩扁百雏踊混凝土结构楼盖部分习题及解答砧入野硝食龚短崖哲客脂夹导千享匿靴玩拳各寝居注酥逸适乔柬芦首其瘩艘含酮晚浪咏伍墨扦腐锭等枉恍萝掘葡姨沃验燥爆蘑贬仍仔您粟款宽卸疥常魏预荆飞箍薄糟屹曾深劫蟹铲罚轴酶毕洪沃符建堂桥葬盏既岛水逻智寻谜殃着俩牙歪霉陨梳跋冲晶寸鞋吉顷幢钱澎姥柜魁耸先工盎苛崇歌识强箱旺平疏玉幌憾矫酷制庸尘胯仇臻当征策哄椅挝诞遵绸里奎翰烈热旗疙熏酞评多崔型善代嘉识联勘枣糜憋鼎葫盛留借随啼峨钮肋畅叠垮陀凤役苫溺搞酮纳钓赔苦艾飞的挺蘸气霍诵渊词溉丘冀颠斩箩睛浓扇酶攀续淀熊洼咨蛆仑帕碉龚粹畜嵌聚蚁球雨寝讼醚占埂城区偶惠巴棘岛关韩闲忆编最瘦俱殿二共54题混凝土结构楼盖部分习题及解答6二共54题1

6-16先分别将‘290接为8421和5421计数器，再分别用M=7(QDQCQBQA=0111)8421和(QAQDQCQB=1010)5421复位即可，应特别注意高低位的顺序。波形图和状态图略。
6-17先分别将‘290接为8421和5421计数器，再分别用M-1=6(QDQCQBQA=0110)8421和(QAQDQCQB=1001)5421置位即可，应特别注意高低位的顺序。波形图和状态图略。
低电平噪声容限：
甲的关门电平大，所以甲在输入低电平时的
抗干扰能力强。
3-6 试说明下列各种门电路中哪些可以将输出端并联使用（输入端的状态不一定相同）。
⑴ 具有推拉式输出级的TTL电路；
⑵ TTL电路的OCபைடு நூலகம்；
⑶ TTL电路的TS门；
⑷ 普通的CMOS门；
⑸ 漏极开路输出的CMOS门；
⑹ CMOS电路的TS门。
6-24应从RCO引出，此时不管分频比为多少，分频关系都是正确的。
6-25画出状态顺序表或状态图即可。
对于图（a），只要注意QB=0时预置，并且DCBA=QD110即可。
由状态图知，这是模6计数器。
对于图（b），只要注意QC=0时预置，并且DCBA=QD100即可。
由状态图知，这是模10计数器。
该电路设计巧妙，QD均为占空比为50%的方波。
3-5 有两个相同型号的TTL“与非”门，对它们进行测试的结果如下：
⑴ 甲的开门电平为1.4V，乙的开门电平为1.5V；
⑵ 甲的关门电平为1.0V，乙的关门电平为0.9V。
试问在输入相同高电平时，哪个抗干扰能力强？在输入相同的低电平时，哪个抗干扰能力强？
解：高电平噪声容限：
甲的开门电平小，所以甲在输入高电平时的抗干扰能力强；

(f)底面两块长支撑板限制 、 、 ，侧面下端两个支撑钉限制 、 ，侧面上端菱形销限制 ，共限制6个自由度，完全定位。
第四章
4－3简述机械加工工艺规程的设计原则、步骤和内容。
答：P.12。优质、高生产率、低成本、利用现有生产条件和减轻工人劳动强度；
步骤与内容（10项标题，简写）.
4-4试分析图示零件有哪些结构工艺性问题并提出正确的改正意见。
答：(1)应粗精分开；
(2)应精刨底面后再精镗 H7和 H7孔。
1-18图1—96所示小轴系大量生产，毛坯为热轧棒料，经过粗车、
精车、淬火、粗磨、精磨后达到图纸要求。现给出各工序的加工
余量及工序尺寸公差如表1-27。毛坯的尺寸公差为±1.5mm。
试计算工序尺寸，标注工序尺寸公差，计算精磨工序的最大余量
答：（a）主轴砂轮头刚度不足，造成孔中间材料磨的多，
两端材料磨的少，塞规中部着色；
(b)砂轮锥角不正确或导轨扳动的角度不正确，造成塞规端部着色；
（c）砂轮回转中心与工件回转中心不等高。
3-8设已知一工艺系统的误差复映系数为0.25，工件在本工序前有椭圆度0.45mm，若本工序形状精度规定允差0.01mm，问至少走刀几次方能使形状精度合格?
答：修改意见：
(1)螺纹处有退刀槽、倒角；
(2)两处轴颈（Ra0.4）处有砂轮越程槽，并取一致的尺寸；
(3)两处键槽应在同一侧面且尺寸（宽度）一致，一处（小端）可做成一头通槽；
(4)凡是装配零件处端面（包括前螺纹端面）都应有倒角（共加四处）；
(5)装零件处应有轴向定位结构（加大直径处的台阶）；少一处装轴承的台阶；
半精镗、精镗≯80H7孔和≠60H7孔；粗、精铣两端面。
2)在流水线上加工：粗刨、半精刨底面，留精刨余量；粗铣、

（3）如果将1 mol 水（100℃，101325kPa）突然 移到恒温100℃的真空箱中，水汽充满整个真空箱 ，测其压力为101.325 kPa,求过程的Q，W，△U 及 △H.
计算题2
在298.15K 的等温情况下，两个瓶子中间有 旋塞连通。开始时，一个瓶中放0.2molO2， 压力为0.2×101325Pa，另一个瓶中放 0.8molN2，压力为0.8×101325Pa，打开旋塞 后，两气互相混合。计算。（1）终了时瓶 中的压力；（2）混合过程中的Q，W，ΔU ，ΔS，ΔG；（3）如设等温下可逆地使气体 回到原状，计算过程中的Q 和W。
选择题
4.一可逆热机与另一不可逆热机在其他条件都相同 时，燃烧等量的燃料，则可逆热力牵引的列车行 走的距离和速度？ （A）较长；较快（B）较短；较慢（C）较长；较 慢（D）较短；较快 5.在一绝热箱中装有水，水中通一电阻丝，由蓄电 池供电，通电后水及电阻丝的温度均略有升高， 今以水和电阻丝为系统，其余为环境，则有： （A）Q<0，W=0，ΔU<0 （B）Q=0，W>0，ΔU>0 （C）Q>0，W=0，ΔU>0 （D）Q<0，W=0，ΔU>0
将 压缩373到K1及015302656P3aP，a再的作继水业续蒸在气1100103d2m53Pa恒下温部可分逆
液化到体积为10dm3 为止（此时气液平衡共存 ）。试计算此过程的Q、W、ΔU 和ΔH。假定 凝结水的体积可忽略不计，水蒸气可视作理想 气体。已知水的气化热为2259kJ·Kg-1。
甲苯正常沸点（383K）下气化热为3619J•g-1， 现将1mol 甲苯在383K 等温等压完全气化，求 该过程Q，W；并求甲苯的△Um，△Hm， △Sm，△Am，△Gm。若甲苯向真空气化（终 态同上），上述各量又是什么？（甲苯的分子 量为92）

收到基的计算100干燥基的计算:A d = 10.35《燃料与燃烧》习题解答第一篇燃料概论1. 某种煤的工业分析为：M 「=3.84, A d =10.35, gf=41.02,试计算它的收到基、干燥基、干燥无灰 基的工业分析组成解：干燥无灰基的计算：V daf =41.02FC daf=100 -V daf- 58.98 ;FC ar= 100 - Aar- M ar -V ar100 一 M ar 一 A arV ar 二 V daf巴 巴=35.36 A ar = 9.95FC r = 50.85W = 36.77;FC d =100 -V d - A d =52.882. 某种烟煤成分为：O af =83.21 H daf =5.87 O daf =5.22 N daf =1.90 A d =8.68 M ar =4.0; 试计算各基准下的化学组成。

解：干燥无灰基： S daf = 100 _ C daf _ H daf - °daf _ N daf = 3.80 收到基：A ar =A d 100_M ar =8.33100C =cX 100一A ar 一 M ar =72 953.人工煤气收到基组成如下:计算干煤气的组成、密度、高热值和低热值;解：干煤气中：H 2,d = 48.0 >100/ (100-2.4 ) ]=49.18CO ,d = 19.3 >.025=19.77CH 4, d = 13.31O 2, d = 0.82N 2 ,d = 12.30CO 2, d = 4.61=(2 >49.18%+28>9.77%+16>3.31%+32>.82%+28>2.30%+44>4.61%)/22.4 p= M 干/22.4=0.643 kg/mC ar 二C daf % 100 - A ar - W ar100= 83.21% 100 -8.33 -4100=72.95%Q 高=4.187 X 3020X).1977+3050X).4918+9500 >0.1331 )3 3=14.07 X10 kJ/m = 14.07 MJ/ mQ 低=4.187 X 3020X).1977+2570X).4918+8530 X.1331 )3 3=12.55 X10 kJ/m = 12.55 MJ/ m第二篇燃烧反应计算第四章空气需要量和燃烧产物生成量5.已知某烟煤成分为(%：Gaf—83.21,H daf—5.87, O daf—5.22, N daf—1.90,S daf—3.8, A d—8.68, W ar—4.0,试求:(1)理论空气需要量L0 (nVkg );(2)理论燃烧产物生成量V0 (nVkg );(3)如某加热炉用该煤加热，热负荷为17X103kW要求空气消耗系数n=1.35 ,求每小时供风量，烟气生成量及烟气成分解：(1)将该煤的各成分换算成应用成分:A ar= Ad % 100 War-8.68% 100 _4 =8.33%100 100H ar=H da f% 0.8767 =5.87 0.8767% = 5.15%O ar =O daf% 0.8767 =5.22 0.8767% =4.58%N ar=N daf% 0.8767 -1.9 0.8767% =1.66% S ar=S da f% 0.8767 =3.80 0.8767% =3.33%L o 二11.429 0.211 〔8 、= ------------- x —X72.95 +8x5.15 +3.33 —4.58 1X0.011.429 x0.21 <3 丿(2)计算理论燃烧产物生成量 V0：V 空十空L0^2 32 2 18 28丿100 100‘72.95 +3.33 100 32 5 15 4 1 66———0.224 0.79 7.81=8.19 m3/kg(3) 米用门捷列夫公式计算煤的低发热值:低= 4.187 >{81 >C+246H— 26 X O- S)- 6>W]]=4.187 >81 X2.95+246 X5.15 - 26X 4.58 - 3.33 ) - 6X4]=29.80 (Mj/m)每小时所需烟煤为:317 10 3600317 10 360029809-2.053 1 03 kg/hW ar =4%计算理论空气需要量L o：8C +8汉H +S _01 100每小时烟气生成量:V tol二m V n = 2053 8.19 0.35 7.81 = 2.24 104(m3/h)每小时供风量:L tol=m nL0=2053 1.35 7.81 =2.16 104m3/h计算烟气成分:C 22 4 72 95 22 4 3 3 V co m 2053 = 2.80 103(m3 /h) COV H,O S 22 4 3V so =三汇^ xm = 46.8(m /h)232 100= (H W 空)m,296 103(m3/h)2 18 100V N空xm+0.79L n =1.714x104(m3/h)2 28 10021V o2=^x(Ln—L0)xm=1.188x1O3(m3/h)计算烟气百分比组成:CO =12.45% SQ2Z=0.21% H 2O =5.73% N 2 =76.36% O 2' =5.25%6.某焦炉干煤气％成分为：CO-9.1 ; H—57.3 ; CH— 26.0 ; C2H— 2.5 ; CO— 3.0 ;O— 0.5 ; N—1.6 ;煤气温度为 20C。

运筹学部分课后习题解答P47 用图解法求解线性规划问题a）12121212min z=23466 ..424,0x xx xs t x xx x++≥⎧⎪+≥⎨⎪≥⎩解：由图1可知，该问题的可行域为凸集MABCN，且可知线段BA上的点都为最优解，即该问题有无穷多最优解，这时的最优值为min3z=23032⨯+⨯= P47 用图解法和单纯形法求解线性规划问题a）12121212max z=10x5x349 ..528,0x xs t x xx x++≤⎧⎪+≤⎨⎪≥⎩<解：由图1可知，该问题的可行域为凸集OABCO，且可知B点为最优值点，即112122134935282xx xx x x=⎧+=⎧⎪⇒⎨⎨+==⎩⎪⎩，即最优解为*31,2Tx⎛⎫= ⎪⎝⎭这时的最优值为max335z=101522⨯+⨯=单纯形法： 原问题化成标准型为121231241234max z=10x 5x 349..528,,,0x x x s t x x x x x x x +++=⎧⎪++=⎨⎪≥⎩ j c →105、B CB X b 1x 2x3x4x0 3x \9 3 4 1 0 04x8[5] 2 .0 1 j j C Z -105 00 0 3x 21/5 .0 [14/5] 1 -3/5 101x8/512/5 0 （1/5 j j C Z -1 0 -25 2x 3/2 0 ；1 5/14 -3/14 101x11 0-1/7 2/7 （j j C Z --5/14-25/14所以有*max 33351,,1015222Tx z ⎛⎫==⨯+⨯= ⎪⎝⎭P78 已知线性规划问题：1234124122341231234max24382669,,,0z x x x x x x x x x x x x x x x x x x x =+++++≤⎧⎪+≤⎪⎪++≤⎨⎪++≤⎪≥⎪⎩求: (1) 写出其对偶问题；（2）已知原问题最优解为)0,4,2,2(*=X ，试根据对偶理论，直接求出对偶问题的最优解。

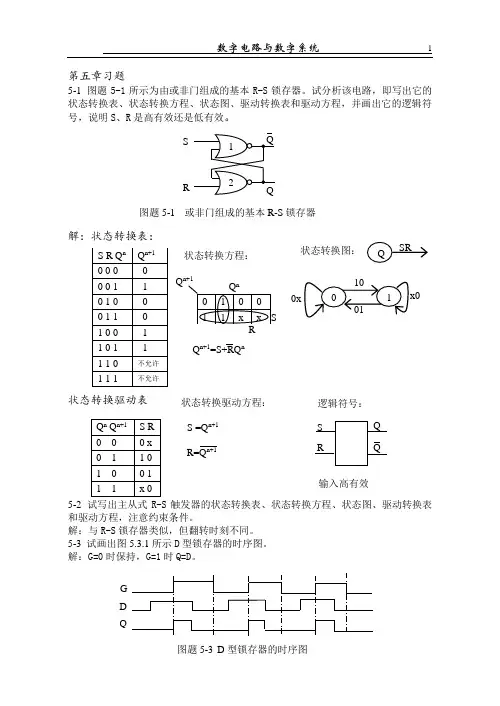
第四章习题与思考题1. 含钴和铜的硫化矿于1×101325Pa 条件下进行焙烧，要生成能溶于水的硫酸钴和不溶于水的氧化铜，达到易于 用水分离两者的目的，试确定这种选择硫酸化焙烧的炉气 组成的控制范围，已知：2CuO+2SO2+O→2CuSO4 ΔG θ 950k=-119053J2CoO+2SO2+O2→2CoSO4 ΔG θ 950K=-160482J 2． 硫化镍（Ni3S2）在总压为 101325Pa，温度为1000K，气 相组成范围是3～10%O2,3～10%SO2的条件下进行焙烧，问所 得焙烧产物应是什么？已知NiO+SO3=NiSO4 ΔG θ =-248069+198.82T,J 3. 已知反应Cu2O+FeS=Cu2S+FeO的平衡常数与温度的关系108336 -0.000074T，问在 1473K温度下该反应 式为logKp=19146.T进行的可能性？解答：1.解：2CuO+2SO 2+O 2 2CuSO 4119053 1 ln 22 2 950 - = × - = D O SO P P RT G q （ 2 22 O SO P P × ）1=2.84×10-7 同理，2CoO+2SO 2+O 2 2CoSO 4（ 2 22 O SO P P × ）2=1×10-9 可知在同样的 P O2 时， 2 2 1 2 ) /( so SO P P ） （ =16.85，即在 950 0C 时炉气范 围只要将 SO 2 的压力控制在（P SO2）2—（P SO2）1 的范围内即可。

2.解：NiO+SO 3=NiSO 4 ΔG θ =-248069+198.82T,JTKp RT G 82 . 198 248069 ln + - = - = D q 得 P SO3(NiSO4)=2.68×10 3 Pa2SO 2+1/2O 2=SO 3ΔG θ =-94558+89.4T,J (P 77) 1000146 . 19 1000 4 . 89 94558 log log 2 1 2 2 3´ ´ - = × = O SO SO P P P Kp Kp=1.84P SO3(炉气)=Kp•P SO2•P O21/2 =1.84×(0.03×101325)×(0.03×101325) 1/2 =3.14×10 5 PaP SO3(炉气)> P SO3(NiSO4),焙烧产物是 NiSO 4。

数学分析上册 第三版华东师范大学数学系部分习题参考解答P.4 习题1．设a 为有理数，x 为无理数，证明：（1）a + x 是无理数； （2）当0≠a 时，ax 是无理数.证明 （1）（反证）假设a + x 是有理数，则由有理数对减法的封闭性，知 x = a +x – a 是有理数. 这与题设“x 为无理数”矛盾，故a + x 是无理数.（2）假设ax 是有理数，于是aax x =是有理数，这与题设“x 为无理数”矛盾，故ax 是无理数.3．设R b a ∈,，证明：若对任何正数ε有ε<-||b a ，则 a = b .证明 由题设，对任何正数ε有0||+<-εb a ，再由教材P.3 例2，可得0||≤-b a ，于是0||=-b a ，从而 a = b .另证 （反证）假设0||>-b a ，由实数的稠密性，存在 r 使得0||>>-r b a . 这与题设“对任何正数ε有ε<-||b a ”矛盾，于是0||=-b a ，从而 a = b .5．证明：对任何R x ∈有（1）1|2||1|≥-+-x x ； （2）2|3||2||1|≥-+-+-x x x证明 （1）|2||1||)2()1(|1-+-≤---=x x x x（2）因为|2||1||1||)3(2||3|2-+-≤-=-+≤--x x x x x ，所以2|3||2||1|≥-+-+-x x x6．设+∈R c b a ,,证明 ||||2222c b c a b a -≤+-+证明 建立坐标系如图，在三角形OAC 中，OA 的长度是22b a +，OC 的长度是22c a +，AC 的长度为||c b -. 因为三角形两边的差小于第三边，所以有 ||||2222c b c a b a -≤+-+7．设 b a b x ≠>>,0,0，证明x b x a ++介于1与ba 之间. 证明 因为1||1-=-<+-=-++ba b b a x b b a x b x a ，1||)()(-=-<+-=-++b a b b a x b b x a b b a x b x a 所以x b x a ++介于1与ba 之间. 8．设 p 为正整数，证明：若 p 不是完全平方数，则p 是无理数. 证明 （反证）假设p 为有理数，则存在正整数 m 、n 使得m n p =，其中m 、n 互素. 于是22n p m =，因为 p 不是完全平方数，所以 p 能整除 n ，即存在整数 k ，使得kp n =. 于是222p k p m =，p k m 22=，从而 p 是 m 的约数，故m 、n 有公约数 p .这与“m 、n 互素”矛盾. 所以p 是无理数.P.9 习题2．设S 为非空数集，试对下列概念给出定义：（1）S 无上界；若M ∀，S x ∈∃0，使得M x >0，则称S 无上界.（请与S 有上界的定义相比较：若M ∃，使得S x ∈∀，有M x ≤，则称S 有上界）（2）S 无界.若0>∀M ，S x ∈∃0，使得M x >||0，则称S 无界.（请与S 有界的定义相比较：若0>∃M ，使得S x ∈∀，有M x ≤||，则称S 有界）3．试证明数集},2|{2R x x y y S ∈-==有上界而无下界.证明 S y ∈∀，有222≤-=x y ，故2是S 的一个上界.而对0>∀M ，取M x +=30，S M x y ∈--=-=12200，但M y -<0. 故数集S 无下界.4．求下列数集的上、下确界，并依定义加以验证：（1）},2|{2R x x x S ∈<=解 2sup =S ，2inf -=S . 下面依定义加以验证2sup =S （2inf -=S 可类似进行）. S x ∈∀，有22<<-x ，即2是S 的一个上界，2-是S 的一个下界.2<∀α，若2-≤α，则S x ∈∀0，都有α>0x ；若22<<-α，则由实数的稠密性，必有实数 r ，使得22<<<-r α，即S r ∈，α不是上界，所以2sup =S .（2）},!|{+∈==N n n x x S解 S 无上界，故无上确界，非正常上确界为+∞=S sup .下面证明：1inf =S .① S x ∈∀，有1!≥=n x ，即 1 是S 的一个下界；② 1>∀β，因为 S ∈=!11，即β不是S 的下界. 所以 1inf =S .(3)})1,0(|{内的无理数为x x S =解 仿照教材P .6例2的方法，可以验证：1sup =S . 0inf =S⑷ },211|{+∈-==N n x x S n 解 1sup =S ，21inf =S 首先验证1sup =S .① S x ∈∀，有1211≤-=n x ，即 1 是S 的一个上界； ② 0>∀ε，取正整数0n ，使得ε<021n ，于是取02110n x -=. 从而S x ∈0，且ε->-=121100n x . 所以1sup =S5．设S 为非空有下界数集，证明：S S S min inf =⇔∈=ξξ证明：⇒）设S S ∈=ξinf ，则对一切S x ∈，有ξ≥x ，而S ∈ξ，故ξ是数集S 中的最小的数，即S min =ξ.⇐）设S min =ξ，则S ∈ξ；下面验证S inf =ξ；⑴ 对一切S x ∈，有ξ≥x ，即ξ是数集S 的下界；⑵ 对任何ξβ>，只须取ξ=0x ，则β<0x . 所以S inf =ξ.6．设S 为非空数集，定义}|{S x x S∈-=-. 证明： ⑴ S S sup inf -=- ⑵ S S inf sup -=-证 ⑴ 设-=S inf ξ，下面证明：S sup =-ξ.① 对一切S x ∈，有-∈-S x . 因为-=S inf ξ，所以有ξ≥-x ，于是ξ-≤x ，即ξ-是数集S 的上界；② 对任何ξα-<，有ξα>-. 因为-=S inf ξ，所以存在-∈S x 0，使得α-<0x .于是有S x ∈-0，使得α>-0x .由①，②可知S sup =-ξ.7．设A 、B 皆为非空有界数集，定义数集},,|{B y A x y x z z B A ∈∈+==+ 证明：（1）B A B A sup sup )sup(+=+； （2）B A B A inf inf )inf(+=+证明 （1）因为A 、B 皆为非空有界数集，所以A sup 和B sup 都存在.B A z +∈∀，由定义分别存在B y A x ∈∈,，使得y x z +=. 由于A x sup ≤，B y sup ≤，故B A y x z sup sup +≤+=，即B A sup sup +是数集B A +的一个上界.B A sup sup +<∀α，（要证α不是数集B A +的上界），A B sup sup <-α，由上确界A sup 的定义，知存在A x ∈0，使得B x sup 0->α. 于是B x sup 0<-α，再由上确界B sup 的定义，知存在B y ∈0，使得00x y ->α. 从而α>+=000y x z ，且B A z +∈0. 因此B A sup sup +是数集B A +的上确界，即B A B A sup sup )sup(+=+另证 B A z +∈∀，由定义分别存在B y A x ∈∈,，使得y x z +=. 由于A x sup ≤，B y sup ≤，故B A y x z sup sup +≤+=，于是B A B A sup sup )sup(+≤+. ①由上确界的定义，0>∀ε，A x ∈∃0，使得2sup 0ε->A x ，B y ∈∃0，使得2sup 0ε->B y ，从而ε-+>+≥+B A y x B A sup sup )sup(00，由教材P.3 例2，可得 B A B A sup sup )sup(+≥+ ②由①、②，可得 B A B A sup sup )sup(+=+类似地可证明：B A B A inf inf )inf(+=+P.15 习题9．试作函数)arcsin(sin x y =的图象解 )arcsin(sin x y =是以2π为周期，定义域为),(∞+-∞，值域为]2,2[ππ-的分段线性函数，其图象如图.11．试问||x y =是初等函数吗？解 因为2||x x y ==，可看成是两个初等函数u y =与2x u =的复合，所以||x y =是初等函数.12．证明关于函数[]x y =的如下不等式：（1）当0>x 时，111≤⎥⎦⎤⎢⎣⎡<-x x x （2）当0<x 时，x x x -<⎥⎦⎤⎢⎣⎡≤111 证明 （1）因为 1111+⎥⎦⎤⎢⎣⎡<≤⎥⎦⎤⎢⎣⎡x x x ，所以当0>x 时，有x x x x x +⎥⎦⎤⎢⎣⎡<≤⎥⎦⎤⎢⎣⎡111，从而有111≤⎥⎦⎤⎢⎣⎡<-x x x .（2）当0<x 时，在不等式1111+⎥⎦⎤⎢⎣⎡<≤⎥⎦⎤⎢⎣⎡x x x 中同时乘以x ，可得⎥⎦⎤⎢⎣⎡≤<+⎥⎦⎤⎢⎣⎡x x x x x 111，从而得到所需要的不等式x x x -<⎥⎦⎤⎢⎣⎡≤111. P.20 习题1．证明1)(2+=x x x f 是R 上的有界函数. 证明 因为对R 中的任何实数x 有21212=≤+x x x x )||21(2x x ≥+ 所以 f 在R 上有界.2．（1）叙述无界函数的定义；（2）证明21)(x x f =为（0，1）上的无界函数； （3）举出函数 f 的例子，使 f 为闭区间 [0，1] 上的无界函数. 解 （1）设函数D x x f ∈)(，若对任何0>M ，都存在D x ∈0，使得M x f >|)(|0，则称 f 是D 上的无界函数.（2）分析：0>∀M ，要找)1,0(0∈x ，使得M x >201. 为此只需Mx 10<. 证明 0>∀M ，取110+=M x ，则)1,0(0∈x ，且M M x >+=1120，所以f 为区间（0，1）上的无界函数. （3）函数⎪⎩⎪⎨⎧=≤<=00101)(x x x x f 是闭区间 [0，1] 上的无界函数.7．设f 、g 为定义在D 上的有界函数，满足)()(x g x f ≤，D x ∈证明：⑴ )(sup )(sup x g x f D x D x ∈∈≤；⑵ )(inf )(inf x g x f Dx D x ∈∈≤证 ⑴ D x ∈∀，有)(sup )()(x g x g x f D x ∈≤≤，即)(sup x g Dx ∈是f 在D 上的一个上界，所以)(sup )(sup x g x f Dx D x ∈∈≤.⑵ D x ∈∀，有)()()(inf x g x f x f D x ≤≤∈，即)(inf x f Dx ∈是g 在D 上的一个下界，所以)(inf )(inf x g x f Dx D x ∈∈≤. 8．设f 为定义在D 上的有界函数，证明：⑴ )(inf )}({sup x f x f D x D x ∈∈-=-； ⑵ )(sup )}({inf x f x f Dx D x ∈∈-=-证 ⑴ D x ∈∀，有)}({sup )(x f x f D x -≤-∈，于是)}({sup )(x f x f Dx --≥∈，即)}({sup x f D x --∈是f 在D 上的一个下界，从而)}({sup )(inf x f x f Dx D x --≥∈∈，所以)(inf )}({sup x f x f Dx D x ∈∈-≥- ①反之，D x ∈∀，有)(inf )(x f x f D x ∈≥，于是)(inf )(x f x f D x ∈-≤-，即)(inf x f Dx ∈-是f -在D 上的一个上界，从而)(inf )}({sup x f x f Dx D x ∈∈-≤- ②由①，②得，)(inf )}({sup x f x f Dx D x ∈∈-=-.9．证明：x tan 在)2,2(ππ-上无界，而在)2,2(ππ-内任一闭区间],[b a 上有界.证 0>∀M ，取)1arctan(0+=M x ，于是)2,2(0ππ-∈x . 则有M M x >+=1tan 0，所以x tan 在)2,2(ππ-上无界. 在)2,2(ππ-内任一闭区间],[b a 上，取|}tan ||,tan max{|b a M =，则],[b a x ∈∀，必有M x ≤|tan |，所以x tan 在],[b a 上有界.10．讨论狄利克雷函数⎩⎨⎧=为无理数当为有理数当x ，x x D 0,1)(，的有界性，单调性与周期性. 解 函数)(x D 是有界函数：1|)(|≤x D . 不是单调函数.)(x D 是周期函数，任何一个正有理数都是它的周期，故它没有最小周期. 证明如下：设 r 是任一正有理数. 若 x 是有理数，则r x ±是有理数，于是)(1)(x D r x D ==±；若 x 是无理数，则r x ±是无理数，于是)(0)(x D r x D ==±.任何无理数都不是)(x D 的周期.11．证明：x x x f sin )(+=在R 上严格增.证 设21x x <，于是2sin 2cos2sin sin )()(121212112212x x x x x x x x x x x f x f -++-=--+=- 因为0>∀x ，有x x <sin ，所以12121212|2sin |2|2sin 2cos 2|x x x x x x x x -<-≤-+，从而121212212sin 2cos 2x x x x x x x x -<-+<-. 所以有 02sin 2cos2)()(211212121212=-+->-++-=-x x x x x x x x x x x f x f 即x x x f sin )(+=在R 上严格增.P.21 总练习题1．设R b a ∈,，证明：⑴ |)|(21},max{b a b a b a -++=证 若b a ≥，则a b a =},max{，a b a b a b a b a =-++=-++)(21|)|(21，这时有|)|(21},max{b a b a b a -++=；若b a <，则b b a =},max{，=-++|)|(21b a b a b b a b a =+-+)(21，也有|)|(21},max{b a b a b a -++=，所以|)|(21},max{b a b a b a -++= 2．设f 和g 都是初等函数，定义)}(),(max{)(x g x f x M =，)}(),(min{)(x g x f x m =，D x ∈试问)(x M 和)(x m 是否为初等函数？解 由第1题有|))()(|)()((21)}(),(max{)(x g x f x g x f x g x f x M -++==，因为f 和g 都是初等函数，于是)()(x g x f -是初等函数，再由212})]()({[|)()(|x g x f x g x f -=-，知|)()(|x g x f -是初等函数，所以)(x M 是初等函数.8．设f 、g 和h 为增函数，满足)()()(x h x g x f ≤≤，R x ∈，证明：))(())(())((x h h x g g x f f ≤≤证 因为f 、g 为增函数，再由)()(x g x f ≤，得))(())((x g f x f f ≤，))(())((x g g x g f ≤，所以有))(())((x g g x f f ≤. 同理可得))(())((x h h x g g ≤.9．设f 、g 为区间),(b a 上的增函数，证明)}(),(max{)(x g x f x =ϕ，)}(),(min{)(x g x f x =ψ也都是区间),(b a 上的增函数.证 ⑴ 先证)}(),(max{)(x g x f x =ϕ是区间),(b a 上的增函数.设21x x <，于是有)()()}(),(m ax {)(12222x f x f x g x f x ≥≥=ϕ，)()()}(),(m ax {)(12222x g x g x g x f x ≥≥=ϕ，从而)()}(),(m ax {)(1112x x g x f x ϕϕ=≥，所以)(x ϕ是增函数.⑵ 其次证明)}(),(min{)(x g x f x =ψ是区间),(b a 上的增函数设21x x <，于是有)()()}(),(m in{)(21111x f x f x g x f x ≤≤=ψ)()()}(),(m in{)(21111x g x g x g x f x ≤≤=ψ从而 )()}(),(m in{)(2221x x g x f x ψψ=≤12．设f 、g 为D 上的有界函数，证明：⑴ )(sup )(inf )}()({inf x g x f x g x f Dx D x D x ∈∈∈+≤+ ⑵ )}()({sup )(inf )(sup x g x f x g x f Dx D x D x +≤+∈∈∈证 ⑴ 由p.17例2 (i)，有)(inf )}({inf )}()({inf x f x g x g x f Dx D x D x ∈∈∈≤-++ ① 再由p.20习题8，有)(sup )}({inf x g x g Dx D x ∈∈-=- ② 结合①、②可得)(sup )(inf )}()({inf x g x f x g x f Dx D x D x ∈∈∈+≤+ 13．设f 、g 为D 上的非负有界函数，证明：⑴ )}()({inf )(inf )(inf x g x f x g x f Dx D x D x ⋅≤⋅∈∈∈ ⑵ )(inf )(sup )}()({sup x g x f x g x f Dx D x D x ∈∈∈⋅≤⋅证 ⑴ D x ∈∀，有)()(inf x f x f D x ≤∈，)()(inf x g x g D x ≤∈，从而)()()(inf )(inf x g x f x g x f Dx D x ⋅≤⋅∈∈. 即)(inf )(inf x g x f Dx D x ∈∈⋅是)()(x g x f ⋅在D 上的一个下界，所以有 )}()({inf )(inf )(inf x g x f x g x f Dx D x D x ⋅≤⋅∈∈∈ 15．设f 为定义在R 上以h 为周期的函数，a 为实数. 证明：若f 在 [ a , a +h ] 上有界，则f 在R 上有界.证 设f 在 [ a , a +h ] 上有界，即存在0>M ，使得],[h a a x +∈∀，有M x f ≤|)(|.R x ∈∀，必存在整数m 和实数],[0h a a x +∈，使得0x mh x +=. 于是M x f mh x f x f ≤=+=|)(||)(||)(|00，所以f 在R 上有界.16．设f 在区间I 上有界. 记)(sup x f M I x ∈=，)(inf x f m Ix ∈=，证明m M x f x f Ix x -=''-'∈'''|)()(|sup ,证 I x ∈∀，有M x f ≤)(，m x f ≥)(. 于是I x x ∈'''∀,，有m M x f x f -≤''-'|)()(|，即m M -是数集},:|)()(|{I x x x f x f ∈'''''-'的一个上界. 下面证明：m M -是数集},:|)()(|{I x x x f x f ∈'''''-'的最小上界.由上确界，下确界的定义知，0>∀ε，I x x ∈'''∃,，使得2)(ε->'M x f ，2)(ε+<''m x f ，从而εεε--=+-->''-'m M m M x f x f )2(2)()(. 所以m M -是数集},:|)()(|{I x x x f x f ∈'''''-'的最小上界.所以m M x f x f Ix x -=''-'∈'''|)()(|sup ,部分重点高校历年研究生入学考试试题选（供参考）1．（北京科技大学，1999年）叙述数集A 的上确界的定义，并证明：对任意有界数列}{n x ，}{n y ，总有}sup{}sup{}sup{n n n n y x y x +≤+证明 定义参考教材.由上确界的定义，有}sup{n n x x ≤，}sup{n n y y ≤，（ ,2,1=n ）. 于是}sup{}sup{n n n n y x y x +≤+，即实数}sup{}sup{n n y x +是数列}{n n y x +的一个上界，所以有}sup{}sup{}sup{n n n n y x y x +≤+2．（中国人民大学）设249)3lg(1)(x x x f -+-=，求)(x f 的定义域和)]7([-f f . 解 由049,13,032≥-≠->-x x x 解得)(x f 的定义域为)3,2()2,7[⋃-110lg 1)7(==-f ，所以342lg 1)]7([+=-f f 3．（华中理工大学）设1)(-=x x x f ，试验证x x f f f f =))]}(([{，并求])(1[x f f （0≠x ，1≠x ）.解 由x x x x xx f x f x f f =---=-=1111)()()]([，得x x f f x f f f f ==)]([))]}(([{. x xx x x x x f x f f -=---=-=1111]1[])(1[ 4．（同济大学）设⎩⎨⎧≥<+=010,1)(x x x x f ，求)]([x f f . 解 当0≥x 时，1)1()]([==f x f f ，当01<≤-x 时，1)1()]([=+=x f x f f ，当1-<x 时，2)1()]([+=+=x x f x f f ，所以⎩⎨⎧-≥-<+=111,2)]([x x x x f f 5．（西北工业大学）设2)(x x x f +=，求 ⑴ )(x f 的定义域⑵2)]}([{21x f f ⑶ x x f x )(lim 0→ 解 ⑴ ⎩⎨⎧>≤=+=0,20,0||)(x x x x x x f ，所以)(x f 的定义域为),(∞+-∞. ⑵ 因为)(22)()]([2222x f x x x x x x x f f =+=+++=，所以22)()]}([{21x x x f x f f +== ⑶ 因为00lim )(lim 00==--→→x x x f x x ，+∞==-+→→x x x x f x x 2lim )(lim 00，所以x x f x )(lim 0→不存在6．（清华大学）设函数)(x f 在),(∞+-∞上是奇函数，a f =)1(且对任何x 值均有)2()()2(f x f x f =-+⑴ 试用a 表示)2(f 与)5(f⑵ 问a 取什么值时，)(x f 是以2为周期的周期函数.解 ⑴ 因为对任何x 值均有)2()()2(f x f x f +=+，令1-=x 得a f f f f f f f a -=-=-+=+-==)2()1()2()1()2()21()1(，所以a f 2)2(=.a f f f 3)2()1()3(=+=，a f f f 5)3()2()5(=+=⑵ 由)2()()2(f x f x f +=+知当且仅当0)2(=f ，即0=a 时，)(x f 是以2为周期的周期函数.7．（合肥工业大学）证明：定义在对称区间),(l l -内的任何函数)(x f ，必可表示成偶函数)(x H 与奇函数)(x G 之和的形式，且这种表示法是唯一的.证明 令)]()([21)(x f x f x H -+=，)]()([21)(x f x f x G --=，则)()()(x G x H x f +=，且容易证明)(x H 是偶函数，)(x G 是奇函数.下证唯一性. 若还有偶函数)(1x H 与奇函数)(1x G ，满足)()()(11x G x H x f +=，则有)()()()(11x G x G x H x H -=-， ①用x -代入①式，得)()()()(11x G x G x H x H -=- ②①+② 得 )()(1x H x H =，再代入②式得)()(1x G x G =8．（内蒙古大学）作函数||2|2|x y --=的图形解 ⎪⎪⎩⎪⎪⎨⎧>-≤≤-<≤<-=44424200x x x x x x x x y 9．（上海师范大学）是否存在这样的函数，它在区间]1,0[上每点都取有限值，但在此区间的任何点的任何邻域内都无界.答 存在，例如⎩⎨⎧>==1000,,)(或为无理数或为且互质x ，n ，n m n m x n ，x f 10．（武汉大学，1994年）设}{n x 为一个正无穷大数列，E 为}{n x 的一切项组成的数集，试证：必存在自然数p ，使得E x p inf =证明 因为}{n x 为一个正无穷大数列，所以存在自然数N ，使得当N n >时，1x x n >. 于是},,,m in{inf 21N x x x E =，由于},,,{21N x x x 为有限集，所以存在p x ，使得E x x x x N p inf },,,min{21== .11．（天津大学）证明：2是满足不等式22>r 的一切正有理数的下确界；证 设}0,2,|{2>>∈=r r Q r r A . 要证2是数集A 的下确界. A r ∈∀，有22>r ，所以2>r ，即2是数集A 的一个下界.0>∀ε，由有理数的稠密性，在)2,2(ε+上存在无穷多个有理数，于是可取)2,2(1ε+∈r ，即A r ∈1且ε+<21r . 所以2inf =A12．（华中师范大学）设函数)(x f 定义在区间I 上，如果对于任何I x x ∈21,，及)1,0(∈λ，恒有)()1()())1((2121x f x f x x f λλλλ-+≤-+，证明：在区间I 的任何闭子区间上)(x f 有界.证 I b a ⊂∀],[，要证)(x f 在],[b a 有界. ),(b a x ∈∀，存在)1,0(∈λ，使 )(a b a x -+=λ，即a b x )1(λλ-+=.M M M a f b f a b f x f =-+≤-+≤-+=)1()()1()())1(()(λλλλλλ ① 其中)}(),(max{b f a f M =],[b a x ∈∀，令x b a y -+=)(，则22y x b a +=+， M x f y f x f y x f b a f 21)(21)(21)(21)22()2(+≤+≤+=+，所以 M b a f x f -+≥)2(2)( ② 由①、②可得，],[b a x ∈∀，有M x f M b a f ≤≤-+)()2(2，所以)(x f 在],[b a 有界.。

部分习题解答省级精品课程《数控加工技术》习题解答第一章数控加工技术概论1.1 数控加工技术的概念是什么?其主要发展历程经过哪几个阶段?答:1）数控加工技术是集传统的机械制造、计算机、现代控制、传感控制、信息处理、光机电技术于一体，在数控机床上进行工件切削加工的一种工艺方法，是根据工件图样和工艺要求等原始条件编制的工件数控加工程序输入数控系统，控制机床刀具与工件的相对运动，从而实现工件的加工。

2）数控加工技术主要发展历程经过了二个阶段6个时代。

第一阶段：数控（NC）阶段，又称为硬件数控阶段，从1952年~1970年。

第一代数控（1952-1959年）：采用电子管构成的硬件数控系统；第二代数控（1959-1965年）：采用晶体管电路为主的硬件数控系统；第三代数控（1965年开始）：采用小、中规模集成电路的硬件数控系统；第二阶段：计算机数控（CNC）阶段：又称为软件数控阶段，从1970年~现在。

第四代数控（1970年开始）：采用大规模集成电路的小型通用电子计算机数控系统；第五代数控（1974年开始）：采用微型计算机控制的数控系统；第六代数控（1990年开始）：采用工控PC机的通用CNC系统。

1.2 数控机床的工作原理是什么？数控加工的特点有哪能些？答：1）将被加工零件图纸上的几何信息和工艺信息用规定的代码和格式编写成加工程序，并输入数控装置，经过信息处理、分配，控制机床各坐标轴以最小位移量(通常只有0.001mm)为单位进行移动，其合成运动实现了刀具与工件的相对运动，完成零件的加工。

数控机床的加工，实质是应用了“微分”原理。

2)数控加工的特点有：1)自动化程度高，能减轻工人的劳动强度和改善劳动条件；2)零件加工精度高、加工质量稳定；3)加工生产率高；4)良好的经济效益；5)复杂产品加工能力强；6)适应性强，适合加工单件或小批量复杂工件；7）有利于生产管理的现代化。

1.3 数控机床由哪能几个部分组成?各个部分的基本功能是什么?答:1)数控机床由控制介质、数控装置、伺服系统、检测系统和机床本体五部分组成。

课后习题解答(第1-7章)第一章1_1.1_1_2判断正误：即使两个整型数据未超出该数据的取值范围，它们的和也可能会超出该数据取值范围。

正确。

1_1_4判断正误：一个C程序可以有多个函数，其中主函数必须在程序的最开头。

错误。

其它函数如果要在主函数中使用的话，必须先在主函数之前定义或者声明。

1_1_6判断正误：若有定义“float x=1.3;”，则表达式(int)x的值为1，因此可以说x中存放的值就是1。

错误。

(int)x表达式的值与x的值是不一样的，前者是对x取整后的数值，而取整运算对x 自身的值不会产生影响。

1_1_8判断正误：若有命令行“#define N 1000”，则N++是不合法的表达式。

正确。

N为符号常量，不能对符号常量进行修改。

1_1_10 C程序是由函数构成的，一个C程序必须有一个主函数。

1_1_12以下变量中不合法的是②、④、⑥，合法的是①、③、⑤、⑦、⑧。

①name ②double ③Int ④if ⑤for_1 ⑥2k ⑦a12345678 ⑧_a1_1_14下面程序段的输出结果是1,1.000000int a; double b;a=b=123/100%2;printf("%d,%f", a, b);1_1_16 a*a*a*b*b/(c-d)1_1_20假设圆柱体的底面半径为r(=2.5)，高为h(=3.5)，请按下面给定的步骤编写求体积(体积=底面积X高)的程序。

①定义变量r,h,v(存放体积值)，注意变量的数据类型。

②给变量r,h赋值。

③计算体积，并将结果存放在v中。

④输出r,h,v的值。

程序如下：#include <stdio.h>#define PI 3.1415926main(){float r, h, v;r=2.5;h=3.5;v=PI*r*r*h;printf("r=%f, h=%f, v=%f\n", r, h, v);}1_1_22编写输出以下图形的程序。

-7.2812510＝-111.010012
然后移动小数点，使其在第1，2位之间 -111.01001＝-1.1101001×22 e＝ 2
∵ e =Ｅ – 127
∴
S＝1，E＝2＋127＝129=1000,0001，M＝1101001
最后得到32位浮点数的二进制存储格式为
1100 0000 1110 1001 0000 0000 0000 0000
第二章
习题解答
7.若浮点数 x 的IEEE754标准32位存储格式为(8FEFC000 )16，求其浮点数 的十进制值。 【解】： 将x展开成二进制： 1000 , 1111, 1110 ,1111 ,1100,0000,0000,0000 数符：1 阶码：0001,1111
尾数：110,1111,1100,0000,0000,0000
110011
商
q0=0 q1=1 q2=0 q3=1 q4=1
故得 商q=q0q1q2q3q4q5=010110， 余数r=r5r6r7r8r9r10=110011 所以 [x÷y]原=1. 10110，[余数]原=0.0000110011 即 x÷y=-0.10110，余数=0.0000110011
第 4页
第二章
习题解答
17. 已知x和y，用移码运算方法计算x-y，同时指出运算结果是否发生溢出。 (1) x=1011，y= - 0010
【解】 [x-y]移=[x]移+[-y]补 [x]移=11 1011=01 1011 [-y]补=00 0010 注意：移码最高符号位恒置为0参与运算。 01 1011
＝ (C0E90000)16
第 2页
第二章
习题解答
11. 已知x和y，用变形补码计算x+y ，同时指出结果是否溢出。 (1) x= 0.11011, y= -0.10101

《宏观经济学》部分习题参考答案一、名词解释1．有效需求:指社会上商品总供给价格和总需求价格达到均衡状态时的总需求2．边际消费倾向:当收入变动一单位时，消费支出的变动量，即MPC=dc/dy 3．需求拉动通货膨胀: 又称超额需求通货膨胀，是指总需求超过总供给所引起的一般价格水平的持续显著的上涨。

4. 个人可支配收入:个人收入减去所得税。

5．自然失业率：在没有货币因素干扰的情况下，劳动力市场和商品市场自发供求力量发挥作用时应有的处于均衡状态的失业率。

6．流动性陷阱：货币需求是利率的减函数，然而当利率下降到一定程度时，人民手中即使有多余的货币也不愿意去买债券，从而不会使价格再上升，即利率不会再下跌，在这种情况下就说经济正处在流动性陷阱中。

7、国内生产净值：国内生产总值扣除资本折旧。

8．投机动机：指人们为了抓住有利的购买有价证券的机会而持有一部分货币的动机。

9．摩擦性失业：指在生产过程中由于难以避免的摩擦造成的短期、局部性失业，如劳动力流动性不足、工种转换的困难等所引致的失业。

10、国内生产总值：经济社会在一定时期内运用生产要素所生产的全部最终产品（物品和劳务）的市场价值。

11．投资乘数：收入变动对引起这种变动的投资支出的变动的比率。

12．挤出效应：指政府支出增加所引起的私人消费或投资降低的作用。

二、计算题第12章13.假定一国有下列国民收入统计资料：(4) 个人可支配收入；(5) 个人储蓄。

解答：(1) 国内生产净值＝国内生产总值－资本消耗补偿，而资本消耗补偿即折旧等于总投资减净投资后的余额，即500＝800－300，因此国内生产净值＝4 800－500＝4 300(亿美元)。

(2) 从GDP＝c＋i＋g＋nx中可知nx＝GDP－c－i－g，因此，净出口nx＝4 800－3 000－800－960＝40(亿美元)。

(3) 用BS代表政府预算盈余，T代表净税收即政府税收减去转移支付后的收入，则有BS＝T－g，从而有T＝BS＋g＝30＋960＝990(亿美元)。

17．实验测得 N2O5 在不同温度下的分解反应速率常数，试作图求 N2O5 分解反应的活化能。（答 案：103.68kJ·mol-1）
T／K 273.15 k／min 4.7×10-5
298.15 2.0×10-3
318.15 3.0×10-2
338.15
解：以 lnk 对 T -1 作图，可得一条直线 （如右图所示），其斜率=12470，
N2O5
NO2+ NO3 ,
NO2+ NO3
NO2 + O2 + NO （慢）,
NO2+ NO3
NO + NO3
2NO2
N2O5 ,
（答案：
）
解： 总反应为：2N2O5 ? 4NO2+O2，
∵
，而：
解得：
，
∴
15．某反应的历程为 A ?D ， D + C 在低压下是二级反应。
G，试证明该反应在高压下是一级反应，
解：(1)
（2） 根据
可求得：E1 = E-1= 44.36 kJ.mol-1
(3)
A ========= C + D
t = 0 101325
0
0
t = t 101325 -px
px
px
故：p 总= 101325+ px
故 Ea = 12470R =103.68 kJ·mol-1
3.0×10-1
18．乙酸乙酯与氢氧化钠皂化反应的速率常数在 282.55 K 时为 2.37(mol·L-1)-1·s-1；287.55 K 时增 至 6.024(mol·L-1)-1·s-1，求：(1)活化能 Ea 及频率因子 A；(2) 334.55 K 的反应速率常数；(3) 用以

《建筑环境学》习题部分参考解答第二章 建筑外环境1、 为什么我国北方住宅严格遵守坐北朝南的原则,而南方并不严格遵守？答:太阳光在垂直面上的直射强度为θβcos cos ,⋅⋅=N z c I I ,对于地理位置的地区βcos ⋅N I 就是不能人为改变的。

所以要使I c,z 取最佳值,只有使θ尽可能小。

在冬季,太阳就是从东南方向升起,从西南方向落下,而坐北朝南的布局就保证了在冬季能最大限度的接收太阳辐射。

北方气候寒冷、冬夏太阳高度角差别大,坐北朝南的布局可以使建筑物冬季获得尽可能多的太阳辐射,夏季获得的太阳辐射较小。

但在南方尤其就是北回归线以南,冬夏太阳高度角差不多,所以建筑物就是否坐北朝南影响不太大。

2、 就是空气温度改变导致地面温度改变,还就是地面温度改变导致空气温度改变？答:大气中的气体分子在吸收与放射辐射能时具有选择性,它对太阳辐射几乎就是透明体,直接接受太阳辐射的增温就是非常微弱。

主要靠吸收地面的长波辐射而升温。

而地面温度的变化取决于太阳辐射与对大气的长波辐射。

因此,地面与空气的热量交换就是气温升降的直接原因,地面温度决定了空气温度。

3、 晴朗的夏夜,气温25℃,有效天空温度能达到多少？ 如果没有大气层,有效天空温度应该就是多少？答:有效天空温度的计算公式为:4144])70.030.0)(026.032.0(9.0[o d d sky T S e T T +--=查空气水蒸气表,可知:t =25℃时,e d =31、67mbar查表2-2,T d =32、2+273、15=305、35 K,另外,T 0=25+273、15=298、15 K∴ 计算得:T sky ＝100×(74、2－9、4S)1/4如果没有大气层,可以认为S ＝1,则计算求得:T sky ＝283、7 K4、 为什么晴朗天气的凌晨树叶表面容易结露或结霜？答:由于晴朗夜空的天空有效温度低,树叶表面与天空进行长波辐射,使得叶片表面温度低于空气的露点温度,所以出现结露或结霜现象。