考研数学第五章+定积分

第五章第三讲、定积分的性质我们列举一些定积分的性质如下：性质 3.1. 设函数 f (x) 在区间[a,b] 上可积（记着 f (x)∈R[a,b]），k 为常数。

则有∫∫b bk f (x)d x =k f (x)d xa a证明：略性质3.2. 设函数 f (x) ，g(x) 在区间[a,b] 上可积，则 f (x)±g(x) 也在区间[a,b] 上可积并且有∫∫∫b b b[ f (x) ±g(x)]d x = f (x) d x ±g(x) d x aa a证明：由定理2.2 可知 f (x)±g(x) 在区间[a,b]上可积，于是按照定积分的定义，我们有左端n=∑±lim [ ( ) ( )]f ξg ξ∆xi i iT →0i=1n n∑∑=+lim ( ) ( )f ξ∆xg ξ∆xi i i iT →0i=1 i=1n n=∑±∑lim ( ) lim ( )f ξ∆xg ξ∆xi i i iT →0 T →0i=1 i=1=右端证毕。

性质3.3. 设函数 f (x) ，区间[α,β]上可积，a,b,c∈[α,β]。

则有∫∫∫b c bf (x) d x = f (x) d x + f (x) d x aa c证明：不妨假设，a,b,c 两两不等（它们中至少有两个相等时，结果显然成立）。

若a <c<b，因 f (x) 在区间[a,b]上可积，所以在分割区间时, 可以永远取c 为分点，于是证毕。

性质3.4. 设函数 f (x) 在区间[a,b] 上可积.若 f (x)≥ 0 ，则∫baf (x) d x ≥0.证明：对于任意分割，所选择的积分和均非负，即n∑i=1f (ξ)∆x≥ 0i i于是nb=∑∆≥∫。

证毕。

f (x)d x lim f (ξ) x 0i ia T →0i=1推论 3.1. 设函数 f (x) ，g(x) 在区间[a,b] 上可积。

一、定积分的定义和性质1. 定积分的概念定积分是微积分学中的重要概念，它是对函数在一个区间上的积分值进行求解的操作。

具体来说，如果函数f(x)在区间[a,b]上是连续的，则我们可以通过定积分的形式来求解函数f(x)在区间[a,b]上的积分值，即∫(a to b) f(x)dx。

这里，∫表示积分符号，a和b分别表示区间的起点和终点，f(x)表示要求解的函数，dx表示积分变量，并代表着在区间[a,b]上x的变化范围。

因此，定积分的求解可以看做是对函数在一个区间上的积分值进行求解的过程。

2. 定积分的性质定积分具有一系列的性质，这些性质在定积分的求解中起着重要的作用。

主要的性质包括线性性、可加性、积性、保号性、保序性等。

具体来说，线性性指的是定积分的线性组合仍然可以进行积分求解；可加性指的是如果一个区间可以分解成若干个子区间，那么对应的积分值也可以进行求和；积性指的是如果一个函数是另一个函数的乘积，那么对应的积分值也可以进行相乘；保号性指的是如果函数在区间上恒大于等于零（小于等于零），那么对应的积分值也恒大于等于零（小于等于零）；保序性指的是如果函数在区间上恒大于等于另一个函数（小于等于另一个函数），那么对应的积分值也恒大于等于（小于等于）另一个函数在相同区间上的积分值。

这些性质在定积分的具体求解中是非常有用的，可以帮助我们简化求解的过程，提高计算的效率。

二、定积分的计算1. 定积分的计算方法定积分的计算方法主要包括定积分的定义法、不定积分法、分部积分法、换元积分法和定积分的几何意义。

其中，定积分的定义法是直接根据定积分的定义进行求解；不定积分法是将定积分转化成不定积分，通过求解不定积分再将得到的结果代入原来的定积分式中，从而得到最终的定积分值；分部积分法是将被积函数进行分解，然后利用分部积分公式对各项进行积分求解；换元积分法是通过变量代换的方法将被积函数进行转化，然后再进行积分求解；定积分的几何意义则是利用定积分代表曲线下面积的特性来进行求解。

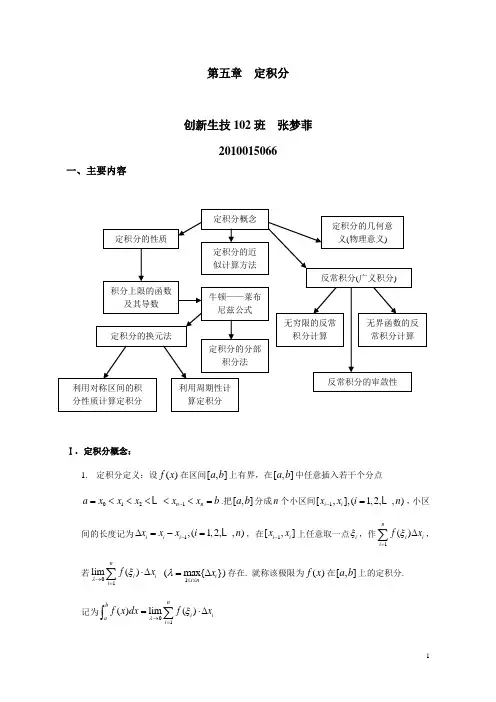
第五章 定积分创新生技102班 张梦菲2010015066一、主要内容Ⅰ. 定积分概念：1. 定积分定义：设()f x 在区间[,]a b 上有界，在[,]a b 中任意插入若干个分点 0121n n a x x x x x b -=<<<<<=.把[,]a b 分成n 个小区间1[,],(1,2,,)i i x x i n -=，小区间的长度记为1,(1,2,,)i i i x x x i n -∆=-=，在1[,]i i x x -上任意取一点i ξ，作1()ni i i f x ξ=∆∑，若01lim()niii f x λξ→=⋅∆∑ 1(max{})ii nx λ≤≤=∆存在. 就称该极限为()f x 在[,]a b 上的定积分.记为1()lim ()nbi i ai f x dx f x λξ→==⋅∆∑⎰当上述极限存在时，称()f x 在[,]a b 上可积. 2. 若()f x 在[,]a b 上连续，则()f x 在[,]a b 上可积。

3. 若()f x 在[,]a b 上有界，且只有有限个间断点，则()f x 在[,]a b 上可积. Ⅱ. 定积分的几何意义 定积分()baf x dx ⎰在几何上表示：由曲线()y f x =，直线x a =和x b =以及x 轴所围图形面积的代数和 (x 轴上方的面积取正，x 轴下方的面积取负) Ⅲ. 定积分的性质1. 补充规定：(1)当a b =时，()0baf x dx =⎰(2)当a b >时,()()baabf x dx f x dx =-⎰⎰2. 性质：(1) [()()]()()bbbaaaf xg x dx f x dx g x dx --+=+⎰⎰⎰(2) ()(),()bba akf x dx k f x dx k =⎰⎰为常数(3) ()()()bc baacf x dx f x dx f x dx =+⎰⎰⎰(4)b adx b a =-⎰(5) 若在[,]a b 上，()0f x ≥，则()0,()baf x dx a b ≥<⎰推论1：若在[,]a b 上，()()f x g x ≤，则()(),()bbaaf x dxg x dx a b ≤<⎰⎰.推论2：()(),()bbaaf x dx f x dx a b ≤<⎰⎰.(6 ) 若在[,]a b 上，()m f x M ≤≤,则()()(),()bam b a f x dx M b a a b -≤≤-<⎰(7) (定积分中值定理)：若()f x 在[,]a b 上连续，则在[,]a b 上至少存在ξ，使()()(),()baf x dx f b a a b ξξ=-≤≤⎰. 3. 连续函数()f x 在[,]a b 上的平均值，1()ba y f x dxb a-=-⎰ Ⅳ. 积分上限函数及其导数 1. 若对任意[,]x a b ∈，()xaf t dt ⎰存在，则称()()xax f t dt Φ=⎰为积分上限的函数.2. 若()f x 在[,]a b 上可积，则()f x 在[,]a b 上有界. 且积分上限函数()()xax f t dt Φ=⎰在[,]a b 上连续.3. 设()f x 在[,]a b 上连续，则()()xax f t dt Φ=⎰在[,]a b 上可导，且'()()(),()xa d x f t dt f x a xb dxΦ==≤≤⎰. 4. 设()f x 连续，()x φ可导，则()''()()[()]()x ad x f t dt f x x dx φφφΦ==⎰. 5. 设()f x 连续，()x φ，()x ϕ可导，则 ()'''()()()[()]()[()]()x x d x f t dt f x x f x x dxφϕφφϕϕΦ==-⎰. Ⅴ. 牛顿——莱布尼兹公式.(微积分基本定理)设()f x 在[,]a b 上连续，()F x 为()f x 在[,]a b 上的一个原函数，则()()()baf x dx F b F a =-⎰.Ⅵ. 定积分的换元法设()f x 在[,]a b 上连续，()x t φ=满足： (1) (),()a b φαφβ==.(2)()t φ在[,]αβ(或[,]βα)上具有连续导数，且()x t φ=的值域不越出[,]a b 的范围，则有'()[()]()baf x dx f t t dt βαφφ=⎰⎰.注：当()t φ的值域[,]R A B φ=越出[,]a b 的范围，但满足其余条件时，只要()f x 在[,]A B 上连续，则换元法的结论仍然成立.Ⅶ. 定积分的分部积分法设()u x 与()v x 在[,]a b 上具有连续导数，则有()()()()()()bbbaaau x dv x u x v x v x du x =-⎰⎰ Ⅷ. 几类特殊的积分公式1. 设()f x 在[,]a a -上连续，则有0()[()()]aaaf x dx f x f x dx -=+-⎰⎰.2()()[,]()()[,]aaaf x dx f x a a f x dx f x a a -⎧-⎪=⎨⎪-⎩⎰⎰当为上连续的偶函数时0当为上连续的奇函数时2. 设()f x 是以l 为周期的连续函数，则对任意实数a ，有()()a llaf x dx f x dx +=⎰⎰.3. 设()f x 在[0,1]上连续，则220(sin )(cos )f x dx f x dx ππ=⎰⎰(sin )(sin )2xf x dx f x dx πππ=⎰⎰20(sin )2(sin )f x dx f x dx ππ=⎰⎰4. 2200123134221242sin cos 13531n n n n n n n n n xdx xdx n n n n πππ--⎧⎪-⎪--⎪==⎨-⎪=⎪⎪⎩⎰⎰为正偶数为大于1的正奇整数1 Ⅸ. 反常积分(广义积分) 1. 无穷限的反常积分(1) 设()f x 在[,)a +∞上连续, ()lim ()ba ab f x dx f x dx ∞→+∞=⎰⎰(2) 设()f x 在(,]b -∞上连续,()lim ()bbaa f x dx f x dx -∞→-∞=⎰⎰(3) 设()f x 在(,)-∞+∞上连续,000()()()lim ()lim ()baa b f x dx f x dx f x dx f x dx f x dx ∞∞-∞-∞→-∞→+∞=+=+⎰⎰⎰⎰⎰若上述各式右端的极限存在，则对应的反常积分收敛，否则称该反常积分发散. 注：(3)的右端是两个独立的极限，只有当两个极限都存在使，才有()f x dx ∞-∞⎰收敛. 只要有一个极限不存在，()f x dx ∞-∞⎰就发散.2. 无界函数的反常积分(1) 设()f x 在(,]a b 上连续，点a 为()f x 的瑕点，()lim ()bba tt af x dx f x dx +→=⎰⎰(2) 设()f x 在[,)a b 上连续，点b 为()f x 的瑕点，()lim ()btaat bf x dx f x dx -→=⎰⎰(3) 设()f x 在[,]a b 上除点c ()a c b <<外连续，点c 为()f x 的瑕点，()()()lim ()lim ()bc b t baacatt ct cf x dx f x dx f x dx f x dx f x dx -+→→=+=+⎰⎰⎰⎰⎰若上述各式右端的极限存在，则对应的反常积分收敛，否则称该反常积分发散. 注：(3)的右端是两个独立的极限，只有当两个极限都存在使，才有()baf x dx ⎰收敛. 只要有一个极限不存在，()baf x dx ⎰就发散.3. 反常积分的审敛法(1) (比较审敛法1) 设()f x 在[,)(0)a a +∞>上连续，且()0f x ≥. 若存在常数0M >及1p >，使得()p Mf x x≤ ()a x ≤<+∞，则反常积分()a f x dx +∞⎰收敛；若存在常数0N >，使得()Nf x x≥ ()a x ≤<+∞，则反常积分()a f x dx +∞⎰发散.(2) (极限审敛法1) 设()f x 在[,)a +∞上连续，且()0f x ≥. 若存在常数1p >，使得lim ()px x f x →∞存在，则反常积分()af x dx +∞⎰收敛；若lim ()0x xf x d →∞=>，(或lim ()x xf x →∞=+∞)则反常积分()af x dx +∞⎰发散.(3) (比较审敛法2)设()f x 在(,]a b 上连续，且()0f x ≥. x a =为()f x 的瑕点.若存在常数0M >及1q <，使得()()()q Mf x a x b x a ≤<≤-，则反常积分()b a f x dx ⎰收敛；若存在常数0N >，使得()Nf x x a≥- ()a x b <≤，则反常积分()b a f x dx ⎰发散.(4) (极限审敛法2) 设()f x 在(,]a b 上连续，且()0f x ≥. x a =为()f x 的瑕点. 若存在常数01q <<，使得l i m ()()qx ax a f x +→-存在，则反常积分()baf x dx ⎰收敛；若lim ()()0x ax a f x d +→-=>，(或lim ()()x ax a f x +→-=+∞)则反常积分()baf x dx ⎰发散.2'0'02)()()(a M dx x M dx x f dx x f dx x f aa aa=≤≤=⎰⎰⎰⎰ξξ.。

凯程考研集训营，为学生引路，为学员服务！考研数学高数公式：定积分第五章：定积分学习要求:1.理解定积分的概念，掌握定积分的性质及定积分中值定理2.理解变上限定积分定义的函数，会求它的导数，掌握牛顿莱布尼茨公式。

3.掌握定积分的换元积分法与分部积分法。

4.了解广义积分的概念，并会计算广义积分。

5.掌握反常积分运算。

定积分的基本公式和定理1、定积分解决的典型问题(1)曲边梯形的面积(2)变速直线运动的路程2、函数可积的充分条件定理设f(x)在区间[a，b]上连续，则f(x)在区间[a，b]上可积，即连续=>可积。

定理设f(x)在区间[a，b]上有界，且只有有限个间断点，则f(x)在区间[a，b]上可积。

3、定积分的若干重要性质性质如果在区间[a，b]上f(x)≥0则∫abf(x)dx≥0.推论如果在区间[a，b]上f(x)≤g(x)则∫abf(x)dx≤∫abg(x)dx.推论|∫abf(x)dx|≤∫ab|f(x)|dx.性质设M及m分别是函数f(x)在区间[a，b]上的最大值和最小值，则m(b-a)≤∫abf(x)dx≤M(b-a)，该性质说明由被积函数在积分区间上的最大值及最小值可以估计积分值的大致范围。

性质(定积分中值定理)如果函数f(x)在区间[a，b]上连续，则在积分区间[a，b]上至少存在一个点ξ，使下式成立：∫abf(x)dx=f(ξ)(b-a)。

4、关于广义积分设函数f(x)在区间[a，b]上除点c(a小提示：目前本科生就业市场竞争激烈，就业主体是研究生，在如今考研竞争日渐激烈的情况下，我们想要不在考研大军中变成分母，我们需要：早开始+好计划+正确的复习思路+好的辅导班（如果经济条件允许的情况下）。

2017考研开始准备复习啦，早起的鸟儿有虫吃，一分耕耘一分收获。

加油！。

5.2　课后习题详解习题5-1　定积分的概念与性质1．利用定积分定义计算由抛物线y ＝x 2＋1，两直线x ＝a 、x ＝b （b ＞a ）及x 轴所围成的图形的面积．解：因为函数f(x)＝x 2＋1在区间[a ，b]上连续，所以函数可积，为计算方便，不妨把[a ，b]分成n 等份，则分点为每个小区间长度为取ξi 为小区间的右端点x i ，则当n→∞时，上式极限为即为所求图形的面积．2．利用定积分定义计算下列积分：解：因为被积函数在积分区间上连续，所以把积分区间分成n等份，并取ξi为小区间的右端点，得到（1）（2）3．利用定积分的几何意义，证明下列等式：证：（1）根据定积分的几何意义，定积分表示由直线y＝2x、x＝1及x轴围成的图形的面积，该图形是底边长为1、高为2的三角形，因此面积为1，即（2）根据定积分的几何意义，定积分表示的是由曲线以及x轴、y轴围成的在第I象限内的图形面积，即单位圆的四分之一的图形，因此有（3）因为函数y＝sinx在区间[0，π]上非负，在区间[－π，0]上非正．根据定积分的几何意义，定积分表示曲线y＝sinx（x∈[0，π]）与x轴所围成的图形D1的面积减去曲线y＝sinx（x∈[－π，0]）与x轴所围成的图形D2的面积，显然图形D1与D2的面积是相等的，所以有（4）因为函数y＝cosx在区间上非负．根据定积分的几何意义，定积分表示曲线与x轴和y轴所围成的图形D1的面积加上曲线与x轴和y轴所围成的图形D2的面积，而图形D1的面积和图形D2的面积显然相等，所以有4．利用定积分的几何意义，求下列积分：解：（1）根据定积分的几何意义，表示的是由直线y＝x，x＝t以及x轴所围成的直角三角形面积，该直角三角形的两条直角边的长均为t，因此面积为因此有（2）根据定积分的几何意义，表示的是由直线x＝－2，x＝4以及x轴所围成的梯形的面积，该梯形的两底长分别为梯形的高为4－（－2）＝6，因此面积为21．因此有（3）根据定积分的几何意义，表示的是由折线y＝|x|和直线x＝－1，x＝2以及x轴所围成的图形的面积．该图形由两个等腰直角三角形组成，一个由直线y＝－x，x＝－1和x轴所围成，其直角边长为1，面积为另一个由直线y＝x，x＝2和x轴所围成，其直角边长为2，面积为2．因此（4）根据定积分的几何意义，表示的是由上半圆周以及x轴所围成的半圆的面积，因此有5．设a＜b，问a、b取什么值时，积分取得最大值？解：根据定积分几何意义，表示的是由y＝x－x2，x＝a，x＝b，以及x轴所围成的图形在x轴上方部分的面积减去x轴下方部分面积．因此如果下方部分面积为0，上方部分面积为最大时，的值最大，即当a＝0，b＝1时，积分取得最大值．6．已知试用抛物线法公式求出ln2的近似值（取n＝10，计算时取4位小数）．解：计算y i并列表表5-2-1按抛物线法公式，求得7．设求解：（1）（2）（3）（4）8．水利工程中要计算拦水闸门所受的水压力．已知闸门上水的压强p与水深h存在函数关系，且有p＝9.8h（kN／m2）．若闸门高H＝3m，宽L＝2m，求水面与闸门顶相齐时闸门所受的水压力P．解：在区间[0，3]上插入n－1个分点，取ξi∈[h i－1，h i]，并记Δh i＝h i－h i－1，得到闸门所受水压力的近似值为根据定积分的定义可知闸门所受的水压力为因为被积函数连续，而连续函数是可积的，因此积分值与积分区间的分法和ξi的取法无关．为方便计算，对区间[0，3]进行n等分，并取ξi为小区间的端点所以。

考研积分知识点总结一、定积分1、定义：设f(x)在区间[a,b]上有界，将[a,b]分成n份，每份的长度为Δx，然后在每份上取一点ξi，令Δx→0时，若极限存在，记为∫abf(x)dx2、性质：（1）可加性：∫ab[f(x)+g(x)]dx=∫abf(x)dx+∫abg(x)dx（2）常数性质：∫abcf(x)dx=c∫abf(x)dx（3）区间可加性：∫abf(x)dx+∫bdf(x)dx=∫acf(x)dx（4）绝对值不等式：|∫abf(x)dx|≤∫ab|f(x)|dx3、微元法：设f(x)在[a,b]上有界，则∫abf(x)dx可看成是多个矩形的面积的和，通过微元法可得到∫abf(x)dx的表达式，即∫abf(x)dx=limΔx→0∑f(ξi)Δx二、不定积分1、定义：设f(x)在区间I上有定义，则函数F(x)称为f(x)在I上的原函数，即F’(x)=f(x)。

不定积分是指对于f(x)进行积分操作，得到一个原函数F(x)，表示为∫f(x)dx=F(x)+C，其中C为任意常数。

2、性质：（1）线性性质：∫[af(x)+bg(x)]dx=a∫f(x)dx+b∫g(x)dx（2）微分求积分关系：若F’(x)=f(x)，则∫F’(x)dx=F(x)+C3、换元法：（1）第一类换元法：若积分中含有复合函数，并且确实有合适的简化形式，可以采用第一类换元法，设u=g(x)，则du=g’(x)dx，∫f(g(x))g’(x)dx=∫f(u)du（2）第二类换元法：当上述第一类换元法不适用时，可以采用第二类换元法，通过变换积分上限和下限的方式，将积分变为已知的形式。

设u=g(x)，则x=h(u)，∫f(x)dx=∫f(h(u))h’(u)du三、区间无穷积分1、无穷远处的积分：（1）定积分的上限或下限为无穷时，这种积分称为无界积分。

（2）若∫abf(x)dx存在且极限为∞或-∞，则∫abf(x)dx称为绝对收敛。

第五章 定积分内容：定积分的概念和性质、微积分基本公式、换元积分法、分部积分法、广义积分。

要求：理解定积分的概念和性质。

掌握牛顿－莱布尼兹公式、定积分的换元法和分部积分法，理解变上限的定积分作为其上限的函数及其求导定理，理解广义积分的概念和计算方法。

重点:定积分的概念和性质；微积分基本公式；换元积分法、分部积分法。

难点:定积分的概念;变上限积分函数及其导数；换元积分法、分部积分法。

§1。

定积分的概念一、实例分析1．曲边梯形的面积设函数)(x f y =∈C[a , b ］, 且)(x f y =〉0。

由曲线0,,),(====y b x a x x f y 围成的图形称为曲边梯形.如何定义曲边梯形的面积? (1) 矩形面积=底高。

（2) 预备一张细长条的纸, 其面积底高。

(3） 预备一张呈曲边梯形状的纸， 将其撕成许多细长条. （4） 启示:将曲边梯形分割为许多细长条， 分割得越细， 误差越小。

第i 个细长条面积)],,[()(11---=∆∈∀∆≈∆i i i i i i i i i x x x x x x f S ξξ曲边梯形面积： ∑=∆≈ni i i x f S 1)(ξ定积分概念示意图.ppt定义： ),,2,1,max {()(lim 10n i x x f S i ni ii =∆=∆=∑=→λξλy =f (x )x =a x =by =f (x )a=x 0 x 1 x i-1 x i x n =b抛开上述过程的几何意义，将其数学过程定义为定积分. 二、定积分的定义 1. 定义设)(x f y =在［a ， b ］有定义， 且有界。

(1) 分割： 用分点b x x x a n =<<<= 10把［a ， b ]分割成n 个小区间：},,2,1,max{,,,2,1],,[11n i x x x x ni x x i i i i i i =∆=-=∆=--λ记(2) 取点: 在每个小区间],[1i i x x -上任取一点i, 做乘积: i i x f ∆)(ξ。