下载文档原格式
小波变换相关实验实验目的1、通过观察小波变换系数建立对小波变换及其有关性质的感性认识。
2、掌握小波变换及重构方法；了解小波变换基本应用。
实验内容1、图像二维离散小波变换及其重构；2、小波变换在去噪、压缩、图像增强上的应用。
实验原理1、“小波”就是小区域、长度有限、均值为0的波形。
所谓“小”是指它具有衰减性；而称之为“波”则是指它的波动性，其振幅正负相间的震荡形式。
与 Fourier变换相比，小波变换是时间(空间)频率的局部化分析，它通过伸缩平移运算对信号（函数)逐步进行多尺度细化，最终达到高频处时间细分，低频处频率细分，能自动适应时频信号分析的要求，从而可聚焦到信号的任意细节，解决了Fourier变换的困难问题，成为继Fourier变换以来在科学方法上的重大突破。
小波转换分成两个大类：离散小波变换 (DWT) 和连续小波转换 (CWT)。
两者的主要区别在于，连续转换在所有可能的缩放和平移上操作，而离散转换采用所有缩放和平移值的特定子集。
小波变换的公式有内积形式和卷积形式，两种形式的实质都是一样的。
它要求的就是一个个小波分量的系数也就是“权”。
其直观意义就是首先用一个时窗最窄，频窗最宽的小波作为尺子去一步步地“量”信号，也就是去比较信号与小波的相似程度。
信号局部与小波越相似，则小波变换的值越大，否则越小。
当一步比较完成后，再将尺子拉长一倍，又去一步步地比较，从而得出一组组数据。
如此这般循环，最后得出的就是信号的小波分解（小波级数）。
当尺度及位移均作连续变化时，可以理解必将产生大量数据，作实际应用时并不需要这么多的数据，因此就产生了离散的思想。
将尺度作二进离散就得到二进小波变换，同时也将信号的频带作了二进离散。
当觉得二进离散数据量仍显大时，同时将位移也作离散就得到了离散小波变换。
2、二维离散小波变换常用函数3、小波图像去噪一般方法如下:1）图像的小波分解。
选择合适的小波函数以及适合的分解层次对图像进行分解。
小波变换在信号处理中的应用一.小波变换应用于噪声抑制：利用Mallet算法对输入信号f(t)进行小波分解，再根据对信号和噪声的先验知识分离信号和噪声。
提过滤波形成新的小波分量，最后重建信号。
f(t)S(t)N(t)W(f)W(S)W(N)小波分解滤波重建信号信号与噪声被小波变换分离：Donoho去噪方法：不同阀值选取算法的去噪结果：研究重点：信号与噪声在小波变换域上的特征。
小波基的选择。
阈值的选取方法。
二.小波变换应用于信号检测：瞬时信号检测问题。
在噪声中检测短时，非平稳，波形和到达时间未知的信号。
H0:H1:某(t)n(t)某(t)S(t)n(t)t[0,T]其中：S(t)只在[t0,t0T0]非零。
n(t)为噪声。
T0T我们可以假设：S(t)Aie某p{ai(tti)}in(i(tti)i)u(tti)i1N其中：Aiaiti信号幅度；衰减系数到达时间频率初始相位ii由cj,kS,j,k|cj,k|在kti两边呈指数衰减，且达到局部极值。
2j由于小波变换得多尺度特性，我们可以选择不同的j,利用不同的时域和频域分辨力，了解信号的的全貌，从而使基于小波变换的信号检测器具有较好的鲁棒性。
可以得到:(1)(2)(3)若在观测时间内，有多个信号到达，我们可以选择适当的j,使时间尺度尽可能的小，从而使不同信号的峰值出现在不同的上，由此分离信号。
k方法：对输入信号进行多尺度的小波变换，检测其变换结果的局部极值点。
性能：优于能量检测器，接近与匹配滤波器。
小波变换应用于信号分析(信号的奇异性分析)若f(t)在某处间断或某阶导数不连续，则称f(t)在此点有奇异性。
Fouier变换可以分析函数的整体的奇异性，但不能推断奇异点的空间(时间)分布情况。
定义：设nn1,若在某点某0,存在常数A与h0,及一个n阶多项式Pn(h),使f(某0h)Pn(h)A|h|a则称f(某)在点某0具有Lipchitz指数0hh0注：()若A和与某0无关，则称为一致1Lipchitz指数。
小波变换在医学图像分析中的应用及其实例医学图像分析是现代医学领域中的重要研究方向之一，其目的是通过对医学图像的处理和分析，提取出有用的信息，帮助医生做出准确的诊断和治疗决策。
而小波变换作为一种有效的信号处理方法，已经被广泛应用于医学图像分析中。
小波变换是一种时频分析方法，与传统的傅里叶变换相比，具有更好的局部性和时频分辨率。
在医学图像分析中，小波变换可以用于图像去噪、边缘检测、特征提取等方面。
首先，小波变换可以用于医学图像的去噪。
在医学图像中，噪声是不可避免的，会影响到医生对图像的判断和分析。
而小波变换通过将图像分解为不同频率的子带，可以更好地分离图像中的噪声和信号。
通过对低频子带进行阈值处理，可以去除图像中的噪声，提高图像的质量。
其次，小波变换可以用于医学图像的边缘检测。
在医学图像中，边缘信息对于病变的定位和诊断非常重要。
而小波变换可以通过对图像进行多尺度分析，提取出不同尺度下的边缘信息。
通过对小波系数进行阈值处理和边缘检测算法，可以准确地提取出图像中的边缘信息，帮助医生做出准确的诊断。
另外，小波变换还可以用于医学图像的特征提取。
在医学图像中，不同病变具有不同的形态和纹理特征，通过提取这些特征可以帮助医生对病变进行分类和诊断。
而小波变换可以通过对图像进行多尺度分析，提取出不同尺度下的纹理特征。
通过对小波系数进行统计分析和特征提取算法，可以得到图像的纹理特征，用于病变的分类和诊断。
举个例子来说明小波变换在医学图像分析中的应用。
假设有一幅乳腺X光片，医生希望通过图像分析来判断是否存在肿瘤。
首先，医生可以使用小波变换对图像进行多尺度分解，得到不同频率的子带图像。
然后，医生可以对低频子带图像进行阈值处理，去除图像中的噪声。
接着，医生可以对高频子带图像进行边缘检测，提取出图像中的边缘信息。
最后，医生可以对小波系数进行统计分析，提取出图像的纹理特征。
通过对这些特征进行分类和诊断，医生可以判断出是否存在肿瘤。
小波变换在医学图像分割中的实际应用案例引言医学图像分割是指将医学图像中感兴趣的区域从背景中分离出来的过程。
这一过程对于医学诊断和治疗具有重要意义。
近年来，小波变换作为一种有效的信号处理工具，在医学图像分割中得到了广泛应用。
本文将通过介绍一个实际应用案例，探讨小波变换在医学图像分割中的实际应用。
案例介绍某医院的放射科经常需要对患者的头部CT图像进行分割，以便更好地观察和分析患者的病情。
然而，由于头部CT图像中存在大量的噪声和干扰，传统的分割方法往往效果不佳。
为了解决这一问题，该医院引入了小波变换技术。
小波变换的原理是将信号分解成不同频率的子信号，然后通过对子信号进行分析和处理，实现对原始信号的分析和处理。
在医学图像分割中，小波变换可以将图像分解成不同频率的子图像，从而更好地提取图像的边缘和纹理信息，进而实现图像的分割。
在这个案例中，医院的放射科使用小波变换对头部CT图像进行分割。
首先，将原始图像进行小波分解，得到一系列不同频率的子图像。
然后，通过对子图像进行阈值处理，将感兴趣的区域从背景中分离出来。
最后，将分割结果进行后处理，去除噪声和干扰，得到最终的分割图像。
实际应用效果通过使用小波变换进行头部CT图像分割，该医院的放射科取得了显著的效果和成果。
与传统的分割方法相比，小波变换能够更好地提取图像的边缘和纹理信息，从而实现更准确的分割结果。
这对于医生的诊断和治疗具有重要意义，可以提高诊断的准确性和治疗的效果。
此外，小波变换还具有较好的鲁棒性和适应性。
对于不同类型的医学图像，小波变换能够根据图像的特点和需求，自动调整参数和分析方法，从而实现更好的分割效果。
这对于医院的放射科而言，可以节省大量的人力和时间成本，提高工作效率和质量。
结论小波变换作为一种有效的信号处理工具，在医学图像分割中具有广泛的应用前景。
通过对医学图像进行小波分解和阈值处理，可以更好地提取图像的边缘和纹理信息，实现图像的分割。
实际应用案例表明，小波变换在医学图像分割中具有较好的效果和成果。
1、 选择()t ϕ或ˆ()ϕω，使{}()k Z t k ϕ∈-为一组正交归一基； 2、 求n h 。
1,(),()n n h t t ϕϕ-=或ˆˆ()(2)/()H ωϕωϕω= 3、 由n h 求n g 。
1(1)n n n g h -=- 或()()i G e H t ωωωπ-=4、 由n g ，()t ϕ构成正交小波基函数()t φ1,()()n n t g t φϕ-=∑或ˆˆ()(/2)(/2)G φωωϕω= Haar 小波的构造1）、选择尺度函数。
101()0t t ϕ ≤≤⎧=⎨ ⎩其他 易知(n)t ϕ-关于n 为一正交归一基。
2）、求n h1,(),()n n h t t ϕϕ-=()2t-n)t dt ϕϕ（其中11(2)220n n t t n ϕ+⎧ ≤≤⎪-=⎨⎪ ⎩其他当n=0时，11(2)20t t ϕ⎧ 0≤≤⎪=⎨⎪ ⎩其他当n=1时，111(21)20t t ϕ⎧ ≤≤⎪-=⎨⎪ ⎩其他故，当n=0，n=1时1()(2)0n n t t n ϕϕ =0,=1⎧•-=⎨⎩其他当n=0时， ()(2)t t n ϕϕ•-1120t ⎧ 0≤≤⎪=⎨⎪ ⎩其他当n=1时，()(2)t t n ϕϕ•-11120t ⎧ ≤≤⎪=⎨⎪ ⎩其他故nh ()2t-n)t dt ϕϕ（1/0n n ⎧=0,=1⎪=⎨ ⎪⎩其他3）、求n g 。
11/0(1)1/10n n n n g h n -⎧=⎪⎪=-=-=⎨⎪ ⎪⎩其他4）、求()t φ。
1,()()n n t g t φϕ-=∑=0-1,011,1()()g t g t ϕϕ-+=(2)(21)t t -=110211120t t ⎧ ≤≤⎪⎪⎪- ≤≤⎨⎪ ⎪⎪⎩其他其图形如下：1、 Haar 尺度函数101()0t t ϕ ≤≤⎧=⎨ ⎩其他 Haar 尺度函数空间：}{,(22),(21),(2),(21),(21),j j j j j x x x x x ϕϕϕϕϕ++-- j 为非负的整数，该空间又称为j 级阶梯函数空间j V 。
小波变换：S 整数变换作业1. 题目：用整数小波的S 或2/6变换对256*256 Lena 灰度图像进行非标准方法的3级分解与重构。
2. 总体设计：本题目的意义在于通过实验体会整数小波变换，由于MA TLAB 自身对矩阵操作的方便性，以及其丰富的库函数（如可以用来直接显示图象），我决定用MATLAB 编程完成本次作业。
要说明的是，这里并不是直接利用MATLAB 中的wavelet 工具箱中的已有小波函数对图象进行整数小波分解，而是用下面的已知分解公式进行小波分解和重构。
分解公式：1,,21,21,,21,[]j k j k j kj k j k j k d s s s s d -+--=-=+ 重构公式：,21,1,,211,,2[]j k j k j k j k j k j k s s d s d s --+-=-=+ ，其中[ ]表示取整。
进行非标准小波分解，即交替进行3次行变换和3次列变换，程序对每次变换后的结果都保存为位图文件，运行后可以在程序所在路径下看到保存的6个分解位图文件和6个重构位图文件。
最后还会在一个图像中显示每次分解后的图像，以便于对比。
3. 实现方法：编写S 变换的分解和重构子程序，分别对图像数据进行一次行列分解和列行重构，程序返回该次变换后的行列矩阵，在主程序中可以连续三次调用行列变换，即完成对原始图像的3级分解和重构，这里的变换是完全可逆的，也就是能够完全恢复原图像数据。
通过对比3次重构后返回的数据与原图像数据后发现它们完全相同。
主要用的MA TLAB 工具函数有：imread( )---------读取图像数据，为uint8类型，需变为double 类型才能进行各种运算 imwrite()---------用于保存图像，这里用它来保存每一级变换后的图像image( )----------显示图像，需要给出色谱表colormap ，这里是灰度图，用colormap ＝gray （256）即可subplot( )--------用于分开绘图，即在一个窗口下绘制多个图像，在这里用于输出变换后的图像，以便对比。
小波变换在图像处理中的应用及其实例引言：随着数字图像处理技术的不断发展，小波变换作为一种重要的数学工具，被广泛应用于图像处理领域。
小波变换具有多尺度分析的特点，能够提取图像的局部特征，对图像进行有效的压缩和去噪处理。
本文将探讨小波变换在图像处理中的应用，并通过实例加以说明。
一、小波变换的基本原理小波变换是将信号或图像分解成一组基函数，这些基函数是由母小波函数进行平移和伸缩得到的。
小波变换的基本原理是将信号或图像在不同尺度上进行分解，得到不同频率的小波系数，从而实现信号或图像的分析和处理。
二、小波变换在图像压缩中的应用图像压缩是图像处理中的重要应用之一。
小波变换通过分解图像，将图像的高频和低频信息分离出来，从而实现图像的有损或无损压缩。
小波变换在图像压缩中的应用主要有以下两个方面：1. 小波变换在JPEG2000中的应用JPEG2000是一种新一代的图像压缩标准，它采用小波变换作为核心算法。
JPEG2000通过小波变换将图像分解成多个子带，然后对每个子带进行独立的压缩，从而实现对图像的高效压缩。
相比于传统的JPEG压缩算法，JPEG2000在保持图像质量的同时，能够更好地处理图像的细节和边缘信息。
2. 小波变换在图像去噪中的应用图像去噪是图像处理中的常见问题，而小波变换能够有效地去除图像中的噪声。
小波变换通过将图像分解成多个尺度的小波系数，对每个尺度的小波系数进行阈值处理，将较小的小波系数置零，从而抑制图像中的噪声。
经过小波变换去噪后的图像能够更清晰地显示图像的细节和边缘。
三、小波变换在图像增强中的应用图像增强是改善图像质量的一种方法，而小波变换能够提取图像的局部特征，从而实现图像的增强。
小波变换在图像增强中的应用主要有以下两个方面：1. 小波变换在图像锐化中的应用图像锐化是增强图像边缘和细节的一种方法，而小波变换能够提取图像的边缘信息。
通过对图像进行小波变换，可以得到图像的高频小波系数，然后对高频小波系数进行增强处理，从而增强图像的边缘和细节。
实验报告课程名称信息隐藏技术实验名称小波变换姓名__ 学号专业班级__）__ _实验日期成绩______ _指导教师____一、实验目的了解小波变换及其变换系数的分布。
二、实验环境(1) PC计算机(2) MatLab软件/语言包括图像处理工具箱(Image Processing Toolbox)(3) 实验所需要的图片三、实验内容与步骤利用Matlab提供的函数对图像进行小波分解与重构。
以下程序是对图像进行一级小波变换及重构：close all；clear；I=imread('图像.bmp);[M,N] = size(I);[A,H,V,D]=dwt2(I,'haar'); %使用haar小波对二维图像进行一级小波分解%A 近似子带；H 水平细节子带；V垂直细节子带；D 对角细节子带J=I;%---------小波分解图像-----J(1:M/2,1:N/2)=A;J(1:M/2,N/2+1:N)=H;J(M/2+1:M,1:N/2)=V;J(M/2+1:M,N/2+1:N)=D;%-----------重构图像----II=idwt2(A,H,V,D,'haar');figureimshow(uint8(J)),title('haar小波一级分解')figureimshow(uint8(II)),title('haar小波重构')六、实验心得与体会思考：1、使用haar小波对图像进行二级小波分解，并将其重构回原图。
close allclearI=imread('Fig4.11(a).jpg');[M.N]=size(I);[A,H,V,D]=dwt2(I,'haar');J(1:M/2,1:N/2)=A;J(1:M/2,N/2+1:N)=H;J(M/2+1:M,1:N/2)=V;J(M/2+1:M.N/2+1:N)=D;[X,Y]=size(A);[cA,cH,cV,cD]=dwt2(A,'haar');Z=J;Z(1:X/2,1:Y/2)=cA;Z(1:X/2,Y/2+1:Y)=cH;Z(X/2+1:X,1:Y/2)=cV;Z(X/2+1:X,Y/2+1:Y)=cD;II=idwt2(cA,cH,cV,cD,'haar');III=idwt2(II,H,V,D,'haar');figureimshow(uint8(Z)),title('haarС²¨¶þ¼¶·Ö½â')figureimshow(uint8(III)),title('haarС²¨Öع¹')2、利用W A VEDEC2函数对图像进行多尺度分解并重构回原图。
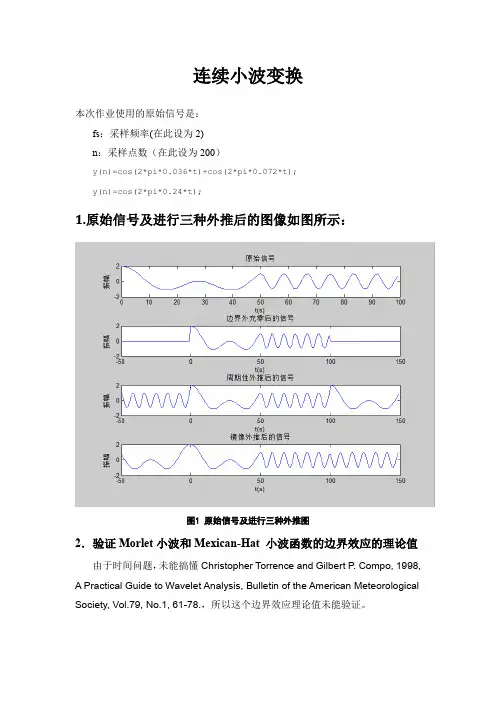
连续小波变换本次作业使用的原始信号是：fs：采样频率(在此设为2)n：采样点数（在此设为200）y(n)=cos(2*pi*0.036*t)+cos(2*pi*0.072*t);y(n)=cos(2*pi*0.24*t);1.原始信号及进行三种外推后的图像如图所示：图1 原始信号及进行三种外推图2．验证Morlet小波和Mexican-Hat 小波函数的边界效应的理论值由于时间问题，未能搞懂Christopher Torrence and Gilbert P. Compo, 1998, A Practical Guide to Wavelet Analysis, Bulletin of the American Meteorological Society, Vol.79, No.1, 61-78.，所以这个边界效应理论值未能验证。
3.试验边界外充零、周期性外推、镜像外推的优劣3.1原始数据作小波变换图2 Mexican Hat小波变换和Morlet小波的变换从图2可以看出：（1）Mexican Hat小波变换在相同的尺度下有更好的时间分辨率；（2）尺度的大小表示小波的宽窄，尺度大，表示小波比较宽，频率就较低；相反，尺度小则表示频率高；而且在经过小波变换后的边界影像范围随尺度的增大而变宽；3.2充零外推后的小波变换：图3 充零外推后的小波变换3.3周期延拓的小波变换：图4 周期延拓的小波变换3.4镜像外推的小波变换：图5 镜像外推的小波变换3.5综合3.2-3.4，可得以下结论：（1）充零外推后的小波变换与原始信号直接小波变换基本上没有什么区别，保证了原始信号的边界效应，但是时间的不连续性可能会导致信号的高频信号的丢失；（2）周期延拓后的小波变换同样会造成时间的不连续性，导致信号的边界效应很明显；（3）镜像外推后的小波变换可以保证时间上的连续，理论上可以应用于各种信号，但仍要与实际相结合使用。
小波分析与时域分析作业1、利用小波包变换和滤波方法实现图像去噪，给出实验仿真程序和实验结果，并对进行分析。
（1）比较不同小波包树结构对图像的影响吗，给出分析理由。
（2）分析小波包变换去噪与滤波方法去噪的特点。
仿真程序：load trees;subplot(2,2,1);image(X);colormap(map);title('原始图像');axis square;init=2055615866;randn('seed',init);X1=X+20*randn(size(X));subplot(2,2,2);image(X1);colormap(map);title('含噪图像');axis square;T=wpdec2(X1,1,'sym2');thr=8.342;NT=wpthcoef(T,0,'s',thr);X2=wprcoef(NT,1);subplot(2,2,3);image(X2);colormap(map);title(‘小波包去噪图像');axis square;K=medfilt2(X1,[4,4]);subplot(2,2,4);image(K);colormap(map);title('中值滤波去噪图像');axis square;实验结果：实验分析：（1）为了比较不同小波包树结构对图像的影响，这里取不同层的小波包树结构对含噪图像进行去噪，实验仿真如下：仿真程序：load trees;subplot(2,2,1);image(X);colormap(map);title('原始图像');axis square;init=2055615866;randn('seed',init);X1=X+20*randn(size(X));subplot(2,2,2);image(X1);colormap(map);title('含噪图像');axis square;T=wpdec2(X1,1,'sym2');thr=8.342;NT=wpthcoef(T,0,'s',thr); X2=wprcoef(NT,1);subplot(2,2,3);image(X2);colormap(map);title('小波包1层去噪图像'); axis square;K=wpdec2(X1,4,'sym2');thr=8.342;NT1=wpthcoef(K,0,'s',thr); X3=wprcoef(NT1,1);subplot(2,2,4);image(X3);colormap(map);title('小波包3层去噪图像'); axis square;实验结果：小波包分解每次对低频和高频都进一步进行处理，舍弃高频，相比于小波分解分得的频段更多。
小波转换在分析化学中的应用摘要：小波变换是80年带发展起来的一种新的数学分支，因为小波变换具有许多其他信号出路方法所不具备的优良特征，如可变的时频分辨率和可调节的局部支持等，所以使它成为信号处理的一种强有力的工具。
本文介绍了小波分析的发展，现状和它在分析化学中的应用，对其可能运用的领域进行了探讨。
关键词：小波：信号；傅立叶变换；分析化学Abstract: Because of the fine properties of flexible time---frequency windows and governedlocalized support, the wavelet transform is a useful tool in signal processing. The text introduced the development and present of Wavelet Analysis. A review of application of Wavelet Analysis in Analytical Chemistry has been presented.Key words: wavelet; signals; Fourier Transform; analytical chemistry小波(又叫子波 )变换的理论是最近发展起来的新的数学方法, 被认为是傅里叶分析理论的重大突破。
小波变换同时在时域和频域中具有较好的局部特性, 将时频统一于一体来研究信号。
而傅里叶变换则与此不同, 它把信号完全变换到频域中研究, 对频率的分辨率是无穷, 但对时间的分辨率是零; 传统的时域分析则完全在时域中分析信号, 它对时间的分辨率是无穷, 但对频率的分辨率为零。
虽然加窗傅里叶变换能部分克服傅里叶变换的不足, 但其窗口大小固定不变, 在应用中也存在它的局限性。
小波变换则同时对时间和频率具有较好的分辨率, 目前已经在若干领域取得了突破性的成果。
小波理论及其应用研究广泛地引起了人们的兴趣。
虽然小波在分析化学中的应用尚处于起步阶段, 但其已广泛应用于许多分析领域 ,是比较理想的对各种信号进行局部频谱分析的数学工具。
1 小波理论的发展及研究现状小波理论的思想形成于本世纪。
Haar 在1910 年提出第一个小波规正交基【1】,即人们所熟知的Haar 系。
1936 年Litterwood 和Paley 对傅立叶级数建立二进制频率分量分组理论L-P 理论,即按二进制频率成份分组傅立叶变换的相位变化。
这是多尺度分析思想的最早起源。
Calderon,Zygmund,Stern 和 Weiss 等人将 L-P 理论推广到高维,并且建立了奇异积分算子理论。
1965 年 Calderon 又给出了再生公式。
1974 年,Coifman 对一维空间和高维空间给出了其原子分解;1975 年Calderon 用他的再生公式给出抛物型空间上H1的原子分解。
这个公式后来成为许多函数分解的出发点，其离散形式已接近小波展开。
此后许多数学家分别对各种不同的目的给出各类函数空间的“原子分解”、“分子分解”、“拟正交展开”、“弱正交展开”、“框架展开”等。
1976 年Peetre 在用L-P 方法给出Besov 空间统一描述的同时,给出Besov 空间的一组基。
其展开系数大小描述了Besov 空间本身；1981年Stromberg 通过对Haar系的改进引入了Sobolev 空间H3正交基, 为小波分析奠定了基础。
小波 Wavelet 变换是由法国数学家 Morlet 于 1980 年提出。
他与法国理论物理学家Grossman 共同提出连续小波变换的几何体系，其基础是平移和伸缩(即放射群)下的不变性【2】。
这使得能将一个信号分解成对空间和尺度(即时间与频率) 的独立贡献 ，同时又不丢失原有信号的信息 ；小波作为函数 ，它的平移伸缩系用于在平方可积空间 L 2(R)展开的概念是由 Grossman 和 Morlet 首先引入； 1985 年法国数学家Meyer 在连续小波理论容许性及重构公式后承认了Calderon 恒等式。
之后又与比利时数学家 Daubechies 以及Grossman 通过构成 L 2(Rn)的一个准正交完全集的方式选取连续小波空间的一个离散子集,称为框架 。
并证明一维小波函数的存在性【3】；Lemarie 将这一理论推广至N 维情形 ，同时 Meyer 和 Battle 又分别给出了具有指数衰减特性的小波函数。
它的平移伸缩系构成 L2(R) 的规范正交基, 从尺度函数出发构造出了小波正交基。
与此同时，小波理论对相关学科发展产生积极的影响：1988 年Mallat 将计算机视觉领域内的多尺度分析的思想引入到小波分析中,提出多分辩分析概念【4】。
用多分辨分析来定义小波,给出了构造正交小波基的一般方法和与 FFT 相对应的快速小波算法-- Mallat 算法,并将这一理论用于图像分析和完全重构【5】；Daubechies 的基于离散滤波器迭代方法构造了紧支集规范正交小波基【6】，证明了具有有限支集正交小波基的存在性。
把在此之前的所有正交小波的构造统一起来 ，并为以后的构造设定了框架 其后的长篇综述【7】,对小波理论的发展和推广起到了促进作用 Mallat 将小波理论与信号处理联系起来,开创了小波理论在信号处理中的应用小波分析已经广泛用于量子场论、 地震勘探、计算机视觉等许多科学领域。
我国对小波的研究起步较晚,在信号的去噪和图像压缩机械故障检测等方面取得了较大的进展。
有关于小波应用的研究主要可以分为两大部分：一部分是利用小波对信号进行消噪处理，以提高解释方法的分辨率。
这部分包括小波变换用于信噪分离、弱信号的提取以及信号奇异点与奇异度的测量和多尺度边缘检测与重构；另一部分是利用小波分析做图像或数据压缩图像经小波分解后可以采用不同的量化处理，针对不同层次的低频系数和高频系数进行量化处理。
对量化后的小波系数进行重构，以达到图像或数据压缩的目的。
2 小波变换在分析化学中的应用各种分析信号的特征是它的时域分布或频域特性 ,小波变换在保持信号局域性的基础上 ,可把信号分解为不同的频率谱块 。
在分析信号处理方面有着广泛的应用。
2 . 1 谱图数据压缩我们分析得到的大量数据中包含了许多无关紧要的信息 ,在保持原有特征的前提下对数据进行压缩处理 , 图谱的存储 、检索和处理都可简化 。
王洪等【8】利用 Daubechies 2小波对5808个聚乙烯红外 光谱数据进行分解 ,把域值在1 . 521以下的变换系数置零 ,大于域值的数据只剩下1104个 ,数据个数压缩了4/5之多 ,但用这些数据重建后的图形却能很好地保持原信号的特征;Bos 等将有机化合物红外光谱数据个数压缩了约 19/20;Chau 等对UV 谱进行数据压缩 ,能很好重建光谱 ,他们还采用小波变换辅以权重优选算法及Huffman 编码技术压缩红外光谱数据 ,优于快速Fourier 变换法及域值法;钱神恩 等【9】亦 把21种 典 型 地 物光 谱 数据 压缩了9/ 10 。
小波函数选择及分解次数不同 ,压缩比也不一样 ;数据取舍的域值是由重建光谱与原始光 谱数据中间的允许误差确定的 ,可先任取一个数为初始值 ,然后计算重建光谱与原始光谱数据的均方差 ,在可接受的误差范围内尽量取较大的值。
小波分析在数据的压缩处理中得到成功应用。
2 . 2 改善分析信号质量 ,提取目标信息2 . 2 . 1 流动注射分析 ( FIA)1992 年Bos等首次将小波变换应用于F IA 中 ,他们对FIA 峰的高斯形状及指数修正的高斯峰进行了模拟研究 ,发现当信噪比 ( S/ N) 为2 时 ,与小波变换得到的FIA 峰强度误差在5 %以内 ,检测限亦有所改善 ,基线漂移也甚小。
2 . 2 . 2 高效液相色谱 ( HPLC)在HPLC定量分析中 , 当样品的浓度较低 , 特别是采用梯度洗脱时 ,存在严重的信噪比低及基线漂移等问题。
对于HPLC数据 ,基线“信号”的频率最低 ,色谱峰信号的频率居中 ,而噪音信号的频率最高。
邵利民等【10】利用Haar小波对HPLC原始信号进行了一定次数的变换 ,得到了高信噪比的光滑曲线 ,检测限及线性亦有了很大改善 ,且峰位不变。
潘忠孝等【11】采用Daubechies小波对HPLC数据进行变换 ,把峰信号的数据置零后重建原始数据 , 得到HPLC的基线信号 ,进而得到扣除基线后的色谱曲线 ,实现了基线信号和色谱信号的分离 ,提高定量分析的准确度及重现性。
邵学广等【12~14】对混合物的HPL C 重叠信号进行小波变换 ,通过对变换后的数据进行分析 ,色谱信号的质量在基线校正后得到改善 ,而且重叠信号的分离度增大 ,变换后各化合物峰信号与其浓度的线性关系良好。
实践证明 ,在提高重叠色谱峰分辨率、提取重叠色谱峰中的组分信息、基线扣除及改善定量分析准确度方面 ,小波变换是一个很有效的工具。
2 . 2 .3 电分析法有人通过对差分脉冲及示波信号小波变换后的数据进行分析 ,结果表明一旦选取了最佳小波函数、分解频率和域值等参数 ,可方便地获得去除了高频噪音和扣除了背景后的信号 ,提高了检测的准确度、重现性和分辨率 ,降低测定的检测限 ,改善多组分分析的准确度。
算法简便快速 ,且无需了解噪音的统计特征及对信号进行预处理【15~18】。
王洪等【19】将小波变换在信号和图象处理中边缘检取的思想引入电位滴定终点判断 ,计算精度达精度下限 ,以氢氧化钠溶液分别滴定了盐酸、醋酸和草酸等溶液 ,滴定终点的计算值与理论值完全相符。
2 . 2 . 4 红外及近红外光谱分析该方面的应用较多。
除上述图谱数据压缩外, 多是对光谱进行去噪处理。
Alsberg 等利用6种小波变换去噪音方法对红外光谱进行处理 ,发现在低信噪比的情况下 ,采用小波变换或Fourier变换效果相近 ,小波变换未显现优势 ;但在高信噪比的情况下 ,小波变换的方法、尤其是HYBRID及VISU两法效果较好 ;另外,Jouan2Rimbaud 等通过采用小波变换对一组近红外光谱数据的噪音及不相关信号进行去除 ,成功地进行了多元校正领域的尝试 ,并指出 ,虽然离散小波变换 ( DWT) 目前应用普遍 ,但小波包变换更有应用价值。
Walczak等利用小波变换对近红外光谱进行标准化 ,优于传统方法 ,尤其在只有很少原始光谱数据可用以提取标准化参数时优势明显。
陈洁等【20】对共聚物的红外光谱小波变换后 ,其特征吸收带得到较好分离 ,提高了红外光谱图的分辨率 ,而相应的Fourier 变换特征吸收带重叠严重。
