光学扫描测金属杆直径
- 格式:ppt
- 大小:3.68 MB
- 文档页数:11

实验6 用光杠杆测量金属的弹性模量(311)一、实验目的1.学习用光杠杆测量微小长度变化的原理,掌握放大法.2.理解视差,掌握消除视差的调整方法.3.学会用逐差法处理数据,掌握对测量结果的标准不确定度进行评定.二、实验仪器杨氏模量测定仪、钢丝、砝码、游标卡尺、卷尺三、实验原理设金属丝的长度为L ,横截面积为S ,沿长度方向受到作用力F 时,金属丝发生弹性形变,伸长(或缩短)△L .比值F /S 是单位横截面上的作用力,称为正应力;比值 △L/L 是相对伸长,称为线应变.胡克定律告诉我们:在物体的弹性限度内正应力与线应变成正比F LES L∆= (9-1) 比例系数E 称为弹性模量(曾称杨氏模量),单位名称为帕[斯卡],单位符号为Pa.实验证明,弹性模量与温度有关,与物体本身材料的化学成分、结构、加工制造方法有关,而与外力、物体的形状及大小无关,是表征固体性质的一个重要物理量.固体中纵波的波速、固体材料的很多力学性质都与弹性模量有关,据此可以提供测弹性模量的不同方法.本实验就是从(9-1)式出发来测量弹性模量。
[装置介绍](9-1)式中F 、S 、L 的测量很容易解决,而△L 很小,用一般工具不易测准,因此可采用光杠杆法。
其装置如图9-1(a )所示,其细部见图9-1(b ):待测金属丝②的上端固定在支架①的顶部,下端固定在“口”形框⑤的上端,“口”形框下端的丝口接砝码托⑦,在托上放置砝码.可上下移动的平台⑥固定在支架的中部,平台上有一个矩形孔,“口”形框穿过此孔并可以在孔中上下自由移动.平面镜③安装在有三只尖脚的镜座④上,前两只尖脚放在平台上,第三只主杆尖脚卡在“口”形框内侧底面中央的接砝码托丝口的凹处,可以随着金属丝的伸长而上下移动.将水准仪放在平台上,调节支架底部的三个螺钉使平台水平.将平面镜的镜面转到与水平面垂直,望远镜⑨正对平面镜,调节目镜与叉丝距离调节手轮⑩和调焦手轮○11,从望远镜中可以看到由平面镜反射过来的标尺⑧的像. 平面镜与镜座构成了光杠杆(见图9-1(b )).光杠杆测微小伸长量的原理见图9-3.当金属丝伸长△L 时,光杠杆的长为b 的主杆尖脚也随之下落△L ,带动平面镜M 转过α角而至M',镜面的法线0on 也转过α角至1on .根据反射定律,0121n on n on α∠=∠=,从标尺的n 2处发出的光线将反射到n 0,从望远镜中看到的是经平面镜反射过来的标尺上n 2处的刻线.由图9-2可以看出图9-1 用光杠杆测量弹性模量装置图tan L b α∆=02tan 2n n on α=因为02n n 是在望远镜中观察到的标尺上刻线的变化,即02n n n =∆,设0on D =,由于α角很小,因此tan L b αα∆≈=2tan 2n Dαα∆≈=消去α得2bL n D∆=∆ (9-2) 从图9-2可以看出,o 相当于杠杆的支点,b+D 相当于杠杆本身,只是D 由光线所代替,所以称为光杠杆。

吉林大学珠海学院课程设计报告设计题目测量金属丝的直径学生姓名学号********学生姓名学号********所属院系电子信息系专业电子信息科学与技术班级电子一班指导教师王天会设计地点实验楼4372016年12月12日一、 实验目的1、 学习读数显微镜的使用方法2、 观察劈尖干涉现象及其特点3、 用劈尖干涉法测量金属丝直径 二、劈尖测量金属丝直径的原理如图1-1所示,G 1、G 2为两片叠放在一起的平板玻璃,起一端的棱边相接触,另一端被一直径为D 的细丝隔开,故在G 1的下边卖女和G 2的上表面之间形成一层空气薄层,叫做空气劈尖。
图中M 为倾斜45°角放置的半透明半反射平面镜,L 为透镜,T 为显微镜。
单色光源S 发出的光经透镜L 后成为平行光,经M 反射后垂直射入劈尖(入射角i=0)。
自空气劈尖上、下两面反射的光相互干涉,从显微镜T 中可观察到明暗交替、均匀分布的干涉条纹,如图1-2所示。
图中相邻两暗纹(或明纹)的中心间距b 叫做劈尖干涉的条纹宽度。
在图1-3中,D 为细丝直径,L 为玻璃片长度,θ为两玻璃片间的夹角。
由于θ实际很小(为清晰期间被,图中θ被夸大),所以在劈尖的上表面处反射的光线都可看作垂直与劈尖表面,他们在劈尖表面处。
相遇并相干叠加。
由于劈尖层空气的折射率n 比比玻璃的折射率n 1小,所以光在劈尖下表面反射时因有相位跃变而产生附加光程差λ/2。
这样,由kλ, k=1,2,…(加强)Δr=2n2d+λ/2=(2k+1), λ/2, k=0,1,2,…(减弱)可得劈尖上下表面反射的两相干光的总光程差为Δ=2nd+λ/2式中d为劈尖上下表面间的距离。
劈尖反射光干涉条纹极大(明纹)的条件为2nd+λ/2=kλ,k=1,2,3,… (1-1)产生干涉条纹极小(暗纹)的条件为2nd+λ/2=(2k+1)λ/2, k=0,1,2,… (1-2)从师1-1和1-2可以看出,凡劈尖内厚度d相同的地方均满足相同的干涉条件。


属杆直径
作者:朱长江
演讲:高健
机械法测量:螺旋测微器,游标卡尺光学测量法:透镜成像法,光学扫描法
激光扫描法原理:菲涅耳直边衍射
实验目的:
用不同的方法测量金属杆的直径;
用激光扫描测量金属杆直径
要求:
几何阴影是如何确定的;
试分析光线经过金属杆表面是怎样传播的。
如何得到测量金属杆较好的实验效果?
直
边界条纹特点:几何阴影内有部分光强,几何阴影外有波动的光强分布,菲涅耳直边衍射的螺旋结构光强分布结果
试验器材:激光,光具座,导轨,透镜,硅光电池,灵敏检流计,细棒
扫描法测细棒直径
激光器
细棒
透镜
光路
透镜
硅光电池
实验步骤
一、按光路图摆好仪器。
二、用辅助棒调节共轴。
三、调节两个透镜,使出射光线平行。
四、调节狭缝大小,使射入硅光电池的光强适中,检流计的最大偏角在40左右。
五、光电检流器在中央暗处使检流器归零。
六、每隔0.1毫米记录一次光强,靠近
边界处每隔0.05记录一次光强,
七、整理数据,分析结果。
对比
两边光强分布与标准分布不相符合,原因所在是透镜的扩展光束并不均匀,中央明亮,两边偏暗。
但光强摆布是明显有的,如果把扩展光束调节的更加均匀,效果将更加明显
直边衍射测金属杆直径运用了菲涅耳直边衍射原理,结合激光的高度相干性,能够很好的测量金属杆直径
THANK YOU。


研究性实验报告光杠杆法测钢丝弹性模量二零一一年十一月目录一、摘要 (3)二、实验原理 (3)三、实验仪器 (5)四、实验步骤 (5)五、数据记录与处理 (6)六、实验讨论 (8)七、总结 (12)一、摘要物体在外力的作用下,或多或少都要发生形变。
当形变不超过某个限度时,外力撤销后形变会随之消失,这种形变称为“弹性形变”。
发生弹性形变时,物体内部会产生恢复原状的内应力。
弹性模量就是描述材料变形与应力关系的重要特征量。
是工程技术中常用的一个参数。
在实验室施加的外力使材料产生的变形相当微小,难以用肉眼观察,同时过大的载荷又会使得材料发生塑形变形,所以要通过将微小变形放大的方法来测量。
本实验通过光杠杆将外力产生的微小位移放大,从而测量出杨氏弹性模量,具有较高的可操作性。
二、实验原理一条各向同性的金属丝,原长为L ,截面积为S ,在外力F 作用下,伸长为△L 。
忽略金属棒本身重力,则棒中任一截面上,内部恢复力必与外力相等。
在弹性限度内,定义:应变L L∆=ε 应力SF =σ 弹性模量E 与外力F 、物体长度L 以及截面积的大小S 均无关,只取决定于棒的材料性质,是表征材料力学性能的一个物理量。
若金属棒为圆柱形,直径为D ,在金属棒下悬一重物产生拉力F 。
则:LD FLE ∆=24π 根据上式,测出等号右边各项,就可算出金属弹性模量,式中的F 、L 、D 可用一般方法测得。
测量难点是,在线弹性限度内,F=mg 不可能很大,相应的不可能很大,只能用采用光杠杆法进行。
一个直立的平面镜装在倾角二次架上,与标尺、望远镜和二次反射镜组成光杆杆测量系统。
如图所示:实验时,将光杠杆两个前足尖放在弹性模量测定仪的固定平台上,后足尖放在待测金属丝的测量端面上。
当金属丝受力后,产生微小伸长,后足尖便随着测量端面一起作微小移动,并使得光杠杆绕前足尖转动一个微小角度,从而带动光杠杆反射镜转动相应的微小角度,这样标尺的像在光杠杆反射镜和二次反射镜之间反射,便把这一微小角位移放大成较大的线位移。

研究性实验报告光杠杆法测钢丝弹性模量二零一一年十一月目录一、摘要 (3)二、实验原理 (3)三、实验仪器 (5)四、实验步骤 (5)五、数据记录与处理 (6)六、实验讨论 (9)七、总结 (12)一、摘要物体在外力的作用下,或多或少都要发生形变。
当形变不超过某个限度时,外力撤销后形变会随之消失,这种形变称为“弹性形变”。
发生弹性形变时,物体内部会产生恢复原状的内应力。
弹性模量就是描述材料变形与应力关系的重要特征量。
是工程技术中常用的一个参数。
在实验室施加的外力使材料产生的变形相当微小,难以用肉眼观察,同时过大的载荷又会使得材料发生塑形变形,所以要通过将微小变形放大的方法来测量。
本实验通过光杠杆将外力产生的微小位移放大,从而测量出杨氏弹性模量,具有较高的可操作性。
二、实验原理一条各向同性的金属丝,原长为L ,截面积为S ,在外力F 作用下,伸长为△L 。
忽略金属棒本身重力,则棒中任一截面上,内部恢复力必与外力相等。
在弹性限度内,定义:应变L L∆=ε 应力SF =σ 弹性模量E 与外力F 、物体长度L 以及截面积的大小S 均无关,只取决定于棒的材料性质,是表征材料力学性能的一个物理量。
若金属棒为圆柱形,直径为D ,在金属棒下悬一重物产生拉力F 。
则:LD FLE ∆=24π根据上式,测出等号右边各项,就可算出金属弹性模量,式中的F 、L 、D 可用一般方法测得。
测量难点是,在线弹性限度内,F=mg 不可能很大,相应的不可能很大,只能用采用光杠杆法进行。
一个直立的平面镜装在倾角二次架上,与标尺、望远镜和二次反射镜组成光杆杆测量系统。
如图所示:实验时,将光杠杆两个前足尖放在弹性模量测定仪的固定平台上,后足尖放在待测金属丝的测量端面上。
当金属丝受力后,产生微小伸长,后足尖便随着测量端面一起作微小移动,并使得光杠杆绕前足尖转动一个微小角度,从而带动光杠杆反射镜转动相应的微小角度,这样标尺的像在光杠杆反射镜和二次反射镜之间反射,便把这一微小角位移放大成较大的线位移。
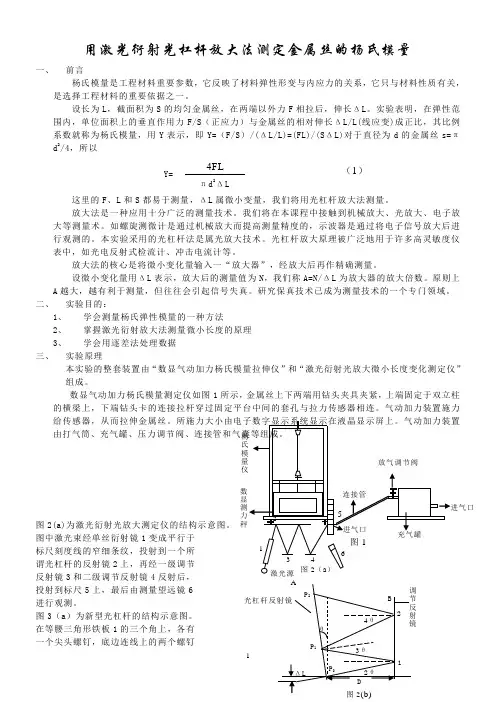
用激光衍射光杠杆放大法测定金属丝的杨氏模量一、 前言杨氏模量是工程材料重要参数,它反映了材料弹性形变与内应力的关系,它只与材料性质有关,是选择工程材料的重要依据之一。
设长为L ,截面积为S 的均匀金属丝,在两端以外力F 相拉后,伸长ΔL 。
实验表明,在弹性范围内,单位面积上的垂直作用力F/S (正应力)与金属丝的相对伸长ΔL/L(线应变)成正比,其比例系数就称为杨氏模量,用Y 表示,即Y=(F/S )/(ΔL/L)=(FL)/(S ΔL)对于直径为d 的金属丝s=πd 2/4,所以Y=这里的F 、L 和S 都易于测量,ΔL 属微小变量,我们将用光杠杆放大法测量。
放大法是一种应用十分广泛的测量技术。
我们将在本课程中接触到机械放大、光放大、电子放大等测量术。
如螺旋测微计是通过机械放大而提高测量精度的,示波器是通过将电子信号放大后进行观测的。
本实验采用的光杠杆法是属光放大技术。
光杠杆放大原理被广泛地用于许多高灵敏度仪表中,如光电反射式检流计、冲击电流计等。
放大法的核心是将微小变化量输入一“放大器”,经放大后再作精确测量。
设微小变化量用ΔL 表示,放大后的测量值为N ,我们称A=N/ΔL 为放大器的放大倍数。
原则上A 越大,越有利于测量,但往往会引起信号失真。
研究保真技术已成为测量技术的一个专门领域。
二、 实验目的:1、 学会测量杨氏弹性模量的一种方法2、 掌握激光衍射放大法测量微小长度的原理3、 学会用逐差法处理数据 三、 实验原理本实验的整套装置由“数显气动加力杨氏模量拉伸仪”和“激光衍射光放大微小长度变化测定仪”组成。
数显气动加力杨氏模量测定仪如图1所示,金属丝上下两端用钻头夹具夹紧,上端固定于双立柱的横梁上,下端钻头卡的连接拉杆穿过固定平台中间的套孔与拉力传感器相连。
气动加力装置施力图2(a)为激光衍射光放大测定仪的结构示意图。
图中激光束经单丝衍射镜1变成平行于 标尺刻度线的窄细条纹,投射到一个所 谓光杠杆的反射镜2上,再经一级调节反射镜3和二级调节反射镜4反射后,投射到标尺5上,最后由测量望远镜6 进行观测。

利用光学衍射的方法测金属的直径摘要:介绍了一种测量金属丝直径的理论方法—光学衍射测量法。
对于已给定的七根直径在(0.1-0.4 mm)范围内的金属丝,我们可以利用已有的实验装置对其进行了测量。
通过测量结果可以看出:多次重复使用这种方法所测量的结果误差不足1%,对于测量直径不同的金属丝所得的结果平均偏差不高于5%。
在做测量金属丝直径的实验中,通常使用得是价格便宜而且实验室必备的的光电二极管和激光器。
所有的实验装置和仪器在实验室中都能找到,测量起来也便于操作。
关键字:细金属丝、直径的测量、激光、光学衍射目录引言 .................................................. 错误!未定义书签。
1 探究衍射的背景 ...................................... 错误!未定义书签。
2 衍射法测细金属丝的直径的研究 ........................ 错误!未定义书签。
2.1衍射分类 ....................................... 错误!未定义书签。
2.2单缝夫朗和费衍射的实验光路 ..................... 错误!未定义书签。
3 测金属直径的实验过程 ................................ 错误!未定义书签。
3.1实验原理 ....................................... 错误!未定义书签。
3.2实验基本装置 ................................... 错误!未定义书签。
3.3金属丝直径的测量过程: ......................... 错误!未定义书签。
4 测量结论和误差分析 .................................. 错误!未定义书签。
小结 .................................................. 错误!未定义书签。


⽤⽴式光学计测量轴的直径实验报告实验⽤⽴式光学计测量轴的直径⼀、实验⽬的1.了解⽴式光学计的测量原理。
2.熟悉⽤⽴式光学计测量外径的⽅法。
3.加深理解计量器具与测量⽅法的常⽤术语。
4. 掌握零件的验收原则和验收⽅法。
⼆、实验设备1.⽴式光学计2.量块三、实验原理及实验设备说明1.⽴式光学计⽴式光学计是⼀种精度较⾼⽽结构简单的常⽤光学机械式长度计量器具。
⽤量块作为长度基准,按⽐较测量法来测量各种⼯件的外形尺⼨。
型号为JD3的⽴式光学计基本技术参数如下:测量范围:0-180mm;分度值:0.001mm;⽰值范围:±0.1mm;仪器最⼤不确定:0.00025 mm;测量最⼤不确定度:±(0.5+L/100)µm图1-1为⽴式光学计外形结构图。
1.投影灯2.投影灯固定螺钉3.⽀柱4.零位微动螺钉5.⽴柱6.⽀臂固定螺钉7.⽀臂8微动偏⼼⼿轮9⽴式测头提升器10.⼯作台调整螺钉11.⼯作台12.壳体13.微动托圈14.微动托圈固定螺钉15.光管定位螺钉16.测量管固定螺钉17.直⾓光管18.测帽19.6V15W变压器图1-1 ⽴式光学计外形图它主要是由带有特殊螺纹的⽴柱5、⽀臂7、直⾓光管17和⼯作台11等⼏部分组成。
⽴式光学计是利⽤光学⾃准原理和机械的正切杠杆原理进⾏测量的仪器。
其光学系统如图1-2a所⽰,由⽩炽灯泡1发出的光线经过聚光镜2和滤光⽚6,通过隔热⽚7照明分划板8的刻线⾯,再通过反射棱镜9后射向准直物镜12。
由于分划板8的刻线⾯置于准直物镜12的焦平⾯上,所以成像光束通过准直物镜12后成为⼀束平⾏光⼊射于平⾯反射镜13上,根据⾃准直原理,分划板刻线的像被平⾯反光镜13反射后,再经准直物镜12被反射棱镜9反射成像在投影物镜4的物平⾯上,然后通过投影物镜4、直⾓棱镜3和反射镜5成像在投影屏10上,通过读数放⼤镜11观察投影屏10上的刻线像。
由于测帽接触⼯件后,其测量杆14使平⾯反光镜倾斜了⼀个⾓度φ,在投影屏上就可以看到刻线的像也随着移动了⼀定的距离,其关系计算如图1-2b 所⽰。
物理实验报告【实验名称】杨氏模量的测定【实验目的】1. 掌握用光杠杆测量微小长度变化的原理和方法,了解其应用。
2. 掌握各种长度测量工具的选择和使用。
3. 学习用逐差法和作图法处理实验数据。
【实验仪器】MYC-1型金属丝杨氏模量测定仪(一套)、钢卷尺、米尺、螺旋测微计、重垂、砝码等。
【实验原理】 一、杨氏弹性模量设金属丝的原长L ,横截面积为S ,沿长度方向施力F 后,其长度改变ΔL ,则金属丝单位面积上受到的垂直作用力F/S 称为正应力,金属丝的相对伸长量ΔL/L 称为线应变。
实验结果指出,在弹性范围内,由胡克定律可知物体的正应力与线应变成正比,即LL Y S F ∆= (1)则ELL SF Y ∆= (2) 比例系数E 即为杨氏弹性模量。
在它表征材料本身的性质,Y 越大的材料,要使它发生一定的相对形变所需要的单位横截面积上的作用力也越大。
Y 的国际单位制单位为帕斯卡,记为Pa (1Pa =12m N ;1GPa =910Pa )。
本实验测量的是钢丝的杨氏弹性模量,如果钢丝直径为d ,则可得钢丝横截面积S 则(2)式可变为EL d FLY ∆=24π (3)可见,只要测出式(3)中右边各量,就可计算出杨氏弹性模量。
式中L (金属丝原长)可由米尺测量,d (钢丝直径),可用螺旋测微仪测量,F (外力)可由实验中钢丝下面悬挂的砝码的重力F=mg 求出,而ΔL 是一个微小长度变化(在此实验中 ,当L ≈1m时,F 每变化1kg 相应的ΔL 约为0.3mm)。
因此,本实验利用光杠杆的光学放大作用实现对钢丝微小伸长量ΔL 的间接测量。
? 二、光杠杆测微小长度变化尺读望远镜和光杠杆组成如图2所示的测量系统。
光杠杆系统是由光杠杆镜架与尺读望远镜组成的。
光杠杆结构见图2(b )所示,它实际上是附有三个尖足的平面镜。
三个尖足的边线为一等腰三角形。
前两足刀口与平面镜在同一平面内(平面镜俯仰方位可调),后足在前两足刀口的中垂线上。
光学扫描法测金属杆直径李美莹;刘凯;李金环【摘要】研究利用光学扫描法测量金属杆直径。
研究根据菲涅尔直边衍射原理获得金属杆衍射光强分布,使用光电池与检流计监测光强分布,利用计算机绘制衍射图像得到待测金属杆的直径(1 cm左右)。
%This study is about measuring the diameter of metal rod using optical scanning method. Based on Fresnel straight edge diffraction theory,we can get the diffraction intensity distribution of metal rod,which is detected by photocell and galvanometer. Diffraction image drawn by computer helps to obtain the diameter ( a-bout 1cm) of metal rod which is to be tested.【期刊名称】《大学物理实验》【年(卷),期】2015(000)004【总页数】3页(P63-65)【关键词】光学扫描法;菲涅尔直边衍射;直径测量【作者】李美莹;刘凯;李金环【作者单位】东北师范大学,吉林长春 130024;东北师范大学,吉林长春 130024;东北师范大学,吉林长春 130024【正文语种】中文【中图分类】TN247光学无损检测已经在食品、农业、医疗等行业得到了广泛的应用[1],在测量行业也具有长足的发展,根据D=Kλ/S可以方便的计算出细丝直径[2],并有办法在理论上将相对测量误差控制在0.4%[3]。
但是这种办法测量的范围很有限,大概在0.05 mm~0.5 mm。
本文介绍一种方法,测量范围在0.5 cm~2 cm 级别依然适用。
当平行光照射到金属杆上时,经过金属杆边缘的光会发生菲涅尔直边衍射,利用光电池与检流计构成的系统可以测定光强与位置坐标之间的关系。