《数值分析及其MATLAB实现》第二篇MATLAB快速入门word第三章 3.9

2.2 数组及其运算一行或一列的矩阵是向量或数组，在MATLAB中向量和数组虽然形式上一致，却是两个不同的概念，遵循不同的运算规则。

2.2.1 数组的输入除了像 1×n矩阵（行向量）一样地输入外，数组常采用“：”和函数linspace两种输入方式，它们的用法可以从下面的例子知道。

在MATLAB 工作窗口输入程序：》a=1:5 %从1到5公差为1的等差数组。

运行后输出结果如下:a=1 2 3 4 5在MA TLAB工作窗口输入程序：》b=1:2:7 %从1到7公差为2的等差数组。

运行后输出结果如下:b=1 3 5 7如果输入b=1:2:8,得到同样结果。

在MA TLAB工作窗口输入程序：》c=6:-3:-6 %从6到-6公差为-3的等差数组。

运行后输出结果如下:c=6 3 0 –3 -6在MA TLAB工作窗口输入程序：》b=[0:2:8,ones(1,3)] %等差数组和行向量拼接。

运行后输出结果如下:b=0 2 4 6 8 1 1 1在MA TLAB工作窗口输入程序：》linspace(0,1,9) %从0到1共9个数值的等差数组。

运行后输出结果如下:ans=0 0.1250 0.2500 0.3750 0.5000 0.6250 0.7 500 0.87500 1.0000linspace(a,b,n)生成从a到b共n个数值的等差数组，公差不必给出。

与它相仿的是logspace(a,b,n)生成从10a到10b共n个数值的等比数组。

4等分π（MATLAB中π的符号是pi）的数组可以用下面两种方式输入。

在MA TLAB工作窗口输入程序：》x=0:pi/4:pi运行后输出结果如下:x=0 0.7854 1.5708 2.3562 3.1416在MA TLAB工作窗口输入程序：》x=linspace(0,pi,5)运行后输出结果如下:x=0 0.7854 1.5708 2.3562 3.14162.2.2 数组的运算数组除了作为1×n矩阵（行向量）遵循矩阵运算规则外，MATLAB还为数组提供了一些特殊的运算：.* 乘法；.^ 乘幂；.\ 左除；./ 右除。

2.3 语句、变量和表达式2.3.1 语句形式MATLAB语句的一般形式为：变量=表达式若变量和“=”省略，则名为ans的变量自动建立。

如果你输入一个语句并以回车结束，则在工作区中显示计算的结果；如果语句以分号“；”结束，MATLAB只进行计算，不显示计算的结果。

如果一个表达式太长，可以用续行号…将其延续到下一行。

此外，一行中可以写几个语句，它们之间要用逗号或分号分开。

如，在MA TLAB工作窗口输入程序：》a=[1 2 3 4 5];b=[1 3 5 7 9];c=a.*b, d=a*b’,e=a'*b运行后输出结果如下:c =1 6 15 28 45d =95e =1 3 5 7 92 6 10 14 183 9 15 21 274 12 20 28 365 15 25 35 452.3.2 变量MATLAB的变量由字母、数字和下划线组成，最多31个字符，区分大小写字母，第一个字符必须是字母。

对于变量，MATLAB不需要任何类型的说明或维数语句。

当输入一个新变量名时MATLAB自动建立变量并为其分配内存空间。

MATLAB有几个特殊的量:pi 圆周率π；eps 最小浮点数；Inf 正无穷大，特指1/0；NaN 不定值，特指0/0；i,j虚数单位。

在MA TLAB工作窗口输入程序：》a=[0 1 0],b=[1 0 0],c=a./b运行后输出结果如下:a =0 1 0b =1 0 0Warning: Divide by zero.c =0 Inf NaN2.3.3 字符串字符串是用单引号括起来的字符集合，可以像向量一样进行拼接和裁剪，如，在MA TLAB工作窗口输入程序：》s1=’Hello’;s2=’every’;s3=’body’;s=[s1,’,’,s2,’ ’,s3],ss=s(1:5)运行后输出结果如下:s=Hello,every bodyss=Hello。

第二篇第四章MA TLAB符号计算4.5 化简和代换符号表达式的初等运算是指符号表达式的变换和化简、符号的代换、复合函数的运算和反函数的运算、加、减、乘、除运算、乘方和开方运算。

有关加、减、乘、除运算、乘方和开方运算在第一章实验的内容中我们已经作了介绍。

下面主要介绍符号表达式的变换和化简、符号的代换、复合函数和反函数的运算。

在MA TLAB中，这些运算的常用函数如表4-5所示。

[例1] 设函数652-=x y 和y z 3=，试求z 关于x 的复合函数。

解 输入>> syms x yz=sqrt(3*y);y =5*x^2-6;z=compose(z,y)运行后屏幕显示为z =3^(1/2)*(5*x^2-6)^(1/2)[例2] 分别求函数=1y e x -和t y sin 2=的反函数。

解 输入>> syms x t y1 y2y1 =exp(-x);y2=sin(t);g1=finverse(y1)g2=finverse(y2,t)运行后屏幕显示为g1 =-log(x)g2 =asin(t)[例3] 求函数)0(5≠++=ac d cx bax y 的反函数。

解 输入>> syms x a b c dy=((a*x+b)/(c*x+d))^(1/5)';g=finverse(y)运行后屏幕显示为g =-(b-conj(x)^5*d)/(a-conj(x)^5*c)为了用符号x 代替表达式g 中的符号conj(x),再输入：>> g=subs(-(b-conj(x)^5*d)/(a-conj(x)^5*c), conj(x),x)运行后屏幕显示为g =(-b+x^5*d)/(a-x^5*c)[例4] 在MA TLAB 工作窗口输入下面程序，运行后，观察其结果，说明所使用MA TLAB 函数collect 、expand 、horner 、factor 和simplify 的意义和用法。

MATLAB 软件为我们提供了众多功能强大的图形绘制函数，用于绘制平面曲线的MATLAB 函数有plot ，ezplot ，polar ，ezpolar ，fplot ，ezcontour 等，绘制空间图形的函数等，下面分别给以介绍。

3.1 函数 plotplot 是MATLAB 中最常用的画平面曲线的函数，它的主要功能是用于绘制显式函数)(x f y =和参数式函数)(),(t y y t x x ==的平面曲线。

Plot 函数的调用格式如下：plot(x,y,’可选项s ’)其中x 是曲线上的横坐标，y 是曲线上的纵坐标，’可选项s ’中通常包含确定曲线颜色、线型、两坐标轴上的比例等等的参数。

用户在作图时可以根据需要选择可选项。

如果用户在绘图时不用可选项，那么Plot 函数将自动选择一组默认值，画出曲线。

下面我们将通过例题逐步介绍。

[例1] 作出通过表3-1中数据点),(i i y x 的折线。

表3-1 例1的数据点),(i i y xx1 2 3 4 5 6 7 8 9 y 0 0.68 0.70 0.99 0.83 0.20 0.80 0.12 0.98解 因为横坐标为序号1，2，…，9，所以作图时，只需输入下列程序：>> y=[0 0.68 0.70 0.99 0.83 0.20 0.80 0.12 0.98];plot(y) ↙运行后屏幕显示数据点),(i i y x 的折线（见图 3-1）。

图 3-1 表3-1中数据点),(i i y x 的折线[例2] 作出函数y =2e x 5.0-cos(3x -4)在区间[0,6π]上的图形。

解 输入下列程序：>> x=linspace(0,6*pi,500);% 在[0,6π]上取500个点y=2*exp(-0.5*x).*cos(3*x-4);plot(x,y)↙运行后屏幕显示函数y =2e x 5.0-cos(3x -4)在区间[0,6π]上500个点连成的光滑的余弦曲线（见图 3-2）。

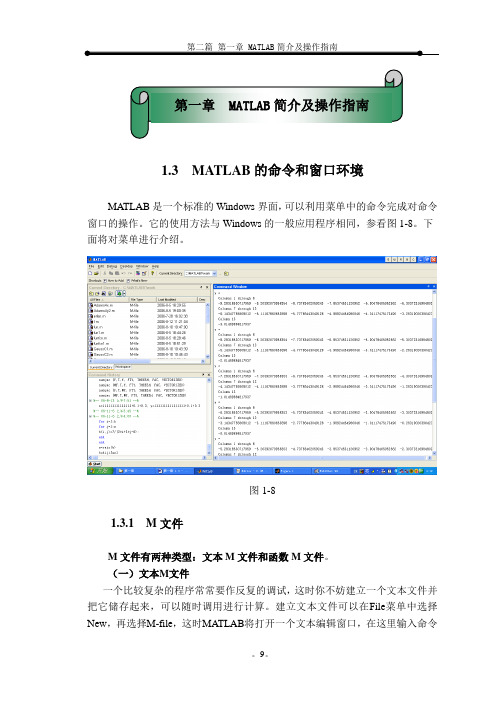
1.3 MA TLAB的命令和窗口环境MA TLAB是一个标准的Windows界面，可以利用菜单中的命令完成对命令窗口的操作。

它的使用方法与Windows的一般应用程序相同，参看图1-8。

下面将对菜单进行介绍。

图1-81.3.1 M文件M文件有两种类型：文本M文件和函数M文件。

（一）文本M文件一个比较复杂的程序常常要作反复的调试，这时你不妨建立一个文本文件并把它储存起来，可以随时调用进行计算。

建立文本文件可以在File菜单中选择New，再选择M-file，这时MA TLAB将打开一个文本编辑窗口，在这里输入命令和数据。

储存时文件名遵循MA TLAB变量命名的原则，但必须以m 为扩展名，其一般形式为< M文件名>.m如juzhen.m, pp.m等。

值得注意的是，文本M文件中的变量都是全局变量，在执行过程中, 文本M 文件中的命令可以使用目前工作区中的变量，它所产生的变量也将成为工作区的一部分。

例如我们把下面的程序保存为名为budijifen1.m的文本M文件：function budijifen1x=-4*pi:0.014*pi;a=1;for C=-3:3y =1/2*(-sin(a*x)+a*x)/a+Cplot(x,y)hold onendgridhold offxlabel('自变量 X')ylabel('因变量 Y')title('不定积分的积分曲线族')legend('不定积分的积分曲线族')然后在MA TLAB工作窗口中输入文件名：>> budijifen1运行后屏幕显示计算结果(略)和图形(见图1-9)。

再如，将下面的一个生成矩阵的程序保存为名为juzhen.m的文本M文件：for i=1:kfor j=1:nb(i,j)=7/(2*i+3*j-6);endenda=rats(b)然后在MA TLAB工作窗口中输入：>> k=3;n=4; juzhen,b图1-9 名为budijifen1.m的文本M文件的图形运行后屏幕显示运行结果如下：a =-7 7/2 7/5 7/87 7/4 1 7/107/3 7/6 7/9 7/12b =-7.0000e+000 3.5000e+000 1.4000e+000 8.7500e-0017.0000e+000 1.7500e+000 1.0000e+000 7.0000e-0012.3333e+000 1.1667e+000 7.7778e-001 5.8333e-001（二）函数M文件函数M文件是另一类M文件，我们可以根据需要建立自己的函数文件，它们能够像库函数一样方便地调用，从而极大地扩展MA TLAB的能力。

第二讲MATLAB的数值分析2-1矩阵运算与数组运算矩阵运算和数组运算是MATLAB数值运算的两大类型，矩阵运算是按矩阵的运算规则进行的，而数组运算则是按数组元素逐一进行的。

因此，在进行某些运算（如乘、除）时，矩阵运算和数组运算有着较大的差别。

在MATLAB中，可以对矩阵进行数组运算，这时是把矩阵视为数组，运算按数组的运算规则。

也可以对数组进行矩阵运算，这时是把数组视为矩阵，运算按矩阵的运算规则进行。

1、矩阵加减与数组加减矩阵加减与数组加减运算效果一致，运算符也相同，可分为两种情况：（1）若参与运算的两矩阵（数组）的维数相同，则加减运算的结果是将两矩阵的对应元素进行加减，如A=[1 1 1;2 2 2;3 3 3];B=A;A+Bans=2 2 24 4 46 6 6（2）若参与运算的两矩阵之一为标量（1*1的矩阵），则加减运算的结果是将矩阵（数组）的每一元素与该标量逐一相加减，如A=[1 1 1;2 2 2;3 3 3];A+2ans=3 3 34 4 45 5 52、矩阵乘与数组乘（1）矩阵乘矩阵乘与数组乘有着较大差别，运算结果也完全不同。

矩阵乘的运算符为“*”，运算是按矩阵的乘法规则进行，即参与乘运算的两矩阵的内维必须相同。

设A、B为参与乘运算的=A m×k B k×n。

因此，参与运两矩阵，C为A和B的矩阵乘的结果，则它们必须满足关系C m×n算的两矩阵的顺序不能任意调换，因为A*B和B*A计算结果很可能是完全不一样的。

如：A=[1 1 1;2 2 2;3 3 3];B=A;A*Bans=6 6 612 12 1218 18 18F=ones(1,3);G=ones(3,1);F*Gans3G*Fans=1 1 11 1 11 1 1（2）数组乘数组乘的运算符为“.*”，运算符中的点号不能遗漏，也不能随意加空格符。

参加数组乘运算的两数组的大小必须相等（即同维数组）。

3.8 画多重线的方法我们用迭代法求解非线性方程组的解时，需要寻找解的初始值，这就需要在同一个坐标系中画出每个方程对应的图形，找这些图形的交点（线）。

在同一个坐标平面中画出许多条曲线的常用方法有三类。

第一类方法是利用循环语句for作多条曲线；第二类方法是用hold on和hold off函数在原有的图形上增加曲线；第三类方法是在plot函数中，填写几条曲线。

我们可以用这些方法在同一个直角坐标系或极坐标系中，画出多条隐函数的图形，显函数的图形，参数函数的图形或极坐标的函数的图形等等。

下面分别给以介绍。

3.8.1 利用循环语句for作多条曲线循环语句for的一边办形式为for <循环参数>=<初值>：<步长>：<终值><语句>end步长为1时可以省略。

对于每一个参数，语句都重复执行。

当作多重循环时，循环语句for可以嵌套使用。

用此方法作概率与数理统计中的散点图和拟合曲线的效果特别好。

下面的例题展示了如何用循环语句for作多条曲线和点。

[例19] 如果我们要画出图3-20中“女人的项链”的图形，只需在MATLAB工作窗口中输入下面的循环语句for的程序：>> t = 0:.02:2*pi;y = zeros(10,length(t));x = zeros(size(t));for k=1:2:19x = x + cos(2.*k*t)/k;y((k+1)/2,:) = x;endplot(y(1:2:9,:)')title('女人的项链')运行后可绘制出图 3-20。

图 3-20 “女人的项链”的图形3.8.2 利用hold on 和hold off 画多重曲线的三种方法 在同一个坐标系中画多条曲线的另一种方法是利用hold on 和hold off 函数在已经画好的图形上再增加曲线。

如果设置hold on ，则MA TLAB 软件将把新的plot 或者ezplot 函数产生的图形画在原来的图形上。

4.5化简和代换符号表达式地初等运算是指符号表达式地变换和化简、符号地代换、复合函数地运算和反函数地运算、加、减、乘、除运算、乘方和开方运算.有关加、减、乘、除运算、乘方和开方运算在第一章实验地内容中我们已经作了介绍.下面主要介绍符号表达式地变换和化简、符号地代换、复合函数和反函数地运算.在MATLAB中，这些运算地常用函数如表4-5所示.[例1] 设函数652-=x y 和y z 3=，试求z 关于x 地复合函数.解 输入>> syms x yz=sqrt(3*y);y =5*x^2-6;z=compose(z,y)运行后屏幕显示为z =3^(1/2)*(5*x^2-6)^(1/2)[例2] 分别求函数=1y e x -和t y sin 2=地反函数.解 输入>> syms x t y1 y2y1 =exp(-x);y2=sin(t);g1=finverse(y1)g2=finverse(y2,t)运行后屏幕显示为g1 =-log(x)g2 =asin(t)[例3] 求函数)0(5≠++=ac dcx b ax y 地反函数. 解 输入>> syms x a b c dy=((a*x+b)/(c*x+d))^(1/5)';g=finverse(y)运行后屏幕显示为g =-(b-conj(x)^5*d)/(a-conj(x)^5*c)为了用符号x 代替表达式g 中地符号conj(x),再输入：>> g=subs(-(b-conj(x)^5*d)/(a-conj(x)^5*c),conj(x),x)运行后屏幕显示为g =(-b+x^5*d)/(a-x^5*c)[例4] 在MATLAB 工作窗口输入下面程序，运行后，观察其结果，说明所使用MATLAB 函数collect 、expand 、horner 、factor 和simplify 地意义和用法.解 在MATLAB 工作窗口输入下面程序：>> syms x y t af1=collect(x^3+2*x^2-5*x^2+4*x-3*x+12-3),f2=collect((1+x)*t+t*x),f3=expand((x-1)*(x-2)*(x-3)),f4=expand(cos(x+y)),f5=expand(cos(3*acos(x))),f6=horner(x^3-6*x^2+11*x-6),f7=horner(1.1+2.2*x+3.3*x^2),f8=factor(x^3-6*x^2+11*x-6),f9=simplify((1-x^2)/(1-x)),f10=simplify(sin(x)^2+cos(x)^2),f11=simplify((1/a^3+6/a^2+12/a+8)^(1/3))运行后屏幕显示如下：f1 =x^3-3*x^2+x+9f2 =2*t*x+tf3 =x^3-6*x^2+11*x-6f4 =cos(x)*cos(y)-sin(x)*sin(y)f5 =4*x^3-3*xf6 =-6+(11+(-6+x)*x)*xf7 =11/10+(11/5+33/10*x)*xf8 =(x-1)*(x-2)*(x-3)f9 =x+1f10 =1f11 =((2*a+1)^3/a^3)^(1/3)请读者观察其结果，说明所使用MA TLAB函数collect等地意义和用法.[例5] 用findsym来确认例4 中地符号表达式f11中地符号.解输入>> findsym(f11)运行后屏幕显示如下：ans =a[例6]工具箱为我们提供了一个强有力地函数simple,它综合运用上面地函数进行化简，并找出长度最短地表达式.（1）请问simple命令常用地调用格式有几种？（2）对于simple命令这些调用格式，选择下面地函数在计算机上演示，并说明它们地功能.（i） f(x)=sin(x)^2+cos(x)^2;（ii） g(x)=(1/a^3+6/a^2+12/a+8)^(1/3).解（1）simple命令常用调用格式有三种，即f=simple(S)，simple(S)和[f,how]=simple(S)（2）（i）f=simple(S)地功能是对表达式S 进行化简，输出长度最短地表达式 f.例如，输入>> syms a xf=simple(sin(x)^2+cos(x)^2)g=simple((1/a^3+6/a^2+12/a+8)^(1/3))运行后屏幕显示：f =1g =(2*a+1)/a（ii）simple(S)地功能是对表达式S 进行化简，输出用各种函数化简地结果，及长度最短地表达式.例如，输入>> simple(sin(x)^2+cos(x)^2)运行后屏幕显示：simplify:1radsimp:sin(x)^2+cos(x)^2combine(trig):1factor:sin(x)^2+cos(x)^2expand:sin(x)^2+cos(x)^2combine:1convert(exp):-1/4*(exp(i*x)-1/exp(i*x))^2+(1/2*exp(i*x)+1/2/exp(i*x ))^2convert(sincos):sin(x)^2+cos(x)^2convert(tan):4*tan(1/2*x)^2/(1+tan(1/2*x)^2)^2+(1-tan(1/2*x)^2)^2/(1+tan(1/ 2*x)^2)^2collect(x):sin(x)^2+cos(x)^2ans =1请读者在计算机上演示g(x).（iii）[f,how]=simple(S)地功能是对表达式S进行化简，输出长度最短地表达式f及f是哪一个函数作用地结果how.例如，输入>> [f,how]=simple((1/a^3+6/a^2+12/a+8)^(1/3)),[g,how]=simple(sin(x)^2+cos(x)^2)运行后屏幕显示：f =(2*a+1)/ahow =radsimpg =1how =combine[例7]工具箱中提供了两种代换函数subs和subexpr.请分别写出它们地一种调用格式，说明它们地功能，并选择下面地函数在计算机上演示.（1）用5代替表达式a+b中地a；（2）分别用alpha和5代替表达式中地a,b；（3）首先用命令t = solve('a*x^3+b*x^2+c*x+d = 0')求方程地根t，然后将求解地结果中地公共部分用s代换.解（1）代换函数subs地一种调用格式为subs(S,old,new)它地功能是用符号new代替表达式S中地符号old.例如，输入>> syms a b,subs(a+b,a,5)f=subs(cos(a)+sin(b),[a,b],[sym('alpha'),5])运行后屏幕显示：ans =5+bf =cos(alpha)+sin(5)（2）代换函数subs地一种调用格式为[Y,SIGMA] = subexpr (X,SIGMA)或[Y,SIGMA] = subexpr (X,'SIGMA')它地功能是将表达式X中地公共部分用SIGMA表示.例如，输入>> t = solve('a*x^3+b*x^2+c*x+d = 0'),[r,s] = subexpr(t,'s')运行后屏幕显示：t =[1/6/a*(36*c*b*a-108*d*a^2-8*b^3+12*3^(1/2)*(4*c^3*a-c ^2*b^2-18*c*b*a*d+27*d^2*a^2+4*d*b^3)^(1/2)*a)^(1/3)-2/3*(3*c* a-b^2)/a/(36*c*b*a-108*d*a^2-8*b^3+12*3^(1/2)*(4*c^3*a-c^2*b^2 -18*c*b*a*d+27*d^2*a^2+4*d*b^3)^(1/2)*a)^(1/3)-1/3*b/a] [ -1/12/a*(36*c*b*a-108*d*a^2-8*b^3+12*3^(1/2)*(4*c^3* a-c^2*b^2-18*c*b*a*d+27*d^2*a^2+4*d*b^3)^(1/2)*a)^(1/3)+1/3*(3 *c*a-b^2)/a/(36*c*b*a-108*d*a^2-8*b^3+12*3^(1/2)*(4*c^3*a-c^2*b^2-18*c*b*a*d+27*d^2*a^2+4*d*b^3)^(1/2)*a)^(1/3)-1/3*b/a+1/2*i*3^(1/2)*(1/6/a*(36*c*b*a-108*d*a^2-8*b^3+12*3^(1/2)*(4*c^3*a-c^2*b^2-18*c*b*a*d+27*d^2*a^2+4*d*b^3)^(1/2)*a)^(1/3)+2/3*(3*c*a-b^2)/a/(36*c*b*a-108*d*a^2-8*b^3+12*3^(1/2)*(4*c^3*a-c^2*b^2-18*c*b*a*d+27*d^2*a^2+4*d*b^3)^(1/2)*a)^(1/3))][ -1/12/a*(36*c*b*a-108*d*a^2-8*b^3+12*3^(1/2)*(4*c^3*a-c^2*b^2-18*c*b*a*d+27*d^2*a^2+4*d*b^3)^(1/2)*a)^(1/3)+1/3*(3*c*a-b^2)/a/(36*c*b*a-108*d*a^2-8*b^3+12*3^(1/2)*(4*c^3*a-c^2*b^2-18*c*b*a*d+27*d^2*a^2+4*d*b^3)^(1/2)*a)^(1/3)-1/3*b/a-1/2*i*3^(1/2)*(1/6/a*(36*c*b*a-108*d*a^2-8*b^3+12*3^(1/2)*(4*c^3*a-c^2*b^2-18*c*b*a*d+27*d^2*a^2+4*d*b^3)^(1/2)*a)^(1/3)+2/3*(3*c*a-b^2)/a/(36*c*b*a-108*d*a^2-8*b^3+12*3^(1/2)*(4*c^3*a-c^2*b^2-18*c*b*a*d+27*d^2*a^2+4*d*b^3)^(1/2)*a)^(1/3))]r =[1/6/a*s^(1/3)-2/3*(3*c*a-b^2)/a/s^(1/3)-1/3*b/a][ -1/12/a*s^(1/3)+1/3*(3*c*a-b^2)/a/s^(1/3)-1/3*b/a+1/2*i*3^(1/2)*(1/6/a*s^(1/3)+2/3*(3*c*a-b^2)/a/s^(1/3))][ -1/12/a*s^(1/3)+1/3*(3*c*a-b^2)/a/s^(1/3)-1/3*b/a-1/2*i*3^(1/2)*(1/6/a*s^(1/3)+2/3*(3*c*a-b^2)/a/s^(1/3))]s =36*c*b*a-108*d*a^2-8*b^3+12*3^(1/2)*(4*c^3*a-c^2*b^2-18*c*b*a*d+27*d^2*a^2+4*d*b^3)^(1/2)*a版权申明本文部分内容，包括文字、图片、以及设计等在网上搜集整理.版权为个人所有This article includes some parts, including text, pictures, and design. Copyright is personal ownership.M2ub6。

学习使用MATLAB进行数值计算和数据分析---第一章：MATLAB的基本介绍MATLAB是一种强大的数值计算和数据分析软件，广泛应用于科学研究、工程设计等领域。

它的主要特点是简洁直观的用户界面和丰富的数学函数库。

在本章中，我们将介绍MATLAB的基本特性和使用方法。

1.1 MATLAB的历史与发展MATLAB是由MathWorks公司于1984年首次推出的。

起初，它作为一个用于矩阵计算的工具被广泛使用。

随着时间的推移，MATLAB逐渐拓展了功能，加入了许多其他数学和工程计算的功能，如符号计算、数据统计和可视化。

如今，MATLAB已经成为一种非常受欢迎的工具。

1.2 MATLAB的安装和环境设置要开始使用MATLAB，首先需要从MathWorks官网下载并安装MATLAB软件。

安装完成后，打开MATLAB并设置工作目录和默认工作文件夹。

工作目录是指存储MATLAB代码和数据文件的文件夹，而默认工作文件夹是指MATLAB打开时默认选择的文件夹。

1.3 MATLAB的基本语法和命令MATLAB的基本语法和命令非常简单易懂。

它采用类似于其他编程语言的命令行交互方式，用户可以直接在命令行输入MATLAB语句并执行。

例如，可以输入"2+2"并按回车键得到结果4。

此外，MATLAB还具有许多内置的数学函数和运算符，可以进行各种数值计算和数据分析。

1.4 MATLAB脚本和函数在MATLAB中，可以使用脚本和函数来组织和执行一系列MATLAB命令。

脚本是一系列命令的集合，可以一次性运行。

函数是一段可以重复使用的代码，可以接受输入参数并返回输出结果。

通过编写脚本和函数，可以提高MATLAB代码的可重复性和可维护性。

第二章：数值计算MATLAB作为一种数值计算工具，提供了丰富的数学函数和算法，可以用于解决各种数值计算问题。

在本章中，我们将介绍MATLAB在数值计算方面的一些常用功能和技巧。

2.1 数值计算方法MATLAB中包含了许多数值计算方法，如数值积分、数值微分、线性代数求解等。