初二数学-图形-专题练习题

初二数学图形练习题题一：周长计算有一个矩形，它的长是8cm，宽是5cm。

请你计算它的周长。

解答：矩形的周长可以通过公式计算：周长 = 2 * (长 + 宽)。

将给定的长和宽代入公式，可以得到周长=2*(8+5)=2*13=26cm。

所以，这个矩形的周长是26cm。

题二：面积计算有一个长方形花坛，它的长是6m，宽是4m。

请你计算它的面积。

解答：长方形的面积可以通过公式计算：面积 = 长 * 宽。

将给定的长和宽代入公式，可以得到面积=6*4=24平方米。

所以，这个长方形花坛的面积是24平方米。

题三：三角形分类将以下三角形分为直角三角形、钝角三角形和锐角三角形：A. 边长分别为3cm、4cm、5cm的三角形B. 边长分别为6cm、8cm、10cm的三角形C. 边长分别为2cm、2cm、2cm的三角形解答：直角三角形是指其中一个角度为90°的三角形；钝角三角形是指其中一个角度大于90°的三角形；锐角三角形是指其中所有角度均小于90°的三角形。

A. 根据勾股定理，可以判断边长为3cm、4cm、5cm的三角形为直角三角形，因为3²+4²=5²。

B. 同样地，边长为6cm、8cm、10cm的三角形也是直角三角形，因为6²+8²=10²。

C. 边长为2cm、2cm、2cm的三角形是等边三角形，因为三条边的长度相等，所以也是锐角三角形。

所以，根据上述分析，A和B是直角三角形，C是锐角三角形。

题四：平行四边形面积计算有一个平行四边形，其底边长为6cm，高为4cm。

请你计算它的面积。

解答：平行四边形的面积可以通过底边长和高进行计算：面积 = 底边长 * 高。

将给定的底边长和高代入公式，可以得到面积=6*4=24平方厘米。

所以，这个平行四边形的面积是24平方厘米。

题五：正方形的特征正方形是一种特殊的矩形，它的特征是四条边长度相等且四个角度均为90°。

初二数学几何图形练习题1. 设△ABC 为等腰直角三角形，其中∠BAC = 90°，∠ABC =∠ACB。

已知 AB = 5cm。

(a) 求 BC 的长度。

(b) 求△ABC 的面积。

2. 在△ABC 中，AD 是边 BC 的中线，且 AB = 3cm，BC = 4cm。

连接 BD，BD 的延长线交 AC 于 E 点。

(a) 求 BD 和 DE 的长度。

(b) 求△ADE 的面积。

3. 在△ABC 中，D、E 两点分别在边 AB、AC 上。

若DE ║ BC，则证明：AD/BD + AE/CE = 1。

4. 已知△ABC 中，∠BAC = 40°，∠ABC = 70°，点 D 在边 BC 上，且满足 BD = AC。

(a) 求∠BDC 的度数。

(b) 求∠ADB 的度数。

5. 在△ABC 中，D、F 分别是边 AB、AC 上的两个点，连接 BF、CD。

已知 AF = 6cm，BF = 4cm，CF = 3cm，FD = 1.5cm。

(a) 求△BFD 的面积。

(b) 求△ABC 的面积。

6. △ABC 的三个内角分别为 60°、75°、45°。

(a) 将△ABC 分别绕着顶点 A，边 BC，边 AC 旋转 90°，分别得到△A'B'C'、△AB'C'、△A'BC。

求△A'B'C'、△AB'C'、△A'BC 的内角。

(b) 证明△A'B'C' 是等腰三角形。

7. 在平面直角坐标系中，点 A(3, 4)、B(-1, -2)、C(-2, 6) 是顶点坐标。

连接 AB、AC，垂直平分 AC 的线段交 AB 的延长线于点 D。

求点 D 的坐标。

8. 已知△ABC 中，点 D、E 分别是边 AB、BC 上的两个点，且 DE ║ AC。

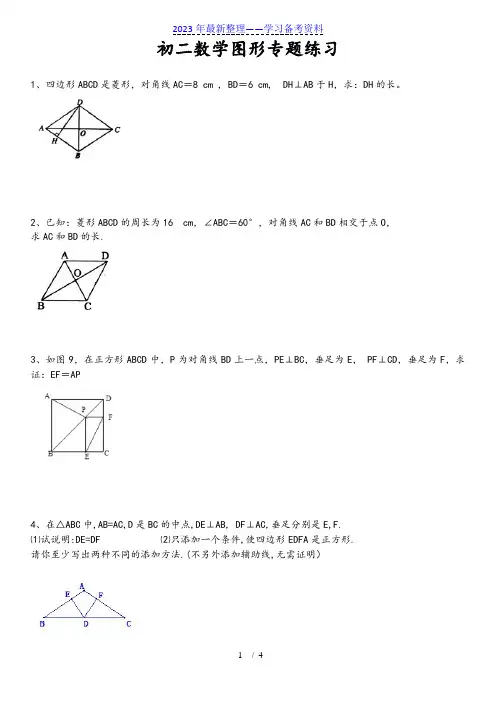
初二数学图形专题练习1、四边形ABCD是菱形，对角线AC＝8 cm , BD＝6 cm, DH⊥AB于H，求：DH的长。

2、已知：菱形ABCD的周长为16 cm，∠ABC＝60°，对角线AC和BD相交于点O，求AC和BD的长.3、如图9，在正方形ABCD中，P为对角线BD上一点，PE⊥BC，垂足为E， PF⊥CD，垂足为F，求证：EF＝AP4、在△ABC中,AB=AC,D是BC的中点,DE⊥AB, DF⊥AC,垂足分别是E,F.⑴试说明:DE=DF ⑵只添加一个条件,使四边形EDFA是正方形.请你至少写出两种不同的添加方法.(不另外添加辅助线,无需证明）5、如图11，ABCD中，AE平分∠BAD交BC于E，EF∥AB交AD于F，试问：四边形ABEF是什么图形吗？请说明理由.6 、△ABC中，∠ACB=900，点D、E分别为AC、AB的中点，点F在BC延长线上，且∠CDF=∠A，求证：四边形DECF是平行四边形；7、平行四边形ABCD，E是CD的中点，△ABE是等边三角形，求证：四边形ABCD是矩形。

8、在平行四边形ABCD中，对角线AC、BD相交于O，EF过点O，且AF⊥BC，求证：四边形AFCE是矩形。

9、平行四边形ABCD中，对角线AC、BD相交于点Ｏ，点Ｐ是四边形外一点，且PA⊥PC，PB⊥PD，垂足为Ｐ。

求证：四边形ABCD为矩形10、已知：如图，平行四边形ABCD的四个内角的平分线分别相交于E、F、G、H，求证：四边形 EFGH 为矩形．11、如图，在已知平行四边形ABCD中，AE平分∠BAD，与BC相交于点E，EF//AB，与AD相交于点F.求证:四边形ABEF是菱形.12、如图，在△ABC中，∠BAC=90°，AD⊥BC于D，CE平分∠ACB，交AD于G，交AB于E，EF⊥BC 于F，四边形AEFG是菱形吗?本文由作者精心整理，校对难免有瑕疵之处，欢迎批评指正，如有需要，请关注下载。

初二数学图形找规律练习题（正文内容）1. 矩形面积规律小明正在学习数学中的图形找规律。

他发现了一组矩形图形，如下所示：矩形1：长为3，宽为2，面积为6矩形2：长为5，宽为3，面积为15矩形3：长为7，宽为4，面积为28小明观察这个序列，发现每个矩形的面积都是其长乘以宽的结果。

小明找到了规律：矩形的面积等于长乘以宽。

这个规律可以用公式表示为 S = L × W，其中 S代表矩形的面积，L代表矩形的长，W代表矩形的宽。

请你根据这个规律，计算以下矩形的面积：矩形4：长为9，宽为6，面积为？矩形5：长为12，宽为8，面积为？矩形6：长为15，宽为10，面积为？2. 正方形周长规律除了矩形，小明还发现了一组正方形图形，如下所示：正方形1：边长为2，周长为8正方形2：边长为4，周长为16正方形3：边长为6，周长为24小明观察这个序列，发现每个正方形的周长都是其边长乘以4的结果。

小明找到了规律：正方形的周长等于边长乘以4。

这个规律可以用公式表示为 P = 4 × S，其中 P代表正方形的周长，S代表正方形的边长。

请你根据这个规律，计算以下正方形的周长：正方形4：边长为8，周长为？正方形5：边长为10，周长为？正方形6：边长为12，周长为？3. 三角形面积规律在继续观察图形时，小明发现了一组三角形图形，如下所示：三角形1：底边长为3，高为2，面积为3三角形2：底边长为5，高为3，面积为7.5三角形3：底边长为7，高为4，面积为14小明观察这个序列，发现每个三角形的面积都是其底边长乘以高再除以2的结果。

小明找到了规律：三角形的面积等于底边长乘以高再除以2。

这个规律可以用公式表示为 S = (B × H) / 2，其中 S代表三角形的面积，B 代表三角形的底边长，H代表三角形的高。

请你根据这个规律，计算以下三角形的面积：三角形4：底边长为9，高为6，面积为？三角形5：底边长为12，高为8，面积为？三角形6：底边长为15，高为10，面积为？（文章结束）。

初二数学图形变换练习题1. 平移变换问题1：将△ABC中的点A向右平移5个单位和向下平移3个单位，得到△A’B’C’。

请绘制△ABC和△A’B’C’两个图形，并计算并比较它们的坐标变化。

问题2：图形PQRST是一个正五边形，将它向左平移2个单位和向上平移4个单位，得到图形P'Q'R'S'T'。

请绘制图形PQRST和P'Q'R'S'T'，并计算并比较它们的坐标变化。

2. 旋转变换问题1：将△ABC以点A为中心逆时针旋转90度，得到△A'B'C'。

请绘制△ABC和△A'B'C'两个图形，并计算并比较它们的坐标变化。

问题2：图形PQRST是一个正方形，以点P为中心顺时针旋转45度，得到图形P'Q'R'S'T'。

请绘制图形PQRST和P'Q'R'S'T'，并计算并比较它们的坐标变化。

3. 对称变换问题1：将图形ABCDE以线段AB为对称轴进行对称变换，得到图形A'B'C'D'E'。

请绘制图形ABCDE和A'B'C'D'E'，并计算并比较它们的坐标变化。

问题2：图形PQRST是一个长方形，以线段PT为对称轴进行对称变换，得到图形P'Q'R'S'T'。

请绘制图形PQRST和P'Q'R'S'T'，并计算并比较它们的坐标变化。

4. 缩放变换问题1：将△ABC以点A为中心放大2倍，得到△A'B'C'。

请绘制△ABC和△A'B'C'两个图形，并计算并比较它们的坐标变化。

问题2：图形PQRST是一个矩形，以点Q为中心缩小一半，得到图形P'Q'R'S'T'。

初二数学几何图形练习题及答案2023一、选择题1. 下图中的几何图形是（）。

A. 直线B. 小数C. 三角形D. 方程式2. 角度为90度的图形是（）。

A. 线段B. 正方形C. 圆形D. 点3. 下列图形中，能构成三角形的是（）。

A. 正方形B. 椭圆形C. 圆形D. 矩形4. 下列图形中，边数最多的是（）。

A. 三角形B. 方形C. 正方形D. 圆形5. 以下哪个图形是圆（）。

A. 三角形B. 正方形C. (x-2)^2 + (y+3)^2 = 16D. 矩形二、填空题1. 正方形的周长是20cm，它的边长是（）cm。

2. 三角形有（）条边。

3. 圆的圆心到任意点的距离相等，这个性质叫做（）。

4. 下图中两个角度之和等于（）度。

（请插入一张图）5. 正方形的对角线长度是20cm，它的边长是（）cm。

三、解答题1. 请根据下图，计算三角形的面积。

（请插入一张图）解：三角形的底为8cm，高为5cm。

面积 = 1/2 ×底 ×高= 1/2 × 8cm × 5cm= 20cm²2. 请根据下图，判断哪两个角度之和为90度。

（请插入一张图）解：根据图可知，∠ABC和∠DBC的两个角度之和为90度。

四、应用题1. 小明的房间是一个长方形，长为6m，宽为4m。

他想贴一块地毯在房间的中央，地毯的形状是正方形，边长为2m。

请问他需要购买多少平方米的地毯？解：房间的面积 = 长 ×宽= 6m × 4m= 24m²地毯的面积 = 边长 ×边长= 2m × 2m= 4m²需要购买的地毯面积 = 房间的面积 - 地毯的面积= 24m² - 4m²= 20m²小明需要购买20平方米的地毯。

2. 小明家的花园是圆形的，半径为5m。

他要在花园的周边围上一圈篱笆，请问他需要多长的篱笆？（π取3.14）解：圆的周长= 2π × 半径= 2 × 3.14 × 5m= 31.4m小明需要使用31.4m长的篱笆。

初二数学图形面积练习题1. 题目：矩形ABC'D'的周长是44cm，对角线AC的长度是15cm。

求该矩形的面积。

解析：根据矩形的性质，矩形的对角线互相垂直且相等。

设矩形的长为a，宽为b。

根据题目可知，2a + 2b = 44cm，AC = 15cm。

根据勾股定理，AC的平方等于矩形两边长度的平方和。

即AC² = a²+ b²。

解方程组：2a + 2b = 44 （1）a² + b² = 15²（2）将（2）式中的b用a表示，然后代入（1）式，得到：2a + 2(15² - a²) = 44化简：2a + 30² - 2a² = 44900 - 2a² = 442a² = 856a² = 428a ≈ 20.69代入（1）式，可以求出b：2(20.69) + 2b = 44b ≈ 1.81因此，该矩形的长约为20.69cm，宽约为1.81cm。

矩形的面积为长乘以宽，约为20.69cm × 1.81cm ≈ 37.41cm²。

所以该矩形的面积约为37.41cm²。

2. 题目：一个长方形花坛的长度是12m，宽度是6m，中间有一条宽度为1m的小道。

计算花坛的面积。

解析：首先计算原始矩形的面积，即12m × 6m = 72m²。

然后计算小道的面积，小道的长度与原始矩形的宽度相等，为6m。

小道的宽度为1m。

所以小道的面积为6m × 1m = 6m²。

将小道的面积从原始矩形的面积中减去，即得到花坛的面积。

花坛的面积 = 原始矩形的面积 - 小道的面积花坛的面积 = 72m² - 6m² = 66m²。

所以花坛的面积为66m²。

3. 题目：一个菱形的对角线长度分别为8cm、10cm，求该菱形的面积。

初二数学几何图形变换练习题在初中数学学习中，几何图形变换是一个重要的内容。

通过对图形进行平移、旋转、反射和放缩等操作，可以帮助我们加深对几何图形性质的理解。

下面将给出一些初二数学几何图形变换的练习题，希望能够帮助同学们巩固与拓展相关知识。

题目一：平移1. ABCD为一个平行四边形，EF是平行四边形的一条对角线。

（1）将平行四边形ABCD沿向量→→→→e向右平移3个单位得到平行四边形A1B1C1D1，连接DD1，证明A1D1∥EF。

（2）将平行四边形ABCD沿向量→→−→−→a向左平移4个单位得到平行四边形A2B2C2D2。

若A1A2的向量表示为→→−→−→b，则求向量→→−→−→b。

题目二：旋转2. 将正方形ABCD顺时针旋转90°得到正方形A1B1C1D1，连接CC1并延长，证明A1C1⊥CC1。

3. 将正方形ABCD顺时针旋转45°得到正方形A2B2C2D2，连接A2C2，若AC的长度为a，则求A2C2的长度。

题目三：反射4. 已知顶点是A(1,-3)的三角形ABC关于x轴反射得到三角形A1B1C1，连接AA1并延长，若直线AA1与x轴交于点D，求点D的坐标。

5. 直线y=x与直线y=2x关于直线y=-x反射，分别得到直线L1和L2。

若L1与L2的交点为P，则求P的坐标。

题目四：放缩6. 图中三角形ABC经过放缩得到三角形A1B1C1，若放缩比例为k，求A1B1 : BC的比值。

解答：题目一：平移1.（1）设向量→→→→AD=a，向量→→→→AC=b，由平移的性质知AA1=a+3，DD1=b+3。

根据平行四边形的性质，有AD=BC，AC=BD。

故A1D1∥EF得证。

（2）设向量→→−→−→a=〈x，y〉，则向量→→−→−→b=〈x-4，y〉。

根据平行四边形的性质，有AB=A1B1，AD=A1D1。

故向量→→−→−→a=AB-AD=〈x，y〉=A1B1-A1D1=向量→→−→−→b=〈-√2，0〉。

初二数学角的图形练习题题目一：平行线与转角在平面直角坐标系中，已知直线l1:y=2x+3，直线l2:y=2x-1。

1. 求l1与l2的交点坐标；2. 画出l1和l2，并标出交点。

解答：1. 求l1与l2的交点坐标：为了求出两条直线的交点，我们可以将它们的方程联立起来，解得交点的坐标。

将直线l1和l2的方程联立，得到：2x + 3 = 2x - 1消去x，得到：0 = -4由于方程无解，说明直线l1与l2没有交点。

2. 画出l1和l2，并标出交点：我们可以画出直线l1和l2，通过观察它们的斜率和截距来确定它们的大致位置，并标出交点。

直线l1的斜率为2，截距为3，我们可以选择x=0和x=1两个点，然后计算出对应的y值，得到点(0, 3)和(1, 5)，然后连接这两个点画出直线l1。

直线l2的斜率也为2，截距为-1，同样选择x=0和x=1两个点，计算出对应的y值，得到点(0, -1)和(1, 1)，然后连接这两个点画出直线l2。

由于题目1中已经说明l1和l2没有交点，所以在图中不会显示交点。

题目二：角的角平分线在平面直角坐标系中，已知直线l:y=x+2，点A(2, 3)和点B(4, 1)。

1. 求点A和点B连线的斜率；2. 求点A和点B连线所在直线的方程；3. 过点A和点B的连线作一条直线l1，使得直线l1和l平行，并且交点在直线l上。

求直线l1的方程。

解答：1. 求点A和点B连线的斜率：根据两点间的斜率公式，我们可以计算出点A和点B连线的斜率。

斜率k = (y2-y1)/(x2-x1) = (1-3)/(4-2) = -12. 求点A和点B连线所在直线的方程：已知点A(2, 3)和斜率k=-1，我们可以使用点斜式的方程形式来表示直线的方程。

直线的点斜式方程：y - y1 = k * (x - x1)代入A点的坐标和斜率值，得到：y - 3 = -1 * (x - 2)化简得到直线的方程：y = -x + 53. 求直线l1的方程：过点A和点B的连线的斜率已经求出为-1（与直线l平行），我们可以使用点斜式的方程形式来表示直线l1的方程。

初二数学图形的平移和旋转练习题题目一：平移图形
给定一个图形，如下所示：
（在这里插入图形示例）
1. 将该图形向右平移4个单位，向上平移3个单位。

请计算平移后的新坐标，并画出平移后的图形。

2. 将平移后的图形再向左平移2个单位，向下平移1个单位。

请计算最终平移后的新坐标，并画出图形。

题目二：旋转图形
给定一个图形，如下所示：
（在这里插入图形示例）
1. 将该图形以原点为中心，逆时针旋转90度。

请计算旋转后的新坐标，并画出旋转后的图形。

2. 将旋转后的图形再顺时针旋转180度。

请计算最终旋转后的新坐标，并画出图形。

题目三：综合练习
给定一个复杂图形，如下所示：
（在这里插入图形示例）
1. 将该图形向右平移5个单位，向上平移2个单位。

请计算平移后的新坐标，并画出平移后的图形。

2. 将平移后的图形以中心为轴顺时针旋转120度。

请计算旋转后的新坐标，并画出旋转后的图形。

3. 将旋转后的图形再向左平移3个单位，向下平移1个单位。

请计算最终平移后的新坐标，并画出图形。

通过以上练习题的实践操作，初二的学生们可以更好地理解和掌握数学图形的平移和旋转。

这些技能在解题过程中能够提高他们的几何思维和空间想象力，同时也为日常生活中的空间定位和方向感提供了基础。

希望同学们能够认真完成这些练习，不断巩固和提升自己的数学能力。

（文章正文结束）。