下载文档原格式
XX八年级数学复习资料：尺规作图◆识记巩固尺规作图的定义：_____________2基本作图包括：_______，_______，________，________，_______3三角形三边的垂直平分线的交点叫三角形的外心，三角形三内角平分线的交点叫三角形的内心，外心到三角形的_______的距离相等，内心到三角形_______的距离相等识记巩固参考答案:限定只能使用圆规和没有刻度的直尺作图2作线段作角作线段的垂直平分线过一点作已知直线的垂线作角平分线3顶点三边◆考点聚焦掌握基本作图，尺规作图的要求与步骤2利用基本作图工具画三角形、四边形、圆以及简单几何体的三视图，对简单的作图能叙述作法3运用基本作图、结合相关的数学知识等进行简单的图案设计4运用基本作图解决实际问题◆备考兵法熟练掌握基本作图2在画几何体的三视图时，要注意其要求，即“长对正”“高平齐”“宽相等”3认真分析题意，善于把实际问题转化为基本作图用直尺和圆规作一个角等于已知角，如图，能得出∠A′′B′=∠AB的依据是（）A．（SAS）B．（SSS）．（ASA）D．（AAS）如图，下面是利用尺规作∠AB的角平分线的作法，在用尺规作角平分线过程中，用到的三角形全等的判定方法是（）作法：①以为圆心，适当长为半径画弧，分别交A，B于点D，E；②分别以D，E为圆心，大于DE的长为半径画弧，两弧在∠AB内交于一点；③画射线，射线就是∠AB的角平分线．A．ASAB．SAS．SSSD．AAS如图，已知在Rt△AB中，∠AB=90°，点D是B边的中点，分别以B、为圆心，大于线段B长度一半的长为半径画弧，两弧在直线B上方的交点为P，直线PD交A于点E，连接BE，则下列结论：①ED⊥B；②∠A=∠EBA；③EB平分∠AED；④ED=AB中，一定正确的是（）A．①②③B．①②④．①③④D．②③④如图，分别以线段A的两个端点A，为圆心，大于A的长为半径画弧，两弧相交于B，D两点，连接BD，AB，B，D，DA，以下结论：①BD垂直平分A；②A平分∠BAD；③A=BD；④四边形ABD是中心对称图形．其中正确的有（）A．①②③B．①③④．①②④D．②③④观察图中尺规作图痕迹，下列结论错误的是（）A．PQ为∠APB的平分线B．PA=PB．点A、B到PQ的距离不相等D．∠APQ=∠BPQ。
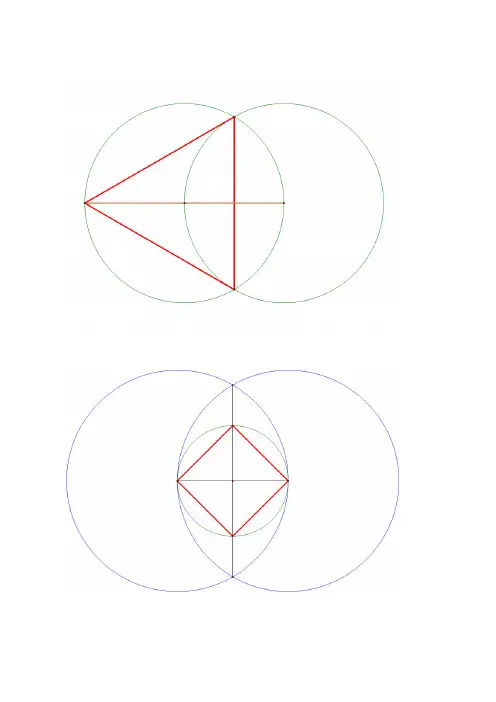
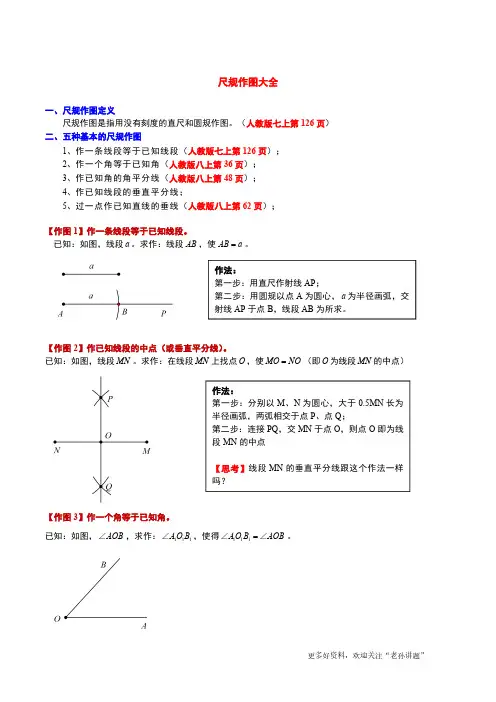
1r===A B C AB BC CA A B C C AB【例1】 A B m n P【分析】 P AB P【解析】 OD OEAB FG OD OE FG 1C 2C【例2】 A (40)O 3y x =+P AOP ∆P【解析】 P P 3y x =+AOP ∆P OA OP =O OA 1P 2P OA AP =A OA PO PA =OA 3P P【例3】 O ⊙'O ⊙R 'R r O ⊙'O ⊙rr【分析】 M ⊙r O ⊙'O ⊙M M O R r +'O 'R r +O ⊙'O ⊙b 2r b <2r b =2r b >【解析】 O ⊙'O ⊙b 2r b >OA R r =+''O B R r =+O 'O R r +'R r +12,M M1OM 2OM R O ⊙D C12M M ，r12,M M ⊙⊙O ⊙'O ⊙R 'R r ()rR >O ⊙'O ⊙【例4】【分析】11【解析】【例5】 ABC ∆【分析】 ABC ∆a h x 212x ah =x 12a h【解析】 ABC ∆a hDEFG ABC DEFG S S ∆=正方形ha D CB AN M12MD a =MD N DN h =MN O O OM O ⊙D DE MN ⊥O ⊙EDE DEFGDEFG【例6】 l M M r O ⊙aal【分析】 M O d O d l【解析】 Rt OAB ∆90A ∠=︒OA r =AB a =O OBl 1M 2M1M 2Ml M Ml M M r O ⊙a【例7】 a b c a b c ∥∥ABC ∆A B C a b cc b aD'DC B Acb a【分析】 ABC ∆A B C a b c AD b ⊥D ABD ∆A 60︒'ACD ∆'D C 60BAC ∠=︒B【解析】a A A ADb ⊥DAD 'ADD'D ''D C AD ⊥c CA AC bB B 'D ACAB AC BC ABC ∆ABC ∆【例8】 P AOB ∠OMPCD ∆90P ∠=︒PC PD =C OA D OBOD'O【解析】 P PE OB ⊥EP l OB ∥l M PM PE ='PM PE =M 'M MC l ⊥'M C l ⊥OA C 'CPC 'PC P PD PC ⊥''PD PC ⊥OB D 'D,PD CD ',''PD C DPCD ∆''PC D ∆【例9】 ABC ∆DEFG D E BC F AC G ABC B AG'F'E'D'GF E D CB A 【分析】 F AC DEFG ''''DEFG ''''D E F G DEFG【解析】AB 'G 'G ''G D BC ⊥'D''G D ''''D E F G 'E 'BD'BF AC FF ''FG F G ∥AB G ''FE F E ∥BC EG ''GD G D ∥BC DDEFG【例10】 ABC ∆BC P l ABC ∆【分析】 AM ABC ∆AM PQ ABC ∆AMC ∆AMP ∆ANP ∆NM AP ∥AMP ∆AMP ∆PN ABC ∆【解析】BC M ,AM APM MN AP ∥AB NP N ll【例11】 ABCDEl l ABCDEF E DC B AM F D C BF D CBNM P CB Al【解析】 AFDE MN O BCDF 'O O 'Oll AE Q BC R RQ P AE BC ABCDE【例12】 071C AB ACBCAB AC =C ABl S 1S 2S 121S S S S =lABC △D AB 2CD ABC △C AB ED DF CE ∥ACF EF 3EF ABC △ 4E ABCD AB E EF AD ∥DC F EF ABCD ABCD ABCD【解析】 CD ABC △ABC △AB h12ADC S AD h =△12BDC S BD h =△12ABC S AB h =△ADCABC S AD S AB =△△BDCADCS BDS AD =△△D ABAD BD AB AD =ADC BDCABC ADCS S S S =△△△△CD ABC △1212S S S ==121S S S S ≠DF CE ∥DEC △FCE △CEDEC FCE S S =△△ A C B 图1 A D B 图2 C A D B 图3 C FE B E A图4EF CD G DGE FGC S S =△△ ADC FGC AFGD S S S =+△△四边形DGE AEF AFGD S S S =+=△△四边形 BDC BEFC S S =△四边形ADC BDC ABC ADC S S S S =△△△△BEFC AEF ABC AEF S S S S =四边形△△△ EF ABC △1EF G G AB DC M NMN ABCD2DF N EN F FM NE ∥AB MMN MN ABCDB E A M （答案图1）B E A M （答案图2）。
北师大版尺规作图的步骤（已知、求作、作法）资料1、将△ABC绕点B按逆时针方向旋转90°后得到△A'BC'，若BC=2，则CC'的长为（;m答案A 解析2、如图，点A在半径为3的⊙O内，OA=，P为⊙O上一点，当∠OPA取最大值时，PA的长等于（答案B 解析3、小琳过14周岁生日，父母为她预定的生日蛋糕如图所示，它的主视图应该是答案B解析考点：简单组合体的三视图．分析：细心观察图中生日蛋糕摆放的位置，根据主视图是从正面看到的图形判定则可．解：生日蛋糕可以看作是三个圆柱，从正面看，它的正视图应该是三个大小不一的矩形．从四个选项中看，只有B选项符合这个条件．故选B．4、下列图中是太阳光下形成的影子是答案A 解析5、在下列各数中： 3.1415926，，0.2，，，，，无理数的个数是A．2B．3C．4D．5 答案A解析6、如图所示，把一个正方形三次对折后沿虚线剪下，则所得的图形是（;）答案C 解析7、“五一”旅游期间，几名同学包租一辆面包车前往“响堂寺”游玩，面包车的租价为180元，出发时，又增加了2名学生，结答案解析8、一个多边形有14条对角线，那么这个多边形的边数是（）A．5B．6C．7D 答案C 解析9、下列所给的几何体中，主视图是三角形的是（）; 答案B 解析10、一件服装标价200元，若以六折销售，仍可获利20℅，则这件服装进价是A．100元B．105元C．108元D．11 答案A 解析11、下列关于单项式的说法中，正确的是答案B 解析冀教版刻画实际问题中变量之间的关系在一个晴朗的天气里，小颖在向正北方向走路时，发现自己的身影向左偏，你知道小颖当时所处的时间是（）A．上午答案A 解析12、解方程的结果是（）A．B．C．D 答案D 解析13、反比例函数y＝的图象位于 -------------------------------------- (m 答案B 解析14。
1：尺规作出正三角形2尺规作出正方形3：尺规作出正六边形4：尺规作出正十边形5：尺规作出正十六边形6:尺规作出正十七边形7：尺规作出正十五边形8：尺规作出正五边形9:单尺作出正八边形10：单尺作出正方形11：单尺作出正六边形12：单尺作出正五边形13：单规找出两点间的三等分点14：单规找出两点间的中点15:单规作出等边三角形16：单规作出正八边形17：单规作出正方形18：单规作出正六边形19：单规作出正十边形20:单规作出正十二边形21：单规作出正十六边形22：单规作出正十五边形23单规作出正五边形24：只有两个刻度的直尺作出正三角形25:只有两个刻度的直尺作出正方形初中数学尺规作图专题讲解张远波尺规作图是起源于古希腊的数学课题.只使用圆规和直尺，并且只准许使用有限次，来解决不同的平面几何作图题。
平面几何作图，限制只能用直尺、圆规.在历史上最先明确提出尺规限制的是伊诺皮迪斯.他发现以下作图法：在已知直线的已知点上作一角与已知角相等。
这件事的重要性并不在于这个角的实际作出,而是在尺规的限制下从理论上去解决这个问题.在这以前，许多作图题是不限工具的.伊诺皮迪斯以后，尺规的限制逐渐成为一种公约，最后总结在《几何原本》之中。
初等平面几何研究的对象,仅限于直线、圆以及由它们（或一部分）所组成的图形，因此作图的工具,习惯上使用没有刻度的直尺和圆规两种。
限用直尺和圆规来完成的作图方法，叫做尺规作图法。
最简单的尺规作图有如下三条:⑴经过两已知点可以画一条直线;⑵已知圆心和半径可以作一圆;⑶两已知直线；一已知直线和一已知圆；或两已知圆,如果相交，可以求出交点;以上三条，叫做作图公法.用直尺可以画出第一条公法所说的直线；用圆规可以作出第二条公法所说的圆;用直尺和圆规可以求得第三条公法所说的交点.一个作图题，不管多么复杂，如果能反复应用上述三条作图公法，经过有限的次数,作出适合条件的图形,这样的作图题就叫做尺规作图可能问题；否则,就称为尺规作图不能问题.历史上，最著名的尺规作图不能问题是：⑴三等分角问题：三等分一个任意角；⑵倍立方问题：作一个立方体，使它的体积是已知立方体的体积的两倍;⑶化圆为方问题：作一个正方形，使它的面积等于已知圆的面积。
中考尺规作图专题复习（含答案）尺规作图定义：用无刻度的直尺和圆规画图，中考中常见画的图是线段的垂线，垂直平分线，角平分线、画等长的线段，画等角。
1.直线垂线的画法：【分析】：以点C为圆心，任意长为半径画弧交直线与A，B两点，再分别以点A，B为圆心，大于12AB的长为半径画圆弧，分别交直线l两侧于点M，N，连接MN，则MN即为所求的垂线2.线段垂直平分线的画法【分析】：作法如下：分别以点A，B为圆心，大于12AB的长为半径画圆弧，分别交直线AB两侧于点C，D，连接CD，则CD即为所求的线段AB的垂直平分线.3.角平分线的画法【分析】1.选角顶点O为圆心，任意长为半径画圆，分别交角两边A，B点，再分别以A，B为圆心，大于12AB的长为半径画圆弧，交H点，连接OH，并延长，则射线OH即为所求的角平分线.4.等长的线段的画法直接用圆规量取即可。
5.等角的画法【分析】以O为圆心，任意长为半径画圆，交原角的两边为A,B两点，连接AB；画一条射线l，以上面的那个半径为半径，l的顶点K为圆心画圆，交l与L，以L为圆心，AB 为半径画圆，交以K为圆心，KL为半径的圆与M点，连接KM，则角LKM即为所求.备注：1.尺规作图时，直尺主要用作画直线，射线，圆规主要用作截取相等线段和画弧；2.求作一个三角形，其实质是依据三角形全等的基本事实或判定定理来进行的；3.当作图要满足多个要求时，应逐个满足，取公共部分.例题讲解例题1.已知线段a，求作△ABC，使AB=BC=AC=a.解：作法如下:①作线段BC=a；（先作射线BD，BD截取BC=a）.②分别以B、C为圆心，以a半径画弧，两弧交于点A；③连接AB、AC.则△ABC 要求作三角形.例2.已知线段a 和∠α，求作△ABC ，使AB=AC=a ，∠A=∠α.解：作法如下：①作∠MAN=∠α；②以点A 为圆心，a 为半径画弧，分别交射线AM ，AN 于点B ，C. ③连接B ，C.△ABC 即为所求作三角形.例3.(深圳中考)如图，已知△ABC ，AB <BC ，用尺规作图的方法在BC 上取一点P ，使得PA ＋PC ＝BC ，则下列选项中，正确的是(D )【解析】由题意知，做出AB 的垂直平分线和BC 的交点即可。
考点名称：尺规作图【学习目标】1．了解什么是尺规作图．2．学会用尺规作图法完成下列五种基本作图：(1)画一条线段等于已知线段；(2)画一个角等于已知角；(3)画线段的垂直平分线；(4)过已知点画已知直线的垂线；(5)画角平分线．3．了解五种基本作图的理由．4．学会使用精练、准确的作图语言叙述画图过程．5．学会利用基本作图画三角形等较简单的图形．6．通过画图认识图形的本质，体会图形的内在美．【基础知识精讲】1．尺规作图：①定义：限定只用直尺和圆规来完成的画图，称为尺规作图．注意：这里所指的直尺是没有刻度的直尺，由于免去了度量，因此，用尺规作图法画出的图形的精确度更高，它在工程绘图等领域应用比较广泛．②步骤：(1)根据给出的条件和求作的图形，写出已知和求作部分；(2)分析作图的方法和过程；(3)用直尺和圆规进行作图； (4)写出作法步骤，即作法。
（根据题目要求来定是否需要写出作法）2．尺规作图中的最基本、最常用的作图称为基本作图．任何尺规作图的步骤均可分解为以下五种.3．基本作图共有五种：(1)画一条线段等于已知线段．如图24-4-1，已知线段DE．求作：一条线段等于已知线段．作法：①先画射线AB．②然后用圆规在射线AB上截取AC＝MN．线段AC就是所要作的线段．(2)作一个角等于已知角．如图24-4-2，已知∠AOB．求作：∠A′O′B′，使∠A′O′B′＝∠AOB．作法：①作射线O′A′；②以点O为圆心，以任意长为半径作弧，交OA于C，交OB于D．③以点O′为圆心，以OC长为半径作弧，交O′A′于C′．④以点C′为圆心，以CD为半径作弧，交前弧于D′．⑤经过点D′作射线O′B′，∠A′O′B′就是所求的角．(3)作线段的垂直平分线．如图24-4-3，已知线段AB．求作：线段AB的垂直平分线．作法：①分别以点A和点B为圆心，大于的长为半径作弧，两弧相交于点C和D．②作直线CD．直线CD就是线段AB的垂直平分线．注意：直线CD与线段AB的交点，就是AB的中点．(4)经过一点作已知直线的垂线．a．经过已知直线上的一点作这条直线的垂线，如图24-4-4．已知：直线AB和AB上一点C，求作：AB的垂线，使它经过点C．作法：作平角ACB的平分线CF．直线CF就是所求的垂线，如图24-4-4．b．经过已知直线外一点作这条直线的垂线．如图24-4-5，已知：直线AB和AB外一点C．求作：AB的垂线，使它经过点C．作法：①任意取一点K，使K和C在AB的两旁．②以C为圆心，CK长为半径作弧，交AB于点D和E．③分别以D和E为圆心，大于的长为半径作弧，两弧交于点F．④作直线CF．直线CF就是所求的垂线．注意：经过已知直线上的一点，作这条直线的垂线转化成画线段垂直平分线的方法解决．(5)平分已知角．如图24-4-6，已知∠AOB．求作：射线OC，使∠AOC＝∠BOC．作法：①在OA和OB上，分别截取OD、OE．②分别以D、E为圆心，大于的长为半径作弧，在∠AOB内，两弧交于点C．③作射线OC．OC就是所求的射线．注意：以上五种基本作图是尺规作图的基础，一些复杂的尺规作图，都是由基本作图组成的，同学扪要高度重视，努力把这部分内容学习好．通过这一节的学习，同学们要掌握下列作图语言：(1)过点×和点×画射线××，或画射线××．(2)在射线××上截取××＝××．(3)以点×为圆心，××为半径画弧．(4)以点×为圆心，××为半径画弧，交××于点×．(5)分别以点×，点×为圆心，以××，××为半径作弧，两弧相交于点×．(6)在射线××上依次截取××＝××＝××．(7)在∠×××的外部或内部画∠×××＝∠×××．注意：学过基本作图后，在作较复杂图时，属于基本作图的地方，不必重复作图的详细过程，只用一句话概括叙述就可以了．如：(1)画线段××＝××．(2)画∠×××＝∠×××．(3)画××平分∠×××，或画∠×××的角平分线．(4)过点×画××⊥××，垂足为点×．(5)作线段××的垂直平分线××，等等．但要注意保留全部的作图痕迹，包括基本作图的操作程序，不能因为作法的叙述省略而作图就不按程序操作，只有保留作图痕迹，才能反映出作图的操作是否合理．【经典例题精讲】例1已知两边及其夹角，求作三角形．如图24-4-7，已知：∠α，线段a、b，求作：△ABC，使∠A＝∠α，AB＝a，AC＝b．作法：①作∠MAN＝∠α．②在射线AM、AN上分别作线段AB＝a，AC＝b．③连结BC．如图24-4-8，△ABC即为所求作的三角形．注意：一般几何作图题，应有下面几个步骤：已知、求作、作法，比较复杂的作图题，在作图之前可根据需要作一些分析．例2如图24-4-9，已知底边a，底边上的高h，求作等腰三角形．已知线段a、h．求作：△ABC，使AB＝AC，且BC＝a，高AD＝h．分析：可先作出底边BC，根据等腰三角形的三线合一的性质，可再作出BC的垂直平分线，从而作出BC边上的高AD，分别连结AB和AC，即可作出等腰△ABC来．作法：(1)作线段BC＝a．(2)作线段BC的垂直平分线MN，MN与BC交于点D．(3)在MN上截取DA，使DA＝h．(4)连结AB、AC．如图24-4-10，△ABC即为所求的等腰三角形．例3已知三角形的一边及这边上的中线和高，作三角形．如图24-4-11，已知线段a，m，h(m>h)．求作：△ABC使它的一边等于a，这边上的中线和高分别等于m和h(m>h)．分析：如图24-4-12，假定△ABC已作出，其中BC＝a，中线AD＝m，高AE＝h，在△AED中AD＝m，AE＝h，∠AED＝90°，因此这个Rt△AED可以作出来(△AED为奠基三角形)．当Rt△AED作出后，由的关系可作出点B和点C，于是△ABC即可得到．作法：(1)作△AED，使∠AED＝90°，AE＝h，AD＝m．(2)延长ED到B，使．(3)在DE或BE的延长线上取．(4)连结AB、AC．则△ABC即为所求作的三角形．注意：因为三角形中，一边上的高不能大于这边上的中线，所以如果h>m，作图题无解；若m＝h，则作出的图形为等腰三角形．例4如图24-4-13，已知线段a．求作：菱形ABCD，使其半周长为a，两邻角之比为1∶2．分析：因为菱形四边相等，“半周长为a”就是菱形边长为，为此首先要将线段a等分，又因为菱形对边平行，则同旁内角互补，由“邻角之比为1∶2”可知，菱形较小内角为60°，则菱形较短对角线将菱形分成两个全等的等边三角形．所以作图时只要作出两个有公共边的等边三角形，则得到的四边形即为所求的菱形ABCD．作法：(1)作线段a的垂直平分线，等分线段a．(2)作线段AC，使．(3)分别以A、C为圆心，为半径，在AC的两侧画弧，两弧分别交于B，D．(4)分别连结AB、BC、CD、DA得到四边形ABCD，则四边形ABCD为所求作的菱形(如图24-4-14)．注意：这种通过先画三角形，然后再画出全部图形的方法即为“三角形奠基法”．例5如图24-4-15，已知∠AOB和C、D两点．求作一点P，使PC＝PD，且使点P到∠AOB的两边OA、OB的距离相等．分析：要使PC＝PD，则点P在CD的垂直平分线上，要使点P到∠AOB的两边距离相等，则P应在∠AOB的角平分线上，那么满足题设的P点就是垂直平分线与角平分线的交点了．作法：(1)连结CD．(2)作线段CD的中垂线l．(3)作∠AOB的角平分线OM，交l于点P，P点为所求．注意：这类定点问题应需确定两线，两直线的交点即为定点，当然这两直线应分别满足题目的不同要求．【中考考点】例6 (2000·安徽省)如图24-4-16，直线表示三条相互交叉的公路，现要建一个货物中转站，要求它到三条公路的距离相等，则可供选择的地址有( )A．一处 B．二处C．三处 D．四处分析：到直线距离相等的点在相交所构成的角的平分线上，可利用作角平分线的方法找到这些点．解：分别作相交所构成的角平分线，共可作出六条，三条角平分线相交的交点共有四个．答案：D．注意：本题应用了角平分线的性质，在具体作图时，不可只作出位于中心位置的一处，而要全面考虑其他满足条件的点．例7 (2002·陕西省)如图24-4-17，△ABC是一块直角三角形余料，∠C＝90°，工人师傅要把它加工成—个正方形零件，使C为正方形的—个顶点，其他三个顶点分别在AB、BC、AC边上．(1)试协助工人师傅用尺规画出裁割线(不写作法，保留作图痕迹)；(2)工人师傅测得AC＝80 cm，BC＝120cm，请帮助工人师傅算出按(1)题所画裁割线加工成的正方形零件的边长．解：(1)作∠ACB的平分线与AB的交点E即为正方形—顶点，作CE线段的中垂线HK 与AC、BC的交点F、D即为所作正方形另两个顶点，如图24-4-17．(2)设这个正方形零件的边长为x cm，∵DE∥AC，∴，∴．∴x＝48．答：这个正方形零件的边长为48cm．注意：本题是几何作图和几何计算相结合题目，要求读者对基本作图务必掌握，同时对作出图形的性质要清楚．例8 (2002·山西省)如图24-4-18①，有一破残的轮片(不小于半个轮)，现要制作一个与原轮片同样大小的圆形零件，请你根据所学的有关知识，设计两种方案，确定这个圆形零件的半径．分析：欲确定这个圆形零件的半径，可以借助三角板，T形尺或尺规作图均可，图②中是这个零件的半径，图③中OB是这个零件半径．解：如图24-4-18②③所示．【常见错误分析】例9如图24-4-19，已知线段a、b、h．求作△ABC，使BC＝a，AC＝b，BC边上的高AD＝h．并回答问题，你作出的三角形唯一吗？从中你可以得到什么结论呢？错解：(1)作法：①作Rt△ADC，使AD＝h，AC＝b．②在直线CD上截取CB＝a．如图24-4-20，则△ABC就是所求作的三角形．(2)作出的三角形唯一．(3)得出结论：有两边及一边上的高对应相等的两三角形全等．误区分析：本题错解在于忽略了三角形的高可能在三角形内部也可能在三角形的外部．正解：如图24-4-21，作法：①作Rt△ADC，使AD＝h，AC＝b．②在直线CD上截取CB＝a(在点C的两侧)．则△ABC，△AB′C都是所求作三角形．(2)作出的三角形不唯一．(3)得出结论有两边及—边上的高对应相等的两三角形不一定全等．注意：与三角形的高有关的题目应慎之又慎．【学习方法指导】学习基本作图，主要是运用观察法，通过具体的操作，了解各种基本作图的步骤，掌握作图语言．【规律总结】画复杂的图形时，如一时找不到作法，—般是先画出一个符合所设条件的草图，再根据这个草图进行分析，逐步寻找画图步骤．有时，也可以根据已知条件和基本作图，先作局部三角形，再以此为基础，根据有关条件画出其余部分，从而完成全图，这种方法称为三角形奠基法．拓展： 1．利用基本作图作三角形：(1)已知三边作三角形； (2)已知两边及其夹角作三角形； (3)已知两角及其夹边作三角形； (4)已知底边及底边上的高作等腰三角形；（5）已知一直角边和斜边作直角三角形．2．与圆有关的尺规作图：(1)过不在同一直线上的三点作圆(即三角形的外接圆)． (2)作三角形的内切圆．（3）作圆的内接正方形和正六边形．附件：尺规作图简史：“规”就是圆规，是用来画圆的工具，在我国古代甲骨文中就有“规”这个字.“矩”就像现在木工使用的角尺，由长短两尺相交成直角而成，两者间用木杠连接以使其牢固，其中短尺叫勾，长尺叫股.矩的使用是我国古代的一个发明，山东历城武梁祠石室造像中就有“伏羲氏手执矩，女娲氏手执规”之图形.矩不仅可以画直线、直角，加上刻度可以测量，还可以代替圆规.甲骨文中也有矩字，这可追溯到大禹治水(公元前2000年)前.《史记》卷二记载大禹治水时“左准绳，右规矩”.赵爽注《周髀算经》中有“禹治洪水，……望山川之形，定高下之势，……乃勾股之所由生也.”意即禹治洪水，要先测量地势的高低，就必定要用勾股的道理.这也说明矩起源于很远的中国古代.春秋时代也有不少著作涉及规矩的论述，《墨子》卷七中说“轮匠(制造车子的工匠)执其规矩，以度天下之方圆.”《孟子》卷四中说“离娄(传说中目力非常强的人)之明，公输子(即鲁班，传说木匠的祖师)之巧，不以规矩，不能成方圆.”可见，在春秋战国时期，规矩已被广泛地用于作图、制作器具了.由于我国古代的矩上已有刻度，因此使用范围较广，具有较大的实用性.古代希腊人较重视规、矩在数学中训练思维和智力的作用，而忽视规矩的实用价值.因此，在作图中对规、矩的使用方法加以很多限制，提出了尺规作图问题.所谓尺规作图，就是只有限次地使用没有刻度的直尺和圆规进行作图.古希腊的安那萨哥拉斯首先提出作图要有尺寸限制.他因政治上的纠葛，被关进监狱，并被判处死刑.在监狱里，他思考改圆成方以及其他有关问题，用来打发令人苦恼的无所事事的生活.他不可能有规范的作图工具，只能用一根绳子画圆，用随便找来的破木棍作直尺，当然这些尺子上不可能有刻度.另外，对他来说，时间是不多了，因此他很自然地想到要有限次地使用尺规解决问题.后来以理论形式具体明确这个规定的是欧几里德的《几何原本》.由于《几何原本》的巨大影响，希腊人所崇尚的尺规作图也一直被遵守并流传下来.由于对尺规作图的限制，使得一些貌似简单的几何作图问题无法解决.最著名的是被称为几何三大问题的三个古希腊古典作图难题：立方倍积问题、三等分任意角问题和化圆为方问题.当时很多有名的希腊数学家，都曾着力于研究这三大问题，虽然借助于其他工具或曲线，这三大难题都可以解决，但由于尺规作图的限制，却一直未能如愿以偿.以后两千年来，无数数学家为之绞尽脑汁，都以失败而告终.直到1637年笛卡尔创立了解析几何，关于尺规作图的可能性问题才有了准则.到了1837年万芝尔首先证明立方倍积问题和三等分任意角问题都属于尺规作图不可能问题.1882年林德曼证明了π是无理数，化圆为方问题不可能用尺规作图解决，这才结束了历时两千年的数学难题公案.•。
（完整）尺规作图专题详尽归纳,推荐⽂档考点名称：尺规作图【学习⽬标】1．了解什么是尺规作图．2．学会⽤尺规作图法完成下列五种基本作图：(1)画⼀条线段等于已知线段；(2)画⼀个⾓等于已知⾓；(3)画线段的垂直平分线；(4)过已知点画已知直线的垂线；(5)画⾓平分线．3．了解五种基本作图的理由．4．学会使⽤精练、准确的作图语⾔叙述画图过程．5．学会利⽤基本作图画三⾓形等较简单的图形．6．通过画图认识图形的本质，体会图形的内在美．【基础知识精讲】1．尺规作图：①定义：限定只⽤直尺和圆规来完成的画图，称为尺规作图．注意：这⾥所指的直尺是没有刻度的直尺，由于免去了度量，因此，⽤尺规作图法画出的图形的精确度更⾼，它在⼯程绘图等领域应⽤⽐较⼴泛．②步骤：(1)根据给出的条件和求作的图形，写出已知和求作部分；(2)分析作图的⽅法和过程；(3)⽤直尺和圆规进⾏作图； (4)写出作法步骤，即作法。
（根据题⽬要求来定是否需要写出作法）2．尺规作图中的最基本、最常⽤的作图称为基本作图．任何尺规作图的步骤均可分解为以下五种.3．基本作图共有五种：(1)画⼀条线段等于已知线段．如图24-4-1，已知线段DE．求作：⼀条线段等于已知线段．作法：①先画射线AB．②然后⽤圆规在射线AB上截取AC＝MN．线段AC就是所要作的线段．(2)作⼀个⾓等于已知⾓．如图24-4-2，已知∠AOB．求作：∠A′O′B′，使∠A′O′B′＝∠AOB．作法：①作射线O′A′；②以点O为圆⼼，以任意长为半径作弧，交OA于C，交OB于D．③以点O′为圆⼼，以OC长为半径作弧，交O′A′于C′．④以点C′为圆⼼，以CD为半径作弧，交前弧于D′．⑤经过点D′作射线O′B′，∠A′O′B′就是所求的⾓．(3)作线段的垂直平分线．如图24-4-3，已知线段AB．求作：线段AB的垂直平分线．作法：①分别以点A和点B为圆⼼，⼤于的长为半径作弧，两弧相交于点C和D．②作直线CD．直线CD就是线段AB的垂直平分线．注意：直线CD与线段AB的交点，就是AB的中点．(4)经过⼀点作已知直线的垂线．a．经过已知直线上的⼀点作这条直线的垂线，如图24-4-4．已知：直线AB和AB上⼀点C，求作：AB的垂线，使它经过点C．作法：作平⾓ACB的平分线CF．直线CF就是所求的垂线，如图24-4-4．b．经过已知直线外⼀点作这条直线的垂线．如图24-4-5，已知：直线AB和AB外⼀点C．求作：AB的垂线，使它经过点C．作法：①任意取⼀点K，使K和C在AB的两旁．②以C为圆⼼，CK长为半径作弧，交AB于点D和E．③分别以D和E为圆⼼，⼤于的长为半径作弧，两弧交于点F．④作直线CF．直线CF就是所求的垂线．注意：经过已知直线上的⼀点，作这条直线的垂线转化成画线段垂直平分线的⽅法解决．(5)平分已知⾓．如图24-4-6，已知∠AOB．求作：射线OC，使∠AOC＝∠BOC．作法：①在OA和OB上，分别截取OD、OE．②分别以D、E为圆⼼，⼤于的长为半径作弧，在∠AOB内，两弧交于点C．③作射线OC．OC就是所求的射线．注意：以上五种基本作图是尺规作图的基础，⼀些复杂的尺规作图，都是由基本作图组成的，同学扪要⾼度重视，努⼒把这部分内容学习好．通过这⼀节的学习，同学们要掌握下列作图语⾔：(1)过点×和点×画射线××，或画射线××．(2)在射线××上截取××＝××．(3)以点×为圆⼼，××为半径画弧．(4)以点×为圆⼼，××为半径画弧，交××于点×．(5)分别以点×，点×为圆⼼，以××，××为半径作弧，两弧相交于点×．(6)在射线××上依次截取××＝××＝××．(7)在∠×××的外部或内部画∠×××＝∠×××．注意：学过基本作图后，在作较复杂图时，属于基本作图的地⽅，不必重复作图的详细过程，只⽤⼀句话概括叙述就可以了．如：(1)画线段××＝××．(2)画∠×××＝∠×××．(3)画××平分∠×××，或画∠×××的⾓平分线．(4)过点×画××⊥××，垂⾜为点×．(5)作线段××的垂直平分线××，等等．但要注意保留全部的作图痕迹，包括基本作图的操作程序，不能因为作法的叙述省略⽽作图就不按程序操作，只有保留作图痕迹，才能反映出作图的操作是否合理．【经典例题精讲】例1已知两边及其夹⾓，求作三⾓形．如图24-4-7，已知：∠α，线段a、b，求作：△ABC，使∠A＝∠α，AB＝a，AC＝b．作法：①作∠MAN＝∠α．②在射线AM、AN上分别作线段AB＝a，AC＝b．③连结BC．如图24-4-8，△ABC即为所求作的三⾓形．注意：⼀般⼏何作图题，应有下⾯⼏个步骤：已知、求作、作法，⽐较复杂的作图题，在作图之前可根据需要作⼀些分析．例2如图24-4-9，已知底边a，底边上的⾼h，求作等腰三⾓形．已知线段a、h．求作：△ABC，使AB＝AC，且BC＝a，⾼AD＝h．分析：可先作出底边BC，根据等腰三⾓形的三线合⼀的性质，可再作出BC的垂直平分线，从⽽作出BC边上的⾼AD，分别连结AB和AC，即可作出等腰△ABC来．作法：(1)作线段BC＝a．(2)作线段BC的垂直平分线MN，MN与BC交于点D．(3)在MN上截取DA，使DA＝h．(4)连结AB、AC．如图24-4-10，△ABC即为所求的等腰三⾓形．例3已知三⾓形的⼀边及这边上的中线和⾼，作三⾓形．如图24-4-11，已知线段a，m，h(m>h)．求作：△ABC使它的⼀边等于a，这边上的中线和⾼分别等于m和h(m>h)．分析：如图24-4-12，假定△ABC已作出，其中BC＝a，中线AD＝m，⾼AE＝h，在△AED中AD＝m，AE＝h，∠AED＝90°，因此这个Rt△AED可以作出来(△AED为奠基三⾓形)．当Rt△AED作出后，由的关系可作出点B和点C，于是△ABC即可得到．作法：(1)作△AED，使∠AED＝90°，AE＝h，AD＝m．(2)延长ED到B，使．(3)在DE或BE的延长线上取．(4)连结AB、AC．则△ABC即为所求作的三⾓形．注意：因为三⾓形中，⼀边上的⾼不能⼤于这边上的中线，所以如果h>m，作图题⽆解；若m＝h，则作出的图形为等腰三⾓形．例4如图24-4-13，已知线段a．求作：菱形ABCD，使其半周长为a，两邻⾓之⽐为1∶2．分析：因为菱形四边相等，“半周长为a”就是菱形边长为，为此⾸先要将线段a等分，⼜因为菱形对边平⾏，则同旁内⾓互补，由“邻⾓之⽐为1∶2”可知，菱形较⼩内⾓为60°，则菱形较短对⾓线将菱形分成两个全等的等边三⾓形．所以作图时只要作出两个有公共边的等边三⾓形，则得到的四边形即为所求的菱形ABCD．作法：(1)作线段a的垂直平分线，等分线段a．(2)作线段AC，使．(3)分别以A、C为圆⼼，为半径，在AC的两侧画弧，两弧分别交于B，D．(4)分别连结AB、BC、CD、DA得到四边形ABCD，则四边形ABCD为所求作的菱形(如图24-4-14)．注意：这种通过先画三⾓形，然后再画出全部图形的⽅法即为“三⾓形奠基法”．例5如图24-4-15，已知∠AOB和C、D两点．求作⼀点P，使PC＝PD，且使点P到∠AOB的两边OA、OB的距离相等．分析：要使PC＝PD，则点P在CD的垂直平分线上，要使点P到∠AOB的两边距离相等，则P应在∠AOB的⾓平分线上，那么满⾜题设的P点就是垂直平分线与⾓平分线的交点了．作法：(1)连结CD．(2)作线段CD的中垂线l．(3)作∠AOB的⾓平分线OM，交l于点P，P点为所求．注意：这类定点问题应需确定两线，两直线的交点即为定点，当然这两直线应分别满⾜题⽬的不同要求．【中考考点】例6 (2000·安徽省)如图24-4-16，直线表⽰三条相互交叉的公路，现要建⼀个货物中转站，要求它到三条公路的距离相等，则可供选择的地址有( )A．⼀处 B．⼆处C．三处 D．四处分析：到直线距离相等的点在相交所构成的⾓的平分线上，可利⽤作⾓平分线的⽅法找到这些点．解：分别作相交所构成的⾓平分线，共可作出六条，三条⾓平分线相交的交点共有四个．答案：D．注意：本题应⽤了⾓平分线的性质，在具体作图时，不可只作出位于中⼼位置的⼀处，⽽要全⾯考虑其他满⾜条件的点．例7 (2002·陕西省)如图24-4-17，△ABC是⼀块直⾓三⾓形余料，∠C＝90°，⼯⼈师傅要把它加⼯成—个正⽅形零件，使C为正⽅形的—个顶点，其他三个顶点分别在AB、BC、AC边上．(1)试协助⼯⼈师傅⽤尺规画出裁割线(不写作法，保留作图痕迹)；(2)⼯⼈师傅测得AC＝80 cm，BC＝120cm，请帮助⼯⼈师傅算出按(1)题所画裁割线加⼯成的正⽅形零件的边长．解：(1)作∠ACB的平分线与AB的交点E即为正⽅形—顶点，作CE线段的中垂线HK 与AC、BC的交点F、D即为所作正⽅形另两个顶点，如图24-4-17．(2)设这个正⽅形零件的边长为x cm，∵DE∥AC，∴，∴．∴x＝48．答：这个正⽅形零件的边长为48cm．注意：本题是⼏何作图和⼏何计算相结合题⽬，要求读者对基本作图务必掌握，同时对作出图形的性质要清楚．例8 (2002·⼭西省)如图24-4-18①，有⼀破残的轮⽚(不⼩于半个轮)，现要制作⼀个与原轮⽚同样⼤⼩的圆形零件，请你根据所学的有关知识，设计两种⽅案，确定这个圆形零件的半径．分析：欲确定这个圆形零件的半径，可以借助三⾓板，T形尺或尺规作图均可，图②中是这个零件的半径，图③中OB是这个零件半径．解：如图24-4-18②③所⽰．【常见错误分析】例9如图24-4-19，已知线段a、b、h．求作△ABC，使BC＝a，AC＝b，BC边上的⾼AD＝h．并回答问题，你作出的三⾓形唯⼀吗？从中你可以得到什么结论呢？错解：(1)作法：①作Rt△ADC，使AD＝h，AC＝b．②在直线CD上截取CB＝a．如图24-4-20，则△ABC就是所求作的三⾓形．(2)作出的三⾓形唯⼀．(3)得出结论：有两边及⼀边上的⾼对应相等的两三⾓形全等．误区分析：本题错解在于忽略了三⾓形的⾼可能在三⾓形内部也可能在三⾓形的外部．正解：如图24-4-21，作法：①作Rt△ADC，使AD＝h，AC＝b．②在直线CD上截取CB＝a(在点C的两侧)．则△ABC，△AB′C都是所求作三⾓形．(2)作出的三⾓形不唯⼀．(3)得出结论有两边及—边上的⾼对应相等的两三⾓形不⼀定全等．注意：与三⾓形的⾼有关的题⽬应慎之⼜慎．【学习⽅法指导】学习基本作图，主要是运⽤观察法，通过具体的操作，了解各种基本作图的步骤，掌握作图语⾔．【规律总结】画复杂的图形时，如⼀时找不到作法，—般是先画出⼀个符合所设条件的草图，再根据这个草图进⾏分析，逐步寻找画图步骤．有时，也可以根据已知条件和基本作图，先作局部三⾓形，再以此为基础，根据有关条件画出其余部分，从⽽完成全图，这种⽅法称为三⾓形奠基法．拓展： 1．利⽤基本作图作三⾓形：(1)已知三边作三⾓形； (2)已知两边及其夹⾓作三⾓形； (3)已知两⾓及其夹边作三⾓形； (4)已知底边及底边上的⾼作等腰三⾓形；（5）已知⼀直⾓边和斜边作直⾓三⾓形．2．与圆有关的尺规作图：(1)过不在同⼀直线上的三点作圆(即三⾓形的外接圆)． (2)作三⾓形的内切圆．（3）作圆的内接正⽅形和正六边形．附件：尺规作图简史：“规”就是圆规，是⽤来画圆的⼯具，在我国古代甲⾻⽂中就有“规”这个字.“矩”就像现在⽊⼯使⽤的⾓尺，由长短两尺相交成直⾓⽽成，两者间⽤⽊杠连接以使其牢固，其中短尺叫勾，长尺叫股.矩的使⽤是我国古代的⼀个发明，⼭东历城武梁祠⽯室造像中就有“伏羲⽒⼿执矩，⼥娲⽒⼿执规”之图形.矩不仅可以画直线、直⾓，加上刻度可以测量，还可以代替圆规.甲⾻⽂中也有矩字，这可追溯到⼤禹治⽔(公元前2000年)前.《史记》卷⼆记载⼤禹治⽔时“左准绳，右规矩”.赵爽注《周髀算经》中有“禹治洪⽔，……望⼭川之形，定⾼下之势，……乃勾股之所由⽣也.”意即禹治洪⽔，要先测量地势的⾼低，就必定要⽤勾股的道理.这也说明矩起源于很远的中国古代.春秋时代也有不少著作涉及规矩的论述，《墨⼦》卷七中说“轮匠(制造车⼦的⼯匠)执其规矩，以度天下之⽅圆.”《孟⼦》卷四中说“离娄(传说中⽬⼒⾮常强的⼈)之明，公输⼦(即鲁班，传说⽊匠的祖师)之巧，不以规矩，不能成⽅圆.”可见，在春秋战国时期，规矩已被⼴泛地⽤于作图、制作器具了.由于我国古代的矩上已有刻度，因此使⽤范围较⼴，具有较⼤的实⽤性.古代希腊⼈较重视规、矩在数学中训练思维和智⼒的作⽤，⽽忽视规矩的实⽤价值.因此，在作图中对规、矩的使⽤⽅法加以很多限制，提出了尺规作图问题.所谓尺规作图，就是只有限次地使⽤没有刻度的直尺和圆规进⾏作图.古希腊的安那萨哥拉斯⾸先提出作图要有尺⼨限制.他因政治上的纠葛，被关进监狱，并被判处死刑.在监狱⾥，他思考改圆成⽅以及其他有关问题，⽤来打发令⼈苦恼的⽆所事事的⽣活.他不可能有规范的作图⼯具，只能⽤⼀根绳⼦画圆，⽤随便找来的破⽊棍作直尺，当然这些尺⼦上不可能有刻度.另外，对他来说，时间是不多了，因此他很⾃然地想到要有限次地使⽤尺规解决问题.后来以理论形式具体明确这个规定的是欧⼏⾥德的《⼏何原本》.由于《⼏何原本》的巨⼤影响，希腊⼈所崇尚的尺规作图也⼀直被遵守并流传下来.由于对尺规作图的限制，使得⼀些貌似简单的⼏何作图问题⽆法解决.最著名的是被称为⼏何三⼤问题的三个古希腊古典作图难题：⽴⽅倍积问题、三等分任意⾓问题和化圆为⽅问题.当时很多有名的希腊数学家，都曾着⼒于研究这三⼤问题，虽然借助于其他⼯具或曲线，这三⼤难题都可以解决，但由于尺规作图的限制，却⼀直未能如愿以偿.以后两千年来，⽆数数学家为之绞尽脑汁，都以失败⽽告终.直到1637年笛卡尔创⽴了解析⼏何，关于尺规作图的可能性问题才有了准则.到了1837年万芝尔⾸先证明⽴⽅倍积问题和三等分任意⾓问题都属于尺规作图不可能问题.1882年林德曼证明了π是⽆理数，化圆为⽅问题不可能⽤尺规作图解决，这才结束了历时两千年的数学难题公案.。
尺规作图大全一、尺规作图定义尺规作图是指用没有刻度的直尺和圆规作图。
（人教版七上第126页）二、五种基本的尺规作图1、作一条线段等于已知线段（人教版七上第126页）；2、作一个角等于已知角（人教版八上第36页）；3、作已知角的角平分线（人教版八上第48页）；4、作已知线段的垂直平分线；5、过一点作已知直线的垂线（人教版八上第62页）；【作图1】作一条线段等于已知线段。
已知：如图，线段a 。
求作：线段AB ，使AB a =。
【作图2】作已知线段的中点（或垂直平分线）。
已知：如图，线段MN 。
求作：在线段MN 上找点O ，使MO NO =（即O 为线段MN 的中点）【作图3】作一个角等于已知角。
已知：如图，AOB ∠，求作：111A O B ∠，使得111A O B AOB =∠∠。
作法：第一步：用直尺作射线AP ；第二步：用圆规以点A 为圆心，a 为半径画弧，交射线AP 于点B ，线段AB 为所求。
作法：第一步：分别以M 、N 为圆心，大于0.5MN 长为半径画弧，两弧相交于点P 、点Q ；第二步：连接PQ ，交MN 于点O ，则点O 即为线段MN 的中点【思考】线段MN 的垂直平分线跟这个作法一样吗？【作图4】作已知角的角平分线。
已知：如图，AOB ∠，求作：射线OC ，使得AOC OC =∠∠B （OC 平分AOB ∠）。
【作图5】经过直线外一点，作已知直线的垂线已知：如图，直线AB 和直线AB 外一点C 。
求作：直线AB 的垂线，使它经过点C 。
作法：第一步：以O 为圆心，任意长为半径画弧，分别交OA 、OB 于点C 、D;第二步：作射线11O A ，以点1O 为圆心，OC 长为半径画弧，交11O A 于点1C ;第三步：以点1C 为圆心，CD 长为半径画弧，与第二步中所画的弧交于点1D ;第四步：过点1D 画射线11O B ，则111A O B AOB =∠∠。
作法：第一步：以点O 为圆心，适当长为半径画弧，交OA 于点M ，OB 于点N ；第二步：分别以M 、N 为圆心，大于0.5MN 的长为半径画弧，两弧在∠AOB 的内部相交于点C ；第三步：画射线OC ，射线OC 即为所求。
完整版)中考数学尺规作图专题复习(含答案)尺规作图是用无刻度的直尺和圆规画图的方法，常见的作图包括线段的垂线、垂直平分线、角平分线、等长线段和等角。
以下是各种作图的具体方法：1.直线垂线的画法：以点C为圆心，任意长为半径画弧交直线与A、B两点，再以点A、B为圆心，大于AB的长为半径画圆弧，分别交直线l两侧于点M、N，连接MN，即可得到所求的垂线。
2.线段垂直平分线的画法：以点A、B为圆心，大于AB的长为半径画圆弧，分别交直线AB两侧于点C、D，连接CD，即可得到线段AB的垂直平分线。
3.角平分线的画法：以角顶点O为圆心，任意长为半径画圆，分别交角两边A、B点，再以A、B为圆心，大于AB的长为半径画圆弧，交点为H，连接OH并延长，即可得到所求的角平分线。
4.等长的线段的画法：直接用圆规量取即可。
5.等角的画法：以O为圆心，任意长为半径画圆，交原角的两边为A、B两点，连接AB；画一条射线l，以上面的半径为半径，l的顶点K为圆心画圆，交l与L，以L为圆心，AB为半径画圆，交以K为圆心，KL为半径的圆与M点，连接KM，则角LKM即为所求。
需要注意的是，直尺主要用于画直线和射线，圆规主要用于截取相等线段和画弧。
在作图时，如果有多个要求，应逐个满足并取公共部分。
例如，对于要求作一个三角形的问题，可以根据三角形全等的基本事实或判定定理来进行作图。
以下是例题解析：例题1：已知线段a，求作△ABC，使AB=BC=AC=a。
作法如下：1.作线段BC=a；2.分别以B、C为圆心，以a半径画弧，两弧交于点A；3.连接AB、AC。
例题2：已知线段a和∠α，求作△ABC，使AB=AC=a，∠A=∠α。
作法如下：1.作∠XXX∠α；2.以点A为圆心，a为半径画弧，分别交射线AM、AN 于点B、C；3.连接B、C。
例题3：已知△ABC，AB<BC，用尺规作图的方法在BC 上取一点P，使得PA+PC=BC。
作法如下：作出AB的垂直平分线，与BC交于点P。
1：尺规作出正三角形2尺规作出正方形3：尺规作出正六边形4：尺规作出正十边形5：尺规作出正十六边形6：尺规作出正十七边形7：尺规作出正十五边形8：尺规作出正五边形9：单尺作出正八边形10：单尺作出正方形11：单尺作出正六边形12：单尺作出正五边形13：单规找出两点间的三等分点14：单规找出两点间的中点15：单规作出等边三角形16：单规作出正八边形17：单规作出正方形18：单规作出正六边形19：单规作出正十边形20：单规作出正十二边形21：单规作出正十六边形22：单规作出正十五边形23单规作出正五边形24：只有两个刻度的直尺作出正三角形25：只有两个刻度的直尺作出正方形初中数学尺规作图专题讲解张远波尺规作图是起源于古希腊的数学课题.只使用圆规和直尺，并且只准许使用有限次，来解决不同的平面几何作图题.平面几何作图，限制只能用直尺、圆规.在历史上最先明确提出尺规限制的是伊诺皮迪斯.他发现以下作图法：在已知直线的已知点上作一角与已知角相等.这件事的重要性并不在于这个角的实际作出，而是在尺规的限制下从理论上去解决这个问题.在这以前，许多作图题是不限工具的.伊诺皮迪斯以后，尺规的限制逐渐成为一种公约，最后总结在《几何原本》之中.初等平面几何研究的对象，仅限于直线、圆以及由它们（或一部分）所组成的图形，因此作图的工具，习惯上使用没有刻度的直尺和圆规两种.限用直尺和圆规来完成的作图方法，叫做尺规作图法.最简单的尺规作图有如下三条：⑴经过两已知点可以画一条直线；⑵已知圆心和半径可以作一圆；⑶两已知直线；一已知直线和一已知圆；或两已知圆，如果相交，可以求出交点；以上三条，叫做作图公法.用直尺可以画出第一条公法所说的直线；用圆规可以作出第二条公法所说的圆；用直尺和圆规可以求得第三条公法所说的交点.一个作图题，不管多么复杂，如果能反复应用上述三条作图公法，经过有限的次数，作出适合条件的图形，这样的作图题就叫做尺规作图可能问题；否则，就称为尺规作图不能问题.历史上，最著名的尺规作图不能问题是：⑴三等分角问题：三等分一个任意角；⑵倍立方问题：作一个立方体，使它的体积是已知立方体的体积的两倍；⑶化圆为方问题：作一个正方形，使它的面积等于已知圆的面积.这三个问题后被称为“几何作图三大问题”.直至1837年，万芝尔（Pierre Laurent Wantzel）首先证明三等分角问题和立方倍积问题属尺规作图不能问题；1882年，德国数学家林德曼（Ferdinand Lindemann）证明π是一个超越数（即π是一个不满足任何整系数代数方程的实数），由此即可推得根号π(即当圆半径1r=时所求正方形的边长）不可能用尺规作出，从而也就证明了化圆为方问题是一个尺规作图不能问题.若干著名的尺规作图已知是不可能的，而当中很多不可能证明是利用了由19世纪出现的伽罗华理论.尽管如此，仍有很多业余爱好者尝试这些不可能的题目，当中以化圆为方及三等分任意角最受注意.数学家Underwood Dudley曾把一些宣告解决了这些不可能问题的错误作法结集成书.还有另外两个著名问题：⑴正多边形作法·只使用直尺和圆规，作正五边形.·只使用直尺和圆规，作正六边形.·只使用直尺和圆规，作正七边形——这个看上去非常简单的题目，曾经使许多著名数学家都束手无策，因为正七边形是不能由尺规作出的.·只使用直尺和圆规，作正九边形，此图也不能作出来，因为单用直尺和圆规，是不足以把一个角分成三等份的.·问题的解决：高斯，大学二年级时得出正十七边形的尺规作图法，并给出了可用尺规作图的正多边形的条件：尺规作图正多边形的边数目必须是2的非负整数次方和不同的费马素数的积，解决了两千年来悬而未决的难题.⑵四等分圆周只准许使用圆规，将一个已知圆心的圆周4等分．这个问题传言是拿破仑·波拿巴出的，向全法国数学家的挑战.尺规作图的相关延伸：用生锈圆规(即半径固定的圆规)作图1.只用直尺及生锈圆规作正五边形2.生锈圆规作图，已知两点A、B，找出一点C使得AB BC CA==.3.已知两点A、B，只用半径固定的圆规，求作C使C是线段AB的中点.4.尺规作图，是古希腊人按“尽可能简单”这个思想出发的，能更简洁的表达吗？顺着这思路就有了更简洁的表达.10世纪时，有数学家提出用直尺和半径固定的圆规作图.1672年，有人证明：如果把“作直线”解释为“作出直线上的2点”，那么凡是尺规能作的，单用圆规也能作出！从已知点作出新点的几种情况：两弧交点、直线与弧交点、两直线交点，在已有一个圆的情况下，那么凡是尺规能作的，单用直尺也能作出！. 五种基本作图：初中数学的五种基本尺规作图为： 1.做一线段等于已知线段 2.做一角等于已知角 3.做一角的角平分线4.过一点做一已知线段的垂线5.做一线段的中垂线下面介绍几种常见的尺规作图方法：⑴ 轨迹交点法：解作图题的一种常见方法.解作图题常归结到确定某一个点的位置.如果这两个点的位置是由两个条件确定的，先放弃其中一个条件，那么这个点的位置就不确定而形成一个轨迹；若改变放弃另一个条件，这个点就在另一条轨迹上，故此点便是两个轨迹的交点.这个利用轨迹的交点来解作图题的方法称为轨迹交点法，或称交轨法、轨迹交截法、轨迹法.【例1】 电信部门要修建一座电视信号发射塔，如下图，按照设计要求，发射塔到两个城镇A 、B 的距离必须相等，到两条高速公路m 、n 的距离也必须相等，发射塔P 应修建在什么位置？m【分析】 这是一道实际应用题，关键是转化成数学问题，根据题意知道，点P 应满足两个条件，一是在线段AB 的垂直平分线上；二是在两条公路夹角的平分线上，所以点P 应是它们的交点.【解析】 ⑴ 作两条公路夹角的平分线OD 或OE ；⑵ 作线段AB 的垂直平分线FG ；则射线OD ，OE 与直线FG 的交点1C ，2C 就是发射塔的位置.【例2】 在平面直角坐标系中，点A 的坐标是(4，0)，O 是坐标原点，在直线3y x =+上求一点P ，使AOP ∆是等腰三角形，这样的P 点有几个？【解析】 首先要清楚点P 需满足两个条件，一是点P 在3y x =+上；二是AOP ∆必须是等腰三角形.其次，寻找P 点要分情况讨论，也就是当OA OP =时，以O 点为圆心，OA 为半径画圆，与直线有两个点1P 、2P ；当OA AP =时，以A 点为圆心，OA 为半径画圆，与直线无交点；当PO PA =时，作OA 的垂直平分线，与直线有一交点3P ，所以总计这样的P 点有3个.【例3】 设O ⊙与'O ⊙相离，半径分别为R 与'R ，求作半径为r 的圆，使其与O⊙及'O ⊙外切.rr【分析】 设M ⊙是符合条件的圆，即其半径为r ，并与O ⊙及'O ⊙外切，显然，点M 是由两个轨迹确定的，即M 点既在以O 为圆心以R r +为半径的圆上，又在以'O 为圆心以'R r +为半径的圆上，因此所求圆的圆心的位置可确定.若O ⊙与'O ⊙相距为b ，当2r b <时，该题无解，当2r b =有唯一解；当2r b >时，有两解.【解析】 以当O ⊙与'O ⊙相距为b ，2r b >时为例：⑴ 作线段OA R r =+，''O B R r =+.⑵ 分别以O ，'O 为圆心，以R r +，'R r +为半径作圆，两圆交于12,M M 两点.⑶ 连接1OM ，2OM ，分别交以R 为半径的O ⊙于D 、C 两点. ⑷ 分别以12M M ，为圆心，以r 为半径作圆. ∴12,M M ⊙⊙即为所求.【思考】若将例3改为：“设O ⊙与'O ⊙相离，半径分别为R 与'R ，求作半径为r ()r R >的圆，使其与O ⊙内切，与'O ⊙外切.”又该怎么作图？⑵ 代数作图法：解作图题时，往往首先归纳为求出某一线段长，而这线段长的表达式能用代数方法求出，然后根据线段长的表达式设计作图步骤.用这种方法作图称为代数作图法.【例4】 只用圆规，不许用直尺，四等分圆周（已知圆心）.【分析】 设半径为1.，也就是说用这个长度去等分圆周.我们的任务就是做出这个长度..1的直角三角.【解析】 具体做法：⑴ 随便画一个圆.设半径为1.⑵ 先六等分圆周.⑶ 以这个距离为半径，分别以两个相对的等分点为圆心，同向作弧，交于一点.（“两个相对的等分点”其实就是直径的两端点啦！两弧交点与“两个相对的等分点”形成的是一个底为2，腰.）⑷【例5】 求作一正方形，使其面积等于已知ABC ∆的面积.【分析】 设ABC ∆的底边长为a ，高为h ，关键是在于求出正方形的边长x ，使得212x ah =，所以x 是12a 与h 的比例中项.【解析】 已知：在ABC ∆中，底边长为a ，这个底边上的高为h ，求作：正方形DEFG ，使得：ABC DEFG S S ∆=正方形haDCBANM作法：⑴ 作线段12MD a =；⑵ 在MD 的延长线上取一点N ，使得DN h =； ⑶ 取MN 中点O ，以O 为圆心，OM 为半径作O ⊙； ⑷ 过D 作DE MN ⊥，交O ⊙于E ， ⑸ 以DE 为一边作正方形DEFG . 正方形DEFG 即为所求.【例6】 在已知直线l 上求作一点M ，使得过M 作已知半径为r 的O ⊙的切线，其切线长为a .al【分析】 先利用代数方法求出点M 与圆心O 的距离d ，再以O 为圆心，d 为半径作圆，此圆与直线l 的交点即为所求.【解析】 ⑴ 作Rt OAB ∆，使得：90A ∠=︒，OA r =，AB a =.⑵ 以O 为圆心，OB 为半径作圆.若此圆与直线l 相交，此时有两个交点1M ，2M . 1M ，2M 即为所求.若此圆与直线l 相切，此时只有一个交点M .M 即为所求.若此圆与直线l 相离，此时无交点.即不存在这样的M 点使得过M 作已知半径为r 的O ⊙的切线，其切线长为a .⑶ 旋转法作图：有些作图题，需要将某些几何元素或图形绕某一定点旋转适当角度，以使已知图形与所求图形发生联系，从而发现作图途径.【例7】 已知：直线a 、b 、c ，且a b c ∥∥.求作：正ABC ∆，使得A 、B 、C 三点分别在直线a 、b 、c 上.c ba D'DCB Acba【分析】 假设ABC ∆是正三角形，且顶点A 、B 、C 三点分别在直线a 、b 、c 上.作AD b ⊥于D ，将ABD∆绕A 点逆时针旋转60︒后，置于'ACD ∆的位置，此时点'D 的位置可以确定.从而点C 也可以确定.再作60BAC ∠=︒，B 点又可以确定，故符合条件的正三角形可以作出.【解析】 作法：⑴ 在直线a 上取一点A ，过A 作AD b ⊥于点D ； ⑵ 以AD 为一边作正三角形'ADD ； ⑶ 过'D 作''D C AD ⊥，交直线c 于C ；⑷ 以A 为圆心，AC 为半径作弧，交b 于B (使B 与'D 在AC 异侧). ⑸ 连接AB 、AC 、BC 得ABC ∆.ABC ∆即为所求.【例8】 已知：如图，P 为AOB ∠角平分线OM 上一点.求作：PCD ∆，使得90P ∠=︒，PC PD =，且C 在OA 上，D 在OB 上.OD'O【解析】 ⑴ 过P 作PE OB ⊥于E .⑵ 过P 作直线l OB ∥;⑶ 在直线l 上取一点M ，使得PM PE =(或'PM PE =)； ⑷ 过M (或'M )作MC l ⊥（或'M C l ⊥），交OA 于C (或'C )点；⑸ 连接PC (或'PC )，过P 作PD PC ⊥(或''PD PC ⊥)交OB 于D （或'D ）点. 连接,PD CD (或',''PD C D ). 则PCD ∆(或''PC D ∆)即为所求.⑷ 位似法作图：利用位似变换作图，要作出满足某些条件的图形，可以先放弃一两个条件，作出与其位似的图形，然后利用位似变换，将这个与其位似得图形放大或缩小，以满足全部条件，从而作出满足全部的条件.【例9】 已知：一锐角ABC ∆.求作:一正方形DEFG ，使得D 、E 在BC 边上，F 在AC 边上，G 在AB 边上.C BAG'F'E'D'G FED CBA【分析】 先放弃一个顶点F 在AC 边上的条件，作出与正方形DEFG 位似的正方形''''D E F G ，然后利用位似变换将正方形''''D E F G 放大（或缩小）得到满足全部条件的正方形DEFG .【解析】 作法：⑴ 在AB 边上任取一点'G ，过'G 作''G D BC ⊥于'D⑵ 以''G D 为一边作正方形''''D E F G ，且使'E 在'BD 的延长线上. ⑶ 作直线'BF 交AC 于F .⑷ 过F 分别作''FG F G ∥交AB 于G ；作''FE F E ∥交BC 于E . ⑸ 过G 作''GD G D ∥交BC 于D . 则四边形DEFG 即为所求.⑸ 面积割补法作图：对于等积变形的作图题，通常在给定图形或某一确定图形上割下一个三角形，再借助平行线补上一个等底等高的另一个三角形，使面积不变，从而完成所作图形.【例10】 如图，过ABC ∆的底边BC 上一定点，P ，求作一直线l ，使其平分ABC ∆的面积.【分析】 因为中线AM 平分ABC ∆的面积，所以首先作中线AM ，假设PQ 平分ABC ∆的面积，在AMC∆中先割去AMP ∆，再补上ANP ∆.只要NM AP ∥，则AMP ∆和AMP ∆就同底等高，此时它们的面积就相等了.所以PN 就平分了ABC ∆的面积.【解析】 作法：⑴ 取BC 中点M ，连接,AM AP ; ⑵ 过M 作MN AP ∥交AB 于N ； ⑶ 过P 、N 作直线l . 直线l 即为所求.NM P CB Al【例11】 如图：五边形ABCDE 可以看成是由一个直角梯形和一个矩形构成.⑴ 请你作一条直线l ，使直线l 平分五边形ABCDE 的面积； ⑵ 这样的直线有多少条？请你用语言描述出这样的直线.FED CBAMFDCBFD CB【解析】 ⑴ 取梯形AFDE 的中位线MN 的中点O ，再取矩形BCDF 对角线的交点'O ，则经过点O ，'O 的直线l 即为所求；⑵ 这样的直线有无数条.设⑴中的直线l 交AE 于Q ，交BC 于R ，过线段RQ 中点P ，且与线段AE 、BC 均有交点的直线均可平分五边形ABCDE 的面积.【例12】 (07江苏连云港)如图1，点C 将线段AB 分成两部分，如果AC BCAB AC=，那么称点C 为线段AB 的黄金分割点．某研究小组在进行课题学习时，由黄金分割点联想到“黄金分割线”，类似地给出“黄金分割线”的定义：直线l 将一个面积为S 的图形分成两部分，这两部分的面积分别为1S ，2S ，如果121S SS S =，那么称直线l 为该图形的黄金分割线．⑴ 研究小组猜想：在ABC △中，若点D 为AB 边上的黄金分割点(如图2)，则直线CD 是ABC △的黄金分割线．你认为对吗？为什么？⑵ 请你说明：三角形的中线是否也是该三角形的黄金分割线？⑶ 研究小组在进一步探究中发现：过点C 任作一条直线交AB 于点E ，再过点D 作直线DF CE ∥，交AC 于点F ，连接EF (如图3)，则直线EF 也是ABC △的黄金分割线．请你说明理由．⑷ 如图4，点E 是ABCD 的边AB 的黄金分割点，过点E 作EF AD ∥，交DC 于点F ，显然直线EF 是ABCD 的黄金分割线．请你画一条ABCD 的黄金分割线，使它不经过ABCD 各边黄金分割点．【解析】 ⑴ 直线CD 是ABC △的黄金分割线．理由如下：设ABC △的边AB 上的高为h ．ACB图1A DB 图2C AD B图3C F E E图412ADC S AD h =△，12BDC S BD h =△，12ABC S AB h =△， ∴ADC ABC S AD S AB =△△，BDC ADC S BD S AD =△△． 又∵点D 为边AB 的黄金分割点， ∴AD BDAB AD=．∴ADC BDC ABC ADC S S S S =△△△△． ∴直线CD 是ABC △的黄金分割线．⑵ ∵三角形的中线将三角形分成面积相等的两部分，此时1212S S S ==，即121S S S S ≠，∴三角形的中线不可能是该三角形的黄金分割线． ⑶ ∵DF CE ∥，∴DEC △和FCE △的公共边CE 上的高也相等， ∴DEC FCE S S =△△．设直线EF 与CD 交于点G ，∴DGE FGC S S =△△． ∴ADC FGC AFGD S S S =+△△四边形DGE AEF AFGD S S S =+=△△四边形， BDC BEFC S S =△四边形．又∵ADC BDCABC ADCS S S S =△△△△，∴BEFC AEF ABC AEF S S S S =四边形△△△． ∴直线EF 也是ABC △的黄金分割线． ⑷ 画法不惟一，现提供两种画法；画法一：如答图1，取EF 中点G ，再过点G 作一直线分别交AB ，DC 于M ，N 点，则直线MN 就是ABCD 的黄金分割线．画法二：如答图2，在DF 上取一点N ，连接EN ，再过点F 作FM NE ∥交AB 于点M ，连接MN ，则直线MN 就是ABCD 的黄金分割线．M （答案图1）M （答案图2）。
