求最大公因数、最小公倍数方法课件

求最大公因数和最小公倍数的方法一、求最大公因数的方法：1.1.基本原理求解最大公因数的方法有很多，其中最常用的方法是欧几里得算法（Euclidean Algorithm）。

基本思想是通过逐步计算两个数的余数，直到余数为0为止。

最后的非零余数即为最大公因数。

1.2.欧几里得算法步骤（1）设两个数为a和b，其中a>=b。

（2）通过除法运算得到a除以b的商q和余数r(a=bq+r)。

（3）如果r=0，则b即为最大公因数。

（4）如果r不等于0，则将b赋值给a，将r赋值给b，然后重复步骤21.3.欧几里得算法示例例如，我们要求解数30和18的最大公因数：Step 1: 30÷18，商为1，余数为12；Step 2: 18÷12，商为1，余数为6；Step 3: 12÷6，商为2，余数为0。

因此，最大公因数为6二、求最小公倍数的方法：2.1.基本原理最小公倍数是指不同整数共同的倍数中，最小的那个数。

求解最小公倍数的方法有多种，其中最常用的方法是通过最大公因数求解。

2.2.通过最大公因数求解最小公倍数最小公倍数等于两个数之积除以最大公因数。

因为最小公倍数是两个数的公共倍数中最小的，所以它必然是两个数的乘积的倍数，而除以最大公因数后，结果就是最小公倍数。

2.3.通过最大公因数求解最小公倍数示例例如，我们要求解数30和18的最小公倍数：首先，求解最大公因数为6、最小公倍数等于30乘以18除以6，结果为90。

三、其他求最大公因数和最小公倍数的方法：除了欧几里得算法外，求解最大公因数和最小公倍数还有其他方法。

3.1.质因数分解法质因数分解是将一个合数写成几个质数的乘积的表示法。

通过质因数分解，可以快速求得两个数的最大公因数和最小公倍数。

以求解30和18的最大公因数和最小公倍数为例：将30和18分别质因数分解，得到：30=2×3×518=2×3×3公共质因数有2和3，所以最大公因数为2×3=6最小公倍数为所有质因数的乘积，即2×3×3×5=90。

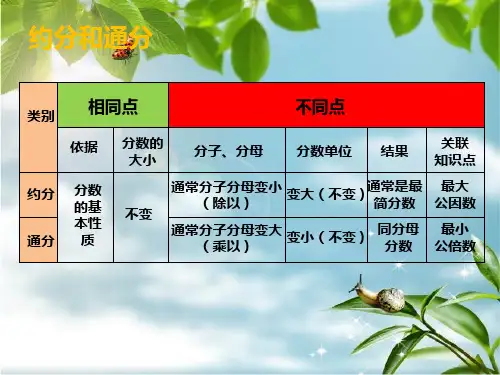
用短除法求最大公因数和最小公倍数课件最大公因数（Greatest Common Divisor，简称GCD）和最小公倍数（Least Common Multiple，简称LCM）是数学中常用的概念。

我们可以使用短除法来求解它们。

首先，让我们来解释一下什么是最大公因数。

最大公因数是指两个或多个整数共有的最大的因数。

我们可以通过短除法来找到最大公因数。

以两个整数a和b为例，我们首先将a除以b，并取得余数r。

然后，将b除以r，并再次取得余数r1。

我们重复这个过程，直到余数为0为止。

此时，最大公因数就是最后一次计算的非零余数。

例如，假设我们要求解整数36和48的最大公因数。

我们首先将36除以48，得到余数12。

然后，将48除以12，得到余数0。

因此，36和48的最大公因数是12。

接下来，让我们来解释一下什么是最小公倍数。

最小公倍数是指两个或多个整数的公有倍数中最小的一个。

我们可以通过短除法来找到最小公倍数。

以两个整数a和b为例，我们首先求解它们的最大公因数GCD。

然后，将a乘以b，再除以最大公因数GCD，即可得到最小公倍数LCM。

例如，假设我们要求解整数36和48的最小公倍数。

首先，我们计算它们的最大公因数，发现它们的最大公因数是12。

然后，我们将36乘以48，得到1728，再除以12，得到144。

因此，36和48的最小公倍数是144。

总结起来，最大公因数是两个或多个整数共有的最大因数，可以通过短除法找到；最小公倍数是两个或多个整数的公有倍数中最小的一个，可以通过将两个整数乘积除以最大公因数来求解。

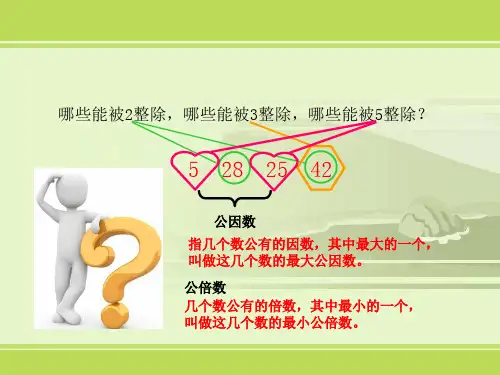
最大公因数和最小公倍数什么是最大公因数？最大公因数（GCD）是指两个或多个数中能够整除它们的最大正整数。

在数学中，最大公因数也被称为最大公约数或者最大公因子。

如何计算最大公因数？有多种方法可以计算最大公因数，其中最常用的方法是欧几里得算法。

这个算法基于如下的数学原理：两个整数a和b的最大公因数即为a除以b的余数c与b的最大公因数。

举个例子，假设我们要计算12和16的最大公因数。

我们可以通过以下步骤来执行欧几里得算法：1.令a等于较大的数字（16），令b等于较小的数字（12）。

2.用b除以a，并计算余数c。

在这种情况下，16除以12等于1，余数为4。

3.然后将b设置为a，而将c设置为新的b。

4.重复上述步骤，直到余数c为0。

此时，b即为最大公因数。

在这个例子中，最大公因数是4。

最大公因数的应用最大公因数在数学中有广泛应用。

例如，在分数运算中，我们可以通过求分子和分母的最大公因数来简化分数。

最大公因数还在密码学中发挥着关键作用。

一些加密算法，如RSA算法，依赖于对两个大质数进行运算，其中最大公因数的计算是一个关键步骤。

什么是最小公倍数？最小公倍数（LCM）是指两个或多个数中能够被它们整除的最小正整数。

最小公倍数也被称为最小公倍数或者最小公倍数。

如何计算最小公倍数？有多种方法可以计算最小公倍数，其中一种常用的方法是通过最大公因数来计算。

假设我们要计算12和16的最小公倍数，我们可以使用以下公式：LCM(a,b) = (a * b) / GCD(a,b)在这个公式中，LCM表示最小公倍数，a和b分别表示两个数字的值，而GCD 表示最大公因数。

使用这个公式，我们可以计算出12和16的最小公倍数：LCM(12,16) = (12 * 16) / 4 = 48所以，12和16的最小公倍数是48。

最小公倍数的应用最小公倍数在数学和实际生活中都有应用。

例如，在时间单位转换中，我们可以通过求两个时间单位的最小公倍数来进行换算。

最小公倍数与最大公因数的求法最小公倍数和最大公因数，听起来像是数学课上那些让人头疼的概念，不过别担心，咱们轻松点儿聊聊。

最小公倍数，简称最小公倍数，其实就是找到几个数共同的倍数，越小越好。

就像找个大家都能接受的时间，约个饭局，大家都好安排。

比如，咱们找 4 和 6 的最小公倍数，4 的倍数有 4、8、12、16，6 的倍数有 6、12、18，嘿，12 是个大家都能接受的选择，最小公倍数就定了。

说到最大公因数，咱们就像在找一群人里能一起干活的那几个，大家干得最起劲儿。

最大公因数，就是能同时整除几个数的最大数。

比如说，8 和 12，这俩数的公因数有 1、2、4，4 就是最大的一个。

想象一下，四个人一起去旅行，大家都能住的地方，就是最大公因数，能同时容得下所有人的那个地方。

找最小公倍数的时候，最简单的办法就是把数列写出来，然后找出最小的那个。

不过，咱们也可以用一种更聪明的方法，叫做“分解质因数”。

这就像拆家，把数拆成最基本的元素。

比如，4 可以拆成2 × 2，6 拆成2 × 3，然后把所有质因数取个最大次数，比如这里的 2 最大出现 2 次，3 最大出现 1 次，最后把它们乘在一起，结果就是 12，哎，这方法简单又高效。

说到最大公因数，咱们同样可以用分解质因数的办法，先把每个数拆解成质因数，然后找出相同的部分。

就像寻找团队里最能干的那几个人，留住最牛的，最终把他们的力量汇聚起来。

比如 8 拆成2 × 2 × 2，12 拆成2 × 2 × 3，嘿，能一起干活的就是2 × 2，最后最大公因数就是 4，找个合适的地方，大家一起把事情做好。

当你在生活中碰到这些数学问题时，别觉得这难上加难。

找最小公倍数和最大公因数其实就像在生活中寻求平衡。

像朋友间的关系，偶尔得妥协，找到一个大家都满意的折中点，才能继续走得更远。

用数学的眼光来看，生活的方方面面都有这些公因数和倍数在潜藏，只是我们未必注意到罢了。