浙江省慈溪市区域性八年级数学竞赛试卷含答案

2021-2022学年第一学期慈溪市八年级学科竞赛数学试题一．选择题（共10小题，每小题3分，共30分）1．下面的图形是以科学家名字命名的，其中是轴对称图形的有()A．1个B．2个C．3个D．4个2．已知a b<，则下列四个不等式中，不正确的是()A．22a b+<+B．1122a b<C．22ac bc<D．2121a b-->--3．小芳有两根长度为4cm和9cm的木条，她想钉一个三角形木框，桌上有下列长度的几根木条，她应该选择长度为()的木条．A．5cm B．3cm C．17cm D．12cm4．把不等式组123xx>-⎧⎨+⎩的解集表示在数轴上，下列符合题意的是()A．B．C．D．5．根据下列条件，能画出唯一ABC∆的是()A．3AB=，4BC=，7CA=B．4AC=， 3.5BC=，60A∠=︒C．45A∠=︒，60B∠=︒，75C∠=︒D．5AB=，4BC=，90C∠=︒6．如图，在ABC∆中，90BAC∠>︒，AB的垂直平分线交BC于点E，AC的垂直平分线交BC于点F，连接AE、AF，若AEF∆的周长为2，则BC的长是() A．2 B．3C．4D．无法确定7．在平面直角坐标系xOy中，对于点(,)P x y，我们把点(1,1)P y x '-++叫做点P 伴随点．已知点1A 的伴随点为2A ，点2A 的伴随点为3A ，点3A 的伴随点为4A ，⋯，这样依次得到点1A ，2A ，3A ，⋯，n A ．若点1A 的坐标为(2,4)，点2021A 的坐标为( )A ．(2,4)B ．(2,2)--C ．(3,1)D ．(3,3)-8．在平面直角坐标系中，点(3,42)P m m --不可能在第( )象限． A ．第一象限B ．第二象限C ．第三象限D ．第四象限9．如图，ABC ∆中，60BAC ∠=︒，BAC ∠的平分线AD 与边BC 的垂直平分线MD 相交于D ，DE AB ⊥交AB 的延长线于E ，DF AC ⊥于F ，现有下列结论：①DE DF =；②DE DF AD +=；③DM 平分EDF ∠；④2AB AC AE +=； 其中正确的是( ) A ．1个 B ．2个C ．3个D ．4个第9题 第10题10．勾股定理是人类最伟大的科学发现之一，我国古算书《周髀算经》中早有记载．如图1，以直角三角形的各边为边分别向外作正方形，再把较小的两张正方形纸片按图2的方式放置在最大正方形内．若知道图中阴影部分的面积，则一定能求出( ) A ．最大正方形与直角三角形的面积和 B ．最大正方形的面积C ． 直角三角形的面积D ．较小两个正方形重叠部分的面积 二．填空题（共6小题，每小题4分，共24分）11．根据数量关系：x 的3倍与1的差不大于2，可列不等式 ． 12．命题“两个全等三角形的面积相等”的逆命题是 命题（填“真”或“假”）. 13．如图，AB AC =，要直接依据ASA 证出ABE ACD ∆∆≌，应添加的一个条件是 ．14．如图，已知60BAC ∠=︒，在BAC ∠的平分线上截取4AD cm =，过点D 作DF AB ⊥于点F ，在AC 上有一点E ，若23AED S cm ∆=，则AE的长为 ．第13题 第14题 第16题15．若关于x 的不等式组2034x x a x-<⎧⎨+>-⎩恰好只有2个整数解，则所有满足条件的 整数a 的值之和是 ．16．如图，在直角坐标系中，已知点(6,0)A ，点B 为y 轴正半轴上一动点，连接AB ，以AB 为一边向下作等边ABC ∆，连接OC ，则OC 的最小值是 ． 三．解答题（共8小题，满分66分）17．（6分）解不等式组：18．（6分）如图，点E 、F 在BC 上，BE FC =，AB DC =，B C ∠=∠．求证：A D ∠=∠．19．（8分）已知y 是x 的一次函数，且当x ＝－3时，y ＝2；当x ＝1时，y ＝10．（1）求y 与x 之间的函数关系式； （2）当y ＝6时，求x 的值；232(2)121123x x x x +>-⎧⎪-+⎨-⎪⎩20．（8分）如图，ABC ∆三个顶点的坐标分别为(1,1)A 、B (4,2)、(3,4)C ．（1）若△111A B C 与ABC ∆关于y 轴成轴对称，则△111A B C 三个顶点坐标分别为：1A ，1B ，1C ；（2）若P 为x 轴上一点，则PA PB +的最小值为 ；21.（8分）已知ABC ∆中，如果过顶点B 的一条直线把这个三角形分割成两个三角形，其中一个为等腰三角形，另一个为直角三角形，则称这条直线为ABC ∆的关于点B 的二分割线．例如：如图1，Rt ABC ∆中90A ∠=︒，20C ∠=︒，若过顶点B 的一条直线BD 交AC 于点D ，若20DBC ∠=︒，显然直线BD 是ABC ∆的关于点B 的二分割线．图3 备用图（1）在图2的ABC ∆中，20C ∠=︒，110ABC ∠=︒，请在图2中画出ABC ∆关于点B 的二分割线，且DBC ∠角度是 ．（2）在图3中，已知20C ∠=︒，A 在射线CP 上，请画出不同于图1、图2的ABC ∆， 所画ABC ∆同时满足：①C ∠为最小角； ②存在关于点B 的二分割线。

2020-2021学年浙江省八年级下学期数学竞赛卷1 一．选择题（共8小题）1．设a＝﹣2，则代数式a3+4a2﹣a+6的值为（）A．6B．4C．2+2D．2﹣2【解答】解：∵a＝﹣2，∴（a+2）2＝（）2，即a2+4a＝1，∴a3+4a2﹣a+6＝a（a2+4a）﹣a+6＝a×1﹣a+6＝6．故选：A．2．关于x的方程x2﹣bx+4＝0有两个相等的正实数根，则b的值为（）A．4B．﹣4C．﹣4或4D．0【解答】解：∵关于x的方程x2+bx+4＝0有两个相等的正实数根，∴△＝b2﹣4×1×4＝b2﹣16＝0，解得：b＝4．故选：A．3．如图所示，∠A+∠B+∠C+∠D+∠E+∠F+∠G＝（）A．360°B．450°C．540°D．720°【解答】解：如图，在四边形ACEH中，∠A+∠C+∠E+∠1＝360°，在四边形BDFP中，∠B+∠D+∠F+∠2＝360°，∵180°﹣∠1+180°﹣∠2+∠G＝180°，∴∠A+∠C+∠E+∠1+∠B+∠D+∠F+∠2+180°﹣∠1+180°﹣∠2+∠G＝360°+360°+180°，∴∠A+∠B+∠C+∠D+∠E+∠F+∠G＝360°+180°＝540°．故选：C．4．如图，在Rt△ABC中，∠C＝90°，AC＝3，以AB为一边向三角形外作正方形ABEF，正方形的中心为O，且OC＝4，那么BC的长等于（）A．3B．5C．2D．【解答】解：如图，作EQ⊥x轴，以C为坐标原点建立直角坐标系，CB为x轴，CA为y轴，则A（0，3）．设B（x，0），由于O点为以AB一边向三角形外作正方形ABEF的中心，∴AB＝BE，∠ABE＝90°，∵∠ACB＝90°，∴∠BAC+∠ABC＝90°，∠ABC+∠EBQ＝90°，∴∠BAC＝∠EBQ，在△ABC和△BEQ中，∴△ACB≌△BQE（AAS），∴AC＝BQ＝3，BC＝EQ，设BC＝EQ＝x，∴O为AE中点，∴OM为梯形ACQE的中位线，∴OM＝，又∵CM＝CQ＝，∴O点坐标为（，），根据题意得：OC＝4＝，解得x＝5，则BC＝5．故选：B．5．如图正方形ABCD的顶点A在第二象限y＝图象上，点B、点C分别在x轴、y轴负半轴上，点D在第一象限直线y＝x的图象上，若S阴影＝，则k的值为（）A．﹣1B．C．D．﹣2【解答】解：如图，过点A作AG⊥x轴，过点D作DE⊥x轴，作DF⊥AG交y轴于H，∴四边形DHOE是矩形∵∠ADC＝∠HDE＝90°∴∠ADC﹣∠FDC＝∠HDE﹣∠FDC∴∠ADF＝∠CDE，∵点D在第一象限直线y＝x的图象上，∴DH＝DE，且∠ADF＝∠CDE，∠DHM＝∠DEN∴△DHM≌△DEN（ASA）∴S△DHM＝S△DNE，∴＝S四边形DHOE＝DH×DE∴DH＝DE＝同理可证：△AFD≌△BGA≌△COB≌△DHC∴AF＝HD＝BG＝OC，AG＝DF＝BO＝HC∴OC＝HD＝＝AF＝BG∴CH＝∴AG＝＝BO∴GO＝∴点A坐标（﹣，）∴k＝﹣×＝﹣故选：B．6．如图，在平行四边形ABCD中，BC＝2AB，CE⊥AB于E，F为AD的中点，若∠AEF＝54°，则∠B＝（）A．54°B．60°C．66°D．72°【解答】解：过F作FG∥AB∥CD，交BC于G；则四边形ABGF是平行四边形，所以AF＝BG，即G是BC的中点；连接EG，在Rt△BEC中，EG是斜边上的中线，则BG＝GE＝FG＝BC；∵AE∥FG，∴∠EFG＝∠AEF＝∠FEG＝54°，∴∠AEG＝∠AEF+∠FEG＝108°，∴∠B＝∠BEG＝180°﹣108°＝72°．故选：D．7．若m是关于x的方程x2﹣2020x+1＝0的根，则（m2﹣2020m+4）•（m2﹣2020m﹣5）的值为（）A．18B．﹣18C．20D．﹣20【解答】解：∵m是关于x的方程x2﹣2020x+1＝0的根，∴m2﹣2020m+1＝0，∴m2﹣2020m＝﹣1，∴（m2﹣2020m+4）•（m2﹣2020m﹣5）＝（﹣1+4）×（1﹣5）＝﹣18．故选：B．8．如图，四边形OABC为平行四边形，A在x轴上，且∠AOC＝60°，反比例函数y＝（k ＞0）在第一象限内过点C，且与AB交于点E．若E为AB的中点，且S△OCE＝8，则OC的长为（）A．8B．4C．D．【解答】解：过点C作CD⊥x轴于点D，过点E作EF⊥x轴于点F，如图：∵四边形OABC为平行四边形，∴OC＝AB，OC∥AB，∴∠EAF＝∠AOC＝60°，在Rt△COD中，∵∠DOC＝60°，∴∠DOC＝30°，设OD＝t，则CD＝t，OC＝AB＝2t，在Rt△EAF中，∵∠EAF＝60°，AE＝AB＝t，∴AF＝，EF＝AF＝t，∵点C与点E都在反比例函数y＝的图象上，∴OD×CD＝OF×EF，∴OF＝＝2t，∴OA＝2t﹣＝t，∴S四边形OABC＝2S△OCE，∴t×t＝2×8，∴解得：t＝（舍负），∴OC＝．故选：D．二．填空题（共6小题）9．已知关于x的一元二次方程（1﹣2k）x2﹣2x﹣1＝0有两个不相等的实数根，则k 的取值范围﹣3≤k＜4且k≠．【解答】解：∵关于x的一元二次方程（1﹣2k）x2﹣2x﹣1＝0有两个不相等的实数根，∴，解得：﹣3≤k＜4且k≠．故答案为：﹣3≤k＜4且k≠．10．若＜0，化简﹣﹣3的结果为﹣2x．【解答】解：由题意得，或，解得，﹣2＜x＜，则原式＝|5﹣3x|﹣|x﹣2|﹣3＝5﹣3x﹣2+x﹣3＝﹣2x，故答案为：﹣2x．11．如图，双曲线y＝（x＞0）的图象上．△OA1B1，△A1A2B2，…，△A n﹣1A n B n均为正三角形，过B1作B1C⊥x轴于C，过B2作B2D⊥x轴于D，则点A n的坐标为（，0）．【解答】解：∵点B1，B2在双曲线y＝（x＞0）的图象上，∴OC•B1C＝3，∵△OA1B1，△A1A2B2，…，△A n﹣1A n B n均为正三角形，∴B1C＝OC，∴OC＝，∴OA1＝2，∴；连接OB2，则OD•B2D＝3，∵OD＝OA1+A1D＝2+，，∴∴，∴，同理可得，，…由上可知，．故答案为：（，0）．12．P是正方形ABCD内一点，AB＝5，P A＝，PC＝5，则PB＝或2．【解答】解：如图所示，∴PB＝＝或PB＝＝2，故答案为：或2．13．已知x1，x2，x3，x4，x5为正整数，任取四个数求和，只能得到44，45，46，47这样四个结果，则这5个数的众数是11．【解答】解：根据题意，设这个重复的和为z，可得：（x1+x2+x3+x4+x5）×4＝44+45+46+47+z，可得：z＝46，可得五个数据之和为57，所以五个数据为：10，11，12，13，11，故答案为：1114．如图，已知直线y＝kx（k＞0）分别交反比例函数y＝和y＝在第一象限的图象于点A，B，过点B作BD⊥x轴于点D，交y＝的图象于点C，连接AC．若△ABC是等腰三角形，则k的值是或．【解答】解：∵点B是y＝kx和y＝的交点，y＝kx＝，∴点B坐标为（，2），同理可求出点A的坐标为（，），∵BD⊥x轴，∴点C横坐标为，纵坐标为，∴BA＝，AC＝，BC＝，∴BA2﹣AC2＝k＞0，∴BA≠AC，若△ABC是等腰三角形，①当AB＝BC时，则＝，解得：k＝±（舍去负值）；②当AC＝BC时，同理可得：k＝；故答案为：或．三．解答题（共4小题）15．已知x﹣y＝6，，求的值．【解答】解：∵x﹣y＝6，∴，∴，∵+＝•+•＝（+）＝9，∴，即，∴＝（﹣）＝×＝4．16．已知实数a，b，c满足：a+b+c＝2，abc＝4．（1）求a，b，c中的最大者的最小值；（2）求|a|+|b|+|c|的最小值．【解答】解：（1）不妨设a是a，b，c中的最大者，即a≥b，a≥c，由题设知a＞0，且b+c＝2﹣a，．于是b，c是一元二次方程的两实根，≥0，a3﹣4a2+4a﹣16≥0，（a2+4）（a﹣4）≥0．所以a≥4．又当a＝4，b＝c＝﹣1时，满足题意．故a，b，c中最大者的最小值为4．（2）因为abc＞0，所以a，b，c为全大于0或一正二负．①若a，b，c均大于0，则由（1）知，a，b，c中的最大者不小于4，这与a+b+c＝2矛盾．②若a，b，c为或一正二负，设a＞0，b＜0，c＜0，则|a|+|b|+|c|＝a﹣b﹣c＝a﹣（2﹣a）＝2a﹣2，由（1）知a≥4，故2a﹣2≥6，当a＝4，b＝c＝﹣1时，满足题设条件且使得不等式等号成立．故|a|+|b|+|c|的最小值为6．17．如图，四边形ABCD是矩形，E是对角线BD上不同于B、D的任意一点，AF＝BE，∠DAF＝∠CBD．（1）求证：△ADF≌△BCE；（2）求证：四边形ABEF是平行四边形；（3）试确定当点E在什么位置时，四边形AEDF为菱形？并说明理由．【解答】（1）证明：∵四边形ABCD是矩形，∴AD＝BC，在△ADF和△BCE中，，∴△ADF≌△BCE（SAS）；（2）证明：∵四边形ABCD是矩形，∴AD∥BC，∠BAD＝90°，∴∠DBC＝∠ADB，∵∠DAF＝∠CBD，∴∠DAF＝∠ADB，∴AF∥BE，∵AF＝BE，∴四边形ABEF是平行四边形；（3）解：当E为BD的中点时，四边形AEDF变为菱形，理由如下：如图所示：∵E为BD的中点，∠BAD＝90°，∴AE＝BE＝DE，∵AF＝BE，AF∥BD，∴AF∥DE，AF＝DE，AF＝AE，∴四边形AEDF是平行四边形，∴四边形AEDF是菱形．18．请你利用直角坐标平面上任意两点（x1，y1），（x2，y2）间的距离公式d＝解答下列问题：已知：反比例函数y＝与正比例函数y＝x的图象交于A，B两点（A在第一象限），点F1（﹣2，﹣2），F2（2，2）在直线y＝x上．设点P（x0，y0）是反比例函数y＝图象上的任意一点，记点P与F1，F2两点之间的距离之差d＝|PF1﹣PF2|．（1）试比较线段AB的长度与d的大小，并由此归纳出双曲线的一个重要定义（用简练的语言表述）．（2）现请你在反比例函数y＝第一象限内的分支上找一点P，使点P到F2（2，2）和点C（6，4）的距离之和最小，求点P的坐标．【解答】：解由y＝和y＝x组成的方程组可得A、B两点的坐标分别为，（，）、（﹣，﹣），线段AB的长度＝4．∵点P（x0，y0）是反比例函数y＝图象上一点，∴y0＝．∴PF1＝＝||，PF2＝＝||，∴d＝|PF1﹣PF2|＝|||﹣|||，当x0＞0时，d＝4；当x0＜0时，d＝4．因此，无论点P的位置如何，线段AB的长度与d一定相等．由此可知：到两个定点的距离之差（取正值）是定值的点的集合（轨迹）是双曲线．（2）由条件PF2＝PF1﹣4，知PF2+PC＝PF1+PC﹣4，由F1，﹣P，C三点共线时最小，此时可解得P（2，1）．。

慈溪数学初二竞赛试题及答案一、选择题（每题3分，共30分）1. 下列哪个数是最小的正整数？A. -3B. 0C. 1D. 22. 如果一个数的平方等于16，那么这个数是？A. 4B. -4C. 4或-4D. 163. 一个直角三角形的两个直角边的长度分别是3和4，那么斜边的长度是多少？A. 5B. 6C. 7D. 84. 如果一个圆的半径是5，那么它的面积是多少？A. 25πB. 50πC. 25D. 505. 一个数列的前三项是1，3，6，那么第四项是多少？A. 10B. 9C. 12D. 156. 一个长方体的长、宽、高分别是4cm、3cm和2cm，它的体积是多少？A. 24cm³B. 36cm³C. 48cm³D. 60cm³7. 一个数的立方根是5，那么这个数是多少？A. 125B. 25C. 5D. 158. 一个分数的分子是15，分母是25，化简后是多少？A. 3/5B. 1/2C. 5/4D. 15/259. 一个正数的倒数是1/4，这个数是多少？A. 4B. 1C. 2D. 310. 一个数的绝对值是5，这个数可能是？A. 5B. -5C. 5或-5D. 0二、填空题（每题2分，共20分）11. 一个数的平方是25，这个数是________。

12. 一个直角三角形的斜边长是13，一个直角边长是5，另一个直角边长是________。

13. 一个圆的周长是44cm，它的半径是________。

14. 一个数列的前四项是1，3，6，10，那么第五项是________。

15. 一个长方体的体积是96cm³，长是4cm，宽是3cm，高是________。

16. 一个数的立方是-27，这个数是________。

17. 一个分数的值是2/3，它的倒数是________。

18. 一个正数的绝对值是3，这个数是________。

19. 一个数的平方根是4，这个数是________。

浙教版八年级数学竞赛试题卷（一、精心选一选（本题有10个小题，每小题4分，共40分）下面每小题给出的四个选项中，只有一个是正确的，请把正确选项前的字母填在相应的括号内。

1． 不论x 、y 为何实数，346422+-+-y y xy x 的值总是 （ ）A.正数B.负数 C . 0 D. 非负数2． 一次函数y=ax-3a+1的图象必通过一定点,此定点坐标是 （ ） A. （1，3） B. （0，1） C. （3，1） D.（0，3）3．若关于x 的方程x 2-2k x-1=0有两个不相等的实数根，则直线y=kx +3必不经过 （ ）A. 第三象限B. 第四象限C. 第一、二象限D. 第三、四象限 4．某商品的进价是100元，标价为150元，商店要求以利润率不低于5%的售价打折出售，售货员最低可打 （ ）A.8折B. 7折C.6折D. 9折 5．梯形的两底角之和为900，上底长为5，下底长为11，则连结两底中点的线段长是 （ ）A. 3B.4C.5D.6 6．已知M （3，2）、N （1，-1），点P 在y 轴上，使PM+PN 最短，则点P 的坐标是（ ）A ．（0，21-） B. （0，0） C. （0，611） D.（0，41-）7．如果等腰三角形一腰上的高线等于腰长的一半,那么它的底角等于 （ ）A ．750 B. 150 C. 300 D 750或1508．如图,D 、E 分别是△ABC 的边BC 、AC 上的点，若AB=AC ，AD=AE ，∠α=300时，则∠CDE （ ） A ．150 B.300 C.450 D.2009．某商店有5袋面粉，各袋重量在25～30公斤之间，店里有一磅秤，但只有能称50～70公斤重量的秤砣，现要确定各袋面粉的重量，至少要称 （ ）A ．4次B ．5次C ．6次 D. 7次10．如图，正方形ABCD 的边长为2，点E 在AB 边上．四边形EFGB 也为正方形，设△AFC 的面积为S ，则 （ ） A ．S=2 B ．S=2.4 C ．S=4 D ．S 与BE 长度有关二．细心填一填（本题有10个小题，每小题4分，共40分）11．如果不等式组⎩⎨⎧<->-01a x x 无解，则a 的取值范围是____________12．如图的号码是由14位数字组成的，每一位数字写在下面的方格中，若任何相邻的三个数字之和都等于14，则x 的值等于13. 若一个数的平方根等于这个数的立方根，则这个数是14．.如图是2002年北京第24届国际数学家大会会标，它由4个全等 的直角三角形拼合而成，若图中大、小正方形的面积分别为13和1， 则直角三角形的较长直角边长为 .15．如图△ABC 中，AC ＞AB ，AB=4，AC=x ，AD 平分∠BAC ，BD ⊥AD 于D ，点E 是BC 的中点，DE=y ，则y 关于x 的 函数关系式为 16．已知1=-b a ，122-=-b a ，则=-20082008b a_________17.已知方程0119992001)2000(2=-⨯-x x 较大的根为α，方程0199919982=-+x x 较小的根为βαβ-则,的值是 。

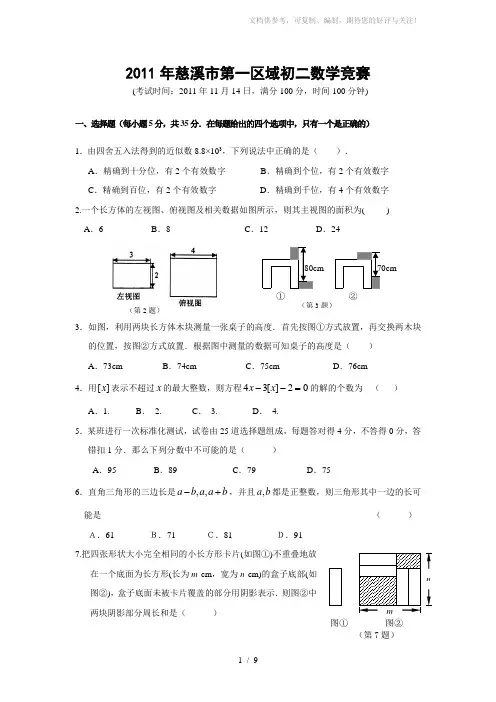
2011年慈溪市第一区域初二数学竞赛(考试时间：2011年11月14日，满分100分，时间100分钟)一、选择题（每小题5分，共35分．在每题给出的四个选项中，只有一个是正确的） 1．由四舍五入法得到的近似数8.8×103，下列说法中正确的是（ ）．A ．精确到十分位，有2个有效数字B ．精确到个位，有2个有效数字C ．精确到百位，有2个有效数字D ．精确到千位，有4个有效数字 2.一个长方体的左视图、俯视图及相关数据如图所示，则其主视图的面积为( ) A ．6 B ．8 C ．12 D ．243．如图，利用两块长方体木块测量一张桌子的高度．首先按图①方式放置，再交换两木块的位置，按图②方式放置．根据图中测量的数据可知桌子的高度是（ ） A ．73cmB ．74cmC ．75cmD ．76cm4．用[]x 表示不超过x 的最大整数，则方程43[]20x x --=的解的个数为 （ ） A ．1. B ． 2. C ． 3. D ． 4.5．某班进行一次标准化测试，试卷由25道选择题组成，每题答对得4分，不答得0分，答错扣1分．那么下列分数中不可能的是（ ） A ．95B ．89C ．79D ．756．直角三角形的三边长是b a a b a +-,,，并且b a ,都是正整数，则三角形其中一边的长可能是 （ ） Ａ．61Ｂ．71 Ｃ．81Ｄ．917.把四张形状大小完全相同的小长方形卡片(如图①)不重叠地放在一个底面为长方形(长为m cm ，宽为n cm)的盒子底部(如图②)，盒子底面未被卡片覆盖的部分用阴影表示．则图②中两块阴影部分周长和是（ ）（第2题）图① 图②nm80cm①70cm②（第3题）(第11题)ADBE C(A) 4n cm (B) 4m cm (C) 2(m +n ) cm (D)4(m －n ) cm二、填空题 (每小题5分，共35分) 8．已知关于x 的分式方程211a x +=+的解是非正数，则a 的取值范围是 . 9．某班共30人，其中15人喜爱篮球运动，10人喜爱兵乓球运动，8人对这两项运动都不喜爱，则喜爱篮球运动但不喜爱乒乓球运动的人数为_ __．10．如图，已知直线1l ∥2l ∥3l ∥4l ，相邻两条平行直线间的距离都是1，如果正方形ABCD的四个顶点分别在四条直线上，则正方形ABCD 的面积是 ．11．如图，在△ABC 中，AB =AC ，D 、E 是△ABC 内两点，AD 平分∠BAC ，∠EBC =∠E =60°，若BE =6cm ，DE =2cm ，则BC = cm ．12．张斌卖起布来了，他自定零售价比批发价高40％．但他发现，由于他所用的米尺不准确，他只赚了39％。

一、选择题（每题5分，共20分）1. 下列各数中，绝对值最小的是（）A. -3B. 2C. 0D. -22. 若x=3，则x²-2x+1的值为（）A. 2B. 3C. 4D. 53. 已知a、b、c是等差数列的前三项，且a+b+c=12，则a²+b²+c²的值为（）A. 36B. 48C. 60D. 724. 在△ABC中，∠A=45°，∠B=60°，则△ABC是（）A. 直角三角形B. 等腰三角形C. 等边三角形D. 不等边三角形5. 已知一元二次方程x²-3x+2=0，则它的解为（）A. x₁=1，x₂=2B. x₁=2，x₂=1C. x₁=1，x₂=3D. x₁=3，x₂=1二、填空题（每题5分，共25分）6. 若m+n=5，m²+n²=23，则m-n的值为______。

7. 在等腰三角形ABC中，底边AB=6，腰AC=8，则三角形ABC的周长为______。

8. 若一元二次方程x²-4x+3=0的两根为a和b，则a²+b²的值为______。

9. 在△ABC中，∠A=45°，∠B=60°，则∠C的度数为______。

10. 若x=2，则x²-4x+3的值为______。

三、解答题（每题10分，共30分）11. （10分）已知等差数列{an}的前三项分别为2，5，8，求该数列的通项公式。

12. （10分）已知等比数列{bn}的前三项分别为1，3，9，求该数列的通项公式。

13. （10分）在△ABC中，∠A=45°，∠B=60°，AB=8，求BC和AC的长度。

四、证明题（10分）14. （10分）证明：在△ABC中，若∠A=45°，∠B=60°，则AC²=2AB×BC。

答案：一、选择题1. C2. C3. B4. C5. A二、填空题6. 17. 228. 169. 75°10. -3三、解答题11. an=3n-112. bn=3^(n-1)13. BC=4√3，AC=4√3四、证明题14. 证明：在△ABC中，∠A=45°，∠B=60°，∠C=75°。

慈溪市2009学年第一学期区域性八年级数学竞赛试卷（2009年12月6日下午1：00—3：00）一、选择题（每小题4分，共24分）1、已知实数a 在数轴上的位置如图所示，则化简|1|a -的结 果为（▲）（2009年湖南长沙中考试题）A 、1B 、1-C 、12a -D 、21a -2、如图2，长方体的长为15，宽为10，高为20，点B 离点C 的距离为5，一只蚂蚁如果要沿着长方体的表面从点A 爬到点B ，需要爬行的最短距离是( ▲ ) （2009年湖北省恩施市中考题）A 、B 、25 C、 D 、 353、如图，已知△ABC 中，∠ABC ＝90°，AB ＝BC ，三角形的顶点在相互平行的三条直线l 1，l 2，l 3上，且l 1，l 2之间的距离为2 , l 2，l 3之间的距离为3 ,则AC 的长是（▲） （2009年浙江省丽江市中考题）A 、172B 、52C 、24D 、74、一宾馆有二人间、三人间、四人间三种客房供游客租住，某旅行团20人准备同时租用这三种客房共7间，如果每个房间都住满，租房方案有（▲） （2009年齐齐哈尔中考题）A 、4种B 、3种C 、2种D 、1种5、如图，点A 的坐标是（2，2），若点P 在x 轴上，且△APO 是等腰三角形，则点P 的坐标不可能．．．是（▲） （2009年重庆綦江中考题）A 、(4，0)B 、（1，0）C 、（－22，0）D 、（2，0）6、某校数学课外小组，在坐标纸上为学校的一块空地设计植树方案如下：第k 棵树种植在点)(k k k y x P ，处，其中11=x ，11=y ，当k ≥2时，⎪⎪⎩⎪⎪⎨⎧---+=----+=--]52[]51[])52[]51([5111k k y y k k x x k k k k ，[a ]表示非负实数a 的整数部分，例如[2.6]=2，[0.2]=0。

按此方案，第2009棵树种植点的坐标为（▲） （2009年杭州市中考题）图2l 1l 2l 3ACBA 、（5，2009）B 、（6，2010）C 、（3，401）D 、（4，402） 二、填空题（每小题5分，共50分）7、某校三个绿化小组一天植树的棵数如下:10，x ，8，已知这组数据只有一个众数且众数等于中位数，那么这组数据的平均数是▲（2009年黑龙江佳木斯市中考题） 8、已知关于的不等式组只有四个整数解，则实数的取值范围是▲（2009年湖南长沙中考题）9、如图，四边形ABCD 中，AB ＝BC ，∠ABC ＝∠CDA ＝90°，BE⊥AD 于点E ，且四边形ABCD 的面积为8，则BE ＝▲ （2009年白银市中考题）10、如图，把一个棱长为3的正方体的每个面等分成9个小正方形，然后沿每个面正中心的一个正方形向里挖空（相当于挖 去了7个小正方体），所得到的几何体的表面积是▲ （2009年湖北省孝感市中考题）11、在中，为的中点，动点从点出发，以每秒1的速度沿的方向运动．设运动时间为，那么当▲秒时，过、两点的直线将的周长分成两个部分，使其中一部分是另一部分的2倍．（2009年襄樊市中考题） 12、如图，在锐角△ABC 中，AB ＝42，∠BAC ＝45°，∠BAC 的平分线交BC 于点D ，M 、N 分别是AD 和AB 上的动点，则BM+MN 的最小值是▲（2009年陕西省中考题）13、在二行三列的方格棋盘上沿骰子的某条棱翻动骰子（相对面上分别标有1点和6点，2点和5点，3点和4点），在每一种翻动方式中，骰子不能后退．开始时骰子如图（1）那样摆放，朝上的点数是2；最后翻动到如图（2）所示的位置，此时骰子朝上的点数不可能．．．的．数 是▲（2009陕西省太原市）14、把一张纸片剪成4块，再从所得的纸片中任取若干块，每块又剪成4块，像这样依次地进行下去，到剪完某一次为止。

一、选择题（每题5分，共25分）1. 若m^2 - 4m + 3 = 0，则m的值为：A. 1B. 2C. 3D. 42. 在等差数列{an}中，若a1 = 3，公差d = 2，则第10项a10的值为：A. 23B. 25C. 27D. 293. 已知一次函数y = kx + b（k≠0），若点（1，2）在直线y = kx + b上，则k 和b的值分别为：A. k = 2，b = 0B. k = 1，b = 1C. k = 2，b = 1D. k = 1，b = 24. 在三角形ABC中，∠A = 45°，∠B = 60°，则∠C的度数为：A. 45°B. 60°C. 75°D. 90°5. 若一个长方体的长、宽、高分别为a、b、c，则它的体积V为：A. V = abcB. V = ab + bc + caC. V = a^2 + b^2 + c^2D. V = (a + b + c)^2二、填空题（每题5分，共25分）6. 若a + b = 5，ab = 6，则a^2 + b^2的值为______。

7. 在直角坐标系中，点P（2，3）关于x轴的对称点坐标为______。

8. 若一个正方形的对角线长为10cm，则它的边长为______cm。

9. 已知圆的半径为r，则它的面积S为______。

10. 若一个三角形的两边长分别为3cm和4cm，第三边长为5cm，则它是一个______三角形。

三、解答题（每题10分，共30分）11. 解方程：2x^2 - 5x + 2 = 0。

12. 已知等差数列{an}中，a1 = 2，公差d = 3，求第n项an的表达式。

13. 已知一次函数y = kx + b（k≠0），若它经过点（1，-2）和点（3，4），求该函数的解析式。

四、应用题（每题15分，共30分）14. 某商店有一种商品，原价为m元，售价为n元。

2010学年第二学期八年级慈溪市部分学校数学竞赛试卷（5月15日下午1：00——3：00 满分120分）一、选择题（每小题4分，共24分）1．在一个不透明的口袋中放着红色、黑色、黄色的橡皮球共有30个，它们除颜色外其它全相同．小刚通过多次摸球试验后发现从中摸到红色球或黄色球的频率稳定在0.15和0.45之间，则口袋中黑色球的个数可能是 （ ▲ ） A ．14 B ．20 C ．9 D ．62．已知点A 的坐标为（2，3），O 为坐标原点，连结OA ，将线段OA 绕点O 按逆时针方向旋转90°得OA 1，再将点A 1作关于x 轴对称得到A 2，则A 2的坐标为（ ） A ．（－2，3）B ．（－2，－3）C ．（－3，2）D ．（－3，－2）3．若不等式组0,122x a x x +⎧⎨->-⎩≥有解，则a 的取值范围是（ ▲ ）A ．1a >-B ．1a ≥-C ．1a ≤D ．1a <4．一些完全相同的小正方形搭成一个几何体，这个几何体从正面和左面看所得的平面图形均如图所示，小正方体的块数可能有（ ▲ ） A ．7种 B ．8种 C ．9种 D ．10种5．如图，在ABC 中，∠BAC 、∠BCA 的平分线相交于点I ，若∠B=35°，BC=AI+AC ，则∠BAC 的度数为（ ▲ ）A ．60°B ．70°C ．80°D ．90°6．如图，△AP 1B 中，BP 1⊥AP 1，AP 1=2，∠A=30°，P 1Q 1⊥AB ，Q 1P 2⊥AP 1，P 2Q 2⊥AB ，Q 2P 3⊥AP 1……，P n Q n ⊥AB ，P n+1Q n ⊥AP 1，则S=P 1Q 1+P 2Q 2+…+P n Q n +…的值为（ ▲ ）ICBA第5题图第6题图30°第４题图第15题图A ．2B ．３C ．４D ．８ 二、填空题（每小题5分，共50分）7．若03=+b a （b ≠0），则22222(1)24b a ab b a b a b++-÷=+- ▲ 8．计算：(30213)(3107)+-+-的值等于 ▲9．一枚质地均匀的正方体骰子的六个面上的数字分别是1，2，2，3，3，4；另一枚质地均匀的正方体骰子的六个面上的数字分别是1，3，4，5，6，8. 同时掷这两枚骰子，则其朝上的面两数之和为5的概率是 ▲ 10．对正实数b a ,定义运算法则b a ab b a ++=*2，若103=*x ，则x 的值是 ▲11．已知42a b n +=+，1=ab ，若221914919a ab b ++的值为2011，则n = ▲ .12．若关于x 的方程223=+-x mx 的解是负数，则m 的取值范围为 ▲ 13．如图，直线y kx b =+经过(21)A ，，(12)B --，两点， 则不等式122x kx b >+>-的解集为 ▲14．将一组数2，2，6，22，10，…，251按图中的方法进行排列若32的位置记为（2，3），27的位置记为（3，2），则这组数中最大的有理数．．．n 的位置记为 ▲ 15．如图，在长方形ABCD 中，AD ＝6，AB ＝4，点E 、G 、H 、F 分别在AB 、BC 、CD 、AD 上，且AF ＝CG ＝2，BE ＝DH ＝1，点P 是直线EF 、GH 之间任意一点，连结PE 、PF 、PG 、PH ，则△PEF 和△PGH 的面积和等于 ▲16．勾股定理有着悠久的历史，它曾引起很多人的兴第16题图yxO A B第13题趣．l955年希腊发行了二枚以勾股图为背景的邮票．所谓勾股图是指以直角三角形的三边为边向外作正方形构成，它可以验证勾股定理．在上图的勾股图中，已知∠ACB=90°，∠BAC=30°，AB= 8．作△PQR 使得∠R=90°，点H 在边QR 上，点D ，E 在边PR 上，点G ，F 在边PQ 上，那么△PQR 的周长等于 ▲三、解答题（共四小题，46分）17（12分）．若已知关于x 的方程2(2)(4)0x x x m --+=有三个实根。

2014年慈溪市“我爱数学”初二数学竞赛(考试时间：2014年12月28日，满分120分，时间120分钟)一、选择题（每小题4分，共32分．在每题给出的四个选项中，只有一个是正确的）1．当y 取某一实数值时，代数式(2)(2)2()()23x y x y x y x y x y -+--+-+的值与x 的取值无关，则这个y 的值为（ A ）A ．23-B ．23C ．1D ．1-原代数式=(32)3x y y -++，因与x 的取值无关，所以，23203y y +=⇒=-2．甲、乙、丙三个同学中有且只有一人做了好事，他们三人各作了如下表述：甲：我没有做好事； 乙：是甲做了好事； 丙：是我做了好事．老师知道他们中只有一人说了假话．聪明的同学你知道是（ C ）做了好事． A ．甲 B ．乙 C ．丙 D ．不能确定谁 列表即可，3．如图，将正方形纸片对折后展开（图④是连续两次对折后再展开），再按图示方法折叠（把 一个直角三角形折叠上去），在图①，②，③，④四个图形中，能够找到一个锐角为30的直 角三角形的图形有（ B ）A ．1 个B ．2个C ．3个D ．4个此题为2012年山东淄博中考题。

如下图只有①②有30度角，而③④中一直角边是另一直角边的一半，不存在30度角4．已知x 为任意实数，a =21x x --+，则1a -最大值为（ C ） A ．2 B ．3 C ．4 D ．5图② 图① 图③ 图④ 甲 乙 丙 结论 假 真 真 不可能 真 假 真 可能 真真假不可能3(1)2112(12)3(2)x a x x x x x <-⎧⎪=--+=--≤≤⎨⎪->⎩5．已知四条直线2x =，1y =，2y =-，5y mx =-所围成的四边形的面积为21，则m = （ D ） A ．12 B ．109- C ．910-或2 D ．12或910- 如图，当0m >时，A （2，1），B （2，-2），C （3(,2)m -，D 6(,1)m所围成的四边形ABCD 的面积为： 3622132122m m m -+-⨯=⇒=当0m <时，同理可得910m =-6．计算：4242424242424242(221)(441)(661)(12121)(331)(551)(771)(13131)++++++++++++++++=（ A ）A ．161 B ．3157 C ．2934 D ．14416942222221(1)(1)(1)a a a a a a a a ++=+-=++-+原式=(73)(2113)(4331)(7357)(11191)(157133)31(137)(3121)(5743)(9173)(133111)(183157)18361⨯⨯⨯⨯⨯⨯==⨯⨯⨯⨯⨯⨯7．如图，在等腰直角△ABC 中，∠ABC =90，点A 在x 轴负半轴上，点B 在y 轴正半轴上， 点C 在第四象限，其横坐标为2，若BC 交x 轴于M ，AM 平分 ∠BAC ，则点C 的纵坐标为（ B ）A ．2-B ．2-C ．3-D ．32-如图，过C 作x 轴的垂线交AB 的延长线于D 点，过C 作y 轴的垂线 交y 轴于E 点，设点(2,)C m ，则 22(0,2),(2,):2(,0)2222m B C m BC y x M m OM m --⇒=+⇒--⇒=-又易证：2AOB BCE OA BE m ≅⇒==-2(2)(2)BCD AOB OM AM OA CD BE m m m ≅⇒=-=-=---=-+由22(2)422m m m m -=-+⇒=⇒=--xyOA B CM （第7题）y=mx-5y=2y=1x=2DCBAO8．某次考试，试题共6题，均为判断题．考生认为对的打“√”，认为错的打“×”，也可不答．记分方法是每道题答对给2分，不答给1分，答错不给分．已知甲、乙、丙、丁、戊、己、庚七名同学 的答案及其中六个人的得分如表中所示，则庚同学的得分为（ C ） A ．4 B ．6 C ．8 D ．10 同学 题号甲 乙 丙 丁 戊 己 庚 1 √ √ √ × × √ 2 √ × × √ × × 3 √ × √ × × × 4 √ √ × × √ √ 5 √ × √ √ × √ 6 √ √ × × × × 得分755597此题是1989年“从小爱数学”邀请赛试题，也曾作2010年国家公务员招聘考试题。