两自由度机械手动力学问题

格式：doc
大小：795.00 KB
文档页数：8

下载文档原格式

/ 8

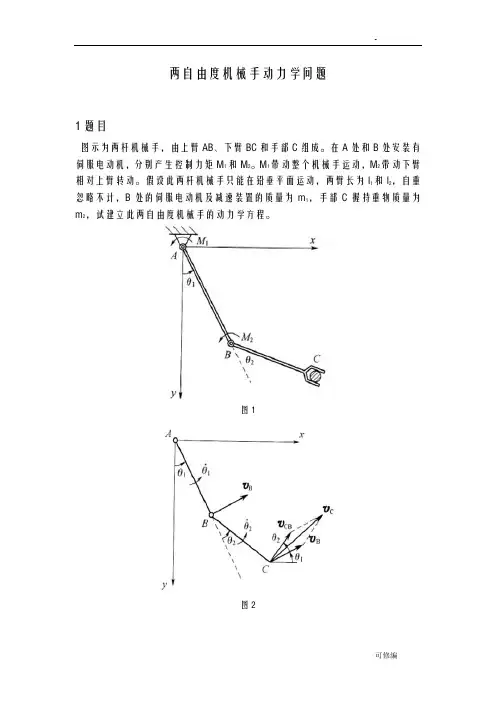
两自由度机械手动力学问题

两自由度机械手动力学问题1题目图示为两杆机械手，由上臂AB、下臂BC和手部C组成。

在A处和B处安装有伺服电动机，分别产生控制力矩M1和M2。

M1带动整个机械手运动，M2带动下臂相对上臂转动。

假设此两杆机械手只能在铅垂平面运动，两臂长为l1和l2，自重忽略不计，B处的伺服电动机及减速装置的质量为m1，手部C握持重物质量为m2，试建立此两自由度机械手的动力学方程。

图1图22数值法求解2.1拉格朗日方程此两杆机械手可以简化为一个双摆系统，改双摆系统在B 、C 出具有质量m 1,m 2,在A 、B 处有控制力矩M 1和M 2作用。

考虑到控制力矩M 2的作用与杆2相对杆1的相对转角θ2有关，故取广义力矩坐标为2211,θθ==q q系统的动能为二质点m 1、m 2的动能之和，即由图2所示的速度矢量关系图可知以A 处为零势能位置，则系统的势能为由拉格朗日函数，动势为：广义力2211,M Q M Q ==求出拉格朗日方程中的偏导数，即代入拉格朗日方程式,整理得:2.2 给定条件（1）角位移运动规律()231*52335.0*1163.0t t t +-=θ，()232*52335.0*1163.0t t t +-=θ21θθ和都是从0到90°，角位移曲线为三次函数曲线。

（2）质量m 1=4㎏ m 2=5kg （3）杆长l 1=0.5m l 2=0.4m2.3 MATLAB 程序t=0:0.1:3;theta1=-0.1163*t.^3+0.52335*t.^2; w1=-0.3489*t.^2+1.0467*t; a1=-0.6978*t+1.0467;theta2=-0.1163*t.^3+0.52335*t.^2; w2=-0.3489*t.^2+1.0467*t; a2=-0.6978*t+1.0467;m1=4; m2=5;l1=0.5; l2=0.4; g=9.8;D11=(m1+m2)*l1.^2+m2*l2.^2+2*m2*l1*l2*cos(theta2); D22=m2*l2.^2;D12=m2*l2.^2+m2*l1*l2*cos(theta2); D21=m2*l2.^2+m2*l1*l2*cos(theta2); D111=0;D122=-m2*l1*l2*sin(theta2); D222=0;D211=m2*l1*l2*sin(theta2); D112=-m2*l1*l2*sin(theta2); D121=-m2*l1*l2*sin(theta2); D212=0; D221=0;D1=(m1+m2)*g*l1*sin(theta1)+m2*g*l2*sin(theta1+theta2); D2=m2*g*l2*sin(theta1+theta2);M1=D11.*a1+D12.*a2+D111.*w1.^2+D122.*w2.^2+D112.*w1.*w2+D121.*w2.*w1+D1; M2=D21.*a2+D22.*a2+D211.*w1.^2+D222.*w2.^2+D212.*w1.*w2+D221.*w2.*w1+D2; T1=polyfit(t,M1,3) T2=polyfit(t,M2,3)subplot(2,1,1),plot(t,M1),grid on,xlabel('时间（s ）'),ylabel('控制力矩（N ·m ）'),title('motion1') subplot(2,1,2),plot(t,M2),grid on,xlabel('时间（s ）'),ylabel('控制力矩（N ·m ）'),title('motion2')2.4 数值计算结果()6167.1*7993.31*7329.3*5685.3t 231+++-=t t t M ()5449.1*9801.25*9481.8*0679.0t 232-+--=t t t M图3 M 1变化规律图图4 M2变化规律图3 ADAMS仿真3.1模型建立图5 模型图3.2 施加运动在两个关节处分别施加位移函数图6 关节运动施加图位移函数为：step(time,0,0,3,pi/2)运动规律如下图所示：图7 关节处运动规律图3.3 运动仿真设置仿真时间为3s,步数为300步，仿真结果如下图所示：图8 关节1处控制力矩仿真结果图图9 关节2处控制力矩仿真结果图4 结果对比图10 控制力矩M1结果对比图图11控制力矩M2结果对比图从函数规律上看，两种求解方法得出的结果几乎一样；从数值上看：t 0 0.5 1.0 1.5 2 2.5 3.0 数值计算M1 7.1699 14.3348 33.4367 49.4650 51.6557 44.8470 40.0971 仿真求解M1 7.4526 14.5646 33.5798 49.5093 51.5775 44.6398 39.8039表2 控制力矩M2数值结果对比由上两表可以看出：数值计算结果与仿真求解结果相差很小，误差围为0.437%-0.731%，出现这种结果的原因可能是因为两种方法计算的精度不同，或者是算法存在差异。

机械系统动力学作业---平面二自由度机械臂运动学分析

机械系统动力学作业---平面二自由度机械臂运动学分析-标准化文件发布号：（9456-EUATWK-MWUB-WUNN-INNUL-DDQTY-KII平面二自由度机械臂动力学分析[摘要] 机器臂是一个非线性的复杂动力学系统。

动力学问题的求解比较困难，而且需要较长的运算时间，因此，这里主要对平面二自由度机械臂进行动力学研究。

本文采用拉格朗日方程在多刚体系统动力学的应用方法分析平面二自由度机械臂的正向动力学。

经过研究得出平面二自由度机械臂的动力学方程，为后续更深入研究做铺垫。

[关键字] 平面二自由度机械臂动力学拉格朗日方程一、介绍机器人是一个非线性的复杂动力学系统。

动力学问题的求解比较困难，而且需要较长的运算时间，因此，简化解的过程，最大限度地减少工业机器人动力学在线计算的时间是一个受到关注的研究课题。

机器人动力学问题有两类：(1) 给出已知的轨迹点上的，即机器人关节位置、速度和加速度，求相应的关节力矩向量Q r。

这对实现机器人动态控制是相当有用的。

(2) 已知关节驱动力矩，求机器人系统相应的各瞬时的运动。

也就是说，给出关节力矩向量τ，求机器人所产生的运动。

这对模拟机器人的运动是非常有用的。

二、二自由度机器臂动力学方程的推导过程机器人是结构复杂的连杆系统，一般采用齐次变换的方法，用拉格朗日方程建立其系统动力学方程，对其位姿和运动状态进行描述。

机器人动力学方程的具体推导过程如下：(1) 选取坐标系，选定完全而且独立的广义关节变量θr ，r=1, 2,…, n。

(2) 选定相应关节上的广义力F r：当θr是位移变量时，F r为力；当θr是角度变量时，F r为力矩。

(3) 求出机器人各构件的动能和势能，构造拉格朗日函数。

(4) 代入拉格朗日方程求得机器人系统的动力学方程。

下面以图1所示说明机器人二自由度机械臂动力学方程的推导过程。

1、分别求出两杆的动能和势能设θ1、θ2 是广义坐标，Q1、Q2是广义力。

两个杆的动能和势能分别为：式中，是杆1质心C1（,）的速度向量，是杆2质心C1（,）的速度向量。

两自由度机械系统动力学

约束方程中不含时间t时为定常约束；约束方程中含有时间t时为非定常约束。
x2 y2 l2
15
第15页/共143页
另外，可以积分的速度约束也是完整约束。例如：直线纯滚动的圆盘，速度满足如下约束关系：
x r
为速度约束，但可以积分，因此还是完整约束。
x r c
本课程只考虑完整约束，而且通常只考虑定常约束情况。
M e
(1)
拉格郎日方程为
d dt

E qi

E qi
Qi
(2)
需要证明(1)是(2)的特例。
65
第65页/共143页
证明：对于单自由度系统，拉格郎日方程应为
d E
dt

E

Me

E

1 2
J e
2

E

Je
( d )
W Fk rk 0
k
（3-3）
18
第18页/共143页
也可以写成分解形式，即
W （X kxk Ykyk Zkzk ) 0
k
（3-4）
19
第19页/共143页
说明：（1）虚位移也叫可能位移，是在约束允许的条件下可能实现的无限小位移。与时间无关，可用变分符号表示。变分与微分很相似，但对时间冻结。（2）力在虚位移上作的功叫虚功，因此虚位移原理也叫虚功原理。（3）理想约束的约束力在虚位移上不做功，所以约束力不在方程中出现。
1 2
m2l2222
46
第46页/共143页
47
第47页/共143页
48
第48页/共143页

一类二自由度并联机器人的动力学分析

ｉｕａｉｎｓｅａｆｇｒｔｏｓａｘｍｐｅ．ｅｋｙｍｏｅｉｈａｆｃｒｒｃｓｏｒｏｎｕｎｈａａｔｒｏｂｍ — ｌｓＴｈｅｄｓｗｈｃｆｅｔｗｏｋｐｅｉｉｎｗｅｅｆｕｄｏｔａｄｔｅｐｒｍｅｅｓｔｅｉ
关键词：动力学分析；模态试验；并联机器人
中图分类号：Ｔｌ；０２ＨＩ３０３９文献标志码：Ａ文章编号：０９ — １７２１）４０２ —７４３２３（０００ —３２０
ＤｙｍｉｓＡｎａｙｉｆａ２ＤＯＦｎａｃｌｓｓｏ一ＰａｒｌｅｂｏａｌｌＲｏｔ
２ＣｌｇｆｃａｉａａｄＥｅｔｎｃａｕｎｉｅｓｙｏｃｎｅｎｅｈｏｏｙａｕｎ００２，Ｃｉａ．ｏｌｅｈｎｌｎｌｒｉ，Ｔｉａｖｒｔｆｉｃｄｃｎｌｇ，Ｔｉａ３０４ｅｏＭｅｃｃｏｙＵｎｉＳｅａＴｙｈｎ）
试验．通过简化模型的模态分析，对样机进行直接的动态性能评估，获得该时变机构的模态参数变换规律．同时分析了该机构在典型位姿处的整体模型的模态，得到影响动平台精度的关键模态，确认了需要改进的结构参数．试验结果可
用于改善机构的动力学性能．过对比分析验证了本研究中提出的试验方法适用于时变模态的试验研究．通
（．天津大学机械程学院，天津３０７；２１００２．太原科技大学机械电子程学院，太原００２）３０４摘要：为了准确评价机构动态性能，以模态试验为主要内容，用Ｌ采ＭＳ动态分析系统对并联机器人进行了动力学

一种两自由度并联机构的动力学分析

针对一种三杆二自由度平面运动并联机构进行了深入的研究，详细推导了该机构的位置逆解、速度及加速度方程，并给出了该机构的雅克比矩阵，推导了该并联机构主要零部件的偏速度和偏角速度矩阵方程，采用凯恩法建立了该并联机构的动力学逆解模型。最后通过数值计算与 ADAMS 仿真相结合的方法验证了所建模型的正确性。
10
韩旭炤等：一种两自由度并联机构的动力学分析
第 10 期
Z
X2
A3
C2
兹
A2
茁2
2a O
l2
Zm B3
X
X1 C1
l1
B（1 B2） Om
Xm
茁1
A1 图 1 并联机构结构简图
Fig.1 Schematic Diagram of the Parallel Mechanism
它由杆 A iBi （i=1，2，3）、A 2A 3、B2B3 和两个滑块 Ci，i=1，，2 组
Dynamic Analysis of a 2-DOF Parallel Mechanism
HAN Xu-zhao，CHEN Yang-yang，GAO Feng，TIAN Lu
（School of Mechanical and Precision Instrument Engineering，Xi’an University of Technology，Shaanxi Xi’an 710048，China）
2 运动学解析
2.1 运动学逆解
所研究的平面二自由度并联机构结构简图，如图 1 所示。
来稿日期：2018-05-18 基金项目：陕西省科技发展计划（2013JQ7009）；陕西省教育厅科技项目（14JK1527）作者简介：韩旭炤，（1979-），男，宁夏人，博士研究生，讲师，主要研究方向：混联机床，机器人及微细加工技术

第二章两自由度机构动力学分析

则：

r
17
F2 s2
M1

r
计算广义力：
动力学方程：
r 1 2m2 r Q1 J11q 2 J q m r Q2 2 22 2
18
1 J12 q 2 Q1 J11q 动力学方程： J q 2 Q2 21 1 J 22 q
差动轮系动力学方程，可以直接应用此结论式。
16
例5：已知：J1 A , m2 , J s 2 , M 1 , F2
重力略，建立运动方程。
s2
M1
F2
分析：选广义坐标： q1 , q2 r
方法1：
1 2 1 3 i21 , i22 2 2
2 0, 即H不动，则：方法2：令q
同理
1 0, 令q
1 i 即1轮不动，则： 2 H i22
3 i22 2
求：i31 , ห้องสมุดไป่ตู้32
1 1 ( ) 8
15
2 J H iH 2
计算广义力：
此为二阶非线性微分方程，用数值解法求解。
13
例4：已知差动轮系中：
，各轮质量略。
1 , H 求：
分析：取广义坐标： q1 1 , q 2 H
1 q1 2, 2 ', 3 q1 , q2
H q2
则：
1 H
14
求：i21 , i22
第二章两自由度机构动力学分析
§2-1 两自由度机构的运动分析例：五杆机构，取 q1 1 , q2 S 4
分析：构件1由 q1 (1 ) 控制，q2 0
构件4由 q2 ( s4 ) 控制，q1 0 件2、3由

二自由度机器人动力学控制及仿真研究

拉格朗日函数方法建立机器人动力学方程，近而确立机器人动力学模型。基于永磁同步电机建立伺服控制系统，利用机器人的位置控制与电流相结合的方式完成机器人的动力学控制。利用自适应控制来完成机器人的位置控制，利用滑模控制算法控制电机。根据控制方法建立机器人和伺服控制模型，利用ＭＡＴＬＡＢ中的Ｓｉｍｕｌｉｎｋ模块进行仿真。仿真结果表明，系统
ｂｙｔｈｅｃｏｍｂｉｎａｔｉｏｎｏｆｔｈｅｐｏｓｉｔｉｏｎｃｏｎｔｒｏｌｏｆｔｈｅｒｏｂｏｔａｎｄｔｈｅｃｕｒｒｅｎｔｃｏｎｔｒｏｌｏｆｔｈｅｍｏｔｏｒＵｓｉｎｇａｄａｐｔｉｖｅｃｏｎｔｒｏｌｌｅｒｔＯ
・
对机器人控制的研究一般是将驱动电机控制和机器人的动
质量表示整个杆的质量；连杆的长度分别为ｄ和ｄ。根据机器人求逆解的方法，已知Ｃ点的运动轨迹，可求得角位移ｑ。拉格朗１３函数Ｌ＝Ｋ — Ｐ。其中，Ｌ是拉格朗１３函数，Ｋ是系统动能，Ｐ是系统位能。
杨彦平潘松峰周真诚（青岛大学自动化与电气工程学院，山东青岛２６６０７１）
摘要：根据所在研究中心机器人的工作模式，把二自由度串联型机器人的关节控制当成经典案例进行深入探讨。利用

二自由度机械臂动力学模型

二自由度机械臂的动力学模型通常涉及到两个主要的方面：几何构型和运动方程。

在建立动力学模型之前，首先需要确定机械臂的几何参数，包括每个关节的转动惯量以及各连杆的长度。

动力学模型可以分为两部分：静力学模型和动力学模型。

静力学模型关注的是力的平衡问题，即在机械臂的任意位置上，作用在机械臂上的所有外力之和等于零，所有外力矩之和也等于零。

动力学模型则进一步考虑了机械臂的运动情况，即在给定的力和力矩作用下，机械臂的运动如何变化。

为了建立动力学模型，我们通常采用牛顿-欧拉方法或者拉格朗日方法。

牛顿-欧拉方法从关节坐标出发，逐步推导出各关节的力和力矩，再结合连杆的长度，得到整个机械臂的动力学方程。

拉格朗日方法则是从能量的角度出发，利用动能和势能的关系来建立动力学方程。

具体来说，对于二自由度机械臂，其动力学方程可以表示为：
M(q)q'' + C(q, q', t)q' + G(q, t) = T(q, q', t)
其中：
- M(q) 是机械臂的质量矩阵，q是关节变量；
- q' 是关节变量的速度；
- q'' 是关节变量的加速度；
- C(q, q', t) 是由关节速度引起的科氏力和离心力等构成的矩阵；
- G(q, t) 是重力矩阵；
- T(q, q', t) 是外部施加的力和力矩。

在实际应用中，还需要对上述方程进行求解，这通常需要借助计算机模拟或数值积分方法。

通过求解动力学方程，可以预测机械臂在特定输入下的动态响应，这对于机械臂的控制系统的设计至关重要。

二自由度机械臂实验报告

二自由度机械臂实验报告实验报告课程名称: 机电系统建模与控制实验项目名称: 二自由度机械臂实验****: **组别：第6组成员：刘仕杰.胡据林.王昊阳.于骁实验日期：2019年12月9日一、实验简介二自由度（DOF）串联柔性（2DSFJ）机械臂包括两个用于驱动谐波齿轮箱（零回转间隙）的直流电机及一个双杆串联机构（）。

两个连接都是刚性的。

主连接通过一个柔性关节耦合到第一个驱动器上，在其端部载有第二个谐波驱动器，该驱动器通过另一个柔性关节与第二个刚性连接耦合。

两个电机及两个柔性关节都装有正交光学编码器。

每一个柔性关节配有两个可更换的弹簧。

使用一个翼形螺钉零件，就可沿着支撑杆，将每根弹簧端移到所希望的不同定位点。

该系统可视为多种手臂式机器人机构的高度近似，是典型的多输入多输入（MIMO）系统。

二、实验内容1. 系统开环时域动态特性和频域特性分析；2. 应用极点配置方法设计控制器，进行时域动态响应特性和频域特性分析（超调量、上升时间、震荡次数等，根据极点分布决定），改变极点分布位置，完成至少 2 组不同闭环参数性能对比；3. 应用 LQR 方法设计反馈控制律，进行时域动态响应特性和频域特性分析（超调量、上升时间、震荡次数等，根据极点分布决定），改变 Q 和 R 的值，完成至少 2 组不同闭环参数性能对比；4. 设计全阶状态观测器，完成物理 PSF 与状态观测（至少两组观测器极点位置）综合作用下的系统性能控制。

三、实验设备1.设备构造与线路图（1）直流电机#1第一台直流电机为一台可在最高27V 下工作的Maxon273759 精密刷电机（90 瓦）。

该电机可提供 3A 的峰值电流，最大连续电流为 1.2A。

注意：施用在电机上的高频信号会对电机刷造成最终损坏。

产生高频噪音的最可能来源是微分反馈。

如果微分增益过高，噪音电压会被输入到电机里。

为保护您的电机，请将您的信号频带限制控制在 50Hz以内。

（2）谐波传动器#1谐波驱动器#1 使用谐波传动器LLC 生产的CS-14-100-1U-CC-SP 谐波减速箱。

二自由度冗余驱动并联机器人的动力学建模及控制

03
二自由度冗余驱动并联机器人模型建立
动力学模型建立
确定机器人结构参数
01
根据机器人结构，确定各部分的结构参数，包括连杆长度、质
量、转动惯量等。
建立动力学方程
02
根据牛顿第二定律，建立机器人的动力学方程，包括关节扭矩
、速度和加速度等。
考虑摩擦与重力影响
03
考虑机器人运动过程中可能受到的摩擦力、重力等影响因素，
与现有技术的比较
我们将所提出的控制算法与现有的控制算法进行了比较。通过比较发现，我们所提出的控制算法在跟踪性能和抗干扰能力方面具有优势。
讨论
虽然我们在实验中取得了令人满意的结果，但仍有许多方面需要进一步研究。例如，我们可以考虑增加更多的传感器和优化机器人的结构以提高其性能。此外，我们还可以研究更复杂的轨迹跟踪和控制任务。
05
实验研究与结果分析
实验平台搭建
硬件平台
为了进行实验研究，我们构建了一个二自由度冗余驱动并联机器人平台。该平台使用高质量的硬件组件，包括高性能电机、高精度编码器和高速控制器等。
软件平台
我们开发了一个基于MATLAB/Simulink的软件平台，用于实现机器人的控制算法和数据采集。
实验结果分析
未来研究展望
01
02
03
研究更加精确的动力学模型，考虑更多的影响因素，以提高机器人的运动性能。
探索更加智能的控制方法，如基于人工智能的控制算法，以提高机器人的自适应性。
对机器人的轨迹跟踪性能进行更全面的评估，包括在不同工况下的表现，以及与其他类型机器人的对比分析。
感谢您的观看
THANKS
研究方法
采用理论分析和实验研究相结合的方法，首先对冗余驱动并联机器人的结构和运动学进行分析，然后建立其动力学模型，并设计相应的控制算法，最后通过实验验证其有效性和可行性。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

两自由度机械手动力学问题
1题目
图示为两杆机械手，由上臂AB、下臂BC和手部C组成。

在A处和B处安装
有伺服电动机，分别产生控制力矩M
1和M
2。

M
1
带动整个机械手运动，M
2
带动下臂
相对上臂转动。

假设此两杆机械手只能在铅垂平面内运动，两臂长为l
1和l
2
，
自重忽略不计，B处的伺服电动机及减速装置的质量为m
1
，手部C握持重物质量
为m
2
，试建立此两自由度机械手的动力学方程。

图1
图2
2数值法求解
拉格朗日方程
此两杆机械手可以简化为一个双摆系统，改双摆系统在B 、C 出具有质量m 1,m 2,在A 、B 处有控制力矩M 1和M 2作用。

考虑到控制力矩M 2的作用与杆2相对杆1的相对转角θ2有关，故取广义力矩坐标为
2211,θθ==q q
系统的动能为二质点m 1、m 2的动能之和，即
由图2所示的速度矢量关系图可知
以A 处为零势能位置，则系统的势能为
由拉格朗日函数，动势为：
广义力2211,M Q M Q ==
求出拉格朗日方程中的偏导数，即
代入拉格朗日方程式,整理得:
给定条件
（1）角位移运动规律
()231*52335.0*1163.0t t t +-=θ，()232*52335.0*1163.0t t t +-=θ
21θθ和都是从0到90°，角位移曲线为三次函数曲线。

（2）质量
m 1=4㎏ m 2=5kg （3）杆长 l 1= l 2=
MATLAB 程序
t=0::3;
theta1=*t.^3+*t.^2; w1=*t.^2+*t; a1=*t+;
theta2=*t.^3+*t.^2; w2=*t.^2+*t; a2=*t+; m1=4; m2=5; l1=; l2=;
g=;
D11=(m1+m2)*l1.^2+m2*l2.^2+2*m2*l1*l2*cos(theta2); D22=m2*l2.^2;
D12=m2*l2.^2+m2*l1*l2*cos(theta2); D21=m2*l2.^2+m2*l1*l2*cos(theta2); D111=0;
D122=-m2*l1*l2*sin(theta2); D222=0;
D211=m2*l1*l2*sin(theta2); D112=-m2*l1*l2*sin(theta2); D121=-m2*l1*l2*sin(theta2); D212=0; D221=0;
D1=(m1+m2)*g*l1*sin(theta1)+m2*g*l2*sin(theta1+theta2); D2=m2*g*l2*sin(theta1+theta2);
M1=D11.*a1+D12.*a2+D111.*w1.^2+D122.*w2.^2+D112.*w1.*w2+D121.*w2.*w1+D1; M2=D21.*a2+D22.*a2+D211.*w1.^2+D222.*w2.^2+D212.*w1.*w2+D221.*w2.*w1+D2; T1=polyfit(t,M1,3) T2=polyfit(t,M2,3)
subplot(2,1,1),plot(t,M1),grid on,xlabel('时间（s ）'),ylabel('控制力矩（N·m）'),title('motion1')
subplot(2,1,2),plot(t,M2),grid on,xlabel('时间（s ）'),ylabel('控制力矩（N·m）'),title('motion2')
数值计算结果
()6167.1*7993.31*7329.3*5685.3t 231+++-=t t t M ()5449.1*9801.25*9481.8*0679.0t 232-+--=t t t M
图3 M1变化规律图
图4 M2变化规律图
3 ADAMS仿真
模型建立
图5 模型图
施加运动
在两个关节处分别施加位移函数
图6 关节运动施加图位移函数为：step(time,0,0,3,pi/2)
运动规律如下图所示：
图7 关节处运动规律图
运动仿真
设置仿真时间为3s,步数为300步，仿真结果如下图所示：
图8 关节1处控制力矩仿真结果图
图9 关节2处控制力矩仿真结果图
4 结果对比
图10 控制力矩M1结果对比图
图11 控制力矩M2结果对比图
从函数规律上看，两种求解方法得出的结果几乎一样；
从数值上看：
表1 控制力矩M1数值结果对比
t02
数值计算M1
仿真求解M1
表2 控制力矩M2数值结果对比
t02
数值计算M2
仿真求解M2
由上两表可以看出：数值计算结果与仿真求解结果相差很小，误差范围为%%，出现这种结果的原因可能是因为两种方法计算的精度不同，或者是算法存在差异。

如果对结果精度要求不是很高，可以认为两种方法求得的结果相等，进一步说明了仿真计算的可靠性。

两自由度机械手动力学问题

合集下载