大学物理实验讲义弦振动与驻波研究

弦振动与驻波实验报告弦振动与驻波实验报告引言：弦振动与驻波是物理学中重要的研究领域，对于理解波动现象和振动特性有着重要的作用。

本次实验旨在通过实验观测和数据分析，探究弦振动和驻波的基本特性，并验证实验结果与理论预期的一致性。

实验装置：实验装置主要由一根细长的弦、固定装置和振动源组成。

弦通过固定装置固定在两端，振动源通过机械手柄产生横向振动，使弦发生振动。

实验过程：1. 调整弦的张力：首先，我们根据实验要求调整弦的张力，使其保持稳定。

通过调节固定装置上的螺钉，可以改变弦的张力，从而影响弦的振动频率和振幅。

2. 观察弦的振动模式：接下来，我们将振动源固定在弦的一个端点，并通过机械手柄产生横向振动。

我们观察到弦在振动过程中形成了不同的振动模式。

当振动源产生的频率与弦的固有频率相等时，弦会形成稳定的驻波。

3. 测量驻波的节点和腹点：我们使用尺子测量弦上的驻波节点和腹点的位置。

节点是弦上振动幅度为零的点，而腹点则是振动幅度最大的点。

通过测量节点和腹点的位置，我们可以计算出弦的波长和振动频率。

4. 计算波长和频率：根据实验测量的数据，我们可以利用以下公式计算弦的波长和频率：波长 = 2 * 节点间距离频率 = 振动源产生的频率实验结果与分析：通过实验观测和数据分析，我们得到了一系列关于弦振动和驻波的结果。

首先，我们发现当振动源产生的频率等于弦的固有频率时，弦会形成稳定的驻波。

这是因为当振动源频率与弦的固有频率一致时，反射波和入射波在弦上形成了干涉，导致驻波的形成。

其次，我们发现驻波的节点和腹点位置与振动源产生的频率有关。

当频率增加时，节点和腹点的位置会发生变化，波长也会相应改变。

这是因为频率的增加导致波长的缩短，从而节点和腹点的位置也会随之改变。

最后，通过计算弦的波长和频率，我们发现实验结果与理论预期相符。

这进一步验证了弦振动和驻波的基本原理和公式的准确性。

结论：通过本次实验，我们深入了解了弦振动和驻波的基本特性，并通过实验结果验证了相关理论。

弦振动与驻波实验报告弦振动与驻波实验报告引言弦振动是物理学中一个经典的实验课题，通过实验可以观察到弦线在不同条件下的振动模式。

本实验旨在通过对弦线振动的研究，探索驻波现象的产生及其特性。

实验目的1. 理解弦振动的基本原理；2. 掌握测量弦线振动频率的方法；3. 观察驻波现象的形成和特性。

实验器材1. 弦线：长度约为2-3米，材质均匀、柔软的弦线；2. 弦线固定装置：用于固定弦线的两端，保持稳定；3. 驱动装置：用于产生弦线的振动；4. 频率计：用于测量弦线的振动频率；5. 各类测量仪器：尺子、计时器等。

实验步骤1. 将弦线固定在实验装置的两端，保持稳定；2. 调整驱动装置，使其产生合适的振动频率；3. 使用频率计测量弦线的振动频率；4. 观察弦线的振动模式，并记录下来；5. 调整驱动装置的频率，观察驻波现象的形成和特性；6. 测量不同驻波节点位置之间的距离，并计算波长。

实验结果与分析通过实验观察，我们可以看到弦线在不同频率下的振动模式。

当驱动频率与弦线固有频率相同时，弦线上形成了驻波现象。

驻波是指波动传播过程中，波峰和波谷相互叠加形成的现象。

在弦线上形成的驻波由一系列波节和波腹组成，波节为振动幅度最小的位置，波腹为振动幅度最大的位置。

在实验中，我们可以通过调整驱动频率，观察驻波现象的形成和特性。

当驱动频率与弦线固有频率相同时，弦线上形成了一个完整的驻波模式。

当驱动频率与弦线固有频率不匹配时，弦线上不会形成驻波，而是呈现出不规则的振动模式。

通过测量不同驻波节点位置之间的距离，我们可以计算出弦线的波长。

波长是指波动中一个完整波动周期所占据的距离。

根据波动理论，波长与频率之间存在着简单的关系，即波速等于波长乘以频率。

因此，通过测量波长和频率，我们可以计算出波速。

实验结论通过本次实验，我们深入了解了弦振动和驻波现象。

弦振动是一种常见的物理现象，通过调整驱动频率可以观察到不同的振动模式。

驻波现象是波动传播中的一个重要现象，通过波节和波腹的叠加形成。

弦振动和驻波实验【实验目的】1、观察固定均匀弦振动传播时形成的驻波波形；2、测量均匀弦线上横波的传播速度及均匀弦线的线密度。

【实验器材】XZDY-B 型固定均匀弦振动仪、磁铁、钩码、滑轮、电子天平等。

【实验原理】驻波是一种波的叠加现象，它广泛存在于各种振动现象中。

本实验通过通有交流电的铜导线在磁场中的振动，观察弦振动驻波的形成，验证横波的波长与弦线中的张力平方根成正比，与线密度的平方根成反比，并利用弦线上产生的驻波，测出驻波的波长。

横波沿弦线传播时，在维持弦线张力不变的情况下，横波的传播速度v 与张力T 及弦线的线密度ρ（即单位长度的质量）之间的关系为：Tv ρ=(1)。

设弦线的振动频率为f ，横波在弦线上传播的波长为λ，则根据v f λ=，有1Tfλρ=（2）。

根据式（2）可知，若弦线的振动频率f 和线密度ρ一定，则波长λ与张力T 的平方根成正比。

如图所示，弦线的一端通过劈尖A ，另一端跨过劈尖B 后通过滑轮挂钩码，当铜导线振动时，振动频率为交流电的频率。

随着振动产生向右传播的横波，此波由A 点传到B 点时发生反射。

由于前进波和反射波的振幅相同、频率相同、振动方向相同，但传播方向相反，所以可互相干涉形成驻波。

在驻波中，弦上各点的振幅出现周期性的变化，有些点振幅最大，称为波腹；有些点振幅为零，称为波节。

两相邻波腹（或波节）之间的距离等于形成驻波的相干波波长的一半。

当弦的长度L （A 、B 两劈尖之间的距离）恰为半波长（2λ）的整数倍时产生共振。

此时驻波的振幅最大且稳定，因此均匀弦振动产生驻波的条件为：(1,2,3......)2L nn λ== （3），式中n 为半波数。

可见，由驻波的半波长的波段数n 和弦长L ，即可求出波长λ，则2(1,2,3......)L n n λ==（4）。

由公式（2）和（4）可得弦线的线密度2224Tn L f ρ=（5）。

【实验内容】1、打开电源，启动弦振动仪，观察均匀弦振动传播时形成的驻波波形。

大学物理《弦振动》实验报告大学物理《弦振动》实验报告（报告内容：目的、仪器装置、简单原理、数据记录及结果分析等）一.实验目的1.观察弦上形成的驻波2.学习用双踪示波器观察弦振动的波形3.验证弦振动的共振频率与弦长、张力、线密度及波腹数的关系二.实验仪器XY弦音计、双踪示波器、水平尺三实验原理当弦上某一小段受到外力拨动时便向横向移动，这时弦上的张力将使这小段恢复到平衡位置，但是弦上每一小段由于都具有惯性，所以到达平衡位置时并不立即停止运动，而是继续向相反方向运动，然后由于弦的张力和惯性使这一小段又向原来的方向移动，这样循环下去，此小段便作横向振动，这振动又以一定的速度沿整条弦传播而形成横波。

理论和实验证明，波在弦上传播的速度可由下式表示：=ρ1------------------------------------------------------- ①另外一方面，波的传播速度v和波长λ及频率γ之间的关系是：v=λγ-------------------------------------------------------- ②将②代入①中得γ=λ1-------------------------------------------------------③ ρ1又有L=n*λ/2 或λ=2*L/n代入③得γn=2L------------------------------------------------------ ④ ρ1四实验内容和步骤1.研究γ和n的关系①选择5根弦中的一根并将其有黄铜定位柱的一端置于张力杠杆的槽内，另一端固定在张力杠杆水平调节旋钮的螺钉上。

②设置两个弦码间的距离为60.00cm，置驱动线圈距离一个弦码大约5.00cm的位置上，将接受线圈放在两弦码中间。

将弦音计信号发生器和驱动线圈及示波器相连接，将接受线圈和示波器相连接。

③将1kg砝码悬挂于张力杠杆第一个槽内，调节张力杠杆水平调节旋钮是张力杠杆水平（张力杠杆水平是根据悬挂物的质量精确确定，弦的张力的必要条件，如果在张力杠杆的第一个槽内挂质量为m的砝码，则弦的张力T=mg，这里g是重力加速度；若砝码挂在第二个槽，则T=2mg；若砝码挂在第三个槽，则T=3mg…….）④置示波器各个开关及旋钮于适当位置，由信号发生器的信号出发示波器，在示波器上同时显示接收器接受的'信号及驱动信号两个波形，缓慢的增加驱动频率，边听弦音计的声音边观察示波器上探测信号幅度的增大，当接近共振时信号波形振幅突然增大，达到共振时示波器现实的波形是清晰稳定的振幅最大的正弦波，这时应看到弦的震动并听到弦振动引发的声音最大，若看不到弦的振动或者听不到声音，可以稍增大驱动的振幅（调节“输出调节”按钮）或改变接受线圈的位置再试，若波形失真，可稍减少驱动信号的振幅，测定记录n=1时的共振频率，继续增大驱动信号频率，测定并记录n=2,3,4,5时的共振频率，做γn图线，导出γ和n的关系。

大学物理实验讲义-弦振动与驻波研究弦振动与驻波研究【实验目的】1．观察在弦上形成的驻波；2．确定弦线振动时驻波波长与张力的关系； 3．学习对数作图和最小二乘法进行数据处理。

【实验原理】在一根拉紧的弦线上，其中张力为T ，线密度为μ，则沿弦线传播的横波应满足下述运动方程：2222x yT t y ∂∂=∂∂μ(1)式中x 为波在传播方向（与弦线平行）的位置坐标，y 为振动位移。

将(1)式与典型的波动方程22222x y V t y ∂∂=∂∂相比较，即可得到波的传播速度: μTV =若波源的振动频率为f ，横波波长为λ，由于波速λf V =，故波长与张力及线密度之间的关系为：μλTf1=(2)为了用实验证明公式(2)成立，将该式两边取对数，得：11lg lg lg lg 22T f λμ=-- (3)固定频率f 及线密度μ，而改变张力T ，并测出各相应波长λ，作lg λ-lg T 图，若得一直线，计算其斜率值（如为21），则证明了λ∝21T的关系成立。

弦线上的波长可利用驻波原理测量。

当两个振幅和频率相同的相干波在同一直线上相向传播时，其所叠加而成的波称为驻波，一维驻波是波干涉中的一种特殊情形。

在弦线上出现许多静止点，称为驻波的波节。

相邻两波节间的距离为半个波长。

【实验仪器】1、可调频率数显机械振动源；2、振动簧片；3、弦线（铜丝）；4、可动刀片支架；5、可动刀口支架；6、标尺；7、固定滑轮；8、砝码与砝码盘；9、变压器;10、实验平台；11、实验桌9123456781011图1 实验装置示意图图2 可调频率数显机械振动源面板图 （1、电源开关 2、频率调节 3、复位键 4、幅度调节 5、频率指示）实验装置如图1所示，金属弦线的一端系在能作水平方向振动的可调频率数显机械振动弦线上驻波实验仪电 源ON复位 幅度 调节上海复旦天欣科教仪器有限公司频率调节H Z1 2 3 45FD-SWE-II源的振簧片上，频率变化范围从0-200Hz 连续可调，频率最小变化量为0.01Hz ，弦线一端通过定滑轮⑦悬挂一砝码盘⑧；在振动装置(振动簧片)的附近有可动刀片支架④，在实验装置上还有一个可沿弦线方向左右移动并撑住弦线的可动刀口⑤。

实验四弦振动的研究两列振幅相等的相干波，在同一直线上沿相反方向传播时，叠加形成驻波。

驻波是波的干涉现象中的一种重要现象，它在声学、光学、无线电工程和检测技术等方面都有广泛的应用，利用驻波现象可以测量波长、波速和频率。

一、实验目的1.了解固定均匀弦振动的传播规律，加深振动与波和干涉的概念。

2.了解固定均匀弦振动传播形成驻波的波形，加深对干涉的特殊形式——驻波的认识。

3.了解固定均匀弦振动固有频率的因素，测量均匀弦线上横波的传播速度及其线密度。

4.了解声音与频率之间的关系。

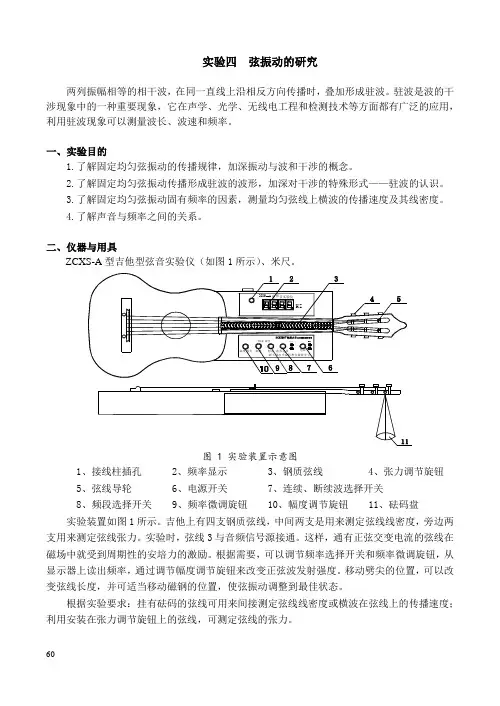
二、仪器与用具ZCXS-A型吉他型弦音实验仪（如图1所示）、米尺。

图 1 实验装置示意图1、接线柱插孔2、频率显示3、钢质弦线4、张力调节旋钮5、弦线导轮6、电源开关7、连续、断续波选择开关8、频段选择开关 9、频率微调旋钮 10、幅度调节旋钮 11、砝码盘实验装置如图1所示。

吉他上有四支钢质弦线，中间两支是用来测定弦线线密度，旁边两支用来测定弦线张力。

实验时，弦线3与音频信号源接通。

这样，通有正弦交变电流的弦线在磁场中就受到周期性的安培力的激励。

根据需要，可以调节频率选择开关和频率微调旋钮，从显示器上读出频率，通过调节幅度调节旋钮来改变正弦波发射强度。

移动劈尖的位置，可以改变弦线长度，并可适当移动磁钢的位置，使弦振动调整到最佳状态。

根据实验要求：挂有砝码的弦线可用来间接测定弦线线密度或横波在弦线上的传播速度；利用安装在张力调节旋钮上的弦线，可测定弦线的张力。

三、实验原理如图1所示，实验时,将弦线3（钢丝）绕过弦线导轮5与砝码盘11连接，并通过接线柱4接通正弦信号源。

在磁场中，通有电流的金属弦线会受到磁场力（称为安培力）的作用，若弦线上接通正弦交变电流时，则它在磁场中所受的与磁场方向和电流方向均为垂直的安培力，也随之发生正弦变化，移动劈尖改变弦长，当弦长是半波长的整倍数时，弦线上便会形成驻波。

移动磁钢的位置，将弦线振动调整到最佳状态，使弦线形成明显的驻波。

大学物理《弦振动》实验报告（报告内容：目的、仪器装置、简单原理、数据记录及结果分析等）一.实验目的1.观察弦上形成的驻波2.学习用双踪示波器观察弦振动的波形3.验证弦振动的共振频率与弦长、张力、线密度及波腹数的关系二.实验仪器XY弦音计、双踪示波器、水平尺三实验原理当弦上某一小段受到外力拨动时便向横向移动，这时弦上的张力将使这小段恢复到平衡位置，但是弦上每一小段由于都具有惯性，所以到达平衡位置时并不立即停止运动，而是继续向相反方向运动，然后由于弦的张力和惯性使这一小段又向原来的方向移动，这样循环下去，此小段便作横向振动，这振动又以一定的速度沿整条弦传播而形成横波。

理论和实验证明，波在弦上传播的速度可由下式表示：=ρ1------------------------------------------------------- ①另外一方面，波的传播速度v和波长λ及频率γ之间的关系是：v=λγ-------------------------------------------------------- ②将②代入①中得γ=λ1-------------------------------------------------------③ρ1又有L=n*λ/2 或λ=2*L/n代入③得γn=2L------------------------------------------------------ ④ρ1四实验内容和步骤1.研究γ和n的关系①选择5根弦中的一根并将其有黄铜定位柱的一端置于张力杠杆的槽内，另一端固定在张力杠杆水平调节旋钮的螺钉上。

②设置两个弦码间的距离为60.00cm，置驱动线圈距离一个弦码大约5.00cm的位置上，将接受线圈放在两弦码中间。

将弦音计信号发生器和驱动线圈及示波器相连接，将接受线圈和示波器相连接。

③将1kg砝码悬挂于张力杠杆第一个槽内，调节张力杠杆水平调节旋钮是张力杠杆水平（张力杠杆水平是根据悬挂物的质量精确确定，弦的张力的必要条件，如果在张力杠杆的第一个槽内挂质量为m的砝码，则弦的张力T=mg，这里g 是重力加速度；若砝码挂在第二个槽，则T=2mg；若砝码挂在第三个槽，则T=3mg…….）④置示波器各个开关及旋钮于适当位置，由信号发生器的信号出发示波器，在示波器上同时显示接收器接受的信号及驱动信号两个波形，缓慢的增加驱动频率，边听弦音计的声音边观察示波器上探测信号幅度的增大，当接近共振时信号波形振幅突然增大，达到共振时示波器现实的波形是清晰稳定的振幅最大的正弦波，这时应看到弦的震动并听到弦振动引发的声音最大，若看不到弦的振动或者听不到声音，可以稍增大驱动的振幅（调节“输出调节”按钮）或改变接受线圈的位置再试，若波形失真，可稍减少驱动信号的振幅，测定记录n=1时的共振频率，继续增大驱动信号频率，测定并记录n=2,3,4,5时的共振频率，做γn图线，导出γ和n的关系。

弦振动与驻波实验报告弦振动与驻波实验报告引言：弦振动是物理学中一个重要的研究领域，对于理解声波、光波等波动现象有着重要的意义。

驻波现象则是弦振动中一个有趣的现象，它产生于两个同频率、相位相反的波在同一介质中相遇并叠加时。

本实验旨在通过观察弦振动和驻波现象，深入理解波动性质以及相关的物理原理。

实验设备与方法：实验中我们使用了一根细而柔软的弦，将其两端固定在实验台上，并通过一个发声装置产生振动。

我们使用一个频率可调的声波发生器，将声波传导到弦上。

同时，我们在弦上设置了一系列固定的振动节点和腹点，用以观察驻波现象的形成。

实验过程与观察：在实验中，我们首先调整发声装置的频率，使其与弦的固有频率相匹配。

随着频率的逐渐增大，我们观察到弦上出现了一系列驻波现象。

通过细致观察，我们发现弦上形成了一些固定的节点和腹点，它们交替出现，并且节点和腹点之间的距离保持不变。

接下来，我们将实验中的发声装置移动到弦的不同位置，重新调整频率，观察到了不同的驻波现象。

我们发现，当发声装置位于弦的中间位置时，形成的驻波现象最为明显，节点和腹点之间的距离也最大。

而当发声装置位于弦的两端时，驻波现象几乎消失，弦上只表现出简单的振动。

实验结果分析：通过实验观察和测量，我们得出了一些结论。

首先，弦上形成的驻波现象是由两个同频率、相位相反的波在弦上相遇叠加形成的。

这两个波分别由弦的两端发出，形成了一个定态的波动模式。

其次，驻波现象的形成与弦的固有频率以及发声装置的频率密切相关。

只有当这两个频率相等时，才能形成稳定的驻波现象。

进一步分析，我们可以得出结论，驻波现象的形成是因为弦两端的波反射与干涉所致。

当波到达弦的固定端时，发生反射并改变相位，然后与原始波相叠加。

如果两个波的相位相反，它们将相互抵消，形成节点。

而如果两个波的相位相同，它们将相互增强，形成腹点。

这种反射与干涉的过程不断重复，最终形成了稳定的驻波现象。

结论：通过本次实验，我们深入理解了弦振动和驻波现象的物理原理。

弦振动和驻波实验[实验目的]1、观察固定均匀弦振动传播时形成的驻波波形。

2、测量均匀弦线上横波的传播速度及均匀弦线的线密度。

[实验仪器] XZDY －B 型固定均匀弦振动仪。

[实验原理]如上图所示，弦长L 为A ，B 两劈尖之间的距离，均匀弦振动产生驻波的条件为：/2(1,2,3......)L n n λ== 式中n 为半波数。

弦线中横波的传播速度为： v = ......... (1) 式中T 为弦线中的张力， ρ为弦线的线密度。

根据v f λ=得：2/v f L n = (2)由（1）（2）两式可得： f = (1,2,3......)n = (3)由（3）式可知，当给定T L ρ、、，频率f 只有满足该式关系才能在弦线上形成驻波。

同理，当外力去驱动弦振动时，外力的频率必须与这些频率一致，才能促使 弦振动的传播形成驻波。

[实验内容]1、打开电源，启动弦振动仪，观察均匀弦振动传播时形成的驻波波形。

2、测定弦线的线密度选取频率100f H z =，张力T 由40g 钩码挂在弦线的一端产生。

调节劈尖A 、B之间的距离，使弦线上依次出现n=1,2,3波段的稳定驻波，记录下相应的弦线长i L ，由（3）式算出i ρ（1,2,3......i =）求出平均值ρ。

3、在张力T 一定的条件下，改变频率f 分别为50、75、100、125、150H z ，调节弦长L，使弦上出现1n=个驻波段。

记下相应f、n、L值，由（2）式n=、2求出弦线上的横波速度v。

4、在频率一定的条件下，改变张力T的大小，测量弦线上横波的传播速度v。

选取75=，张力T由钩码挂在弦线的一端产生。

以30g钩码为起点每次增f H z加10g直至钩码质量达到60g。

在各张力作用下调节弦长L，使弦长出现1n=、n=个驻波段。

记下相应T、n、L值，由（2）式计算出弦线上横波的速度v 25、数据处理（表格自拟）[思考练习]1、能否将细铜丝弦线换成细铁丝或是细线？为什么？。

实验七 固定均匀弦振动在自然界中，振动现象是广泛存在，广义地说，任何一个物理量存在 一个定值附近作往复变化，都可称为振动。

振动是产生波动的根源，波动是振动的传播。

波动具有自己特征，首先它具有一定的传播速度，且伴随能量的传播；另外，波动还具有反射、折射、干涉和衍射现象，本实验研究波的特征之一，干涉现象的特例：驻波。

【实验目的】1、了解固定均匀弦振动的传播规律。

2、观察固定均匀弦振动的传播时形成驻波的波形。

3、测量均匀弦上横波的传播速度和均匀弦线的线密度。

【实验仪器】均匀弦振动实验装置，如图1所示。

【实验原理】设一均匀弦线，一端由劈尖A 支柱，另一端由劈尖B 支撑。

如图所示，对均匀通电弦线在磁场的扰动下，引起弦线上各质点的振动，于是波动就由A 端朝B 端方向传播，称为入射波；再由B 端反射沿弦线朝A 端传播，称为反射波。

入射波与反射波在同一弦线上沿相反方向传播时将相互干涉，移动劈尖B 到适当的位置，即2λ⋅=n L AB ，弦线上的波就形成稳定的驻波。

这时弦线上的波被分成几段且每段波两端的点始终静止不动，而中间的点振幅最大。

这始终静止不动的点称为波节，振幅最大的点称为波腹。

驻波的形成如图2所示。

设图2中的两列波是沿x 轴相反方向传播的振幅相等、频率相同的简谐波，向右传播的波用细实线表示，向左传播的波用细虚线表示，它们形成的驻波用粗实线表示，由图二可见两个波腹间的距离都是等于半个波长，这可从波动方程推倒出来。

驻波是由振幅相同的两列相干波（同频率、同振动方向、相位差恒定），在同一直线上沿相反方向传播时叠加而成的一种特殊形式的干涉现象。

下面用简谐表达式对驻波进行定量描述。

设沿x 轴正方向传播的波为入射波，沿x 轴负方向传播的波为反射波，取它们振动位相始终相同的点作坐标原点，且在0=x 处，振动质点向上达到最大位移开始计时，则它们的波动方程为：)(2cos 1λπxft A y -= ; )(2cos 2λπxft A y +=式中A 为简谐振动的振幅，f 为频率，λ为波长，x 为弦线上质点的坐标位置。

大学物理演示实验探究1151914 李海鹏一、实验名称：弦驻波现象的探究二、主要装置：振荡器（调节振动源的振幅和频率），振动源，松紧带（充当驻波的介质）三、物理原理：当振动频率，振幅和振动方向相同的两列简谐波，在同一直线沿着相反的方向传播时，产生特殊的干涉现象，即驻波。

在波的传播过程中，当波由波密媒质进入波疏媒质时，在分界面处，反射波与入射波同相位，没有半波损失。

当波由波疏媒质进入波密媒质时，在分界面处，反射波与入射波有π的相位突变，有半波损失。

所以驻波在两固定端形成的是波节。

相邻波节和波腹的距离为因为波长有一定限制，一波长和松紧带的长度应满足如下条件是才能形成驻波。

四、实验现象：当振动频率，振幅和振动方向相同的两列简谐波，在同一直线沿着相反的方向传播时，产生特殊的干涉现象，即驻波。

松紧带的两端分别与振动源和固定端（入射波反射点）相连。

当振荡器开启时，将会形成简谐波，入射波和反射波干涉，当频率波长满足条件时将在松紧带上形成驻波。

因为波长有一定限制，一波长和松紧带的长度满足如下条件时才能形成驻波。

调节合适的频率与振幅使得驻波形成之后，可以看到在驻波中，直线上的某些始终静止不动，这样的点叫做波节。

某些点的振幅具有最大值，这些点称为波腹。

波腹处的振幅等于一个波的振幅的两倍。

固定端形成的永远是波节。

波形上的不同点以不同的振幅在波节两边以相同的频率做往复运动。

两波节中间的点，振幅最大；越靠近波节，振幅越小。

此时绳上的各点，只有段与段之间的相位突变，没有震动状态或相位的逐点传播，没有什么能量向外传播。

每一个节点的两侧的各点总是向相反方向运动，当右边的点向上移动时，左边的点向下移动，说明节点两边的位相相反。

而相邻两节点间的各点，虽然它们的振幅不同，但它们却同时经过平衡点，同时达到最大值，和最小值，各点的向相同方向运动，说明它们具有相同的位相。

分别改变振动频率以及振幅，观察松紧带的振动情况。

频率增大，驻波形成的越多，即两波节之间的距离越小。

物理实验报告哈工大物理实验中心班号33006学号1190501917姓名刘福田教师签字实验日期2020.4.19预习成绩学生自评分总成绩(注：为方便登记实验成绩，班号填写后5位，请大家合作。

）实验(三)弦振动和驻波实验一．实验目的1、在弦线张力不变时，用实验确定驻波波长与振动频率的关系；2、在振动源频率不变时，用实验确定驻波波长与张力的关系；3、观察弦振动及驻波的形成。

二．实验原理在一根拉紧的弦线上，张力为T，线密度为μ，则沿弦线传播的横波应满足运动方程其中x：波在传播方向（与弦线平行）的位置坐标；y：振动位移；而典型的波动方程为通过比较（1）、（2），可得到波的传播速度；若波源的振动频率为f，横波波长为λ，则横波沿弦线传播的速度可表示为波长与张力及线密度之间的关系可表示为两边取对数，得到公式波长的测量：驻波方法图像如图所示三．实验主要步骤或操作要点1、在弦线张力不变时，用实验确定驻波波长与振动频率的关系；①将弦线一端固定在鞋盒侧面，线跨过鞋盒沿，另一端下垂并悬挂一水瓶。

实验装置如图3-1图3-1②在保持张力不变的情况下，移动筷子位置，使半波长λ/2分别为10、15、20、25、30c m。

③用牙签波动弦线发出声音，利用P h y p h o x分别测出线的振动频率f2、在振动源频率不变时，用实验确定驻波波长与张力的关系①固定A B之间的距离并测量②利用小量杯等量地增加水瓶中水的体积，即等量地改变弦线的张力T③波动弦线，用软件p h y p h o x测量不同张力下弦线的振动频率f3、验证三分损益法①保持弦线张力不变，先将A B的距离固定，测出此时的频率，并将音调定为基准音D o，算出相应的F a,S o l,L a,高音D o的理论频率。

②移动筷子，缩短A B距离，波动弦线，先粗略听出F a音，再微调距离使得P h y p h o x 测出的频率恰为理论的F a音频率。

测出相应的A B距离。

标记F a位置。

弦振动与弦驻波实验波是一种重要的物理现象，我们通过前进的波和反射波叠加可以得到驻波。

在和振动源连接的一根拉紧的弦线上，可以直观而清楚地了解弦振动时驻波形成的过程。

用它可以研究弦振动的基频与张力、弦长的关系，从而测量在弦线上横波的传播速度，并由此求出振动源的频率，一、实验目的1．观察弦振动时形成的驻波，学习与弦振动有关的物理知识和规律；2．通过实验测量振动源的频率。

二、实验设备THQZB-2型弦振动仪信号源、THQZB-2型弦振动实验仪。

图1 THQZB-2型弦振动仪信号源面板示意图（一）THQZB-2型弦振动仪信号源弦振动仪信号源主要由以下几部分组成，如图1所示：频率计：用于显示信号源频率；扬声器接口：用于连接信号源与实验仪中扬声器接口，驱动扬声器工作；复位按键：用于当仪器出现死机或其他异常时使其恢复到初始状态；频率调节旋钮：用于调节信号源输出信号的频率；幅度调节旋钮：用于调节信号源输出信号的幅度。

（二）THQZB-2型弦振动实验仪弦振动实验仪结构如图2所示：图2 THQZB-2 型弦振动实验仪结构简图弦振动实验仪由振子（扬声器）、滑块1（固定）、滑块2（可移动）、滑轮、弦线、砝码、标尺、导轨等几部分组成。

三、实验原理1．弦线上横波的传播速度在拉紧的弦线上，波沿某方向传播的速度（大学物理课中讲过）为（1）式（1）中为波速，为弦线张力，是弦线密度。

2．振动频率与横波波长、弦线张力及线密度的关系如图2所示，将细弦线的一端固定在振动源上，另一端绕过滑轮悬挂砝码。

当振子振动时，弦线也在振子的带动下振动，即振子的振动沿弦线传播，弦线振动频率和振子振动频率相等。

选择适当的砝码重量，可在弦线上形成稳定的驻波。

驻波波长为，则弦线上横波传播的速度为：（2）将式（2）代入式（1）得（3）设弦线长为L，形成稳定驻波时，弦线上的半波（波腹）数为，则，即（4）将式（4）代入式(9)得（5）式（5）表明线密度、长度和张力与弦振动频率的关系。

大学物理演示实验探究1151914 李海鹏一、实验名称：弦驻波现象的探究二、主要装置：振荡器（调节振动源的振幅和频率），振动源，松紧带（充当驻波的介质）三、物理原理：当振动频率，振幅和振动方向相同的两列简谐波，在同一直线沿着相反的方向传播时，产生特殊的干涉现象，即驻波。

在波的传播过程中，当波由波密媒质进入波疏媒质时，在分界面处，反射波与入射波同相位，没有半波损失。

当波由波疏媒质进入波密媒质时，在分界面处，反射波与入射波有π的相位突变，有半波损失。

所以驻波在两固定端形成的是波节。

相邻波节和波腹的距离为因为波长有一定限制，一波长和松紧带的长度应满足如下条件是才能形成驻波。

四、实验现象：当振动频率，振幅和振动方向相同的两列简谐波，在同一直线沿着相反的方向传播时，产生特殊的干涉现象，即驻波。

松紧带的两端分别与振动源和固定端（入射波反射点）相连。

当振荡器开启时，将会形成简谐波，入射波和反射波干涉，当频率波长满足条件时将在松紧带上形成驻波。

因为波长有一定限制，一波长和松紧带的长度满足如下条件时才能形成驻波。

调节合适的频率与振幅使得驻波形成之后，可以看到在驻波中，直线上的某些始终静止不动，这样的点叫做波节。

某些点的振幅具有最大值，这些点称为波腹。

波腹处的振幅等于一个波的振幅的两倍。

固定端形成的永远是波节。

波形上的不同点以不同的振幅在波节两边以相同的频率做往复运动。

两波节中间的点，振幅最大；越靠近波节，振幅越小。

此时绳上的各点，只有段与段之间的相位突变，没有震动状态或相位的逐点传播，没有什么能量向外传播。

每一个节点的两侧的各点总是向相反方向运动，当右边的点向上移动时，左边的点向下移动，说明节点两边的位相相反。

而相邻两节点间的各点，虽然它们的振幅不同，但它们却同时经过平衡点，同时达到最大值，和最小值，各点的向相同方向运动，说明它们具有相同的位相。

分别改变振动频率以及振幅，观察松紧带的振动情况。

频率增大，驻波形成的越多，即两波节之间的距离越小。

弦振动与驻波研究【实验目的】1．观察在弦上形成的驻波；2．确定弦线振动时驻波波长与张力的关系； 3．学习对数作图和最小二乘法进行数据处理。

【实验原理】在一根拉紧的弦线上，其中张力为T ，线密度为μ，则沿弦线传播的横波应满足下述运动方程：2222x yT t y ∂∂=∂∂μ (1)式中x 为波在传播方向（与弦线平行）的位置坐标，y 为振动位移。

将(1)式与典型的波动方程 22222xy V t y ∂∂=∂∂ 相比较，即可得到波的传播速度: μTV =若波源的振动频率为f ，横波波长为λ，由于波速λf V =，故波长与张力及线密度之间的关系为：μλTf1=(2)为了用实验证明公式(2)成立，将该式两边取对数，得：11lg lg lg lg 22T f λμ=-- (3) 固定频率f 及线密度μ，而改变张力T ，并测出各相应波长λ，作lg λ-lg T 图，若得一直线，计算其斜率值（如为21），则证明了λ∝21T 的关系成立。

弦线上的波长可利用驻波原理测量。

当两个振幅和频率相同的相干波在同一直线上相向传播时，其所叠加而成的波称为驻波，一维驻波是波干涉中的一种特殊情形。

在弦线上出现许多静止点，称为驻波的波节。

相邻两波节间的距离为半个波长。

【实验仪器】1、可调频率数显机械振动源；2、振动簧片；3、弦线（铜丝）；4、可动刀片支架；5、可动刀口支架；6、标尺；7、固定滑轮；8、砝码与砝码盘；9、变压器;10、实验平台；11、实验桌图1 实验装置示意图图2 可调频率数显机械振动源面板图（1、电源开关2、频率调节 3、复位键 4、幅度调节5、频率指示）实验装置如图1所示，金属弦线的一端系在能作水平方向振动的可调频率数显机械振动源的振簧片上，频率变化范围从0-200Hz连续可调，频率最小变化量为0.01Hz，弦线一端通过定滑轮⑦悬挂一砝码盘⑧；在振动装置(振动簧片)的附近有可动刀片支架④，在实验装置上还有一个可沿弦线方向左右移动并撑住弦线的可动刀口⑤。

物理实验报告哈工大物理实验中心班号33006学号1190501917姓名刘福田教师签字实验日期2020.4.19预习成绩学生自评分总成绩(注：为方便登记实验成绩，班号填写后5位，请大家合作。

）实验(三)弦振动和驻波实验一．实验目的1、在弦线张力不变时，用实验确定驻波波长与振动频率的关系；2、在振动源频率不变时，用实验确定驻波波长与张力的关系；3、观察弦振动及驻波的形成。

二．实验原理在一根拉紧的弦线上，张力为T，线密度为μ，则沿弦线传播的横波应满足运动方程其中x：波在传播方向（与弦线平行）的位置坐标；y：振动位移；而典型的波动方程为通过比较（1）、（2），可得到波的传播速度；若波源的振动频率为f，横波波长为λ，则横波沿弦线传播的速度可表示为波长与张力及线密度之间的关系可表示为两边取对数，得到公式波长的测量：驻波方法图像如图所示三．实验主要步骤或操作要点1、在弦线张力不变时，用实验确定驻波波长与振动频率的关系；①将弦线一端固定在鞋盒侧面，线跨过鞋盒沿，另一端下垂并悬挂一水瓶。

实验装置如图3-1图3-1②在保持张力不变的情况下，移动筷子位置，使半波长λ/2分别为10、15、20、25、30c m。

③用牙签波动弦线发出声音，利用P h y p h o x分别测出线的振动频率f2、在振动源频率不变时，用实验确定驻波波长与张力的关系①固定A B之间的距离并测量②利用小量杯等量地增加水瓶中水的体积，即等量地改变弦线的张力T③波动弦线，用软件p h y p h o x测量不同张力下弦线的振动频率f3、验证三分损益法①保持弦线张力不变，先将A B的距离固定，测出此时的频率，并将音调定为基准音D o，算出相应的F a,S o l,L a,高音D o的理论频率。

②移动筷子，缩短A B距离，波动弦线，先粗略听出F a音，再微调距离使得P h y p h o x 测出的频率恰为理论的F a音频率。

测出相应的A B距离。

标记F a位置。

弦振动驻波的研究【实验目的】1．观察弦振动时驻波的形成；2．验证弦振动时驻波波长与张力的关系； 3．验证弦线波传播规律ρTV =，λ⋅=f V 。

【实验仪器】本实验用产生稳定驻波的实验装置产生驻波（如图1所示）。

波源A 是由电力驱动的电动音叉，能够产生机械波。

B 是一个定滑轮，称为节点。

从音叉A 的端部引出一根弦线穿过B 点后弯折，弦线的另一端悬挂一重物M 。

重物产生的重力就是加在弦线上的张力。

【实验原理】1. 求弦线线密度的原理机械波在介质中的传播速度与介质本身的物理属性有关系。

当一列横波沿弦线传播时，若维持张力T 不变，则横波的传播速度v 与弦线上的张力T 及弦线的线密度ρ的关系为ρTv =。

若弦线的振动频率为f ，横波在弦线上传播的波长为λ，则ρλTf v =⋅=，即ρλTf1=，若f 、ρ固定，则 λ∝T 。

精确测定λ和T ，作λ～T 图线，若其为一过原点的直线，则上述观点得到验证。

若知道f ，T ，λ则可求出弦线的线密度。

2. 用驻波法求波长的原理从波源A 发出的机械波沿着弦线向前传播。

机械波传播到节点B 后即被反射，反射回来的机械波仍然沿弦线传播。

发射波（波1）与反射波（波2）在C 点相遇，如图2。

波1比波图1 驻波发生装置源A 的相位延迟了πλϕ21⋅=x。

波2比波源A 的相位延迟了ππλϕ+⋅-=222xL 。

其中2ϕ里面附加的相位π是由于在节点B 的位置处，波是由波疏介质（弦线）入射到波密介质（金属定滑轮），因此产生半波损失，产生π的相位突变。

波1和波2在C 点处的相位差ππλϕϕϕ+⋅-=-=∆22212xL c 。

对于C 点来说，两列波的相位差恒定。

且两列波是从同一个波源发出的，故频率相同，振幅相同，满足机械波波的相干条件（频率相同，振幅相近，相位差恒定），会产生波的干涉现象。

图2 驻波原理当波源到节点的距离为半波长的整数倍的时候，即2λ⋅=m L ，m 为整数，在C 点处相遇的两束波的相位差为πλππππλλϕ22222⋅-+=+⋅-=∆xm xm c 。