钢结构基本原理(第二版)习题参考解答第六章

钢结构第二版课后习题答案钢结构第二版课后习题答案钢结构是一门重要的工程学科，它涉及到建筑、桥梁、车辆等领域的设计和施工。

在学习钢结构的过程中，课后习题是非常重要的一部分，它可以帮助学生巩固所学知识，提高解决问题的能力。

本文将为大家提供钢结构第二版课后习题的答案，希望对大家的学习有所帮助。

第一章：钢结构基础知识1. 钢结构的优点有哪些？答：钢结构具有重量轻、强度高、施工周期短、可重复利用等优点。

2. 钢结构的分类有哪些？答：钢结构可以分为工业建筑钢结构、桥梁钢结构和特殊用途钢结构等。

3. 钢结构设计的基本原则是什么？答：钢结构设计的基本原则是满足强度、刚度和稳定性的要求。

第二章：钢结构的材料性能1. 钢材的强度是指什么？答：钢材的强度是指其抵抗外力破坏的能力。

2. 钢材的塑性是指什么？答：钢材的塑性是指其在受力作用下可以发生塑性变形而不断延展。

3. 钢材的屈服点是什么意思？答：钢材的屈服点是指在拉伸过程中，材料开始发生塑性变形的点。

第三章：钢结构的连接方式1. 钢结构的连接方式有哪些？答：钢结构的连接方式包括焊接连接、螺栓连接和铆接连接等。

2. 焊接连接的优点是什么？答：焊接连接具有连接强度高、结构刚度大、施工简便等优点。

3. 螺栓连接的优点是什么？答：螺栓连接具有拆卸方便、可重复利用、施工速度快等优点。

第四章：钢结构的设计原则1. 钢结构的设计原则是什么？答：钢结构的设计原则是满足强度、刚度和稳定性的要求，并考虑施工的可行性和经济性。

2. 钢结构的荷载有哪些？答：钢结构的荷载包括自重、活载、风荷载、地震荷载等。

3. 钢结构的稳定性是指什么？答：钢结构的稳定性是指在受力作用下，结构不发生失稳现象。

第五章：钢结构的施工工艺1. 钢结构的施工工艺包括哪些环节？答：钢结构的施工工艺包括制作、运输、安装和验收等环节。

2. 钢结构的制作工艺有哪些？答：钢结构的制作工艺包括切割、焊接、钻孔和组装等。

3. 钢结构的安装工艺有哪些？答：钢结构的安装工艺包括起吊、定位、连接和调整等。

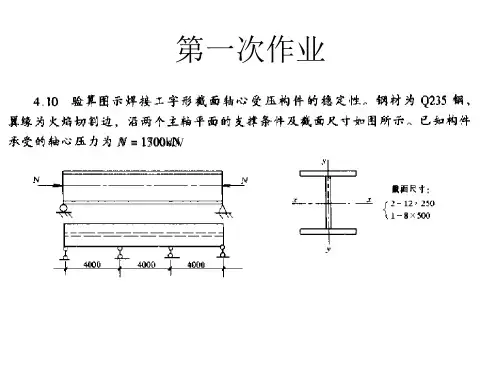
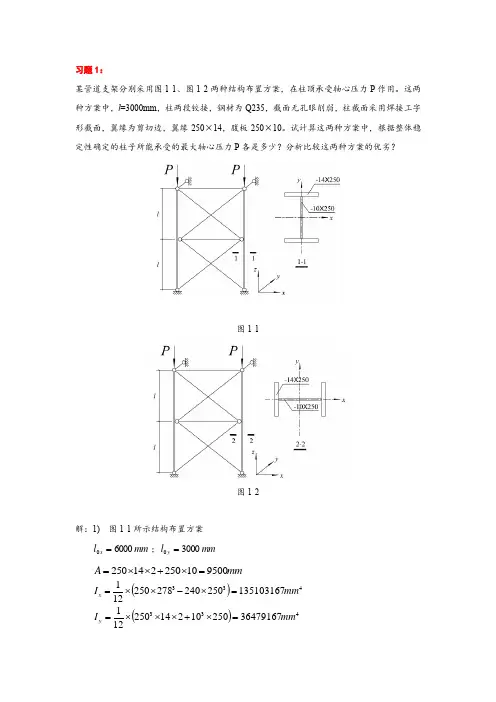
习题1：某管道支架分别采用图1-1、图1-2两种结构布置方案，在柱顶承受轴心压力P 作用。

这两种方案中，l =3000mm ，柱两段铰接，钢材为Q235，截面无孔眼削弱，柱截面采用焊接工字形截面，翼缘为剪切边，翼缘-250×14，腹板-250×10。

试计算这两种方案中，根据整体稳定性确定的柱子所能承受的最大轴心压力P 各是多少？分析比较这两种方案的优劣？图1-1图1-2解：1) 图1-1所示结构布置方案mm l x 60000=；mm l y 30000=mm A 950010250214250=⨯+⨯⨯=()433135103167250240278250121mm I x =⨯-⨯⨯=()4333647916725010214250121mm I y =⨯+⨯⨯⨯=mm A I i x x 3.1199500135103167===；mm AI i y y 0.62950036479167===3.503.11960000===x x x i l λ；4.480.6230000===y y y i l λ此截面对x 轴为b 类，对y 轴为c 类，查表得855.0=x ϕ(附表4-4)；785.0=y ϕ(附表4-5)应根据y ϕ确定柱子整体稳定的承载力kN Af P d y 16032159500785.0max =⨯⨯==ϕ2) 图1-2所示结构布置方案mm l x 60000=；mm l y 30000=mm A 9500=；mm i x 0.62=；mm i y 3.119= 8.960.6260000===x x x i l λ；1.253.11930000===y y y i l λ此截面对x 轴为c 类，对y 轴为b 类，查表得478.0=x ϕ(附表4-5)；953.0=y ϕ(附表4-4)应根据x ϕ确定柱子整体稳定的承载力kN Af P d x 9762159500478.0max =⨯⨯==ϕ3) 分析比较两种结构布置方案所使用的材料完全相同，但是图1-1所示方案（为下文表述的方便，以后简称方案A ）的承载力为1603kN ，而图1-2所示方案（为下文表述的方便，以后简称方案B ）的承载力仅为976kN 。

4-1解：kN N N N QK Q GK G 420315324.1315312.1=⨯⨯+⨯⨯=+=γγ焊缝质量为三级，用引弧板施焊。

查表得E43焊条的2/185mm N f W t =，Q235钢的2/215mm N f =。

mm bf N t W t 35.11185200104203=⨯⨯=≥ 故取mm t 12=。

4-2解：k k k QK Q GK G N N N N N N 36.18.04.12.02.1=⨯+⨯=+=γγ焊缝质量为二级，2/215mm N f W t =未用引弧板施焊mm l W 376122400=⨯-=tl Nf W W t =，k W W t N t l f N 36.1== kN t l f N W W t k 3.71336.11237621536.1=⨯⨯==4-4解：1）焊脚尺寸f h背部尺寸⎪⎩⎪⎨⎧=⨯=≤=⨯=≥mmt h mmt h f f 6.982.12.174.4105.15.1min 1max 1趾部尺寸()()⎪⎩⎪⎨⎧=-=-≤=⨯=≥mm t h mmt h f f 7~62~182~174.4105.15.1min2max 2为方便备料，取mm h h h f f f 621===，满足上述要求。

2）轴心力N 的设计值kN N N N QK Q GK G 4.2481809.04.11801.02.1=⨯⨯+⨯⨯=+=γγ按角钢背与趾部侧面角焊缝内力分配系数可知:等边角钢内力分配系数3.01=b e 7.02=be对角钢趾部取力矩平衡得: 21Ne b N =kN N N be N 52.744.2483.03.021=⨯===kN N N N N 88.1734.2487.07.012=⨯==-=3)焊缝长度。

当构件截面为一只角钢时，考虑角钢与节点板单面连接所引起的偏心影响， W t f 应乘以折减系数0-85。

角钢趾：mm h mm f h N l f W f f W 48813016085.067.01052.7485.07.0311=>=⨯⨯⨯⨯=⋅≥取mm l 1401= （mm h f 1422130=+，取10mm 的整数倍） 角钢背：mm h mm f h N l f W f f W 3606030416085.067.01088.17385.07.0322=<=⨯⨯⨯⨯=⋅≥ 取mm l 3202= （mm h f 3162304=+，取10mm 的整数）4-5解：腹板受到轴心拉力k N 作用kN N N N QK Q GK G 4.5984408.04.14402.02.1=⨯⨯+⨯⨯=+=γγ焊脚尺寸f hmmt h f 6.55.1max =≥，mmt h f 9~8)2~1(min =-≤取mm h f 6=时，mm h mm f h N l f Wf f W 360602.44516067.02104.5987.023=>=⨯⨯⨯⨯=⨯≥ 不可行；取mm h f 7=时，mm l w 6.381≥，mm h l f w 42060=≤ 可行，mm h l f 6.39526.381=+=，取mm l 400= 取mm h f 9=时，mm l w 8.296≥，mm h l f w 54060=< 可行，mm h l f 8.31428.296=+=，取mm l 320=故最小的焊脚尺寸可取mm 7，钢板搭接长度为mm 400 最大的焊脚尺寸可取mm 9，钢板搭接长度为mm 3204-7解：（1）直接计算法m kN Nl M ⋅=⨯==102.0502262/1.148862407.0101067.0mm N h h l h M ff W f f =⨯⨯==σ23/6.2972407.010507.0mm N h h l h N ff W f f =⨯⨯==τW f f ff f ≤+⎪⎪⎭⎫⎝⎛22τβσ 1606.29722.11.148822≤⎪⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫ ⎝⎛f f h h 解得：mm h f 85.7= 采用()mmt mmt mmh f 9~82~136.6185.15.18min max =-≤=⨯=≥=，可（2）试算法()⎩⎨⎧=-≤=⨯=≥mm t mmt h f 9~82~136.6185.15.1min max 取mm h f 8=2134424087.07.0mm l h l h A W f W e W =⨯⨯=== 3225376024087.06161mm l h W W e W =⨯⨯⨯==2262/0.186624087.0101067.0mm N l h M W f f =⨯⨯⨯==σ 23/2.3724087.010507.0mm N l h N W f f =⨯⨯⨯==τ222222/160/9.1562.3722.1186mm N f mm N W f f ff =≤=+⎪⎭⎫ ⎝⎛=+⎪⎪⎭⎫ ⎝⎛τβσ，可 故mm h f 8=4-8解：kN R R R k k 405%754.1%252.1=⨯+⨯=mm l 300= mm l h 701080=-=取焊脚尺寸mm h f 6= mm h h f e 2.47.0== （1）几何关系水平焊缝计算长度mm h l l f h Wh 64670=-=-= 全部焊缝计算长度mm l l l Wh W 4286423002=⨯+=+= 全部焊缝有效截面W e W l h A = 形心位置cm h h A l l h x e e WWhWh e 96.08.4224.64.6222=⨯⨯⨯⨯=⋅=略去3e h 项423236.21542304.642.02123042.02212cm l l h l h I Wh e e x =⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛⨯⨯⨯+⨯=⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛⋅+=42232238.4796.04.642.096.024.64.642.0124.642.022122cm x l h x l l h l h I Wh e Wh Wh e Wh e y =⨯⨯+⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛-⨯⨯+⨯⨯=+⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛-+= 焊缝有效截面对形心O 的极惯性矩404.22028.476.2154cm I I I y x =+=+=（2）强度验算kN RV 5.2022== mm x a 4.7080=-= m kN Ra T ⋅=⨯⨯==-3.142104.7040523 mm x l x Wh 4.546.9641=-=-= mm ly 15021==↑=⨯⨯⨯==24601/3.35104.22024.54103.14mm N I Tx Tfσ ←=⨯⨯⨯==2461/4.97104.2202150103.14mm N I Ty Tfτ↑=⨯⨯==23/7.1124282.4105.202mm N A V V fσ剪力和扭矩共同作用下的强度条件()222222/160/6.1554.9722.17.1123.35mmN f mm N W f Tf f Vf Tf =≤=+⎪⎭⎫ ⎝⎛+=+⎪⎪⎭⎫⎝⎛+τβσσ，可5-1解：QK Q GK G N N N γγ+=则：N N k 8.772560%904.1560%102.1=⨯⨯+⨯⨯=查表，得：钢板螺栓孔壁承压承载力设计值：2/405mm N f b c = 螺栓的强度设计值为：2/190mm N f b v =)(32.1191019044002432kN f d n N bv e vbv =⨯⨯⨯⨯==-ππ)(1621040520203kN tf d N bc b c =⨯⨯⨯=∑=-取)(32.119},min{kN N N N b c b v b == 需要的螺栓数目：48.632.1198.772===b N N n 最少采用7=n试取螺栓距mm mm d p o 655.613≈== 端距mm mm d a o 45412≈== 边距mm mm d c o 3575.305.1≈==因为板宽mm b 250=，若边距为mm 35则不满足间距不大于mm t 12012=要求，故最外排每列螺栓应设3个，取螺栓横向间距为mm 90，端距为mm 45，螺栓数增加为8个。

2023钢结构基本原理第二版（沈祖炎著）课后答
案下载
2023钢结构基本原理第二版（沈祖炎著）课后答案下载
前言
第一章绪论.
第一节钢结构的特点和应用
第二节钢结构设计要求与设计方法
第三节钢结构的发展方向
第四节本课程的主要内容、特点和学习方法
思考题
第二章钢结构的材料
第一节钢结构对材料的要求
第二节钢材的塑性破坏和脆性破坏
第三节钢材的主要性能
第四节影响钢材性能的因素
第五节钢材的疲劳
第六节钢材的种类和规格
思考题
钢结构基本原理第二版（沈祖炎著）：内容简介
点击此处下载钢结构基本原理第二版（沈祖炎著）课后答案
钢结构基本原理第二版（沈祖炎著）：图书目录
本书主要依据国家标准《钢结构设计规范》(GB 50017--)编写。

全书共分七章，基本内容包括绪论、钢结构的材料、钢结构的'连接、轴心受力构件、受弯构件设计、拉弯压弯构件和钢结构最新技术。

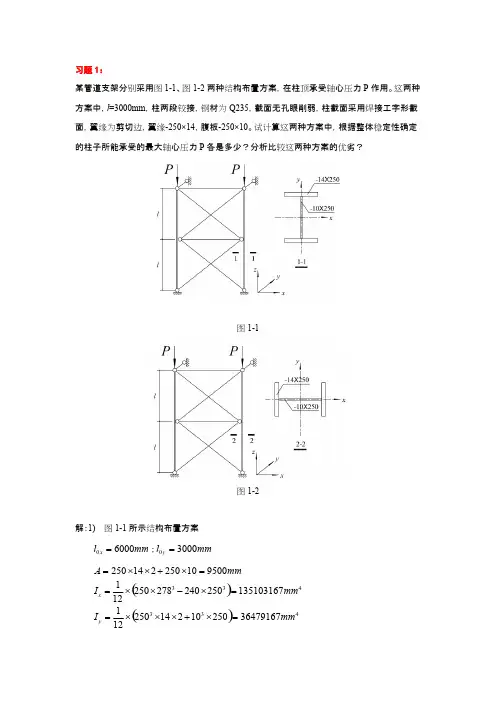
习题1：某管道支架分别采用图1-1、图1-2两种结构布置方案，在柱顶承受轴心压力P 作用。

这两种方案中，l =3000mm ，柱两段铰接，钢材为Q235，截面无孔眼削弱，柱截面采用焊接工字形截面，翼缘为剪切边，翼缘-250×14，腹板-250×10。

试计算这两种方案中，根据整体稳定性确定的柱子所能承受的最大轴心压力P 各是多少？分析比较这两种方案的优劣？图1-1图1-2解：1) 图1-1所示结构布置方案；mm l x 60000=mml y 30000=mmA 950010250214250=⨯+⨯⨯=()433135103167250240278250121mm I x =⨯-⨯⨯=()4333647916725010214250121mm I y =⨯+⨯⨯⨯=；mm A I i x x 3.1199500135103167===mmAI i y y 0.62950036479167===；3.503.11960000===x x x i l λ4.480.6230000===y y y i l λ此截面对x 轴为b 类，对y 轴为c 类，查表得(附表4-4)；(附表4-5)855.0=x ϕ785.0=y ϕ应根据确定柱子整体稳定的承载力y ϕkNAf P d y 16032159500785.0max =⨯⨯==ϕ2) 图1-2所示结构布置方案；mm l x 60000=mml y 30000=；；mm A 9500=mm i x 0.62=mmi y 3.119=；8.960.6260000===x x x i l λ1.253.11930000===y y y i l λ此截面对x 轴为c 类，对y 轴为b 类，查表得(附表4-5)；(附表4-4)478.0=x ϕ953.0=y ϕ应根据确定柱子整体稳定的承载力x ϕkNAf P d x 9762159500478.0max =⨯⨯==ϕ3) 分析比较两种结构布置方案所使用的材料完全相同，但是图1-1所示方案（为下文表述的方便，以后简称方案A ）的承载力为1603kN ，而图1-2所示方案（为下文表述的方便，以后简称方案B ）的承载力仅为976kN 。

钢结构第六章作业参考答案-标准化文件发布号：（9456-EUATWK-MWUB-WUNN-INNUL-DDQTY-KII习题6.1 有一两端铰接长度为4m 的偏心受压柱，用Q235的HN400x200x8x13做成，压力的设计值为490KN ，两端偏心距相同，皆为20cm 。

试验算其承载力。

解：（1）截面的几何特性A = 84.12 cm 2 I X = 23700cm 4 I y = 1740cm 4i x = 16.8cm i y = 4.54cm w x = 1190cm 3(2) 验算强度 N= 490kN M= N x e 0 =490x0.2=98kN •mAn N + X Mx r Wnx = 324901084.1210⨯⨯ + 6398101.05119010⨯⨯⨯ = 58.25+78.43=136.68N/mm 2 < f =215 N/mm 2(3) 验算弯矩作用平面内的稳定λx = x x li = 40016.8= 23.8< [λ] =150 查附表4.2（b 类截面） ϕx = 0.958'Ex N = 22X 1.1EA πλ = 2220600084121.123.8π⨯⨯⨯ = 2744.86kN mx β=1.0 x A N ϕ + mx X 1x 'Mx r W (10.8)ExN N β- = 3490100.9588412⨯⨯ +631.098104901.05119010(10.8)2744.86⨯⨯⨯⨯-=152.30N/mm 2 < f =215 N/mm 2可见平面内不失稳。

（4）验算弯矩作用平面外的稳定 λy =4004.54=88.1 查附表4.2 （b 类截面） ϕy = 0.634ϕb = 1.07 - 2y 44000λ = 1.07-288.144000=0.894 tx β=1.0 , η=1.0y A N ϕ + b 1tx x x M W βηϕ = 3490100.6348412⨯⨯ + 631.098101.00.894119010⨯⨯⨯⨯⨯ =184 N/ mm 2 < f = 215 N/mm 2平面外不失稳。

6.1 工字形焊接组合截面简支梁，其上密铺刚性板可以阻止弯曲平面外变形。

梁上均布荷载（包括梁自重）4/q kN m =，跨中已有一集中荷载090F kN =，现需在距右端4m 处设一集中荷载1F 。

问根据边缘屈服准则，1F 最大可达多少。

设各集中荷载的作用位置距梁顶面为120mm ，分布长度为120mm 。

钢材的设计强度取为2300/N mm 。

另在所有的已知荷载和所有未知荷载中，都已包含有关荷载的分项系数。

图6-34 题6.1解：（1）计算截面特性2250122800812400A mm =⨯⨯+⨯=339411250824(2508)800 1.33101212x I mm =⨯⨯-⨯-⨯=⨯ 633.229102x x I W mm h==⨯ 32501240640082001858000m S mm =⨯⨯+⨯⨯= 31250124061218000S mm =⨯⨯=（2）计算0F 、1F 两集中力对应截面弯矩()210111412901263422843F M F kN m =⨯⨯+⨯⨯+⨯=+⋅ ()1118128248489012824424333F M F kN m =⨯-⨯⨯+⨯⨯⨯+⨯=+⋅ 令10M M >，则当1147F kN >，使弯矩最大值出现在1F 作用截面。

（3）梁截面能承受的最大弯矩63.22910300968.7x M W f kN m ==⨯⨯=⋅令0M M =得：1313.35F kN =；令1M M =得：1271.76F kN =故可假定在1F 作用截面处达到最大弯矩。

（4）a ．弯曲正应力61max 68(244)1033003.22910x x F M W σ+⨯==≤⨯ ① b.剪应力1F 作用截面处的剪力1111122412449053()2233V F F kN ⎛⎫=⨯⨯-⨯+⨯+=+ ⎪⎝⎭311max 925310185800031.33108m x F V S I t τ⎛⎫+⨯⨯ ⎪⎝⎭==≤⨯⨯ ② c.局部承压应力 在右侧支座处：()312244510330081205122120c F σ⎛⎫++⨯ ⎪⎝⎭=≤⨯+⨯+⨯ ③ 1F 集中力作用处：()311030081205122120c F σ⨯=≤⨯+⨯+⨯ ④ d.折算应力1F 作用截面右侧处存在很大的弯矩，剪力和局部承压应力，计算腹板与翼缘交界处的分享应力与折算应力。