高中数学 充分条件与必要条件、第一章 集合与简易逻辑的复习 .

高中数学第一章-集合考试内容：集合、子集、补集、交集、并集．逻辑联结词．四种命题．充分条件和必要条件．考试要求： （1）理解集合、子集、补集、交集、并集的概念；了解空集和全集的意义；了解属于、包含、相等关系的意义；掌握有关的术语和符号，并会用它们正确表示一些简单的集合．（2）理解逻辑联结词“或”、“且”、“非”的含义理解四种命题及其相互关系；掌握充分条件、必要条件及充要条件的意义．§01. 集合与简易逻辑 知识要点一、知识结构:本章知识主要分为集合、简单不等式的解法（集合化简）、简易逻辑三部分：二、知识回顾：（一）集合1.基本概念：集合、元素；有限集、无限集；空集、全集；符号的使用.2.集合的表示法：列举法、描述法、图形表示法.集合元素的特征：确定性、互异性、无序性. 集合的性质：①任何一个集合是它本身的子集，记为；②空集是任何集合的子集，记为；③空集是任何非空集合的真子集；如果，同时，那么A = B.如果.[注]：①Z = {整数}（√） Z ={全体整数} （×）②已知集合S 中A 的补集是一个有限集，则集合A 也是有限集.（×）（例：S=N ； A=，则C s A= {0}）A A ⊆A ⊆φB A ⊆A B ⊆C A C B B A ⊆⊆⊆，那么，+N③空集的补集是全集.④若集合A=集合B，则C B A=，C A B =C S（C A B）=D（注：C A B =）.3. ①{（x，y）|xy =0，x∈R，y∈R}坐标轴上的点集.②{（x，y）|xy＜0，x∈R，y∈R二、四象限的点集.③{（x，y）|xy＞0，x∈R，y∈R} 一、三象限的点集.[注]：①对方程组解的集合应是点集.例：解的集合{(2，1)}.②点集与数集的交集是. （例：A ={(x，y)| y =x+1} B={y|y =x2+1} 则A∩B =）4. ①n个元素的子集有2n个. ②n个元素的真子集有2n－1个. ③n个元素的非空真子集有2n－2个.5. ⑴①一个命题的否命题为真，它的逆命题一定为真. 否命题逆命题.②一个命题为真，则它的逆否命题一定为真. 原命题逆否命题.例：①若应是真命题.，则a+b = 5，成立，所以此命题为真.②.1或y = 2.,故是的既不是充分，又不是必要条件.⑵小范围推出大范围；大范围推不出小范围.3.例：若.4.集合运算：交、并、补.5.主要性质和运算律（1）包含关系：（2）等价关系：（3）集合的运算律：交换律：结合律:分配律:.∅∅∅}⎩⎨⎧=-=+1323yxyxφ∅⇔⇔325≠≠≠+baba或，则且1≠x3≠y1≠∴yx且3≠+yx21≠≠yx且255xxx或，⇒{|,}{|}{,}A B x x A x BA B x x A x BA x U x A⇔∈∈⇔∈∈⇔∈∉U交：且并：或补：且C,,,,,;,;,.UA A A A U A UA B B C A C A B A A B B A B A A B B⊆Φ⊆⊆⊆⊆⊆⇒⊆⊆⊆⊇⊇CUA B A B A A B B A B U⊆⇔=⇔=⇔=C.;ABBAABBA==)()();()(CBACBACBACBA==)()()();()()(CABACBACABACBA==0-1律：等幂律：求补律：A∩C U A=φA∪C U A=U C U U=φ C Uφ=U反演律：C U(A∩B)= (C U A)∪(C U B) C U(A∪B)= (C U A)∩(C U B)6.有限集的元素个数定义：有限集A的元素的个数叫做集合A的基数，记为card( A)规定 card(φ) =0.基本公式：(3) card( U A)= card(U)- card(A)(二)含绝对值不等式、一元二次不等式的解法及延伸1.整式不等式的解法根轴法（零点分段法）①将不等式化为a0(x-x1)(x-x2)…(x-x m)>0(<0)形式，并将各因式x的系数化“+”；(为了统一方便)②求根，并在数轴上表示出来；③由右上方穿线，经过数轴上表示各根的点（为什么？）；④若不等式（x的系数化“+”后）是“>0”,则找“线”在x轴上方的区间；若不等式是“<0”,则找“线”在x轴下方的区间.（自右向左正负相间）则不等式的解可以根据各区间的符号确定.特例①一元一次不等式ax>b解的讨论；②一元二次不等式ax2+box>0(a>0)解的讨论.>∆0=∆0<∆二次函数cbxaxy++=2（0>a）的图象,,,A A A U A A U A UΦ=ΦΦ===.,AAAAAA==(1)()()()()(2)()()()()()()()()card A B card A card B card A Bcard A B C card A card B card Ccard A B card B C card C Acard A B C=+-=++---+x)0)((002211><>++++--aaxaxaxa nnnn原命题若p 则q否命题若┐p 则┐q 逆命题若q 则p 逆否命题若┐q 则┐p 互为逆否互逆否互为逆否互互逆否互一元二次方程()的根002>=++a c bx ax 有两相异实根)(,2121x x x x <有两相等实根ab x x 221-== 无实根的解集)0(02>>++a c bx ax {}21x x x x x ><或⎭⎬⎫⎩⎨⎧-≠a b x x 2R 的解集)0(02><++a c bx ax {}21x x x x << ∅∅2.分式不等式的解法（1）标准化：移项通分化为>0(或<0)； ≥0(或≤0)的形式，（2）转化为整式不等式（组）3.含绝对值不等式的解法（1）公式法：,与型的不等式的解法.（2）定义法：用“零点分区间法”分类讨论.（3）几何法：根据绝对值的几何意义用数形结合思想方法解题.4.一元二次方程根的分布一元二次方程ax 2+bx+c=0(a≠0)（1）根的“零分布”：根据判别式和韦达定理分析列式解之.（2）根的“非零分布”：作二次函数图象，用数形结合思想分析列式解之.（三）简易逻辑1、命题的定义：可以判断真假的语句叫做命题。

知识点总结1 集合与简易逻辑一、集合(一)元素与集合1.集合的含义某些指定对象的部分或全体构成一个集合．构成集合的元素除了常见的数、点等数学对象外，还可以是其他对象．2.集合元素的特征(1)确定性：集合中的元素必须是确定的，任何一个对象都能明确判断出它是否为该集合中的元素．(2)互异性：集合中任何两个元素都是互不相同的，即相同元素在同一个集合中不能重复出现．(3)无序性：集合与其组成元素的顺序无关．3.元素与集合的关系元素与集合之间的关系包括属于(记作a A ∈)和不属于(记作a A ∉)两种．4.集合的常用表示法集合的常用表示法有列举法、描述法、图示法(韦恩图)．5.常用数集的表示 数集 自然数集 正整数集 整数集 有理数集 实数集符号 NN ∗或N + Z Q R (二)集合间的基本关系1.集合A 为集合B 的子集 ，记作A B ⊆（或B A ⊇），读作“A 包含于B ”（或“B 包含A ”）.(2)真子集：若A B ⊆，且存在b B ∈，但b A ∉，则集合A 是集合B 的真子集，记作AB （或B A ⊃≠）. 读作“A 真包含于B ”或“B 真包含A ”.(3)相等：对于两个集合A 与B ，如果A B ⊆，同时B A ⊆，那么集合A 与B 相等，记作A =B ．(4)空集：把不含任何元素的集合叫做空集，记作∅；(三)集合的基本运算(1)交集：由所有属于集合A 且属于集合B 的元素组成的集合，叫做A 与B 的交集，记作A B ⋂， 即{}|A B x x A x B ⋂=∈∈且．(2) 并集：由所有属于集合A 或属于集合B 的元素组成的集合，叫做A 与B 的并集，记作A B ⋃，(3) 即{}|A B x x A x B ⋃=∈∈或．(3)补集：对于一个集合A ，由全集U 中不属于集合A 的所有元素组成的集合称为集合A 相对于全集U 的补集，简称为集合A 的补集，记作U C A ，即{|,}U C A x x U x A =∈∉且．(四)集合的运算性质(1)集合的运算性质：①交换律：A ∪B ＝B ∪A ；A ∩B ＝B ∩A ；②结合律：(A ∪B )∪C ＝A ∪(B ∪C )；(A ∩B )∩C ＝A ∩(B ∩C )；③分配律：(A ∩B )∪C ＝(A ∪C )∩(B ∪C )；(A ∪B )∩C ＝(A ∩C )∪(B ∩C )；【集合常用结论】1.子集个数：含有n个元素的有限集合M，其子集个数为2n；其真子集个数为2n－1；其非空子集个数为2n－1；其非空真子集个数为2n－2.2. 是任何集合的子集，是任何非空集合的真子集.3.∁U(A∪B)＝(∁U A)∩(∁U B)；∁U(A∩B)＝(∁U A)∪(∁U B)；4.A∪B＝A⇔B⊆A；A∩B＝B⇔B⊆A.5.集合运算中的常用方法若已知的集合是不等式的解集，用数轴求解；若已知的集合是点集，用数形结合法求解；若已知的集合是抽象集合，用Venn图求解.二、简易逻辑(一).全称命题、特称(存在性)命题及其否定(1)全称命题p：∀x∈M，p(x)，其否定为特称(存在性)命题：¬p：∃x0∈M，¬p(x0).(2)特称(存在性)命题p：∃x0∈M，p(x0)，其否定为全称命题：¬p：∀x∈M，¬p(x).(二).充分条件与必要条件的判定方法(1)定义法：若p⇒q，则p是q的充分条件(或q是p的必要条件)；若p⇒q，且q⇏p，则p是q的充分不必要条件(或q是p的必要不充分条件).(2)集合法：利用集合间的包含关系。

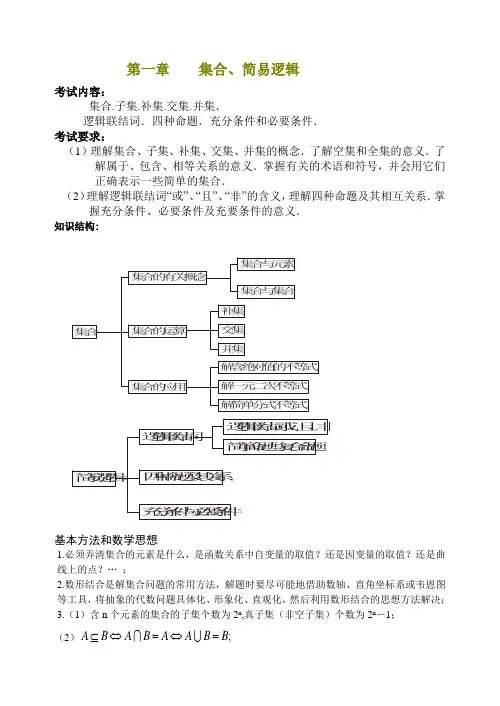
第一章 集合、简易逻辑考试内容：集合.子集.补集.交集.并集．逻辑联结词．四种命题．充分条件和必要条件．考试要求：（1）理解集合、子集、补集、交集、并集的概念．了解空集和全集的意义．了解属于、包含、相等关系的意义．掌握有关的术语和符号，并会用它们正确表示一些简单的集合．（2）理解逻辑联结词“或”、“且”、“非”的含义，理解四种命题及其相互关系．掌握充分条件、必要条件及充要条件的意义．知识结构:基本方法和数学思想1.必须弄清集合的元素是什么，是函数关系中自变量的取值？还是因变量的取值？还是曲线上的点？… ；2.数形结合是解集合问题的常用方法，解题时要尽可能地借助数轴、直角坐标系或韦恩图等工具，将抽象的代数问题具体化、形象化、直观化，然后利用数形结合的思想方法解决；3.（1）含n 个元素的集合的子集个数为2n ,真子集（非空子集）个数为2n －1；（2）;B B A A B A B A =⇔=⇔⊆（3）;)(,)(B C A C B A C B C A C B A C I I I I I I ==4、一元二次不等式20(0)ax bx c ++><或2(0,40)a b ac ≠∆=->，如果a 与2ax bx c ++同号，则其解集在两根之外；如果a 与2ax bx c ++异号，则其解集在两根之间.简言之：同号两根之外，异号两根之间.121212()()0()x x x x x x x x x <<⇔--<<；121212,()()0()x x x x x x x x x x <>⇔--><或.5.一个语句是否为命题，关键要看能否判断真假，陈述句、反诘问句都是命题，而祁使句、疑问句、感叹句都不是命题；6.判断命题的真假要以真值表为依据。

原命题与其逆否命题是等价命题 ，逆命题与其否命题是等价命题 ，一真俱真，一假俱假，当一个命题的真假不易判断时，可考虑判断其等价命题的真假；7.判断命题充要条件的三种方法：（1）定义法；（2）利用集合间的包含关系判断，若B A ⊆，则A 是B 的充分条件或B 是A 的必要条件；若A=B ，则A 是B 的充要条件；（3）等价法：即利用等价关系"A B B A "⇒⇔⇒判断，对于条件或结论是不等关系（或否定式）的命题，一般运用等价法；高考热点分析集合与简易逻辑是高中数学的重要基础知识，是高考的必考内容.本章知识的高考命题热点有以下两个方面：一是集合的运算、集合的有关述语和符号、集合的简单应用、判断命题的真假、四种命题的关系、充要条件的判定等作基础性的考查，题型多以选择、填空题的形式出现；二是以函数、方程、三角、不等式等知识为载体，以集合的语言和符号为表现形式，结合简易逻辑知识考查学生的数学思想、数学方法和数学能力，题型常以解答题的形式出现.。

高中数学会考基础知识汇总 第一章 集合与简易逻辑：一．集合1、 集合的有关概念和运算（1）集合的特性：确定性、互异性和无序性；（2）元素a 和集合A 之间的关系：a ∈A ，或a ∉A ；2、子集定义：A 中的任何元素都属于B ，则A 叫B 的子集 ；记作：A ⊆B ， 注意：A ⊆B 时，A 有两种情况：A ＝φ与A ≠φ3、真子集定义：A 是B 的子集 ，且B 中至少有一个元素不属于A ；记作：B A ⊂；4、补集定义：},|{A x U x x A C U ∉∈=且；5、交集与并集 交集：}|{B x A x x B A ∈∈=且 ；并集：}|{B x A x x B A ∈∈=或6、集合中元素的个数的计算： 若集合A 中有n 个元素，则集合A 的所有不同的子集个数为_________，所有真子集的个数是__________，所有非空真子集的个数是 。

二．简易逻辑：1．复合命题： 三种形式：p 或q 、p 且q 、非p ； 判断复合命题真假：2.真值表：p 或q ，同假为假，否则为真；p 且q ，同真为真；非p ，真假相反。

3.四种命题及其关系：原命题：若p 则q ； 逆命题：若q 则p ；否命题：若⌝p 则⌝q ； 逆否命题：若⌝q 则⌝p ； 互为逆否的两个命题是等价的。

原命题与它的逆否命题是等价命题。

4.充分条件与必要条件：若q p ⇒，则p 叫q 的充分条件； 若q p ⇐，则p 叫q 的必要条件； 若q p ⇔，则p 叫q 的充要条件；第二章 函数一． 函数1、映射：按照某种对应法则f ，集合A 中的任何一个元素，在B 中都有唯一确定的元素和它对应， 记作f ：A →B ，若B b A a ∈∈,，且元素a 和元素b 对应，那么b 叫a 的象，a 叫b 的原象。

2、函数：（1）、定义：设A ，B 是非空数集，若按某种确定的对应关系f ，对于集合A 中的任意一个数x ，集合B 中都有唯一确定的数f （x ）和它对应，就称f ：A →B 为集合A 到集合B 的一个函数，记作y=f （x ）， （2）、函数的三要素：定义域，值域，对应法则；3、求定义域的一般方法：①整式：全体实数R ；②分式：分母0≠，0次幂：底数0≠； ③偶次根式：被开方式0≥，例：225x y -=；④对数：真数0>，例：)11(log xy a -=4、求值域的一般方法：①图象观察法：||2.0x y =；②单调函数法： ]3,31[),13(log 2∈-=x x y ③二次函数配方法：)5,1[,42∈-=x x x y ， 222++-=x x y④“一次”分式反函数法：12+=x xy ；⑥换元法：x x y 21-+= 5、求函数解析式f （x ）的一般方法：①待定系数法：一次函数f （x ），且满足172)1(2)1(3+=--+x x f x f ，求f （x ） ②配凑法：,1)1(22xx xx f +=-求f （x ）；③换元法：x x x f 2)1(+=+，求f （x ） 6、函数的单调性：（1）定义：区间D 上任意两个值21,x x ，若21x x <时有)()(21x f x f <，称)(x f 为D 上增函数； 若21x x <时有)()(21x f x f >，称)(x f 为D 上减函数。

第六节 充分条件与必要条件一、基础知识（一）充分条件、必要条件和充要条件1．充分条件：如果A 成立那么B 成立，则条件A 是B 成立的充分条件。

2．必要条件：如果A 成立那么B 成立，这时B 是A 的必然结果，则条件B 是A 成立的必要条件。

B A ⇒3．充要条件：如果A 既是B 成立的充分条件，又是B 成立的必要条件，则A 是B 成立的充要条件；同时B 也是A 成立的充要条件。

（二）充要条件的判断1若B A ⇒成立则A 是B 成立的充分条件，B 是A 成立的必要条件。

2．若B A ⇒且B A ，则A 是B 成立的充分且不必要条件，B 是A 成立必要且非充分条件。

3．若B A ⇔成立则A 、B 互为充要条件。

证明A 是B 的充要条件，分两步：（1）充分性：把A 当作已知条件，结合命题的前提条件推出B ；（2）必要性：把B 当作已知条件，结合命题的前提条件推出A 。

（三）反证法运用的两个难点：1）何时使用反证法 2）如何得到矛盾。

二、范例选讲例1．（04重庆）一元二次方程2210,(0)ax x a ++=≠有一个正根和一个负根的充分不必要条件是（ C ）（A ）0a < （B ）0a > （C ）1a <- （D ）1a >练习1设f(x)=x 2-4x(x ∈R)，则f(x)>0的一个必要而不充分条件是（ C ）A 、x<0B 、x<0或x>4C 、│x-1│>1D 、│x-2│>3例2．填空题;______)1(条件的是则若p q q p ⌝⌝⇒;______00,_______00)2(条件的是条件的是≥≥>>ba ab b a ab (3)若A 是B 的充分条件，B 是C 的充要条件，D 是C 的必要条件，则A 是D 的 条件. 答案：(1)充分条件 (2)充要、必要不充分 (3)A ＝> B <＝> C ＝> D 故填充分。

2021年高考数学复习专题01 集合与简易逻辑命题及其关系、充分条件与必要条件考点剖析主标题：命题及其关系、充分条件与必要条件副标题：为学生详细的分析命题及其关系、充分条件与必要条件的高考考点、命题方向以及规律总结。

关键词：命题，充分条件，必要条件难度：2重要程度：4考点剖析：1．理解命题的概念．2．了解“若p，则q”形式的命题的逆命题、否命题与逆否命题，会分析四种命题的相互关系．3．理解充分条件、必要条件与充要条件的含义.命题方向：充分、必要条件的判断；全称命题与存在性命题的否定. 考查形式一般为选择题、填空题，多为容易题．规律总结：1．一个区别否命题与命题的否定是两个不同的概念．否命题同时否定原命题的条件和结论，命题的否定仅仅否定原命题的结论(条件不变)．2．三个防范一是分清命题中的条件和结论，并搞清楚其中的关键词，如“≠”与“＝”，“＞”与“≤”，“且”与“或”，“是”与“不是”，“都不是”与“至少一个是”，“都是”与“不都是”等互为否定；二是弄清先后顺序：“A的充分不必要条件是B”是指B⇒A，且AB；而“A是B的充分不必要条件”则是指A⇒B且B A；三是注意题中的大前提．方法：1．判断充分条件和必要条件的方法(1)命题判断法：设“若p，则q”为原命题，那么：①原命题为真，逆命题为假时，p是q的充分不必要条件；②原命题为假，逆命题为真时，p是q的必要不充分条件；③原命题与逆命题都为真时，p是q的充要条件；④原命题与逆命题都为假时，p是q的既不充分也不必要条件．(2)集合判断法：从集合的观点看，建立命题p，q相应的集合：p：A＝{x|p(x)成立}，q：B＝{x|q(x)成立}，那么：①若A⊆B，则p是q的充分条件；若AB时，则p是q的充分不必要条件；②若B⊆A，则p是q的必要条件；若BA时，则p是q的必要不充分条件；③若A⊆B且B⊆A，即A＝B时，则p是q的充要条件．(3)等价转化法：p是q的什么条件等价于綈q是綈p的什么条件．2．转化与化归思想由于互为逆否命题的两个命题具有相同的真假性，因而当判断一个命题的真假比较困难时，可转化为判断它的逆否命题的真假．知识梳理1．四种命题及其关系(1)四种命题间的相互关系(2)四种命题的真假关系①两个命题互为逆否命题，它们具有相同的真假性．②两个命题为互逆命题或互否命题时，它们的真假性没有关系．2．充分条件、必要条件与充要条件的概念若p⇒q，则p是q的充分条件，q是p的必要条件p是q的充分不必要条件p⇒q且qpp是q的必要不充分条件pq且q⇒pp是q的充要条件p⇔qp是q的既不充分也不必要条件p q且qp33345 8241 艁ev37363 91F3 釳23884 5D4C 嵌 36748 8F8C 辌21289 5329 匩l 34962 8892 袒QbUa。

高一数学充足条件与必需条件、第一章会合与简略逻辑的复习人教版【本讲教育信息】一. 教课内容：1.充足条件与必需条件2.第一章会合与简略逻辑的复习二. 本周重、难点：1.对于充要条件的判断2.本章综合知识的应用【典型例题】p 是 q 的什么条件？[ 例 1] 判断以下各组命题中（ 1）p：ab 0 ， q ：a2 b 2 0（ 2）p：xy 0 ，q：x y x y（ 3）p：m 0， q ：方程x2 x m 0 有实根（ 4）p：ax2 ax 1 0 的解集为R，q：0 a 4解：（1）p是q的必需不充足条件（2）p是q的充足不用要条件（3）p是q的充足不用要条件（4）p是q的必需不充足条件[ 例 2] 已知：p：x2 8x 20 0 ，q： x2 2x 1 a 2 0 ，若p是q的充足而不用要条件。

求正实数 a 的取值范围。

解：p ： x 10 或 x 2 又∵ a 0 ∴ q ： x 1 a 或 x 1 aa 0由题意 p q 但q / p 如图则有 1 a 2 解得 0 a 31 a 10∴实数 a 的取值范围是0 a 3[ 例 3] 已知p是r的充足条件，而r 是q的必需条件，同时又是S 的充足条件，q是 S 的必要条件。

（1）S 是p的什么条件？（2）p是q的什么条件？（3）此中有哪几对条件互为充要条件？解：p r q r ∴r S Sq∴（ 1） S 是 p 的必需条件（ 2） p 是 q 的充足条件（ 3） r 与 S ， r 与 q ， S 与 q 三对分别互为充要条件[ 例 4] 当且仅当 m 取何整数值时，对于 x 的方程。

mx 24x 40 ①x 24mx 4m 24m5 0 ②的根都是整数解：方程①有实根的充要条件是： 16 16m0 解得 m 1方程②有实根的充要条件是：16 m 2 4(4 m 24 5)解得 m5m45∴m 14由 m 为整数知： m1，0，1当 m1时，方程①为 x24x 4 0 它没有整数根当 m 0 时，方程②为 x 2 5 0 它也没有整数根当 m1时，方程①、②的根都是整数[ 例 5] 设 a 、b 、c 为 ABC 的三边， 求证：方程 x 2 2ax b 20 与 x 2 2cx b 20 有公共根的充要条件是A 90证明：（ 1）充足性∵A 90∴ a 2b 2c 2∴ x 22ax b 20 可化为： x 2 2ax a 2c 2 0[ x (ac)][ x (a c)] 0 ∴ x 1 a c ， x 2a c同理： x 2 2cx b 20 可化为：x 2 2cx c 2 a 2 0[ x (c a)][ x ( c a)] 0 ∴ x 3 a c ， x 4 c a∴ 双方程有公共根 a c（ 2）必需性设双方程有公共根2 2a b 2 0 ∴22( a c)0则2cb 2 02又 ∵0 若0 代入任一方程得 b 20 即 b 0 这与已知 b 是三角形的边长 b0 相矛盾∴ a c把 a c 代入上边方程组与任何一个式子，均可得a 2b 2c 2∴ A90[例 6] 设 a 1 、 b 1 、 c 1 、 a 2 、 b 2 、 c 2 均为非零实数，不等式 a 1 x2b 1xc 1 0 和 a 2 x 2b 2 xc 2 0 的解集分别为M 和 N ，那么“a 1b 1c 1 ”是“ M=N ”的（ ）a 2b 2c 2A. 充足不用要条件B. 必需不充足条件C. 充要条件D. 既不充足与不用要条件解： 对于 x2x 2 0 和 x2x2 0 有 112，但其解集分别为11 2{ x | 1 x2} 和 { x | x 1或 x 2} 不相等，∴ 充足条件不建立又对于x2x 1的解集为 ， x 2 2x4 0的解集为 ， 1111 24∴ 必需条件不建立∴a1b 1c 1 是 M=N 的既不充足也不用要条件。