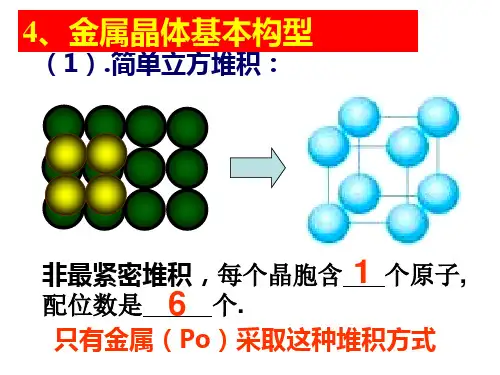
金属晶体的堆积模型

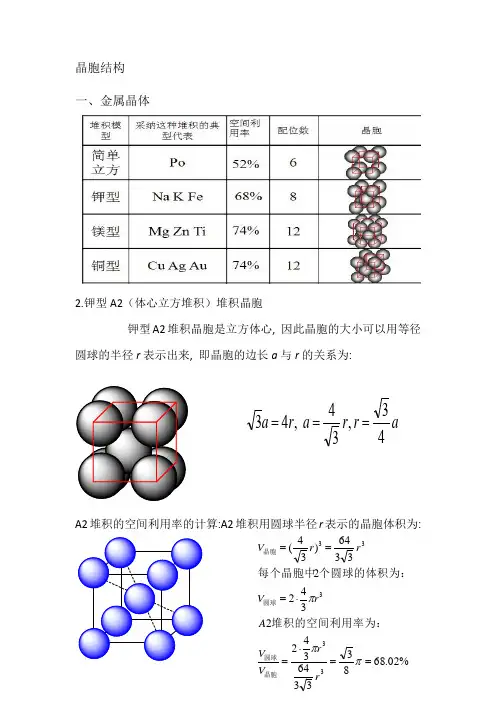
晶胞结构一、金属晶体2.钾型A2（体心立方堆积）堆积晶胞钾型A2堆积晶胞是立方体心, 因此晶胞的大小可以用等径圆球的半径r 表示出来, 即晶胞的边长a 与r 的关系为:A2堆积的空间利用率的计算:A2堆积用圆球半径r 表示的晶胞体积为:ar r a r a 43,34 ,43===%02.68833364342234223364)34(33333==⋅=⋅===πππr r V V A rV rr V 晶胞圆球圆球晶胞堆积的空间利用率为：个圆球的体积为：每个晶胞中3.六方最密堆积（4）A1（面心立方最密堆积）A1是ABCABCABC······型式的堆积，从这种堆积中可以抽出一个立方面心点阵，因此这种堆积型式的最小单位是一个立方面心晶胞。

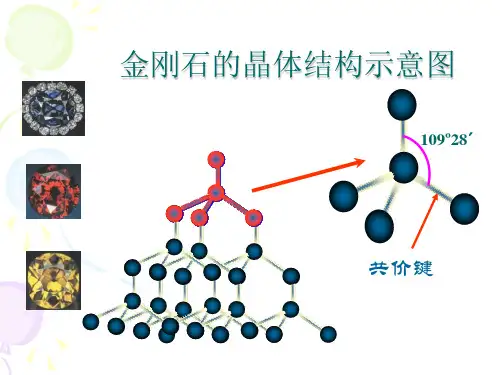
A1堆积晶胞是立方面心, 因此晶胞的大小可以用等径圆球的半径r 表示出来, 即晶胞的边长a 与r 的关系为:A1堆积空间利用率的计算:A1堆积用圆球半径r 表示的晶胞体积为:（5）A4堆积形成晶胞A4堆积晶胞是立方面心点阵结构, 因此晶胞的大小可以用等径圆球的半径r 表示出来, 即晶胞的边长a 与r 的关系为:A4堆积的空间利用率的计算:A4堆积用圆球半径r 表示的晶胞体积为: ra r a 22 ,42==%05.742312163441344 4216)22(33333==⋅=⋅===πππr r V V A r V r r V 晶胞圆球圆球晶胞堆积的空间利用率为：个圆球的体积为：每个晶胞中ar r a r r a 83,38 ,8243===⨯=%01.34163335123484348 833512)38(33333==⋅=⋅===πππr r V V A r V r r V 晶胞圆球圆球晶胞堆积的空间利用率为：个圆球的体积为：每个晶胞中二、原子晶体1.金刚石立体网状结构，每个碳原子形成4个共价键，任意抽出2个共价键，每两个单键归两个六元环所有，而不是只归一个六元环所有（如图所示，红色的两个碳碳单键，可以构成蓝色和紫红色的两个六元环）。

金属晶体的四种堆积模型
金属晶体是由金属原子按照一定的排列构成的固体，它们具有规则的晶体结构，其中最常见的是四种堆积模型：面心立方模型、面心六方模型、空心六方模型和空心八方模型。

面心立方模型是最常见的金属晶体堆积模型，它由八个原子组成，每个原子都位于晶体的八个顶点上，形成一个立方体。

这种模型的特点是，每个原子都与其他七个原子有相同的距离，因此它具有良好的稳定性。

面心六方模型是一种比面心立方模型更复杂的晶体堆积模型，它由十二个原子组成，每个原子都位于晶体的六个面上，形成一个六面体。

这种模型的特点是，每个原子都与其他五个原子有不同的距离，因此它具有较高的热稳定性。

空心六方模型是一种比面心六方模型更复杂的晶体堆积模型，它由十八个原子组成，每个原子都位于晶体的六个面上，形成一个空心六面体。

这种模型的特点是，每个原子都与其他十一个原子有不同的距离，因此它具有较高的热稳定性和机械稳定性。

空心八方模型是一种比空心六方模型更复杂的晶体堆积模型，它由二十四个原子组成，每个原子都位于晶体的八个面上，形成一个空心八面体。

这种模型的特点是，每个原子都与其他十七个原子有不同的距离，同样具有较高的热稳定性和机械稳定性。

总之，金属晶体的四种堆积模型是面心立方模型、面心六方模型、空心六方模型和空心八方模型，它们各自具有不同的特点，可以满足不同的应用需求。

金属晶体的原子堆积模型一、核心思想学生发展核心素养倡导培养学生的科学精神和学会学习的能力，那么以课堂为载体、将核心素养的培养内化到学生学习过程中是我们每节课的追求目标。

为实现培养学生能力和突破教学重难点的双重目标，本节课通过开展活动探究式教学，让学生“动手做、动眼看、动口议、动笔写、动脑思”，加强学生自主探究活动，培养他们的理性思维能力、批判质疑精神和勇于探究精神，真正体现学生的主体地位。

二、教学内容分析1教材分析本节课是鲁科版选修三第三章第一节第二课时的内容，第三章的主题是物质的聚集状态与物质性质，旨在让学生通过本章的学习，了解四种基础晶体类型，能从晶体结构的视角认识物质的性质，进一步形成有关物质结构的概念。

2价值分析（1）学科价值：在教材中承上启下，帮助学生了解金属晶体的原子堆积模型；（2）应用价值：能够判断金属晶体的晶胞类型；（3）学生发展价值：从微观角度认识世界。

3学情分析（1）知识层面：学生已初步了解分子晶体、原子晶体的定义及结构特点。

（2）能力层面：有学习热情，有一定的探究能力、分析思维能力和自主学习能力，主动探究能力有待提升。

（3）可能遇到的问题：语言表达能力不足、不会表达或化学用语不规范；知识迁移运用能力不足，分析问题、解决问题的能力有待提高。

三、教学目标分析1课程目标（1）了解金属晶体的四种基本堆积模型：简单立方堆积、体心立方堆积、六方最密堆积和面心立方最密堆积。

（2）认识四种基本堆积模型的晶胞、能判断金属原子的配位数及四种堆积方式的空间利用率的计算。

2学生核心素养目标（1）科学精神：理性思维能力、严谨求知的态度，勇于探究的精神。

（2）自主发展：乐学善学、学习方法的习得，信息意识。

3方法目标（1）通过观察和制作堆积模型训练学生的空间想象能力和动手能力。

（2）通过小组合作培养学生的合作互助意识。

四、教学重点和难点1教学重点：金属原子在三维空间的四种堆积方式2教学难点：四种堆积方式晶胞、配位数、原子利用率的区别五、教学方法活动探究式学习六、设计思想本节课的设计思想如下，逐步开展三个思考与交流活动以及4个探究环节、梯度螺旋化上升，符合学生认知规律。

金属晶体的四种堆积模型总结Metal crystals can be classified into four main stacking models: Close-packed cubic (FCC), Close-packed hexagonal (HCP), Body-centered cubic (BCC), and Simple cubic (SC). These models represent different ways in which metal atoms arrange themselves in a crystal lattice. Close-packed cubic structures have atoms arranged in layers of repeating ABCABC... pattern, giving them high packing efficiency.金属晶体可以分为四种主要的堆积模型：密堆立方（FCC）、密堆六方（HCP）、体心立方（BCC）和简单立方（SC）。

这些模型代表了金属原子在晶格中排列的不同方式。

密堆立方结构中，原子按照重复ABCABC...模式排列在不同层中，使得具有较高的填充效率。

Close-packed hexagonal structures, on the other hand, consist of layers with an ABAB... stacking sequence. This type of arrangement gives rise to a compact structure with a hexagonal unit cell. Body-centered cubic structures have atoms arranged in a simple cubic lattice with an additional atom at the center of the cube. This arrangement provides good mechanical properties due to thepresence of the central atom, which enhances the strength of the crystal lattice.另一方面，密堆六方结构由具有ABAB...堆叠序列的层组成。