平行四边形的判定定理

平面向量的平行四边形定理和平行四边形法则平面向量是解决空间中几何问题的重要工具之一。

在平面向量的运算中，平行四边形定理和平行四边形法则是非常基础且重要的内容。

本文将为你详细介绍平行四边形定理和平行四边形法则的概念、性质及应用。

一、平行四边形定理的概念和性质平行四边形定理是关于平行四边形的平面向量性质的定理。

根据平行四边形定理，如果平面上四个向量AB、BC、CD和DA构成一个平行四边形，那么这四个向量之和为零。

也就是说，AB + BC + CD + DA = 0。

平行四边形定理的性质可以推导出以下几个重要的结论：1. 如果ABCD是一个平行四边形，那么向量AB = DC，向量AD = BC。

2. 如果平行四边形ABCD的一组对角线向量相等，即向量AC = BD，那么它是一个平行四边形。

二、平行四边形法则的概念和性质平行四边形法则是平行四边形定理的逆定理，即如果一个平面上四个向量AB、BC、CD和DA满足向量AB + BC + CD + DA = 0，那么这四个向量构成一个平行四边形。

根据平行四边形法则的性质，可以推导出以下几个重要结论：1. 如果向量AB = DC，向量AD = BC，那么四边形ABCD是一个平行四边形。

2. 如果向量AC = BD，那么四边形ABCD是一个平行四边形。

三、平行四边形定理和平行四边形法则的应用平行四边形定理和平行四边形法则在解决平面向量问题时，常用于以下几个方面的应用：1. 平行四边形的判定：通过使用平行四边形定理和平行四边形法则，可以判断给定的四个向量是否能够构成一个平行四边形。

2. 向量之间的关系：根据平行四边形定理和平行四边形法则的性质，可以得到向量之间的关系。

例如，如果向量AB = DC，那么可以推导出向量AB和向量DC平行。

3. 向量的线性运算：平行四边形定理和平行四边形法则可以应用于向量的线性运算中。

例如，如果已知向量AB = DC，向量AD = BC，则可以通过平行四边形定理推导出向量AC = BD。

平行四边形的判定定理五条
一、求余边定理：
如果两条相邻边之间的倾斜角相等，那么两条边之间的连接边就必然是平行的。

二、定位定理：
如果四个点形成一个平行四边形，那么这四个点的位置的距离必定相等。

三、折射定律：
如果给定一个平行四边形，那么它的对边必定是平行的，而且它的节点位置也会折射出其他的平行直线。

四、向量定理：
若 ab 为交点 A 的一条边，CD 为另一条边，则AB ⊥ CD 并且AB·CD = 0，其中AB 为标量向量，CD 为向量 B 向量 C 的合向量
五、三角形定理：
如果AB和CD是平行四边形的两条相邻边，则对应角AB＝CD，AB·CD=0，AB和CD垂直于BC 且两个三角形ABC，DBC具有相同的度数。

平行四边形性质定理和判定定理总结
平行四边形
性质定理和判定定理
矩形菱形
性质定理
边对边平行且相等对边平行且相等对边平行，四边相等
角对角相等，邻角互补四个角都是直角对角相等，邻角互补
对角线对角线互相平分对角线互相平分且相等对角线互相垂直且平分
每条对角线平分一组对角对称性中心对称图形，对称中心是对角线的交点轴对称图形中心对称图形，轴对称图形
判定定理边两组对边分别平行的四边形（定义）
两组对边分别相等的四边形
一组对边平行且相等的四边形
一组邻边相等的平行四边形（定义）
四条边相等的四边形
角两组对角分别相等的四边形有一个角是直角的平行四边形（定义）
有三个角是直角的四边形
对角线对角线互相平分对角线相等的平行四边形对角线互相垂直的平行四边形。

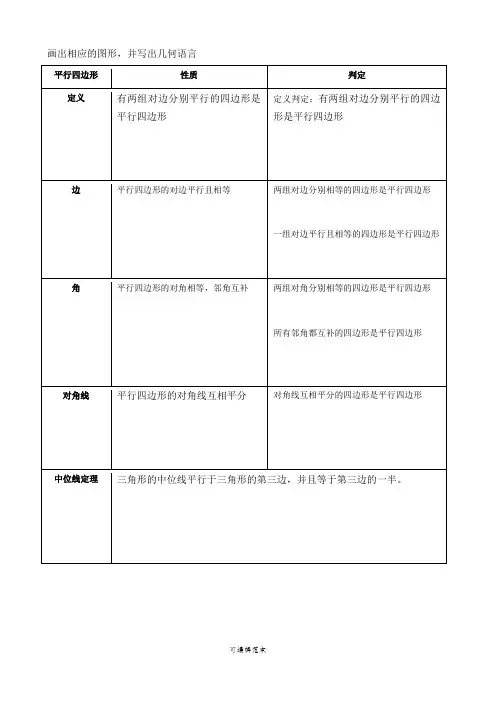
画出相应的图形，并写出几何语言
其他判定方法：
1. 一组对边平行，一组对角相等的四边形是平行四边形。

如图，在四边形
ABCD 中，AB ∥CD ，∠A=∠C ，求证：四边形ABCD 是平行四边形。

2. 熟练掌握平行四边形角平分线的相关问题
(1). 如图，在平行四边形ABCD 中，∠BAD 、∠BCD 的平分线分别交BC 、AD 于点E 、F ．四边形AECF 是平行四边形吗？为什么？
(2). □ABCD 中，DE 平分∠ADC 交BC 的延长线于E ，BF 平分∠ABC 交AB 形 DEBF 是平行四边形
3. 总结求证四边形是平行四边形的方法
已知一组对边平行
已知一组对边相等
[此文档可自行编辑修改，如有侵权请告知删除，感谢您的支持，我们会努力把内容做得更好]
F
E
C
D
B。

平行四边形
定义：
在同一平面内有两组对边分别平行的四边形叫做平行四边形。

性质：
（1）平行四边形对边平行且相等。

（2）平行四边形两条对角线互相平分。

（3）平行四边形的对角相等，两邻角互补
判定：
1.两组对边分别平行的四边形是平行四边形（定义判定法）；
2.一组对边平行且相等的四边形是平行四边形；
3.对角线互相平分的四边形是平行四边形；
4.两组对角分别相等的四边形是平行四边形；
5.两组对边分别相等的四边形是平行四边形。

矩形
定义：有一个角是直角的平行四边形是矩形。

性质
矩形是特殊的平行四边形，矩形具有平行四边形的所有性质，从而矩形的性质可归结为从三个方面来看：
（1）平行四边形与矩形共有的性质：
①从边看，矩形对边平行且相等。

（2）矩形特有的性质：
②从角看，矩形四个角都是直角。

③从对角线看，矩形对角线互相平分且相等。

④矩形的代表：正方形——具有菱形和平行四边形的一切性质。

判定
①定义：有一个角是直角的平行四边形是矩形
②有三个角是直角的四边形是矩形
③对角线互相平分且相等的四边形是矩形性质定理2
直角三角形斜边中线等于斜边一半
矩形的四个角都是直角
矩形的对角线相等。

1. 定义: 两组对边分别平行的四边形叫做平行四边形。

2.性质:⑴如果一个四边形是平行四边形，那么这个四边形的两组对边分别相等。

（简述为“平行四边形的对边相等”）⑵如果一个四边形是平行四边形，那么这个四边形的两组对角分别相等。

（简述为“平行四边形的对角相等”）⑶夹在两条平行线间的平行线段相等。

⑷如果一个四边形是平行四边形，那么这个四边形的两条对角线互相平分。

（简述为“平行四边形的两条对角线互相平分”）⑸平行四边形是中心对称图形，对称中心是两条对角线的交点。

3.判定：（1）如果一个四边形的两组对边分别相等，那么这个四边形是平行四边形。

（简述为“两组对边分别相等的四边形是平行四边形”）（2）如果一个四边形的一组对边平行且相等，那么这个四边形是平行四边形。

（简述为“一组对边平行且相等的四边形是平行四边形”）（3）如果一个四边形的两条对角线互相平分，那么这个四边形是平行四边形。

（简述为“对角线互相平分的四边形是平行四边形”）（4）如果一个四边形的两组对角分别相等，那么这个四边形是平行四边形。

（简述为“两组对角分别相等的四边形是平行四边形”（5）如果一个四边形的两组对边分别平行，那么这个四边形是平行四边形。

（简述为“两组对边分别平行的四边形是平行四边形”）矩形的性质和判定定义：有一个角是直角的平行四边形叫做矩形.性质：①矩形的四个角都是直角；②矩形的对角线相等 .注意：矩形具有平行四边形的一切性质 .判定：①有一个角是直角的平行四边形是矩形；②有三个角是直角的四边形是矩形；③对角线相等的平行四边形是矩形 .菱形的性质和判定定义：有一组邻边相等的平行四边形叫做菱形.性质：①菱形的四条边都相等；②菱形的对角线互相垂直，并且每一条对角线平分一组对角 .注意：菱形也具有平行四边形的一切性质 .判定：①有一组邻边相等的平行四边形是菱形；②四条边都相等的四边形是菱形；③对角线互相垂直的平行四边形是菱形(4).有一条对角线平分一组对角的平行四边形是菱形正方形的性质和判定定义：有一组邻边相等并且有一角是直角的平行四边形叫做正方形.性质：①正方形的四个角都是直角，四条边都相等；②正方形的两条对角线相等，并且互相垂直平分，每条对角线平分一组对角 .判定：因为正方形具有平行四边形、矩形、菱形的一切性质，所以我们判定正方形有三个途径①四条边都相等的平行四边形是正方形②有一组临边相等的矩形是正方形③有一个角是直角的菱形是正方形梯形及特殊梯形的定义梯形：一组对边平行而另一组对边不平行的四边形叫做梯形.（一组对边平行且不相等的四边形叫做梯形.）等腰梯形：两腰相等的梯形叫做等腰梯形. 直角梯形：一腰垂直于底的梯形叫做直角梯形.等腰梯形的性质1、等腰梯形两腰相等、两底平行；2、等腰梯形在同一底上的两个角相等；3、等腰梯形的对角线相等；4、等腰梯形是轴对称图形，它只有一条对称轴，一底的垂直平分线是它的对称轴. 等腰梯形的判定1、两腰相等的梯形是等腰梯形；2、在同一底上的两个角相等的梯形是等腰梯形；3、对角线相等的梯形是等腰梯形.平行四边形性质定理1 平行四边形的对角相等平行四边形性质定理2 平行四边形的对边相等且平行平行四边形性质定理3 平行四边形的对角线互相平分平行四边形判定定理1 两组对角分别相等的四边形是平行四边形平行四边形判定定理2 两组对边分别相等的四边形是平行四边形平行四边形判定定理3 对角线互相平分的四边形是平行四边形平行四边形判定定理4 一组对边平行相等的四边形是平行四边形矩形性质定理1 矩形的四个角都是直角矩形性质定理2 矩形的对角线相等矩形判定定理1 有一个角是直角的平行四边形是矩形矩形判定定理2 对角线相等的平行四边形是矩形正方形性质定理1正方形的四个角都是直角，四条边都相等正方形性质定理2正方形的两条对角线相等，并且互相垂直平分，每条对角线平分一组对角菱形性质定理1 菱形的四条边都相等菱形性质定理2 菱形的对角线互相垂直菱形面积=对角线乘积的一半，即S=（a×b）÷2菱形判定定理1 四边都相等的四边形是菱形菱形判定定理2 对角线互相垂直的平行四边形是菱形菱形判定定理3是对称轴图形的平行四边形是菱形。

平行四边形的判定定理平行四边形是一种特殊的四边形，具有以下特点：对边平行且对角线相等。

在数学中，判定一个四边形是否为平行四边形有多种方法。

方法一：利用对边平行的性质判定一个四边形ABCD是否为平行四边形时，可以先利用对边平行的性质进行判断。

步骤：1.检查边AB和边CD是否平行。

2.检查边BC和边AD是否平行。

如果边AB和边CD以及边BC和边AD都是平行的，则可以断定四边形ABCD是一个平行四边形。

方法二：利用对角线相等的性质判定一个四边形ABCD是否为平行四边形时，可以利用对角线相等的性质进行判断。

步骤：1.计算对角线AC的长度。

2.计算对角线BD的长度。

如果对角线AC的长度等于对角线BD的长度，则可以断定四边形ABCD是一个平行四边形。

方法三：利用对边比例相等的性质判定一个四边形ABCD是否为平行四边形时，还可以利用对边比例相等的性质进行判断。

步骤：1.计算边AB与边CD的长度比（AB/CD）。

2.计算边BC与边AD的长度比（BC/AD）。

如果边AB与边CD的长度比等于边BC与边AD的长度比，即AB/CD = BC/AD，那么四边形ABCD是一个平行四边形。

方法四：利用四个角的性质判定一个四边形ABCD是否为平行四边形时，也可以利用四个角的性质进行判断。

步骤：1.检查角A与角C是否相等。

2.检查角B与角D是否相等。

如果角A与角C相等，并且角B与角D相等，则可以断定四边形ABCD是一个平行四边形。

总结通过以上四种方法，我们可以判定一个四边形是否为平行四边形。

可以根据实际情况选择其中一种或多种方法来进行判定，以便快速准确地得出结论。

请注意，以上的判定定理仅适用于四边形，其他多边形无法用这些方法判定是否为平行四边形。

在实际应用中，合理选择合适的方法，结合几何定理，可以更好地解决相关问题。

希望本文能对你理解和应用平行四边形的判定定理有所帮助。

平行四边形的判定定理(基础)【学习目标】1. 平行四边形的四个判定定理及应用，会应用判定定理判断一个四边形是不是平行四边形.2. 会综合应用平行四边形的性质定理和判定定理解决简单的几何问题. 【要点梳理】要点一、平行四边形的判定1. 两组对边分别平行的四边形是平行四边形；2. 一组对边平行且相等的四边形是平行四边形；3. 两组对边分别相等的四边形是平行四边形；4. 两组对角分别相等的四边形是平行四边形；5. 对角线互相平分的四边形是平行四边形.要点诠释：(1)这些判定方法是学习本章的基础，必须牢固掌握，当几种方法都能判定同一个行四边形时，应选择较简单的方法(2)这些判定方法既可作为判定平行四边形的依据，也可作为“画平行四边形”的依据. 【典型例题】类型一、平行四边形的判定1、如图所示，E、F分别为四边形ABCD勺边AD BC上的点，且四边形AECF和DEBF 都是平行四边形，AF和BE相交于点G DF和CE相交于点H.求证：四边形EGFH为平行四边形.A E D【思路点拨】欲证四边形EGFH为平行四边形，只需证明它的两组对边分别平行，即EG/ FH, FG// HE可用来证明四边形EGFH为平行四边形.【答案与解析】证明：••• 四边形AECF为平行四边形，••• AF // CE•••四边形DEBF为平行四边形，•BE // DF.•四边形EGFH为平行四边形.【总结升华】平行四边形的定义既包含平行四边形的性质，又可以用来判定一个四边形是平行四边形，即平行四边形的两组对边分别平行，两组对边分别平行的四边形是平行四边形.举一反三：【变式】(2015?厦门校级一模)如图，在四边形ABCD中, AB//CD / BAD的平分线交直线BC于点E,交直线DC于点F,若CE=CF求证：四边形ABCD是平行四边形.证明：•••/ BAD 的平分线交直线 BC 于点E ,•••/ 仁/ 2,•/ AB// CD•••/ 仁/ F ,•/ CE=CF•••/ F=Z 3,•••/ 仁/ 3,•••/ 2=Z 3,• AD// BC ,•/ AB// CD•四边形ABCD 是平行四边形.【思路点拨】(1)根据全等三角形的判定方法，判断出厶ADE ◎△ CBF ，即可推得DE=BF . (2)首先判断出 DE // BF ;然后根据一组对边平行且相等的四边形是平行四边形，推得四 边形DEBF 是平行四边形即可.【答案与解析】证明：(1)v 四边形ABCD 是平行四边形,• AD // CB , AD=CB , •••/ DAE= / BCF , 在厶ADE 和厶CBF 中， r AD=CB• ZDAE=ZBCFt AE=CF• △ ADE CBF , • DE=BF .（2）由（1）,可得△ ADE ◎△ CBF ,•••/ ADE= / CBF ,•••/ DEF= / DAE + Z ADE ，/ BFE= / BCF + Z CBF ,? ABCD 中，点E , F 在对角线 AC 上，且AE=CF .求证:D(1) DE=BF ;(2) 四边形DEBF 是平行四边形.•••/ DEF= Z BFE ,• DE // BF ,又••• DE=BF ,•四边形DEBF是平行四边形.【总结升华】此题主要考查了平行四边形的判定和性质的应用，以及全等三角形的判定和性质的应用，要熟练掌握.3、（2015?张掖校级模拟）已知：如图四边形ABCD是平行四边形，P、Q是直线AC上的点，且AP=CQ求证：四边形PBQD是平行四边形.【思路点拨】证明四边形是平行四边形有很多种方法，此题可由对角线互相平分来证明.【答案与解析】证明：连接BD交AC与O点，•••四边形ABCD是平行四边形，•AO=CO BO=DO又••• AP=CQ• AP+AO=CQ3Q即PO=QO•四边形PBQD是平行四边形.【总结升华】本题主要考查平行四边形的判定，利用“对角线互相平分的四边形是平行四边形”来证明.举一反三：0A=0C 0D=0B 推出 0E=0F 得出平 【变式】如图，在△ ABC 中，D 是BC 边上的一点，E 是AD 的中点，过点 A 作BC 的平行线交 BE 的延长线于F ,且AF=DC 连接CF.试说明：D 是BC 的中点.【答案】证明：••• AF// BC,•••/ AFE=/ DBE••• E 是AD 的中点，• AE=DE在厶AEF 和厶DEB 中,.AFE = DBE , ••• <NAEF = Z DEB,AE = DE,• △ AEF ^A DEB( AAS ,• AF=BD•/ AF=DC• BD=DC• D 是BC 的中点.类型二、平行四边形的性质定理与判定定理的综合运用G e 如图，在平行四边形ABC 州E 、F 是对角线AC 上的点，且AE=CF(1)猜想探究：BE 与DF 之间的关系： ____________________【思路点拨】(1) BE 平行且等于DF ;(2)连接BD 交AC 于O 根据平行四边形的性质得出 行四边形BEDF 即可.【答案与解析】(1) 解：BE 和 DF 的关系是：BE=DF BE / DF ,故答案为：平行且相等.(2) 证明：连接BD 交AC 于0,••• ABCD 是平行四边形，• 0A=0C 0B=0D•/ AE=CF D•••OE=OF••• BFDE是平行四边形，• BE=DF BE// DF.【总结升华】本题考查了平行四边形的性质和判定的应用，能否熟练地运用平行四边形的性质和判定进行推理是你解决本题的关键，题型较好，通过此题培养了学生分析问题和解决问题的能力，同时培养了学生的观察能力和猜想能力.举一反三：变式：如图，在「ABCD中, E、F分别在AD BC边上，且AE=CF请你猜想BE与DF的关系，并说明理由.解：猜想BE与DF的关系是BE=DF BE/ DF,理由是：•••四边形ABCD是平行四边形，• AD// BC, AD=BC•/ AE=CF• AD-AE=BC-CF即DE=BF•••DE// BF,•四边形BFDE是平行四边形，• BE=DF BE/ DF.5、如图，四边形ABCD的对角线AC BD交于点P,过点P作直线交AD于点E,交BC 于点F.若PE=PF,且AP+AE=CP+C.F(1)求证：PA=PC(2)若AD=12 AB=15 / DAB=60 ,求四边形ABCD勺面积.【思路点拨】(1)首先在PA和PC的延长线上分别取点M N,使AM=AE CN=CF可得PN=PM 则易证四边形EMFN是平行四边形，则可得ME=FN / EMA M CNF,即可证得厶EAM^A FCN 则可得PA=PC(2)由PA=PC EP=PF,可证得四边形AFCE为平行四边形，易得△ PED^A PFB,则可得四边形ABCD为平行四边形，由AB=15 , AD=12 / DAB=60 ,即可求得四边形ABCD的面积.【答案与解析】(1 )证明：在PA和PC的延长线上分别取点M N,使AM=AE CN=CF•/ AP+AE=CP+CF•PN=PM•/ PE=PF,•四边形EMFN是平行四边形••• ME=FN / EMA2 CNF又•••/ AME M AEM / CNF=Z CFN•△ EAM^A FCN•AM=CN•/ PM=PN• PA=PC(2)解：T PA=PC EP=PF•四边形AFCE为平行四边形.• AE// CF.•••/ PED玄PFB, M EPD M FPB EP=PF•△ PED^A PFB• DP=PB由( 1)知PA=PC•四边形ABCD为平行四边形.•/ AB=15, AD=12 M DAB=60 ,•四边形ABCD勺面积为90 3 .【总结升华】此题考查了平行四边形的判定与性质，以及全等三角形的判定与性质等知识. 题图形比较复杂，难度适中，解题的关键是数形结合思想的应用.。

判定定理以及性质定理四边形判定定理四边形一、平行四边形：一、平行四边形：判定：判定：）两组对边分别平行的四边形是平行四边形。

（1）两组对边分别平行的四边形是平行四边形。

）两组对边分别相等的四边形是平行四边形。

（2）两组对边分别相等的四边形是平行四边形。

（3）一组对边平行且相等的四边形是平行四边形。

）一组对边平行且相等的四边形是平行四边形。

）对角线互相平分的四边形是平行四边形。

（4）对角线互相平分的四边形是平行四边形。

）两组对角分别相等的四边形是平行四边形。

（5）两组对角分别相等的四边形是平行四边形。

性质：性质：）平行四边形两组对边分别平行。

（1）平行四边形两组对边分别平行。

（2）平行四边形的对变相等。

）平行四边形的对变相等。

）平行四边形的对角相等。

（3）平行四边形的对角相等。

）平行四边形的两条对角线互相平分。

（4）平行四边形的两条对角线互相平分。

（5）平行四边形是中心对称图形，对称中心是两条对角线的交点。

）平行四边形是中心对称图形，对称中心是两条对角线的交点。

二、矩形：二、矩形：判定：判定：）有一个内角是直角的平行四边形是矩形。

（1）有一个内角是直角的平行四边形是矩形。

）有三个内角是直角的四边形是矩形。

（2）有三个内角是直角的四边形是矩形。

）对角线相等平行四边形是矩形。

（3）对角线相等平行四边形是矩形。

性质：性质：）矩形的四个角都是直角。

（1）矩形的四个角都是直角。

）矩形的两条对角线相等。

（2）矩形的两条对角线相等。

三、菱形：三、菱形：判定：判定：）有一组邻边相等的平行四边形叫做菱形。

（1）有一组邻边相等的平行四边形叫做菱形。

）四条边都相等的四边形是菱形。

（2）四条边都相等的四边形是菱形。

）对角线互相垂直的平行四边形是菱形。

（3）对角线互相垂直的平行四边形是菱形。

性质：性质：）菱形的四条边都相等。

（1）菱形的四条边都相等。

）菱形的对角线互相垂直，并且每一条对角线平分一组对角。

（2）菱形的对角线互相垂直，并且每一条对角线平分一组对角。

性质（1）假如一个四边形是平行四边形,那么这个四边形的两组对边分离相等.（简述为“平行四边形的两组对边分离相等”[2]）（2）假如一个四边形是平行四边形,那么这个四边形的两组对角分离相等.（简述为“平行四边形的两组对角分离相等”[2]）（3）假如一个四边形是平行四边形,那么这个四边形的邻角互补.（简述为“平行四边形的邻角互补”）（4）夹在两条平行线间的平行的高相等.（简述为“平行线间的高距离处处相等”）（5）假如一个四边形是平行四边形,那么这个四边形的两条对角线互相等分.（简述为“平行四边形的对角线互相等分”[2]）（6）衔接随意率性四边形各边的中点所得图形是平行四边形.（推论）（7）平行四边形的面积等于底和高的积.（可视为矩形.）（8）过平行四边形对角线交点的直线,将平行四边形分成全等的两部分图形.（9）平行四边形是中间对称图形,对称中间是两对角线的交点.（10）平行四边形不是轴对称图形,但平行四边形是中间对称图形.矩形和菱形是轴对称图形.注：正方形,矩形以及菱形也是一种特别的平行四边形,三者具有平行四边形的性质.（11）平行四边形ABCD中（如图）E为AB的中点,则AC和DE互相三等分,一般地,若E为AB上接近A的n等分点,则AC和DE互相(n+1)等分.（12）平行四边形ABCD中,AC.BD是平行四边形ABCD的对角线,则各四边的平方和等于对角线的平方和.（13）平行四边形对角线把平行四边形面积分成四等份.（14）平行四边形中,两条在不合对边上的高所构成的夹角,较小的角等于平行四边形中较小的角,较大的角等于平行四边形中较大的角.（15）平行四边形的面积等于相邻双方与其夹角正弦的乘积平行四边形的剖断办法（共6种）1.两组对边分离平行的四边形是平行四边形（界说剖断法）;2.一组对边平行且相等的四边形是平行四边形;3.对角线互相等分的四边形是平行四边形;4.两组对角分离相等的四边形是平行四边形;5.所有邻角（每一组邻角）都互补的四边形是平行四边形;6.两组对边分离相等的四边形是平行四边形.帮助线作法一.衔接对角线或平移对角线.二.过极点尴尬刁难边的垂线构成直角三角形.三.衔接对角线交点与一边中点,或过对角线交点作一边的平行线,构成线段平行或中位线.四.衔接极点与对边上一点的线段或延伸这条线段,结构类似三角形或等积三角形.五.过极点尴尬刁难角线的垂线,构成线段平行或三角形全等.平行四边形的界说：在统一平面内有两组对边分离平行的四边形叫做平行四边形.平行四边形的界说.性质：（1）平行四边形对边平行且相等.（2）平行四边形两条对角线互相等分.（菱形和正方形）（3）平行四边形的对角相等,两邻角互补（4）衔接随意率性四边形各边的中点所得图形是平行四边形.(推论）（5）平行四边形的面积等于底和高的积.（可视为矩形）（6）平行四边形是扭转对称图形,扭转中间是两条对角线的交点.（7）过平行四边形对角线交点的直线,将平行四边形分成全等的两部分图形.（8）平行四边形是中间对称图形,对称中间是两对角线的交点.（9）一般的平行四边形不是轴对称图形,菱形是轴对称图形.（10）平行四边形ABCD中,AC.BD是平行四边形ABCD的对角线,则各四边的平方和等于对角线的平方和（可用余弦定理证实）.（11）平行四边形对角线把平行四边形面积分成四等分.剖断：（1）两组对边分离相等的四边形是平行四边形; （2）对角线互相等分的四边形是平行四边形; （3）一组对边平行且相等的四边形是平行四边形; （4）两组对边分离平行的四边形是平行四边形; （5）两组对角分离相等的四边形是平行四边形; （6）一组对边平行一组对角线互相等分的四边形是平行四边形; （7）一组对边平行一组对角相等的四边形是平行四边形;。

四边形的判定定理
平行四边形的判定:
1)两组对边分别平行的四边形是平行四边形．
2)两组对边分别相等的四边形是平行四边形．
3)一组对边平行且相等的四边形是平行四边形．
4)两组对角分别相等的四边形是平行四边形．
5)对角线互相平分的四边形是平行四边形．
矩形的判定：
1)一个角是直角的平行四边形是矩形
2)对角线相等的平行四边形是矩形
3)有三个角是直角的四边形是矩形
4)对角线相等且互相平分的四边形是矩形
菱形的判定：
1)四条边相等的平行四边形是菱形
2)对角线互相垂直的平行四边形是菱形(对角线互相垂直且平分的四边形是菱形）
3)一组邻边相等的平行四边形是菱形
4)一组对角线平分一组对角的平行四边形是菱形
正方形的判定：
1)对角线相等的菱形是正方形。

2)有一个角为直角的菱形是正方形。

3)对角线互相垂直的矩形是正方形。

4)一组邻边相等的矩形是正方形。

5)一组邻边相等且有一个角是直角的平行四边形是正方形。

6)对角线互相垂直且相等的平行四边形是正方形。

7)对角线相等且互相垂直平分的四边形是正方形。

8)一组邻边相等，有三个角是直角的四边形是正方形。

9)既是菱形又是矩形的四边形是正方形。

THANKS !!!
致力为企业和个人提供合同协议，策划案计划书，学习课件等等
打造全网一站式需求
欢迎您的下载，资料仅供参考。

四边形的性质和判定一、平行四边形的性质和判定（一）平行四边形性质：1、平行四边形的两组对边平行且相等2、平行四边形的两组对角相等,邻角互补3、平行四边形的两条对角线互相平分4、平行四边形是中心对称图形，对称中心是两条对角线的交点（二）平行四边形的判定：1、两组对边分别平行2、两组对边分别相等3、一组对边平行且相等4、两条对角线互相平分5 两组对角分别相等以上五个条件均可判定一个四边形是平行四边形，都是平行四边形的判定定理。

二、菱形的性质和判定：（一）菱形的性质：1、对角线互相垂直且平分；2、四条边都相等；3、对角相等,邻角互补；4、每条对角线平分一组对角．5、菱形是中心对称图形，对称中心是两条对角线的交点也是轴对称图形，对称轴是两条对角线（二）菱形的判定三、矩形的性质和判定（一）矩形的性质1、从边看，矩形对边平行且相等。

2、从角看，矩形四个角都是直角。

3、从对角线看，矩形对角线互相平分且相等。

4、矩形是轴对称图形，它有两条对称轴，它也是中心对称图形，对称中心是对角线的交点（二）矩形判定：1.有一个角是直角的平行四边形是矩形2、对角线相等的平行四边形是矩形2.有三个角是直角的四边形是矩形四、正方形的性质和判定（一）正方形的性质1、四边相等，四个角是直角2、对角线相等、相互平分、相互垂直3、既是中心对称图形又是轴对称图形（二）正方形的判定1、有一个角是直角的菱形是正方形2、有一组邻边相等的矩形是正方形3、有一组邻边相等且有一个角是直角的平行四边形是正方形4、对角线相等的菱形是正方形5、对角线相互垂直的矩形是正方形。