中考数学中的最值问题解法(学生版)
- 格式:docx
- 大小:517.61 KB
- 文档页数:27
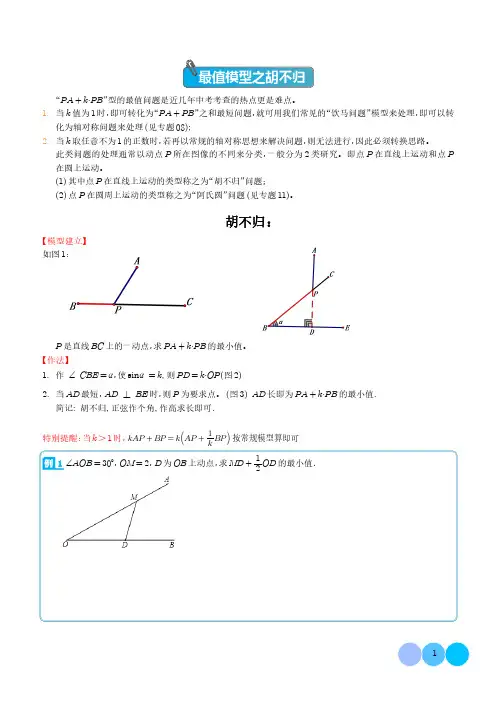
最值模型之胡不归“PA+k·PB”型的最值问题是近几年中考考查的热点更是难点。
1.当k值为1时,即可转化为“PA+PB”之和最短问题,就可用我们常见的“饮马问题”模型来处理,即可以转化为轴对称问题来处理(见专题08);2.当k取任意不为1的正数时,若再以常规的轴对称思想来解决问题,则无法进行,因此必须转换思路。
此类问题的处理通常以动点P所在图像的不同来分类,一般分为2类研究。
即点P在直线上运动和点P 在圆上运动。
(1)其中点P在直线上运动的类型称之为“胡不归”问题;(2)点P在圆周上运动的类型称之为“阿氏圆”问题(见专题11)。
胡不归:【模型建立】如图1:P是直线BC上的一动点,求PA+k·PB的最小值。
【作法】1.作∠CBE=α,使sinα=k,则PD=k·OP(图2)2.当AD最短,AD⊥BE时,则P为要求点。
(图3)AD长即为PA+k·PB的最小值.简记:胡不归,正弦作个角,作高求长即可.特别提醒:当k>1时,kAP+BP=k AP+1k BP按常规模型算即可1∠AOB=30°,OM=2,D为OB上动点,求MD+12OD的最小值.2(1)【问题探究】如图1,点E是等边△ABC高AD上的一定点,请在AB上找一点F,使EF=12AE,并说明理由;(2)【问题解决】如图2,在△ACD中,CO⊥AD,垂足为O,若AD=32,AC=2,OC=3,点P在OC上,求DP+12PC的最小值.(3)【问题拓展】如图3,△ABC中,AB=AC=10,tan∠A=2,BE⊥AC于点E,D是线段BE上的一个动点,求CD+ 55BD的最小值.1.实战训练1一.选择题(共8小题)1如图,在△ABC 中,P 为平面内的一点,连接AP 、PB 、PC ,若∠ACB =30°,AC =8,BC =10,则4PA +2PB +23PC 的最小值是()A.489B.36C.410+25+67D.1610-102如图,△ABC 为等边三角形,BD 平分∠ABC ,AB =2,点E 为BD 上动点,连接AE ,则AE +12BE 的最小值为()A.1B.2C.3D.23如图,在平面直角坐标系中,抛物线y =-49x 2+83x 与x 轴的正半轴交于点A ,B 点为抛物线的顶点,C 点为该抛物线对称轴上一点,则3BC +5AC 的最小值为()A.24B.25C.30D.364如图,在等边△ABC 中,AB =6,点E 为AC 中点,D 是BE 上的一个动点,则CD +12BD 的最小值是()A.3B.33C.6D.3+35如图,在菱形ABCD中,AB=AC=6,对角线AC、BD相交于点O,点M在线段AC上,且AM= 2,点P是线段BD上的一个动点,则MP+12PB的最小值是()A.2B.23C.4D.436如图,在Rt△ABC中,∠ACB=90°,∠A=30°,则AB=2BC.请在这一结论的基础上继续思考:若AC=2,点D是AB的中点,P为边CD上一动点,则AP+12CP的最小值为()A.1B.2C.3D.27如图,△ABC中,AB=AC=10,tan A=2,BE⊥AC于点E,D是线段BE上的一个动点,则CD +55BD的最小值是()A.25B.45C.53D.108如图,在菱形ABCD中,∠ABC=60°,E是边BC的中点,P是对角线BD上的一个动点,连接AE,AP,若AP+12BP的最小值恰好等于图中某条线段的长,则这条线段是()A.ABB.AEC.BDD.BE2二.填空题(共9小题)1如图,AC垂直平分线段BD,相交于点O,且OB=OC,∠BAD=120°.(1)∠ABC=.(2)E为BD边上的一个动点,BC=6,当AE+12BE最小时BE=2 .2如图,在△ABC中,∠A=90°,∠C=30°,AB=2,若D是BC边上的动点,则2AD+DC的最小值为.3如图,在平面直角坐标系中,直线y=-x+4的图象分别与y轴和x轴交于点A和点B.若定点P的坐标为(0,63),点Q是y轴上任意一点,则12PQ+QB的最小值为3 .4如图,直线y=x-3分别交x轴、y轴于B、A两点,点C(0,1)在y轴上,点P在x轴上运动,则2PC+PB的最小值为.5如图,抛物线y=x2-2x-3与x轴交于A、B两点,过B的直线交抛物线于E,且tan∠EBA=4 3,有一只蚂蚁从A出发,先以1单位/s的速度爬到线段BE上的点D处,再以1.25单位/s的速度沿着DE爬到E点处觅食,则蚂蚁从A到E的最短时间是 649 s.6如图,在平面直角坐标系中,二次函数y=x2-2x+c的图象与x轴交于A、C两点,与y轴交于点B (0,-3),若P是x轴上一动点,点D(0,1)在y轴上,连接PD,则C点的坐标是,2PD+PC的最小值是.7如图,四边形ABCD是菱形,AB=4,且∠BAD=30°,P为对角线AC(不含A点)上任意一点,则DP+12AP的最小值为.8如图,四边形ABCD中,AB=62,∠ABC=45°,E是BD上一点,若∠ABD=15°,则AE+12BE的最小值为.9如图,矩形OABC中,点A、C分别在x轴,y轴的正半轴上,且OA=3,AB=1,点P为线段OA上一动点,则12OP+PB最小值为.3三.解答题(共5小题)1如图,在平面直角坐标系中,二次函数y=ax2+bx+c的图象经过点A(-1,0),B(0,-3),C(2,0),其对称轴与x轴交于点D.(1)求二次函数的表达式及其顶点坐标;(2)点M为抛物线的对称轴上的一个动点,若平面内存在点N,使得以A,B,M,N为顶点的四边形为菱形,求点M的坐标;(3)若P为y轴上的一个动点,连接PD,求12PB+PD的最小值.2如图抛物线y=ax2+bx-4与x轴交于A(-1,0),B(4,0)两点,与y轴交于点C.(1)求抛物线解析式.(2)连接BC,点P为BC下方上一动点,连接BP,CP.当△PBC的面积最大时,求点P的坐标和△PBC 面积的最大值.(3)点N为线段OC上一点,连接AN,求AN+12CN的最小值.3如图,在平面直角坐标系xOy中,已知抛物线y=x2+bx+c与x轴交于点A、B两点,其中A(1,0),与y轴交于点C(0,3).(1)求抛物线解析式;(2)如图1,过点B作x轴垂线,在该垂线上取点P,使得△PBC与△ABC相似,请求出点P坐标;(3)如图2,在线段OB上取一点M,连接CM,请求出CM+12BM的最小值.4(1)【问题探究】如图1,点E是等边△ABC高AD上的一定点,请在AB上找一点F,使EF=12AE,并说明理由;(2)【问题解决】如图2,在△ACD中,CO⊥AD,垂足为O,若AD=32,AC=2,OC=3,点P在OC上,求DP+12PC的最小值.(3)【问题拓展】如图3,△ABC中,AB=AC=10,tan∠A=2,BE⊥AC于点E,D是线段BE上的一个动点,求CD+ 55BD的最小值.。

备战2020中考数学之解密压轴解答题命题规律专题10 二次函数与线段关系及最值定值问题【类型综述】图形运动的过程中,求两条线段之间的函数关系,是中考数学的热点问题.产生两条线段间的函数关系,常见的情况有两种,一是勾股定理,二是比例关系.还有一种不常见的,就是线段全长等于部分线段之和.由比例线段产生的函数关系问题,在两种类型的题目中比较常用. 一是由平行线产生的对于线段成比例,二是相似三角形的对应边成比例.一般步骤是先说理产生比例关系,再代入数值或表示数的字母,最后整理、变形,根据要求写出定义域.关键是寻找比例关系,难点是有的整理、变形比较繁琐,容易出错.【方法揭秘】由勾股定理产生的函数关系,在两种类型的题目中比较常用.类型一,已知“边角边”,至少一边是动态的,求角的对边.如图1,已知点A 的坐标为(3, 4),点B 是x 轴正半轴上的一个动点,设OB =x ,AB =y ,那么我们在直角三角形ABH 中用勾股定理,就可以得到y 关于x 的函数关系式.类型二,图形的翻折.已知矩形OABC 在坐标平面内如图2所示,AB =5,点O 沿直线EF 翻折后,点O 的对应点D 落在AB 边上,设AD =x ,OE =y ,那么在直角三角形AED 中用勾股定理就可以得到y 关于x 的函数关系式.图1 图2【典例分析】【例1】如图①,矩形ABCD 中,2,5,1AB BC BP ===,090MPN ∠=,将MPN ∠绕点P 从PB 处开始按顺时针方向旋转,PM 交边AB (或AD )于点E ,PN 交边AD (或CD )于点F .当PN 旋转至PC 处时,MPN ∠的旋转随即停止.(1)特殊情形:如图②,发现当PM 过点A 时,PN 也恰好过点D ,此时ABP ∆是否与PCD ∆相似?并说明理由;(2)类比探究:如图③,在旋转过程中,PEPF的值是否为定值?若是,请求出该定值;若不是,请说明理由; (3)拓展延伸:设AE t =时,EPF ∆的面积为S ,试用含t 的代数式表示S ;①在旋转过程中,若1t =时,求对应的EPF ∆的面积; ②在旋转过程中,当EPF ∆的面积为4.2时,求对应的t 的值.【例2】如图1,在矩形ABCD 中,AB =8,AD =10,E 是CD 边上一点,连接AE ,将矩形ABCD 沿AE 折叠,顶点D 恰好落在BC 边上点F 处,延长AE 交BC 的延长线于点G . (1)求线段CE 的长;(2)如图2,M ,N 分别是线段AG ,DG 上的动点(与端点不重合),且∠DMN =∠DAM ,设AM =x ,DN =y . ①写出y 关于x 的函数解析式,并求出y 的最小值;②是否存在这样的点M ,使△DMN 是等腰三角形?若存在,请求出x 的值;若不存在,请说明理由.【例3】抛物线2(0)y ax bx c a =++≠与x 轴交于,A B 两点(点A 在点B 的左侧),与y 轴交于点(0,4)C -.已知(2,0)A -,抛物线的对称轴l 交x 轴于点(1,0)D . (1)求出,,a b c 的值;(2)如图1,连接BC ,点P 是线段BC 下方抛物线上的动点,连接,PB PC .点,M N 分别在y 轴,对称轴l 上,且MN y ⊥轴.连接,AM PN .当PBC ∆的面积最大时,请求出点P 的坐标及此时AM MN NP ++的最小值;(3)如图2,连接AC ,把AOC ∆按照直线y x =对折,对折后的三角形记为A OC ∆'',把A OC ∆''沿着直线BC 的方向平行移动,移动后三角形的记为A O C ∆''''',连接DA '',DC '',在移动过程中,是否存在DA C ∆''''为等腰三角形的情形?若存在,直接写出点C ''的坐标;若不存在,请说明理由.【例4】如图在锐角△ABC 中,BC =6,高AD =4,两动点M 、N 分别在AB 、AC 上滑动(不包含端点),且MN ∥BC,以MN 为边长向下作正方形MPQN,设MN =x,正方形MPQN 与△ABC 公共部分的面积为y . (1)如图(1),当正方形MPQN 的边P 恰好落在BC 边上时,求x 的值;(2)如图(2),当PQ 落△ABC 外部时,求出y 与x 的函数关系式(写出x 的取值范围)并求出x 为何值时y 最大,最大是多少?【例5】如图,抛物线y=12-x2+mx+m(m>0)的顶点为A,交y轴于点C.(1)求出点A的坐标(用含m的式子表示);(2)若直线y=﹣x+n经过点A,与抛物线交于另一点B,证明:AB的长是定值;(3)连接AC,延长AC交x轴于点D,作直线AD关于x轴对称的直线,与抛物线分别交于E、F两点.若∠ECF=90°,求m的值.【例6】如图,在平面直角坐标系中,二次函数y=x2+bx+c的图象与x轴交于A、B两点,A点在原点的左侧,B 点的坐标为(3,0),与y轴交于点C(0,﹣3).(1)求二次函数解析式;(2)若点Q为抛物线上一点,且S△ABQ=12S△ACQ,求点Q的坐标;(3)若直线l:y=mx+n与抛物线有两个交点M,N(M在N的左边),P为抛物线上一动点(不与M,N重合).过P作PH平行于y轴交直线l于点H,若HM HNHP⋅=5,求m的值.【变式训练】1.如图,抛物线y =ax 2+4x +c (a ≠0)与反比例函数y =5x的图象相交于点B ,且点B 的横坐标为5,抛物线与y 轴交于点C (0,6),A 是抛物线的顶点,P 和Q 分别是x 轴和y 轴上的两个动点,则AQ +QP +PB 的最小值为_____.2.如图,在平面直角坐标系中,菱形OABC 的顶点 A 在 x 轴正半轴上,顶点 C 的坐标为(4,3),D 是抛物线 y =﹣x 2+6x 上一点,且在x 轴上方,则△BCD 面积的最大值为__________3.己知抛物线2114y x =+具有如下性质:该抛物线上任意一点到定点F(0,2)的距离与到x 轴的距离始终相等,如图,点M 的坐标为(3,3),P 是抛物线2114y x =+上一个动点,则△PMF 周长的最小值是__________.4.如图,在Rt △ABC 中,∠BAC =90°,AB =AC =16cm ,AD 为BC 边上的高,动点P 从点A 出发,沿A →D 方向以2/s 的速度向点D 运动,过P 点作PE ∥BC 交AC 于点E ,过E 点作EF ⊥BC 于点F ,设△ABP 的面积为S 1,四边形PDFE 的面积为S 2,则点P 在运动过程中,S 1+S 2的最大值为______.5.在平面直角坐标系中,已知()A 2,4、()P 1,0,B 为y 轴上的动点,以AB 为边构造ABC V ,使点C 在x 轴上,BAC 90.M ∠=o 为BC 的中点,则PM 的最小值为______.6.如图,在平面直角坐标系中,抛物线y=﹣x 2+4x 与x 轴交于点A,点M 是x 轴上方抛物线上一点,过点M 作MP ⊥x 轴于点P,以MP 为对角线作矩形MNPQ,连结NQ,则对角线NQ 的最大值为_________.7.如图,在平面直角坐标系中,过A (-1,0)、B (3,0)两点的抛物线交y 轴于点C,其顶点为点D,设△ACD 的面积为S 1,△ABC 的面积为S 2.小芳经探究发现:S 1︰S 2是一个定值.这个定值为________.8.如图,在平面直角坐标系中,有二次函数23333y x x =--+,顶点为H ,与x 轴交于A 、B 两点(A 在B 左侧),易证点H 、B 关于直线3:33l y x =+对称,且A 在直线l 上.过点B 作直线//BK AH 交直线l 于K 点,M 、N 分别为直线AH 和直线l 上的两个动点,连接HN 、NM 、MK ,则HN NM MK ++的最小值为________9.如图,抛物线2(0)y ax bx c a =++≠与直线1y x =+相交于(1,0)A -,(4,)B m 两点,且抛物线经过点(5,0)C(1)求抛物线的解析式.(2)点P 是抛物线上的一个动点(不与点A 点B 重合),过点P 作直线PD x ⊥轴于点D ,交直线AB 于点E .当2PE ED =时,求P 点坐标;(3)如图所示,设抛物线与y 轴交于点F ,在抛物线的第一象限内,是否存在一点Q ,使得四边形OFQC 的面积最大?若存在,请求出点Q 的坐标;若不存在,说明理由.10.如图,在矩形ABCD 中,AB=18,AD=12,点M 是边AB 的中点,连结DM,DM 与AC 交于点G ,点E,F 分别是CD 与DG 上的点,连结EF,(1)求证:CG=2AG .(2)若DE=6,当以E,F,D 为顶点的三角形与△CDG 相似时,求EF 的长.(3)若点E 从点D 出发,以每秒2个单位的速度向点C 运动,点F 从点G 出发,以每秒1个单位的速度向点D 运动.当一个点到达,另一个随即停止运动.在整个运动过程中,求四边形CEFG 的面积的最小值.11.如图①,抛物线y=a(x 2+2x-3)(a≠0)与x 轴交于点A 和点B,与y 轴交于点C,且OC=OB.(1)直接写出点B 的坐标是( , ),并求抛物线的解析式;(2)设点D 是抛物线的顶点,抛物线的对称轴是直线l,连接BD,线段OC 上的点E 关于直线l 的对称点E'恰好在线段BD 上,求点E 的坐标;(3)若点F 为抛物线第二象限图象上的一个动点,连接BF,CF,当△BCF 的面积是△ABC 面积的一半时,求此时点F 的坐标.12.如图,抛物线y =﹣x 2+mx +2与x 轴交于点A ,B ,与y 轴交于点C ,点A 的坐标为(1,0) (1)求抛物线的解析式(2)在抛物线的对称轴l 上找一点P ,使PA +PC 的值最小,求出点P 的坐标 (3)在第二象限内的抛物线上,是否存在点M ,使△MBC 的面积是△ABC 面积的12?若存在,求出点M 的坐标,若不存在,请说明理由.13.如图,抛物线212y x mx n =++交x 轴于A 、B 两点,直线y=kx+b 经过点A,与这条抛物线的对称轴交于点M (1,2),且点M 与抛物线的顶点N 关于x 轴对称.(1)求抛物线的函数关系式;(2)设题中的抛物线与直线的另一交点为C,已知P(x,y)为线段AC上一点,过点P作PQ⊥x轴,交抛物线于点Q.求线段PQ的最大值及此时P坐标;(3)在(2)的条件下,求△AQC面积的最大值.14.如图,抛物线y=﹣12x2+bx+c与x轴交于A、B两点,与y轴交于点C,且OA=2,OC=3.(1)求抛物线的解析式;(2)点D(2,2)是抛物线上一点,那么在抛物线的对称轴上,是否存在一点P,使得△BDP的周长最小,若存在,请求出点P的坐标;若不存在,请说明理由.(3)连接AD并延长,过抛物线上一点Q(Q不与A重合)作QN⊥x轴,垂足为N,与射线交于点M,使得QM=3MN,若存在,请直接写出点Q的坐标;若不存在,请说明理由.15.如图,在平面直角坐标系中,点A在抛物线y=- x2 + 4x上,且横坐标为1,点B与点A关于抛物线的对称轴对称,直线AB与y轴交于点C,点D为抛物线的顶点,点E的坐标为(1,1).(1)求线段AB 的长.(2)点P 为线段AB .上方抛物线上的任意一点,过点P 作AB 的垂线交AB 于点H,点F 为y 轴上一点,当∆PBE 的面积最大时,求PH + HF + 12FO 的最小值. (3)在(2)中,PH+HF+12方FO 取得最小值时,将∆CFH 绕点C 顺时针旋转60°后得到∆CF'H',过点F'作CF'的垂线与直线AB 交于点Q,点R 为抛物线对称轴上的一点,在平面直角坐标系中是否存在点S,使以点D,Q,R,S 为顶点的四边形为菱形,若存在,请直接写出点S 的坐标,若不存在,请说明理由.16.已知,二次函数24y x x c =-+的图像与x 轴的一个交点为O(0,0),点P (m,0)是x 轴正半轴上的一个动点.(1)如图1,求二次函数的图像与x 轴另一个交点的坐标; (2)如图2,过点P 作x 轴的垂线交直线33y x =与点C,交二次函数图像于点D, ①当PD=2PC 时,求m 的值;如图3,已知A (3,-3)在二次函数图像上,连结AP,求12AP OP +的最小值;(3如图4,在第(2)小题的基础上,作直线OD,作点C关于直线OD的对称点C’,当C’落在坐标轴上时,请直接写出m的值.17.如图1,已知抛物线y =ax2+bx +c 经过A(-3,0),B (1,0 ),C (0,3 )三点,其顶点为D,对称轴是直线l , l 与x 轴交于点H .(1)求该抛物线的解析式;(2)若点P 是该抛物线对称轴l 上的一个动点,求∆PBC 周长的最小值;(3)如图2,若 E 是线段AD 上的一个动点(E 与A, D 不重合),过 E 点作平行于y 轴的直线交抛物线于点 F ,交x 轴于点G ,设点 E 的横坐标为m ,四边形AODF 的面积为S 。
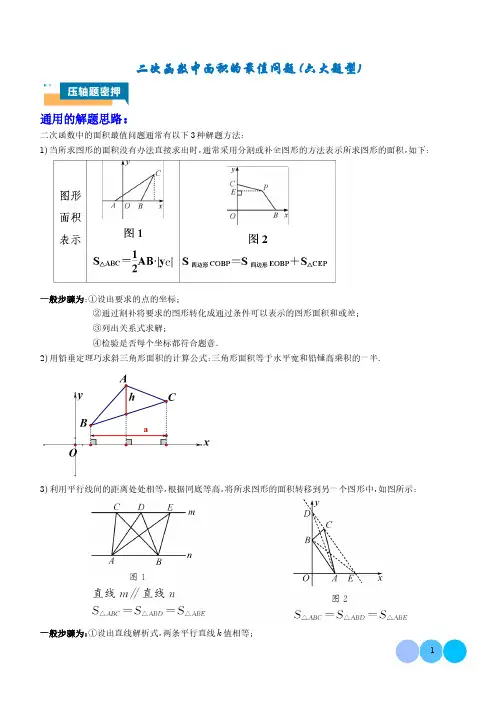
二次函数中面积的最值问题(六大题型)通用的解题思路:二次函数中的面积最值问题通常有以下3种解题方法:1)当所求图形的面积没有办法直接求出时,通常采用分割或补全图形的方法表示所求图形的面积,如下:一般步骤为:①设出要求的点的坐标;②通过割补将要求的图形转化成通过条件可以表示的图形面积和或差;③列出关系式求解;④检验是否每个坐标都符合题意.2)用铅垂定理巧求斜三角形面积的计算公式:三角形面积等于水平宽和铅锤高乘积的一半.3)利用平行线间的距离处处相等,根据同底等高,将所求图形的面积转移到另一个图形中,如图所示:一般步骤为:①设出直线解析式,两条平行直线k值相等;②通过已知点的坐标,求出直线解析式;③求出题意中要求点的坐标;④检验是否每个坐标都符合题意.题型01三角形面积最值问题1(2024·宁夏银川·一模)如图,二次函数y =-x 2+6x 的图象与x 轴的正半轴交于点A ,经过点A 的直线与该函数图象交于点B 1,5 ,与y 轴交于点C .(1)求直线AB 的函数表达式及点C 的坐标;(2)点P 是二次函数图象上的一个动点,且在直线AB 上方,过点P 作直线PE ⊥x 轴于点E ,与直线AB 交于点D ,设点P 的横坐标为m .①当PD =12OC 时,求m 的值;②设△PAB 的面积为S ,求S 关于m 的函数表达式,并求出S 的最大值.2(2024·新疆克孜勒苏·二模)如图,抛物线y =x ²+bx +c (b ,c 是常数)的顶点为C ,与x 轴交于A ,B 两点,A 2,0 ,AB =6,点P 为线段AB 上的动点,过P 作PQ ∥BC 交AC 于点Q .(1)求抛物线的解析式;(2)求△CPQ 面积的最大值,并求此时P 点坐标.3(23-24九年级下·湖北武汉·开学考试)如图,抛物线y =ax 2-4ax +3a 交x 轴于A ,B 两点(点A 在点B 的左侧),交y 轴正半轴于点C ,OB =OC ,点P 在抛物线上.(1)求抛物线的解析式;(2)若tan∠ACP=2,求点P的横坐标.(3)平面上有两点M m,-m-3,求△PMN的面积的最小值.,N m+2,-m-54(23-24九年级下·辽宁沈阳·阶段练习)△ABC中,∠BAC=90°,AB=2,AC=4,点P从点C出发,沿射线CA方向运动,速度为每秒1个单位长度,同时点Q以相同的速度从点B出发,沿射线BA方向运动.设运动时间为x(x≠2且x≠4)秒,△APQ的面积为S.(1)当0<x<2时,如图①,求S与x的函数关系式;(2)当2<x<4时,如图②,求S的最大值;(3)若在运动过程中,存在两个时刻x1,x2,对应的点P和点Q分别记为P1,P2和Q1,Q2,对应的△AP1Q1和△AP2Q2的面积分别记为S1和S2,且当CP1=P1P2时,S1=S2,请求出x1的值.5(2023·山东聊城·二模)如图,抛物线y=x2+bx+c与x轴交于A,B两点(点A在点B的左侧),点A 的坐标为-1,0,直线CD:y=2x-3与x轴交于点D.动点M在抛物线上运动, ,与y轴交于点C0,-3过点M作MP⊥x轴,垂足为点P,交直线CD于点N.(1)求抛物线的表达式;(2)当点P在线段OD上时,△CDM的面积是否存在最大值,若存在,请求出最大值;若不存在,请说明理由;(3)点M在运动过程中,能否使以C,N,M为顶点的三角形是以NM为腰的等腰直角三角形?若存在,请直接写出点M的坐标.6(2024·浙江宁波·模拟预测)如图,一次函数y=33x+3的图象与坐标轴交于点A、B,抛物线y=-33x2+bx+c的图象经过A、B两点.(1)求二次函数的表达式;(2)若点P为抛物线上一动点,在直线AB上方是否存在点P使△PAB的面积最大?若存在,请求出△PAB 面积的最大值及点P的坐标,请说明理由.7(2024·甘肃陇南·一模)如图,在平面直角坐标系xOy中,已知直线y=-x-3与x轴交于点A,与y轴交于点C,过A,C两点的抛物线y=ax2+bx+c与x轴交于另一点B1,0,抛物线对称轴为直线l.(1)求抛物线的解析式;(2)点M为直线AC下方抛物线上一点,当△MAC的面积最大时,求点M的坐标;(3)点P是抛物线上一点,过点P作l的垂线,垂足为D,E是l上一点.要使得以P,D,E为顶点的三角形与△BOC全等,请直接写出点P的坐标.8(2024·江苏盐城·模拟预测)已知抛物线y=x2+bx-3与x轴交于A,B(点A在点B的左侧),与y轴交于点C,且OB=OC.(1)求抛物线的解析式和点A的坐标;(2)如图1,点P为直线BC下方抛物线上一点,求△PBC的最大面积;(3)如图2,M、N是抛物线上异于B,C的两个动点,若直线BN与直线CM的交点始终在直线y=2x-9上,求证:直线MN必经过一个定点,并求该定点坐标.9(2024·四川广元·二模)如图,在平面直角坐标系中,抛物线y1=-x2+bx+c与x轴交于点B,A(-3, 0),与y轴交于点C(0,3).(1)求直线AC和抛物线的解析式.(2)若点M是抛物线对称轴上的一点,是否存在点M,使得以M,A,C三点为顶点的三角形是以AC为底的等腰三角形?若存在,请求出点M的坐标;若不存在,请说明理由.(3)若点P是第二象限内抛物线上的一个动点,求△PAC面积的最大值.10(2024·安徽安庆·一模)如图,抛物线y=ax2+bx+3与x轴交于点A1,0两点,与y轴交于、B3,0点C.(1)求此抛物线对应的函数表达式;(2)点E为直线BC上的任意一点,过点E作x轴的垂线与此抛物线交于点F.①若点E在第一象限,连接CF、BF,求△CFB面积的最大值;②此抛物线对称轴与直线BC交于点D,连接DF,若△DEF为直角三角形,请直接写出E点坐标.11(2024·安徽合肥·一模)如图,直线y=x-3与x轴交于点B,与y轴交于点C,抛物线y=x2+bx+c 经过B、C两点,抛物线与x轴负半轴交于点A.(1)求抛物线的函数表达式;(2)直接写出当x-3>x2+bx+c时,x的取值范围;(3)点P是位于直线BC下方抛物线上的一个动点,过点P作PE⊥BC于点E,连接OE.求△BOE面积的最大值及此时点P的坐标.12(2024·天津西青·一模)已知抛物线y=-x2-4ax-12a(a<0)与x轴交于A,B两点(点A在点B左边),与y轴交于点C.(1)若点D4,12在抛物线上.①求抛物线的解析式及点A的坐标;②连接AD,若点P是直线AD上方的抛物线上一点,连接PA,PD,当△PAD面积最大时,求点P的坐标及△PAD面积的最大值;(2)已知点Q的坐标为-2a,-8a,连接QC,将线段QC绕点Q顺时针旋转90°,点C的对应点M恰好落在抛物线上,求抛物线的解析式.13(2024·山东临沂·二模)如图,抛物线y=ax2+32x+c与x轴交于点A和点B4,0,与y轴交于点C0,2,连接BC,点D在抛物线上.(1)求抛物线的解析式;(2)小明探究点D位置时发现:如图1,点D在第一象限内的抛物线上,连接BD,CD,△BCD面积存在最大值,请帮助小明求出△BCD面积的最大值;(3)小明进一步探究点D位置时发现:如图2,点D在抛物线上移动,连接CD,存在∠DCB=∠ABC,请帮助小明求出∠DCB=∠ABC时点D的坐标.14(2024·广东深圳·二模)如图,在平面直角坐标系中,二次函数y=-x2+bx+c的图象与轴交于A,B 点,与y轴交于点C0,3,点B的坐标为3,0,点P是抛物线上一个动点.(1)求二次函数解析式;(2)若P点在第一象限运动,当P运动到什么位置时,△BPC的面积最大?请求出点P的坐标和△BPC面积的最大值;(3)连接PO,PC,并把△POC沿CO翻折,那么是否存在点P,使四边形POP C为菱形;若不存在,请说明理由.15(2024·湖北·模拟预测)如图,抛物线y=x-12+k与x轴相交于A,B两点(点A在点B的左侧),与y轴相交于点C0,-3.设P点在抛物线上运动,横坐标为m.(1)求此抛物线的解析式;(2)当P点位于第四象限时,求△BCP面积的最大值,并求出此时P点坐标;(3)设此抛物线在点C与点P之间部分(含点C和点P)最高点与最低点的纵坐标之差为h.① 求h关于m的函数解析式,并写出自变量m的取值范围;② 根据h的不同取值,试探索点P的个数情况.16(22-23九年级下·重庆·阶段练习)抛物线y=ax²+bx+5经过点A1,0和点B5,0.该抛物线与直线y=12x+5相交于C、D两点,点P是抛物线上的动点且位于x轴下方,直线PM∥y轴,分别与x轴和直线CD交于点M、N.(1)求该抛物线所对应的函数解析式;(2)连接PC、PD,如图1,在点P运动过程中,△PCD的面积是否存在最大值?若存在,求出这个最大值;若不存在,说明理由;(3)连接PB,过点C作CQ⊥PM,垂足为点Q,如图2,是否存在点P,使得△CNQ与△PBM相似?若存在,求出满足条件的点P的坐标;若不存在,说明理由.17(2024·江苏宿迁·一模)如图1,在平面直角坐标系xOy中,抛物线y=ax2+bx+3与x轴分别相交于A、B两点,与y轴相交于点C,已知点A的坐标为(-1,0),点B的坐标为(3,0).(1)求出这条抛物线的函数表达式;(2)如图2,点D是第一象限内该抛物线上一动点,过点D作直线l∥y轴,直线l与△ABD的外接圆相交于点E.①仅用无刻度直尺找出图2中△ABD外接圆的圆心P.②连接BC、CE,BC与直线DE的交点记为Q,如图3,设△CQE的面积为S,在点D运动的过程中,S是否存在最大值?如果存在,请求出S的最大值;如果不存在,请说明理由.18(2024·新疆乌鲁木齐·一模)如图,在△ABC中,AB=AC,AD⊥BC于点D,BC=10cm,AD=8cm,点P从点B出发,在线段BC上以每秒3cm的速度向点C匀速运动,与此同时,垂直于AD的直线m 从底边BC出发,以每秒2cm的速度沿DA方向匀速平移,分别交AB、AC、AD于E、F、H,当点P到达点C,点P与直线m同时停止运动,设运动时间为t秒t>0.(1)AH=,EF=(用含t的式子表示).(2)在整个运动过程中,所形成的△PEF的面积存在最大值,当△PEF的面积最大时,求线段BP的长;(3)是否存在某一时刻t,使△PEF为直角三角形?若存在,请求出此时刻t的值;若不存在,请说明理由.19(2024·重庆·模拟预测)如图,在平面直角坐标系中,抛物线y=ax2+bx+c过点(3,-4),交x轴于点A(-1,0),B两点,交y轴于点C(0,2).(1)求抛物线的表达式;(2)连接AC ,BC ,M 为线段AB 上一动点,过点M 作MD ∥BC 交直线AC 于点D ,连接MC ,求△MDC 面积的最大值及此时M 点的坐标;(3)在(2)中△MDC 面积取得最大值的条件下,将该抛物线沿射线BC 方向平移2个单位长度,P 是平移后的抛物线上一动点,连接CP ,当∠PCM 与△OBC 的一个内角相等时,请直接写出所有符合条件的点P 的坐标.20(2024·湖南衡阳·一模)如图,已知抛物线y =ax 2+bx +c 经过A 1,0 ,B -3,0 ,C 0,3 三点.(1)求抛物线的解析式;(2)若点D 为第二象限内抛物线上一动点,求△BCD 面积的最大值;(3)设点P 为抛物线的对称轴上的一个动点,求使△BPC 为直角三角形的点P 的坐标.21(2024·甘肃天水·一模)如图,在平面直角坐标系中,开口向下的抛物线与x 轴交于A ,B 两点,D 是抛物线的顶点.O 为坐标原点.A ,B 两点的横坐标分别是方程x 2-4x -12=0的两根,且cos ∠DAB =22.(1)求抛物线的函数解析式;(2)作AC ⊥AD ,AC 交抛物线于点C ,求点C 的坐标及直线AC 的函数解析式;(3)在(2)的条件下,在x 轴上方的抛物线上是否存在一点P ,使△APC 的面积最大?如果存在,请求出点P 的坐标和△APC 的最大面积;如果不存在,请说明理由.22(2024·山东聊城·一模)在平面直角坐标系中,抛物线y =ax 2+bx -3与x 轴交于点A -1,0 和点B 3,0 ,与y 轴交于点C .(1)求抛物线的解析式及顶点坐标;(2)若点P 为第四象限内抛物线上一点,当△PBC 面积最大时,求点P 的坐标;(3)若点P 为抛物线上一点,点Q 是线段BC 上一点(点Q 不与两端点重合),是否存在以P 、Q 、O 为顶点的三角形是等腰直角三角形,若存在,请直接写出满足条件的点P 的坐标;若不存在,请说明理由.23(2024·吉林长春·一模)如图,在平面直角坐标系中,直线y =x +2分别交x 轴、y 轴于A 、B 两点,过点C 2,2 作x 轴垂线,垂足为D ,连接BC .现有动点P 、Q 同时从A 点出发,分别沿AB 、AD 向终点B 和终点D 运动,若点P 的运动速度为每秒2个单位长度,点Q 的运动速度为每秒2个单位长度.设运动的时间为t 秒.(1)求A、B两点的坐标;(2)当CQ∥AB时,t=;(3)设△CPQ的面积为y,写出y与t的函数关系式,并求△CPQ面积的最大值;(4)当△CPQ为轴对称图形时,直接写出t的值.24(2023·湖南娄底·中考真题)如图,抛物线y=x2+bx+c过点A-1,0,交y轴于点C.、点B5,0(1)求b,c的值.(2)点P x0,y0是抛物线上的动点0<x0<5①当x0取何值时,△PBC的面积最大?并求出△PBC面积的最大值;②过点P作PE⊥x轴,交BC于点E,再过点P作PF∥x轴,交抛物线于点F,连接EF,问:是否存在点P,使△PEF为等腰直角三角形?若存在,请求出点P的坐标;若不存在,请说明理由.25(2024·河南安阳·模拟预测)如图,在平面直角坐标系xOy中,抛物线y=ax2+bx+c与抛物线y=-x2+x-1的形状相同,且与x轴交于点-1,0.直线y=kx+2分别与x轴、y轴交于点A,B,和4,0与y=ax2+bx+c于点C,D(点C在点D的左侧).(1)求抛物线的解析式;(2)点P是直线y=kx+2上方抛物线上的任意一点,当k=2时,求△PCD面积的最大值;(3)若抛物线y=ax2+bx+c与线段AB有公共点,结合函数图象请直接写出k的取值范围.26(2024·湖南长沙·一模)如图,抛物线y=x2-bx+c与x轴交于A-1,0两点,与y轴交于,B m,0点C0,-3,顶点为D,直线BD交y轴于点E.(1)求抛物线的解析式.(2)设点P为线段BD上一点(点P不与B,D两点重合),过点P作x轴的垂线与抛物线交于点F,连接DF,BF,求△BDF面积的最大值.(3)连接CD,在线段BD上是否存在点Q,使得∠BDC=∠QCE?若存在,求出点Q的坐标;若不存在,请说明理由.27(2024·江西萍乡·一模)如图,已知抛物线y=-x2+bx+c与x轴交于A、B两点,与y轴交于点C,抛物线的对称轴交x轴于点D.已知A3,0,连接AC,BC.,C0,3(1)求抛物线的函数解析式;(2)在抛物线的对称轴上找一点P,使得以A、D、P为顶点的三角形与△OBC相似,求出点P的坐标;(3)若点M是抛物线上的一个动点,且位于第一象限内,连接MC,MA.设△ACM的面积为S,试求S的最大值.28(2024·四川广元·二模)如图1,抛物线y=ax²+bx+c与x轴交于A,B两点,且点B的坐标为5,0,与y轴交于点C,该抛物线的顶点坐标为(3,-4).(1)求抛物线和直线BC的解析式.(2)在抛物线上是否存在点M,使得△BCM是以BC为底边的等腰三角形?若存在,求出所有点M的坐标;若不存在,请说明理由.(3)如图2,以点B 为圆心,画半径为2的圆,点P 为⊙B 上的一个动点,连接AC ,求△ACP 面积的最大值.29(2023·山东青岛·中考真题)如图,在菱形ABCD 中,对角线AC ,BD 相交于点O ,AB =10cm ,BD =45cm .动点P 从点A 出发,沿AB 方向匀速运动,速度为1cm/s ;同时,动点Q 从点A 出发,沿AD 方向匀速运动,速度为2cm/s .以AP ,AQ 为邻边的平行四边形APMQ 的边PM 与AC 交于点E .设运动时间为t s 0<t ≤5 ,解答下列问题:(1)当点M 在BD 上时,求t 的值;(2)连接BE .设△PEB 的面积为S cm 2 ,求S 与t 的函数关系式和S 的最大值;(3)是否存在某一时刻t ,使点B 在∠PEC 的平分线上?若存在,求出t 的值;若不存在,请说明理由.30(2023·湖南怀化·中考真题)如图一所示,在平面直角坐标系中,抛物线y =ax 2+bx -8与x 轴交于A (-4,0)、B (2,0)两点,与y 轴交于点C .(1)求抛物线的函数表达式及顶点坐标;(2)点P 为第三象限内抛物线上一点,作直线AC ,连接PA 、PC ,求△PAC 面积的最大值及此时点P 的坐标;(3)设直线l 1:y =kx +k -354交抛物线于点M 、N ,求证:无论k 为何值,平行于x 轴的直线l 2:y =-374上总存在一点E ,使得∠MEN 为直角.31(2024·海南省直辖县级单位·一模)如图,已知抛物线y =ax 2+2x +c a ≠0 ,与x 轴交于点A -1,0 和点B 3,0 ,与y 轴交于点C ,E 为抛物线的顶点.图1图2(1)求该抛物线的函数表达式;(2)如图1,点P 是第一象限内抛物线上一动点,连接PC 、PB 、BC ,设点P 的横坐标为t .①当t 为何值时,△PBC 的面积最大?并求出最大面积;②当t 为何值时,△PBC 是直角三角形?(3)如图2,过E 作EF ⊥x 轴于F ,若M m ,0 是x 轴上一动点,N 是线段EF 上一点,若∠MNC =90°,请直接写出实数m 的取值范围.32(2024·四川成都·一模)如图,直线y =-x -4分别交x 轴,y 轴于A ,C 两点,点B 在x 轴正半轴上.抛物线y =15x 2+bx +c 过A ,B ,C 三点.(1)求抛物线的解析式;(2)过点B 作BD ∥AC 交y 轴于点D ,交抛物线于点F .若点P 为直线AC 下方抛物线上的一动点,连接PD 交AC 于点E ,连接EB ,求S △PEB 的最大值及最大值时点P 的坐标;(3)如图2,将原抛物线进行平移,使其顶点为原点,进而得到新抛物线,直线y =-2x 与新抛物线交于O ,G 两点,点H 是线段OG 的中点,过H 作直线RQ (不与OG 重合)与新抛物线交于R ,Q 两点,点R 在点Q 左侧.直线GR 与直线OQ 交于点T ,点T 是否在某条定直线上?若是,请求出该定直线的解析式,若不是,请说明理由.33(2024·江苏苏州·一模)如图,在平面直角坐标系中,抛物线y =ax 2-8ax +10a -1a <0 与x 轴的交点分别为A x 1,0 ,B x 2,0 ,其中(0<x 2<x 1),且AB =4,与y 轴的交点为C ,直线CD ∥x 轴,在x 轴上有一动点E t ,0 ,过点E 作直线l ⊥x 轴,与抛物线、直线CD 的交点分别为P 、Q .(1)求抛物线的解析式;(2)当0<t ≤8时,求△APC 面积的最大值;(3)当t >2时,是否存在点P ,使以C 、P 、Q 为顶点的三角形与△OBC 相似?若存在,求出此时t 的值;若不存在,请说明理由.题型02四边形面积最值问题1(2024·安徽阜阳·一模)如图,抛物线y =ax 2+bx +3与x 轴交于A -1,0 ,B 3,0 两点,与y 轴交于点C .(1)求抛物线的解析式;(2)在抛物线的对称轴上找一点P ,使△PAC 的周长最小,求△PAC 的周长的最小值及此时点P 的坐标;(3)若M 为抛物线在第一象限内的一动点,求出四边形OCMB 的面积的最大值及此时点M 的坐标.2(2024·山东临沂·一模)如图,在平面直角坐标系中,抛物线y =-14x 2+bx +c 与x 轴交于点A (-2,0)和点B ,与y 轴交于点C (0,4),点P 是直线BC 上方的抛物线上一点(点P 不与点B ,C 重合),过点P 作PD ∥y 轴交直线BC 于点D .(1)求抛物线的函数表达式;(2)求线段PD 长的最大值;(3)连接CP ,BP ,请直接写出四边形ABPC 的面积最大值为.3(2024·山西运城·一模)综合与探究如图,抛物线y=ax2+bx-3a≠0与x轴交于A-1,0、B两点,与y轴交于点C,点D-2,9 2在抛物线上,点P是抛物线在第四象限内的一个动点,过点P作PQ∥y轴交直线BD于点Q,连接PA、PB、QA,设点P的横坐标为m.(1)求抛物线的函数表达式;(2)求四边形PAQB面积的最大值及此时点P的坐标;(3)若点M是抛物线上任意一点,是否存在点M,使得∠MAB=2∠ACO,若存在,请直接写出所有符合条件的点M的坐标,若不存在,请说明理由.4(2024·安徽合肥·一模)在平面直角坐标系中,点O是坐标原点.抛物线y=ax2+bx-3a≠0与x轴交于A,B两点,直线l:y=kx+2与抛物线交于A,C两点,且A-1,0,B3,0.(1)求a,b,k的值;(2)点M是线段OB上的动点,点N在x轴上,MN=2,且点N在M的左边.过点M作MP⊥x轴,交抛物线于点P.过点N作x轴的垂线,交抛物线于点Q,交直线l于点R.①当以P,Q,R,M为顶点的四边形是平行四边形时,求点M的坐标.②记以P,Q,R,M为顶点的四边形面积为S,求S的最大值.5(2024·安徽蚌埠·一模)如图1,已知直线y=-x+5与坐标轴相交于A、B,点C坐标是-1,0,抛物线经过A、B、C三点.点P是抛物线上的一点,过点P作y轴的平行线,与直线AB交于点D,与x轴相交于点F.(1)求抛物线的解析式;(2)当点P在第一象限时,连接CP交OA于点E,连接EF,如图2所示;①求AE+DF的值;②设四边形AEFB的面积为S,则点P在运动过程中是否存在面积S的最大值,若存在,请求出此时点P的坐标;若不存在,请说明理由.6(2024·安徽马鞍山·一模)如图,过原点的二次函数y=ax2+bx的图象与x轴正半轴交于点A,经过点A的直线与该函数交于B1,-3,与y轴交于点C0,-4.(1)分别求此二次函数与直线AB的解析式.(2)点P是第四象限内二次函数图象上的一个动点,过点P作直线PE⊥x轴于点E,与直线AB交于点D,设点P的横坐标为t.①当PD=12OC时,求t的值;②当点P在直线AB下方时,连接OP,过点B作BQ⊥x轴于点Q,BQ与OP交于点F,连接DF,求四边形FQED面积的最大值.7(2024·山东济南·一模)如图,直线y=-12x+3交y轴于点A,交x轴于点C,抛物线y=-14x2+bx+c经过点A,点C,且交x轴于另一点B.(1)求抛物线的解析式;(2)在直线AC上方的抛物线上有一点M,求四边形ABCM面积的最大值及此时点M的坐标;(3)将线段OA绕x轴上的动点P m,0顺时针旋转90°得到线段O A ,若线段O A 与抛物线只有一个公共点,请结合函数图象,求m的取值范围.8(2024·四川广元·二模)如图,二次函数y=ax2+bx+c的图象与x轴交于原点O和点A4,0,经过点A的直线与该函数图象交于另一点B1,3,与y轴交于点C.(1)求直线AB的函数解析式及点C的坐标.(2)点P是抛物线上位于直线AB上方的一个动点,过点P作直线PE⊥x轴于点E,与直线AB交于点D,过点B作BF⊥x轴于点F,连接OP,与BF交于点G,连接DG.求四边形GDEF面积的最大值.(3)抛物线上是否存在这样的点Q,使得∠BOQ=45°?若存在,请求出点Q的坐标;若不存在,请说明理由.9(2024·广东珠海·一模)如图,抛物线y=-x2+3x+4和直线y=x+1交于A-1,0点,点B,B3,4在直线x=3上,直线x=3与x轴交于点C.(1)求∠BAC的度数.(2)点P从点A出发,以每秒2个单位长度的速度沿线段AB向点B运动,点Q从点C出发,以每秒2个单位长度的速度沿线段CA向点A运动,点P,Q同时出发,当其中一点到达终点时,另一个点也随之停止运动,设运动时间为t秒t>0.以PQ为边作矩形PQNM,使点N在直线x=3上.①当t为何值时,矩形PQNM的面积最小?并求出最小面积;②直接写出当t为何值时,恰好有矩形PQNM的顶点落在抛物线上.10(2024·安徽宿州·二模)如图1,抛物线y=ax2+bx-3(a,b是常数且a>0)与x轴交于点A-1,0和点B(点B在点A的右侧),点D是抛物线的顶点,CD是抛物线的对称轴且交x轴于点C1,0.(1)求a,b的值;(2)点P是抛物线上一点且位于点A和点D之间.(i)如图2,连接AP,DP,BD,求四边形ABDP面积的最大值;(ii)如图3,连接AP并延长交CD延长线于点Q,连接BP交CD于点E,求CE+CQ的值.11(2024·安徽·二模)如图1,在平面直角坐标系中,抛物线y=ax2+bx-4交x轴于点A-1,0,B4,0,交y轴于点C,点M在该抛物线上,横坐标为m,将该抛物线M,C两点之间(包括M,C两点)的部分记为图象W.(1)求抛物线的解析式;(2)图象W的最大值与最小值的差为4时,求m的值;(3)如图2,若点M位于BC下方,过点A作AE∥BC交拋物线于点E,点D为直线AE上一动点,连接CM, CD,BM,BD,求四边形CDBM面积的最大值及此时点M的坐标.12(2024·四川广安·二模)如图,抛物线y=-x2+bx+c交x轴于A-4,0.,B两点,交y轴于点C0,4(1)求抛物线的函数解析式.(2)点D在线段OA上运动,过点D作x轴的垂线,与AC交于点Q,与抛物线交于点P,连接AP、CP,求四边形AOCP的面积的最大值.(3)在抛物线的对称轴上是否存在点M,使得以点A、C、M为顶点的三角形是直角三角形?若存在,请求出点M的坐标;若不存在,请说明理由.13(23-24九年级上·重庆渝北·期末)二次函数y=ax2+bx+4经过点A-1,0,点C,点D,点B4,0分别二次函数与y轴的交点和顶点,点M为二次函数图象上第一象限内的一个动点.(1)求二次函数的解析式;(2)如图1,连接BC ,过点A 作BC 的平行线交二次函数于点E ,连接CM ,BM ,BE ,CE .求四边形CMBE 面积的最大值以及此时点M 的坐标;(3)如图2,过点M 作MN ∥y 轴,交BC 于点N (点M 不与点D 重合),过点D 作DH ∥y 轴,交BC 于点H ,当DM =HN 时,直接写出点M 的坐标.题型03面积比最值问题14(2024·安徽合肥·一模)在平面直角坐标系xOy 中,已知抛物线y =a x +1 x -4 与x 轴交于A 、 B 两点,与y 轴交于点C 0,-2 .(1)求a 的值;(2)点D 为第四象限抛物线上一点①求△BCD 的面积最大值②连接AD ,BC 交于点E ,连接BD ,记△BDE 的面积为S 1,△ABE 的面积为S 2,求S 1S 2的最大值;15(2023·四川遂宁·中考真题)在平面直角坐标系中,O 为坐标原点,抛物线y =14x 2+bx +c 经过点O (0,0),对称轴过点B (2,0),直线l 过点C 2,-2 ,且垂直于y 轴.过点B 的直线l 1交抛物线于点M 、N ,交直线l 于点Q ,其中点M 、Q 在抛物线对称轴的左侧.(1)求抛物线的解析式;(2)如图1,当BM :MQ =3:5时,求点N 的坐标;(3)如图2,当点Q 恰好在y 轴上时,P 为直线l 1下方的抛物线上一动点,连接PQ 、PO ,其中PO 交l 1于点E ,设△OQE 的面积为S 1,△PQE 的面积为S 2.求S2S 1的最大值.16(2024·湖北省直辖县级单位·一模)抛物线y =x 2-4x 与直线y =x 交于原点O 和点B ,与x 轴交于另一点A ,顶点为D .(1)求出点B 和点D 的坐标;(2)如图①,连接OD ,P 为x 轴的负半轴上的一点,当tan ∠PDO =12时,求点P 的坐标;(3)如图②,M 是点B 关于抛物线的对称轴的对称点,Q 是抛物线上的动点,它的横坐标为m 0<m <5 ,连接MQ ,BQ ,MQ 与直线OB 交于点E ,设△BEQ 和△BEM 的面积分别为S 1和S 2,求S1S 2的最大值.17(2023·湖南永州·中考真题)如图1,抛物线y =ax 2+bx +c (a ,b ,c 为常数)经过点F 0,5 ,顶点坐标为2,9 ,点P x 1,y 1 为抛物线上的动点,PH ⊥x 轴于H ,且x 1≥52.(1)求抛物线的表达式;(2)如图1,直线OP :y =y 1x 1x 交BF 于点G ,求S △BPG S △BOG的最大值;(3)如图2,四边形OBMF 为正方形,PA 交y 轴于点E ,BC 交FM 的延长线于C ,且BC ⊥BE ,PH =FC ,求点P 的横坐标.18(2024·四川南充·一模)抛物线y =-38x 2+bx +c b >0 与x 轴分别交于A ,B 两点(点A 在点B 的左侧),与y 轴交于点C 0,3 ,抛物线对称轴为x =1,点P 是抛物线在第一象限上动点,连接CB ,PB .(1)求抛物线和直线BC 的解析式;(2)如图,连接PA ,交BC 于点M ,设△ABM 的面积为S 1,△PBM 的面积为S 2,求S 1S 2的最小值及此时点P的坐标.19(2024·湖北孝感·一模)如图1,已知抛物线y=ax2+bx+3与x轴交于点A-1,0,B3,0,与y轴交于点C,连接BC.(1)求a,b的值及直线BC的解析式;(2)如图1,点P是抛物线上位于直线BC上方的一点,连接AP交BC于点E,过P作PF⊥x轴于点F,交BC于点G,(ⅰ)若EP=EG,求点P的坐标,(ⅱ)连接CP,CA,记△PCE的面积为S1,△ACE的面积为S2,求S1S2的最大值;(3)如图2,将抛物线位于x轴下方面的部分不变,位于x轴上方面的部分关于x轴对称,得到新的图形,将直线BC向下平移n个单位,得到直线l,若直线l与新的图形有四个不同交点,请直接写出n的取值范围.题型04面积和最值问题1(2024·吉林长春·一模)在平面直角坐标系中,抛物线y=ax2+bx+3交x轴于点A(-1,0)、B(3,0),交y轴于点C,连结AC、BC.点D在该抛物线上,过点D作DE∥AC,交直线BC于点E,连结AD、AE、BD.设点D横坐标为m(m>0),△DAE的面积为S1,△DBE的面积为S2.(1)求a,b的值;(2)设抛物线上D、B两个点和它们之间的部分为图象G,当图象G的最高点的纵坐标与m无关时,求m的取值范围;(3)当点D在第一象限时,求S1+S2的最大值;(4)当S1:S2=2:1时,直接写出m的值.题型05面积差最值问题1(2024·安徽合肥·一模)如图1,在平面直角坐标系xOy中,抛物线y=x2+bx+c的对称轴为直线x=。

中考数学复习重难点与压轴题型专项突围训练(全国通用版)专题13一次函数的实际应用中最值问题【典型例题】1.(2022·河南汝阳·九年级期末)为满足市场需求,某超市在新年来临前夕,购进一款商品,每盒进价是40元.超市规定每盒售价不得少于45元.根据以往销售经验发现;当售价定为每盒45元时,每天可以卖出700盒,如果每盒售价每提高1元,则每天要少卖出20盒.(1)试求出每天的销售量y(盒)与每盒售价x(元)之间的函数关系式;(2)要使每天销售的利润为6000元,且让顾客得到最大的实惠.售价应定为多少元?(3)当每盒售价定为多少元时,每天销售的利润P(元)最大?最大利润是多少?【专题训练】一、解答题1.(2022·山东青岛·模拟预测)“菊润初经雨,橙香独占秋”,如图,橙子是一种甘甜爽口的水果,富含丰维生素C.某水果商城为了了解两种橙子市场销售情况,购进了一批数量相等的“血橙”和“脐橙”供客户对比品尝,其中购买“脐橙”用了420元,购买“血橙”用了756元,已知每千克“血橙”进价比每千克“脐橙”贵8元.(1)求每千克“血橙”和“脐橙”进价各是多少元?(2)若该水果商城决定再次购买同种“血橙”和“脐橙”共40千克,且再次购买的费用不超过600元,且每种橙子进价保持不变.若“血橙”的销售单价为24元,“脐橙”的销售单价为14元,则该水果商城应如何进货,使得第二批的“血橙”和“脐橙”售完后获得利润最大?最大利润是多少?2.(2022·山东莱芜·九年级期末)2022年冬奥会即将在北京召开,某网络经销商购进了一批以冬奥会为主题的文化衫进行销售,文化衫的进价每件40元,每月销售量y(件)与销售单价x(元)之间的函数关系如图所示,设每月获得的利润为W(元).(1)求出每月的销售量y(件)与销售单价x(元)之间的函数关系式;(2)这种文化衫销售单价定为多少元时,每月的销售利润最大?最大利润是多少元?(3)为了扩大冬奥会的影响,物价部门规定这种文化衫的销售单价不高于60元,该商店销售这种文化衫每月要获得最大利润,销售单价应定为多少元?每月的最大利润为多少元?3.(2022·河南·郑州中学九年级期末)冰墩墩(Bing Dwen Dwen),是2022年北京冬季奥运会的吉祥物.将熊猫形象与富有超能量的冰晶外壳相结合,头部外壳造型取自冰雪运动头盔,装饰彩色光环,整体形象酷似航天员.冬奥会来临之际,冰墩墩玩偶非常畅销.小冬在某网店选中A,B两款冰墩墩玩偶,决定从该网店进货并销售.两款玩偶的进货价和销售价如表:(1)第一次小冬550元购进了A,B两款玩偶共30个,求两款玩偶各购进多少个.(2)第二次小冬进货时,网店规定A款玩偶进货数量不得超过B款玩偶进货数量的一半.小冬计划购进两款玩偶共30个,应如何设计进货方案才能获得最大利润,最大利润是多少?(3)小冬第二次进货时采取了(2)中设计的方案,并且两次购进的玩偶全部售出,请从利润率的角度分析,对于小冬来说哪一次更合算?(注:利润率=(利润÷成本)×100%).4.(2021·山东青岛·一模)某学校为进一步做好疫情防控工作,计划购进A,B两种口罩.已知每箱A种口罩比每箱B种口罩多10包,每箱A种口罩和每箱B种口罩的价格分别是630元和600元,而每包A种口罩和每包B种口罩的价格分别是这一批口罩平均每包价格的0.9倍和1.2倍.(1)求这一批口罩平均每包的价格是多少元.(2)如果购进A,B两种口罩共5500包,最多购进3500包A种口罩,为了使总费用最低,应购进A种口罩和B种口罩各多少包?总费用最低是多少元?5.(2022·江苏滨湖·八年级期末)小李在某网店选中A、B两款玩偶,确定从该网店进货并销售.两款玩偶的进货价和销售价如表:(1)第一次小李用1100元购进了A、B两款玩偶共30个,求两款玩偶各购进多少个?(2)第二次小李进货时,网店规定A款玩偶进货数量不得超过B款玩偶进货数量的一半,小李计划购进两款玩偶60个.设小李购进A款玩偶m个,售完两款玩偶共获得利润W元,问应如何设计进货方案才能获得最大利润?并求W的最大值.6.(2021·山东北区·一模)六一前夕,某商场采购A、B两种品牌的卡通笔袋,已知每个A品牌笔袋的进价,比每个B品牌笔袋的进价多2元;若用3000元购进A品牌笔袋的数量,与用2400元购进B品牌笔袋的数量相同.(1)求每个A品牌笔袋和每个B品牌笔袋的进价分别是多少元;(2)该商场计划用不超过7220元采购A、B两种品牌的笔袋共800个,且其中B品牌笔袋的数量不超过400个,求该商场共有几种进货方式;(3)若每个A品牌笔袋售价16元,每个B品牌笔袋售价12元,在第(1)(2)问的前提下,不计其他因素,将所采购的A、B两种笔袋全部售出,求该商场可以获得的最大利润为多少元.7.(2022·四川简阳·八年级期末)某校准备组织八年级280名学生和5名老师参加研学活动,已知用1辆小客车和2辆大客车每次可运送120人;用3辆小客车和1辆大客车每次可运送135人.(1)每辆小客车和每辆大客车各能坐多少人?(2)若学校计划租用小客车m辆,大客车n辆,一次送完,且恰好每辆车都坐满.①请你设计出所有的租车方案;②若小客车每辆需租金6000元,大客车每辆需租金7500元,总租金为W元,写出W与m的关系式,根据关系式选出最省钱的租车方案,并求出最少租金.8.(2022·山东城阳·八年级期末)七月份河南暴雨,鸿星尔克因捐款5000万爆红网络,为表达对品牌的支持,国人掀起购物潮.我区一家鸿星尔克门店有库存上衣和裤子共1450件,若上衣按每件获利50元卖,裤子按每件获利80元卖,则售完这些库存共可获利92000元.(1)该门店库存有上衣、裤子各多少件?。

中考数学最值问题专题知识点概述在中学数学题中,最值题是常见题型,围绕最大(小)值所出的数学题是各种各样,就其解法,主要分为几何最值和代数最值两大部分。
一、解决几何最值问题的要领(1)两点之间线段最短;(2)直线外一点与直线上所有点的连线段中,垂线段最短;(3)三角形两边之和大于第三边或三角形两边之差小于第三边(重合时取到最值)。
二、解决代数最值问题的方法要领1.二次函数的最值公式二次函数y ax bx c =++2(a 、b 、c 为常数且a ≠0)其性质中有 ①若a >0当x b a=-2时,y 有最小值。
y ac b a min =-442; ②若a <0当x b a=-2时,y 有最大值。
y ac b a max =-442。
2.一次函数的增减性.一次函数y kx b k =+≠()0的自变量x 的取值范围是全体实数,图象是一条直线,因而没有最大(小)值;但当m x n ≤≤时,则一次函数的图象是一条线段,根据一次函数的增减性,就有最大(小)值。
3. 判别式法.根据题意构造一个关于未知数x 的一元二次方程;再根据x 是实数,推得∆≥0,进而求出y 的取值范围,并由此得出y 的最值。
4.构造函数法.“最值”问题中一般都存在某些变量变化的过程,因此它们的解往往离不开函数。
5. 利用非负数的性质.在实数范围内,显然有a b k k 22++≥,当且仅当a b ==0时,等号成立,即a b k 22++的最小值为k 。
6. 零点区间讨论法.用“零点区间讨论法”消去函数y 中绝对值符号,然后求出y 在各个区间上的最大值,再加以比较,从中确定出整个定义域上的最大值。
7. 利用不等式与判别式求解.在不等式x a ≤中,x a =是最大值,在不等式x b ≥中,x b =是最小值。
8. “夹逼法”求最值.在解某些数学问题时,通过转化、变形和估计,将有关的量限制在某一数值范围内,再通过解不等式获取问题的答案,这一方法称为“夹逼法”。
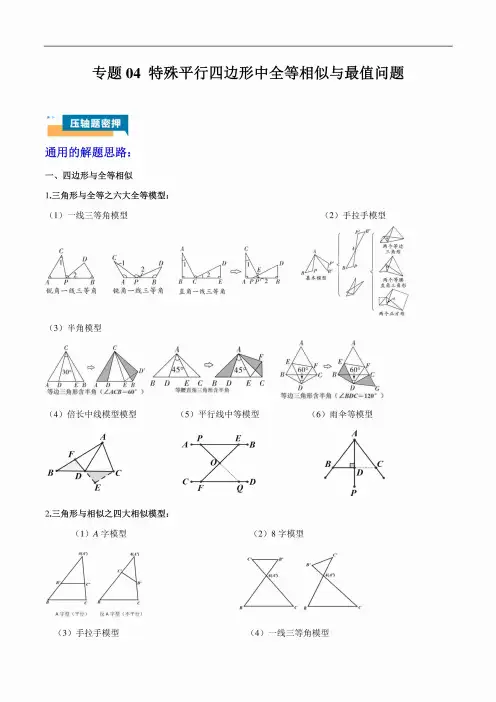
专题04特殊平行四边形中全等相似与最值问题通用的解题思路:一、四边形与全等相似1.三角形与全等之六大全等模型:(1)一线三等角模型锐角一线三等角(2)手拉手模型(3)半角模型(4)倍长中线模型模型(6)雨伞等模型(5)平行线中等模型2.三角形与相似之四大相似模型:(1)A字模型(3)手拉手模型(2)8字模型(4)一线三等角模型B 二、四边形线段最值问题囹 1 C B D 02B (1)将军饮马模型两定一动模型一定两动模型两线段相减的最大值模型(三点共线)• B(2)费马点模型:将边以A 为顶点逆时针旋转60。
,得到AQE,连接P0则^APQ 为等边三角形,PA=PQ O1. (2023-r 东深圳•中考真题)(1)如图,在矩形ABCD 中,E 为AD 边上一点,连接BE,①若= 过C 作CFLBE 交BE 于点、F ,求证:AABE^AFCB ;②若S 矩形倔8 = 2。
时,则BECF=(2)如图,在菱形ABCD 中,cosA = |,过。
作CE1AB 交A8的延长线于点E,过E 作EF _LAD 交AD 于点、F ,若S 菱形*d =24时,求EF BC 的值.(3)如图,在平行四边形ABCD 中,匕4 = 60。
,AB = 6, AD=5,点E 在CD 上,且CE = 2,点F 为BC 上一点,连接时,过E 作EGLEF 交平行四边形ABCD 的边于点G,若EF ・EG = 70时,请直接写出AG 的长.D,E E a C C A B AB备用图2.(2022广东广州•中考真题)如图,在菱形ABCQ中,0BAD=120°,AB=6,连接8Q.⑴求BQ的长;⑵点E为线段BQ上一动点(不与点B,。
重合),点E在边AQ上,且BE二也DF,①当CE±AB时,求四边形的面积;②当四边形的面积取得最小值时,CE+右CT的值是否也最小?如果是,求CE+也CF的最小值;如果不是,请说明理由.题型一特殊平行四边形中全等相似计算1.(2024-P东汕头•一模)(1)如图1,在矩形ABCD中,E为AD边上一点,连接8E,①若BE=BC,过。

备战2020中考数学之解密压轴解答题命题规律专题13 几何中的最值与定值问题【类型综述】线段和差的最值问题,常见的有两类:第一类问题是“两点之间,线段最短”.两条动线段的和的最小值问题,常见的是典型的“牛喝水”问题,关键是指出一条对称轴“河流”第二类问题是“两点之间,线段最短”结合“垂线段最短”.【方法揭秘】两条动线段的和的最小值问题,常见的是典型的“牛喝水”问题,关键是指出一条对称轴“河流”(如图1).三条动线段的和的最小值问题,常见的是典型的“台球两次碰壁”或“光的两次反射”问题,关键是指出两条对称轴“反射镜面”(如图2).两条线段差的最大值问题,一般根据三角形的两边之差小于第三边,当三点共线时,两条线段差的最大值就是第三边的长.如图3,P A与PB的差的最大值就是AB,此时点P在AB的延长线上,即P′.解决线段和差的最值问题,有时候求函数的最值更方便,本讲不涉及函数最值问题.图1 图2 图3如图4,正方形ABCD的边长为4,AE平分∠BAC交BC于E.点P在AE上,点Q在AB上,那么△BPQ周长的最小值是多少呢?如果把这个问题看作“牛喝水”问题,AE是河流,但是点Q不确定啊.第一步,应用“两点之间,线段最短”.如图5,设点B关于“河流AE”的对称点为F,那么此刻PF+PQ的最小值是线段FQ.第二步,应用“垂线段最短”.如图6,在点Q运动过程中,FQ的最小值是垂线段FH.这样,因为点B和河流是确定的,所以点F是确定的,于是垂线段FH也是确定的.图4 图5 图6【典例分析】【例1】如图1,△ABC是边长为8的等边三角形,AD⊥BC于点D,DE⊥AB于点E.(1)求证:AE=3EB(2)若点F是AD的中点,点P是BC边上的动点,连接PE,PF,如图2所示,求PE+PF的最小值及此时BP 的长;(3)在(2)的条件下,连接EF,当PE+PF取最小值时,△PEF的面积是______.【例2】问题探究()1请在图①的正方形ABCD的对角线BD上作一点P,使PA PC+最小;()2如图②,点P为矩形ABCD的对角线BD上一动点,AB2=,BC3=点E为BC边的中点,请作一点+最小,并求这个最小值;P,使PE PC问题解决()3如图③,李师傅有一块边长为1000米的菱形采摘园ABCD,AC1200=米,BD为小路,BC的中点E为一水池,李师傅现在准备在小路BD上建一个游客临时休息纳凉室P,为了节省土地,使休息纳凉室P到水池E与大门C的距离之和最短,那么是否存在符合条件的点P?若存在,请作出点P的位置,并求出这个最短距离;若不存在,请说明理由.【例3】在平面直角坐标系中,点A (0,4),B (m ,0)在坐标轴上,点C ,O 关于直线AB 对称,点D 在线段AB 上.(1)如图1,若m =8,求AB 的长;(2)如图2,若m =4,连接OD ,在y 轴上取一点E ,使OD =DE ,求证:CE =2DE ;(3)如图3,若m =43,在射线AO 上裁取AF ,使AF =BD ,当CD +CF 的值最小时,请在图中画出点D 的位置,并直接写出这个最小值.【例4】如图,一次函数122y x =-+的图像与坐标轴交于A 、B 两点,点C 的坐标为(1,0)-,二次函数2y ax bx c =++的图像经过A 、B 、C 三点.(1)求二次函数的解析式(2)如图1,已知点(1,)D n 在抛物线上,作射线BD ,点Q 为线段AB 上一点,过点Q 作QM y ⊥轴于点M ,作QN BD ⊥于点N ,过Q 作//QP y 轴交抛物线于点P ,当QM 与QN 的积最大时,求点P 的坐标;(3)在(2)的条件下,连接AP ,若点E 为抛物线上一点,且满足APE ABO ∠=∠,求点E 的坐标.【例5】如图,在平面直角坐标系中,抛物线y =﹣235333x x ++与x 轴交于A 、B 两点(点A 在点B 左侧),与y 轴交于点C .(1)求出△ABC 的周长.(2)在直线BC 上方有一点Q ,连接QC 、QB ,当△QBC 面积最大时,一动点P 从Q 出发,沿适当路径到达y 轴上的M 点,再沿与对称轴垂直的方向到达对称轴上的N 点,连接BN ,求QM +MN +BN 的最小值.(3)在直线BC 上找点G ,K 是平面内一点,在平面内是否存在点G ,使以O 、C 、G 、K 为顶点的四边形是菱形?若存在,求出K 的坐标;若不存在,请说明理由.【例6】在平面直角坐标系中,抛物线y =﹣x 2+bx +c 经过点A 、B ,C ,已知A (﹣1,0),C (0,3).【变式训练】一、单选题1.如图,APB △中,4,3AP BP ==,在AB 的同侧作正ABD △、正APE V 和正BPC △,则四边形PCDE 面积的最大值是( )A .12B .15C .20D .252.如图,在Rt ABC ∆中, 90BAC =︒∠,45ACB ∠=︒,22AB =,点P 为BC 上任意一点,连结PA ,以PA ,PC 为邻边作平行四边形PAQC ,连结PQ ,则PQ 的最小值为( )A .2B .2C .22D .43.如图,矩形ABCD 中,3AB =,8BC =,点P 为矩形内一动点,且满足PBC PCD ∠=∠,则线段PD 的最小值为( )A .5B .1C .2D .34.已知:AB 是O e 的直径,AD ,BC 是O e 的切线,P 是O e 上一动点,若10AD =,4OA =,16BC =,则PCD ∆的面积的最小值是( )A .36B .32C .24D .10.45.⊙O 是半径为1的圆,点O 到直线L 的距离为3,过直线L 上的任一点P 作⊙O 的切线,切点为Q ;若以PQ 为边作正方形PQRS,则正方形PQRS 的面积最小为( )A .7B .8C .9D .106.在△ABC 中,AB=BC,点D 在AC 上,BD=6cm,E ,F 分别是AB ,BC 边上的动点,△DEF 周长的最小值为6 cm,则ABC ∠=( )A .20°B .25°C .30°D .35°7.如图,已知点(1,3)A -,(5,1)B -,点(,0)P m 是x 轴上一动点,点Q 是y 轴上一动点,要使四边形ABPQ 的周长最小,m 的值为( )A .3.5B .4C .7D .2.58.如图,四边形ABCD 中,∠BAD=130°,∠B=∠D=90°,在BC 、CD 上分别找一点M 、N,使三角形AMN 周长最小时,则∠AMN+∠ANM 的度数为( )A .80°B .90°C .100°D .130°二、填空题9.如图,ABC ∆是等边三角形,13AD AB =,点E 、F 分别为边AC 、BC 上的动点,当DEF ∆的周长最小时,FDE ∠的度数是______________.10.如图,△ABC 中,AB=8,AC=5,BC=7,点D 在AB 上一动点,线段CD 绕点C 逆时针旋转60°得到线段CE,AE 的最小值为________11.在Rt △ABC 中,∠BAC =90,AB =AC ,AD ⊥BC 于点D ,P 是线段AD 上的一个动点,以点P 为直角的顶点,向上作等腰直角三角形PBE ,连接DE ,若在点P 的运动过程中,DE 的最小值为3,则AD 的长为____.12.如图示,在Rt ABC ∆中,90ACB ∠=︒,3AC =,3BC =,点P 在Rt ABC ∆内部,且PAB PBC ∠=∠,连接CP ,则CP 的最小值等于______.13.如图,在半径为2的⊙O 中,弦AB ⊥直径CD ,垂足为E ,∠ACD =30°,点P 为⊙O 上一动点,CF ⊥AP 于点F . ①弦AB 的长度为_____;②点P 在⊙O 上运动的过程中,线段OF 长度的最小值为_____.14.如图,矩形ABCD 中,6AB =,8BC =,M 是AD 边上的一点,且2AM =,点P 在矩形ABCD 所在的平面中,且90BPD ∠=︒,则PM 的最大值是_________.三、解答题15.如图,在平面直角坐标系中,矩形OABC 的两边OA OC 、分别在x 轴、y 轴的正半轴上,8,4OA OC ==.点P 从点O 出发,沿x 轴以每秒2个单位长的速度向点A 匀速运动,当点P 到达点A 时停止运动,设点P 运动的时间是t 秒.将线段CP 的中点绕点P 按顺时针方向旋转90o ,得点D ,点D 随点P 的运动而运动,连接DP DA 、.(1)请用含t 的代数式表示出点D 的坐标. (2)求t 为何值时,DPA ∆的面积最大,最大为多少?(3)在点P 从O 向A 运动的过程中,DPA ∆能否成为直角三角形?若能,求t 的值:若不能,请说明理由. (4)请直接写出整个运动过程中,点D 所经过的长度.16.已知矩形纸片OBCD 的边OB 在x 轴上,OD 在y 轴上,点C 在第一象限,且86OB OD ==,.现将纸片折叠,折痕为EF (点E,F 是折痕与矩形的边的交点),点P 为点D 的对应点,再将纸片还原。


(全国通用)专题14二次函数与线段数量关系最值定值问题图形运动的过程中,求两条线段之间的函数关系,是中考数学的热点问题.产生两条线段间的函数关系,常见的情况有两种,一是勾股定理,二是比例关系.还有一种不常见的,就是线段全长等于部分线段之和.由比例线段产生的函数关系问题,在两种类型的题目中比较常用.一是由平行线产生的对于线段成比例,二是相似三角形的对应边成比例.一般步骤是先说理产生比例关系,再代入数值或表示数的字母,最后整理、变形,根据要求写出定义域.关键是寻找比例关系,难点是有的整理、变形比较繁琐,容易出错.【例1】(2022•武汉模拟)抛物线y=x2﹣2x+m的顶点A在x轴上,与y轴交于点B.(1)求抛物线的解析式;(2)如图1,直线CD∥AB交抛物线于C,D两点,若,求△COD的面积;(3)如图2,P为抛物线对称轴上顶点下方的一点,过点P作直线交抛物线于点E,F,交x轴于点M,求的值.【例2】(2022•黄石)如图,抛物线y=﹣x2+x+4与坐标轴分别交于A,B,C三点,P是第一象限内抛物线上的一点且横坐标为m.(1)A,B,C三点的坐标为,,.(2)连接AP,交线段BC于点D,①当CP与x轴平行时,求的值;②当CP与x轴不平行时,求的最大值;(3)连接CP,是否存在点P,使得∠BCO+2∠PCB=90°,若存在,求m的值,若不存在,请说明理由.【例3】(2022•河南三模)如图,抛物线y=ax2+bx﹣4交x轴于A,B两点,交y轴于点C,OB=2OC=4OA,连接AC,BC.(1)求抛物线的解析式;(2)点D是抛物线y=ax2+bx﹣4的图象上在第四象限内的一动点,DE⊥x轴于点E,交BC于点F.设点D的横坐标为m.①请用含m的代数式表示线段DF的长;②已知DG∥AC,交BC于点G,请直接写出当时点D的坐标.【例4】(2021•大庆)如图,抛物线y=ax2+bx+c与x轴交于原点O和点A,且其顶点B关于x轴的对称点坐标为(2,1).(1)求抛物线的函数表达式;(2)抛物线的对称轴上存在定点F,使得抛物线y=ax2+bx+c上的任意一点G到定点F的距离与点G到直线y=﹣2的距离总相等.①证明上述结论并求出点F的坐标;②过点F的直线l与抛物线y=ax2+bx+c交于M,N两点.证明:当直线l绕点F旋转时,+是定值,并求出该定值;(3)点C(3,m)是该抛物线上的一点,在x轴,y轴上分别找点P,Q,使四边形PQBC周长最小,直接写出P,Q的坐标.1.(2020•道里区二模)已知:在平面直角坐标系中,点O为坐标原点,抛物线y=﹣+bx+3交x轴于A、B两点(点B在点A的右边)交y轴于点C,OB=3OC.(1)如图1,求抛物线的解析式;(2)如图2,点E是第一象限抛物线上的点,连接BE,过点E作ED⊥OB于点D,tan∠EBD=,求△BDE的面积;(3)如图3,在(2)的条件下,连接BC交DE于点Q,点K是第四象限抛物线上的点,连接EK交BC于点M,交x轴于点N,∠EMC=45°,过点K作直线KT⊥x轴于点T,过点E作EL∥x轴,交直线KT于点L,点F是抛物线对称轴右侧第一象限抛物线上的点,连接ET、LF,LF的延长线交ET于点P,连接DP并延长交EL于点S,SE=2SL,求点F的坐标.2.(2020•三明二模)如图,抛物线y=x2+mx(m<0)交x轴于O,A两点,顶点为点B.(Ⅰ)求△AOB的面积(用含m的代数式表示);(Ⅱ)直线y=kx+b(k>0)过点B,且与抛物线交于另一点D(点D与点A不重合),交y轴于点C.过点C作CE∥AB交x轴于点E.(ⅰ)若∠OBA=90°,2<<3,求k的取值范围;(ⅱ)求证:DE∥y轴.3.(2022•杜尔伯特县一模)如图,已知抛物线y=x2+bx+c与x轴相交于A(﹣1,0),B(m,0)两点,与y轴相交于点C(0,﹣3),抛物线的顶点为D.(1)求抛物线的解析式;(2)若点E在x轴上,且∠ECB=∠CBD,求点E的坐标.(3)若P是直线BC下方抛物线上任意一点,过点P作PH⊥x轴于点H,与BC交于点M.①求线段PM长度的最大值.②在①的条件下,若F为y轴上一动点,求PH+HF+CF的最小值.4.(2020•江岸区校级一模)已知:抛物线y=x2+x+m交x轴于A,B两点,交y轴于点C,其中点B在点A的右侧,且AB=7.(1)如图1,求抛物线的解析式;(2)如图2,点D在第一象限内抛物线上,连接CD,AD,AD交y轴于点E.设点D的横坐标为d,△CDE的面积为S,求S与d之间的函数关系式(不要求写出自变量d的取值范围);(3)如图3,在(2)的条件下,过点D作DH⊥CE于点H,点P在DH上,连接CP,若∠OCP=2∠DAB,且HE:CP=3:5,求点D的坐标及相应S的值.5.(2020•涡阳县一模)如图,抛物线y=ax2+bx+c(a≠0)与直线y=x+1相交于A(﹣1,0),B(4,m)两点,且抛物线经过点C(5,0).(1)求抛物线的解析式.(2)点P是直线上方的抛物线上的一个动点,求△ABP的面积最大时的P点坐标.(3)若点P是抛物线上的一个动点(不与点A点B重合),过点P作直线PD⊥x轴于点D,交直线AB 于点E.当PE=2ED时,求P点坐标;(4)设抛物线与y轴交于点F,在抛物线的第一象限内,是否存在一点M,使得AM被FC平分?若存在,请求出点M的坐标;若不存在,说明理由.6.(2021•桂林)如图,已知抛物线y=a(x﹣3)(x+6)过点A(﹣1,5)和点B(﹣5,m),与x轴的正半轴交于点C.(1)求a,m的值和点C的坐标;(2)若点P是x轴上的点,连接PB,P A,当=时,求点P的坐标;(3)在抛物线上是否存在点M,使A,B两点到直线MC的距离相等?若存在,求出满足条件的点M的横坐标;若不存在,请说明理由.7.(2021•甘肃)如图,在平面直角坐标系中,抛物线y=x2+bx+c与坐标轴交于A(0,﹣2),B(4,0)两点,直线BC:y=﹣2x+8交y轴于点C.点D为直线AB下方抛物线上一动点,过点D作x轴的垂线,垂足为G,DG分别交直线BC,AB于点E,F.(1)求抛物线y=x2+bx+c的表达式;(2)当GF=时,连接BD,求△BDF的面积;(3)①H是y轴上一点,当四边形BEHF是矩形时,求点H的坐标;②在①的条件下,第一象限有一动点P,满足PH=PC+2,求△PHB周长的最小值.8.(2021•丽水)如图,已知抛物线L:y=x2+bx+c经过点A(0,﹣5),B(5,0).(1)求b,c的值;(2)连结AB,交抛物线L的对称轴于点M.①求点M的坐标;②将抛物线L向左平移m(m>0)个单位得到抛物线L1.过点M作MN∥y轴,交抛物线L1于点N.P是抛物线L1上一点,横坐标为﹣1,过点P作PE∥x轴,交抛物线L于点E,点E在抛物线L对称轴的右侧.若PE+MN=10,求m的值.9.(2020•陕西)已知抛物线L:y=﹣x2+bx+c过点(﹣3,3)和(1,﹣5),与x轴的交点为A,B(点A 在点B的左侧).(1)求抛物线L的表达式;(2)若点P在抛物线L上,点E、F在抛物线L的对称轴上,D是抛物线L的顶点,要使△PEF∽△DAB (P的对应点是D),且PE:DA=1:4,求满足条件的点P的坐标.10.(2020•盘锦)如图1,直线y=x﹣4与x轴交于点B,与y轴交于点A,抛物线y=﹣x2+bx+c经过点B和点C(0,4),△ABO沿射线AB方向以每秒个单位长度的速度平移,平移后的三角形记为△DEF (点A,B,O的对应点分别为点D,E,F),平移时间为t(0<t<4)秒,射线DF交x轴于点G,交抛物线于点M,连接ME.(1)求抛物线的解析式;(2)当tan∠EMF=时,请直接写出t的值;(3)如图2,点N在抛物线上,点N的横坐标是点M的横坐标的,连接OM,NF,OM与NF相交于点P,当NP=FP时,求t的值.11.(2022•深圳三模)如图1,抛物线y=ax2+bx经过点A(﹣5,0),点B(﹣1,﹣2).(1)求抛物线解析式;(2)如图2,点P为抛物线上第三象限内一动点,过点Q(﹣4,0)作y轴的平行线,交直线AP于点M,交直线OP于点N,当点P运动时,4QM+QN的值是否变化?若变化,说明变化规律,若不变,求(3)如图3,长度为的线段CD(点C在点D的左边)在射线AB上移动(点C在线段AB上),连接OD,过点C作CE∥OD交抛物线于点E,线段CD在移动的过程中,直线CE经过一定点F,直接写出定点F的坐标与的最小值.12.(2022•阿克苏地区一模)如图1.抛物线与x轴交于A、B两点,与y轴交于点C,连接BC,已知点B(4,0).(1)若C(0,3),求抛物线的解析式.(2)在(1)的条件下,P(﹣2,m)为该抛物线上一点,Q是x轴上一点求的最小值,并求此时点Q的坐标.(3)如图2.过点A作BC的平行线,交y轴与点D,交抛物线于另一点E.若DE=7AD,求c的值.13.(2022•松江区二模)如图,在平面直角坐标系中,已知直线y=2x+8与x轴交于点A、与y轴交于点B,抛物线y=﹣x2+bx+c经过点A、B.(1)求抛物线的表达式;(2)P是抛物线上一点,且位于直线AB上方,过点P作PM∥y轴、PN∥x轴,分别交直线AB于点M、①当MN=AB时,求点P的坐标;②联结OP交AB于点C,当点C是MN的中点时,求的值.14.(2022•游仙区模拟)如图,抛物线与坐标轴分别交于A(﹣1,0),B(3,0),C(0,3).(1)求抛物线的解析式;(2)抛物线上是否存在点P,使得∠CBP=∠ACO,若存在,求出点P的坐标;若不存在,说明理由;(3)如图2,Q是△ABC内任意一点,求++的值.15.(2022•龙岩模拟)抛物线y=ax2+bx+c经过A(﹣1,0),B(3,4)两点,与y轴交于点C.(1)求抛物线的解析式(用含a的式子表示);(2)当a>0时,连接AB,BC,若tan∠ABC=,求a的值;(3)直线y=﹣x+m与线段AB交于点P,与抛物线交于M,N两点(点M在点N的左侧),若PM•PN =6,求m的值.16.(2022•雷州市模拟)如图(1),抛物线y=ax2+bx+6与x轴交于点A(﹣6,0)、B(2,0),与y轴交于点C,抛物线对称轴交抛物线于点M,交x轴于点N.点P是抛物线上的动点,且位于x轴上方.(1)求抛物线的解析式.(2)如图(2),点D与点C关于直线MN对称,若∠CAD=∠CAP,求点P的坐标.(3)直线BP交y轴于点E,交直线MN于点F,猜想线段OE、FM、MN三者之间存在的数量关系,并证明.17.(2022•马鞍山二模)如图,抛物线y=ax2+bx﹣3交x轴于点A(﹣1,0)、B(3,0),与y轴交于C点,直线y=kx(k<0)交线段BC下方抛物线于D点,交BC于E点(1)分别求出a、b的值;(2)求出线段BC的函数关系式,并写出自变量取值范围;(3)探究是否有最大值,若存在,请求出此时k值,若不存在,请说明理由.18.(2022•南岗区校级二模)如图1,在平面直角坐标系中,O为坐标原点,抛物线y=﹣ax2+6ax+6与y 轴交于点B,交x轴的负半轴于点A,交x轴的正半轴于点C,且S△ABC=30.(1)求抛物线的解析式;(2)如图2,点P为第一象限抛物线上一点,其横坐标为t,PD⊥x轴于点D,设tan∠P AD等于m,求m与t之间的函数关系式;(3)如图3,在(2)的条件下,当m=时,过点B作BN⊥AB交∠P AC的平分线于点N,点K在线段AB上,点M在线段AN上,连接KM、KN,∠MKN=2∠BNK,作MT⊥KN于点T,延长MT交BN 于点H,若NH=4BH,求直线KN的解析式.19.(2022•江汉区校级模拟)如图1,已知抛物线y=ax2+bx+c(a>0)与x轴交于A(﹣1,0),B(3,0),与y轴交于点C.(1)若C(0,﹣3),求抛物线的解析式;(2)在(1)的条件下,E是线段BC上一动点,AE交抛物线于F点,求的最大值;(3)如图2,点N为y轴上一点,AN、BN交抛物线于E、F两点,求•的值.20.(2022•成都模拟)如图,抛物线与x轴交于A,B两点(点A在点B的左侧),与y 轴交于点C.(1)求点A,B,C的坐标及抛物线的对称轴;(2)如图1,点P(1,m),Q(1,m﹣2)是两动点,分别连接PC,QB,请求出|PC﹣QB|的最大值,并求出m的值;(3)如图2,∠BAC的角平分线交y轴于点D,过D点的直线l与射线AB,AC分别于E,F,当直线l 绕点D旋转时,是否为定值,若是,请求出该定值;若不是,请说明理由.21.(2022•沈阳模拟)如图,在平面直角坐标系中,抛物线y=﹣x2+x+2与x轴交于A,B两点(点A 在点B左侧),与y轴交于点C,直线l:y=kx+b经过点B,点C,点P是抛物线上一动点,连接OP交直线BC于点D.(1)求直线l的解析式;(2)当=时,求点P的坐标;(3)在(2)的条件下,点N是直线BC上一动点,连接ON,过点D作DF⊥ON于点F,点F在线段ON上,当OD=DF时,请直接写出点N的坐标.22.(2022•沈阳模拟)如图,在平面直角坐标系中,抛物线y=ax2+bx﹣过点A(3,2)和点B (,0),与x轴的另一个交点为点C.(1)求抛物线的函数表达式.(2)判断△ABC的形状,并说明理由.(3)点D在线段BC上,连接AD,作DE⊥AD,且DE=AD,连接AE交x轴于点F.点F不与点C 重合,射线DP⊥AE,交AE于点P,交AC于点Q.①当AD=AF时,请直接写出∠CAE的度数;②当=时,请直接写出CQ的长.。

求最值中的几何模型题型解读|模型构建|通关试练模型01 将军饮马模型将军饮马模型在考试中主要考查转化与化归等的数学思想,该题型综合考查学生的理解和数形结合能力具有一定的难度,也是学生感觉有难度的题型.在解决几何最值问题主要依据是:①将军饮马作对称点;②两点之间,线段最短;③垂线段最短,涉及的基本知识点还有:利用轴对称变换化归到“三角形两边之和大于第三边”、“三角形两边之差小于第三边”等;希望通过本专题的讲解让大家对这类问题有比较清晰的认识. 模型02 建桥选址模型建桥选址模型,即沿一个方向平移的定长线段两端到两个定点距离和最小,解题时需要理清楚是否含有定长平移线段,且利用平移求出最短路径位置.求解长度时若有特殊角,通常采用构造直角三角形利用勾股定理求解的方法.该题型主要考查了在最短路径问题中的应用,涉及到的主要知识点有矩形的性质、平行四边形的性质、等腰直角三角形的性质、勾股定理,解题的关键在于如何利用轴对称找到最短路径.模型03 胡不归模型胡不归PA+k·PB”型的最值问题:当k等于1时,即为“PA+PB”之和最短问题,可用我们常见的“将军饮马”问题模型来处理,即可以转化为轴对称问题来处理.当k不等于1时,若再以常规的轴对称思想来解决问题,则无法进行,因此必须转换思路.此类问题的处理通常以动点P所在图象的不同来分类,一般分为两类研究.即点P在直线上运动和点P在圆上运动.其中点P在直线上运动的类型通常为“胡不归”问题.模型01将军饮马模型考|向|预|测将军饮马模型问题该题型主要以选择、填空形式出现,综合性大题中的其中一问,难度系数较大,在各类考试中都以中高档题为主.本题考查的是轴对称--最短路线问题、勾股定理、等边三角形的判定和性质、含30°角的直角三角形的性质、垂线段最短,解这类问题的关键是将所给问题抽象或转化为数学模型,把两条线段的和转化为一条线段,属于中考选择或填空题中的压轴题.答|题|技|巧 第一步: 观察所求为横向还是纵向的线段长度(定长),将线段按照长度方向平移第二步: 同侧做对称点变异侧,异侧直接连线第三步: 结合两点之间,线段最短;垂线段最短;三角形两边之和大于第三边等常考知识点 第四步: 利用数学的转化思想,将复杂模型变成基本模型(1)点A 、B 在直线m 两侧两点连线,线段最短例1.(2023·四川)如图,等边三角形ABC 的边BC 上的高为6,AD 是BC 边上的中线,M 是线段AD 上的-一个动点,E 是AC 中点,则EM CM +的最小值为 .【答案】6【详解】解:连接BE ,与AD 交于点M .∵AB=AC ,AD 是BC 边上的中线,mA B P m AB∴B 、C 关于AD 对称,则EM+CM=EM+BM ,则BE 就是EM+CM 的最小值.∵E 是等边△ABC 的边AC 的中点,AD 是中线∴BE=AD=6,∴EM+CM 的最小值为6,故答案为:6.(2)点A 、B 在直线同侧例2.(2022·安徽)如图,在锐角△ABC 中,AB =6,∠ABC =60°,∠ABC 的平分线交AC 于点D ,点P ,Q 分别是BD ,AB 上的动点,则AP +PQ 的最小值为( )A .6B .C .3D .【答案】D 【详解】解:如图,在BC 上取E ,使BE =BQ ,连接PE ,过A 作AH ⊥BC 于H ,∵BD 是∠ABC 的平分线,∴∠ABD =∠CBD ,∵BP =BP ,BE =BQ ,∴△BPQ ≌△BPE (SAS ),m ABm∴PE =PQ ,∴AP +PQ 的最小即是AP +PE 最小,当AP +PE =AH 时最小,在Rt △ABH 中,AB =6,∠ABC =60°,∴AH =33,∴AP +PQ 的最小为33, 故选:D .模型02 建桥选址模型考|向|预|测建桥选址模型该题型也主要以选择、填空的形式出现,一般较为靠后,有一定难度,该题型主要考查轴对称---最短路径问题、勾股定理、三角形及平行四边形的判定与性质,要利用“两点之间线段最短”等,但许多实际问题没这么简单,需要我们将一些线段进行转化,即用与它相等的线段替代,从而转化成两点之间线段最短的问题.目前,往往利用对称性、平行四边形的相关知识进行转化.答|题|技|巧 第一步: 观察点或图形的变化规律,根据图形的变化规律求出已知关键点的坐标;第二步: 分析变化规律得到一般的规律看是否具有周期性(如点变的循环规律或点运动的循环规律,点的横、纵坐标的变化规律等)第三步: 周期性的求最小周期看余数,不是周期性的可以罗列求解几组以便发现规律,根据最后的变化次数或者运动时间登,确定要求的点与哪个点重合或在同一象限,或与哪个关键点的横纵坐标相等;第四步: 利用有理数的运算解题(1)两个点都在直线外侧:辅助线:连接AB 交直线m 、n 于点P 、Q ,则PA +PQ +QB 的最小值为AB .例1.(2022·湖北)如图,在Rt △ABC 中,∠ACB =90°,∠ABC =30°,AC =2,以BC 为边向左作等边△BCE ,点D 为AB 中点,连接CD ,点P 、Q 分别为CE 、CD 上的动点.求PD +PQ +QE 的最小值为 .n QP n mAP'Q'【答案】4.【详解】如图,连接,PA QB ,BCE QV 和ADC 都是等边三角形,60BCE ∴∠=︒,60ACD ∠=︒,1302ACE ACB BCE ACD ∴∠=∠−∠=︒=∠,CE ∴垂直平分AD ,PA PD ∴=, 同理可得:CD 垂直平分BE ,QB QE ∴=,PD PQ QE PA PQ QB ∴++=++,由两点之间线段最短可知,当点,,,A P Q B 共线时,PA PQ QB ++取得最小值AB ,故PD PQ QE ++的最小值为4.(2)一个点在内侧,一个点在外侧:辅助线:过点B 作关于定直线n 的对称点B’,连接AB’交直线m 、n 于点P 、Q ,则PA +PQ +QB 的最小值为AB ’.例2.(2023·山东)如图,在ABC 中,6AB =,7BC =,4AC =,直线m 是ABC 中BC 边的垂直平分线,P 是直线m 上的一动点,则APC △的周长的最小值为_________.n mn【答案】10【详解】解:∵直线m 垂直平分BC ,∴B 、C 关于直线m 对称,设直线m 交AB 于D ,∴当P 和D 重合时,AP +CP 的值最小,最小值等于AB 的长,∴△APC 周长的最小值是6+4=10.故答案为:10.(3)如图3,两个点都在内侧:辅助线:过点A 、B 作关于定直线m 、n 的对称点A’ 、B’ ,连接A’B’ 交直线m 、n 于点P 、Q ,则PA +PQ +QA 的最小值为A ’B’.例3.(2023.浙江)如图所示,∠AOB =50°,∠BOC =30°,OM =12,ON =4.点P 、Q 分别是OA 、OB 上动点,则MQ +PQ +NP 的最小值是 .【答案】4【详解】解:如图,作点N 关于OA 的对称点N ′,则NP =N ′P ,nmn作点M关于OB的对称点M′,则MQ=M′Q,∴MQ+PQ+NP=M′Q+PQ+N′P,当N′M′在同一条直线上时取最小值,连接ON′,OM′,∵∠AOB=50°,∠BOC=30°则∠N′OA=∠AOC=∠AOB﹣∠BOC=20°,∠BOM′=∠BOA=50°,∴∠N′OM′=2×20°+30°+50°=120°,∵ON′=ON=4,OM′=OM=12,∴∠AON=∠AOB﹣∠BOC=50°﹣30°=20°,先作射线ON'与射线ON关于OA对称,由对称的性质可知∠AON'=20°,PN=PN',同理作射线OM'与射线OM关于OB对称,同理∠BOM'=50°,QM=QM′,当N'、P、Q、M'四点共线时,MQ+PQ+NP最小,则∠N′OM′=∠N′OP+∠AOB+∠BPM′=20°+50°+50°=120°,作N'垂直OM'的延长线交于点E,∴∠EON'=60°,∴ON'=ON=4,在Rt△N'OE中,∠EN'O=30°,根据30°角所对的直角边是斜边的一半可知OE=2,则EN'=2,OM=OM'=12,∴EM′=OE+OM′=12+2=14,则N′M===4.故答案为:4.模型03胡不归模型考|向|预|测胡不归模型可看作将军饮马衍生,主要考查转化与化归等的数学思想,近年在中考数学和各地的模拟考中常以压轴题的形式考查,学生不易把握.本专题就最值模型中的胡不归问题进行梳理及对应试题分析,方便掌握.在解决胡不归问题主要依据是:点到线的距离垂线段最短.答|题|技|巧第一步:构造与kPB相等的线段,将“PA+kPB”型问题转化为“PA+PC”型;第二步:借助三角函数,构造锐角α,将另一个系数也化为1;第三步:利用“垂线段最短”原理构造最短距离;第四步:数形结合解题【答案】42【详解】解:如图,过点P 作PE ⊥AD ,交AD 的延长线于点E ,∵AB CD ∥,∴∠EDP=∠DAB=45°,∴sin EP EDP DP ∠==,∴EP PD =,∴2PB PD PB PE +=+, ∴当点B ,点P ,点E 三点共线且BE ⊥AD 时,PB+PE 有最小值,即最小值为BE ,∵sin BE A AB ∠=,∴BE AB =故答案为:1.(2023·江苏扬州)如图所示,军官从军营C 出发先到河边(河流用AB 表示)饮马,再去同侧的D 地开会,应该怎样走才能使路程最短?你能解决这个著名的“将军饮马”问题吗?下列给出了四个图形,你认为符合要求的图形是( )A .B .C .D .【答案】D【详解】解:由选项D 中图可知:作D 点关于直线AB 的对称点D ¢,连接CD '交AB 于点N ,由对称性可知,DN D N '=,CN DN CN D N CD ∴+=≥''+,当C 、N 、D ¢三点共线时,CN DN +的距离最短,故选:D2.(2023.浙江)如图,等边△ABC 的边长为4,AD 是BC 边上的中线,F 是AD 边上的动点,E 是AC 边上一点,若AE =2,当EF +CF 取得最小值时,则∠ECF= .【答案】∠ECF =30º【详解】过E 作EM ∥BC ,交AD 于N ,如图所示:∵AC =4,AE =2,∴EC =2=AE ,∴AM =BM =2,∴AM =AE ,∵AD 是BC 边上的中线,△ABC 是等边三角形,∴AD ⊥BC ,∵EM ∥BC ,∴AD ⊥EM ,∵AM =AE ,∴E 和M 关于AD 对称,连接CM 交AD 于F ,连接EF ,则此时EF +CF 的值最小, ∵△ABC 是等边三角形,∴∠ACB =60º,AC =BC ,∵AM =BM ,∴∠ECF =∠ACB =30º.故答案为30°3.(2022·安徽)如图,在平面直角坐标系中,∠AOB =30°,P (5,0),在OB 上找一点M ,在OA 上找一点N ,使△PMN 周长最小,则此时△PMN 的周长为 .【答案】5【详解】作点P 关于OB 的对称点C ,作P 点关于AO 的对称点D ,连接CD 交OA 于N ,交OB 于M ,连接MP ,NP ,OC ,OD ,∴CM =MP ,NP =DN ,∴PM+PN+MN =CM+MN+DN≥CD ,∴当C 、M 、N 、D 点共线时,△PMN 的周长最小,∵∠BOA =30°,OP =OC =OB ,∴∠COD =60°,∴△OCD 是等边三角形,∴CD =OP ,∵P (5,0),∴OP =5,∴CD =5,∴△PMN 的周长最小值为5,故答案为:5.4.(2023·广东)如图,在Rt ABC 中,ACB 90∠=︒,AC 9=,BC 12=,15AB =,AD 是BAC ∠的平分线,若点P 、Q 分别是AD 和AC 上的动点,则PC PQ +的最小值是 .【答案】365【详解】解:如图,作Q 关于AP 的对称点O ,则PQ=PO ,所以O 、P 、C 三点共线时,CO=PC+PO=PC+PQ ,此时PC+PQ 有可能取得最小值,∵当CO 垂直于AB 即CO 移到CM 位置时,CO 的长度最小,∴PC+PQ 的最小值即为CM 的长度, ∵111591222ABC S AB CM AC CB CM =⨯=⨯∴=⨯,,∴CM=91236155⨯=,即PC+PQ 的最小值为 365, 故答案为365.5.(2023·江苏)如图,高速公路的同一侧有A ,B 两城镇,它们到高速公路所在直线MN 的距离分别为2km AC =,4km BD =,8km CD =.要在高速公路上C ,D 之间建一个出口P ,使A ,B 两城镇到P 的距离之和最小,则这个最短距离为 .【答案】10km【详解】解:如图所示:作A 点关于直线MN 的对称点A ',再连接A B ',交直线MN 于点P ,则此时AP PB +最小,过点B 作BE CA ⊥交延长线于点E ,∵2km AC =,4km BD =,8km CD =.∴m 422k AE =−=,4km AA '=,∴6km A E '=,km 8BE CD ==,在Rt A EB '△中,10km A B '==,则AP PB +的最小值为10km .故答案为:10km .【答案】B【详解】解:如图:等腰Rt △DEF 中,过点D 作DM ⊥EF 于点M ,过E 、F 分别作∠MEP=∠MFP=30°,则EM=DM=1,故cos30°=EM EP ,解得:,则PM=,故DP=1﹣,则PD+PE+PF=2×+1﹣1. 故选B .A .42B .33 【答案】A 【详解】解:延长AD ,过点B 作BE AD ⊥交CD 于点P ,∵四边形ABCD 为平行四边形,∴AB CD ∥,∴45DEP DAB ∠=∠=︒,∵BE AD ⊥,∴DE PE =,则22222DE PE DE PD +==,则2DE PD =,同理可得:BE AB =,∴2PB PD PB PE +=+,∴当点E 、P 、B 在同一条直线上时,PB PD 的值最小,∵8AB =,∴22P E BE A B PD B P B P +===+=故选:A .8.(2023·四川)如图,在ABC 中,90,60,4BAC B AB ∠=︒∠=︒=,若D 是BC 边上的动点,则2AD DC +的最小值是( )A .6B .8C .10D .12【答案】D 【详解】解:过点C 作射线CE ,使30BCE ∠=︒,再过动点D 作DF CE ⊥,垂足为点F ,连接AD ,如图所示:在t R DFC △中,30DCF ∠=︒,∴12DF DC =,∵122()2AD DC AD DC +=+=2()AD DF +,∴当A ,D ,F 在同一直线上,即AF CE ⊥时,AD DF +的值最小,最小值等于垂线段AF 的长, 此时,60B ADB ︒∠=∠=,∴ABD △是等边三角形,∴4===AD BD AB ,在t R ABC 中,90,60,4A B AB ∠=∠=︒=︒,∴8BC =,∴4DC =,∴12,2DF DC ==,∴426AF AD DF =+=+=,∴2()212AD DF AF +==,∴2()AD DC +的最小值为12,故选:D .9.(2023·湖南)某班级在探究“将军饮马问题”时抽象出数学模型:直线l 同旁有两个定点A 、B ,在直线l 上存在点P ,使得PA PB +的值最小.解法:如图1,作A 点关于直线l 的对称点A ',连接A B ',则A B '与直线l 的交点即为P ,且PA PB +的最小值为A B '.请利用上述模型解决下列问题:(1)几何应用:如图2,ABC 中,90C ∠=︒,2AC BC ==,E 是AB 的中点,P 是BC 边上的一动点,则PA PE+的最小值为 ;(2)几何拓展:如图3,ABC 中,2AC =,30A ∠=︒,若在AB 、AC 上各取一点M 、N 使CM MN +的值最小,画出图形,求最小值并简要说明理由.【答案】【详解】(1)解:如图2所示,作点A 关于BC 的对称点A ',连接A E '交BC 于P ,此时PA PE +的值最小.连接BA ',由勾股定理得, BA BA '==∵E 是AB 的中点,∴12BE BA ===∵90C ∠=︒,2AC BC ==,∴45A BC ABC '∠=∠=︒,∴90A BA '∠=︒,∴PA PE +的最小值A E '===;(2)解:如图3,作点C 关于直线AB 的对称点C ',作C N AC '⊥于N ,交AB 于M ,连接AC ',则2C A CA '==,30C AB CAB '∠=∠=︒,60C AC '∴∠=︒∴C AC '△为等边三角形,∴30AC N '∠=︒,∴112AN C A '==,∴CM MN +的最小值为C N '=10.(2023·陕西)在学习对称的知识点时,我们认识了如下图所示的“将军饮马”模型求最短距离. 问题提出:(1)如图1所示,已知A ,B 是直线l 同旁的两个定点.在直线l 上确定一点P ,并连接AP 与BP ,使PA PB +的值最小.问题探究:(2)如图2所示,正方形ABCD 的边长为2,E 为AB 的中点,P 是AC 上一动点.连接EP 和BP ,则PB PE +的最小值是___________;问题解决:(3)某地有一如图3所示的三角形空地AOB ,已知45AOB ∠=︒,P 是AOB 内一点,连接PO 后测得10PO =米,现当地政府欲在三角形空地AOB 中修一个三角形花坛PQR ,点Q R ,分别是OA OB ,边上的任意一点(不与各边顶点重合),求PQR 周长的最小值.【答案】(1)见解析(3)【详解】(1)解:如图所示,当P 点在如图所示的位置时,PA PB +的值最小;(2)解:如下图所示,∵四边形ABCD 是正方形,∴AC 垂直平分BD ,∴PB PD =,由题意易得:PB PE PD PE DE +=+≥,当D 、P 、E 共线时,在ADE V 中,根据勾股定理得,DE =(3)解:如下图所示,分别作点P 关于OA ,OB 的对称点M N ,,连接OM ON MN ,,,MN 交OA ,OB 于点Q R ,,连接PR PQ ,,此时PQR 周长的最小值等于MN .由轴对称性质可得,10OM ON OP MOA POA NOB POB ===∠=∠∠=∠,,,∴224590MON AOB ∠=∠=⨯︒=︒,在Rt MON △中,MN ===即PQR 周长的最小值等于上一动点,则ACBD【答案】A【详解】解:连接CD ,设,CD AB 交于点G ,如图所示,∵四边形ABCD 是平行四边形,∴CG GD =,AG GB =,∵()0,8A ,()0,2B −∴()0,3G ,∴当CG 取得最小值时,CD 取得最小值,∴当CG EF ⊥时,CG 取得最小值,∵()05E ,,()5,0F −,∴OE OF =,2EG =,∴OEF 是等腰直角三角形,∴此时CGE 是直角三角形,且EG 是斜边,∵2EG =,∴CG =ACBD 的对角线CD 的最小值是,故选:A .2.(2023·上虞市)如图,点P 是∠AOB 内任意一点,OP =6cm ,点M 和点N 分别是射线OA 和射线OB 上的动点,若△PMN 周长的最小值是6 cm ,则∠AOB 的度数是( )A .15B .30C .45D .60【答案】B 【详解】分别作点P 关于OA 、OB 的对称点C 、D ,连接CD ,分别交OA 、OB 于点M 、N ,连接OC 、OD 、PM 、PN 、MN ,如图所示:∵点P 关于OA 的对称点为D ,关于OB 的对称点为C ,∴PM=DM ,OP=OD ,∠DOA=∠POA ; ∵点P 关于OB 的对称点为C ,∴PN=CN ,OP=OC ,∠COB=∠POB ,∴OC=OP=OD ,∠AOB=12∠COD , ∵△PMN 周长的最小值是6cm ,∴PM+PN+MN=6,∴DM+CN+MN=6,即CD=6=OP ,∴OC=OD=CD ,即△OCD 是等边三角形,∴∠COD=60°,∴∠AOB=30°,故选:B .【答案】B 【详解】解:如图,过点G 作GH ⊥AB 于H ,过点G 作MN ∥AB ,∵四边形ABCD 是矩形,AB =112,BC =3,∴∠B =90°,CD =112,AD =3,∵AE =1,∴BE =92,∵∠GHE =∠A =∠GEF =90°,∴∠GEH +∠EGH =90°,∠GEH +∠FEA =90°,∴∠EGH =∠FEA ,又∵GE =EF ,∴△GEH ≌△EFA (AAS ),∴GH =AE =1,∴点G 在平行AB 且到AB 距离为1的直线MN 上运动,∴当F 与D 重合时,CG 有最小值,此时AF =EH =3,∴CG52, 故选B .【答案】B 【详解】解:连接AM 、AC ,AM 交BD 于P ,此时PM+PC 最小,连接CP ,∵四边形ABCD 是菱形,∴OA=OC ,AC ⊥BD ,∴C 和A 关于BD 对称,∴AP=PC ,∵∠A=120°,∴∠ABC=60°,∴△ABC 是等边三角形,∴AC=AB=2,∵M 是BC 的中点,∴AM ⊥BC ,∴∠BAM=30°,∴BM=1,∴故选B .5.(2023·湖北)如图,将△ABC 沿AD 折叠使得顶点C 恰好落在AB 边上的点M 处,D 在BC 上,点P 在线段AD 上移动,若AC =6,CD =3,BD =7,则△PMB 周长的最小值为 .【答案】18【详解】解:由翻折的性质可知,AM =AC ,PM =PC ,∴M 点为AB 上一个固定点,则BM 长度固定, ∵△PMB 周长=PM +PB +BM ,∴要使得△PMB 周长最小,即使得PM +PB 最小,∵PM =PC ,∴满足PC +PB 最小即可,显然,当P 、B 、C 三点共线时,满足PC +PB 最小,如图所示, 此时,P 点与D 点重合,PC +PB =BC ,∴△PMB 周长最小值即为BC +BM ,此时,作DS ⊥AB 于S 点,DT ⊥AC 延长线于T 点,AQ ⊥BC 延长线于Q 点,由题意,AD 为∠BAC 的角平分线,∴DS =DT ,∵1122ACD S AC DT CD AQ ==,1122ABD S AB DS BD AQ ==, ∴11221122ABDACD AB DS BD AQ S S AC DT CD AQ ==,即:AB BD AC CD =,∴763AB =,解得:AB =14, ∵AM =AC =6,∴BM =14-6=8,∴△PMB 周长最小值为BC +BM =3+7+8=18,故答案为:18.6.(2023·北京)如图,P 是AOB ∠内一定点,点M ,N 分别在边OA ,OB 上运动,若30AOB ∠=︒,3OP =,则PMN 的周长的最小值为 .【答案】3【详解】如图,作P 关于OA ,OB 的对称点C ,D .连接OC ,OD .则当M ,N 是CD 与OA ,OB 的交点时,△PMN 的周长最短,最短的值是CD 的长.∵点P 关于OA 的对称点为C ,∴PM=CM ,OP=OC ,∠COA=∠POA ;∵点P 关于OB 的对称点为D ,∴PN=DN ,OP=OD ,∠DOB=∠POB ,∴OC=OD=OP=3,∠COD=∠COA+∠POA+∠POB+∠DOB=2∠POA+2∠POB=2∠AOB=60°,∴△COD 是等边三角形,∴CD=OC=OD=3.∴△PMN 的周长的最小值=PM+MN+PN=CM+MN+DN≥CD=3.【答案】【详解】解:如图,过点P 作PE ⊥AB 于点E ,过点D 作DF ⊥AB 于点F,∵四边形ABCD 是菱形,且∠B =120°,∴∠DAC =∠CAB =30°,∴PE =12AP;∵∠DAF =60°,∴∠ADF =30°,∴AF =12AD =12×6=3;∴DF = ∵12AP+PD =PE+PD,∴当点D ,P ,E 三点共线且DE ⊥AB 时,PE+DP 的值最小,最小值为DF 的长,∴12AP+PD 的最小值为故答案为: 8.(2023·广东)如图,在Rt ABC △中,90BAC ∠=︒,2AB =,4AC =.D ,E 分别是边AB ,AC 上的动点,且2CE AD =,则2BE CD +的最小值为 .【答案】【详解】如图,作Rt CEF ADC ∽,连接BF ,过B 点作BG AC ⊥的延长线与G 点,Rt Rt CEF ADC ∽,且2CE AD =,21CF EF EC AC DC AD ∴===,282,CF AC EF DC ∴===,2BE CD BE EF ∴+=+.BE EF BF +≥,∴当B 、E 、F 三点共线时,BE EF BF +=,此时2BE CD +的值最小,为BF .90FCA ∠=︒,90ACG ∴∠=︒.又90A ∠=︒,90BGC ∠=︒,∴四边形ABGC 是矩形,4BG AC ∴==,2GC AB ==,8210FG FC CG ∴=+=+=,BF ∴==故答案为:9.(2023·内蒙古)如图,已知菱形ABCD的边长为8,点M是对角线AC上的一动点,且∠ABC=120°,则MA+MB+MD的最小值是________.【答案】【详解】解:如图,过点D作DE⊥AB于点E,连接BD,∵菱形ABCD中,∠ABC=120°,∠MAE=30°,∴∠DAB=60°,AD=AB=DC=BC,MD=MB,∴△ADB是等边三角形,∵∠MAE=30°,∴AM=2ME,∵MD=MB,∴MA+MB+MD=2ME+2DM=2DE,根据垂线段最短,此时DE MA+MB+MD最小,∵菱形ABCD的边长为8,∴=∴MA+MB+MD的最小值是故答案为:10.(2023·浙江)如图,河的两岸有A,B两个水文观测点,为方便联络,要在河上修一座木桥MN(河的两岸互相平行,MN垂直于河岸),现测得A,B两点到河岸的距离分别是5米,4米,河宽3米,且A,++的最小值是米.B两点之间的水平距离为12米,则AM MN NB【答案】18【详解】作BB '垂直于河岸,使BB '等于河宽,连接AB ',与靠近A 的河岸相交于M ,作MN 垂直于另一条河岸, 过点A 作'⊥AC BB 交BB '的延长线于点C ,则MN BB '∥且MN BB '=,于是MNBB '为平行四边形,故MB BN '=,当AM MB AB '+=时,AM BN +最小,也就是AM MN NB ++最短,∵12AC =(米),54312BC =++=(米),1239B C '=−=(米)∴在Rt AB C '△中,15AB '(米),∴AM MN NB ++的最小值为:15318+=(米)故答案为:18 .11.(2023·广东)如图所示,已知O 为坐标原点,矩形ABCD (点A 与坐标原点重合)的顶点D 、B 分别在x 轴、y 轴上,且点C 的坐标为()4,8−,连接BD ,将ABD △沿直线BD 翻折至A BD ',交CD 于点E .(1)求点A '坐标.(2)试在x 轴上找点P ,使A P PB '+的长度最短,请求出这个最短距离.【答案】(1)3216,55A ⎛⎫'− ⎪⎝⎭;(2)A P PB '+的长度的最短距离为.【详解】(1)点C 的坐标为(4,8)−,4OD BC ∴==,8CD OB ==,连接AA ',与BD 交于点G ,过A '作A F OB '⊥于点F ,由折叠知,8A B OA '==,OG A G '=,OA BD '⊥, ∴11··22OBD S BD OG OD OB ==,∴·OD OB OG BD ==,∴2OA OG '==, 设OF x =,则8BF x =−,22222OA OF A F A B BF '''−==−,即()222288x x −=−−⎝⎭, 解得,165x =,即165OF =,∴325A F '==, 3216,55A ⎛⎫∴− ⎪⎝⎭';(2)作A '点关于x 轴的对称点A ',连接BA '',与x 轴交于点P ,则A P PB A P PB A B '''''+=+=的值最小,3216,55A ⎛⎫∴−−' ⎝'⎪⎭, (0,8)B ,∴A B =='' 故A P PB '+的长度的最短距离为.吉林)数学兴趣活动课上,小致将等腰的底边,在中,,在中,作在中,,得到线段ABC ABC 120︒ABP ABC 60【答案】(1)2;(2;(3)3.【详解】(1)如图,过点A 作,此时AP 的值最小.∵,,,故答案为:2.(2)根据小致的思路作出图形,可知当时的值最小,如图:∵,,∴,∵,∴(3)如图3中,在上取一点,使得,连接,.,,,,,,,,,时,的值最小,最小值为3,的最小值为3.13.(2023·河南)唐朝诗人李颀的诗《古从军行》开头两句说:“白日登山望烽火,黄昏饮马傍交河.”诗中隐含着一个有趣的数学问题——将军饮马问题:如图1所示,诗中将军在观望烽火之后从山脚下的A 点出发,走到河旁边的P 点饮马后再到B 点宿营.请问怎样走才能使总的路程最短?作法如下:如图1,从B 出发向河岸引垂线,垂足为D ,在BD 的延长线上,取B 关于河岸的对称点B ',连接AB ',与河岸线相交于P ,则P 点就是饮马的地方,将军只要从A 出发,沿直线走到P ,饮马之后,再由P 沿直线走到B ,所走的路程就是最短的.⊥AP BC 4,120AB AC BAC ==∠=︒30ABC ∴∠=︒122AP AB ∴==PN AB ⊥PE EF +30ABC ∠=︒122AP AB ==BP =1122BP AP AB PN ⋅=⋅PN =AB K AK AC =CK DK 90ACB ∠=︒30B ∠=︒60CAK ∴∠=︒PAD CAK ∴∠=∠PAC DAK ∴∠=∠PA DA =CA KA =()PAC DAK SAS ∴△≌△PC DK ∴=KD BC ⊥KD PC ∴(1)观察发现如图2,在等腰梯形ABCD 中,2,120AB CD AD D ===∠=︒,点E 、F 是底边AD 与BC 的中点,连接EF ,在线段EF 上找一点P ,使BP AP +最短.作点B 关于EF 的对称点,恰好与点C 重合,连接AC 交EF 于一点,则这点就是所求的点P ,故BP AP +的最小值为_______.(2)实践运用如图3,已知O 的直径1MN =,点A 在圆上,且AMN ∠的度数为30︒,点B 是弧AN 的中点,点P 在直径MN 上运动,求BP AP +的最小值.(3)拓展迁移如图,已知抛物线()20y ax bx c a =++≠的对称轴为1x =,且抛物线经过()()1,00,3A C −−、两点,与x 轴交于另一点B .①求这条抛物线所对应的函数关系式;②在抛物线的对称轴直线1x =上找到一点M ,使ACM △周长最小,请求出此时点M 的坐标与ACM △周长最小值.【答案】(1)(2)PA PB +的最小值为(3)①2=23y x x −−;②点M 的坐标为()12−,;ACM △【详解】(1)解:过点A 作AM BC ⊥于点M ,作DN BC ⊥于点N ,如图所示:则AM DN ∥,∵四边形ABCD 为等腰梯形,∴AD BC ∥,120BAD ADC ∠=∠=︒,∴18060ABM BAD ∠=︒−∠=︒,18060DCN ADC ∠=︒−∠=︒,∴1cos 60212BM AB =⨯︒=⨯=,sin 602AM AB =⨯︒== 1cos 60212CN CD =⨯︒=⨯=,∵AD BC ∥,AM DN ∥,∴四边形AMND 为平行四边形,∴2MN AD ==,∴123CM CN MN =+=+=,∴AC ==即BP AP +的最小值为故答案为:(2)解:取点A 关于MN 的对称点A ',连接OA '、OB 、OA 、MB 、A B ',MN 与A B '交于点P ',当点P 在点P '时,PA PB +最小,且最小值为A B ',如图所示:∵A 关于MN 的对称点A ',MN 为直径,∴点A '在O 上,∵30AMN ∠=︒,∴260AON AMN ∠=∠=︒,∵点A 关于MN 的对称点A ',∴60A ON AON '∠=∠=︒,∵点B 是弧AN 的中点, ∴1152BMN AMN ∠=∠=︒, ∴230BON BMN ∠=∠=︒,∴603090BOA '∠=︒+︒=︒,∵直径1MN =, ∴12OA OB '==,∴A B ==', 即PA PB +的最小值为2.(3)解:①∵抛物线()20y ax bx c a =++≠的对称轴为1x =,且抛物线经过()1,0A −, ∴抛物线与x 轴的另外一个交点B 的坐标为:()3,0, ∴抛物线的解析式为:()()13y a x x =+−, 把()0,3C −代入得:()()30103a −=+−,解得:1a =,∴抛物线的解析式为:()()21323y x x x x =+−=−−.②连接CB 交直线1x =于一点,该点即为点M ,连接AM ,AC ,如图所示:∵点A 、B 关于直线1x =对称,∴AM BM =,∴AM CM CM BM +=+,∵两点之间线段最短,∴CM BM +最小,即AM CM +最小,∵AC 为定值,∴此时ACM △的周长最小,∵AC =BC = ∴ACM △;设直线BC 的解析式为()0y kx b k =+≠,把()0,3C −,()3,0B 代入得:330b k b =−⎧⎨+=⎩,解得:13k b =⎧⎨=−⎩,∴直线BC 的解析式为3y x =−,把1x =代入得:132y =−=−,∴点M 的坐标为()12−,.。
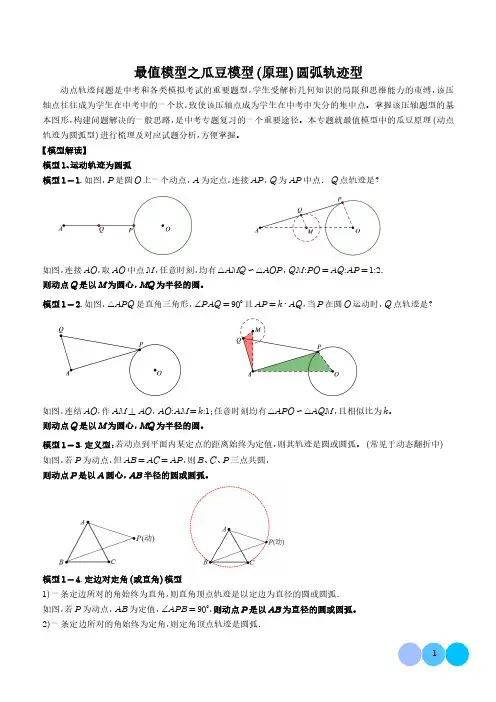
最值模型之瓜豆模型(原理)圆弧轨迹型动点轨迹问题是中考和各类模拟考试的重要题型,学生受解析几何知识的局限和思维能力的束缚,该压轴点往往成为学生在中考中的一个坎,致使该压轴点成为学生在中考中失分的集中点。
掌握该压轴题型的基本图形,构建问题解决的一般思路,是中考专题复习的一个重要途径。
本专题就最值模型中的瓜豆原理(动点轨迹为圆弧型)进行梳理及对应试题分析,方便掌握。
【模型解读】模型1、运动轨迹为圆弧模型1-1. 如图,P是圆O上一个动点,A为定点,连接AP,Q为AP中点.Q点轨迹是?如图,连接AO,取AO中点M,任意时刻,均有△AMQ∽△AOP,QM:PO=AQ:AP=1:2.则动点Q是以M为圆心,MQ为半径的圆。
模型1-2. 如图,△APQ是直角三角形,∠PAQ=90°且AP=k⋅AQ,当P在圆O运动时,Q点轨迹是?如图,连结AO,作AM⊥AO,AO:AM=k:1;任意时刻均有△APO∽△AQM,且相似比为k。
则动点Q是以M为圆心,MQ为半径的圆。
模型1-3. 定义型:若动点到平面内某定点的距离始终为定值,则其轨迹是圆或圆弧。
(常见于动态翻折中)如图,若P为动点,但AB=AC=AP,则B、C、P三点共圆,则动点P是以A圆心,AB半径的圆或圆弧。
模型1-4. 定边对定角(或直角)模型1)一条定边所对的角始终为直角,则直角顶点轨迹是以定边为直径的圆或圆弧.如图,若P为动点,AB为定值,∠APB=90°,则动点P是以AB为直径的圆或圆弧。
2)一条定边所对的角始终为定角,则定角顶点轨迹是圆弧.如图,若P为动点,AB为定值,∠APB为定值,则动点P的轨迹为圆弧。
【模型原理】动点的轨迹为定圆时,可利用:“一定点与圆上的动点距离最大值为定点到圆心的距离与半径之和,最小值为定点到圆心的距离与半径之差”的性质求解。
1(2023·山东泰安·统考中考真题)如图,在平面直角坐标系中,Rt△AOB的一条直角边OB在x轴上,点A的坐标为(-6,4);Rt△COD中,∠COD=90°,OD=43,∠D=30°,连接BC,点M是BC中点,连接AM.将Rt△COD以点O为旋转中心按顺时针方向旋转,在旋转过程中,线段AM的最小值是()A.3B.62-4C.213-2D.22(2023·四川广元·统考一模)如图,线段AB为⊙O的直径,点C在AB的延长线上,AB=4,BC=2,点P是⊙O上一动点,连接CP,以CP为斜边在PC的上方作Rt△PCD,且使∠DCP=60°,连接OD,则OD长的最大值为.3(2023·四川宜宾·统考中考真题)如图,M是正方形ABCD边CD的中点,P是正方形内一点,连接BP,线段BP以B为中心逆时针旋转90°得到线段BQ,连接MQ.若AB=4,MP=1,则MQ的最小值为.4(2023·湖南·统考中考真题)如图,在矩形ABCD中,AB=2,AD=7,动点P在矩形的边上沿B→C→D→A运动.当点P不与点A、B重合时,将△ABP沿AP对折,得到△AB P,连接CB ,则在点P的运动过程中,线段CB 的最小值为.5(2023·山东·统考中考真题)如图,在四边形ABCD中,∠ABC=∠BAD=90°,AB=5,AD=4,AD< BC,点E在线段BC上运动,点F在线段AE上,∠ADF=∠BAE,则线段BF的最小值为.6(2023·浙江金华·九年级校考期中)如图,点A,C,N的坐标分别为(-2,0),(2,0),(4,3),以点C为圆心、2为半径画⊙C,点P在⊙C上运动,连接AP,交⊙C于点Q,点M为线段QP的中点,连接MN,则线段MN的最小值为.7(2023上·江苏连云港·九年级校考阶段练习)已知矩形ABCD,AB=6,BC=4,P为矩形ABCD内一点,且∠BPC=135°,若点P绕点A逆时针旋转90°到点Q,则PQ的最小值为.8(2023下·陕西西安·九年级校考阶段练习)问题提出:(1)如图①,在△ABC中,AB=AC,∠BAC=120°,BC=43,则AB的长为;问题探究:(2)如图②,已知矩形ABCD,AB=4,BC=5,点P是矩形ABCD内一点,且满足∠APB= 90°,连接CP,求线段CP的最小值;问题解决:(3)如图③所示,我市城市绿化工程计划打造一片四边形绿地ABCD,其中AD∥BC,AD= 40m,BC=60m,点E为CD边上一点,且CE:DE=1:2,∠AEB=60°,为了美化环境,要求四边形ABCD的面积尽可能大,求绿化区域ABCD面积的最大值.课后专项训练1(2023·安徽合肥·校考一模)如图,在△ABC中,∠B=45°,AC=2,以AC为边作等腰直角△ACD,连BD,则BD的最大值是()A.10-2B.10+3C.22D.10+22(2023春·广东·九年级专题练习)已知:如图,在△ABC中,∠BAC=30°,BC=4,△ABC面积的最大值是( ).A.8+43B.83+4C.83D.8+833(2022秋·江苏扬州·九年级校考阶段练习)如图,A是⊙B上任意一点,点C在⊙B外,已知AB=2,BC=4,△ACD是等边三角形,则△BCD的面积的最大值为()A.43+4B.4C.43+8D.64(2023·山东济南·一模)正方形ABCD中,AB=4,点E、F分别是CD、BC边上的动点,且始终满足DE=CF,DF、AE相交于点G.以AG为斜边在AG下方作等腰直角△AHG使得∠AHG=90°,连接BH.则BH的最小值为()A.25-2B.25+2C.10-2D.10+25(2023上·江苏连云港·九年级统考期中)如图,在矩形ABCD中,已知AB=3,BC=4,点P是BC边上一动点(点P不与点B,C重合),连接AP,作点B关于直线AP的对称点M,连接CM,则CM的最小值为.6(2023春·广东深圳·九年级专题练习)如图,点G是△ABC内的一点,且∠BGC=120°,△BCF是等边三角形,若BC=3,则FG的最大值为.7(2023·江苏泰州·九年级专题练习)如图,在矩形ABCD中,AD=10,AB=16,P为CD的中点,连接BP.在矩形ABCD外部找一点E,使得∠BEC+∠BPC=180°,则线段DE的最大值为.8(2023·陕西渭南·三模)如图,在矩形ABCD中,AB=6,BC=5,点E在BC上,且CE=4BE,点M 为矩形内一动点,使得∠CME=45°,连接AM,则线段AM的最小值为.9(2023江苏扬州·三模)如图,在等边△ABC和等边△CDE中,AB=6,CD=4,以AB、AD为邻边作平行四边形ABFD,连接AF.若将△CDE绕点C旋转一周,则线段AF的最小值是.10(2023秋·湖北武汉·九年级校考阶段练习)如图,△ABC为等腰直角三角形,∠BAC=90°,AB= AC=22,点D为△ABC所在平面内一点,∠BDC=90°,以AC、CD为边作平行四边形ACDE,则CE的最小值为.11(2023·福建泉州·统考模拟预测)如图,点E是正方形ABCD的内部一个动点(含边界),且AD= EB=8,点F在BE上,BF=2,则以下结论:①CF的最小值为6;②DE的最小值为82-8;③CE= CF;④DE+CF的最小值为10;正确的是.12(2021·广东·中考真题)在△ABC中,∠ABC=90°,AB=2,BC=3.点D为平面上一个动点,∠ADB=45°,则线段CD长度的最小值为.13(2023·广东·深圳市二模)如图,在矩形ABCD中,AB=3,BC=4,E为边BC上一动点,F为AE 中点,G为DE上一点,BF=FG,则CG的最小值为.14(2023秋·广东汕头·九年级校考期中)如下图,在正方形ABCD中,AB=6,点E是以BC为直径的圆上的点,连接DE,将线段DE绕点D逆时针旋转90°,得到线段DF,连接CF,则线段CF的最大值与最小值的和.15(2023·陕西渭南·统考一模)如图,在矩形ABCD中,AB=2,BC=4,Q是矩形ABCD左侧一点,连接AQ、BQ,且∠AQB=90°,连接DQ,E为DQ的中点,连接CE,则CE的最大值为.16(2023·安徽亳州·统考模拟预测)等腰直角△ABC 中,BAC =90°,AB =5,点D 是平面内一点,AD =2,连接BD ,将BD 绕D 点逆时针旋转90°得到DE ,连接AE ,当DAB =(填度数)度时,AE 可以取最大值,最大值等于.17(2023·河北廊坊·统考二模)已知如图,△ABC 是腰长为4的等腰直角三角形,∠ABC =90°,以A 为圆心,2为半径作半圆A ,交BA 所在直线于点M ,N .点E 是半圆A 上仟意一点.连接BE ,把BE 绕点B 顺时针旋转90°到BD 的位置,连接AE ,CD .(1)求证:△EBA ≌△DBC ;(2)当BE 与半圆A 相切时,求弧EM的长;(3)直接写出△BCD 面积的最大值.18(2022·北京·中考真题)在平面直角坐标系xOy 中,已知点M (a ,b ),N .对于点P 给出如下定义:将点P 向右(a ≥0)或向左(a <0)平移a 个单位长度,再向上(b ≥0)或向下(b <0)平移b 个单位长度,得到点P ',点P '关于点N 的对称点为Q ,称点Q 为点P 的“对应点”.(1)如图,点M (1,1),点N 在线段OM 的延长线上,若点P (-2,0),点Q 为点P 的“对应点”.①在图中画出点Q;②连接PQ,交线段ON于点T.求证:NT=12 OM;(2)⊙O的半径为1,M是⊙O上一点,点N在线段OM上,且ON=t12<t<1,若P为⊙O外一点,点Q为点P的“对应点”,连接PQ.当点M在⊙O上运动时直接写出PQ长的最大值与最小值的差(用含t的式子表示)19(2023下·广东广州·九年级校考阶段练习)如图,△ABC为等边三角形,点P是线段AC上一动点(点P不与A,C重合),连接BP,过点A作直线BP的垂线段,垂足为点D,将线段AD绕点A逆时针旋转60°得到线段AE,连接DE,CE.(1)求证:BD=CE;(2)连接CD,延长ED交BC于点F,若△ABC的边长为2;①求CD的最小值;②求EF的最大值.20(2023·江苏常州·统考二模)如图,在平面直角坐标系中,二次函数y=-13x2+bx-3的图像与x轴交于点A和点B9,0,与y轴交于点C.(1)求二次函数的表达式;(2)若点P是抛物线上一点,满足∠PCB+∠ACB=∠BCO,求点P的坐标;(3)若点Q在第四象限内,且cos∠AQB=35,点M在y轴正半轴,∠MBO=45°,线段MQ是否存在最大值,如果存在,直接写出最大值;如果不存在,请说明理由.。
专题13二次函数与胡不归型最值问题胡不归问题:模型分析:“PA+k·PB”型的最值问题,当k=1时通常为轴对称之最短路径问题,而当k>0时,若以常规的轴对称的方式解决,则无法进行,因此必须转换思路.如图,直线BM,BN交于点B,P为BM上的动点,点A在射线BM,BN同侧,已知sin∠MBN=k.过点A作AC⊥BN于点C,交BM于点P,此时PA+k·PB取最小值,最小值即为AC的长.证明 如图,在BM 上任取一点Q ,连结AQ ,作QD ⊥BN 于点D .由sin ∠MBN =k ,可得QD = k ·QB .所以QA +k ·QB =QA +QD ≥AC ,即得证.【例1】(2022•济南)抛物线y =ax 2+x ﹣6与x 轴交于A (t ,0),B (8,0)两点,与y 轴交于点C ,直线y =kx ﹣6经过点B .点P 在抛物线上,设点P 的横坐标为m .(1)求抛物线的表达式和t ,k 的值;(2)如图1,连接AC ,AP ,PC ,若△APC 是以CP 为斜边的直角三角形,求点P 的坐标;(3)如图2,若点P 在直线BC 上方的抛物线上,过点P 作PQ ⊥BC ,垂足为Q ,求CQ +PQ 的最大值.【例2】(2022•宜宾)如图,抛物线y =ax 2+bx +c 与x 轴交于A (3,0)、B (﹣1,0)两点,与y 轴交于点C (0,3),其顶点为点D ,连结AC .(1)求这条抛物线所对应的二次函数的表达式及顶点D 的坐标;(2)在抛物线的对称轴上取一点E ,点F 为抛物线上一动点,使得以点A 、C 、E 、F 为顶点、AC 为边的四边形为平行四边形,求点F 的坐标; P B AM N N M AB C PD Q(3)在(2)的条件下,将点D向下平移5个单位得到点M,点P为抛物线的对称轴上一动点,求PF+ PM的最小值.【例3】(2022•东西湖区模拟)如图1,抛物线y=x2+(m﹣2)x﹣2m(m>0)与x轴交于A,B两点(A 在B左边),与y轴交于点C.连接AC,BC.且△ABC的面积为8.(1)求m的值;(2)在(1)的条件下,在第一象限内抛物线上有一点T,T的横坐标为t,使∠ATC=60°.求(t﹣1)2的值.(3)如图2,点P为y轴上一个动点,连接AP,求CP+AP的最小值,并求出此时点P的坐标.【例4】(2022•成都模拟)如图,在平面直角坐标系xOy中,二次函数y=ax2+bx+c(a≠0)的图象与y轴,x轴分别相交于A(0,2),B(2,0),C(4,0)三点,点D是二次函数图象的顶点.(1)求二次函数的表达式;(2)点P为抛物线上异于点B的一点,连接AC,若S△ACP=S△ACB,求点P的坐标;(3)M是第四象限内一动点,且∠AMB=45°,连接MD,MC,求2MD+MC的最小值.1.(2022•河北区二模)已知抛物线y=﹣x2+bx+c(b,c为常数)的图象与x轴交于A(1,0),B两点(点A在点B左侧).与y轴相交于点C,顶点为D.(Ⅰ)当b=2时,求抛物线的顶点坐标;(Ⅱ)若点P是y轴上一点,连接BP,当PB=PC,OP=2时,求b的值;(Ⅲ)若抛物线与x轴另一个交点B的坐标为(4,0),对称轴交x轴于点E,点Q是线段DE上一点,点N为线段AB上一点,且AN=2BN,连接NQ,求DQ+NQ的最小值.2.(2021•南海区二模)如图1,抛物线y=x2+bx+c与x轴交于A、B两点,点A、B分别位于原点左、右两侧,且AO=2BO=4,过A点的直线y=kx+c交y轴于点C.(1)求k、b、c的值;(2)在抛物线的对称轴上是否存在一点P,使△ACP为直角三角形?若存在,直接写出所有满足条件的点的坐标;若不存在,请说明理由;(3)如图2,点M为线段AC上一点,连接OM,求AM+OM的最小值.3.(2021•宝安区模拟)(1)已知二次函数经过点A(﹣3,0)、B(1,0)、C(0,3),请求该抛物线解析式;(2)点M为抛物线上第二象限内一动点,BM交y轴于点N,当BM将四边形ABCM的面积分为1:2两部分时,求点M的坐标;(3)点P为对称轴上D点下方一动点,点Q为直线y=x第一象限上的动点,且DP=OQ,求BP+ BQ的最小值并求此时点P的坐标.4.(2021•南沙区一模)已知,抛物线y=mx2+x﹣4m与x轴交于点A(﹣4,0)和点B,与y轴交于点C.点D(n,0)为x轴上一动点,且有﹣4<n<0,过点D作直线l⊥x轴,且与直线AC交于点M,与抛物线交于点N,过点N作NP⊥AC于点P.点E在第三象限内,且有OE=OD.(1)求m的值和直线AC的解析式.(2)若点D在运动过程中,AD+CD取得最小值时,求此时n的值.(3)若△ADM的周长与△MNP的周长的比为5:6时,求AE+CE的最小值.5.(2021•射阳县三模)如图,抛物线y=ax2+bx+c经过A(﹣1,0)、B(3,0)、C(0,3)三点,对称轴与抛物线相交于点P,与直线BC相交于点M,连接AC,PB.(1)求该抛物线的解析式;(2)设对称轴与x轴交于点N,在对称轴上是否存在点G,使以O、N、G为顶点的三角形与△AOC相似?如果存在,请求出点G的坐标;如果不存在,请说明理由;(3)抛物线上是否存在一点Q,使△QMB与△PMB的面积相等,若存在,求点Q的坐标;若不存在,请说明理由;(4)点E是y轴上的动点,连接ME,求ME+CE的最小值.6.(2021•深圳模拟)如图1,抛物线y=﹣x2+bx+c交x轴于A、B两点,其中点A坐标为(﹣3,0),与y 轴交于点C(0,3),点D为抛物线y=﹣x2+bx+c的顶点.(1)求抛物线的函数表达式;(2)若点E在x轴上,且∠ECA=∠CAD,求点E的坐标;(3)如图2,点P为线段AC上方的抛物线上任一点,过点P作PH⊥x轴于点H,与AC交于点M.①求△APC的面积最大时点P的坐标;②在①的条件下,若点N为y轴上一动点,求HN+CN的最小值.7.(2021•深圳模拟)已知:如图,点A(1,0),B(3,0),D(2,﹣1),C是y轴上的点,且OC=3.(1)过点A作AM⊥BC,垂足为M,连接AD、BD,求证:四边形ADBM为正方形;(2)若过A、B、C三点的抛物线对称轴上有一动点P,当PC﹣PB的值最大时,求出点P的坐标;(3)设Q为线段OC上的一动点,问:AQ+QC是否存在最小值?若存在,求出这个最小值;若不存在,请说明理由.8.(2021•资阳)抛物线y=﹣x2+bx+c与x轴交于A、B两点,与y轴交于点C,且B(﹣1,0),C(0,3).(1)求抛物线的解析式;(2)如图1,点P是抛物线上位于直线AC上方的一点,BP与AC相交于点E,当PE:BE=1:2时,求点P的坐标;(3)如图2,点D是抛物线的顶点,将抛物线沿CD方向平移,使点D落在点D'处,且DD'=2CD,点M是平移后所得抛物线上位于D'左侧的一点,MN∥y轴交直线OD'于点N,连结CN.当D'N+CN的值最小时,求MN的长.9.(2022•杜尔伯特县一模)如图,已知抛物线y=x2+bx+c与x轴相交于A(﹣1,0),B(m,0)两点,与y轴相交于点C(0,﹣3),抛物线的顶点为D.(1)求抛物线的解析式;(2)若点E在x轴上,且∠ECB=∠CBD,求点E的坐标.(3)若P是直线BC下方抛物线上任意一点,过点P作PH⊥x轴于点H,与BC交于点M.①求线段PM长度的最大值.②在①的条件下,若F为y轴上一动点,求PH+HF+CF的最小值.10.(2020•自贡)在平面直角坐标系中,抛物线y=ax2+bx+3与x轴交于点A(﹣3,0)、B(1,0),交y 轴于点N,点M为抛物线的顶点,对称轴与x轴交于点C.(1)求抛物线的解析式;(2)如图1,连接AM,点E是线段AM上方抛物线上一动点,EF⊥AM于点F,过点E作EH⊥x轴于点H,交AM于点D.点P是y轴上一动点,当EF取最大值时:①求PD+PC的最小值;②如图2,Q点为y轴上一动点,请直接写出DQ+OQ的最小值.11.(2022•中山市三模)如图,抛物线y=ax2+bx﹣3与x轴交于A、B两点,与y轴交于点C,抛物线的对称轴为直线x=1,点A(﹣1,0),过B的直线交y轴于点D,交抛物线于E,且.(1)求抛物线的解析式;(2)在抛物线第四象限的图象上找一点P,使得△BDP的面积最大,求出点P的坐标;(3)点M是线段BE上的一点,求的最小值,并求出此时点M的坐标.12.(2021•南山区校级三模)如图,已知抛物线y=ax2+bx+c(a≠0)与y轴相交于点C(0,﹣2),与x 轴分别交于点B(3,0)和点A,且tan∠CAO=1.(1)求抛物线解析式.(2)抛物线上是否存在一点Q,使得∠BAQ=∠ABC,若存在,请求出点Q坐标,若不存在,请说明理由;(3)抛物线的对称轴交x轴于点D,在y轴上是否存在一个点P,使PC+PD值最小,若存在,请求出最小值,若不存在,请说明理由.13.(2021•津南区一模)已知抛物线y=x2﹣2x+c交x轴于A,B两点,且点B的坐标为(3,0),其对称轴交x轴于点C.(Ⅰ)求该抛物线的顶点D的坐标;(Ⅱ)设P是线段CD上的一个动点(点P不与点C,D重合).①过点P作y轴的垂线l交抛物线(对称轴右侧)于点Q,连接QB,QD,求△QBD面积的最大值;②连接PB,求PD+PB的最小值.14.(2021•防城区模拟)如图,已知抛物线y=ax2﹣2ax﹣8a(a>0)与x轴从左至右依次交于A,B两点,与y轴交于点C,经过点B的直线y=﹣x+与抛物线的另一交点为D,且点D的横坐标为﹣5.(1)求抛物线的函数表达式;(2)若点P(x,y)在该二次函数的图象上,且S△BCD=S△ABP,求点P的坐标;(3)设F为线段BD上的一个动点(异于点B和D),连接AF.是否存在点F,使得2AF+DF的值最小?若存在,分别求出2AF+DF的最小值和点F的坐标,若不存在,请说明理由.15.(2021秋•沈北新区校级月考)如图,在平面直角坐标系中,点O为坐标原点,抛物线y=ax2﹣2x+c与x轴交于点A(1,0),点B(﹣3,0),与y轴交于点C,连接BC,点P在第二象限的抛物线上,连接PC、PO,线段PO交线段BC于点E.(1)求抛物线的表达式;(2)若△PCE的面积为S1,△OCE的面积为S2,当=时,求点P的坐标;(3)已知点C关于抛物线对称轴的对称点为点N,连接BN,点H在x轴上,当∠HCB=∠NBC时,①求满足条件的所有点H的坐标;②当点H在线段AB上时,平面内点M,且HM=1,直接写出AM+CM的最小值.16.(2021•香洲区校级三模)如图,抛物线y=﹣x2﹣6x+7交x轴于A,B两点(点A在点B左侧),交y轴于点C,直线y=x+7经过点A、C,点M是线段AC上的一动点(不与点A,C重合).(1)求A,B两点的坐标;(2)当点P,C关于抛物线的对称轴对称时,求PM+AM的最小值及此时点M的坐标;(3)连接BC,当△AOM与△ABC相似时,求出点M的坐标.17.(2021•涪城区校级模拟)已知:如图所示,抛物线y=﹣x2﹣x+c与x轴交于A、B两点,与y轴的正半轴交于点C,点A在点B的左侧,且满足tan∠CAB•tan∠CBA=1.(1)求A、B两点的坐标;(2)若点P是抛物线y=﹣x2﹣x+c上一点,且△P AC的内切圆的圆心正好落在x轴上,求点P的坐标;(3)若M为线段AO上任意一点,求MC+AM的最小值.18.(2021•青山区模拟)已知抛物线y=ax2﹣4ax﹣12a与x轴相交于A,B两点,与y轴交于C点,且OC =OA.设抛物线的顶点为M,对称轴交x轴于点N.(1)求抛物线的解析式;(2)如图1,点E(m,n)为抛物线上的一点,且0<m<6,连接AE,交对称轴于点P.点F为线段BC上一动点,连接EF,当P A=2PE时,求EF+BF的最小值.(3)如图2,过点M作MQ⊥CM,交x轴于点Q,将线段CQ向上平移t个单位长度,使得线段CQ与抛物线有两个交点,求t的取值范围.19.(2021•罗湖区校级模拟)已知抛物线y=ax2+bx(a,b为常数,a≠0)与x轴的正半轴交于点A,其顶点C的坐标为(2,4).(Ⅰ)求抛物线的解析式;(Ⅱ)点P是抛物线上位于直线AC上方的一个动点,求△P AC面积的最大值;(Ⅲ)点Q是抛物线对称轴上的一个动点,连接QA,求QC+QA的最小值.20.(2020•东胜区二模)如图,在平面直角坐标系中,二次函数y=ax2+bx+c的图象经过点A(﹣2,0),B (0,),C(1,0),其对称轴与x轴交于点E,顶点坐标为D.(1)求二次函数的表达式;(2)点P为抛物线的对称轴上的一个动点,且在第二象限内,若平面内存在点Q,使得以B,C,P,Q 为顶点的四边形为菱形,求点Q的坐标;(3)若M为y轴上的一个动点,连接ME,求MB+ME的最小值.。
最值问题之将军饮马一、模型精讲最小?基础模型:如图,在直线上找一点P使得PA+PB模型解析:作点A关于直线的对称点A',连接PA',则PA'=PA,所以PA+PB=PA'+模型变式:1.两定一动之点点周长最小.在OA、OB上分别取点M、N,使得△PMN2.两定两动之点点的周长最小。
在OA、OB上分别取点M、N使得四边形PMNQ3.一定两动之点线12在OA 、OB 上分别取M 、N 使得PM +MN最小。
此处M 点为折点,作点P 关于OA 对称的点P ',将折线段PM +MN 转化为P 'M +MN ,即过点P '作OB 垂线分别交OA 、OB 于点M 、N ,得PM +MN 最小值(点到直线的连线中,垂线段最短)二、针对训练一、单选题1如图,正方形ABCD 的边长为4,点M 在DC 上,且DM =1,N 是AC 上一动点,则DN +MN 的最小值为()A.4B.42C.25D.52如图所示,在△ABC 中,∠ABC =68°,BD 平分∠ABC ,P 为线段BD 上一动点,Q 为 边AB 上一动点,当AP +PQ 的值最小时,∠APB的度数是()A.118°B.125°C.136°D.124°3如图,Rt △ABC 中,∠C =90°,AC =4,BC =3,点P 为AC 边上的动点,过点P 作PD ⊥AB 于点D ,则PB +PD的最小值为() A.154 B.245 C.5 D.2034如图所示,已知A (1,y 1),B (2,y 2)为反比例函数y =2x图象上的两点,动点P (x ,0)在x 轴正半轴上运动,当线段3AP 与线段BP 之差达到最大值时,点P 的坐标是()A.(3,0)B.72,0C.53,0D.52,05如图,如图,⊙M 的半径为2,圆心M 的坐标为(3,4),点P 是⊙M 上的任意一点,PA ⊥PB ,PA ,PB 与x 轴分别交于A ,B 两点,若点A 、点B 关于原点O 对称,则AB 的最小值为()A.3B.4C.5D.66如图,等边△ABC 的边长为6,AD 是BC 边上的中线,M 是AD 上的动点,E 是边AC 上一点,若AE =2,则EM +CM的最小值为()A.26B.33C.27D.427如图,点M 是菱形ABCD 的边BC 的中点,P 为对角线BD 上的动点,若AB =2,∠A =120°,则PM +PC的最小值为()A.2B.3C.2D.18如图1,正方形ABCD 中,点E 是BC 的中点,点P 是对角线AC 上的一个动点,设AP =x ,PB +PE =y ,当点P 从A 向点C 运动时,y 与x 的函数关系如图2所示,其中点M 是函数图象的最低点,则点M 的坐标是()4A.42,35 B.22,35 C.35,22 D.35,429如图,E 为正方形ABCD 边AD 上一点,AE =1,DE =3,P 为对角线BD 上一个动点,则PA+PE 的最小值为()A.5B.42C.210D.1010如图,在矩形ABCD 中,AB =8,AD =4,点E 是矩形ABCD 内部一动点,且∠BEC =90°,点P 是AB 边上一动点,连接PD 、PE ,则PD+PE 的最小值为()A.8B.45C.10D.45-2二、填空题11如图,在△ABC 中,∠BAC =90°,AB =3,AC =4,EF 垂直平分BC ,点P 为直线EF 上任意一点,则AP +BP 的最小值是.12如图,在等边△ABC 中,BD ⊥AC 于D ,AD =3cm .点P ,Q 分别为AB ,AD 上的两个定点且BP =AQ =1cm ,点M 为线段BD 上一动点,连接PM ,QM ,则PM +QM 的最小值为cm .513如图,牧童在A 处,A 、B 处相距河岸的距离AC ,BD 的长分别为700m 和500m ,且C ,D 两地距离为500m ,天黑前牧童从A 处将牛牵到河边饮水,再赶回家,那么牧童最少要走.14如图,菱形草地ABCD 中,沿对角线修建60米和80米两条道路AC <BD ,M 、N 分别是草地边BC 、CD 的中点,在线段BD 上有一个流动饮水点P ,若要使PM +PN 的距离最短,则最短距离是米.15在平面直角坐标系中,点A 0,-3 ,点O 0,0 ,若有一点B 2a +1,-2a +2 ,当BA +BO 的值最小时,a =.16如图,直线y =x +4与x 轴,y 轴分别交于A 和B ,点C 、D 分别为线段AB 、OB 的中点,P 为OA 上一动点,当PC +PD的值最小时,点P 的坐标为.17如图,点P 是∠AOB 内任意一点,OP =3cm ,点M 和点N 分别是射线OA 和射线OB 上的动点,∠AOB =30°,则△PMN 周长的最小值是.618如图,在周长为12的菱形ABCD 中,DE =1,DF =2,若P 为对角线AC 上一动点,则EP +FP 的最小值为.19如图,在Rt △ABC 中,∠ACB =90°,AC =BC,点C 在直线MN 上,∠BCN =30°,点P 为MN 上一动点,连接AP ,BP .当AP +BP 的值最小时,∠CBP 的度数为度.20如图,抛物线y =x 2-4x +3与x 轴分别交于A ,B两点(点A 在点B 的左侧),与y 轴交于点C ,在其对称轴上有一动点M ,连接MA ,MC ,AC ,则△MAC 周长的最小值是.三、解答题21如图,抛物线y =x 2+bx +c 与x 轴交于A -1,0 ,B 3,0 两点.(1)求该抛物线的解析式;(2)观察函数图象,直接写出当x 取何值时,y >0?(3)设(1)题中的抛物线交y 轴于C 点,在该抛物线的对称轴上是否存在点Q ,使得△QAC 的周长最小?若存在,求出Q 点的坐标;若不存在,请说明理由.22教材呈现:下图是华师版八年级下册数学教材第111页的部分内容.7(1)问题解决:请结合图①,写出例1的完整解答过程.(2)问题探究:在菱形ABCD 中,对角线AC 、BD 相交于点O ,AB =4,∠BAD =2∠ABC .过点D 作DE ⎳AC 交BC 的延长线于点E .如图②,连结OE ,则OE 的长为.(3)如图③,若点P 是对角线BD 上的一个动点,连结PC 、PE ,则PC+PE 的最小值为.23在平面直角坐标系中,矩形OACB 的顶点O 在坐标原点,顶点A 、B 分别在x 轴、y 轴的正半轴上,A (3,0),B (0,4),D 为边OB 的中点.(1)若E 为边OA 上的一个动点,求△CDE 的周长最小值;(2)若E 、F 为边OA 上的两个动点,且EF =1,当四边形CDEF 的周长最小时,求点E 、F 的坐标.24如图,在Rt △ABC 中,∠ACB =90°,斜边AB =8,AB 经过原点O ,点C 在y 轴的正半轴上,AC 交x 轴于点D ,且CD :AD =4:3,反比例函数y =k x的图象经过A 、B 两点.(1)求反比例函数的解析式.(2)点P 为直线AC 上一动点,求BP +OP 的最小值.25如图,已知抛物线y =ax 2+bx -6与x 轴的交点A (-3,0),B (1,0),与y 轴的交点是点C .8(1)求抛物线的解析式;(2)点P 是抛物线对称轴上一点,当PB +PC 的值最小时,求点P 的坐标;(3)点M 在抛物线上运动,点N 在y 轴上运动,是否存在点M ,N ,使得∠CMN =90°且以点C ,M ,N 为顶点的三角形与△OAC 相似?若存在,求出点M 和点N 的坐标;若不存在,说明理由.26如图,直线l 1经过A 92,0、B 2,-5两点,直线l 2:y =-x +3与直线l 1交于点C ,与x 轴交于点D .(1)求点C 的坐标;(2)点P 是y 轴上一点,当四边形PDCB 的周长最小时,求四边形PDCB 的面积;(3)把直线l 1沿y 轴向上平移9个单位长度,得到新直线l 3与直线l 2交于点E ,试探究在x 轴上是否存在点Q ,在平面内存在点F 使得以点D ,Q ,E ,F 为顶点的四边形是菱形(含正方形)?若存在,直接写出符合条件的点Q 的坐标;若不存在,说明理由.27如图,已知一次函数y =kx +b 的图像经过A (1,4),B (4,1)两点,并且交x 轴于点C ,交y 轴于点D .(1)求该一次函数的表达式;(2)若y 轴存在一点P 使PA +PB 的值最小,求此时点P 的坐标及PA +PB 的最小值;(3)在x 轴上是否存在一点M ,使△MOA 的面积等于△AOB 的面积;若存在请直接写出点M 的坐标,若不存在请说明理由.28如图,在平面直角坐标系中,直线AB 分别与x 轴的负半轴、y 轴的正半轴交于A 、B 两点,其中OA =2,S △ABC =12,点C 在x 轴的正半轴上,且OC =OB .9(1)求直线AB 的解析式;(2)将直线AB 向下平移6个单位长度得到直线l 1,直线l 1与y 轴交于点E ,与直线CB 交于点D ,过点E 作y 轴的垂线l 2,若点P 为y 轴上一个动点,Q 为直线l 2上一个动点,求PD +PQ +DQ 的最小值;(3)若点M 为直线AB 上的一点,在y 轴上是否存在点N ,使以点A 、D 、M 、N 为顶点的四边形为平行四边形,若存在,请直接写出点N 的坐标;若不存在,请说明理由.29在Rt △ABC 中,AB =BC ,在Rt △CEH 中,∠CEH =45°,∠ECH =90°,连接AE.(1)如图1,若点E 在CB 延长线上,连接AH ,且AH =6,求AE 的长;(2)如图2,若点E 在AC 上,F 为AE 的中点,连接BF 、BH ,当BH =2BF ,∠EHB +12∠HBF =45°时,求证:AE =CE ;(3)如图3,若点E 在线段AC 上运动,取AE 的中点F ,作FH '∥BC 交AB 于H ,连接BE 并延长到D ,使得BE =DE ,连接AD 、CD ;在线段BC 上取一点G ,使得CG =AF ,并连接EG ;若点E 在线段AC 上运动的过程中,当ACD 的周长取得最小值时,△AED 的面积为25,请直接写出GE +BH ′的值.。
问题分析“费马点”指的是位于三角形内且到三角形三个顶点距高之和最短的点。
主要分为两种情况:(1)当三角形三个内角都小于120°的三角形.通常将某三角形绕点旋转60度.从而将“不等三爪图”中三条线段转化在同一条直线上.利用两点之间线段最短解决问题。
(2)当三角形有一个内角大于120°时.费马点就是此内角的顶点.费马点问题解题的核心技巧:旋转60° 构造等边三角形将“不等三爪图”中三条线段转化至同一直线上利用两点之间线段最短求解问题模型展示:如图.在△ABC内部找到一点P.使得PA+PB+PC的值最小.当点P满足△APB=△BPC=△CPA=120º.则PA+PB+PC的值最小.P点称为三角形的费马点.特别地.△ABC中.最大的角要小于120º.若最大的角大于或等于120º.此时费马点就是最大角的顶点A(这种情况一般不考.通常三角形的最大顶角都小于120°)费马点的性质:1.费马点到三角形三个顶点距离之和最小。
2.费马点连接三顶点所成的三夹角皆为120°。
最值解法:以△ABC任意一边为边向外作等边三角形.这条边所对两顶点的距离即为最小值。
证明过程:几何最值之费马点问题方法技巧将△APC 边以A 为顶点逆时针旋转60°.得到AQE.连接PQ.则△APQ 为等边三角形.PA=PQ 。
即PA+PB+PC=PQ+PB+PC.当B 、P 、Q 、E 四点共线时取得最小值BE【例1】如图.四边形 ABCD 是菱形.A B =6.且△ABC =60° .M 是菱形内任一点.连接AM .BM .CM .则AM +BM +CM 的最小值为________.【答案】63【详解】将△BMN 绕点B 顺时针旋转60度得到△BNE .△BM =BN .△MBN =△CBE =60°.△MN=BM△MC=NE△AM +MB +CM =AM +MN +NE .当A 、M 、N 、E 四点共线时取最小值AE .△AB =BC =BE =6.△ABH =△EBH =60°.△BH △AE .AH =EH .△BAH =30°.△BH =12AB =3.AH =3BH =33.△AE =2AH =63.故答案为63.题型精讲【例2】如图.四边形ABCD 是正方形.△ABE 是等边三角形.M 为对角线BD (不含B 点)上任意一点.将BM 绕点B 逆时针旋转60°得到BN.连接EN 、AM 、CM.(1)求证:△AMB△△ENB ;(2)△当M 点在何处时.AM +CM 的值最小; △当M 点在何处时.AM +BM +CM 的值最小.并说明理由;(3)当AM +BM +CM 的最小值为13 时.求正方形的边长.【答案】(1)△AMB△△ENB.证明略。
专题08 二次函数背景下面积最值问题【典型例题】——铅垂高类最值问题
如图,已知抛物线过A(4,0)、B(0,4)、C(-2,0)三点,P是抛物线上一点(1)求抛物线解析式
(2)若P在直线AB上方,求四边形PBCA面积最大值,
(3)若P在直线AB上方,作PF⊥AB,F在线段AB上,求PF最大值x
x
(4)若P在直线AB上方,作PF⊥AB,交线段AB于F,作PE∥y轴交AB于E,求△PEF周长和面积的最大值
(5)若P在直线AB上方,连接OP,交AB于D,求PD
OD
的最大值
x
x
(6) 若P 在直线AB 上方,连接CP ,交AB 于D ,△PDA 面积为S 1,△CDA 面积为S 2,求2
1
S S 的最小
值
(7) 点D 是点B 关于关于x 轴的对称点,连接CD ,点P 是第一象限上一点,求△PCD 面积最大值
【模型解读】——铅垂高
x
x。
最值模型之胡不归模型胡不归模型可看作将军饮马衍生,主要考查转化与化归等的数学思想,近年在中考数学和各地的模拟考中常以压轴题的形式考查,学生不易把握。
本专题就最值模型中的胡不归问题进行梳理及对应试题分析,方便掌握。
在解决胡不归问题主要依据是:点到线的距离垂线段最短。
【模型背景】从前有个少年外出求学,某天不幸得知老父亲病危的消息,便立即赶路回家.根据“两点之间线段最短”,虽然从他此刻位置A 到家B 之间是一片砂石地,但他义无反顾踏上归途,当赶到家时,老人刚咽了气,小伙子追悔莫及失声痛哭.邻居告诉小伙子说,老人弥留之际不断念叨着“胡不归?胡不归?”看到这里很多人都会有一个疑问,少年究竟能不能提前到家呢?假设可以提早到家,那么他该选择怎样的一条路线呢?这就是今天要讲的“胡不归”问题.知识储备:在直角三角形中锐角A 的对边与斜边的比叫做∠A 的正弦,记作sin A ,即sin A =∠A 的对边斜边。
【模型解读】一动点P 在直线MN 外的运动速度为V 1,在直线MN 上运动的速度为V 2,且V 1<V 2,A 、B 为定点,点C 在直线MN 上,确定点C 的位置使AC V 2+BC V 1的值最小.(注意与阿氏圆模型的区分)1)AC V 2+BC V 1=1V 1BC +V 1V 2AC,记k =V 1V 2,即求BC +kAC 的最小值.2)构造射线AD 使得sin ∠DAN =k ,CH AC=k ,CH =kAC ,将问题转化为求BC +CH 最小值.3)过B 点作BH ⊥AD 交MN 于点C ,交AD 于H 点,此时BC +CH 取到最小值,即BC +kAC 最小.【解题关键】在求形如“PA+kPB”的式子的最值问题中,关键是构造与kPB相等的线段,将“PA+kPB”型问题转化为“PA+PC”型.(若k>1,则提取系数,转化为小于1的形式解决即可)。
【最值原理】两点之间线段最短及垂线段最短。
最值问题4-“AP+k•PB”最小值(胡不归型)胡不归型(“AP+k•PB”型)(2)如图,P 为正方形ABCD 对角线BD 上一动点,若AB=2,则AP+BP+CP 的最小值.作图、2.如图,抛物线y=﹣x2+x+6交x轴于A、B两点,点A在点B的右侧,交y轴于点C,点D为顶点.(1)求点A、D的坐标;(2)若点P是抛物线上位于第一象限内对称轴右侧的一个动点,当S△ABP=45时,在线段AC上有一动点Q,当PQ+QA的值最小时,求Q的坐标和PQ+QA的最小值;3. 如图1,在平面直角坐标系中,抛物线y=x2﹣x﹣与x轴交于A、B、两点(点A在点B的左侧),与y轴交于点C.(1)判断△ABC形状,并说明理由.(2)在抛物线第四象限上有一点,它关于x轴的对称点记为点P,点M是直线BC上的一动点,当△PBC的面积最大时,求PM+MC的最小值;4.如图,抛物线y=ax2+bx+c交x轴于点A、B两点,点A在点B的右侧,交y轴于点C,它顶点的横坐标为,直线AC的解析式为y=﹣+3.(1)求抛物线的解析式;(2)若点P是抛物线上位于第一象限内对称轴右侧的一个动点,当S△ABP=5时,在线段AC上有动点Q,当PQ+QC的值最小时,求PQ+QC的最小值.5.如图,抛物线y=ax2+bx+c(a≠0)与x轴交于点A(﹣1,0)和点B,与y轴交于点C,点C关于抛物线对称轴的对称点为点D,抛物线顶点为H(1,2).(1)求抛物线的解析式;(2)点P为直线AD上方抛物线的对称轴上一动点,连接P A,PD.当S△P AD=3,若在x 轴上存在一动点Q,使PQ+QB最小,求此时点Q的坐标及PQ+QB的最小值.6. 如图,抛物线y=﹣x2+x+3 与x 轴交于点A,点B,与y 轴交于点C,点D 与点C关于x 轴对称,点P 是x 轴上的一个动点,设点P 的坐标为(m,0),过点P 作x 轴的垂线l 交抛物线于点Q.(1)求直线BD的解析式;(2)当点P在线段OB上运动时,直线l 交BD 于点M,当△DQB面积最大时,在x轴上找一点E,使QE+EB的值最小,求E的坐标和最小值.7. 如图1,二次函数y=x2﹣2x+1的图象与一次函数y=kx+b(k≠0)的图象交于A,B两点,点A的坐标为(0,1),点B在第一象限内,点C是二次函数图象的顶点,点M是一次函数y=kx+b(k≠0)的图象与x轴的交点,过点B作x轴的垂线,垂足为N,且S△AMO:S四边形AONB=1:48.(1)求直线AB和直线BC的解析式;(2)点P是线段AB上一点,点D是线段BC上一点,PD∥x轴,射线PD与抛物线交于点G,过点P作PE⊥x轴于点E,PF⊥BC于点F.当PF与PE的乘积最大时,在线段AB上找一点H(不与点A,点B重合),使GH+BH的值最小,求点H的坐标和GH+BH的最小值.8. 如图,在平面直角坐标系中,点A在抛物线y=﹣x2+4x上,且横坐标为1,点B与点A 关于抛物线的对称轴对称,直线AB与y轴交于点C,点D为抛物线的顶点,点E的坐标为(1,1).(1)求线段AB的长;(2)点P为线段AB上方抛物线上的任意一点,过点P作AB的垂线交AB于点H,点F 为y轴上一点,当△PBE的面积最大时,求PH+HF+FO的最小值.9. 如图1,抛物线y=﹣x2+x+2的图象与x轴交于点A、B,与y轴交于点C,连接BC,过点A作AD∥BC交抛物线的对称轴于点D.(1)求点D的坐标;(2)如图2,点P是抛物线在第一象限内的一点,作PQ⊥BC于Q,当PQ的长度最大时,在线段BC上找一点M(不与点B、点C重合),使PM+BM的值最小,求点M的坐标及PM+BM的最小值.10. 如图1,抛物线y=﹣x2+x+2与x轴交于A,B两点(点A在点B左侧),与y轴交于点C,连结BC.(1)求直线BC的解析式;(2)如图2,点D是CB上方抛物线上一动点,连结DC,DB,过点A作CB的平行线,交对称轴于点E,交DB的延长线于点F,连接CF,当△CDF的面积最大时,在对称轴上找一点R,使得DR+RE的值最小,求出此时点R的坐标;11. 如图1,抛物线y=﹣x2﹣x+3与x轴交于A、B两点(点A在点B的右侧),交y轴于点C,点D的坐标为(0,﹣1),直线AD交抛物线于另一点E,点P是第二象限抛物线上的一点,作PQ∥y轴交直线AE于Q,作PG⊥AD于G,交x轴于点H(1)求线段DE的长;(2)设d=PQ﹣PH,当d的值最大时,在直线AD上找一点K,使PK+EK的值最小,求出点K的坐标和PK+EK的最小值;12.如图,顶点为D的抛物线y=﹣x2+x+4与y轴交于点A,与x轴交于两点B、C(点B在点C的左边),点A与点E关于抛物线的对称轴对称,点B、E在直线y=kx+b(k,b为常数)上.(1)求k,b的值;(2)点P为直线AE上方抛物线上的任意一点,过点P作AE的垂线交AE于点F,点G为y轴上任意一点,当△PBE的面积最大时,求PF+FG+OG的最小值.13.如图①,在平面直角坐标系中,抛物线y=ax2+bx+4与x轴交于A,B两点(点A在点B左侧),与y轴交于点C,抛物线的顶点为点D,且3OC=4OB,对称轴为直线x=,点,连接CE交对称轴于点F,连接AF交抛物线于点G.(1)求抛物线的解析式和直线CE的解析式;(2)如图②,过E作EP⊥x轴交抛物线于点P,点Q是线段BC上一动点,当QG+QB 最小时,线段MN在线段CE上移动,点M在点N上方,且MN=,请求出四边形PQMN周长最小时点N的横坐标;14.如图1,在平面直角坐标系中,抛物线y=﹣x2+x+与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,对称轴与x轴交于点D.(1)求直线BC的解析式;(2)如图2,点P为直线BC上方抛物线上一点,连接PB、PC.当△PBC的面积最大时,在线段BC上找一点E(不与B、C重合),使PE+BE的值最小,求PE+BE的最小值和点P的坐标.15.如图,在平面直角坐标系中,抛物线y=﹣x﹣3交x轴于A,B两点(点A在点B的左侧),交y轴于点C.(1)求直线AC的解析式;(2)点P是直线AC上方抛物线上的一动点(不与点A,点C重合),过点P作PD⊥AC于点D,当线段PD的长度最大时,点Q从点P出发,先以每秒一个单位的速度沿适当的路径运动到y轴上的点M处,再沿MC以每秒个单位的速度运动到点C停止.当点Q在整个运动中用时最少时,求点M的坐标.16.如图1,抛物线y=﹣x2﹣x+3与x轴交于A、B两点(点A在点B的右侧),交y轴于点C,点D的坐标为(0,﹣1),直线AD交抛物线于另一点E,点P是第二象限抛物线上的一点,作PQ∥y轴交直线AE于Q,作PG⊥AD于G,交x轴于点H(1)求线段DE的长;(2)设d=PQ﹣PH,当d的值最大时,在直线AD上找一点K,使PK+EK的值最小,求出点K的坐标和PK+EK的最小值;。
中考数学几何最值问题解法在平面几何的动态问题中,当某几何元素在给定条件变动时,求某几何量(如线段的长度、图形的周 长或面积、角的度数以及它们的和与差)的最大值或最小值问题,称为最值问题。
解决平面几何最值问题的常用的方法有: (1)应用两点间线段最短的公理 求最值;( 2)应用垂线段最短的性质求最值; ( 3)应用轴对称的性质求最值;5)应用其它知识求最值。
下面通过近年全国各地中考的实例探讨其解法。
应用两点间线段最短的公理(含应用三角形的三边关系)求最值例 4. 在△ABC 中,AB =5,AC =3,AD 是 BC 边上的中线,则 AD 的取值范围是练习题:1. 如图,长方体的底面边长分别为 2cm 和 4cm ,高为 5cm . 若一只蚂蚁从 P 点开始经 过 4 个侧面爬行一圈到达 Q 点,则蚂蚁爬行的最短路径长为【 】2. 如图,圆柱的底面周长为 6cm , AC 是底面圆的直径,高 BC=6cm ,点 P 是母线 BC 上一2点,且 PC= BC .一只蚂蚁从 A 点出发沿着圆柱体的表面爬行到点P 的最短距离是 【 】3含应用三角形的三边关系) 4)应用二次函数求最值; 典型例题:例 1. 如图,∠ MON=9°0 ,矩形 ABCD 的顶点 A 、 B 分别在边 OM , 运动时, A 随之在边 OM 上运动, 矩形 ABCD 的形状保持不变,其中 程中,点 D 到点 O 的最大距离为B . 5C . 145 55D .例 2. 在锐角三角形 ABC 中, BC=4 2 ,∠ ABC=45°, BD 平分∠ ABC , M 、 N 分别是BC 上的动点,则 CM+MN 的最小值是例 3. 如图, 圆柱底面半径为 2cm ,高为 9 cm ,点 上的点,且 A 、B 在同一母线上,用一棉线从 A 顺着圆柱侧面绕 3 圈到 B ,求棉线 最短为cm 。
A.13cmB.12cmC.10cmD.8cmON 上,当 B 在边 ON上AB=2,BC=1,运动过A 、B 分别是圆柱两底面圆周的最小值为【 】 A . 1B . 3C . 2D . 3 + 1例 3. 已知梯形 ABCD , AD ∥ BC , AB ⊥ BC ,等,为什么?问题 2:如图 2,若 P 为 AB 边上一点,以 PD , PC 为边作平行四边形小值?如果存在,请求出最小值,如果不存在,请说明理由.问题 3:若 P 为 AB 边上任意一点,延长 PD 到 E ,使 DE =PD ,再以 PE , PC 为边作平行四边形 PCQE ,请探 究对角线 PQ 的长是否也存在最小值?如果存在,请求出最小值,如果不存在,请说明理由.问题 4:如图 3,若 P 为 DC 边上任意一点,延长 PA 到 E ,使 AE =nPA (n 为常数),以 PE 、PB 为边作平行四边形 PBQE ,请探究对角线 PQ 的长是否也存在最小值?如果存在,请求出最小值,如果不存在,请说明理A 、 (4 ㎝B 、 5cmC 、35 ㎝ D 、 7cm3. 如图所示,在边长为 2 的正三角形 ABC 中, E 、 F 、 G 分别为 AB 、 点 P 为线段 EF 上一个动点, 连接 BP 、GP ,则△ BPG 的周长的最小值是 二、应用垂线段最短的性质求最值:典型例题: 例 1. 在△ABC 中,AB = AC =5,BC =6.若点 P 在边 AC 上移动,则 例 2. 如图,菱形 ABCD 中, AB=2,∠ A=120°,点P ,Q ,K 分别为线段 BC ,CD ,BD 上的任 意一点,则 PK+QKAD =1,AB =2,BC =3, 问题 1:如图 1,P 为 AB 边上的一点,以 PD , PC 为边作平行四边形 PQ ,DC 的长能否相PCQD ,请问对角线 PQ 的长是否存在最 PCQD ,请问对角线由.AB=8cm ,AD=6cm ,按下列步骤进行裁剪和拼图:第一步: 如图①,在线段 AD 上任意取一点 E ,沿 EB ,EC 剪下一个三角形纸片 EBC (余下部分不再使用 ) ; 第二步:如图②,沿三角形 EBC 的中位线 GH 将纸片剪成两部分,并在线段 GH 上任意取一点 M ,线段BC 上任意取一点 N ,沿 MN 将梯形纸片 GBCH 剪成两部分;第三步:如图③,将 MN 左侧纸片绕 G 点按顺时针方向旋转 180°,使线段 GB 与 GE 重合,将 MN 右侧 纸片绕 H 点按逆时针方向旋转 180°,使线段 HC 与 HE 重合,拼成一个与三角形纸片 EBC 面积相等的四边 形纸片. ( 注:裁剪和拼图过程均无缝且不重叠 )例 4. 如图,点 A 的坐标为( -1 ,0),点 B 在直线 y x 上运动,当线段 AB 最短时,点 B 的坐标为【】A. (0,0)1 1 B.(,)22EF .在此运动变化的过程中,有下列结论:① △DFE 是等腰直角三角形; ② 四边形 CEDF 不可能为正方形;③ 四边形 CEDF 的面积随点 E 位置的改变而发生变化; ④ 点 C 到线段 EF 的最大距离为 . 其中正确结论的个数是【 】A .1个B .2个C .3 个D .4 个B. C. ( 2, 2222)D.222)例 5. 如图,在△ ABC 中, ∠ C=90°,在 AC 、 BC 边上运动(点 E 不与点 A 、C 重合),且保持 AE=CF ,连接AC=BC=,4 D 是 AB 的中点,点 E 、F 分别 DE 、DF 、例 6. 如图,则拼成的这个四边形纸片的周长的最小值为cm ,最大值为cm例7. 如图,在△ ABC中,∠ C=90°,AC=BC=,4 D是AB的中点,点E、F 分别在AC、BC边上运动(点E不与点A、C重合),且保持AE=CF,连接DE、DF、EF.在此运动变化的过程中,有下列结论:①△DFE是等腰直角三角形;②四边形CEDF不可能为正方形;③四边形CEDF的面积随点 E 位置的改变而发生变化;④点 C 到线段EF的最大距离为.其中正确结论的个数是【】例8. 如图,△ ABC中,∠ BAC=60°,∠ ABC=45°,AB=2 2 ,D 是线段BC上的一个动点,以AD为直径画⊙O分别交AB,AC于E,F,连接EF,则线段EF长度的最小值为例9. 如图所示,在菱形ABCD中,AB=4,∠BAD=12°0 ,△AEF为正三角形,点E、F 分别在菱形的边BC.CD 上滑动,且E、F 不与B.C.D重合.(1)证明不论E、F 在BC.CD上如何滑动,总有BE=CF;(2)当点E、F 在BC.CD上滑动时,分别探讨四边形AECF和△CEF的面积是否发生变化?如果不变,求出这个定值;如果变化,求出最大(或最小)值.例10.在锐角△ ABC中,AB=4,BC=5,∠ACB=45°,将△ AB C绕点B按逆时针方向旋转,得到△A 1BC1.(1)如图1,当点C1在线段CA的延长线上时,求∠ CC 1A1的度数;(2)如图2,连接AA1,CC1.若△ ABA1的面积为4,求△ CBC1的面积;(3)如图3,点E为线段AB中点,点P是线段AC上的动点,在△ ABC 绕点B按逆时针方向旋转过程中,点P 的对应点是点P1,求线段EP1 长度的最大值与最小值.例11. 如图,在△ ABC 中,点D、 E 分别在边BC、AC上,连接AD、DE,且∠ 1=∠B=∠C.(1)由题设条件,请写出三个正确结论:(要求不再添加其他字母和辅助线,找结论过程中添加的字母和辅助线不能出现在结论中,不必证明)答:结论一:;结论二:;结论三:.(2)若∠ B=45°,BC=2,当点D在BC上运动时(点D不与B、C重合),①求CE的最大值;②若△ ADE是等腰三角形,求此时BD的长.(注意:在第(2)的求解过程中,若有运用(1)中得出的结论,须加以证明)练习题:1. 如图,OP平分∠ MON,PA⊥ON于点A,点Q是射线OM上的一个动点,若PA=2,则PQ的最小值为【】A、1B、 2 C 、3 D、42. 如图,等腰梯形ABCD中,AD∥BC,AD=AB=CD=,2∠ C=60°,M是BC的中点.(1)求证:△ MDC是等边三角形;(2)将△ MDC绕点M旋转,当MD(即MD′)与AB交于一点E,MC(即MC′)同时与AD交于一点 F 时,点E,F和点 A 构成△ AEF.试探究△AEF 的周长是否存在最小值.如果不存在,请说明理由;如果存在,请计算出△ AEF 周长的最小值.3. 如图,⊙O 的半径为2,点O到直线l 的距离为3,点P是直线l 上的一个动点,PQ切⊙O 于点Q,则PQ的最小值为【】4. 如图,在四边形ABCD中,∠A=90°,AD=4,连接BD,BD⊥ CD,∠ADB=∠C.若P 是BC边上一动点,则DP长的最小值为.5. 如图,在Rt△ABC中,∠C=90°,AB=10cm,AC:BC=4:3,点P 从点A出发沿AB方向向点 B 运动,速度为1cm/s ,同时点Q从点B出发沿B→C→A方向向点 A 运动,速度为2cm/s,当一个运动点到达终点时,另一个运动点也随之停止运动.1)求AC、BC的长;2A.13 B .5 C .3 D . 2(2)设点P 的运动时间为x (秒),△ PBQ的面积为y (cm2),当△ PBQ存在时,求y 与x 的函数关系式,并写出自变量x 的取值范围;(3)当点Q在CA上运动,使PQ⊥AB 时,以点B、P、Q为定点的三角形与△ ABC 是否相似,请说明理由;4)当x=5 秒时,在直线PQ上是否存在一点M,使△ BCM得周长最小,若存在,求出最小周长,若不存在,请说明理由.、应用轴对称的性质求最值:典型例题:例 1. ( 2012山东青岛 3 分)如图,圆柱形玻璃杯高为12cm、底面周长为18cm,在杯内离杯底4cm的点C 处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿4cm与蜂蜜相对的点 A 处,则蚂蚁到达蜂蜜的最短距离为cm例 2. 如图,四边形ABCD中,∠ BAD=120°,∠ B=∠D=90°,在BC、CD上分别找一点M、N,使△ AMN周长最小时,则∠ AMN+∠ANM 的度数为【】A.130° B .120° C .110° D .100°例 3. 点A、B均在由面积为1 的相同小矩形组成的网格的格点上,建立平面直角坐标系如图所示.若P是x轴上使得PA PB的值最大的点,上使得QA十QB的值最小的点,则OP OQ =例 4. 如图,正方形ABCD中,AB=4,E是BC的中点,点P 是对角线AC上一动点,则PE+PB的最小值为.例 5. 如图,MN为⊙O的直径,A、B是O上的两点,过 A 作AC⊥MN于点C,过B 作BD⊥MN于点D,P为DC上的任意一点,若MN=20,AC=8,BD=6,则PA +PB的最小值是。