综合探究题专题

初二生物实验探究综合题汇编经典及答案一、实验探究综合题1．鸟的全身都是为了飞行而设计的，我们可以从以下几点看出来：（1）鸟的体形呈流线型，能减少飞行时的______。

（2）鸟的体表被覆羽毛，前肢变成______，因而具有迅速飞翔的能力。

（3）鸟的骨骼薄而轻，长骨中空，这减轻了______。

（4）鸟用______呼吸，身体内还有______来辅助呼吸。

（5）鸟类的生活习性不同，形态结构也常常不同，如鸟的生活习性常常与趾的形态相适应。

如图为几种鸟趾的形态，请据图分析问题：家燕的趾如图中①所示，适于在地面行走；鹰以小动物为食，趾强健有力且特别锋利，它的趾应如图[__]所示；啄木鸟善于攀援，用爪抓握树干，用细长的喙啄食害虫，它的趾应如图[___]所示；鸭善于游泳，常在水面活动，取食水底的小动物，它的趾应如图[_]所示；图[___]所示为鸵鸟的趾，它适于在沙地中飞奔。

答案：阻力翼体重肺气囊② ③ ⑤ ④【分析】本题考查的是鸟类的主要特征，首先明确的是鸟类的形态结构特征是和飞行生活相适应的。

【解析：阻力翼体重肺气囊② ③ ⑤ ④【分析】本题考查的是鸟类的主要特征，首先明确的是鸟类的形态结构特征是和飞行生活相适应的。

【详解】（1）鸟的体形呈流线型，能减少飞行时的阻力。

（2）鸟的体表被覆羽毛，前肢变成翼，因而具有迅速飞翔的能力。

（3）鸟的骨骼薄而轻，长骨中空，减轻体重，利于飞行。

（4）鸟用肺呼吸，身体内还有气囊来辅助呼吸。

鸟类在飞行时，需要消耗很多的能量，鸟类有气囊，与肺相通，主要功能是贮存空气，使鸟类每呼吸一次，在肺内进行两次气体交换，这种现象称为双重呼吸。

双重呼吸是鸟类适应飞行生活的一种呼吸方式，提高了气体交换的效率，为飞行提供充足的氧气，才能分解更多的有机物，释放出较多的能量，满足飞行的需要。

（5）家燕的趾如图中①所示，适于在地面行走；②为老鹰的足锐利、具有钩爪，适于捕捉小动物；③为啄木鸟的足两只朝前，两只朝后，便于抓握树干，能抓握和钩挂在树上，适于攀援在树上；④为鸵鸟的足，趾短粗有力，适于奔走；⑤为野鸭的足趾间有蹼，适于在水中游泳。

八年级上册生物实验探究综合题测试卷附答案一、实验探究综合题1．图为蝗虫的外部形态示意图。

（1）根据动物体内有无脊柱分类，蝗虫属于_______________动物。

（2）蝗虫身体的三个部分中，[_____] (填序号)是蝗虫的运动中心；（3）蝗虫适应陆地生活的特点是身体表面有一层坚韧的___________，虽然会限制身体的发育和长大，但能保护体内柔软器官并防止体内____________蒸发（或散失）的作用；（4）蝗虫的体表有与呼吸有关的结构是____________。

答案：（1）无脊椎（2）⑪（3）外骨骼水分（4）气门【分析】蝗虫是无脊椎动物中的节肢动物，图中①复眼，②单眼，③触角，④口器，⑤前足，⑥中足，⑦后足，⑧气门，⑨翅，⑩腹解析：（1）无脊椎（2）⑪（3）外骨骼水分（4）气门【分析】蝗虫是无脊椎动物中的节肢动物，图中①复眼，②单眼，③触角，④口器，⑤前足，⑥中足，⑦后足，⑧气门，⑨翅，⑩腹部，⑪胸部，⑫头部，据此解答。

（1）蝗虫的体内无脊柱，身体有许多体节构成，并且分部，体表有外骨骼，可以起到保护和支持，以及减少体内水分的散失的作用，触角和足也分节，所以属于无脊椎动物中的节肢动物。

（2）由图中可以看出，蝗虫的身体分为三部分：①头部、②胸部、③腹部，其中头部有触角、胸部有足和翅、腹部有气门，因此蝗虫的⑪胸部是运动中心。

（3）蝗虫的体表具有外骨骼，坚韧的外骨骼既保护和支持了内部结构，又能有效的防止体内水分的蒸发，这是节肢动物适应干旱陆地生活的重要原因。

（4）在蝗虫胸腹部的左右两侧有一些小孔是气门，为气体进出蝗虫体内的门户，与呼吸有关。

2．下图是我们生活中常见的几种动物，请分析回答。

（1）图示动物中，不能较好地在陆地干燥环境中生活的有___________、___________（用图中字母表示），原因是___________。

（2）B、C俩类动物在发育方面的共同特征为___________。

一、中考初中化学科学探究题1．某化学实验兴趣小组为了测定某纯碱样品（只含有Na2CO3、NaCl）中Na2CO3的质量分数。

取5g样品，往其中加入一定质量的稀盐酸，产生气体的质量与所加稀盐酸的质量变化如图，试计算：（1）其产生______g二氧化碳。

（2）该纯碱样品中Na2CO3的质量分数。

（3）求恰好完全反应时所得溶液的质量分数？【答案】（1）1.76；（2）84.8%；（3）10%【解析】（1）根据图中提供的信息可知，产生的二氧化碳为1.76g；设混合物中碳酸钠的质量为X，生成氯化钠的质量为YNa2CO3+2HCl==2NaCl+H2O+CO2↑106 117 44X y 1.76g106/44=X/1.76g 117/44=y/1.76gX=4.24g y=4.68g（2）碳酸钠的质量分数为：4.24g/5g×100%=84.8%（3）溶液中氯化钠的质量为：4.68g+（5g-4.24=5.44g溶液的质量为：51.16g+5g-1.76g=54.4g恰好完全反应时所得溶液的质量分数为：=5.44g/54.4g×100%=10%2．小东、小林和小雨同学对氢氧化钠溶液使酚酞溶液变红的现象很感兴趣，决定做实验进行探究：氢氧化钠溶液中到底是哪一种粒子使酚酞溶液变红？实验中可供使用的用品有盐酸、氯化钠溶液、氯化钙溶液、氢氧化钠溶液、碳酸钠溶液、酚酞溶液及若干支试管。

（提出假设）假设（1）：使酚酞溶液变红的是H2O。

假设（2）：使酚酞溶液变红的是Na+。

假设（3）：使酚酞溶液变红的是________。

小东认为不做实验即可说明假设（1）不成立，原因是 ___________________。

（实验验证）（完成下列实验操作、实验现象及实验结论）实验步骤实验操作实验现象实验结论小雨认为向实验步骤（1）后的试管中加入盐酸也可得出正确结论，你同意她的观点吗？_________（填“同意”或“不同意”）。

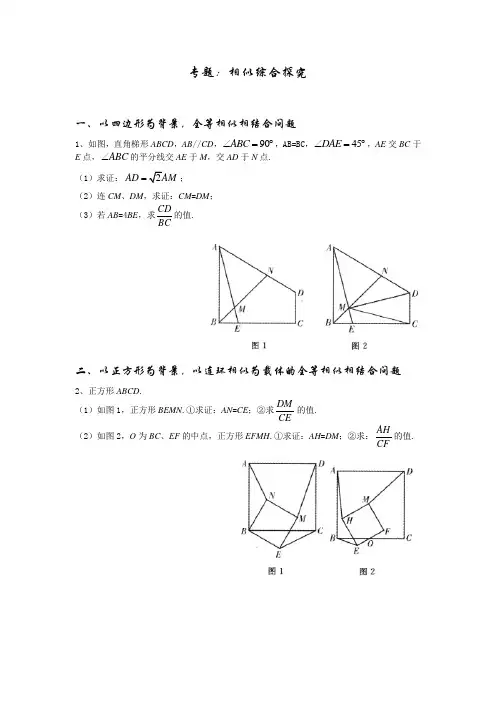
专题：相似综合探究一、以四边形为背景，全等相似相结合问题1、如图，直角梯形ABCD ，AB //CD ，90ABC ∠=︒，AB=BC ，45DAE ∠=︒，AE 交BC 于E 点，ABC ∠的平分线交AE 于M ，交AD 于N 点. （1）求证：2AD AM =；（2）连CM 、DM ，求证：CM =DM ； （3）若AB =4BE ，求CDBC的值.二、以正方形为背景，以连环相似为载体的全等相似相结合问题2、正方形ABCD .（1）如图1，正方形BEMN .①求证：AN =CE ；②求DMCE的值. （2）如图2，O 为BC 、EF 的中点，正方形EFMH .①求证：AH =DM ；②求：AHCF的值.3、如图，正方形ABCD ，点F 在CD 上，连AF 交BC 的延长线于E 点. （1）求证：2AD BE DF =⋅；（2）如图2，O 点为正方形对角线的交点，连OF ，求证：DOF BED ∠=∠； （3）若AB =6，DF =2CF ，延长OF 交DE 于M ，则OM 长为多少？三、以三角形为背景，以比例置换为载体的几何综合问题4、如图，等腰直角△BCD ，90BDC ∠=︒，E 为CD 的中点，DF ⊥BE 于F ，连CF 交BD 于H .（1）求证：2DE EF EB =⋅； （2）求DHBH； （3）过B 点作BG ⊥BC 交CH 的延长线于G 点，求证：BC =2BG .四、以三角形为背景，以连环相似为载体的全等相似相结合问题5、如图1，正△ABC ，D 、E 分别在BC 、AC 上，若CD =AE . （1）求证：△ABE ≌△CAD ；（2）如图2，连DE 、CF ，求证：ADE ACF ∠=∠；（3）如图3，①过E 点作EG //CF 交AD 于G 点，求证：BF =DG ；②若15ABE ∠=︒，求AFDF.。

2023年高三化二轮复习——化学反应原理综合题型探究专题训练知识梳理化学反应原理主要考查热化学、电化学、化学反应速率和化学平衡等主干理论知识，主要命题点有盖斯定律的应用、反应速率和化学平衡的分析、化学平衡常数的表达式书写与计算、反应条件的分析选择、生产生活中的实际应用等，试题常以填空、读图、作图、计算等形式呈现。

试题一般以与生产、生活紧密联系的物质为背景材料命制组合题，各小题之间又有一定的独立性。

主要考查学生的信息处理能力、学科内综合分析能力，应用反应原理解决生产实际中的具体问题，体现了“变化观念与平衡思想”的核心素养。

在近几年的相关考题中，对单一因素影响的考查已经越来越少了，主要以“多因素影响”出现，考查考生的综合分析判断能力。

以实际情景(场景)为背景，更能体现核心素养的要求。

而在实际生产过程中，影响因素是多元化、多方位和多层次的。

强化训练1．(2022·湖北，19)自发热材料在生活中的应用日益广泛。

某实验小组为探究“CaO—Al—H 2O ”体系的发热原理，在隔热装置中进行了下表中的五组实验，测得相应实验体系的温度升高值(ΔT )随时间(t )的变化曲线，如图所示。

回答下列问题： (1)已知： ①CaO(s)＋H 2O(l)Ca(OH)2(s) ΔH 1＝－65.17 kJ·mol －1 ②Ca(OH)2(s)Ca 2＋(aq)＋2OH －(aq) ΔH 2＝－16.73 kJ·mol －1③Al(s)＋OH －(aq)＋3H 2O(l)[Al(OH)4]－(aq)＋32H 2(g) ΔH 3＝－415.0 kJ·mol －1则CaO(s)＋2Al(s)＋7H 2O(l)===Ca 2＋(aq)＋2[Al(OH)4]－(aq)＋3H 2(g)的ΔH 4＝_______kJ·mol －1。

(2)温度为T时，K sp[Ca(OH)2]＝x，则Ca(OH)2饱和溶液中c(OH－)＝__________(用含x的代数式表示)。

题型十一综合探究题类型四与旋转有关的探究题（专题训练）D为BC的中点，E，F分1.(2022·重庆市B卷)在△ABC中，∠BAC=90°，AB=AC=别为AC，AD上任意一点，连接EF，将线段EF绕点E顺时针旋转90°得到线段EG，连接FG，AG．(1)如图1，点E与点C重合，且GF的延长线过点B，若点P为FG的中点，连接PD，求PD的长；(2)如图2，EF的延长线交AB于点M，点N在AC上，∠AGN=∠AEG且GN=MF，求证：AM+AF=；(3)如图3，F为线段AD上一动点，E为AC的中点，连接BE，H为直线BC上一动点，连接EH，将△BEH沿EH翻折至△ABC所在平面内，得到△B′EH，连接B′G，直接写出线段B′G的长度的最小值．【答案】(1)解：如图1，连接CP，由旋转知，CF=CG，∠FCG=90°，∴△FCG为等腰直角三角形，∵点P是FG的中点，∴CP⊥FG，∵点D是BC的中点，BC，∴DP=12在Rt△ABC中，AB=AC==4，∴BC=∴DP=2；(2)证明：如图2，过点E作EH⊥AE交AD的延长线于H，∴∠AEH=90°，由旋转知，EG=EF，∠FEG=90°，∴∠FEG=∠AEH，∴∠AEG=∠HEF，∵AB=AC，点D是BC的中点，∴∠BAD=∠CAD=1∠BAC=45°，2∴∠H=90°―∠CAD=45°=∠CAD，∴AE=HE，∴△EGA≌△EFH(SAS)，∴AG=FH，∠EAG=∠H=45°，∴∠EAG=∠BAD=45°，∵∠AMF=180°―∠BAD―∠AFM=135°―∠AFM，∵∠AFM=∠EFH，∴∠AMF=135°―∠EFH，∵∠HEF=180°―∠EFH―∠H=135°―∠EFH，∴∠AMF=∠HEF，∵△EGA≌△EFH，∴∠AEG=∠HEF，∵∠AGN=∠AEG，∴∠AGN=∠HEF，∴∠AGN=∠AMF，∵GN=MF，∴△AGN≌△AMF(AAS)，∴AG=AM，∵AG=FH，∴AM=FH，∴AF +AM =AF +FH =AH；(3)解：∵点E 是AC 的中点，∴AE =12AC 根据勾股定理得，BE ==由折叠直，BE =B′E∴点B′是以点E由旋转知，EF =EG ，∴点G 是以点E 为圆心，EG 为半径的圆上，∴B′G 的最小值为B′E ―EG ，要B′G 最小，则EG 最大，即EF 最大，∵点F 在AD 上，∴点在点A 或点D 时，EF∴线段B′G2.（湖南省郴州市2021年中考数学试卷）如图1，在等腰直角三角形ABC 中，90BAC Ð=°．点E ，F 分别为AB ，AC 的中点，H 为线段EF 上一动点（不与点E ，F 重合），将线段AH 绕点A 逆时针方向旋转90°得到AG ，连接GC ，HB ．（1）证明：AHB AGC V V ≌；（2）如图2，连接GF ，HC ，AF 交AF 于点Q ．①证明：在点H 的运动过程中，总有90HFG Ð=°；②若4AB AC ==，当EH 的长度为多少时，AQG V 为等腰三角形？【答案】（1）见详解；（2）①见详解；②当EH 的长度为2时，AQG V 为等腰三角形【分析】（1）由旋转的性质得AH=AG ，∠HAG=90°，从而得∠BAH=∠CAG ，进而即可得到结论；（2）①由AHB AGC V V ≌，得AH=AG ，再证明AEH AFG V V ≌，进而即可得到结论；②AQG V 为等腰三角形，分3种情况：（a ）当∠QAG=∠QGA=45°时，（b ）当∠GAQ=∠GQA=67.5°时，（c ）当∠AQG=∠AGQ=45°时，分别画出图形求解，即可．【详解】解：（1）∵线段AH 绕点A 逆时针方向旋转90°得到AG ，∴AH=AG ，∠HAG=90°，∵在等腰直角三角形ABC 中，90BAC Ð=°，AB=AC ，∴∠BAH=90°-∠CAH=∠CAG ，∴AHB AGC V V ≌；（2）①∵在等腰直角三角形ABC 中，AB=AC ，点E ，F 分别为AB ，AC 的中点，∴AE=AF ，AEF V 是等腰直角三角形，∵AH=AG ，∠BAH =∠CAG ，∴AEH AFG V V ≌，∴∠AEH=∠AFG=45°，∴∠HFG=∠AFG+∠AFE=45°+45°=90°，即：90HFG Ð=°；②∵4AB AC ==，点E ，F 分别为AB ，AC 的中点，∴AE=AF=2，∵∠AGH=45°，AQG V 为等腰三角形，分3种情况：（a ）当∠QAG=∠QGA=45°时，如图，则∠HAF=90°-45°=45°，∴AH 平分∠EAF ，∴点H 是EF 的中点，∴12==（b）当∠GAQ=∠GQA=（180°-45°）÷2=67.5°时，如图，则∠EAH=∠GAQ=67.5°，∴∠EHA=180°-45°-67.5°=67.5°，∴∠EHA=∠EAH，∴EH=EA=2；（c）当∠AQG=∠AGQ=45°时，点H与点F重合，不符合题意，舍去，V为等腰三角形．综上所述：当EH的长度为2时，AQG【点睛】本题主要考查等腰直角三角形的性质，旋转的性质，全等三角形的判定和性质，勾股定理，熟练掌握全等三角形的判定定理，根据题意画出图形，进行分类讨论，是解题的关键．3.（2021·四川中考真题）在等腰ABC V 中，AB AC =，点D 是BC 边上一点（不与点B 、C 重合），连结AD ．（1）如图1，若60C Ð=°，点D 关于直线AB 的对称点为点E ，结AE ，DE ，则BDE Ð=________；（2）若60C Ð=°，将线段AD 绕点A 顺时针旋转60°得到线段AE ，连结BE ．①在图2中补全图形；②探究CD 与BE 的数量关系，并证明；（3）如图3，若AB AD k BC DE==，且ADE C Ð=Ð，试探究BE 、BD 、AC 之间满足的数量关系，并证明．【答案】（1）30°；（2）①见解析；②CD BE =；见解析；（3）()AC k BD BE =+，见解析【分析】（1）先根据题意得出△ABC 是等边三角形，再利用三角形的外角计算即可（2）①按要求补全图即可②先根据已知条件证明△ABC 是等边三角形，再证明AEB ADC △≌△，即可得出CD BE=（3）先证明AC BC AD DE=，再证明ACB ADE △∽△，得出BAC EAD Ð=Ð，从而证明AEB ADC △≌△，得出BD BE BC +=，从而证明()AC k BD BE =+【详解】解：（1）∵AB AC =，60C Ð=°∴△ABC 是等边三角形∴∠B=60°∵点D 关于直线AB 的对称点为点E∴AB ⊥DE ，∴BDE Ð=30°故答案为：30°；（2）①补全图如图2所示；②CD 与BE 的数量关系为：CD BE =；证明：∵AB AC =，60BAC Ð=°．∴ABC V 为正三角形，又∵AD 绕点A 顺时针旋转60°，∴AD AE =，60EAD Ð=°，∵60BAD DAC Ð+Ð=°，60BAD BAE Ð+Ð=°，∴BAE DAC Ð=Ð，∴AEB ADC △≌△，∴CD BE =．（3）连接AE ．∵AB AD k BC DE ==，AB AC =，∴AC AD BC DE=．∴AC BC AD DE =．又∵ADE C Ð=Ð，∴ACB ADE △∽△，∴BAC EAD Ð=Ð．∵AB AC =，∴AE AD =，∴BAD DAC BAD BAE Ð+Ð=Ð+Ð，∴DAC BAE Ð=Ð，∴AEB ADC △≌△，CD BE =．∵BD DC BC +=，∴BD BE BC +=．又∵AC k BC=，∴()AC k BD BE =+．【点睛】本题考查相似三角形的证明及性质、全等三角形的证明及性质、三角形的外角、轴对称，熟练进行角的转换是解题的关键，相似三角形的证明是重点4.（2021·浙江嘉兴市·中考真题）小王在学习浙教版九上课本第72页例2后，进一步开展探究活动：将一个矩形ABCD 绕点A 顺时针旋转()090αα°<≤°，得到矩形'''AB C D [探究1]如图1，当90α=°时，点'C 恰好在DB 延长线上．若1AB =，求BC 的长．[探究2]如图2，连结'AC ，过点'D 作'//'D M AC 交BD 于点M ．线段'D M 与DM 相等吗？请说明理由．[探究3]在探究2的条件下，射线DB 分别交'AD ，'AC 于点P ，N （如图3），MN ，PN 存在一定的数量关系，并加以证明．【答案】[探究1]BC =；[探究2]'D M DM =，证明见解析；[探究3]2MN PN DN =×，证明见解析【分析】[探究1] 设BC x =，根据旋转和矩形的性质得出''//D C DA ，从而得出''D C B ADB D D ∽，得出比例式'''D C D B AD AB=，列出方程解方程即可；[探究2] 先利用SAS 得出''AC D DBA D D ≌，得出'DAC ADB Ð=Ð，'ADB AD M Ð=Ð，再结合已知条件得出''MDD MD D Ð=Ð，即可得出'D M DM =；[探究3] 连结AM ，先利用SSS 得出ADM ADM D D ≌，从而证得MN AN =，再利用两角对应相等得出NPA NAD D D ∽，得出PN AN AN DN=即可得出结论．【详解】[探究1]如图1，设BC x =．∵矩形ABCD 绕点A 顺时针旋转90°得到矩形'''AB C D ，∴点A ，B ，'D 在同一直线上．∴'AD AD BC x ===，'1DC AB AB ===，∴''1D B AD AB x =-=-．∵'90BAD D Ð=Ð=°，∴//D C DA ¢¢．又∵点'C 在DB 延长线上，∴''D C B ADB D D ∽，∴''D C AD 1x =解得1x =2x （不合题意，舍去）∴BC =[探究2] 'D M DM =．证明：如图2，连结'DD ．∵'//'D M AC ，∴'''AD M D AC Ð=Ð．∵'AD AD =，''90AD C DAB Ð=Ð=°，''D C AB =，∴()''AC D DBA SAS D D ≌．∴'D AC ADB ¢Ð=Ð，'ADB AD M Ð=Ð，∵AD AD =，''ADD AD D Ð=Ð，∴''MDD MD D Ð=Ð，∴'D M DM =．[探究3]关系式为2MN PN DN =×．证明：如图3，连结AM ．∵'D M DM =，'AD AD =，AM AM =，∴()ADM AD M SSS ¢D D ≌．∴'MAD MAD Ð=Ð，∵AMN MAD NDA Ð=Ð+Ð，'NAM MAD NAP Ð=Ð+Ð，∴AMN NAM Ð=Ð，∴MN AN =．在NAP D 与NDA D 中，ANP DNA Ð=Ð，NAP NDA Ð=Ð，∴NPA NAD D D ∽，∴PN AN AN DN=，∴2AN PN DN =×．∴2MN PN DN =×．【点睛】本题考查了矩形的性质，旋转的性质，全等三角形的判定和性质，相似三角形的判定和性质，解一元二次方程等，解题的关键是灵活运用这些知识解决问题．5.（2021·浙江中考真题）如图，在菱形ABCD 中，ABC Ð是锐角，E 是BC 边上的动点，将射线AE 绕点A 按逆时针方向旋转，交直线CD 于点F ．（1）当AE BC EAF ABC ，^Ð=Ð时，①求证：AE AF =；②连结BD EF ，，若25EF BD =，求ABCDn ＡＥＦ菱形ＳＳ的值；（2）当12EAF BAD Ð=Ð时，延长BC 交射线AF 于点M ，延长DC 交射线AE 于点N ，连结AC MN ，，若42AB AC ==，，则当CE 为何值时，AMN V 是等腰三角形．【答案】（1）①见解析；②825；（2）当43CE =或2或45时，AMN V 是等腰三角形．【分析】（1）根据菱形的性质得到边相等，对角相等，根据已知条件证明出BAE DAF Ð=Ð，得到ABE ADF V V ≌，由=AE AF ，CE CF =，得到AC 是EF 的垂直平分线，得到//EF BD ，CEF CBD ∽△△，再根据已知条件证明出AEF BAC V V ∽，算出面积之比；（2）等腰三角形的存在性问题，分为三种情况：当AM AN =时，ANC MAC V V ≌，得到CE=43；当NA NM =时，CEN BEA V V ≌，得到CE=2；当=MA MN 时，CEN BEA ∽△△，得到CE=45．【详解】（1）①证明：在菱形ABCD 中，//AB AD ABC ADC AD BC ，，=Ð=Ð，AE BC AE AD Q ，^\^，90ABE BAE EAF DAF \Ð+Ð=Ð+Ð=°，,EAF ABC BAE DAF Ð=Ð\Ð=ÐQ ，∴ABE ADF V V ≌（ASA），∴=AE AF ．②解：如图1，连结AC ．由①知，ABE ADF BE DF CE CF V V ≌，，\=\=，AE AF AC EF Q ，=\^．在菱形ABCD 中，//AC BD EF BD CEF CBD V V ，，∽^\\，∴25EC EF BC BD ==，设=2EC a ，则534AB BC a BE a AE a ，，===\=．AE AF AB BC EAF ABC Q ，，==Ð=Ð，∴AEF BAC V V ∽，∴22625=415AEF BAC S AE a S AB a V V æöæöç÷ç÷==ç÷ç÷èøèø，∴1168222525AEF AEF BAC ABCD S S S S V V V 菱形==´=． （2）解：在菱形ABCD 中，1122BAC BAD EAF BAD Q ，Ð=ÐÐ=Ð，BAC EAF BAE CAM ，\Ð=Ð\Ð=Ð，//C AB CD BAE AN ANC CAM Q ，，\Ð=Ð\Ð=Ð，同理，AMC NAC Ð=Ð，∴AC AM MAC ANC CN NAV V ∽，\=．AMN V 是等腰三角形有三种情况：①如图2，当AM AN =时，ANC MAC V V ≌，2CN AC \==，//AB CN CEN BEA Q V V ，∽\，142CE CN AB BE AB Q ，=\==，14433BC CE BC Q ，=\==．②如图3，当NA NM =时，NMA NAM BAC BCA Ð=Ð=Ð=Ð，12AM AC ANM ABC AN AB V V ∽，\==，24CN AC CEN BEA V V ，≌\==\，∴122CE BE BC ===．③如图4，当=MA MN 时，MNA MAN BAC BCA AMN ABC V V ，∽Ð=Ð=Ð=Ð\，1212AM AB CN AC AN AC ，\==\==，14CE CN CEN BEA BE AB QV V ∽，\==，1455CE BC \==．综上所述，当43CE =或2或45时，AMN V 是等腰三角形．【点睛】本题主要考查了菱形的基本性质、相似三角形的判定与性质、菱形中等腰三角形的存在性问题，解决本题的关键在于画出三种情况的等腰三角形（利用两圆一中垂），通过证明三角形相似，利用相似比求出所需线段的长．6.（2020·山东中考真题）在等腰△ABC 中，AC ＝BC ，ADE V 是直角三角形，∠DAE ＝90°，∠ADE ＝12∠ACB ，连接BD ，BE ，点F 是BD 的中点，连接CF ．（1）当∠CAB ＝45°时．①如图1，当顶点D 在边AC 上时，请直接写出∠EAB 与∠CBA 的数量关系是 ．线段BE 与线段CF 的数量关系是 ；②如图2，当顶点D 在边AB 上时，（1）中线段BE 与线段CF 的数量关系是否仍然成立？若成立，请给予证明，若不成立，请说明理由；学生经过讨论，探究出以下解决问题的思路，仅供大家参考：思路一：作等腰△ABC 底边上的高CM ，并取BE 的中点N ，再利用三角形全等或相似有关知识来解决问题；思路二：取DE 的中点G ，连接AG ，CG ，并把CAG V 绕点C 逆时针旋转90°，再利用旋转性质、三角形全等或相似有关知识来解快问题．（2）当∠CAB ＝30°时，如图3，当顶点D 在边AC 上时，写出线段BE 与线段CF 的数量关系，并说明理由．【答案】（1）①EAB ABC Ð=Ð，12CF BE =；②仍然成立，证明见解析；（2）BE =，理由见解析．【分析】（1）①如图1中，连接BE ，设DE 交AB 于T ．首先证明,,AD AE BD BE ==再利用直角三角形斜边中线的性质解决问题即可．②解法一：如图2﹣1中，取AB 的中点M ，BE 的中点N ，连接CM ，MN ．证明CMF BMN V V ≌（SAS ），可得结论．解法二：如图2﹣2中，取DE 的中点G ，连接AG ，CG ，并把CAG V 绕点C 逆时针旋转90°得到CBT V ，连接DT ，GT ，BG ．证明四边形BEGT 是平行四边形，四边形DGBT 是平行四边形，可得结论．（2）结论：BE ＝．如图3中，取AB 的中点T ，连接CT ，FT ．证明BAE CTF V V ∽，可得结论．【详解】解：（1）①如图1中，连接BE ，设DE 交AB 于T ．∵CA＝CB，∠CAB＝45°，∴∠CAB＝∠ABC＝45°，∴∠ACB＝90°，∵∠ADE＝12∠ACB＝45°，∠DAE＝90°，∴∠ADE＝∠AED＝45°，∴AD＝AE，90,DAEÐ=°Q45, EAB DAT ABC\Ð=Ð=Ð=°∴AT⊥DE，DT＝ET，∴AB垂直平分DE，∴BD＝BE，∵∠BCD＝90°，DF＝FB，∴CF＝12BD，∴CF＝12BE．故答案为：∠EAB＝∠ABC，CF＝12BE．②结论不变．解法一：如图2﹣1中，取AB的中点M，BE的中点N，连接CM，MN．∵∠ACB ＝90°，CA ＝CB ，AM ＝BM ，∴CM ⊥AB ，CM ＝BM ＝AM ，由①得：,AD AE =设AD ＝AE ＝y ．FM ＝x ，DM ＝a ，Q 点F 是BD 的中点，则DF ＝FB ＝a+x ，∵AM ＝BM ，∴y+a ＝a+2x ，∴y ＝2x ，即AD ＝2FM ，∵AM ＝BM ，EN ＝BN ，∴AE ＝2MN ，MN ∥AE ，∴MN ＝FM ，∠BMN ＝∠EAB ＝90°，∴∠CMF ＝∠BMN ＝90°，∴CMF BMN V V ≌（SAS ），∴CF ＝BN ，∵BE ＝2BN ，∴CF ＝12BE ．解法二：如图2﹣2中，取DE 的中点G ，连接AG ，CG ，并把△CAG 绕点C 逆时针旋转90°得到CBT V ，连接DT ，GT ，BG ．∵AD ＝AE ，∠EAD ＝90°，EG ＝DG ，∴AG ⊥DE ，∠EAG ＝∠DAG ＝45°，AG ＝DG ＝EG ，∵∠CAB ＝45°，∴∠CAG ＝90°，∴AC ⊥AG ，∴AC ∥DE ，∵∠ACB ＝∠CBT ＝90°，//,AC BT \∴AC ∥BT ∥DE ，∵AG ＝BT ，∴DG ＝BT ＝EG ，∴四边形BEGT 是平行四边形，四边形DGBT 是平行四边形，∴BD 与GT 互相平分，,BE GT =∵点F 是BD 的中点，∴BD 与GT 交于点F ，∴GF ＝FT ，由旋转可得；,90,CG CT GCT =Ð=°\ GCT V 是等腰直角三角形，∴CF ＝FG ＝FT ，∴CF ＝12BE ．（2）结论：BE ＝．理由：如图3中，取AB 的中点T ，连接CT ，FT ．∵CA ＝CB ，∴∠CAB ＝∠CBA ＝30°，∠ACB ＝120°，∵AT ＝TB ，∴CT ⊥AB ，tan 30CT AT \°==∴AT ，∴AB ＝，∵DF ＝FB ，AT ＝TB ，∴TF ∥AD ，AD ＝2FT ，∴∠FTB ＝∠CAB ＝30°，∵∠CTB ＝∠DAE ＝90°，∴∠CTF ＝∠BAE ＝60°，∵∠ADE ＝12∠ACB ＝60°，tan 60AE AD\°==∴AE ＝，∴AB AE CT FT==，∴BAE CTF V V ∽，∴BE BA CF CT ==，∴BE =．【点睛】本题属于相似形综合题，考查了等腰三角形的性质，全等三角形的判定和性质，平行四边形的判定和性质，相似三角形的判定和性质,锐角三角函数的应用，解题的关键是学会添加常用辅助线，构造全等三角形或相似三角形解决问题，属于中考压轴题．7.（2021·江苏中考真题）已知正方形ABCD 与正方形AEFG ，正方形AEFG 绕点A 旋转一周．(1)如图①，连接BG 、CF ，求CF BG的值；(2)当正方形AEFG 旋转至图②位置时，连接CF 、BE ，分别去CF 、BE 的中点M 、N ，连接MN 、试探究：MN 与BE 的关系，并说明理由；(3)连接BE 、BF ，分别取BE 、BF 的中点N 、Q ，连接QN ，AE=6，请直接写出线段QN 扫过的面积．【答案】（12）1;2MN BE MN BE ^=；（3）9p 【分析】（1）由旋转的性质联想到连接AF AC 、，证明CAF BAG D D ∽即可求解；（2）由M 、N 分别是CF 、BE 的中点，联想到中位线，故想到连接BM 并延长使BM=MH ，连接FH 、EH ，则可证BMC HMF D D ≌即可得到HF BC BA ==，再由四边形BEFC 内角和为360°可得BAC HFE Ð=Ð，则可证明BAE HFE D D ≌，即BHE D 是等腰直角三角形，最后利用中位线的性质即可求解；（3）Q 、N 两点因旋转位置发生改变，所以Q 、N 两点的轨迹是圆，又Q 、N 两点分别是BF 、BE 中点，所以想到取AB 的中点O ，结合三角形中位线和圆环面积的求解即可解答．【详解】解：（1）连接AF AC、Q 四边形ABCD 和四边形AEFG 是正方形,,90AB BC AG FG BAD GAE CBA AGF \==Ð=Ð=Ð=Ð=°Q AF AC 、分别平分,EAG BADÐÐ45BAC GAF \Ð=Ð=°BAC CAG GAF CAG \Ð+Ð=Ð+Ð即BAG CAFÐ=Ð且,ABC AGF D D 都是等腰直角三角形AC AF AB AG\==CAF BAG \D D ∽CF AC BG AB \==（2）连接BM 并延长使BM=MH ，连接FH 、EHM Q 是CF 的中点CM MF\=又CMB FMHÐ=ÐCMB FMH\D D ≌,BC HF BCM HFM\=Ð=Ð在四边形BEFC 中360BCM CBE BEF EFC Ð+Ð+Ð+Ð=°又90CBA AEF Ð=Ð=°3609090180BCM ABE AEB EFC \Ð+Ð+Ð+Ð=°-°-°=°即180HFM EFC ABE AEB Ð+Ð+Ð+Ð=°即180HFE ABE AEB Ð+Ð+Ð=°180BAE ABE AEB Ð+Ð+Ð=°Q HFE BAE\Ð=Ð又四边形ABCD 和四边形AEFG 是正方形,BC AB FH EA EF\===BAE HFE\D D ≌.BE HE BEA HEF\=Ð=Ð90HEF HEA AEF Ð+Ð=Ð=°Q 90BEA HEA BEH\Ð+Ð=°=Ð\三角形BEH 是等腰直角三角形Q M 、N 分别是BH 、BE 的中点1//,2MN HE MN HE \=190,2MNB HEB MN BE \Ð=Ð=°=1,2MN BE MN BE \^=（3）取AB 的中点O ，连接OQ 、ON ，连接AF在ABF D 中，O 、Q 分别是AB 、BF 的中点12OQ AF \=同理可得12ON AE =AF ==Q3OQ ON \==所以QN扫过的面积是以O为圆心，3为半径的圆环的面积(2239\=-=．S p p p【点睛】本题考察旋转的性质、三角形相似、三角形全等、正方形的性质、中位线的性质与应用和动点问题，属于几何综合题，难度较大．解题的关键是通过相关图形的性质做出辅助线．8.（2020•内江）如图，正方形ABCD中，P是对角线AC上的一个动点（不与A、C重合），连结BP，将BP绕点B顺时针旋转90°到BQ，连结QP交BC于点E，QP延长线与边AD交于点F．（1）连结CQ，求证：AP＝CQ；（2）若AP=1AC，求CE：BC的值；4（3）求证：PF＝EQ．【分析】（1）证明△BAP≌△BCQ（SAS）可得结论．AC，可以假设AP＝CQ＝a，则（2）过点C作CH⊥PQ于H，过点B作BT⊥PQ于T．由AP=14PC＝3a，解直角三角形求出CH．BT，利用平行线分线段成比例定理解决问题即可．（3）证明△PGB≌△QEB，推出EQ＝PG，再证明△PFG是等腰直角三角形即可．【解答】（1）证明：如图1，∵线段BP绕点B顺时针旋转90°得到线段BQ，∴BP＝BQ，∠PBQ＝90°．∵四边形ABCD 是正方形，∴BA ＝BC ，∠ABC ＝90°．∴∠ABC ＝∠PBQ ．∴∠ABC ﹣∠PBC ＝∠PBQ ﹣∠PBC ，即∠ABP ＝∠CBQ ．在△BAP 和△BCQ 中，∵BA =BC ∠ABP =∠CBQ BP =BQ，∴△BAP ≌△BCQ （SAS ）．∴CQ ＝AP ．（2）解：过点C 作CH ⊥PQ 于H ，过点B 作BT ⊥PQ 于T ．∵AP =14AC ，∴可以假设AP ＝CQ ＝a ，则PC ＝3a ，∵四边形ABCD 是正方形，∴∠BAC ＝∠ACB ＝45°，∵△ABP ≌△CBQ ，∴∠BCQ ＝∠BAP ＝45°，∴∠PCQ ＝90°，∴PQ ==，∵CH ⊥PQ ，∴CH =PC ⋅CQ PQ =，∵BP ＝BQ ，BT ⊥PQ ，∴PT ＝TQ ，∵∠PBQ ＝90°，∴BT =12PQ =，∵CH ∥BT ，∴CEEB =CH BT ==35，∴CE CB =38．（3）解：结论：PF ＝EQ ，理由是：如图2，当F 在边AD 上时，过P 作PG ⊥FQ ，交AB 于G ，则∠GPF ＝90°，∵∠BPQ＝45°，∴∠GPB＝45°，∴∠GPB＝∠PQB＝45°，∵PB＝BQ，∠ABP＝∠CBQ，∴△PGB≌△QEB，∴EQ＝PG，∵∠BAD＝90°，∴F、A、G、P四点共圆，连接FG，∴∠FGP＝∠FAP＝45°，∴△FPG是等腰直角三角形，∴PF＝PG，∴PF＝EQ．9.（2020•郴州）如图1，在等腰直角三角形ADC中，∠ADC＝90°，AD＝4．点E是AD的中点，以DE为边作正方形DEFG，连接AG，CE．将正方形DEFG绕点D顺时针旋转，旋转角为α（0°＜α＜90°）．（1）如图2，在旋转过程中，①判断△AGD与△CED是否全等，并说明理由；②当CE＝CD时，AG与EF交于点H，求GH的长．（2）如图3，延长CE交直线AG于点P．①求证：AG⊥CP；②在旋转过程中，线段PC的长度是否存在最大值？若存在，求出最大值；若不存在，请说明理由．【分析】（1）①结论：△AGD≌△CED．根据SAS证明即可．②如图2中，过点A作AT⊥GD于T．解直角三角形求出AT，GT，再利用相似三角形的性质求解即可．（2）①如图3中，设AD交PC于O．利用全等三角形的性质，解决问题即可．②因为∠CPA＝90°，AC是定值，推出当∠ACP最小时，PC的值最大，推出当DE⊥PC时，∠ACP的值最小，此时PC的值最大，此时点F与P重合（如图4中）．【解析】（1）①如图2中，结论：△AGD≌△CED．理由：∵四边形EFGD是正方形，∴DG＝DE，∠GDE＝90°，∵DA＝DC，∠ADC＝90°，∴∠GDE＝∠ADC，∴∠ADG＝∠CDE，∴△AGD≌△CED（SAS）．②如图2中，过点A作AT⊥GD于T．∵△AGD≌△CED，CD＝CE，∴AD＝AG＝4，∵AT⊥GD，∴TG＝TD＝1，∴AT==∵EF∥DG，∴∠GHF＝∠AGT，∵∠F＝∠ATG＝90°，∴△GFH∽△ATG，∴GHAG =FGAT，=∴GH∴GH=（2）①如图3中，设AD交PC于O．∵△AGD≌△CED，∴∠DAG＝∠DCE，∵∠DCE+∠COD＝90°，∠COD＝∠AOP，∴∠AOP+∠DAG＝90°，∴∠APO＝90°，∴CP⊥AG．②∵∠CPA＝90°，AC是定值，∴当∠ACP最小时，PC的值最大，∴当DE⊥PC时，∠ACP的值最小，此时PC的值最大，此时点F与P重合（如图4中），∵∠CED＝90°，CD＝4，DE＝2，∴EC==∵EF＝DE＝2，∴CP＝CE+EF＝∴PC的最大值为。

微专题4过氧化钠与水、二氧化碳反应的综合实验探究题1．过氧化钠与水反应实质的实验探究例1用脱脂棉包住约0.2 g过氧化钠粉末，置于石棉网上，往脱脂棉上滴水，可观察到脱脂棉剧烈燃烧起来。

(1)由实验现象所得出的有关Na2O2和H2O反应的结论是：a．有氧气生成；b．__________________________________________________________________________。

(2)某学校研究性学习小组拟用如图所示装置进行实验，以证明上述结论。

①用以验证结论a的实验操作方法及现象是_______________________________________。

②用以验证结论b的实验_______________________________________________________。

(3)该研究性学习小组的同学认为Na2O2和H2O反应可生成H2O2，现请你设计一个简单的实验证明Na2O2和足量的H2O充分反应后的溶液中有H2O2存在。

试剂：_______________________________________________________________________。

操作及现象：_________________________________________________________________。

答案(1)该反应是放热反应(2)①将带火星的木条靠近导管口p处，木条复燃②将导管口q放入水槽中，反应过程中有气泡冒出(3)MnO2向反应后的溶液中加入少量MnO2粉末，立即冒出大量气泡，将带火星的木条放到瓶口，发现木条复燃2．过氧化钠与二氧化碳反应的实验探究例2(2019·北京西城区期末)某课外活动小组设计了如图所示装置，验证CO 2跟Na2O2反应时需要与水接触。

【装置分析】(1)装置①中反应的离子方程式是_________________________________________________。

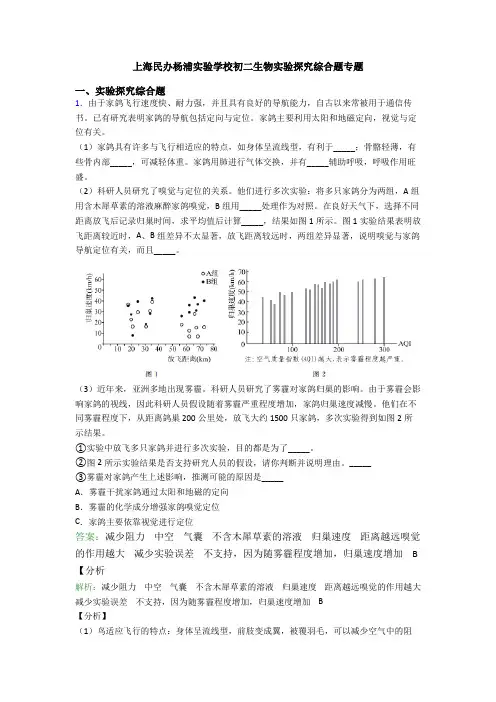
上海民办杨浦实验学校初二生物实验探究综合题专题一、实验探究综合题1．由于家鸽飞行速度快、耐力强，并且具有良好的导航能力，自古以来常被用于通信传书。

已有研究表明家鸽的导航包括定向与定位。

家鸽主要利用太阳和地磁定向，视觉与定位有关。

（1）家鸽具有许多与飞行相适应的特点，如身体呈流线型，有利于_____；骨骼轻薄，有些骨内部_____，可减轻体重。

家鸽用肺进行气体交换，并有_____辅助呼吸，呼吸作用旺盛。

（2）科研人员研究了嗅觉与定位的关系。

他们进行多次实验：将多只家鸽分为两组，A组用含木犀草素的溶液麻醉家鸽嗅觉，B组用_____处理作为对照。

在良好天气下，选择不同距离放飞后记录归巢时间，求平均值后计算_____，结果如图1所示。

图1实验结果表明放飞距离较近时，A、B组差异不太显著，放飞距离较远时，两组差异显著，说明嗅觉与家鸽导航定位有关，而且_____。

（3）近年来，亚洲多地出现雾霾。

科研人员研究了雾霾对家鸽归巢的影响。

由于雾霾会影响家鸽的视线，因此科研人员假设随着雾霾严重程度增加，家鸽归巢速度减慢。

他们在不同雾霾程度下，从距离鸽巢200公里处，放飞大约1500只家鸽，多次实验得到如图2所示结果。

①实验中放飞多只家鸽并进行多次实验，目的都是为了_____。

②图2所示实验结果是否支持研究人员的假设，请你判断并说明理由。

_____③雾霾对家鸽产生上述影响，推测可能的原因是_____A．雾霾干扰家鸽通过太阳和地磁的定向B．雾霾的化学成分增强家鸽嗅觉定位C．家鸽主要依靠视觉进行定位答案：减少阻力中空气囊不含木犀草素的溶液归巢速度距离越远嗅觉的作用越大减少实验误差不支持，因为随雾霾程度增加，归巢速度增加 B 【分析解析：减少阻力中空气囊不含木犀草素的溶液归巢速度距离越远嗅觉的作用越大减少实验误差不支持，因为随雾霾程度增加，归巢速度增加 B【分析】（1）鸟适应飞行的特点：身体呈流线型，前肢变成翼，被覆羽毛，可以减少空气中的阻力；胸肌发达，利于牵动两翼；骨薄而轻，长骨中空，内充满空气，可以减轻体重；直肠短，没有膀胱，粪便可以随时排出体外，能减轻体重；食量大，消化能力强；体内有气囊，辅助肺完成双重呼吸，可以供给充足的氧气。

2023北京初三一模道德与法治汇编综合探究题餐厅就餐时，适量点餐、光盘行动就是文明。

对外交往中，尊重彼此的文化和习俗就是文明。

邻里相处，见面打招呼、遇事多帮忙就是文明。

在学校里，_____________________________就是文明。

(1)请将小明的话补充完整。

中国共产党根本宗旨：全心全意为人民服务最高理想：实现共产主义初心使命：______________________________3月5日学习雷锋活动日学期中“六个一”实践活动12月4日宪法宣传活动日……社区实践活动……参考答案1．(1)C(2)宪法是国家的根本法，在国家法律体系中具有最高的法律地位、法律权威和法律效力，任何法律都不得与宪法的原则和精神相违背。

有利于加强宪法监督，维护宪法权威有利于坚持依宪治国，更好地发挥宪法在治国理政中的重要作用。

【分析】考点考查：宪法的地位。

能力考查：运用所学知识分析材料，解答问题的能力。

核心素养：法治观念。

【详解】（1）本题考查宪法的构成，可结合教材知识作答。

（2）第一步：审设问，明确主体、作答范围及作答角度。

本题的设问主体为公民，需要运用宪法的有关知识，从理由类习题的角度进行作答。

第二步：审材料，提取关键词，链接教材知识。

关键词①：立法应当符合宪法的规定、原则和精神→可链接宪法是国家的根本法，宪法具有最高的法律地位、法律权威和法律效力；关键词②：涉及的合宪性问题以及重要的不同意见应当在审议结果报告中予以说明→可链接加强宪法监督，更好地发挥宪法在治国理政中的重要作用。

第三步：整合信息，组织答案。

2．(1)①实施乡村振兴战略，努力缩小城乡之间的发展差距；②建设文化强国，为物质文明建设提供动力；③坚持走绿色发展的道路，建设生态文明；④推进“一带一路”建设，促进沿线国家发展。

(2)“日月不肯迟，四时相催迫。

”在这个属于奋斗者的新时代，人人都有追梦的权利，人人也都是梦想的筑造者。

青年兴则国家兴，青年强则国家强，广大青年要勇扣时代使命，不驰于空想、不骛于虚声，在奔跑中奋力逐梦，做新时代的追梦人。