高一数学 三角函数化简和求值超难方法汇总
- 格式:doc
- 大小:565.50 KB
- 文档页数:15
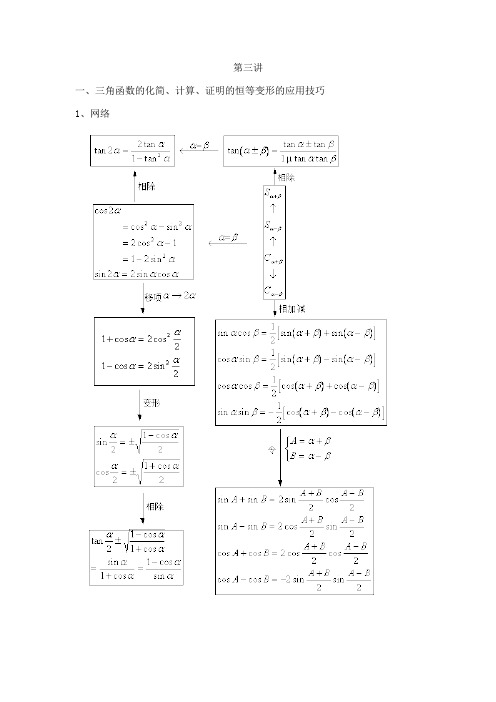
第三讲一、三角函数的化简、计算、证明的恒等变形的应用技巧1、网络2、三角函数变换的方法总结(1)变换函数名对于含同角的三角函数式,通常利用同角三角函数间的基本关系式及诱导公式,通过“切割化弦”,“切割互化”,“正余互化”等途径来减少或统一所需变换的式子中函数的种类,这就是变换函数名法.它实质上是“归一”思想,通过同一和化归以有利于问题的解决或发现解题途径。
【例1】已知θ同时满足和,且a、b 均不为0,求a、b的关系。
练习:已知sin(α+β)=,cos(α-β)=,求的值。
2)变换角的形式对于含不同角的三角函数式,通常利用各种角之间的数值关系,将它们互相表示,改变原角的形式,从而运用有关的公式进行变形,这种方法主要是角的拆变.它应用广泛,方式灵活,如α可变为(α+β)-β;2α可变为(α+β)+(α-β);2α-β可变为(α-β)+α;α/2可看作α/4的倍角;(45°+α)可看成(90°+2α)的半角等等。
【例2】求sin(θ+75°)+cos(θ+45°)-cos(θ+15°)的值。
练习已知,求的值【例3】已知sinα=Asin(α+β)(其中cosβ≠A),试证明:tan(α+β)=提示:sin[(α+β)-β]=Asin (α+β)(3)以式代值利用特殊角的三角函数值以及含有1的三角公式,将原式中的1或其他特殊值用式子代换,往往有助于问题得到简便地解决。
这其中以“1”的变换为最常见且最灵活。
“1”可以看作是sin2x+cos2x, sec2x-tan2x, csc2x -cot2x,tanxcotx, secxcosx, tan45°等,根据解题的需要,适时地将“1”作某种变形,常能获得较理想的解题方法。
【例4】化简:(4)和积互化积与和差的互化往往可以使问题得到解决,升幂和降次实际上就是和积互化的特殊情形。
这往往用到倍、半角公式。


第三讲一、三角函数的化简、计算、证明的恒等变形的应用技巧1、网络2、三角函数变换的方法总结(1)变换函数名对于含同角的三角函数式,通常利用同角三角函数间的基本关系式及诱导公式,通过“切割化弦”,“切割互化”,“正余互化”等途径来减少或统一所需变换的式子中函数的种类,这就是变换函数名法.它实质上是“归一”思想,通过同一和化归以有利于问题的解决或发现解题途径。
【例1】已知θ同时满足和,且a、b 均不为0,求a、b的关系。
练习:已知sin(α+β)=,cos(α-β)=,求的值。
2)变换角的形式对于含不同角的三角函数式,通常利用各种角之间的数值关系,将它们互相表示,改变原角的形式,从而运用有关的公式进行变形,这种方法主要是角的拆变.它应用广泛,方式灵活,如α可变为(α+β)-β;2α可变为(α+β)+(α-β);2α-β可变为(α-β)+α;α/2可看作α/4的倍角;(45°+α)可看成(90°+2α)的半角等等。
【例2】求sin(θ+75°)+cos(θ+45°)-cos(θ+15°)的值。
练习已知,求的值【例3】已知sinα=Asin(α+β)(其中cosβ≠A),试证明:tan(α+β)=提示:sin[(α+β)-β]=Asin (α+β)(3)以式代值利用特殊角的三角函数值以及含有1的三角公式,将原式中的1或其他特殊值用式子代换,往往有助于问题得到简便地解决。
这其中以“1”的变换为最常见且最灵活。
“1”可以看作是sin2x+cos2x, sec2x-tan2x, csc2x -cot2x,tanxcotx, secxcosx, tan45°等,根据解题的需要,适时地将“1”作某种变形,常能获得较理想的解题方法。
【例4】化简:(4)和积互化积与和差的互化往往可以使问题得到解决,升幂和降次实际上就是和积互化的特殊情形。
这往往用到倍、半角公式。

高中数学三角函数解题技巧和公式大全
大家好,我是洪老师,今天给大家推荐的是关于高中数学三角函数解题技巧和公式大全!
如下这些均是有word文档,可以下载下来进行打印的。
有需要的,可以发是送私信063给洪老师,又或者点洪老师头像以后,点洪粉必看的菜单按钮(菜单就在屏幕底下)
那么今天给大家上来的是关于三角函数的最值的求解的问题!
总共有三种方法!
求三角函数的最值常用方法有:配方法、化一法、数形结合法、换元法、基本不等式法等等。
在高考各种题型均有出现如选择题、填空题和解答题,其试题难度属中档题.
方法一配方法
方法二化一法
方法三直线斜率法。

三角函数的化简1、三角函数式的化简:(1)常用方法:①直接应用公式进行降次、消项;②切割化弦,异名化同名,异角化同角;③ 三角公式的逆用等。
(2)化简要求:①能求出值的应求出值;②使三角函数种数尽量少;③使项数尽量少;④尽量使分母不含三角函数;⑤尽量使被开方数不含三角函数2、三角函数的求值类型有三类:(1)给角求值:一般所给出的角都是非特殊角,要观察所给角与特殊角间的关系,利用三角变换消去非特殊角,转化为求特殊角的三角函数值问题;(2)给值求值:给出某些角的三角函数式的值,求另外一些角的三角函数值,解题的关键在于“变角”,如2(),()()ααββααβαβ=+-=++-等,把所求角用含已知角的式子表示,求解时要注意角的范围的讨论;(3)给值求角:实质上转化为“给值求值”问题,由所得的所求角的函数值结合所求角的范围及函数的单调性求得角。
3、三角等式的证明:(1)三角恒等式的证题思路是根据等式两端的特征,通过三角恒等变换,应用化繁为简、左右同一等方法,使等式两端的化“异”为“同”;(2)三角条件等式的证题思路是通过观察,发现已知条件和待证等式间的关系,采用代入法、消参法或分析法进行证明。
一、化简 【例1】求值:︒+︒︒⋅︒+︒+︒80cot 40csc 10sin 20tan 10cos 20sin 2.【变式】1、求值()︒+︒︒+︒+︒10cos 110tan 60tan 110cos 40cos 2【变式】2、求0020210sin 21)140cos 1140sin 3(⋅-。
【例2】(三兄弟)已知23523sin cos παπαα<<=-,且,求αααtan 1sin 22sin 2-+的值【变式】(05天津)已知727sin(),cos 241025παα-==,求sin α及tan()3πα+.【例3】(最值辅助角)已知函数f (x )=2a sin 2x -23a sin x cos x +a +b -1,(a 、b 为常数,a <0),它的定义域为[0,2π],值域为[-3,1],试求a 、b 的值。

高中数学三角函数知识点解题技巧总结高中数学三角函数知识点总结高中数学三角函数知识点解题方法总结一、见“给角求值”问题,运用“新兴”诱导公式一步到位转换到区间(-90o,90o)的公式.1.sin(kπ+α)=(-1)ksinα(k∈Z);2.cos(kπ+α)=(-1)kcosα(k∈Z);3.tan(kπ+α)=(-1)ktanα(k∈Z);4.cot(kπ+α)=(-1)kcotα(k∈Z).二、见“sinα±cosα”问题,运用三角“八卦图”1.sinα+cosα;0(或0(或|cosα|óα的终边在Ⅱ、Ⅲ的区域内;4.|sinα|“化弦为一”:已知tanα,求sinα与cosα的齐次式,有些整式情形还可以视其分母为1,转化为sin2α+cos2α.六、见“正弦值或角的平方差”形式,启用“平方差”公式:1.sin(α+β)sin(α-β)=sin2α-sin2β;2.cos(α+β)cos(α-β)=cos2α-sin2β.七、见“sinα±cosα与sinαcosα”问题,起用平方法则:(sinα±cosα)2=1±2sinαcosα=1±sin2α,故1.若sinα+cosα=t,(且t2≤2),则2sinαcosα=t2-1=sin2α;2.若sinα-cosα=t,(且t2≤2),则2sinαcosα=1-t2=sin2α.八、见“tanα+tanβ与tanαtanβ”问题,启用变形公式:tanα+tanβ=tan(α+β)(1-tanαtanβ).思考:tanα-tanβ=???九、见三角函数“对称”问题,启用图象特征代数关系:(A≠0)1.函数y=Asin(wx+φ)和函数y=Acos(wx+φ)的图象,关于过最值点且横向于y轴的直线分别成直线型;2.函数y=Asin(wx+φ)和函数y=Acos(wx+φ)的图象,关于其中间零点分别成中心对称;3.同样,利用图象也可以得到向量y=Atan(wx+φ)和函数y=Acot(wx+φ)的对称性质。
三角函数化简与求值,4种突破口,展现恒等变换常用技巧
利用三角公式进行化简与求值时要注意三看:一看角,即看式子里面各角之间的联系。
二看函数名称,即看是同名还是异名,是"弦"还是"切"。
三看式子的结构特征,即看式子是积与商的形式还是和与差的形式等。
从角入手,化复角为单角
从形入手,利用配方法,先对二次项配方
从名入手,化异名为同名
从幂入手,利用降幂公式先降次
选择不同的突破口,就有不同的解法,正可谓是"条条大路通罗马"!本题展现了三角函数恒丰变换中的几种常用技巧,是一个典型的范例!
更多高考数学知识,敬请关注头条号,数学教育!。
学不会这些三角函数化简技巧,三角函数寸步难行
三角函数两大主线分别是三角函数性质以及解斜三角形,但这两条主线都要以三角函数化简技巧为核心
所以要想学好此部分内容,需要彻底掌握三角函数化简的技巧,特别对于已知条件的敏感关键词一定要引起重视:
【三角函数化简绝招】
1、统一名:其中包含齐次化切,以及切化弦
2、统一角:单角转倍角,倍角转单角
3、降幂:但不能违背统一角的原则
4、遇到特殊角拆
5、边转角,角转变
6、归一原则
7、配角原则
今天重点分享切化弦以及边转角和角转变。
三角函数化简公式及方法三角函数化简就是对复杂的三角函数进行变形,从而变成简单的三角函数,接下来给大家分享三角函数化简常用的公式。
三角函数化简原则(1)看角的特点,充分利用角之间的关系,尽量向同角转化,利用已知角构建求特角;(2)看函数名的特点,向同名函数转化,弦切互相转化;(3)看式子的结构特点,从整体出发,正用、逆用、变形应用这些公式。
另外,根据式子的特点,还可以使用辅助角公式。
三角函数化简常用公式半角公式sin(A/2)=±√((1-cosA)/2)cos(A/2)=±√((1+cosA)/2)tan(A/2)=±√((1-cosA)/((1+cosA))三角函数和差化积公式sinA+sinB=2sin[(A+B)/2]cos[(A-B)/2]sinA-sinB=2cos[(A+B)/2]sin[(A-B)/2]cosA+cosB=2cos[(A+B)/2]cos[(A-B)/2]cosA-cosB=-2sin[(A+B)/2]sin[(A-B)/2]tanA+tanB=sin(A+B)/cosAcosB=tan(A+B)(1-tanAtanB)tanA-tanB=sin(A-B)/cosAcosB=tan(A-B)(1+tanAtanB)三角函数积化和差公式sinAsinB=-[cos(A+B)-cos(A-B)]/2cosAcosB=[cos(A+B)+cos(A-B)]/2sinAcosB=[sin(A+B)+sin(A-B)]/2cosAsinB=[sin(A+B)-sin(A-B)]/2三角函数降幂公式sin^2(α)=(1-cos(2α))/2=versin(2α)/2cos^2(α)=(1+cos(2α))/2=vercos(2α)/2tan^2(α)=(1-cos(2α))/(1+cos(2α))三角函数辅助角公式asinα+bcosα=(√a^2+b^2)sin(α+β),tanβ=b/a 三角函数化简方法(1)切割化弦;(2)降幂公式;(3)用三角公式转化出特殊角;(4)异角化同角;(5)异名化同名;(6)高次转低次;(7)辅助角公式;(8)分解因式。
第九讲 三角函数式的恒等变形1基本知识与基本方法 1.1基本知识介绍①两角和与差的基本关系式βαβαβαsin sin cos cos )cos( =±;βαβαβαsin cos cos sin )sin(±=±;.tan tan 1tan tan )tan(βαβαβα ±=±②和差化积与积化和差公式2cos()2sin(2sin sin βαβαβα-+=+,2sin()2cos(2sin sin βαβαβα-+=-)2cos()2cos(2cos cos βαβαβα-+=+)2sin()2sin(2cos cos βαβαβα-+-=-[])sin()sin(21cos sin βαβαβα-++=[])sin()sin(21sin cos βαβαβα--+=[])cos()cos(21cos cos βαβαβα-++=[])cos()cos(21sin sin βαβαβα--+-=③倍角公式αααcos sin 22sin =ααααα2222sin 211cos 2sin cos 2cos -=-=-=.tan 1tan 22tan 2ααα-=④半角公式⎪⎭⎫⎝⎛2sin α2)cos 1(α-±=, ⎪⎭⎫⎝⎛2cos α2)cos 1(α+±=,=⎪⎭⎫⎝⎛2tan α)cos 1()cos 1(αα+-±=.sin )cos 1()cos 1(sin αααα-=+⑤辅助角公式如果b a ,是实数且022≠+b a ,则)sin(cos sin 22ϕααα++=+b a b a ,其中ϕ满足22sin ba b +=ϕ22cos ba a +=ϕ.1.2基本方法介绍①变角思想在三角化简、求值中,往往出现较多相异的角,可根据角与角之间的关系,通过配凑,整体把握公式,消去差异,达到统一角的目的,使问题求解.如已知βα、均为锐角,并且,31)tan(,54cos -=-=βαα求βcos 的值.观察到目标角与已知角不同,应寻找它们的关系,将目标角转化为已知角,即)(βααβ--=,所以求出10103)cos(,53sin =-=βαα1010)sin(-=-βα,则[])sin(sin )cos(cos )(cos cos βααβααβααβ-+-=--= 50109= .②变名思想当条件与所求的三角函数名不一样时,可以利用三角函数关系实现弦切、弦割互化,还可通过诱导公式实现正、余函数名的互化,使问题得到解决.如)10tan 31(50sin 00+的值,可先将正切化成弦,即=+=+)10cos 10sin 31(50sin )10tan 31(50sin 0180sin 100sin 10cos 50cos 250sin 10cos 10sin 310cos 50sin 000000000===+=. ③配对偶式法对偶式是指与原数学式子结构对称,或结构相似的数学式.根据原数学式子结构,构造一个对偶式,共同参与运算或变换,使问题得以巧妙的解决,这种解题方法叫做对偶式法.在化简求值或证明一些三角问题时,如果能灵活的运用对偶的数学思想,合理的构造出对偶式,并对原式和对偶式进行和、差或积的计算,则可以使问题得到巧妙的解决. 比如说计算0072cos 36cos 的值,可以设000072sin 36sin ,72cos 36cos ==y x ,则将它们两边相乘,y xy 4136sin 72sin 41144sin 72sin 410000===, 4172cos 36cos 00==x . ④消元思想对于三角变换的多元问题,需要根据题意尽量将多元向单元(或二元)转化,防止多元变量对我们解题的干扰.如锐角γβα,,满足βγαβγαcos cos cos ,sin sin sin =-=+,求βα-的值.考虑将γ角消去,由条件,γβαγαβcos cos cos ,sin sin sin =-=-, 再将两式两边平方再相加,得1)cos(22=--βα,21)cos(=-βα.由条件)0,2(πβα-∈-,得3πβα-=-.⑤1的代换三角函数中常遇到1的变形,主要有1cot tan ,1sec cos csc sin =⋅=⋅=⋅αααααααααααα22222200cot csc tan sec cos sin 1,45tan 90sin 1-=-=+===.如已知,31tan -=α求ααcos sin 11-的值,不需求ααcos ,sin ,可以将1看作αα22cos sin +,即原式=13109139101tan tan 1tan cos sin cos sin cos sin 222222==+-+=-++ααααααααα. 2基本知识应用 2.1基本三角公式的应用基本三角公式向我们揭示了同角或异角的三角函数之间的关系,利用它们可以在已知与未知之间进行转化,帮助我们进行化简、求值、求角.【例1】已知41)2sin(,312cos(=--=-βαβα,且,2,223πβππαπ<<<<求 2cos βα+的值.解: 由条件可观察得到 2)2()2(βαβαβα+=---由πβππαπ<<<<2,223, 所以 224,472πβαππβαπ<-<-<-< 又41)2sin(,312cos(=--=-βαβα 所以415)2cos(,322)2sin(=--=-βαβα所以121522)2(2(cos 2cos+-=⎥⎦⎤⎢⎣⎡---=+βαβαβα .【例2】已知,αβ为锐角,且3cos cos cos()2αβαβ+-+=求,αβ的值.解: 由题意,得012cos 2cos 42cos 42=+-+-+βαβαβα配成完全平方式可得 02sin )2cos 2cos 2(22=-+--+βαβαβα所以02cos 2cos 2=--+βαβα 且 02sin =-βα.因为,αβ为锐角,所以22πβαπ<-<- . 由02sin =-βα, 得βα=.将βα=代入02cos 2cos 2=--+βαβα,得212cos=+βα. 所以32πβα=+. 又βα=, 得3πβα==.在利用三角公式化简、求值时应找出已知条件与欲求的值之间的差异,主要是角及函数名称的差异,然后对已知式与欲求式施以适当的变形,消除它们的差异,以达到解决问题的目的。
求值时要注意角的范围限制对结果的影响. 2.2辅助角公式的应用在三角化简中经常会出现ααcos sin b a +的结构,我们可以把它化成一个角的三角函数,简化三角式的结构,这就需要引入辅助角ϕ,)sin(cos sin 22ϕααα++=+b a b a ,其中ϕ满足22sin ba b +=ϕ22cos ba a +=ϕ.【例3】求])10tan 31(10sin 40cos 220cos 1000+++o 的值.解: 原式=10cos 10sin 310cos 10sin 40cos 2(10cos 2000++ ⎥⎦⎤⎢⎣⎡++=)10sin 2310cos 21(10sin 40cos 10cos 2200000630cos 22)40sin 10sin 40cos 10(cos 2200000==+=.将ααcos sin b a +的结构化成一个角的三角函数,其方式并不唯一,注意公式的正负号,另外也要熟悉公式的反用与变用.3基本方法应用 3.1配对偶式法三角函数中,正弦函数和与余弦函数,正切函数与余切函数,正割函数与余割函数称为互余函数,利用互余函数来构造对偶式,通过运算使问题获得解决.【例4】求值:︒︒-︒+︒80sin 40sin 50cos 10cos 22︒︒-︒+︒=80sin 40sin 50cos 10cos 22x 令︒︒-︒+︒=80cos 40cos 50sin 10sin 22y0000040cos 2)80sin 40sin 80cos 40(cos 2-=+-=+y x 则 00000080sin 40sin 80cos 40cos )80cos 20(cos -+-=-y x 又2140cos 2150sin 120cos )30sin(50sin 200000-=-=+--= 两式相加得232122=-=x ,所以43=x .某些结构特殊的三角函数问题,如果加以观察、利用,构造出与之匹配的对偶结构式整体求解,常常可以达到意想不到的效果.3.2消元思想在三角函数的问题中,往往会出现多个角,多个函数名,在变角或变名过程中,可先设法减少角(或名)的个数(种类),这种思想称为消元思想.【例5】已知0cos cos cos sin sin sin =++=++z y x z y x , 求z y x z y x S tan tan tan )tan(+++=的值.解: 由已知得z y x z y x cos cos cos ,sin sin sin -=+-=+平方相加,得1sin sin 2cos cos 22=++y x y x ,即21)cos(-=-y x同理21)cos(-=-z y ,21)cos(-=-x z .不妨设)(,23211Z k k y x ∈++=ππ)(,23222Z k k z y ∈++=ππ),(,)(2342121Z k k k k z x ∈+++=ππ所以π)12(2321+++=++k k z z y x .z z z z z y x z y x S tan )32tan()34tan(3tan tan tan tan )tan(ππ+++=+++= 0tan 3tan(3tan(3tan =-++=z z z z ππ.【例6】设12π≥≥≥z y x ,且2π=++z y x ,求乘积z y x cos sin cos 的最大值和最小值.解:由已知条件,0)sin(,0)sin(,31222)(2≥-≥-=⨯-≤+-=z y y x z y x ππππ于是,[])sin(cos 21)sin()sin(cos 21cos sin cos z y x z y z y x z y x +≥-++=813cos 21cos 2122=≥=πx (当且仅当12,3ππ===z y x 时取等号). 又[])sin(cos 21)sin()sin(cos 21cos sin cos y x z y x y x z z y x +≤--+=83212cos 21cos 2122+=≤=πz (当且仅当12,245ππ===z y x 时取等号).消元法可以减少三角问题中的变元,使问题的条件变得简洁,能够让我们容易观察条件之间的联系,从而准确地寻找突破口,运用相关知识进行解决. 3.3 1的代换在三角函数中的应用三角函数中1有着特殊的地位,在求值、化简中为了进一步变形的需要,往往将1作灵活的代换,主要方式有αααα222200tan sec cos sin 1,45tan 90sin 1-=+===等等.【例7】设b a ,是非零实数,R x ∈,若,2224241cos sin ba b xa x +=+求2006200820062008cos sin bxa x +的值.(表示用b a ,)解: 已知,2224241cos sin ba b x a x +=+ ………………①将①改写成x ba x ab x x 42242244cos sin cos sin 1+++=.而 x x x x x x 2244222cos sin 2cos sin )cos (sin 1++=+=, 所以有0cos cos sin 2sin 42222422=+-x ba x x x ab . 即0cos sin 222=⎪⎭⎫ ⎝⎛-x b a x a b , 也即4444cos sin b xa x = 将该值记为C. 则由(1)知,22221b a C b C a +=+。