弹性力学作业总结
- 格式:doc
- 大小:1.76 MB
- 文档页数:25
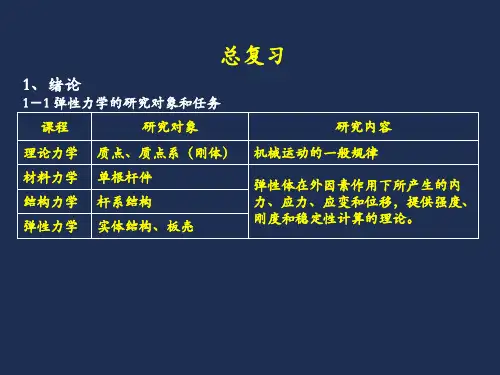
1、绪论1-1 弹性力学的研究对象和任务课程研究对象研究内容理论力学质点、质点系(刚体)机械运动的一般规律材料力学单根杆件弹性体在外因素作用下所产生的内力、应力、应变和位移,提供强度、刚度和稳定性计算的理论。
结构力学杆系结构弹性力学实体结构、板壳总复习z y x σσσ,,zxyz xy τττ,,zy x εεε,,zxyz xy γγγ,,wv u ,,zy x f f f ,,zy x ff f ,,基本量符号量纲正负号规定应力分量正应力N/m 2正面上沿坐标轴正向为正负面上沿坐标轴负向为正切应力N/m 2应变分量正应变无量纲线段伸长为正切应变无量纲线段间夹角变小为正位移分量m 沿坐标轴正向为正外力体力分量N/m 3面力分量N/m 21-2 弹性力学的基本量直角坐标表示的基本量基本假定引用后的结果物理假设(理想弹性体假设)连续性应力、应变和位移可用坐标的连续函数表示均匀性物理的弹性常数不随坐标位置而改变各向同性物理的弹性常数不随方向而改变完全弹性保证了应力与应变之间的一一对应的线性关系几何假设小变形基本方程化为线性方程,可引用硬化原理、叠加原理1-3 弹性力学的基本假定1-4 弹性力学问题已知量:物体的形状和大小(边界);物体的弹性常数(E、 、G);物体的体力、面力;物体的边界约束。
待求量:应力分量、形变分量、位移分量。
超静定问题。
物理量平面应力问题平面应变问题Oxy平面内的分量(基本未知量)Z方向的分量(不存在或不独立)Oxy平面内的分量(基本未知量)Z方向的分量(不存在或不独立)位移分量仅是x、y的函数,与z无关由积分得到仅是x、y的函数,与z无关应变分量应力分量弹性体形状特征物体厚度方向(Z向)的尺寸远小于板面尺寸(X、Y)的等厚度薄板。
物体长度方向(Z向)的尺寸远大于截面尺寸(X、Y)的等截面柱体。
弹性体受力特征外力平行于板面,作用在板的周边,沿厚度不变;板面上无面力,都为零。
外力垂直于柱体轴线,且沿长度方向(Z向)不变。

弹性力学总结弹性力学是研究物体在外力作用下的变形和应力的科学。
它是力学的一个分支,广泛应用于工程领域中的结构设计和材料力学等方面。
在本文中,我将对弹性力学进行总结,从基本概念到应用和发展趋势等方面进行阐述。
弹性力学的基本概念可以追溯到17世纪,当时有很多科学家开始研究物体的变形和力的关系。
罗伯特·胡克被公认为弹性力学的奠基人,他提出了著名的胡克定律,即物体的变形与受力成正比。
根据胡克定律,当外力作用在一个物体上时,它将引起物体的变形,而变形与外力之间存在线性关系。
在弹性力学中,常用的变形参数有拉伸、压缩、剪切和弯曲等。
通过测量这些变形参数,可以得到物体的应力分布。
应力是物体内部的力和单位面积之比,它反映了物体受力的程度。
根据应力的不同分布规律,可以确定物体的受力状态,从而进行结构设计和材料力学分析。
弹性力学的应用广泛,特别是在工程领域中。
在建筑设计中,弹性力学可以用于确定结构的强度和稳定性,从而确保结构的安全性。
在机械工程中,弹性力学可以用于设计和分析弹性元件,如弹簧和悬挂系统等。
此外,弹性力学还可以应用于材料研究、地质学和天体物理学等领域。
近年来,随着科学技术的发展,弹性力学也取得了一系列的进展。
例如,弹性力学在纳米材料研究中的应用日益广泛。
由于纳米材料具有特殊的力学性能,如尺寸效应和表面效应等,弹性力学理论需要进行适应性调整,以准确描述纳米材料的力学行为。
此外,基于弹性力学的模拟方法也在逐渐发展。
通过数值模拟和计算机仿真,可以更全面地研究物体的变形和应力分布。
这为结构设计和材料力学提供了更多的参考依据。
总之,弹性力学是研究物体变形和应力分布的重要科学,它在工程领域中有着广泛的应用。
通过研究物体的变形和应力分布,可以确保结构和材料的安全性和性能。
随着科学技术的进步,弹性力学也在不断发展,适应越来越复杂的材料和结构需求。
弹性力学的研究将有助于推动科技进步和实现更安全和可靠的工程设计。

弹性力学总结第一章绪论一、弹性力学的内容:弹性力学的研究对象、内容和范围。
二、弹性力学的基本量1、外力(1)体力(2)面力2、内力——应力3、应变4、位移以上基本量要求掌握其定义、表达式、分量的符号、正负号规定、量纲。
三、弹性力学中的基本假定1、连续性2、完全弹性3、均匀性4、各向同性以上是对材料性质的假定,凡符合以上四个假定的物体,称为理想弹性体。
5、小变形假定(对物体的变形状态所作的假定)要求掌握各假定的内容和意义(在建立弹性力学基本方程时的作用)。
习题举例:1、弹性力学,是固体力学的一个分支,它的任务是研究弹性体由于受外力作用、边界约束或温度改变等原因而发生的(),从而解决各类工程中所提出的强度、刚度和稳定问题。
A.应力、应变和位移;B.弯矩、扭矩和剪力;C.内力、挠度和变形;D.弯矩、应力和挠度。
2、在弹性力学中,作用于物体的外力分为()。
A.体力和应力;B.应力和面力;C.体力和面力;D.应力和应变。
3、重力和惯性力为(C )。
A .应力;B .面力;C .体力;D .应变。
4、分布在物体体积内的力称为( C )。
A .应力;B .面力;C .体力;D .应变。
5、物体在体内某一点所受体力的集度的表达式及体力分量的量纲为( A )。
A .0lim V F f V∆→∆=∆,-2-2L MT ; B .0lim S F f S ∆→∆=∆,-1-2L MT ; C .0lim A F p A ∆→∆=∆,-1-2L MT ; D .0lim V F f V ∆→∆=∆,-1-2L MT 。
6、弹性力学研究中,在作数学推导时可方便地运用连续和极限的概念,是利用了( )假定。
A .完全弹性;B .连续性;C .均匀性;D .各向同性。
7、( A )四个假设是对物体的材料性质采用的基本假设,凡是符合这四个假设的物体,就称为理想弹性体。
A .完全弹性,连续性,均匀性和各向同性;B .完全弹性,连续性,均匀性和小变形;C .连续性,均匀性,各向同性和小变形;D .完全弹性,连续性,小变形和各向同性。

弹塑性力学总结弹塑性力学的任务是分析各种结构物或其构件在弹性阶段和塑性阶段的应力和位移,校核它们是否具有所需的强度、刚度和稳定性,并寻求或改进它们的计算方法。
并且弹塑性力学是以后有限元分析、解决具体工程问题的理论基础,这就要求我们掌握其必要的基础知识和具有一定的计算能力。
通过一学期的弹塑性力学的学习,对其内容总结如下:一、弹性力学1、弹性力学的基本假定求解一个弹性力学问题,通常是已知物体的几何形状(即已知物体的边界),弹性常数,物体所受的外力,物体边界上所受的面力,以及边界上所受的约束;需要求解的是物体内部的应力分量、应变分量与位移分量。
求解问题的方法是通过研究物体内部各点的应力与外力所满足的静力平衡关系,位移与应变的几何学关系以及应力与应变的物理学关系,建立一系列的方程组;再建立物体表面上给定面力的边界以及给定位移约束的边界上所给定的边界条件;最后化为求解一组偏分方程的边值问题。
在导出方程时,如果考虑所有各方面的因素,则导出的方程非常复杂,实际上不可能求解。
因此,通常必须按照研究对象的性质,联系求解问题的范围,做出若干基本假定,从而略去一些暂不考虑的因素,使得方程的求解成为可能。
(1)假设物体是连续的。
就是说物体整个体积内,都被组成这种物体的物质填满,不留任何空隙。
这样,物体内的一些物理量,例如:应力、应变、位移等,才可以用坐标的连续函数表示。
(2)假设物体是线弹性的。
就是说当使物体产生变形的外力被除去以后,物体能够完全恢复原来形状,不留任何残余变形。
而且,材料服从虎克定律,应力与应变成正比。
(3)假设物体是均匀的。
就是说整个物体是由同一种质地均匀的材料组成的。
这样,整个物体的所有部分才具有相同的物理性质,因而物体的弹性模量和泊松比才不随位置坐标而变。
(4)假设物体是各向同性的。
也就是物体内每一点各个不同方向的物理性质和机械性质都是相同的。
(5)假设物体的变形是微小的。
即物体受力以后,整个物体所有各点的位移都小于物体的原有尺寸,因而应变和转角都远小于1。

弹性⼒学作业总结⼀、综述这学期我们有幸跟着邱⽼师学习了弹性⼒学这门课程,虽然我本科是学习机械专业的,但经过这学期的系统学习,使我对弹性⼒学的认识也越发的清晰,我对平⾯问题、空间问题等基本知识有了较为清晰的了解与掌握,会⽤逆解法、半逆解法、差分法、变分法和有限元法解决⼀些基础的弹性⼒学问题。
弹性⼒学是固体⼒学的⼀个分⽀,研究弹性体由于外⼒作⽤或温度改变等原因⽽发⽣的应⼒、形变和位移。
它是学习塑性⼒学、断裂⼒学、有限元⽅法的基础,⼴泛应⽤于建筑、机械、化⼯、航天等⼯程领域。
本课程较为完整的表现了⼒学问题的数学建模过程,建⽴了弹性⼒学的基本⽅程和边值条件,并对⼀些问题进⾏了求解。
弹性⼒学基本⽅程的建⽴为进⼀步的数值⽅法奠定了基础。
⼆、绪论弹性⼒学所依据的基本规律有三个:变形连续规律、应⼒-应变关系和运动(或平衡)规律,它们有时被称为弹性⼒学三⼤基本规律。
弹性⼒学中许多定理、公式和结论等,都可以从三⼤基本规律推导出来。
通过对弹性⼒学的学习,我感觉整本书就讲了⼗五个控制⽅程解⼗五个未知数。
⽽剩下的问题就是如何求解这些⽅程的问题,这也是数学和⼒学结合最紧密的地⽅。
⽽求解的⽅法⽆外乎有:基于位移的求解(位移法)和基于应⼒的求解(应⼒函数法),差分法、变分法。
⽽前⼈的研究⼤部分都是如何使这些⽅程求解起来更⽅便。
弹性⼒学思路清晰,但是⽅程和公式复杂。
1.⼯程⼒学问题建⽴⼒学模型的过程,⼀般要对三⽅⾯进⾏简化:结构简化、材料简化及受⼒简化。
建模过程如右图:结构简化:如空间问题向平⾯问题的简化,向轴对称问题的简化,实体结构向板、壳结构的简化。
受⼒简化:根据圣维南原理,复杂⼒系简化为等效⼒系。
材料简化:根据各向同性、连续、均匀等假设进⾏简化。
在建⽴数学模型的过程中,通常要注意分清问题的性质进⾏简化:线性化和实验验证。
2.弹性⼒学的基本内容就是研究研究弹性体由于外⼒作⽤或温度改变等原因⽽发⽣的应⼒、形变和位移。
应⽤在⼯程中的实例有⽐赛斜塔,⽔轮机以及各种齿轮等等。

弹性力学总结弹性力学概述弹性力学是研究物体在受力作用下的变形和恢复行为的物理学分支。
它主要研究物体在力的作用下如何发生形变,并在去除外力后如何回复到原来的状态。
弹性力学在工程、材料科学和地震学等领域都有广泛的应用。
弹性力学的基本原理弹性力学的基本原理主要包括胡克定律和变形的描述。
胡克定律胡克定律是弹性力学研究的基石之一,它描述了弹性物质的应力和应变之间的关系。
根据胡克定律,弹性物体在小应变范围内,应力与应变成正比。
公式表示为:σ = Eε其中,σ代表应力,E代表弹性模量,ε代表应变。
胡克定律适用于各向同性的线性弹性材料。
变形的描述弹性变形通常分为线弹性和非线性弹性两种情况。
线弹性是指应力与应变之间成线性关系的弹性变形,而非线性弹性则是指应力与应变之间存在非线性关系的弹性变形。
在弹性力学中,常用的变形描述方法有拉伸、压缩、剪切和扭转等。
这些变形可以通过位移场、应变场和应力场来描述。
弹性体的应力分析弹性体在受力作用下会发生应力分布。
根据应力的分布规律,可以得出一些重要结论。
平面应力和轴对称应力问题在平面应力问题中,物体受力平面上只有两个应力分量,另一个应力分量为零。
这种情况下,可以根据累积概率法或复数变量法求解。
轴对称应力问题是较为常见的一类问题,这类问题的特点是应力场只与径向位置有关。
通过解析方法或数值方法,可以得到轴对称弹性体的应力分布。
弹性体的本构关系弹性体的本构关系以描述应力和应变之间的关系。
弹性体的本构关系可以是线性的或非线性的。
常见的线性弹性体本构关系有:胡克弹性体、准胡克弹性体和线弹性体。
这些本构关系常用于弹性力学计算中,可以通过试验数据或材料参数得到。
非线性弹性体的本构关系较为复杂,常用的描述方法有牛顿-拉普森方程和本构方程等。
弹性力学应用弹性力学在各个领域都有广泛的应用。
以下是几个常见领域:工程领域在工程领域中,弹性力学主要用于材料的强度计算、结构的稳定性分析和振动问题的研究。
通过弹性力学的理论,工程师可以预测材料在受力下的变形和破坏情况,并设计出更加安全和可靠的结构。

弹塑性力学课程学习总结弹塑性力学主要是对物体在发生变形时进行的弹性力学和塑性力学分析,由于塑性力学比较复杂,发展还不够完善,所以以弹性力学为主要内容。
下面是对本课程的学习总结。
弹性力学是固体力学的重要分支,它研究物体在外力和其它外界因素作用下产生的弹性变形和内力。
它是材料力学、结构力学、塑性力学和某些交叉学科的基础,广泛应用于建筑、机械、化工、航天等工程领域。
塑性力学研究的是物体发生塑性变形时的应力和应变。
物体变形包括弹性变形与塑性变形。
在外力作用下产生形变车去外力可以恢复原状是塑性变形;当外力达到一定值后,撤去外力,不再恢复原状是塑性变形。
当外力由小到大,物体变形由弹性变为弹塑性最后变为塑性直至破坏。
弹性变形是应力与应变一一对应。
主要任务是研究物体弹塑性的本构关系和荷载作用下物体内任一点应力变形。
为了便于研究我们常需要做一些假设,弹塑性力学的假设为:1、均匀连续性假设2、材料的弹性性质对塑性变形无影响3、时间对材料性质无影响4、稳定材料,荷载缓慢增加5、小变形假设。
弹性力学在研究对象上与材料力学和结构力学之间有一定的分工。
材料力学基本上只研究杆状构件;结构力学主要是在材料力学的基础上研究杆状构件所组成的结构,即所谓杆件系统;而弹性力学研究包括杆状构件在内的各种形状的弹性体。
在材料力学和结构力学中主要是采用简化的可用初等理论描述的数学模型;在弹性力学中,则将采用较准确的数学模型。
有些工程问题(例如非圆形断面柱体的扭转,孔边应力集中,深梁应力分析等问题)用材料力学和结构力学的理论无法求解,而在弹性力学中是可以解决的。
有些问题虽然用材料力学和结构力学的方法可以求解,但无法给出精确可靠的结论,而弹性力学则可以给出用初等理论所得结果可靠性与精确度的评价。
弹性力学包括平面问题,空间问题,柱体扭转,能量原理,虚功原理和有限元法等。
在研究过程中,需要列出基本方程,空间问题有15个基本方程,包括平衡方程,物理方程,变形协调方程和边界条件。

弹性力学学习心得范文弹性力学是一门研究物体在外力作用下产生的形变和变形恢复过程的力学学科。
在学习弹性力学的过程中,我深刻认识到弹性力学的重要性和应用广泛性,并通过实例分析和解决问题的方法,提高了自己的问题解决能力和学习能力。
以下是我对于弹性力学学习心得的总结。
首先,在学习弹性力学的过程中,我了解到了弹性力学作为应用数学领域中的一个重要分支,具有广泛的应用前景。
弹性力学可以应用于结构设计、材料力学、地震工程等领域,并且在工程学、医学、生物学等多个领域中都有重要的应用。
其次,在学习弹性力学的过程中,我掌握了一些基本的概念和理论。
弹性力学主要研究物体在外力作用下的弹性变形,其中包括应力、应变、弹性模量等重要概念。
通过学习弹性力学基本原理和应用方法,我对弹性体的弹性变形规律有了较为深入的了解。
然后,在学习弹性力学的过程中,我通过实例分析和解决问题的方法,提高了自己的问题解决能力和学习能力。
我将所学的理论运用到实际问题中,通过分析和计算,找到了解决问题的方法,并且在实践中加深了对弹性力学的理解和应用。
最后,在学习弹性力学的过程中,我认识到了科学研究的重要性和严谨性。
科学研究需要以客观的态度去研究问题,通过实验和计算来验证理论,从而得出科学结论。
通过学习弹性力学,我对科学研究的方法和过程有了更为清晰的认识。
总结起来,通过学习弹性力学,我不仅掌握了一门重要的力学学科,而且提高了自己的问题解决能力和学习能力。
弹性力学作为应用数学的一个重要分支,具有广泛的应用前景,对于工程学、医学、生物学等多个领域都有重要的意义。
因此,我将继续深入学习弹性力学,并将其应用于实际问题中,为社会发展做出更大的贡献。

弹性力学总结弹性力学关于应力变分法问题一、起源及发展1687年,Newton 在《自然哲学的数学原理》中提出第一个变分问题——定轴转动阻力最小的旋转曲面形状问题; 1696年,Bernoulli 提出了著名的最速降线问题;到18世纪,经过Euler ,Lagrange 等人的努力,逐渐形成变分法。
古典变分法的基本内容是确定泛函的极值和极值点,它为许多数学、物理、科技、工程问题提供了强有力地数学工具。
现代理论证明,微分方程(组)中的变分法是把微分方程(组)化归为其对应泛函的临界点(即化为变分问题),以证明其解的存在性及解的个数。
讨论对应泛函临界点的存在性及其个数的基本方法是Morse 理论与极小极大理论(Minimax Theory )。
变分法有着深刻的物理背景,某种意义上,自然界一切物质运动均可以用某种形式的数理方程表示,一般数理方程又与一定的泛函相对应,所以一切物质运动规律都遵从“变分原理”。
由于弹性力学变分解法,实质上就是数学中的变分法应用于解弹性力学问题,虽然在讨论的近似解法中使用变分计算均甚简单(类似微分),但“变分”的概念却极为重要,它关系到我们队一系列力学变分原理中“虚”的概念的建立与理解。
以下,就应力变分法进行讨论。
二、定义及应用(1)、应力变分方程设有任一弹性体,在外力的作用下处于平衡。
命ij σ为实际存在的应变分量,它们满足平衡微分方程和应力边界条件,也满足相容方程,其相应的位移还满足位移边界条件。
现在,假想体力和应变边界条件上给定的面力不变而应力分量发生了微小的改变ij δσ,即所谓虚应力或应力的变分,使应力分量成为ij ij δσσ+ 假定他们只满足平衡微分方程和应力边界条件。
既然两组应力分量都满足同样体力和面力作用下的平衡微分方程和应力边界条件,应力分量的变化必然满足无体力时的平衡微分方程。
即0,0,0x xy zx y yz xy z zx yz x y z y z x z x y δσδτδτδσδτδτδσδτδτ⎫∂∂∂++=⎪∂∂∂⎪⎪∂∂∂++=⎬∂∂∂⎪⎪∂∂∂++=⎪∂∂∂⎭。

一、引言力学作为物理学的基础学科,对于培养学生的科学素养和实际操作能力具有重要意义。
在大学期间,我们学习了大量的力学理论知识,但理论知识的学习并不能完全代替实践。
通过力学实践作业,我深刻体会到了理论与实践相结合的重要性,以下是我对力学实践作业的一些心得体会。
二、实践作业的内容与过程1. 实践作业的内容本次力学实践作业主要包括以下几个方面:力的合成与分解、牛顿运动定律的应用、功与能的计算、转动动力学、振动与波动等。
2. 实践作业的过程(1)预习:在实践作业开始前,我首先查阅了相关资料,了解了实验原理、实验步骤和注意事项。
(2)实验:在实验过程中,我严格按照实验步骤进行操作,认真观察实验现象,并记录实验数据。
(3)数据处理:将实验数据进行分析和处理,得出实验结果。
(4)撰写实验报告:在实验报告中对实验过程、实验结果、实验结论进行分析和总结。
三、实践作业的心得体会1. 理论与实践相结合的重要性通过力学实践作业,我深刻体会到了理论与实践相结合的重要性。
在实验过程中,我发现理论知识与实际操作之间存在一定的差距,只有将理论知识与实际操作相结合,才能更好地理解和掌握力学知识。
2. 培养实际操作能力力学实践作业不仅有助于我们掌握理论知识,还能提高我们的实际操作能力。
在实验过程中,我学会了如何使用实验仪器、如何观察实验现象、如何处理实验数据等,这些能力对于今后从事科学研究或工程实践具有重要意义。
3. 培养科学素养力学实践作业要求我们严谨、细致、认真,这些品质对于培养我们的科学素养具有重要作用。
在实验过程中,我学会了如何发现问题、分析问题、解决问题,这些能力将对我今后的学习和工作产生积极影响。
4. 团队合作意识在力学实践作业中,我们需要与同学进行合作,共同完成实验任务。
这使我认识到了团队合作的重要性,学会了如何与他人沟通、协调,提高了我的团队协作能力。
5. 增强学习兴趣力学实践作业使我对力学产生了浓厚的兴趣。
在实验过程中,我感受到了力学知识的魅力,从而激发了我进一步学习力学的动力。

第1篇一、引言力学实验是物理学科中重要的实践环节,通过实验可以加深对力学理论的理解,培养实验操作能力和分析问题、解决问题的能力。
本报告将对全套力学实验进行总结,包括实验目的、原理、方法、结果分析及实验心得体会。
二、实验内容1. 力学基本实验(1)实验目的:验证牛顿运动定律,研究力与运动的关系。
(2)实验原理:通过测量物体的运动状态和受力情况,分析物体所受的合外力,验证牛顿运动定律。
(3)实验方法:利用打点计时器、天平等实验仪器,测量物体的位移、速度、加速度等参数,分析受力情况。
(4)结果分析:通过实验数据,验证牛顿运动定律的正确性,分析力与运动的关系。
2. 弹性力学实验(1)实验目的:研究弹性力学的基本理论,验证胡克定律。
(2)实验原理:利用弹簧测力计、杠杆等实验仪器,测量弹簧的伸长量与所受拉力之间的关系,验证胡克定律。
(3)实验方法:通过改变拉力大小,测量弹簧的伸长量,分析伸长量与拉力的关系。
(4)结果分析:通过实验数据,验证胡克定律的正确性,研究弹性力学的基本理论。
3. 材料力学实验(1)实验目的:研究材料力学的基本理论,验证材料的力学性能。
(2)实验原理:利用拉伸试验机、万能试验机等实验仪器,测量材料的应力、应变等参数,分析材料的力学性能。
(3)实验方法:通过拉伸、压缩等试验,测量材料的应力、应变等参数,分析材料的力学性能。
(4)结果分析:通过实验数据,验证材料的力学性能,研究材料力学的基本理论。
4. 振动实验(1)实验目的:研究振动的基本理论,验证振动方程。
(2)实验原理:利用单摆、弹簧振子等实验仪器,研究振动系统的振动特性,验证振动方程。
(3)实验方法:通过改变振动系统的参数,测量振动频率、振幅等参数,分析振动系统的振动特性。
(4)结果分析:通过实验数据,验证振动方程的正确性,研究振动的基本理论。
5. 流体力学实验(1)实验目的:研究流体力学的基本理论,验证流体流动规律。
(2)实验原理:利用风洞、水槽等实验仪器,研究流体流动特性,验证流体流动规律。
弹性力学学习心得范本通过这次学习弹性力学,我对固体力学和材料力学有了更深入的了解和认识。
弹性力学是研究固体变形和应力分布的学科,具有广泛的应用领域和重要的理论价值。
以下是我在学习过程中的心得体会。
首先,深入理解弹性力学的基本概念和原理是非常重要的。
在学习弹性力学的过程中,我通过分析和推导弹性体的应力-应变关系等基本公式,掌握了弹性力学基本概念和原理。
这有助于我理解和解决弹性体的变形和应力分布问题。
其次,掌握弹性体的力学性能和性质是弹性力学学习的重点。
弹性体的力学特性可以通过应力-应变曲线等力学性能来描述。
在学习中,我深入了解了应力-应变曲线的构成和性质,以及弹性模量、剪切模量和泊松比等重要的力学性能参数。
同时,我也学习了弹性体的各种力学特性,如杨氏模量、屈服强度和硬度等。
这些知识对于分析材料性能和应用具有重要的意义。
第三,学习和应用弹性力学的方法和技巧是提高学习效果和解决实际问题的关键。
在学习过程中,我通过课堂讲解、实验演示和数值计算等多种方法学习和掌握弹性力学的基本理论和方法。
我也了解了一些经典问题的解决方法,如悬臂梁的计算、圆盘的变形分析和杆件的应力计算等。
这些方法和技巧对于发展弹性力学理论和解决实际问题有着重要的意义。
第四,实践和应用是深化理解和巩固知识的有效途径。
在学习弹性力学过程中,我通过实验和实例分析等实践活动,加深了对弹性力学理论和实际应用的理解。
例如,我通过拉伸试验和弯曲试验等实验,观察和分析了材料的应力-应变行为和破坏机理。
另外,我还通过实例分析弹性体的变形和应力分布,结合实际问题进行计算和解决。
这使我对弹性力学的理论和应用有了更深入的理解和认识。
最后,深化对弹性力学的学习需要坚持不懈的努力和持续的实践。
学习弹性力学是一个长期的过程,需要不断学习和实践,加深对理论的理解和应用的掌握。
因此,在学习弹性力学过程中,我将继续不断提高自己的理论水平和实践能力,力争成为一名优秀的弹性力学专业人才。
弹性力学文献阅读报告水坝的应力计算问题及其讨论文章题目:Stress Analysis of the Rectangular Retaining Wall Under Water Pressure Based on Elasticity Mechanics作者:Yongwei Wang Yanqin Guo Huanghe Science and Technology College Institute of Technology, Henan Province, china 一、对文章的理解及讨论在工程实践中,我们经常需要了解坝体的应力分布情况,来确定坝体的危险截面,给我们的工程设计和应用带来参考。
这篇文章中将水坝简化为矩形坝体,并用弹性力学的方法分析坝体的应力和位移。
水坝在工程实际中主要受到两种力,即自身体力和液体的压力。
这里取水坝的一个横截面进行分析,将其视为平面应变问题,示意图如图1所示:水坝力学模型1.水坝力学模型图1.这里假设坝体的密度为ρ1,左侧的液体密度为ρ2。
文章中采用的是半逆解法,由应力的表达式假设出应力函数求解,过程如以下公式所示:所以可以假设出应力函数的表达式为:这里文章中并没有解释σx假设成这样的原因,我认为这里之所以将σx假设成这样是因为坝体内的应力由两部分影响组成,即自重ρ1gy和水压ρ2gy,这两部分均为关于y的正比例函数,故σx假设成如上的形式。
将应力函数代入相容方程得:因为上式要对无数y值成立,所以各次项系数都要为0,即:积分可得到下式:将其代入应力函数的表达式,,可得:将其代入应力函数的表达式利用应力函数求出应力分量为:分析主要边界的应力边界条件可得:运用圣维南原理列出次要边界的应力边界条件:这里原文中运用了圣维南原理对上表面的σy 积分为0,其实是对应力边界的一种放松要求,不过由验算得知,这里放松之后的结果和严格遵循边界条件的计算结果相同。
由以上的边界可以解得各应力分量为:再由物理方程求水平位移分量:文章的内容到这里就结束了,在介绍中提到求解应力分量是为了确定危险截面,但是文章正文内容并没有提及。
2024年粘弹性力学学习心得范本经过一个学期的弹性力学学习,说实话,学起来还真的比较的抽象,有很多知识理解起来不是很清楚,比如一些公式的推导以及解题方法。
不过经过弹性力学的学习,还是了解到了一些相关的基本理论和一些解题思想。
弹性力学,是固体力学的一个分支,研究弹性体由于受外力作用、边界约束或温度改变等原因而发生的应力、形变和位移。
弹性力学的研究对象是完全弹性体,弹性体是变形体的一种,在外力作用下物体变形,当外力不超过某一限度时,出去外力后,除去外力后物体即恢复原状。
根据问题的性质,忽略一些很小的次要因素,对物体的材料性质采用了一些基本假定,即弹性力学的基本假定,主要有连续性、完全弹性、均匀性、各向同性,符合以上假定的物体,就称为理想弹性体;此外,假定位移和形变是微小的。
在物体的任意一点,应力分量s____,sy,sz,tyz,tz____,t____y,这六个应力分量就可以完全确定该点的应力状态;形变分量e____,ey,ez,gyz,gz____,g____y,这六个应变分量就可以完全确定该点的形变状态。
物体任意一点的位移,用它在____、y、z三轴上的投影表示。
研究讨论的平面应力弹性体的形状为等厚度均匀薄板,厚度方向的尺寸小于其他两个方向的尺寸。
在解决弹性力学平面问题时,需要建立基本方程:平衡方程—应力与外力之间的关系;几何方程—位移与应变之间的关系;物理方程—应变与应力之间的关系。
以及边界条件的建立,边界条件表示在边界上位移与约束,或应力与面力之间的关系式。
位移分量已知的边界,建立位移边界;给定了面力分量,建立应力边界条件。
圣维南原理,面力的改变,就只会使近处产生显著的应力改变,而远处的应力改变可以忽略不计。
在解决平面问题时,按位移求解平面以及在问题或按应力求解平面问题。
2024年粘弹性力学学习心得范本(2)粘弹性力学是材料力学的一个重要分支,研究材料在加载和卸载过程中的变形行为。
在粘弹性力学的学习过程中,我深入学习了粘弹性材料的力学性质、应力应变关系和变形机制等相关知识,并结合实际案例进行分析和探讨。