理论塔板数的计算

第五节 理论板数的求法所谓求理论塔板数，就是利用前面讨论的平衡关系，()n n x f y =和操作关系，()()m n n x f y x f y ''='=+或1计算达到指定分离要求所须的汽化-冷凝次数。

（1）逐板计算法每利用一次平衡关系和一次操作关系，即为一块理论板。

提馏段也是一样。

（2）图解法通常采用直角梯级图解法，其实质仍然是以平衡关系与操作关系为依据，将两者绘在y x -图上，便可图解得出达到指定分离任务所须的理论塔板数及加料板位置。

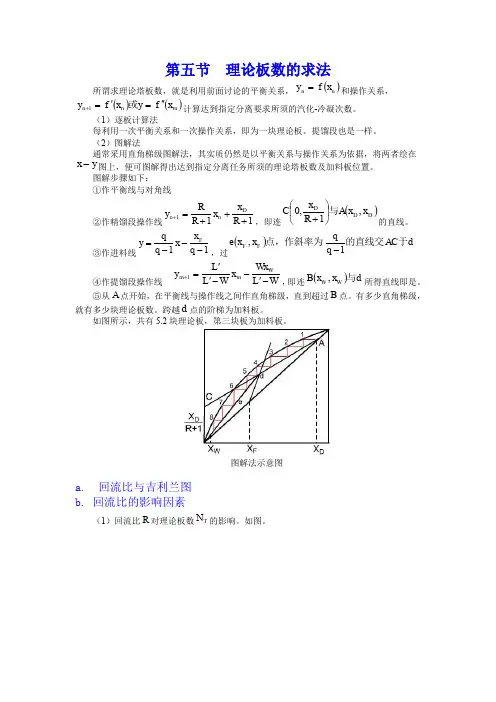
图解步骤如下： ①作平衡线与对角线②作精馏段操作线111+++=+R x x R R y D n n ，即连()D D D x x A R x C ,1,0与⎪⎭⎫ ⎝⎛+的直线。

③作进料线11---=q x x q qy F，过()d AC q q x x e F F 于的直线交点，作斜率为1,- ④作提馏段操作线W L Wx x W L L y W m m -'--''=+1，即连()d x x B W W 与,所得直线即是。

⑤从A 点开始，在平衡线与操作线之间作直角梯级，直到超过B 点。

有多少直角梯级，就有多少块理论板数。

跨越d 点的阶梯为加料板。

如图所示，共有5.2块理论板，第三块板为加料板。

图解法示意图a. 回流比与吉利兰图b. 回流比的影响因素（1）回流比R 对理论板数T N 的影响。

如图。

回流比对T N 的影响↑+↓1R x R D ，，操作线靠近平衡线，↑T N 反之，↓+↑1R x R D ，，操作线远离平衡线，↓T N 即 T N 正比于R 1（2）回流比对设备费与操作费的影响 ()D R D L V 1+=+=↑↑V R ,，塔直径↑，冷凝器↑，蒸馏釜↑ 设备费↑↓↑T N R ,，塔高下降，设备费↓↑↑V R ,，冷却水量↑，加热蒸汽量↑， 操作费↑须选一个合适回流比R ，使总费用最省。

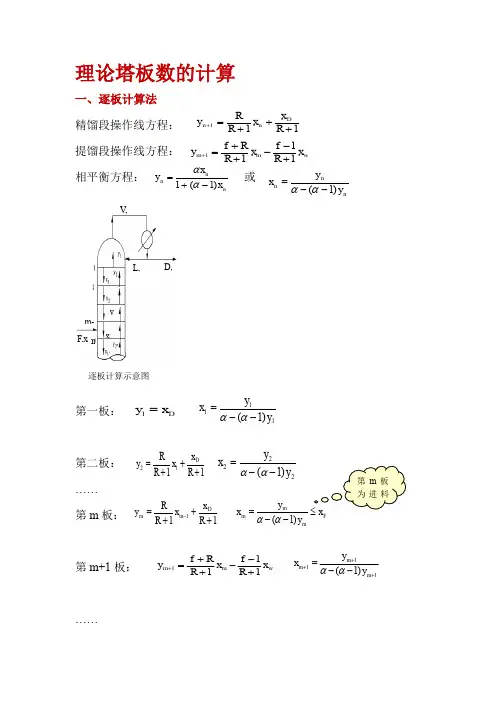
理论塔板数的计算一、逐板计算法精馏段操作线方程： 提馏段操作线方程： 相平衡方程： 或第一板：第二板：…… 第m 板：第m+1板： (1)11+++=+R x x R R y D n n w m m x R f x R R f y 1111+--++=+nn n x x y )1(1-+=ααnn n y y x )1(--=ααD, V, L, xD F,xx y m m-逐板计算示意图 111)1(y y x --=ααDx y =11112+++=R x x R R y D 222)1(y y x --=αα111+++=-R x x R R y D m m F m m m x y y x ≤--=)1(αα第m 板为进料111)1(+++--=m m m y y x ααw m m x R f x R R f y 1111+--++=+第N 板：在计算过程中, 每使用一次平衡关系, 表示需要一层理论板. 由于一般再沸器相当于一层理论板.结果: 塔内共有理论板N 块, 第N 板为再沸器, 其中精馏段m-1块, 提馏段N-m+1块 (包括再沸器), 第m 板为进料板。

二、图解法图解法求理论板层数的基本原理与逐板计算法的完全相同,只不过是用平衡曲线和操作线分别代替平衡方程和操作线方程,用简便的图解法代替繁杂的计算而已。

1、操作线的作法首先根据相平衡数据, 在直角坐标上绘出待分离混合物的x-y 平衡曲线, 并作出对角线.W NN N x y y x ≤--=)1(ααw N N x R f x R R f y 1111+--++=-在x=xD 处作铅垂线, 与对角线交于点a, 再由精馏段操作线的截距xD /(R+1) 值, 在y 轴上定出点b, 联ab. ab为精馏段操作线.在x=xF 处作铅垂线, 与精馏段操作线ab交于点d.在x=xW 处作铅垂线, 与对角线交于点c, 联cd. cd为提留段操作线.2、求N 的步骤自对角线上a点始, 在平衡线与精馏段操作线间绘出水平线及铅垂线组成的梯级.当梯级跨过两操作线交点d 时, 则改在平衡线与提馏操作线间作梯级, 直至某梯级的垂直线达到或小于xw为止.每一个梯级代表一层理论板. 梯级总数即为所需理论板数.3、梯级含义：如第一梯级:由a点作水平线与平衡线交于点1(y1, x1), 相当于用平衡关系由y1求得x1；再自点1作垂线与精馏段操作线相交, 交点坐标为(y2, x1), 即相当于用操作线关系由x1求得y2。

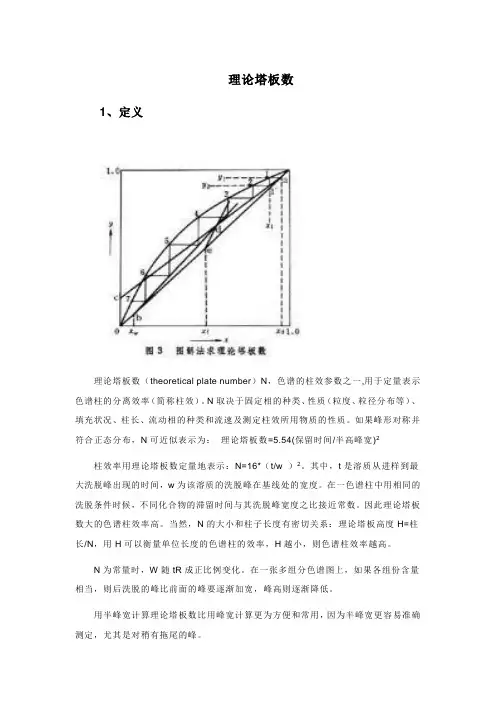
理论塔板数1、定义理论塔板数（theoretical plate number）N，色谱的柱效参数之一,用于定量表示色谱柱的分离效率（简称柱效）。

N取决于固定相的种类、性质（粒度、粒径分布等）、填充状况、柱长、流动相的种类和流速及测定柱效所用物质的性质。

如果峰形对称并符合正态分布，N可近似表示为：理论塔板数=5.54(保留时间/半高峰宽)2柱效率用理论塔板数定量地表示：N=16*（t/w ）2。

其中，t是溶质从进样到最大洗脱峰出现的时间，w为该溶质的洗脱峰在基线处的宽度。

在一色谱柱中用相同的洗脱条件时候，不同化合物的滞留时间与其洗脱峰宽度之比接近常数。

因此理论塔板数大的色谱柱效率高。

当然，N的大小和柱子长度有密切关系：理论塔板高度H=柱长/N，用H可以衡量单位长度的色谱柱的效率，H越小，则色谱柱效率越高。

N为常量时，W随tR成正比例变化。

在一张多组分色谱图上，如果各组份含量相当，则后洗脱的峰比前面的峰要逐渐加宽，峰高则逐渐降低。

用半峰宽计算理论塔板数比用峰宽计算更为方便和常用，因为半峰宽更容易准确测定，尤其是对稍有拖尾的峰。

N与柱长成正比，柱越长，N越大。

用N表示柱效时应注明柱长，，如果未注明，则表示柱长为1米时的理论塔板数。

（一般HPLC柱的N在1000以上。

）若用调整保留时间（tR′）计算理论塔板数，所得值称为有效理论塔板数（N有效或Neff）=16(tR′/W)2我们知道实际操作过程中，峰会出现拖尾的情况，所以，实用半峰宽比使用峰宽要准确一些，当然这也不是绝对的。

理论塔板高度和理论塔板数都是柱效指标，，由于峰宽或半峰宽是组分分子在色谱柱内离散的度量，总的离散程度是单位柱长内分子离散的累计，其与柱长成正比。

理论塔板数首先应该是和柱子的性能是有关系的，像填料，柱长什么的，和你的流动相，流速，样品分子量大小都是有关系的。

每个峰的理论塔板数肯定是不同的，理论塔板数越高峰形越好。

2、理论塔板数下降后可以考虑色谱柱再生（1）、反相柱分别用甲醇：水=90：10，纯甲醇（HPLC级），异丙醇（HPLC级），二氯甲烷（HPLC级）等溶剂作为流动相，依次冲洗，每种流动相流经色谱柱不少于20倍的色谱柱体积，然后再以相反的次序冲洗。

板式吸收塔理论塔板数的计算14404806 龙益如通常在吸收操作中，大多采用填料塔。

然而，填料式吸收塔不是在所有情况下均适用，仅在处理量较小，塔径在600毫米以下时（文献得知），采用填料塔比较经济。

当塔径较大时，可能出现严重的壁流和沟流现象，导致吸收效率下降。

故，处理量较大时，采用板式吸收塔。

另外，填料塔不能像板式塔一样设置人孔进行检修和清洗，故此方面依旧板式塔更优。

下面进行板式吸收塔的理论塔板数的计算，主要参照板式精馏塔采用逐级计算法和图解法，另外由查阅文献介绍解析法等其他方法。

方法一：首先，我们假定板式吸收塔中每一块塔板均为理想板，即塔板上的液相组成是均匀的，且离开该板的气液两相处于平衡状态，即所谓理论板。

同时，在气相中采用惰性组分的摩尔比为基准，在液相中采用吸收剂的摩尔比为基准，且满足吸收过程中惰性组分吸收剂的流量均可视为恒定，即各板上升的惰性组分的摩尔流量V均相等，各板下降的吸收剂的摩尔流量L均相等。

基于以上讨论，参照板式精馏塔的处理方式，进行计算：如图所示，在全塔范围内对溶质进行物料衡算得VY b+LX a=VY a+LX b(1-1)V(Y b−Y a)=L(X b−X a)(1-2)在吸收塔的任意两板间（i和i+1）分别与塔顶或者塔底的范围内，对溶质A进行物料衡算得VY i+1+LX a=VY a+LX i移项，得Y i+1=LV X i+(Y a−LVX a)(1-3)即为板式吸收塔的操作线方程。

由以上部分计算对比教材上填料式吸收塔的计算可知，此部分两者的处理方法基本相同。

故，后续部分计算直接采用书上已有公式。

其中，Y a=Y b(1−φA) (1-4)而最小液气比（LV ）min=Y b−Y aY bm−X a(1-5)又实际液气比为L V =（1.1~1.2）（LV）min（1-6）图1-1一般情况下，进行吸收操作时，处理量V、进塔气体组成Y b、出塔气体组成Y a以及进塔吸收剂组成X a均为设计时已经确定的量，故式1-2、1-5、1-6可求得出塔吸收液组成X b。

精馏过程的物料衡算和塔板数的计算一、理论塔板连续精馏计算的主要对象是精馏塔的理论塔板数。

所谓的理论塔板是指气液在塔板上充分接触，有足够长的时间进行传热传质，当气体离开塔板上升时与离开塔板下降的液体已达平衡，这样的塔板称为理论塔板。

实际上，由于塔板上气液接触的时间及面积均有限，因而任何形式的塔板上气液两相都难以达到平衡状态，也就是说理论塔板是不存在的，它仅是一种理想的板，是用来衡量实际分离效率的依据和标准。

通常在设计中先求出按生产要求所需的理论塔板数N T然后用塔板效率η予以校正，即可求得精馏设备中的实际塔板数N P二、计算的前提由于精馏过程是涉及传热、传质的复杂过程，影响因素众多。

为处理问题的方便作如下假设，这些就是计算的前提条件。

（1）塔身对外界是绝热的，即没有热损失。

（2）回流液由塔顶全凝器供给，其组成与塔顶产品相同。

（3）塔内上升蒸气由再沸器加热馏残液使之部分气化送入塔内而得到。

（4）恒摩尔气化在精馏操作时，在精馏段内，每层塔板上升的蒸气的摩尔流量都是相等的，提馏段内也是如此，即：精馏段：V1 = V2 = …………＝Ｖn= Vmol/s(下标为塔板序号，下同）提馏段：Ｖ′n+1 =V′n+2 =…………＝V′m= V′mol/s但Ｖn不一定与Ｖ′m相等，这取决于进料状态。

（５）恒摩尔溢流（或称为恒摩尔冷凝）精馏操作时，在精馏段内每层塔板下降的液体的摩尔流量都是相等的，提馏段也是如此，即：Ｌ1 = L2=…………= L n = L mol/sL′n+1= L′n+2=………… = L′m= L′ mol/s但Ｌ不一定与Ｌ′相等，这也取决于进料的状态。

（６）塔内各塔板均为理论塔板。

三、物料衡算和操作线方程１、全塔物料衡算图4-10 全塔物料衡算示意图如图４－１０所示，设入塔进料流量为Ｆ，轻组分含量为x F,塔顶产量流量为Ｄ，轻组分含量为x D,塔底产品流量为Ｗ，轻组分含量为x w，流量单位均为mol/s，含量均为摩尔分率。

理论塔板数定义理论塔板数（theoretical plate number），N色谱的柱效参数之一,用于定量表示色谱柱的分离效率（简称柱效）。

N取决于固定相的种类、性质（粒度、粒径分布等）、填充状况、柱长、流动相的种类和流速及测定柱效所用物质的性质。

如果峰形对称并符合正态分布，N可近似表示为：理论塔板数=5.54(保留时间/半高峰宽)2 (2是平方)柱效率用理论塔板数定量地表示：N=16*（t/w ）2。

其中，t是溶质从进样到最大洗脱峰出现的时间，w为该溶质的洗脱峰在基线处的宽度。

在一色谱柱中用相同的洗脱条件时候，不同化合物的滞留时间与其洗脱峰宽度之比接近常数。

因此理论塔板数大的色谱柱效率高。

当然，N的大小和柱子长度有密切关系：理论塔板高度H=柱长/N，用H可以衡量单位长度的色谱柱的效率，H越小，则色谱柱效率越高。

N为常量时，W随tR成正比例变化。

在一张多组分色谱图上，如果各组份含量相当，则后洗脱的峰比前面的峰要逐渐加宽，峰高则逐渐降低。

用半峰宽计算理论塔板数比用峰宽计算更为方便和常用，因为半峰宽更容易准确测定，尤其是对稍有拖尾的峰。

N与柱长成正比，柱越长，N越大。

用N表示柱效时应注明柱长，，如果未注明，则表示柱长为1米时的理论塔板数。

（一般HPLC柱的N在1000以上。

）若用调整保留时间（tR’）计算理论塔板数，所得值称为有效理论塔板数（N有效或Neff）=16(tR’/W)2处理方法理论塔板数下降后可以考虑色谱柱再生1.反相柱分别用甲醇:水=90:10,纯甲醇（HPLC级）,异丙醇（HPLC级）,二氯甲烷（HPL C级）等溶剂作为流动相,依次冲洗,每种流动相流经色谱柱不少于20倍的色谱柱体积.然后再以相反的次序冲洗.2.正相柱分别用正己烷（HPLC级）,异丙醇（HPLC级）,二氯甲烷（HPLC级）,甲醇（H PLC级）等溶剂做流动相,顺次冲洗,每种流动相流经色谱柱不少于20倍的柱体积(异丙醇粘度大,可降低流速,避免压力过高).注意使用溶剂的次序不要颠倒,用甲醇冲洗完后,再以相反的次序冲洗至正己烷.所有的流动相必须严格脱水.3.离子交换柱长时间在缓冲溶液中使用和进样,将导致色谱柱离子交换能力下降,.用稀酸缓冲溶液冲洗可以使阳离子柱再生,反之,用稀碱缓冲溶液冲洗可以使阴离子柱再生.另外,还可以选择能溶解柱内污染物的溶剂为流动相做正方向和反方向冲洗.但再生后的色谱柱柱效是不可能恢复到新柱的水平的.如果柱子装反了,可以调回来,但可能会造成柱内担体塌陷.在不得已的情况下尽量不要反装色谱柱.梯度洗脱科技名词定义中文名称：梯度洗脱英文名称：gradient elution定义：梯度性地改变洗脱液的组分(成分、离子强度等)或pH，以期将层析柱上不同的组分洗脱出来的方法。