chap13_stata面板数据分析

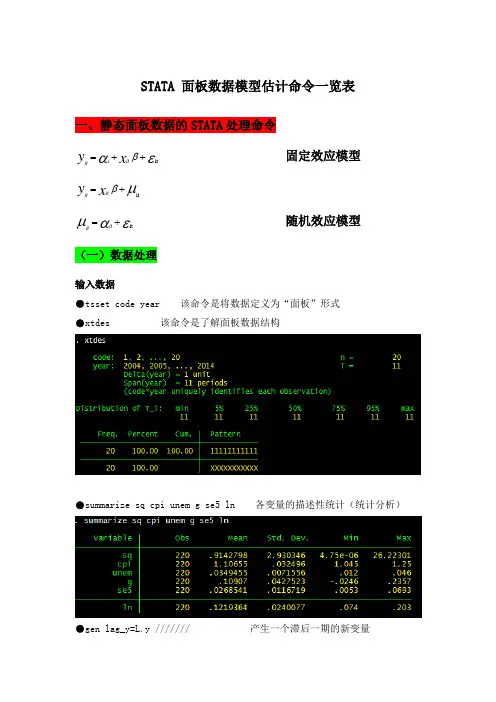
STATA 面板数据模型估计命令一览表 一、静态面板数据的STATA 处理命令εαβit ++=x y it i it 固定效应模型μβit +=x y it itεαμit +=it it 随机效应模型（一）数据处理输入数据●tsset code year 该命令是将数据定义为“面板”形式●xtdes 该命令是了解面板数据结构●summarize sq cpi unem g se5 ln 各变量的描述性统计（统计分析）●gen lag_y=L.y /////// 产生一个滞后一期的新变量gen F_y=F.y /////// 产生一个超前项的新变量gen D_y=D.y /////// 产生一个一阶差分的新变量gen D2_y=D2.y /////// 产生一个二阶差分的新变量（二）模型的筛选和检验●1、检验个体效应（混合效应还是固定效应）（原假设：使用OLS混合模型）●xtreg sq cpi unem g se5 ln,fe对于固定效应模型而言，回归结果中最后一行汇报的F统计量便在于检验所有的个体效应整体上显著。

在我们这个例子中发现F统计量的概率为0.0000，检验结果表明固定效应模型优于混合OLS模型。

●2、检验时间效应（混合效应还是随机效应）（检验方法：LM统计量）（原假设：使用OLS混合模型）●qui xtreg sq cpi unem g se5 ln,re (加上“qui”之后第一幅图将不会呈现) xttest0可以看出，LM检验得到的P值为0.0000，表明随机效应非常显著。

可见，随机效应模型也优于混合OLS模型。

●3、检验固定效应模型or随机效应模型（检验方法：Hausman检验）原假设：使用随机效应模型（个体效应与解释变量无关）通过上面分析，可以发现当模型加入了个体效应的时候，将显著优于截距项为常数假设条件下的混合OLS模型。

但是无法明确区分FE or RE的优劣，这需要进行接下来的检验，如下：Step1：估计固定效应模型，存储估计结果Step2：估计随机效应模型，存储估计结果Step3：进行Hausman检验●qui xtreg sq cpi unem g se5 ln,feest store fequi xtreg sq cpi unem g se5 ln,reest store rehausman fe (或者更优的是hausman fe,sigmamore/ sigmaless)可以看出，hausman检验的P值为0.0000，拒绝了原假设，认为随机效应模型的基本假设得不到满足。

STATA面板数据模型操作命令讲解编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（STATA面板数据模型操作命令讲解）的内容能够给您的工作和学习带来便利。

同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。

本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为STATA面板数据模型操作命令讲解的全部内容。

STATA 面板数据模型估计命令一览表一、静态面板数据的STATA 处理命令 固定效应模型εαβit ++=x y it i it μβit +=x y it it随机效应模型εαμit +=it it (一）数据处理输入数据●tsset code year 该命令是将数据定义为“面板”形式●xtdes 该命令是了解面板数据结构●summarize sq cpi unem g se5 ln 各变量的描述性统计(统计分析)●gen lag_y=L.y /////// 产生一个滞后一期的新变量gen F_y=F 。

y /////// 产生一个超前项的新变量gen D_y=D.y /////// 产生一个一阶差分的新变量gen D2_y=D2。

y /////// 产生一个二阶差分的新变量（二）模型的筛选和检验●1、检验个体效应（混合效应还是固定效应)（原假设：使用OLS混合模型）●xtreg sq cpi unem g se5 ln，fe对于固定效应模型而言，回归结果中最后一行汇报的F统计量便在于检验所有的个体效应整体上显著。

在我们这个例子中发现F统计量的概率为0。

0000，检验结果表明固定效应模型优于混合OLS模型。

●2、检验时间效应(混合效应还是随机效应)(检验方法:LM统计量）(原假设:使用OLS混合模型)●qui xtreg sq cpi unem g se5 ln，re （加上“qui"之后第一幅图将不会呈现）xttest0可以看出，LM检验得到的P值为0.0000，表明随机效应非常显著。

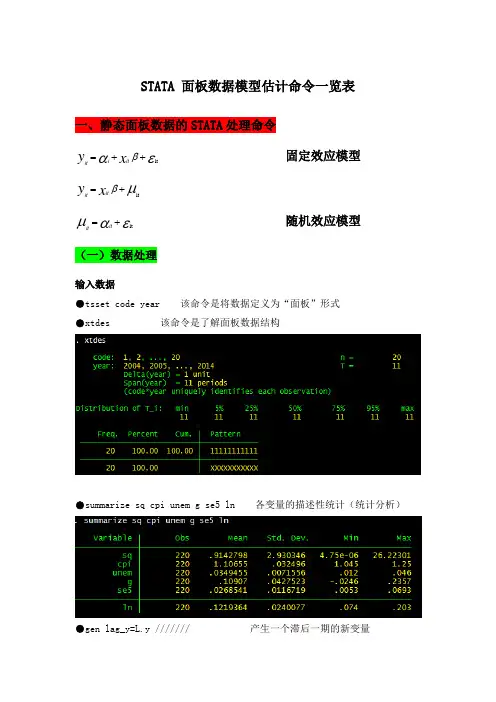
STATA 面板数据模型估计命令一览表 一、静态面板数据的STATA 处理命令εαβit ++=x y it i it 固定效应模型μβit +=x y it itεαμit +=it it 随机效应模型（一）数据处理输入数据●tsset code year 该命令是将数据定义为“面板”形式●xtdes 该命令是了解面板数据结构●summarize sq cpi unem g se5 ln 各变量的描述性统计（统计分析）●gen lag_y=L.y /////// 产生一个滞后一期的新变量gen F_y=F.y /////// 产生一个超前项的新变量gen D_y=D.y /////// 产生一个一阶差分的新变量gen D2_y=D2.y /////// 产生一个二阶差分的新变量（二）模型的筛选和检验●1、检验个体效应（混合效应还是固定效应）（原假设：使用OLS混合模型）●xtreg sq cpi unem g se5 ln,fe对于固定效应模型而言，回归结果中最后一行汇报的F统计量便在于检验所有的个体效应整体上显著。

在我们这个例子中发现F统计量的概率为0.0000，检验结果表明固定效应模型优于混合OLS模型。

●2、检验时间效应（混合效应还是随机效应）（检验方法：LM统计量）（原假设：使用OLS混合模型）●qui xtreg sq cpi unem g se5 ln,re (加上“qui”之后第一幅图将不会呈现) xttest0可以看出，LM检验得到的P值为0.0000，表明随机效应非常显著。

可见，随机效应模型也优于混合OLS模型。

●3、检验固定效应模型or随机效应模型（检验方法：Hausman检验）原假设：使用随机效应模型（个体效应与解释变量无关）通过上面分析，可以发现当模型加入了个体效应的时候，将显著优于截距项为常数假设条件下的混合OLS模型。

但是无法明确区分FE or RE的优劣，这需要进行接下来的检验，如下：Step1：估计固定效应模型，存储估计结果Step2：估计随机效应模型，存储估计结果Step3：进行Hausman检验●qui xtreg sq cpi unem g se5 ln,feest store fequi xtreg sq cpi unem g se5 ln,reest store rehausman fe (或者更优的是hausman fe,sigmamore/ sigmaless)可以看出，hausman检验的P值为0.0000，拒绝了原假设，认为随机效应模型的基本假设得不到满足。

经济统计学中的面板数据分析面板数据分析是经济统计学中的一项重要研究方法，它能够提供更加全面和准确的经济数据分析结果。

在经济学领域，我们经常需要研究多个个体或单位在不同时间点上的经济行为和变化趋势。

传统的横截面数据和时间序列数据分析方法无法完全满足这种需求，而面板数据分析则能够充分利用横截面和时间序列的信息，从而更好地解释和预测经济现象。

面板数据是指在一段时间内对多个个体或单位进行观察和测量的数据。

这些个体可以是不同的国家、地区、企业或个人，而时间可以是连续的或离散的。

面板数据分析的核心思想是将个体和时间作为两个维度，通过同时考虑个体和时间的变化，来探索它们之间的关系和影响。

面板数据分析方法的一个重要应用是面板回归分析。

面板回归模型可以通过同时考虑个体特征和时间变化，来解释和预测经济现象。

在面板回归模型中，我们可以引入个体固定效应和时间固定效应，以控制个体间和时间间的异质性。

这样一来，我们就能够更准确地估计变量之间的关系，并得出更可靠的结论。

除了面板回归模型，面板数据分析还可以应用于其他经济统计学方法，如面板单位根检验、面板协整分析和面板数据的动态模型等。

这些方法在经济学研究中起着重要的作用，能够帮助我们深入理解经济现象的本质和规律。

面板数据分析的优势在于它能够提供更加精确和全面的经济数据分析结果。

相比传统的横截面数据和时间序列数据分析方法，面板数据分析能够更好地控制个体和时间的异质性，从而减少估计误差和偏差。

此外，面板数据分析还能够提供更多的信息，比如个体间的相关性和时间的趋势性，从而更好地解释经济现象和预测未来趋势。

然而，面板数据分析也存在一些挑战和限制。

首先，面板数据的获取和整理相对困难，需要耗费大量的时间和精力。

其次，面板数据中可能存在缺失值和异常值，需要进行适当的处理和修正。

另外，面板数据分析方法的选择和应用也需要根据具体问题和数据特点进行合理的判断和决策。

总之，经济统计学中的面板数据分析是一种重要的研究方法，能够提供更加全面和准确的经济数据分析结果。

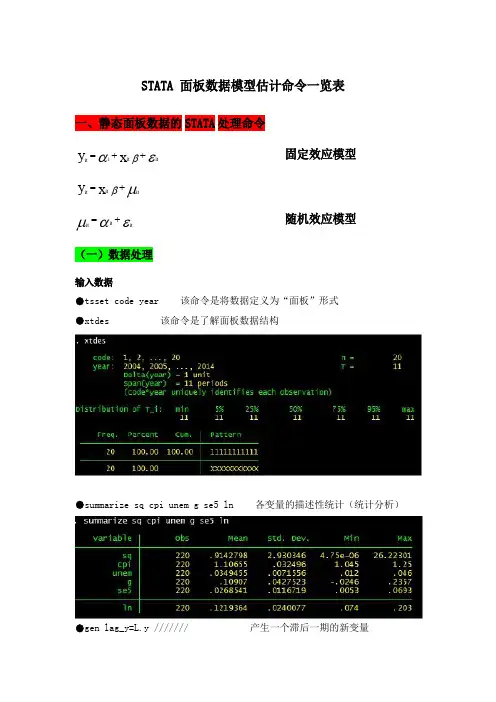
STATA面板数据模型估计命令一览表一、静态面板数据的STATA处理命令y it=αi+x itβ+εit固定效应模型y it=x itβ+μitμit=αit+εit随机效应模型（一）数据处理输入数据●tsset code year该命令是将数据定义为“面板”形式●xtdes该命令是了解面板数据结构●summarize sq cpi unem g se5ln各变量的描述性统计（统计分析）●gen lag_y=L.y///////产生一个滞后一期的新变量gen F_y=F.y///////产生一个超前项的新变量gen D_y=D.y///////产生一个一阶差分的新变量gen D2_y=D2.y///////产生一个二阶差分的新变量（二）模型的筛选和检验●1、检验个体效应（混合效应还是固定效应）（原假设：使用OLS混合模型）●xtreg sq cpi unem g se5ln,fe对于固定效应模型而言，回归结果中最后一行汇报的F统计量便在于检验所有的个体效应整体上显著。

在我们这个例子中发现F统计量的概率为0.0000，检验结果表明固定效应模型优于混合OLS模型。

●2、检验时间效应（混合效应还是随机效应）（检验方法：LM统计量）（原假设：使用OLS混合模型）●qui xtreg sq cpi unem g se5ln,re(加上“qui”之后第一幅图将不会呈现) xttest0可以看出，LM检验得到的P值为0.0000，表明随机效应非常显著。

可见，随机效应模型也优于混合OLS模型。

●3、检验固定效应模型or随机效应模型（检验方法：Hausman检验）原假设：使用随机效应模型（个体效应与解释变量无关）通过上面分析，可以发现当模型加入了个体效应的时候，将显著优于截距项为常数假设条件下的混合OLS模型。

但是无法明确区分FE or RE的优劣，这需要进行接下来的检验，如下：Step1：估计固定效应模型，存储估计结果Step2：估计随机效应模型，存储估计结果Step3：进行Hausman检验●qui xtreg sq cpi unem g se5ln,feest store fequi xtreg sq cpi unem g se5ln,reest store rehausman fe(或者更优的是hausman fe,sigmamore/sigmaless)可以看出，hausman检验的P值为0.0000，拒绝了原假设，认为随机效应模型的基本假设得不到满足。

STATA面板数据模型操作命令讲解面板数据模型主要用于分析在一段时间内，多个个体上观察到的数据。

在面板数据模型中，个体可以是个人、家庭、公司等。

面板数据模型的分析主要包括汇总统计、描述性统计、回归分析等。

下面是一些STATA中常用的面板数据分析命令的介绍和使用说明：1. xtset命令：该命令用于设置数据集的面板数据特征。

在使用面板数据模型之前，需要先将数据集设置为面板数据。

使用xtset命令可以指定面板数据集的个体维度和时间维度。

示例：xtset id year该命令将数据集按照id（个体）和year（时间）进行分类。

2. xtsummary命令：该命令用于生成面板数据的汇总统计信息，包括平均值、标准差、最小值、最大值等。

示例：xtsummary var1 var2该命令将变量var1和var2的汇总统计信息显示出来。

3. xtreg命令：该命令用于进行固定效应模型（Fixed Effects Model）的估计，其中个体效应被视为固定参数，时间效应被视为随机参数。

示例：xtreg y x1 x2, fe该命令将变量y对x1和x2进行固定效应模型估计。

4. xtfe命令：该命令用于进行固定效应模型的估计，并提供了更多的选项和功能。

示例：xtfe y x1 x2, vce(robust)该命令将变量y对x1和x2进行固定效应模型估计，并使用鲁棒标准误。

5. xtlogit命令：该命令用于进行面板Logistic回归分析，适用于因变量为二分类变量的情况。

示例：xtlogit y x1 x2, re该命令将变量y对x1和x2进行面板Logistic回归分析，并进行随机效应的估计。

6. areg命令：该命令用于进行差别法（Difference-in-Differences）模型的估计，适用于时间和个体差异的面板数据分析。

上述命令只是STATA中一部分常用的面板数据模型操作命令。

在实际应用中，根据具体的研究需求和数据特征，还可以使用其他面板数据模型命令进行分析，如xtlogit、xtprobit等。

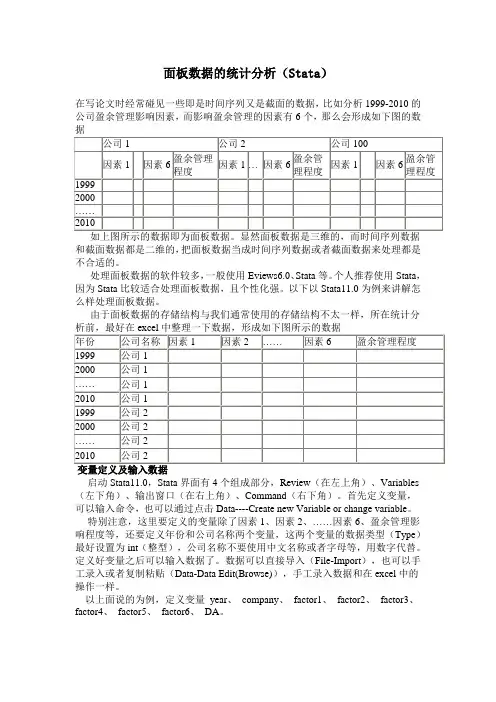
面板数据的统计分析（Stata）在写论文时经常碰见一些即是时间序列又是截面的数据，比如分析1999-2010的公司盈余管理影响因素，而影响盈余管理的因素有6个，那么会形成如下图的数和截面数据都是二维的，把面板数据当成时间序列数据或者截面数据来处理都是不合适的。

处理面板数据的软件较多，一般使用Eviews6.0、Stata等。

个人推荐使用Stata，因为Stata比较适合处理面板数据，且个性化强。

以下以Stata11.0为例来讲解怎么样处理面板数据。

由于面板数据的存储结构与我们通常使用的存储结构不太一样，所在统计分启动Stata11.0，Stata界面有4个组成部分，Review（在左上角）、Variables （左下角）、输出窗口（在右上角）、Command（右下角）。

首先定义变量，可以输入命令，也可以通过点击Data----Create new Variable or change variable。

特别注意，这里要定义的变量除了因素1、因素2、……因素6、盈余管理影响程度等，还要定义年份和公司名称两个变量，这两个变量的数据类型（Type）最好设置为int（整型），公司名称不要使用中文名称或者字母等，用数字代替。

定义好变量之后可以输入数据了。

数据可以直接导入（File-Import），也可以手工录入或者复制粘贴（Data-Data Edit(Browse)），手工录入数据和在excel中的操作一样。

以上面说的为例，定义变量year、company、factor1、factor2、factor3、factor4、factor5、factor6、DA。

变量company 和year分别为截面变量和时间变量。

显然，通过这两个变量我们可以非常清楚地确定panel data 的数据存储格式。

因此，在使用STATA 估计模型之前，我们必须告诉它截面变量和时间变量分别是什么，所用的命令为tsset，命令为：tsset company year输出窗口将输出相应结果。

Stata面板数据回归分析中的倾向得分匹配方法面板数据回归分析是经济学和社会科学研究中常用的方法之一，能够帮助研究者研究变量之间的关系。

然而，在面板数据回归分析中，处理观测数据之间的非随机性分布可能会导致结果的偏误。

为了解决这个问题，倾向得分匹配方法被引入到面板数据回归分析中，该方法能够降低处理效应的偏误，提高研究的可靠性。

一、倾向得分匹配方法的基本原理倾向得分匹配方法是一种非随机化的处理效应评估方法，它的基本原理是通过在处理组和对照组之间寻找类似的个体来减少处理效应的偏误。

具体而言，倾向得分匹配方法首先根据个体的一些特征和自变量，建立预测处理的倾向得分模型。

然后，根据该模型计算出每个个体的倾向得分，并将处理组的个体与对照组的个体进行匹配。

最后，通过对匹配的样本进行回归分析来评估处理效应。

二、倾向得分匹配方法的步骤1. 数据准备：在进行倾向得分匹配方法之前，我们需要准备好面板数据，确保数据的可靠性和完整性。

同时，将个体的一些特征和自变量作为匹配的指标。

2. 倾向得分模型的建立：倾向得分模型是通过将处理组的个体与对照组的个体进行比较，找出其特征与处理状态之间的关系，并验证该模型的拟合度。

建立倾向得分模型可以使用Logistic回归模型，也可以使用其他适合的模型，如贝叶斯回归、决策树等。

3. 计算倾向得分：在建立完倾向得分模型后，根据该模型计算每个个体的倾向得分。

倾向得分通常是在0到1之间的概率值，表示个体属于处理组的概率。

4. 匹配处理组和对照组个体：接下来，根据计算得到的倾向得分，将处理组的个体与对照组的个体进行匹配。

一般而言，可以使用最近邻匹配、卡尺匹配、卡尔曼滤波匹配等方法将倾向得分相似的个体进行配对。

5. 分析匹配样本：在完成匹配后，我们可以对匹配的样本进行回归分析，以评估处理效应。

在回归分析中，通常应该控制其他可能影响结果的因素，以达到更准确的结论。

三、倾向得分匹配方法的优点与应用1. 减少选择性偏误：倾向得分匹配方法可以通过减小处理组和对照组之间的差异，降低选择性偏误的发生。

STATA⾯板数据模型操作命令讲解STATA ⾯板数据模型估计命令⼀览表⼀、静态⾯板数据的STATA 处理命令εαβit ++=xy itiit固定效应模型µβit +=xy ititεαµit+=itit随机效应模型（⼀）数据处理输⼊数据●tsset code year 该命令是将数据定义为“⾯板”形式●xtdes 该命令是了解⾯板数据结构●summarize sq cpi unem g se5 ln 各变量的描述性统计（统计分析）●gen lag_y=L.y /////// 产⽣⼀个滞后⼀期的新变量gen F_y=F.y /////// 产⽣⼀个超前项的新变量gen D_y=D.y /////// 产⽣⼀个⼀阶差分的新变量gen D2_y=D2.y /////// 产⽣⼀个⼆阶差分的新变量（⼆）模型的筛选和检验●1、检验个体效应（混合效应还是固定效应）（原假设：使⽤OLS混合模型）●xtreg sq cpi unem g se5 ln,fe对于固定效应模型⽽⾔，回归结果中最后⼀⾏汇报的F统计量便在于检验所有的个体效应整体上显著。

在我们这个例⼦中发现F统计量的概率为0.0000，检验结果表明固定效应模型优于混合OLS模型。

●2、检验时间效应（混合效应还是随机效应）（检验⽅法：LM统计量）（原假设：使⽤OLS混合模型）●qui xtreg sq cpi unem g se5 ln,re (加上“qui”之后第⼀幅图将不会呈现) xttest0可以看出，LM检验得到的P值为0.0000，表明随机效应⾮常显著。

可见，随机效应模型也优于混合OLS模型。

●3、检验固定效应模型or随机效应模型（检验⽅法：Hausman检验）原假设：使⽤随机效应模型（个体效应与解释变量⽆关）通过上⾯分析，可以发现当模型加⼊了个体效应的时候，将显著优于截距项为常数假设条件下的混合OLS模型。

但是⽆法明确区分FE or RE的优劣，这需要进⾏接下来的检验，如下：Step1：估计固定效应模型，存储估计结果Step2：估计随机效应模型，存储估计结果Step3：进⾏Hausman检验●qui xtreg sq cpi unem g se5 ln,feest store fequi xtreg sq cpi unem g se5 ln,reest store rehausman fe (或者更优的是hausman fe,sigmamore/ sigmaless)可以看出，hausman检验的P值为0.0000，拒绝了原假设，认为随机效应模型的基本假设得不到满⾜。

Stata软件操作教程第15章：面板数据分析面板数据是指在时间上具有一定连续性的多个个体观测值，例如不同地区连续多年的经济数据、同一个企业在多个时间点的财务数据等。

面板数据具有时间序列和截面两个维度，因此在分析面板数据时需要考虑个体间的相关性和时间序列的影响。

在Stata中，面板数据的操作和分析可以使用如下的一些命令：1. 导入面板数据：使用`use`命令导入面板数据文件，例如`use filename, clear`，其中filename为数据文件名。

2. 面板数据的描述性统计：使用`summarize`命令计算面板数据的平均值、标准差等描述性统计量。

例如，`summarize varname, detail`计算变量varname的描述性统计量。

3. 面板数据的时间序列图：使用`tsline`命令绘制面板数据的时间序列图。

例如，`tsline varname`绘制变量varname的时间序列图。

4. 固定效应模型（Fixed Effects Model）：使用`xtreg`命令估计固定效应模型，该模型考虑了个体间的固定效应。

例如，`xtreg dependent var independent var, fe`估计固定效应模型。

5. 随机效应模型（Random Effects Model）：使用`xtreg`命令估计随机效应模型，该模型考虑了个体间的随机效应。

例如，`xtreg dependent var independent var, re`估计随机效应模型。

6. 混合效应模型（Mixed Effects Model）：使用`xtmixed`命令估计混合效应模型，该模型既考虑了个体间的固定效应，又考虑了个体间的随机效应。

例如，`xtmixed dependent var independent var ，groupvar:`估计混合效应模型。

7. 模型检验和诊断：使用`xttest0`命令进行固定效应模型的F检验；使用`xtserial`命令进行个体效应的序列相关性检验；使用`xtgee`命令进行广义估计方程的估计和推断。

Chp8 Panel Data一直想把看Panel模型时的感悟整理成笔记，但终因懒惰而未能成行。

今天终于下决心开了个头，可遗憾的是，这个开头却是从本章的结尾写起，因为这一部分最容易写。

不过，凡事有了好的开头基本上也算成功一半了，所以后面的整理工作还要有劳各位的督促。

文中的不足还望不吝指出。

8.1简介8.2一般模型8.2.1固定效应模型（Fixed Effect Model）8.2.2随机效应模型（Random Effect Model）8.3自相关性8.4动态Panel Data8.5门槛Panel Data8.6非稳定Panel Data及协整8.7Panel V AR8.8Stata8.0实现在介绍了Panel Data的基本理论后，下面我们介绍如何使用STATA8.0软件包来实现模型的估计。

前面我们已经提到，Panel Data具有如下数据存储格式：company year invest mvalue11951755.94833.011952891.24924.9119531304.46241.7119541486.75593.621951588.22289.521952645.52159.421953641.02031.321954459.32115.531951135.21819.431952157.32079.731953179.52371.631954189.62759.9其中，变量company和year分别为截面变量和时间变量。

显然，通过这两个变量我们可以非常清楚地确定panel data的数据存储格式。

因此，在使用STATA8.0估计模型之前，我们必须告诉它截面变量和时间变量分别是什么，所用的命令为tsset1，命令格式如下：tsset panelvar timevar这里需要指出的是，由于Panel Data本身兼具截面数据和时间序列二者的特性，所以对时间序列进行操作的运算同样可以应用到Panel Data身上。

STATA 面板数据模型估计命令一览表一、静态面板数据的 STATA 处理命令固定效应模型随机效应模型（一）数据处理输入数据• tsset code year 该命令是将数据定义为“面板”形式 • xtdes该命令是了解面板数据结构・ xtdescode: 1i 2, ■■■( 20n 工 20 year : 3004, 2005, ■…,2014T =11Delta(year) =1 unit span(year) =11 periods(code*year uniquely identifies eachobservation)Distribution of:min 8%2璃50^ 75% 95%max1111 11111111 11Freq. Percent Cum. Pattern20 100.00 100.00 1111111111120100.00XXXXXXXXXXX・ summarize sc I cpi unem gse5 InvariableObs Mean Std ・ Dev.Mi nMax sq 220 .Q142798 2.9303464.75e-0626.22301cpi2201*10655 *032496 1.045 1. 25 unem22Q .0349455 .0071556 .012 ,046 g220,10907 .0427523 0246 .2357220 .0268541 011671? .0053.0693220.1219364.0240077,074,203• summarize sq cpi unem g se5 In各变量的描述性统计（统计分析）• gen lag_y=L.y ///////产生一个滞后一期的新变量*= Xitit• ;itto U 一 if对于固定效应模型而言，回归结果中最后一行汇报的F 统计量便在于检验所 有的个体效应整体上显著。

stata⾯板数据计量知识及参考资料计量知识：1、横截⾯数据、时间序列、⾯板数据：横截⾯数据是在同⼀时间，不同统计单位相同统计指标组成的数据列。

横截⾯数据是按照统计单位排列的。

因此，横截⾯数据不要求统计对象及其范围相同，但要求统计的时间相同。

也就是说必须是同⼀时间截⾯上的数据。

,Pr i t emium ,1Pr i t emiun -H A Turnover Tutnover A H Size +/H A H SO SO +22/A H σσDummy时间序列数据：在不同时间点上收集到的数据，这类数据反映了某⼀事物、现象等随时间的变化状态或程度。

⾯板数据：是截⾯数据与时间序列数据综合起来的⼀种数据类型。

其有时间序列和截⾯两个维度，当这类数据按两个维度排列时，是排在⼀个平⾯上，与只有⼀个维度的数据排在⼀条线上有着明显的不同，整个表格像是⼀个⾯板,所以把panel data 译作“⾯板数据”。

举例：如：城市名：北京、上海、重庆、天津的GDP 分别为10、11、9、8（单位亿元）。

这就是截⾯数据，在⼀个时间点处切开，看各个城市的不同就是截⾯数据。

如：2000、2001、2002、2003、2004各年的北京市GDP 分别为8、9、10、11、12（单位亿元）。

这就是时间序列，选⼀个城市，看各个样本时间点的不同就是时间序列。

如：2000、2001、2002、2003、2004各年中国所有直辖市的GDP 分别为：北京市分别为8、9、10、11、12；上海市分别为9、10、11、12、13；天津市分别为5、6、7、8、9；重庆市分别为7、8、9、10、11（单位亿元）。

这就是⾯板数据。

*变量合并2、截⾯数据，多重共线性和异⽅差都需要考虑，截⾯数据不需要检测DW 值！你做出来R ⽅⽐较⼩，可能原因是你的回归⽅程中没有纳⼊关键变量，建议你采⽤逐步回归⽅法，以提⾼R ⽅！对于截⾯数据来说，R ⽅⼀般在0.7左右都能接受！相关分析不是必要做的，在模型中加⼊什么变量进⾏回归，主要是依据前期的理论分析和研究⽬的！仅就计量回归⽽⾔，这些步骤只是告诉你，⾃变量与因变量的相关性会影响变量在模型中的显著性，⽽⾃变量间的相关则会带来多重共线性！3、线性相关，也叫⾃相关：可以⽤来看x和y的相关性，常⽤来考察各个x ⾃变量之间是否存在相关关系。

【原创】5分钟搞定Stata面板数据分析简易教程ver2.0作者：张达5分钟搞定Stata面板数据分析简易教程步骤一：导入数据原始表如下，数据请以时间（1998，1999，2000，2001⋯⋯）为横轴，样本名（北京，天津，河北⋯⋯）为纵轴将中文地名替换为数字。

注意：表中不能有中文字符，否则会出现错误。

面板数据中不能有空值。

去除年份的一行，将其余部分复制到stata的data editor中，或保存为csv格式。

打开stata，调用数据。

方法一：直接复制到data editor中。

方法二：使用口令：insheet using 文件路径调用例如：insheet using C:\STUDY\paper\taxi.csv 其中csv格式可用excel的“另存为”导出如图：步骤二：调整格式首先请将代表样本的var1重命名口令：rename var1 样本名例如：rename var1 province也可直接在var1处双击，在弹出的窗口中修改:接下来将数据转化为面板数据的格式口令：reshape long var, i(样本名)例如：reshape long var, i(province)其中var代表的是所有的年份（var2,var3,var4⋯⋯）转化后的格式如图：转化成功后继续重命名，其中_j 这里代表原始表中的年份，var代表该变量的名称口令例如：rename _j yearrename var taxi也可直接在需要修改的名称处双击，在弹出的窗口中修改如图：步骤三：排序口令：sort 变量名例如：sort province year意思为将province按升序排列，然后再根据排好的province数列排year这一列如图：（虽然很多时候在执行sort前数据就已经符合要求了，但以防万一请务必执行此操作）最后，保存。

至此，一个变量的前期数据处理就完成了，请如法炮制的处理所有的变量，也就是说每个变量都做一个dta文件。

Stata面板数据回归分析理论与实践面板数据回归分析是计量经济学中一种常用的经验分析方法，它结合了时间序列数据与横截面数据的特点，能够有效地控制个体之间的异质性，并提供更为准确的估计结果。

Stata软件作为一种功能强大、使用方便的统计分析工具，广泛应用于面板数据回归分析的实践中。

本文将介绍Stata面板数据回归分析的基本理论和实践技巧。

一、面板数据回归分析的基本理论面板数据回归分析要求样本数据包含时间维度和个体维度，其中时间维度表示时间序列，个体维度表示横截面数据。

在进行面板数据回归分析之前，需要对数据进行合理的整理和准备工作。

首先，应对数据进行面板单位的定义和标识，即确定个体和时间的标识符。

常见的面板单位标识符有个体编号和时间标识，可以用数字或字符进行表示。

其次，需要进行面板数据的平衡性检验。

平衡面板数据是指同一时间期内没有个体缺失的数据，通常是为了保证面板数据的可靠性而进行的处理。

最后，应对面板数据进行描述性分析，包括统计个体和时间的数量、观测变量的分布情况等。

这些分析可以帮助我们更好地理解数据的特征和结构。

二、Stata面板数据回归分析的实践技巧在使用Stata软件进行面板数据回归分析时，需要掌握一些常用的命令和技巧，以便有效地进行数据操作和模型估计。

1. 面板数据的导入和保存使用Stata软件导入面板数据的基本命令是"import"，可以导入多种格式的数据文件，如Excel文件、文本文件等。

导入后的数据可以使用"save"命令保存为Stata数据文件格式，方便后续的分析和处理。

2. 面板数据的变量操作在进行面板数据回归分析时，可能需要对数据进行变量操作，如生成新的变量、删除不需要的变量等。

Stata提供了一系列的命令，如"generate"、"drop"等，可以帮助我们方便地进行变量操作。

3. 面板数据的描述性统计通过Stata软件提供的命令，可以对面板数据进行描述性统计，包括计算平均值、标准差、相关系数等统计量。

STATA面板数据模型估计命令一览表输入数据•tsset code year 该命令是将数据定义为“面板”形式•xtdes 该命令是了解面板数据结构• summarize sq cpi unem g se5 In 各变量的描述性统计（统计分析）• gen lag_y=L.y /////// 产生一个滞后一期的新变量to U 一 if对于固定效应模型而言，回归结果中最后一行汇报的F 统计量便在于检验所 有的个体效应整体上显著。

在我们这个例子中发现 F 统计量的概率为0.0000 , 检验结果表明固定效应模型优于混合 OLS 模型。

合效应还是随机效应） （检验方法：LM 统计量）（原假设：使用OLS 混合模型） • qui xtreg sq cpi unem g se5 ln,re（加上"qui ”之后第一幅图将不会呈现 ）xttest0xizretg s-<q cpifgen F_y=F.y /////// gen D_y=D.y /////// gen D2_y=D2.y ///////产生一个超前项的新变量 产生一个一阶差分的新变量 产生一个二阶差分的新变量（二）模型的筛选和检验• 1检验个体效应 （混合效应还是固定效应）（原假设：使用OLS 混合模型） • xtreg sq cpi unem g se5 ln,fe3C"t 『U<3 SCI C.IPm feor r Cu iO-23OZ O. O<7i67 O- 匕 Qm -Bk T -:<?■£ f 3 X dmts m 工■zd s d z mAm - -5 -1s u a 工一67 ■r.QB€BJL£3;4M 4Liny;工G-RO 丄 bo --A - « _ QprlsrlQ --mA6.2:sGctg scs0'.x丄z skJ>4y-- -S4S"0 Get 一一一GftlxJ2 IKqg4岭济34工Lu -^-3 ■■MB : od JL X QX 丄炮丄• 2、检验时间效应O- SZ £>&■ J d rn可以看出，LM检验得到的P值为0.0000，表明随机效应非常显著。