tensorflow常用函数介绍

tf.greater函数tf.greater函数是TensorFlow的一个函数，其主要作用是比较两个张量（Tensor）的元素是否符合大于关系。

在本文档中，我们将介绍tf.greater函数的使用方法、函数原型、返回类型以及实例应用。

## 函数原型在TensorFlow中，tf.greater函数的原型定义如下：```python tf.greater(x, y, name=None) ```其中，参数x和y是需要比较的两个张量，name是可选参数，用于给当前操作命名。

## 返回类型tf.greater函数返回的是一个张量（Tensor），其值的类型为bool型。

如果x的某个元素的值大于y的对应元素的值，则返回True，否则返回False。

如果x和y的shape不一样，则会使用广播规则进行自动填充。

例如，如果x的shape为(3,1)，y的shape为(1,4)，则用广播规则将它们自动填充为(3,4)的shape。

## 使用方法tf.greater函数的使用方法非常简单，只需要调用该函数并将需要比较的两个张量作为参数传入即可。

例如，以下代码比较了两个张量x和y的大小关系：```python import tensorflow as tfx = tf.constant([1, 3, 5, 7]) y =tf.constant([3, 1, 7, 5])greater = tf.greater(x, y)with tf.Session() as sess:print(sess.run(greater)) ```该代码将输出结果为：[False True False True]。

这说明，x中第1个元素的值比y中对应的元素的值小，x 中第2个元素的值比y中对应的元素的值大，x中第3个元素的值比y中对应元素的值小，x中第4个元素的值比y中对应的元素的值大。

实际应用时，tf.greater函数常常和其他TensorFlow 函数一起使用。

TensorFlow的embedding函数参数1.导言在使用深度学习进行自然语言处理（N LP）任务时，词嵌入（W or dE mb ed di ng）是一个重要的概念。

它将自然语言中的词语转化为低维稠密向量，可以在机器学习模型中使用。

Te ns or Fl ow是一个广泛应用于深度学习的开源框架，其中的em be dd i ng函数可以帮助我们实现词嵌入的功能。

本文将详细介绍Te ns or Flo w的e mb ed di ng函数以及其参数的使用方法。

2. Te nsorFlo w的e m b e d d i n g函数T e ns or Fl ow的e mbe d di ng函数是一个非常强大和灵活的函数，用于实现词嵌入的功能。

它将一个整数序列作为输入，并将其转换为对应的词嵌入向量序列。

具体来说，e mb ed di ng函数将整数序列表示为矩阵的形式，其中每一行都是一个词嵌入向量。

3. em bedding函数的参数在使用e mb ed di ng函数时，我们可以根据需要设置不同的参数。

下面是一些常用的参数：3.1i n p u t_d i mi n pu t_di m参数指定了输入序列中不同词语的个数。

它是一个正整数。

例如，如果我们的输入序列中有10000个不同的词语，那么i np ut_d im应该设置为10000。

3.2o u t p u t_d i mo u tp ut_d im参数指定了每个词语的词嵌入向量的维度。

它是一个正整数。

例如，如果我们希望每个词语的词嵌入向量是100维的，那么o u tp ut_d im应该设置为100。

3.3i n p u t_l e n g t hi n pu t_le ng th参数指定了输入序列的长度。

它允许我们指定不同序列的长度。

例如，如果我们的输入序列的长度是10，那么i n pu t_le ng th应该设置为10。

3.4e m b e d d i n g s_i n i t i a l i z e re m be dd in gs_i ni tia l iz er参数指定了词嵌入矩阵的初始化方法。

tf函数的用法TensorFlow是一个由谷歌开发、广泛应用于机器学习和深度学习领域的开源软件库。

在TensorFlow中，tf函数是其重要之一的组成部分。

本文将详细介绍tf函数的用法，帮助读者在应用TensorFlow时更加高效、方便地进行代码编写和调试。

1. tf函数简介tf函数是TensorFlow库中封装了一系列常用数学函数或深度学习模块的函数集合。

这些函数大大简化了机器学习模型的设计和实现，同时也极大地加速了模型的训练和测试过程。

tf函数中包含的模块有：数学运算模块、矩阵运算模块、卷积运算模块、激活函数模块、损失函数模块、优化器模块等。

2. 数学运算模块数学运算模块主要包含了常见的算术运算、逻辑运算、统计运算和向量运算等。

例如，可以使用tf.add()函数实现两个张量的加法；使用tf.subtract()函数实现向量的减法等。

这些函数的调用方式也非常简单，例如tf.add(a,b)，其中a和b 是需要相加的两个张量。

调用方式非常方便，大大简化了代码编写的难度。

3. 矩阵运算模块矩阵运算模块主要包含了矩阵加、矩阵减、矩阵点乘、矩阵转置等常见操作。

例如，可以使用tf.matmul()函数实现两个矩阵的点乘；使用tf.transpose()函数实现矩阵的转置等。

这些函数的调用方式也非常简单，且高度优化。

使用TensorFlow 进行矩阵运算时，速度非常快，并且集成了GPU加速功能，但是并不需要显式地写出GPU加速代码，TensorFlow会自动进行加速。

4. 卷积运算模块卷积运算模块主要用于卷积神经网络(Convolutional Neural Networks, CNN)中的卷积运算。

例如，可以使用tf.nn.conv2d()函数实现二维卷积运算；使用tf.nn.conv3d()函数实现三维卷积运算等。

这些函数的调用方式也非常简单，只需传入合适的参数就可以进行卷积运算。

同时，TensorFlow会自动进行优化，使运算速度更快。

一、介绍TensorFlow是一个开源的人工智能框架，它可以用于构建和训练深度神经网络模型。

在TensorFlow中，预测函数是非常重要的一部分，它可以用来计算模型对输入数据的预测结果。

本文将介绍TensorFlow 中预测函数的计算公式及其相关内容。

二、预测函数的计算公式在TensorFlow中，预测函数的计算公式通常遵循以下基本步骤：1. 加权求和输入数据会经过一系列的输入层、隐藏层和输出层，每一层都包含一组权重参数。

在预测函数中，输入数据会分别与对应的权重进行相乘，并将结果进行求和。

这个过程可以用如下公式表示：h = Wx + b其中，h是预测函数的输出，W是权重参数矩阵，x是输入数据，b是偏置项。

2. 激活函数在加权求和之后，通常会使用一个激活函数来对预测结果进行非线性转换。

常见的激活函数包括sigmoid函数、ReLU函数、tanh函数等，它们可以有效地增加模型的表达能力。

激活函数的计算公式如下：a = f(h)其中，a是激活函数的输出，f是激活函数。

3. 输出结果经过激活函数的转换后，我们就可以得到模型对输入数据的预测结果。

在分类问题中，通常会使用softmax函数对预测结果进行归一化，以获得每一类别的概率值。

在回归问题中，预测结果即为最终的输出值。

通过上述三个步骤，我们可以得到TensorFlow中预测函数的计算公式。

这个公式被广泛应用在深度学习模型中，并为模型带来了强大的预测能力。

三、预测函数的优化在实际应用中，预测函数的性能往往会受到多种因素的影响，包括数据质量、模型结构、参数设置等。

为了获得更好的预测性能，我们可以对预测函数进行优化。

以下是一些常见的优化方法：1. 参数调优通过调整模型的超参数，包括学习率、正则化项、批量大小等，可以提高预测函数的泛化能力，从而提升模型的预测性能。

2. 特征工程合理的特征工程可以有助于提取有效的特征信息，从而改进预测函数的输入数据质量，提升模型的预测效果。

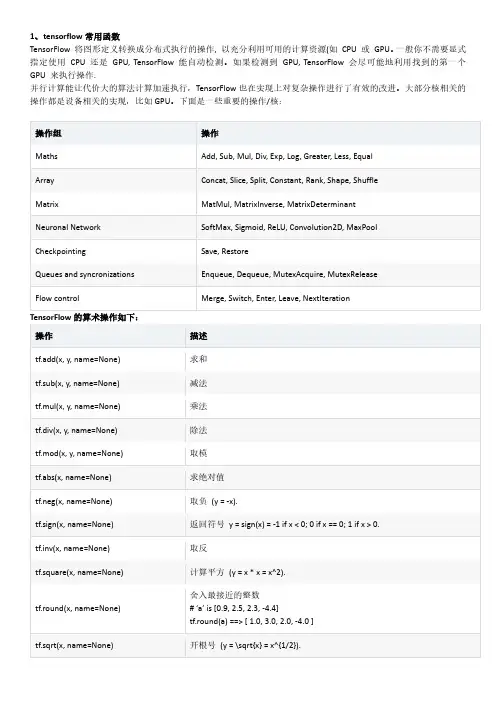
1、tensorflow常用函数TensorFlow 将图形定义转换成分布式执行的操作, 以充分利用可用的计算资源(如CPU 或GPU。

一般你不需要显式指定使用CPU 还是GPU, TensorFlow 能自动检测。

如果检测到GPU, TensorFlow 会尽可能地利用找到的第一个GPU 来执行操作.并行计算能让代价大的算法计算加速执行，TensorFlow也在实现上对复杂操作进行了有效的改进。

大部分核相关的操作都是设备相关的实现，比如GPU。

下面是一些重要的操作/核：操作组操作Maths Add, Sub, Mul, Div, Exp, Log, Greater, Less, EqualArray Concat, Slice, Split, Constant, Rank, Shape, ShuffleMatrix MatMul, MatrixInverse, MatrixDeterminantNeuronal Network SoftMax, Sigmoid, ReLU, Convolution2D, MaxPoolCheckpointing Save, RestoreQueues and syncronizations Enqueue, Dequeue, MutexAcquire, MutexReleaseFlow control Merge, Switch, Enter, Leave, NextIterationTensorFlow的算术操作如下：操作描述tf.add(x, y, name=None) 求和tf.sub(x, y, name=None) 减法tf.mul(x, y, name=None) 乘法tf.div(x, y, name=None) 除法tf.mod(x, y, name=None) 取模tf.abs(x, name=None) 求绝对值tf.neg(x, name=None) 取负(y = -x).tf.sign(x, name=None) 返回符号y = sign(x) = -1 if x < 0; 0 if x == 0; 1 if x > 0.tf.inv(x, name=None) 取反tf.square(x, name=None) 计算平方(y = x * x = x^2).tf.round(x, name=None) 舍入最接近的整数# ‘a’ is [0.9, 2.5, 2.3, -4.4]tf.round(a) ==> [ 1.0, 3.0, 2.0, -4.0 ]tf.sqrt(x, name=None) 开根号(y = \sqrt{x} = x^{1/2}).tf.pow(x, y, name=None) 幂次方# tensor ‘x’ is [[2, 2], [3, 3]]# tensor ‘y’ is [[8, 16], [2, 3]]tf.pow(x, y) ==> [[256, 65536], [9, 27]]tf.exp(x, name=None) 计算e的次方tf.log(x, name=None) 计算log，一个输入计算e的ln，两输入以第二输入为底tf.maximum(x, y, name=None) 返回最大值(x > y ? x : y)tf.minimum(x, y, name=None) 返回最小值(x < y ? x : y)tf.cos(x, name=None) 三角函数cosinetf.sin(x, name=None) 三角函数sinetf.tan(x, name=None) 三角函数tantf.atan(x, name=None) 三角函数ctan张量操作Tensor Transformations•数据类型转换Casting操作描述tf.string_to_number(string_tensor, out_type=None, name=None) 字符串转为数字tf.to_double(x, name=’ToDouble’) 转为64位浮点类型–float64tf.to_float(x, name=’ToFloat’) 转为32位浮点类型–float32tf.to_int32(x, name=’ToInt32’) 转为32位整型–int32tf.to_int64(x, name=’ToInt64’) 转为64位整型–int64tf.cast(x, dtype, name=None) 将x或者x.values转换为dtype# tensor a is [1.8, 2.2], dtype=tf.floattf.cast(a, tf.int32) ==> [1, 2] # dtype=tf.int32•形状操作Shapes and Shaping操作描述tf.shape(input, name=None) 返回数据的shape# ‘t’ is [[[1, 1, 1], [2, 2, 2]], [[3, 3, 3], [4, 4, 4]]] shape(t) ==> [2, 2, 3]tf.size(input, name=None) 返回数据的元素数量# ‘t’ is [[[1, 1, 1], [2, 2, 2]], [[3, 3, 3], [4, 4, 4]]]]size(t) ==> 12tf.rank(input, name=None) 返回tensor的rank注意：此rank不同于矩阵的rank，tensor的rank表示一个tensor需要的索引数目来唯一表示任何一个元素也就是通常所说的“order”, “degree”或”ndims”#’t’ is [[[1, 1, 1], [2, 2, 2]], [[3, 3, 3], [4, 4, 4]]]# shape of tensor ‘t’ is [2, 2, 3]rank(t) ==> 3tf.reshape(tensor, shape, name=None) 改变tensor的形状# tensor ‘t’ is [1, 2, 3, 4, 5, 6, 7, 8, 9]# tensor ‘t’ has shape [9]reshape(t, [3, 3]) ==>[[1, 2, 3],[4, 5, 6],[7, 8, 9]]#如果shape有元素[-1],表示在该维度打平至一维# -1 将自动推导得为9:reshape(t, [2, -1]) ==>[[1, 1, 1, 2, 2, 2, 3, 3, 3],[4, 4, 4, 5, 5, 5, 6, 6, 6]]tf.expand_dims(input, dim, name=None) 插入维度1进入一个tensor中#该操作要求-1-input.dims()# ‘t’ is a tensor of shape [2]shape(expand_dims(t, 0)) ==> [1, 2]shape(expand_dims(t, 1)) ==> [2, 1]shape(expand_dims(t, -1)) ==> [2, 1] <= dim <= input.dims()•切片与合并（Slicing and Joining）操作描述tf.slice(input_, begin, size, name=None) 对tensor进行切片操作其中size[i] = input.dim_size(i) - begin[i]该操作要求0 <= begin[i] <= begin[i] + size[i] <= Di for i in [0, n]#’input’ is#[[[1, 1, 1], [2, 2, 2]],[[3, 3, 3], [4, 4, 4]],[[5, 5, 5], [6, 6, 6]]] tf.slice(input, [1, 0, 0], [1, 1, 3]) ==> [[[3, 3, 3]]]tf.slice(input, [1, 0, 0], [1, 2, 3]) ==>[[[3, 3, 3],[4, 4, 4]]]tf.slice(input, [1, 0, 0], [2, 1, 3]) ==>[[[3, 3, 3]],[[5, 5, 5]]]tf.split(split_dim, num_split, value, name=’split’) 沿着某一维度将tensor分离为num_split tensors # ‘value’ is a tensor with shape [5, 30]# Split ‘value’ into 3 tensors along dimension 1 split0, split1, split2 = tf.split(1, 3, value)tf.shape(split0) ==> [5, 10]tf.concat(concat_dim, values, name=’concat’) 沿着某一维度连结tensort1 = [[1, 2, 3], [4, 5, 6]]t2 = [[7, 8, 9], [10, 11, 12]]tf.concat(0, [t1, t2]) ==> [[1, 2, 3], [4, 5, 6], [7, 8, 9], [10, 11, 12]] tf.concat(1, [t1, t2]) ==> [[1, 2, 3, 7, 8, 9], [4, 5, 6, 10, 11, 12]] 如果想沿着tensor一新轴连结打包,那么可以：tf.concat(axis, [tf.expand_dims(t, axis) for t in tensors])等同于tf.pack(tensors, axis=axis)tf.pack(values, axis=0, name=’pack’) 将一系列rank-R的tensor打包为一个rank-(R+1)的tensor # ‘x’ is [1, 4], ‘y’ is [2, 5], ‘z’ is [3, 6]pack([x, y, z]) => [[1, 4], [2, 5], [3, 6]]# 沿着第一维packpack([x, y, z], axis=1) => [[1, 2, 3], [4, 5, 6]]等价于tf.pack([x, y, z]) = np.asarray([x, y, z])tf.reverse(tensor, dims, name=None) 沿着某维度进行序列反转其中dim为列表，元素为bool型，size等于rank(tensor) # tensor ‘t’ is[[[[ 0, 1, 2, 3],#[ 4, 5, 6, 7],#[ 8, 9, 10, 11]],#[[12, 13, 14, 15],#[16, 17, 18, 19],#[20, 21, 22, 23]]]]# tensor ‘t’ shape is [1, 2, 3, 4]# ‘dims’ is [False, False, False, True]reverse(t, dims) ==>[[[[ 3, 2, 1, 0],[ 7, 6, 5, 4],[ 11, 10, 9, 8]],[[15, 14, 13, 12],[19, 18, 17, 16],[23, 22, 21, 20]]]]tf.transpose(a, perm=None, name=’transpose’) 调换tensor的维度顺序按照列表perm的维度排列调换tensor顺序，如为定义，则perm为(n-1…0)# ‘x’ is [[1 2 3],[4 5 6]]tf.transpose(x) ==> [[1 4], [2 5],[3 6]]# Equivalentlytf.transpose(x, perm=[1, 0]) ==> [[1 4],[2 5], [3 6]] tf.gather(params, indices, validate_indices=None,name=None)合并索引indices所指示params中的切片tf.one_hot(indices, depth, on_value=None, off_value=None, axis=None, dtype=None, name=None) indices = [0, 2, -1, 1] depth = 3on_value = 5.0off_value = 0.0axis = -1#Then output is [4 x 3]: output =[5.0 0.0 0.0] // one_hot(0) [0.0 0.0 5.0] // one_hot(2) [0.0 0.0 0.0] // one_hot(-1) [0.0 5.0 0.0] // one_hot(1)矩阵相关运算操作描述tf.diag(diagonal, name=None) 返回一个给定对角值的对角tensor # ‘diagonal’ is [1, 2, 3, 4]tf.diag(diagonal) ==>[[1, 0, 0, 0][0, 2, 0, 0][0, 0, 3, 0][0, 0, 0, 4]]tf.diag_part(input, name=None) 功能与上面相反tf.trace(x, name=None) 求一个2维tensor足迹，即对角值diagonal之和tf.transpose(a, perm=None, name=’transpose’) 调换tensor的维度顺序按照列表perm的维度排列调换tensor顺序，如为定义，则perm为(n-1…0)# ‘x’ is [[1 2 3],[4 5 6]]tf.transpose(x) ==> [[1 4], [2 5],[3 6]]# Equivalentlytf.transpose(x, perm=[1, 0]) ==> [[1 4],[2 5], [3 6]]tf.matmul(a, b, transpose_a=False,transpose_b=False, a_is_sparse=False, 矩阵相乘tf.matrix_determinant(input, name=None)返回方阵的行列式tf.matrix_inverse(input, adjoint=None,name=None)求方阵的逆矩阵，adjoint 为True 时，计算输入共轭矩阵的逆矩阵tf.cholesky(input, name=None)对输入方阵cholesky 分解，即把一个对称正定的矩阵表示成一个下三角矩阵L 和其转置的乘积的分解A=LL^Ttf.matrix_solve(matrix, rhs, adjoint=None, name=None) 求解tf.matrix_solve(matrix, rhs, adjoint=None, name=None) matrix 为方阵shape 为[M,M],rhs 的shape 为[M,K]，output 为[M,K] 复数操作 操作描述plex(real, imag, name=None)将两实数转换为复数形式# tensor ‘real’ is [2.25, 3.25] # tensor imag is [4.75, 5.75]plex(real, imag) ==> [[2.25 + 4.75j], [3.25 + 5.75j]] plex_abs(x, name=None)计算复数的绝对值，即长度。

conv1d函数Conv1d函数卷积是深度学习模型中常用的操作之一，而在卷积神经网络中，卷积层则是整个模型中最为重要的一环。

在TensorFlow中，我们可以使用conv1d函数来构建卷积层。

一、conv1d函数的基本形式TensorFlow中的conv1d函数可以使用以下形式：```tf.nn.conv1d(input, filters, stride, padding, use_cudnn_on_gpu=None,data_format=None, name=None)```其中，- input：待卷积的输入数据。

它是一个4维的Tensor，形状为[batch_size, input_length, input_channels]。

- filters：卷积核。

它是一个4维的Tensor，形状为[filter_length,input_channels, output_channels]。

- stride：卷积核移动的步长。

它是一个长度为1的整数。

- padding：卷积的边界处理方式。

可以是"VALID"（有效边缘处理）或"SAME"（相同边缘处理）。

- use_cudnn_on_gpu：是否使用CUDA加速。

如果设为True，则使用CUDA加速；如果设为False，则不使用CUDA加速。

默认值是None。

- data_format：数据的格式。

可以是"NHWC"（表示样本数×高×宽×通道数）或"NCHW"（表示样本数×通道数×高×宽）。

默认值是None，表示使用"TWC"格式。

- name：操作的名称。

默认值是None。

二、使用conv1d函数构建卷积层在使用conv1d函数构建卷积层时，我们通常需要依次指定以下三个参数：1. 卷积核的数量```num_filters = 32```这里我们定义了卷积核的数量为32。

tensort view对应的函数摘要：一、引言二、张量视图的概念与作用三、Python中常用的张量视图函数1.TensorFlow中的张量视图函数2.PyTorch中的张量视图函数四、张量视图函数的实际应用与举例五、总结正文：一、引言在深度学习和人工智能领域，张量（Tensor）是处理多维数组的重要数据结构。

张量视图（Tensor View）则是在原有张量基础上，提供了一种更高效地操作和访问张量的方法。

本文将详细介绍张量视图的概念以及对应的函数，并通过实例演示其应用。

二、张量视图的概念与作用张量视图是张量的一种表示方式，可以看作是对张量的一种切片或者子集。

通过张量视图，我们可以更方便地对张量中的特定部分进行操作，而不必修改原始张量。

同时，张量视图可以有效地减少内存占用，提高计算效率。

三、Python中常用的张量视图函数1.TensorFlow中的张量视图函数在TensorFlow中，我们可以通过tf.Tensor.view()函数创建张量视图。

示例代码如下：```pythonimport tensorflow as tfa = tf.constant([[1, 2, 3], [4, 5, 6]])b = a.view([2, 3]) # 从2x3的张量视图```2.PyTorch中的张量视图函数在PyTorch中，我们可以通过torch.Tensor.view()函数创建张量视图。

示例代码如下：```pythonimport torcha = torch.tensor([[1, 2, 3], [4, 5, 6]])b = a.view(2, 3) # 从2x3的张量视图```四、张量视图函数的实际应用与举例假设我们有一个4x4的张量，我们想要提取其对角线上的元素，可以通过张量视图函数来实现。

```pythonimport tensorflow as tfa = tf.constant([[1, 2, 3, 4], [5, 6, 7, 8], [9, 10, 11, 12], [13, 14, 15, 16]])b = a.view([4, 4])```通过上述代码，我们可以得到一个4x4的张量视图。

size_lookup函数的用法(一)Size_lookup函数的用法在深度学习中，我们常常需要将输入数据调整为指定的形状和尺寸。

而size_lookup函数则是一种常用的工具，在TensorFlow中被广泛应用于数据重塑和尺寸调整的场景。

本文将介绍size_lookup函数的用法，希望能对读者有所帮助。

什么是size_lookup函数？size_lookup函数是TensorFlow中的一个操作符，用于查询给定数据的形状和尺寸。

它可以将数据从一个形状转换为另一个形状，同时调整数据的尺寸和维度。

size_lookup函数常用于卷积神经网络、循环神经网络、自编码器等深度学习模型中，以帮助实现数据的重塑和尺寸调整。

size_lookup函数的语法size_lookup函数的语法比较简单，下面是它的基本语法：tf.size_lookup(input, output_shape)其中，input表示待重塑的数据；output_shape表示重塑后的形状。

size_lookup函数的应用下面通过几个例子，来演示size_lookup函数的应用。

例子1：数据重塑假设我们有一个形状为[batch_size, height, width, channels]的数据，现在需要将它重塑为[batch_size, height*width, channels]的形状。

这时，可以使用size_lookup函数来方便地实现数据的重塑。

input= tf.placeholder(tf.float32, shape=[None, 28, 28, 3])output_shape = tf.constant([1,-1,3])output = tf.reshape(input, tf.size_lookup(input, output_shape))在上面的例子中，我们首先定义了一个输入数据input和一个目标形状output_shape，然后使用size_lookup函数查询出目标形状对应的尺寸，并将input按照目标尺寸进行重塑。

tensorflow reshape函数TensorFlow是一个广泛使用的机器学习框架，在深度学习领域有着重要的地位。

其中的reshape函数是一个非常常用的函数，它能够改变张量的形状，为后续的计算提供便利。

本文将详细介绍TensorFlow中的reshape函数及其用法。

一、reshape函数的定义与作用reshape函数是TensorFlow中的一个重要函数，它的作用是改变张量的形状，即重新定义张量的维度。

在深度学习中，数据的维度往往非常重要，而reshape函数能够灵活地改变数据的形状，满足不同计算的需求。

二、reshape函数的基本用法reshape函数的基本用法非常简单，它的语法如下：tf.reshape(tensor, shape)其中，tensor表示需要改变形状的张量，shape表示目标形状。

需要注意的是，改变形状前后张量的元素数量必须保持一致，否则会报错。

下面我们通过一个具体的例子来演示reshape函数的使用。

假设我们有一个形状为(2, 3)的张量t，即有2行3列的矩阵。

我们可以使用reshape函数将其转换为一个形状为(3, 2)的矩阵，代码如下：import tensorflow as tft = tf.constant([[1, 2, 3], [4, 5, 6]])t_reshape = tf.reshape(t, [3, 2])print(t_reshape)运行以上代码，输出结果如下：tf.Tensor([[1 2][3 4][5 6]], shape=(3, 2), dtype=int32)可以看到，原始的(2, 3)矩阵被成功转换为了(3, 2)矩阵。

三、reshape函数的高级用法除了基本的形状转换外，reshape函数还可以实现一些更加复杂的操作。

比如，我们可以使用reshape函数将一个多维数组展平为一维数组，或者将一维数组转换为多维数组。

下面我们通过一些示例来进一步说明reshape函数的高级用法。

tensorflow中的zeros函数详解Tensorflow（简称TF）是谷歌开源的一个数值计算工具包，它可广泛应用于各种机器学习领域，如人工智能、语音处理、自然语言处理等。

在TF中，使用zeros函数可以创建指定大小的全零张量，下面就详细介绍一下这个函数。

一、函数原型在TF中，zeros函数的原型为：```pythontf.zeros(shape,dtype=tf.float32,name=None)```函数参数分别为：- shape：tf.TensorShape对象，指定新张量的形状。

- dtype：tf.DType类型，指定新张量中元素的数据类型。

默认情况下创建的张量类型为tf.float32。

- name：可选参数，张量的名称。

二、函数使用实例下面通过示例来说明zeros函数的使用。

```pythonimport tensorflow as tf# 创建形状为 [2, 3] 的全零浮点型张量a = tf.zeros([2, 3], dtype=tf.float32)# 创建形状为 [3, 3] 的全零整型张量b = tf.zeros([3, 3], dtype=tf.int32)# 输出张量print(a)print(b)```运行上述代码可以得到以下输出：```tf.Tensor([[0. 0. 0.][0. 0. 0.]], shape=(2, 3), dtype=float32)tf.Tensor([[0 0 0][0 0 0][0 0 0]], shape=(3, 3), dtype=int32)```这里我们调用了两次zeros函数，每次都创建了不同形状和数据类型的全零张量。

通过调整shape和dtype参数，我们可以自由地创建不同形状和数据类型的全零张量。

三、函数实现原理在TF中，zeros函数的实现原理其实很简单，它会调用底层的c++库，先创建一个指定大小的全零张量，然后将其转化为TensorFlow 中的张量类型，最后返回。

Tensorflow中dense（全连接层）各项参数TensorFlow中的dense（全连接层）是神经网络中常用的一种层类型。

它可以将输入数据与权重矩阵相乘，并添加偏置项，然后通过激活函数处理最终输出。

在TensorFlow中，dense层的参数包括输入形状、输出形状、权重初始化方法、激活函数等等。

下面将详细介绍每个参数。

1. 输入形状（input_shape）：输入形状是指数据进入dense层的形状。

在TensorFlow中，输入形状可以是一个整数或者一个元组。

例如，如果输入是一个维度为(32, 32, 3)的图像，那么输入形状可以写为(32, 32, 3)。

2. 输出形状（units）：输出形状是指dense层的输出大小。

在TensorFlow中，输出形状可以是一个整数。

例如，如果希望输出一个大小为64的向量，那么输出形状可以写为643. 权重初始化方法（kernel_initializer）：权重初始化方法是指权重矩阵的初始值。

在TensorFlow中，权重矩阵的初始值可以通过选择不同的初始化方法进行设置。

常用的初始化方法包括'glorot_uniform'、'glorot_normal'、'he_uniform'、'he_normal'等。

这些方法可以根据不同的网络架构和任务来选择合适的参数初始化方法。

4. 偏置项初始化方法（bias_initializer）：偏置项初始化方法是指偏置项的初始值。

在TensorFlow中，偏置项的初始值可以通过选择不同的初始化方法进行设置。

常用的初始化方法包括'zeros'、'ones'等。

可以根据具体情况来选择适合的偏置项初始化方法。

5. 权重正则化参数（kernel_regularizer）：权重正则化参数是指权重矩阵的正则化方法。

在TensorFlow中，可以通过'L1'、'L2'等正则化方法来约束权重矩阵的大小。

tensorflow tf.gather_nd的用法TensorFlow中的tf.gather_nd函数是一个非常有用的操作，用于根据给定的索引从给定的张量中获取特定的元素或子集。

它可以用于多种场景，例如提取特定的像素点、从多维数组中提取特定的元素等。

在本文中，我们将详细介绍tf.gather_nd函数的用法，并提供一些示例来帮助读者更好地理解其使用方法。

1. 理解tf.gather_nd的基本用法在TensorFlow中，tf.gather_nd函数的基本语法如下：tf.gather_nd(params, indices, name=None)它接受两个参数：- params：一个张量，表示我们要从中提取元素的源张量。

- indices：一个张量，表示我们要提取的元素的索引。

2. 了解indices的形状在理解tf.gather_nd的使用方法之前，我们首先要了解indices张量的形状。

indices张量的形状决定了我们最终获取的元素的个数。

具体来说，indices张量的形状应为[K, N]，其中K是我们要提取的元素的个数，N是每个元素的索引的维度。

例如，如果我们要从一个2维张量中提取3个元素，则索引张量应具有形状为[3, 2]的形状。

3. 使用tf.gather_nd提取元素接下来，我们将使用一些示例来说明如何使用tf.gather_nd来提取元素。

示例1 - 提取特定像素点的值：假设我们有一张图像，形状为[height, width, channels]，我们想要提取特定坐标处像素的值。

假设我们的图像为img，我们可以使用以下代码来提取坐标为(x, y)处像素的值：pythoncoord = tf.constant([[x, y]])pixel_value = tf.gather_nd(img, coord)这样，我们就可以得到坐标为(x, y)处像素的值。

示例2 - 提取多维数组的特定元素：假设我们有一个4维张量，形状为[batch_size, height, width, depth]，我们想要提取每个示例的特定像素的值。

tf常见的损失函数（LOSS）总结运算公式1、均⽅差函数均⽅差函数主要⽤于评估回归模型的使⽤效果，其概念相对简单，就是真实值与预测值差值的平⽅的均值，具体运算公式可以表达如下：Q=1mm∑i=1(f(x i)−y i)2其中f(x i)是预测值，y i是真实值在⼆维图像中，该函数代表每个散点到拟合曲线y轴距离的总和，⾮常直观。

2、交叉熵函数出⾃信息论中的⼀个概念，原来的含义是⽤来估算平均编码长度的。

在机器学习领域中，其常常作为分类问题的损失函数。

Q=−1mm∑i=1(y i log(f(x i))+(1−y i)los(1−f(x i)))其中f(x i)是预测值，y i是真实值交叉熵函数是怎么⼯作的呢？假设在分类问题中，被预测的物体只有是或者不是，预测值常常不是1或者0这样绝对的预测结果，预测是常⽤的做法是将预测结果中⼤于0.5的当作1，⼩于0.5的当作0。

此时假设如果存在⼀个样本，预测值接近于0，实际值却是1，那么在交叉熵函数的前半部分：y i log(f(x i))其运算结果会远远⼩于0，取符号后会远远⼤于0，导致该模型的损失函数巨⼤。

通过减⼩交叉熵函数可以使得模型的预测精度⼤⼤提升。

tensorflow种损失函数的表达1、均⽅差函数loss = tf.reduce_mean(tf.square(logits-labels))loss = tf.reduce_mean(tf.square(tf.sub(logits, labels)))loss = tf.losses.mean_squared_error(logits,labels)2、交叉熵函数loss = tf.nn.sigmoid_cross_entropy_with_logits(labels=y,logits=logits)#计算⽅式：对输⼊的logits先通过sigmoid函数计算，再计算它们的交叉熵#但是它对交叉熵的计算⽅式进⾏了优化，使得结果不⾄于溢出。

broadcast函数
broadcast函数是一种用于在TensorFlow中执行广播操作的功能。

广播操作是一种类似于numpy的操作，用于对不同大小和形状的张量进行计算。

在执行广播操作时，TensorFlow会在不增加存储和内存开销的情况下，对输入张量进行扩展，使其具有相同的形状和大小，以便能够进行计算。

TensorFlow中的broadcast函数可以通过使用以下代码进行调用：
tf.broadcast(tensor, shape)
其中，tensor是要进行广播操作的张量，shape是指定广播操作后输出张量的形状（由Python列表表示）。

broadcast函数的主要用途是在神经网络和其他深度学习模型中，对多个不同形状和大小的张量进行运算。

通过广播操作，可以将这些张量进行扩展和对齐，以便进行计算。

例如，当乘以一个向量或矩阵时，如果输入张量的形状不同，则可以使用broadcast函数将它们扩展为相同的形状，然后进行计算。

在深度学习中，广播操作特别有用，因为它可以提高代码的效率并减少内存使用。

在训练大型神经网络时，内存是一项非常重要的资源，并且往往很容易超出预算。

通过使用广播操作，可以避免创建大量临时变量，从而节省内存开销。

除了广播函数之外，TensorFlow还提供了一些其他的广播操作，例如add_n和multiply。

这些操作和broadcast函数类似，可以对任意形状的张量进行运算，并将它们广播到一个公共形状。

在TensorFlow中，广播操作是一种非常常见和重要的操作，它在深度学习中发挥着关键作用。

tf常用函数TensorFlow是一个开源的深度学习框架，它提供了许多常用的函数和工具，用于构建和训练神经网络模型。

以下是一些常用的TensorFlow函数和它们的功能：tf.constant()：创建一个常量张量，用于定义一个不可变的数值。

tf.placeholder()：创建一个占位符张量，用于在运行图中插入一个变量或常量。

tf.Variable()：创建一个变量张量，用于定义模型的可训练参数。

tf.data.Dataset()：创建一个数据集对象，用于处理数据输入。

tf.Session()：创建一个会话对象，用于运行TensorFlow图。

tf.train.Optimizer()：创建一个优化器对象，用于更新模型的参数。

tf.nn.softmax()：对输入张量的每一行应用softmax函数，将其转换为概率分布。

tf.nn.sigmoid()：对输入张量的每一行应用sigmoid函数，将其转换为0到1之间的值。

tf.nn.relu()：对输入张量的每一行应用ReLU（Rectified Linear Unit）函数，将其转换为非负值。

tf.nn.l2_normalize()：对输入张量的每一行应用L2归一化操作，将其长度变为1。

tf.matmul()：对两个张量进行矩阵乘法运算。

tf.reduce_mean()：计算输入张量的均值。

tf.reduce_sum()：计算输入张量的和。

tf.argmax()：返回输入张量中最大值的索引。

tf.argmin()：返回输入张量中最小值的索引。

tf.where()：根据条件对输入张量中的元素进行取舍。

tf.case()：根据条件对输入张量中的元素进行取舍，类似于Python中的switch-case语句。

tf.while_loop()：创建一个循环结构，类似于Python中的while循环。

tf.map_fn()：对输入张量中的每个元素应用指定的函数，并返回一个新的张量。

tensorflowjs predict结果解析-概述说明以及解释1.引言1.1 概述概述部分的内容可以写成如下：概述部分旨在为读者提供对于本篇文章的整体了解以及背景知识的介绍。

本文主要讨论的是tensorflow.js predict方法的结果解析，以帮助读者更好地理解和应用这个方法。

随着人工智能技术的快速发展，深度学习成为了解决各种复杂问题的一种有效方法。

TensorFlow.js作为谷歌开发的开源机器学习框架TensorFlow的JavaScript版本，在浏览器中实现了深度学习的训练和推断功能，为前端开发者提供了强大的工具。

其中，predict方法是TensorFlow.js中一个非常重要且常用的函数。

它用于对给定的数据进行预测并返回预测结果。

这个方法的灵活性和高效性使得它在各种深度学习任务中得到广泛的应用，包括图像分类、文本生成、语音识别等。

然而，在面对predict方法的结果时，往往需要对其进行解析和分析，以获取更具体、更实际的信息。

因此，本文将重点探讨如何解析tensorflow.js predict方法的结果，以便读者能够更好地利用这些结果进行进一步的处理和应用。

整体来说，本文将从tensorflow.js简介开始，介绍predict方法的作用和用法，并深入探讨解析predict结果的重要性以及具体的解析方法和步骤。

通过阅读本文，读者将能够更好地理解和应用tensorflow.js predict 方法的结果，进而提升深度学习的应用能力。

下一节中，将详细介绍tensorflow.js的概念以及predict方法的作用和用法。

1.2 文章结构文章结构:本文主要分为三个部分：引言、正文和结论。

在引言部分，我们将概述本文的主要内容和目的，介绍本文的结构和组织方式。

在正文部分，首先我们会对tensorflowjs进行简介，介绍它的背景和基本概念。

然后，我们会着重讲解predict方法的作用和用法，包括如何准备输入数据和调用predict方法进行预测。

tensorflow模型中input的用法TensorFlow是一个广泛使用的机器学习框架，它提供了丰富的工具和功能来训练和部署机器学习模型。

在TensorFlow中，input的用法非常重要，它决定了如何将数据输入到模型中进行训练和预测。

本文将详细介绍TensorFlow模型中input的用法。

在TensorFlow中，可以使用多种方式来定义和处理input。

下面将分别介绍常用的input方法。

1. tf.placeholdertf.placeholder是一种占位符，用于在模型中定义输入的形状和数据类型。

它允许在运行模型时，将真实数据传递到TensorFlow计算图中。

使用tf.placeholder时，需要指定数据类型和形状。

例如，可以使用以下代码定义一个tf.placeholder: ```input_data = tf.placeholder(tf.float32, shape=[None, 784])```在上述例子中，tf.float32指定了数据类型，[None, 784]指定了输入的形状。

其中，None表示这个维度可以为任意大小，784表示每个输入的维度为784。

通过这种方式，可以在运行时根据实际数据来确定输入的大小。

2. tf.data.Datasettf.data.Dataset是TensorFlow中用于处理大规模数据的API。

它提供了一种高效的数据输入流水线来加载、处理和预处理数据。

使用tf.data.Dataset，可以从多种数据源中读取数据，并进行处理、转换和批处理等操作。

例如，可以使用以下代码来创建一个tf.data.Dataset:```dataset = tf.data.Dataset.from_tensor_slices((input_data, target_data))```上述例子中，input_data和target_data是输入数据和目标数据，可以是Numpy 数组、Pandas Dataframe或Tensor对象。

一、介绍在深度学习领域，TensorFlow是一种广泛使用的开源机器学习框架。

它提供了丰富的函数库，使得开发者能够快速构建和训练各种复杂的神经网络模型。

本文将介绍一些常用的TensorFlow函数，帮助读者更好地理解和应用TensorFlow框架。

二、基本数据操作1. tf.constant()tf.constant()函数可以创建一个常量张量，其值在图构建时就已经确定。

这个函数的参数包括value和dtype，分别表示张量的值和数据类型。

例如：```pythona = tf.constant([1, 2, 3], dtype=tf.float32)```2. tf.Variable()tf.Variable()函数用于创建一个可训练的变量。

其参数包括initial_value和dtype，分别表示变量的初始值和数据类型。

例如： ```pythonw = tf.Variable(initial_value=tf.random_normal([2, 2]),dtype=tf.float32)```3. tf.placeholder()tf.placeholder()函数用于创建一个占位符，其值在图执行时才会被指定。

这个函数的参数包括dtype和shape，分别表示占位符的数据类型和形状。

例如：```pythonx = tf.placeholder(dtype=tf.float32, shape=[None, 784])```三、神经网络构建1. yers.dense()yers.dense()函数用于创建一个全连接层。

其参数包括inputs、units和activation，分别表示输入张量、输出单元数和激活函数。

例如：```pythonh = yers.dense(inputs=x, units=128, activation=tf.nn.relu) ```2. tf.nn.conv2d()tf.nn.conv2d()函数用于创建一个二维卷积层。

tensorflow相除的函数
在TensorFlow中，我们可以使用`tf.divide`函数来进行张量之间的相除操作。

这个函数的语法是`tf.divide(x, y)`，其中x和y是要相除的张量。

例如，我们可以这样使用这个函数：
python.
import tensorflow as tf.
# 创建两个张量。

a = tf.constant([10, 20, 30], dtype=tf.float32)。

b = tf.constant([2, 4, 6], dtype=tf.float32)。

# 使用tf.divide进行相除操作。

result = tf.divide(a, b)。

# 创建会话并打印结果。

with tf.Session() as sess:
output = sess.run(result)。

print(output)。

在这个例子中，我们首先导入了TensorFlow库，然后创建了两个常量张量a和b。

接下来，我们使用`tf.divide`函数来计算a和b之间的相除操作，最后通过会话执行并打印结果。

除了`tf.divide`函数，我们还可以使用`/`运算符来进行相除操作。

例如：
python.
result = a / b.
这两种方法在功能上是等价的，都可以用来实现张量的相除操作。

希望这个回答能够帮助到你理解TensorFlow中的相除函数。

tf⼀些函数1.tf.reduce_mean(a) ：求平均值2.tf.truncated_normal([3,2],stddev=0.1) : 从正态分布中输出随机值，标准差为0,1，构造矩阵为3*2的3.tf.argmax(vector, 1)：返回的是vector中的最⼤值的索引号，如果vector是⼀个向量，那就返回⼀个值，如果是⼀个矩阵，那就返回⼀个向量，这个向量的每⼀个维度都是相对应矩阵⾏的最⼤值元素的索引号。

A = [[1,3,4,5,6]]B = [[1,3,4], [2,4,1]]with tf.Session() as sess:print(sess.run(tf.argmax(A, 1)))print(sess.run(tf.argmax(B, 1)))输出：[4][2 1]4.tf.equal(A, B)是对⽐这两个矩阵或者向量的相等的元素，如果是相等的那就返回True，反正返回False，返回的值的矩阵维度和A是⼀样的A = [[1,3,4,5,6]]B = [[1,3,4,3,2]]with tf.Session() as sess: print(sess.run(tf.equal(A, B)))输出：[[ True True True False False]]5.tf.cast()强制转换类型使⽤案例：import tensorflow as tfx = tf.constant([1.8, 2.2], dtype=tf.float32)r = tf.cast(x, tf.int32)sess = tf.Session()print(sess.run(r)) # [1, 2], dtype=tf.int326.mnist.train.next_batch(100):拿出100个样本来7.Dropout就是在不同的训练过程中随机扔掉⼀部分神经元。

tf.nn.dropout(x, keep_prob, noise_shape=None, seed=None,name=None)上⾯⽅法中常⽤的是前两个参数：第⼀个参数x：指输⼊第⼆个参数keep_prob: 设置神经元被选中的概率8.transpose函数import tensorflow as tf#x = tf.constant([[1, 2 ,3],[4, 5, 6]])x = [[[1,2,3,4],[5,6,7,8],[9,10,11,12]],[[21,22,23,24],[25,26,27,28],[29,30,31,32]]]#a=tf.constant(x)a=tf.transpose(x, [0, 1, 2]) # 正常情况下，0，1，2b=tf.transpose(x, [0, 2, 1]) # 将1和2的位置换了⼀下，原来是2*（3*4），后⾯的2个3和4换了⼀下以后，现在是2*（4*3）c=tf.transpose(x, [1, 0, 2]) # 所有矩阵的第⼀⾏拼成⼀个矩阵，第⼆⾏。