电路(第五版).-邱关源原著-电路教案--第8章相量法
- 格式:doc
- 大小:3.97 MB
- 文档页数:13









第5章含有运算放大器的电阻电路●本章重点1、理想运算放大器的两个特性;2、节点法分析含理想运算放大器的电阻电路。
●本章难点分析电路时理解虚断、虚短的含义。
●教学方法本章是通过一些典型电路讲述了含运算放大器的电阻电路的分析方法。
采用讲授为主,自学为辅的教学方法。
共用2课时。
通过讲例题加以分析,深入浅出,举一反三,理论联系实际,使学生能学会学懂。
●授课内容运算放大器是一种电压放大倍数很高的放大器,不仅可用来实现交流信号放大,而且可以实现直流信号放大,还能与其他元件组合来完成微分、积分等数学运算,因而称为运算放大器。
目前它的应用已远远超出了这些范围,是获得最广泛应用的多端元件之一。
5.1运算放大器的电路模型a端—-反相输入端:在o端输出时相位相反。
b端—-同相输入端:在o端输出时相位相同。
o baau_+o 端—-输出端A —-放大倍数,也称作“增益”(开环放大倍数:输入端不受o 端影响)。
''''''()o ao bo o o b a u Au u Au u u u A u u =-=⇒=+=-差动输入方式二、端口方程:()o b a u Au u =- 三、电路模型:i o ioR R R R ----输入电阻输出电阻高输入,低输出电阻,0,""0000,""a i b o b a b a i R i R u u u u a b A ≈⎫→∞⎬≈⎭→⎫-≈≈⎬→∞⎭理想状态下,虚断电流可以为,但不能把支路从电路里断开。
虚短,但不能在电路中将、两点短接。
四、常用接法理想化:u a ≈0。
“虚地”:可把a 点电位用0代入,但不能直接作接地处理。
5.2含理想运放的电路分析分析方法:节点电压法。
采用概念:“虚短”,“虚断”,“虚地”。
避免问题:对含有运放输出端的节点不予列方程。
_o ao uao。
+__+a ub u0i ≈i R R0u+__ +a ub ua ii R R0u求解次序:由最末一级的运放输入端开始,逐渐前移。
《电路》邱关源第五版课后习题答案答案第一章 电路模型和电路定律【题1】:由U A B =5V 可得:I AC .=-25A :U D B =0:U S .=125V 。
【题2】:D 。
【题3】:300;-100。
【题4】:D 。
【题5】:()a i i i =-12;()b u u u =-12;()c ()u u i i R =--S S S ;()d ()i i R u u =--S SS 1。
【题6】:3;-5;-8。
【题7】:D 。
【题8】:P US1=50 W ;P U S 26=- W ;P U S 3=0;P I S 115=- W ;P I S 2 W =-14;P I S 315=- W 。
【题9】:C 。
【题10】:3;-3。
【题11】:-5;-13。
【题12】:4(吸收);25。
【题13】:0.4。
【题14】:3123I +⨯=;I =13A 。
【题15】:I 43=A ;I 23=-A ;I 31=-A ;I 54=-A 。
【题16】:I =-7A ;U =-35V ;X 元件吸收的功率为P U I =-=-245W 。
【题17】:由图可得U E B =4V ;流过2 Ω电阻的电流I E B =2A ;由回路ADEBCA 列KVL 得U I A C =-23;又由节点D 列KCL 得I I C D =-4;由回路CDEC 列KVL 解得;I =3;代入上式,得UAC=-7V。
【题18】:PPII12122222==;故I I1222=;I I12=;⑴ KCL:43211-=I I;I185=A;U I IS=-⨯=218511V或16.V;或I I12=-。
⑵ KCL:43211-=-I I;I18=-A;US=-24V。
第二章电阻电路的等效变换【题1】:[解答]I=-+9473A=0.5A;U Ia b.=+=9485V;IU162125=-=a b.A;P=⨯6125.W=7.5W;吸收功率7.5W。
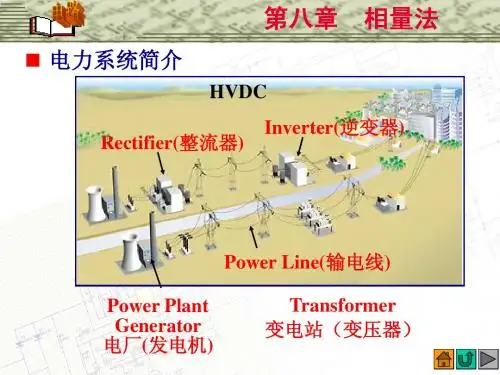
第八章相量法求解电路的正弦稳态响应,在数学上是求非齐次微分方程的特解.引用相量法使求解微分方程特解的运算变为复数的代数运运算,从儿大大简化了正弦稳态响应的数学运算.所谓相量法,就是电压、电流用相量表示, RLC元件用阻抗或导纳表示,画出电路的相量模型,利用KCL,KVL和欧姆定律的相量形式列写出未知电压、电流相量的代数方程加以求解,因此,应用相量法应熟练掌握:(1)正弦信号的相量表示;(2) KCL,KVL的相量表示;(3) RLC元件伏安关系式的相量形式;(4) 复数的运算.这就是用相量分析电路的理论根据.8-1将以下复数化为极坐标形式:(1) Fi=-5-j5;⑵ F2 =-4+ j3;⑶ F3 =20+j40;(4) F4=j10; (5) F5=-3; (6) F6=2.78 +j9.20o解:(1) F1 =-5-j5 = a Z0a = (-5)2 (-5)2 =5.2-5 v1-arctan ——=-135 -5 (因F1在第三象限)故F1的极坐标形式为F1=5%'2/ -135-(2) F2 =—4 + j3=C(Y)2+32/arctan⑶—4)=52143.13:(F2在第二象限)(3)F3 =20+ j40 = J202 +402N arctan(40/20) =44.72/63.43二(4) F4 =10j =10/90 二⑸ F5=-3 = 3/180 二(6)F6 =2.78 + j 9.20 = 32.782+9.202/arctan(9.20/2.78) = 9.61,73.19 :注:一个复数可以用代数型表示,也可以用极坐标型或指数型表示,即F=a1+ j a2 =a/e =ae ja它们相互转换的关系为:2 2 1-arctan—a〞0 a2 a i和a1 = acosi a2= asin?需要指出的,在转换过程中要注意F在复平面上所在的象限,它关系到日的取值及实部a i和虚部a2的正负.8-2将以下复数化为代数形式:〔1〕F i=10/—73;〔2〕F2 =15/112.6:;〔3〕F3 =1.2/152;〔4〕F4=10/-90 :〔5〕F i =5Z-180=;〔6〕 F i =10/ -1351解:〔1〕 F i =10/— 73°=10xcos〔—73二〕十j10xsin〔—73〕= 2.92 —j9.56⑵ F2=15/112.6〞 = 15cos112.6、15sin112.6' = -5.76+j13.85〔3〕 F3 =1.2/152 口=1.2cos152' + 1.2sin152 0 = —1.O6 + jO.56〔4〕F4 =10=-90*=-jIO〔5〕F1 =5/-180口= -5〔6〕 F i =10/-135,0cos〔-135:〕+10sin〔-135二〕=-7.07-j7.078 —3假设IO./.“十A260 °= 175/中.求A和中.解:原式=100+ Acos600+ ja sin600=175c o s9 + j175s in中根据复数相等的定义,应有实部和实部相等,即Acos60 100 =175cos虚部和虚部相等Asin60 =175sin「把以上两式相加,得等式A2 100 A -20625 -0-100主,1002+4乂20625 1 102.07A = ---------------------------------- 二+解得 2 「202.069.3102.07 ——Asin602sin =-------------- = --------------- — 175 175=30.348-4求8—1题中的F ,F6和F 2/F6.解:F 2 F6=(—4 j3) (2.78 j9.20) =5 143.13 9.61 73.19= 48.05. 216.32 =48.05. -143.684 j3 5. 143.13F 2 F6 = ------------ --- = ----------------- = 0.52 69.942.78 j9.20 9.61 73.198 — 5求8 —2题中的F 1 +巳和E/F 5 o解:F 1 F 5 - 10. - 73 5. - 180= 10cos(-73 ) j10sin(-73 ) -5 =-2.08 - j9.56 =9.78 -102.2710. -73F 1 F 5= ---------------------------- = 2 -73180 =2 1075/-1808 —6 假设.i 1 = -5cos(314t +60)Ai 2 = 10sin(314t + 60)A,i 3 =4cos(314t 60 )A(1)写出上述电流的相量,并绘出它们的相量图; (2)1与心和i1与)的相位差;(3)绘出3的波形图;(4)假设将3表达式中的负号去掉将意味着什么? (5)求的周期T 和频率f .解:(1) i 1 二 一5cos(314t+601 =5cos(314t+60 = —180=) =5cos(314t —120bi 2 =10sin(314t 60 ) = 10cos(314t - 30 )=0.505 所以故i 1 , i 2和i 3的相量表达式为(4)假设将i i (t)中的负号去掉,意味着i i 的初相位超前了 180二.即i i 的 参考方向反向.(5) i i (t)的周期和频率分别为2 二 2 二T =——= ------ =0.02s = 20ms314 .1■ ■1f =一 =——= ---- =50 HzT 2 二 0.02注:定义两个同频率的正弦信号的相位差等于它们的初相之差,因此在 比拟相位差时,两个正弦量必须满足(1)同频率;(2)同函数,即都是正 弦或都是余弦;(3)同符合,即都为正号或都为负号,才能进行比拟.8-7 假设两个同频正弦电压的相量分别为U i =50/30 V ,5 =T00/-150 V ,其频率 f=100Hz .求:5I i : 一 120 A,1210 4:——30 A,13 :——60 A2 2(3) i i (t)的波形图见题解图(b)所示.13 =1 - 3 - -120 -60 - -180其相量图如题解图(a)所示.(1)写出u i,出的时域形式;(2) 3与弘的相位差.(1)u1(t) = 50.. 2 cos(2 ft 30 ) = 50 .. 2 cos(628t 30 )Vu2(t) =-100.2cos(2二ft-150 ) =100..2cos(628t-150 =180 )V 二100,2cos(628t 30 )V(2)由于U1=50. 30 V ,U2=-100/-150 V =100. 30 V故相位差为中=30<30' = 0:即u1与u2同相位.8-8 :3(t) =22072cos(314t—120 1Vu2(t) =220,2 cos(314t 30 )V(1)画出它们的波形图,求出它们的有效值、频率f和周期T;(2)写出它们的相量和画出其相量图,求出它们的相位差;(3)如果把电压电的参考方向反向,重新答复(1), (2).解:(1)波形如题解8—8图(a)所示.有效值为u1 =u2 = 220V u2314f1 = f2 =——= ---------------------- =50Hz频率2二2二1 1T1 = T2 0.02 s周期 f 50(2) 5和弘的相量形式为U1 =220 -120 V U2=220 30 V故相位差为 =i - :2 =-120 -30 <-150 相量图见题解图(b)所示.(3)U2的参考方向反向,u2 (t)变为一u2 (t),有效值、频率和周期均 不变,—U 2(t )的相量为 U'2 =220/30—180口=200/—150V故U1和U2的相位差为*=91-中2=-120 -(-150)=30 波形图和向量图见题解图(a)和(b).8 — 9一段电路的电压、电流为:3,u =10sin(10 t - 20 )V i =2cos(103t -50 )A(1)画出它们的波形图和向量图;(2)求出它们的相量差.33解:(1) u =10s lM10 t—20 )=10cos10 t —110 )V ,故 u 和 i 的相量分别为U a =22072cos 侬t +10)V , U b =22045cosgt -110 =)V , U c = 220 2 cos( t 130 )V求:(1) 3个电压的和;(2) U ab ,U bc ; (3)画出它们的相量图--------- ------------- 0 .2 I =-50 A210U =-110 V60 o8-10图示三个电压源的电压分别为:u(a) +1 -------处+e ; c ~ +题解8—10图解:“,u b, U c的相量为U a = 220 10 VU b=220. -110VU c =220. 130 V(1)应用相量法有U a U b U c=220 10 220/ -110 220 130a c=0即三个电压的和u a⑴u b(t) u c⑴=0⑵ U ab =U a -U b =220/10 220/-110 := 220 3 40 VU bc =U b -U c =220 -110 -220 130= 220.3 -80 V(3)相量图如题解8—10图所示u c(a)中电压表读数为V 1:30V ; V 2:60V ;图(b)中的V 1 :15V ; 100V .(电压表的读数为正弦电压的有效值.)求图中电压U s .题8—11图解法一:(a)图:设回路中电流「=1/0:根据元件的电压、电流相量关系,可得题8-11图U R = RI = RI 0 =3.0 V U L = jX L l = X L I 90 =6.90 V那么总电压 U S =U R -U L =30 • j60V所以U s 的有效值为US =痴2 +602 = 67.08V(b)图:设回路中电流相量I =1/0二A,由于U R = RI = RI 0 =15 0 VU L —X L I =X L I 90 =80 90 V8-11 图 V 2 :80V . V 3 :题解8—10图元件相量关系后效值关系相位关系相量图电阻R UR = RI R U R =RI R仇=%U C=-jX C I =X C I -90 =100 -90 V所以总电压U S =U R U L U C =15 j80 -100j =15-j 20V故U s的有效值为U S=J132+202=25V解法二:利用相量图求解.设电流「=1/0 '为参考相量,电阻电压U R与「同相位,电感电压U L超前I'90 :电容电压U c要滞后「90[总电压U s与各元件电压向量构成一直角三角形.题解8-11图〔a〕和〔b〕为对应原图〔a〕和〔b〕的相量图.由题解图〔a〕可得U S = . U R U L = 302 602 = 67.08V由题解图〔b〕可得U S = ,U R 〔U C-U L〕2 = 152〔100 -80〕2 = 258V题解8—11图注:这一题的求解说明,R, L, C元件上电压与电流之间的相量关系、有效值和相位关系〔如下表所示〕是我们分析正弦稳态电路的根底,必须很好地理解和掌握.电感LU L = jX L I LU L = jX L 「 仇=仇+90二电容CU C = - jX C I C U C = X C I C仇=d -90二1 -----------------------------8—12图示正弦电流电路中,电流表的读数分别为 A :5A ; A 2:2°A;A 3 :25A o 求:〔1〕图中电流表A 的读数;〔2〕如果维持A 的读数不变,而把电 源的频率提升一倍,再求电流表 A 的读数.解法一:〔1〕 R, L, C 并联,设元件的电压为U R 二二U L 二U C 二U 二U 0根据元件电压、电流的相量关系,可得U U I R5/0 AR RU UI L =——=——-90 A - - j20A jXL X L应用KLC 的相量形式,总电流相量为I = I R I L I C =5-j20 j25 = 5 j5 =5' 2 45 A故总电流表的读数.・' =I =5、.2 =7.07A(2)设U R ==U L =U C =U -U — 0U U,,…—『一 ,、一 , I R =- =— =5,0 A. 当电流的频率提图一倍后,由于 R R不变,所以UR -U不I CU- jX C90 = 25 90 = j 25A题8—12图U UIc == = 2 25. 90 =50. 90 A一jX C _j ; 2 cI =I R I L 1c =5-j10 j50 =5 j40即,电流表的读数解法二: 利用相量图求解.设U =U /00=U R =U L =Uc 为参考向量,根据元件电压、电流的相位关系知,I R 和U 同相位,1c 超前90: I L 滞后U 901 ■ ■ ■ 相量图如题解8—12图所示,总电流「与I R, I c 和I L 组成一个直角三角形.故 电流表的读数为... =\IR(I c -I L )2A即 (1)@ =,52 +(25 -20)2 =7.07A⑵ @ =,52 +(25 -10)2 =40.31A注:从8—11题的解法二,可以体会到应用向量图分析电路的要点,那就是 首先要选好一个参考相量,这个参考相量的选择,必须能方便地将电路中其它电变,而X L =2^L 增大一倍,26C 减小一倍,因此,有U 1 ——=—20.jX L j2 L 2所以A - -52 402 -40.31A题解8—12图压、电流相量,根据电路的具体结构及参数特点逐一画出,把所给的条件转化成 相量图中的几何关系.最后根据相量图中的相量关系,使问题得到解决.一般对 串联电路,选电流作参考方向较方便,如 8-11题.对并联电路,那么选电压作参 考相量较方便,如8-12题.有些问题通过相量图分析将很直观和简便.8-13 对RL 串联电路作如下两次测量:(1)端口加90V 直流电压=0)时, 输入电流为3A; (2)端口加f =50H z 的正弦电压90V 时,输入电流为1.8A .求R 和L 的值.题解8—13图解:由题意画电路如题解8—13图所示.(1)当u s 为90V 直流电压时,电感L 看作短路,那么电阻RU-(2)当u s 为90V 交流电压时,设电流「=1/0口=1.8/0二A,根据相量法,U S = RI jX L I =30 1.8 jX L 1.8 U S =90 = 1.8 , 302 X i 2X L= (90)2 -302 =40 】1.8, X L X L 40L = ----- = ------- = -------- 解得 • 2开 100二8-14某一元件的电压、电流(关联方向)分别为下述 4种情况时,它可能是U0.127H 庆什么元件?'u =10cos(10t 十 45 1V (D i =2sin(10t +135)AU = 10. 45 V2即电压、电流同相位,根据元件电压、电流相位关系可知这是一个 5建的电阻元件.(1)把电压变为余弦形式有u=cos(100t - j 90 )V102 U 45 I =0 A(2) u 和i 的相量为J 2V 2U5一二5 45 (1 j); R jX L 那么I.. 255R : ---- :. iX L :--- :. i即这是一个 「2 的电阻和v 2 的电感的串联组合.3,、.,8—15电路由电压源u s n 00 cos(10 t)V 及R 和L= 0.025H 串联组成.电感端电 压的有效值为25V .求R 值和电流的表达式.解:由题意画电路的相量模型如题解 8—15图(a)所示,相量图如题解图 (b)所示.由于100U.2 0X L = L=103 0.025= 25」u =10sin(100t)V(2) i =2cos(100t)AU = -10costV (3) 、i=-sintA;u = 10cos(314t+451V (4)、 i =2cos(314t)A解:(1)把电流变为余弦形式有= 2cos(10t +135、901=2cos(10t + 45°)A,u和i 的相量为题解8—15图由图〔b〕知电阻电压的有效值为U R 66.144R = —R = -------- =66.144' 1所以电阻为I 1「滞后U S的角度(由于是感性电路)为.U L . 25Z= arcsin——=arcsin -------- -- - 20.70U S100 2因此电流的瞬时表达式为i(t) = 2cos(103t -20.70 )A100■ _________I U S— = ------------------------ 2—— =1 -20.70 A也可根据R jX L 66.144 j25得i(t) = 2cos(103t -20.70 )A8-16图示电路I1 =I2 =10A.求I和U S.■ ■ ■ ■ ■解:设U S为参考相量.I1与U S同相位,I2超前U S901相量图如题解8-题解8—16图题解8—16图I = J l2-12 = J102・ 102 =10、,2 A12Z= arctan = arctanl = 4511由电路图知U S = RI1 =10 10 = 100V故U s和「分别为U S -100. 0 VI = I. :Z =10,2 45 A8-17图示电路中1s=2/0 A.求电压u o■■' u u1s = I R ' I L =二 '解:R jX Lu - I S -2 0= 2 45V1 .2 —451即j题8—17图。
第8章相量法8.1 复习笔记一、复数相关知识点1.复数的表示形式如图8-1-1所示,在复平面内有一个向量F,可以用以下几种方式表示:(1)代数形式(2)三角函数形式F=|F|(cosθ+jsinθ)(3)指数形式F=|F|e jθe jθ=cosθ+jsinθ(欧拉公式)(4)极坐标形式F=|F|∠θ图8-1-12.复数运算设有两个复数分别为F1=a1+jb1,F2=a2+jb2。
(1)加减运算F1±F2=(a1+jb1)±(a2+jb2)=(a1±a2)+j(b1±b2)复数的加减运算在复平面上符合平行四边形求和法则,如图8-1-2所示。
图8-1-2 复数的加减运算(2)乘法运算所以|F1F2|=|F1||F2|arg(F1F2)=arg(F1)+arg(F2)(3)除法运算所以(4)旋转因子①e jθ=1∠θ,若则②e jπ/2=j,e-jπ/2=-j,e jπ=-1,e j2π=1。
二、相量法基础(1)正弦量的表达式:u(t)=U m cos(ωt+φ)。
式中,U m为振幅,ω为角频率,φ为初相,三者称为正弦量的三要素。
有效值即其均方根值相量:表征正弦时间函数的复值常数。
(2)有效值相量:U▪=U∠φu,复值常数的模表示有效值,由此可知(3)正弦量的相量表示法:分为有效值相量和最大值相量。
例如,正弦量其有效值相量I▪=10∠50°A。
其对应的最大值相量三、电路定律的相量形式(1)KCL、KVL定律的相量形式∑I▪=0∑U▪=0(2)电路元件VCR的相量形式①电阻元件:U▪=R I▪。
即电阻上的电压和电流同相位,相量图如图8-1-3所示。
图8-1-3②电感元件:U▪=jωL I▪。
即电感上的电压超前电流90°,相量图如图8-1-4所示。
图8-1-4③电容元件:U▪=I▪/(jωC)即电容上的电压滞后电流90°,相量图如图8-1-5所示。
电路(第五版).-邱关源原著-电路教案--第8章相量法第8章 相量法● 本章重点1、正弦量的两种表示形式;2、相量的概念;3、KVL 、KCL 及元件VCR 的相量形式。
● 本章难点1、 正确理解正弦量的两种表示形式的对应关系;2、 三种元件伏安关系的相量形式的正确理解。
● 教学方法本章是相量法的基础,对复数和正弦量两部分内容主要以自学为主,本章主要讲授相量法的概念、电路定律的相量形式以及元件V AR 的相量形式。
讲述中对重点内容不仅要讲把基本概念讲解透彻,而且要讲明正弦量的相量与正弦时间函数之间的对应关系;元件V AR 的相量形式与时域形式之间的对应关系,使学生加深对内容的理解并牢固掌握。
本章对元件的功率和能量这部分内容作了简单讲解,以便为下一章的学习打下基础。
本章共用4课时。
● 授课内容8.1复数1. 复数的三种表示bj a A += 直角坐标=θ∠r 极坐标 =θj re 指数形式θθθsin cos 22r b r a ab arctgb a r ==⇒=+=⇒直极极直θθsin cos jr r A += 三角表示形式欧拉公式:θθθsin cos j e j +=2. 复数的运算已知:11111θ∠=+=r jb a A ,22222θ∠=+=r jb a A求:212121,,A AA A A A ⋅±i()()212121b b j a a A A ±+±=±212121212121θθθθ+∠=+∠=⋅r r A A r r A A 8.2正弦量一、正弦量:随时间t 按照正弦规律变化的物理量,都称为正弦量,它们在某时刻的值称为该时刻的瞬时值,则正弦电压和电流分别用小写字母i 、u 表示。
周期量:时变电压和电流的波形周期性的重复出现。
周期T :每一个瞬时值重复出现的最小时间间隔,单位:秒(S ); 频率f : 是每秒中周期量变化的周期数,单位:赫兹(Hz )。
显然,周期和频率互为倒数,即f =1/T。
交变量:一个周期量在一个周期内的平均值为零。
可见,正弦量不仅是周期量,而且还是交变量。
二、正弦量的表达式 1. 函数表示法:m ()cos(f t F t ωψ=+m F —t ωψ+—相位,反映正弦量变动的进程;ω—角频率(rad /s ),反映正弦量变化的快慢。
22,2T f Tπωπωπ=== ()ψπψπ-≤≤—初相位,反映正弦量初值的大小、正负。
m F ,ω,ψ—正弦量的三要素。
已知m 10A,50Hz,15o I f ψ===-, 则()10cos(31415)A o i t t =-。
2. 波形表示法0t ωψ+=, t ωψ=-。
当0>ψ时,最大值点由坐标原点左移ψ。
如下图。
t这样正弦量的数学表达式写为 ()cos()f t t ωψ+。
因此,正弦量的有效值可以代替最大值作为它的一个要素。
对于正弦电流i =I m cos(ωt+φi ) 的有效值为I =I m /2=0.707I m同理,正弦电压u =U m cos(ωt+φu )的有效值为U =U m /2=0.707U m在工程上,一般所说的正弦电压、电流的大小都是指有效值。
例如交流测量仪表所指示的读数、交流电气设备铭牌上的额定值都是指有效值。
我国所使用的单相正弦电源的电压U =220V ,就是正弦电压的有效值,它的最大值U m =2U =1.414×220=311V 。
应当指出,并非在一切场合都用有效值来表征正弦量的大小。
例如,在确定各种交流电气设备的耐压值时,就应按电压的最大值来考虑。
8.3 相量法的基本概念一、 相量:可以表示一个正弦量的复值常数称为相量。
令正弦量m ()cos()cos()f t F t t ωψωψ=++,根据欧拉公式,可知 j e cos jsin x x x =+,取x t ωψ=+ 则 ()cos()jsin()j t e t t ωψωψωψ+=+++j()cos()Re t t e ωψωψ+⎡⎤+=⎣⎦ j ()sin()Im t t e ωψωψ+⎡⎤+=⎣⎦于是 j()j()m m ()Re Re t t f t F e F e ωψωψ++⎡⎤⎡⎤==⎣⎦⎣⎦j j j m m Re Re t t F e e F e ψωω⎡⎤⎡⎤==⎣⎦⎢⎥⎣⎦j m m m F F e F ψψ==∠ —最大值相量。
m ()30)V 220230V u t t U =+⇔=∠ F F ψ=∠ —有效值相量 m 2F F =上述表明,可以通过数学的方法,把一个实数域的正弦时间函数与一个复数域的复指数函数一一对应起来,而复指数函数的复常数部分是用正弦量的有效值(最大值)和初相结合成一个复数表示出来的。
运用相量进行正弦稳态电路的分析和计算,可同时将正弦量(最大值)的有效值和初相计算出来。
有效值(最大值)上方加的小圆点是用来与普通复数相区别的记号,在数学运算上与一般复数的运算并无区别。
相量既然是复数,它也可以在复平面上用一条有向线段表示。
如下图所示为正弦电流i =2I cos (ωt +Ψi )的相量,其中Ψi >0。
相量。
I 的长度是正弦电流的有效值I,相量。
I与正实轴的夹角是正弦电流的初相。
这种表示相量的图称为相量图。
为了简化起见,相量图中不画出虚轴,而实轴改画为水平的虚线,如下图所示。
iI I ψ=∠二、旋转因子j teω复指数函数的另一部分e jωt,是一个随时间变化的旋转因子,它在复平面上是一个以原点为中心、以角速度ω等速旋转、模为l的复数。
j1()cos jsinte t t tωωωω=∠=+取j2,j2t eππω==;取j()2,j2t eππω-=-=-;于是j,1±-—旋转因子。
三、正弦量为旋转相量在实轴上的投影相量(。
F=F e jφ)乘以旋转因子e jωt再乘以2,即2。
F e jωt,所以将它称为旋转相量,2。
F称为旋转相量的复振幅相量,如图(a)所示。
jm()Re tf t F eω⎡⎤=⎢⎥⎣⎦旋转相量。
(a) (b)旋转相量与正弦波iψ+1+jIiψ1 +1+jω+1+jI--I--jj II一个正弦量在任何时刻的瞬时值,等于对应的旋转相量该时刻在实轴上的投影。
这个关系可以用图(a)、(b)分别所示的旋转相量2。
F e jωt 和正弦量f (t )的波形图之间的对应关系来说明。
对于任何正弦时间函数都可以找到唯一的与其对应的复指数函数,建立起一一对应关系,从而得到表示这个正弦量的相量。
由于这种对应关系非常简单,因而可以直接写出。
四、 同频率正弦量的相量运算1 同频率正弦量的加减法例1:11m 1()cos()u t U t ωψ=+,22m 2()cos()u t U t ωψ=+。
求12()()u t u t +。
解:j 1m 11m 1()cos()Re t u t U t U e ωωψ⎡⎤=+=⎢⎥⎣⎦j 2m 22m 2()cos()Re t u t U t U e ωωψ⎡⎤=+=⎢⎥⎣⎦j 12m m ()()cos()Re t u t u t U t U e ωωψ⎡⎤+=+=⎢⎥⎣⎦j j 1m 2m 12()()()Re Re t t u t u t u t U e U e ωω⎡⎤⎡⎤=+=+⎢⎥⎢⎥⎣⎦⎣⎦j j 1m 2m m Re ()Re t t U U e U e ωω⎡⎤⎡⎤=+=⎢⎥⎢⎥⎣⎦⎣⎦m 1m 2m U U U =+上述计算也可以根据平行四边形法则在相量图上进行。
相量的加减法只对应同频率正弦量的加减法。
2相量的微分运算 设m ()cos()f t F t ωψ=+ 则[]m m ()sin()cos(90)df t F t F t dtωωψωωψ=-+=++ 而j m ()Re t f t F e ω⎡⎤=⎢⎥⎣⎦则 j j j m m m ()(Re )Re ()Re j t t t df t d d F e F e F e dt dt dt ωωωω⎡⎤⎡⎤⎡⎤===⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦于是 ()m df t j F dtω⇔m (j 90)m F F ωωψ=∠+当()(-1)01-1sm (-1)()()()()cos()n n n n s n n d f t d f t df t a a a a f t U t dt dt dtωψ++++=+ 其中,稳态响应p m ()cos()f t F t ωψ=+ p m m ()f t F F ψ⇒=∠()p m ()(j )k k k d f F dt ω⇒Sm S Sm S ()u t U U ψ⇒=∠ (1)Sm 0m 1m 1m m (j )(j )(j )n n n n a F a F a F a F U ωωω--++++=(1)Sm m 011/[(j )(j )j ]n n n n F U a a a a ωωω--=++++8.4 电路定律的相量形式 一、KCL 的相量形式KCL 时域形式∑=mk 1i k =0当线性正弦稳态电路的电流都是同频率的正弦量时,j m m i ()cos()Re t k k k k i t i t I e ωωψ⎡⎤=+=⎢⎥⎣⎦因此,在所有时刻,对任一节点的KCL 可表示为j j j j mm ()Re[]Re[()]Re[2()]Re[0]0t t t t ki t Ie I e I e e ωωωω====⨯=∑∑∑∑于是很容易推导出KCL 的相量形式,即m 0 0k k II ==∑∑ KCL 的相量形式其中 。
Im k = I m kikjeψ= I m k /ψik。
I k = I k ik je ψ = I k /ψik为流出该节点的第k 条支路正弦电流i k 对应的相量。
二、 KVL 的相量形式同理,在正弦稳态电路中,沿任一回路,KVL 可表示为∑=mk 1。
Um k = 0∑=mk 1。
U k = 0 KVL 的相量形式式中。
Um k 、。
U k 为回路中第k 条支路的电压相量。
必须强调指出,KCL 、KVL 的相量形式所表示的是相量的代数和恒等于零,并非是有效值的代数和恒等于零。
三、R 、L 、C 的相量模型在正弦稳态电路中,三种基本电路元件R 、L 、C 的电压、电流之间的关系都是同频率正弦电压、电流之间的关系,所涉及的有关运算都可以用相量进行,因此这些关系的时域形式都可以转换为相量形式。
1、 正弦交流电路中的电阻元件在电压和电流的参考方向关联时,电阻R 的伏安关系的时域形式R R ()()u t R i t =⋅当正弦电流i R =2I R cos(ωt +ψi )通过电阻R 时,则 R Rm i u ()cos()cos()Rm u t RI t U t ωψωψ=+=+Rm Rm R R U RI U RI=⎫⎬=⎭电压、电流的最大值(有效值)之间符合欧姆定律;u i u i0ψψϕψψ=⎫⎬=-=⎭R u 与Ri 同相令:R R R i RR R R u R i ()()i t I I u t U U RI R I ψψψ⇒=∠⇒=∠=∠= 则在电压和电流关联参考方向下电阻的伏安关系的相量形式为R R U R I = Rm Rm U R I =线性电阻的相量电路、相量图如下。