青岛版初一数学上第一章几何图形复习
- 格式:ppt
- 大小:493.00 KB
- 文档页数:34


Fpg
Fpg 初一上數學知識點匯總第一章基本の幾何圖形
現實生活中の物體我們只管它の形狀、大小、位置而得到の圖形,叫做幾何圖形。
長方體、正方體、球、圓柱、圓錐等都是立體圖形,此外棱柱、棱錐也是常見の立體圖形。
許多立體圖形是由一些平面圖形圍成の,將它們適當の剪開,就可以展開成平面圖形。
幾何體也簡稱體。
長方體、正方體、圓柱、圓錐、球、棱柱、棱錐等都是幾何體。
包圍著體の是面。
面有平の面和曲の面兩種。
面和面相交の地方形成線。
線和線相交の地方是點。
幾何圖形都是由點、線、面、體組成の,點是構成圖形の基本元素。
“點動成線”、“線動成面”、“面動成體”,注意要會舉實例。
線段有兩個端點。
將線段向一個方向無限延伸就得到射線,射線有一個端點。
將線段向兩個方向無限延伸就得到線段,線段有兩個端點。
注意:線段、射線、直線の表示方法,要會畫圖形。
點與直線の位置關系有兩種:
1. 點A在直線AB上(直線AB經過點A)
2. 點P在直線AB外(直線AB不經過點P)
直線公理:經過兩點有一條直線,並且只有一條直線。
兩點確定一條直線。
線段公理:兩點の所有連線中,線段最短。
簡單說成:兩點之間,線段最短。
兩點之間線段の長度,叫做這兩點之間の距離。
線段AB分成相等の兩條線段AM與MB,點M叫做線段ABの中點。
類似の還有線段の三等分點、四等分點等。
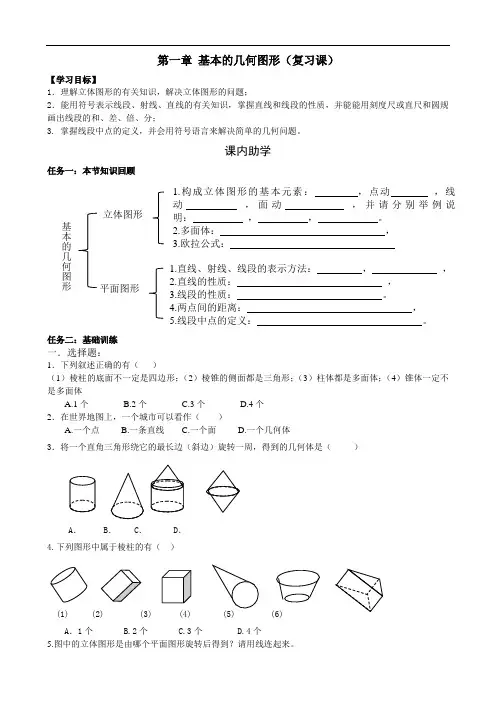
第一章 基本的几何图形(复习课)【学习目标】1.理解立体图形的有关知识,解决立体图形的问题;2.能用符号表示线段、射线、直线的有关知识,掌握直线和线段的性质,并能能用刻度尺或直尺和圆规画出线段的和、差、倍、分;3. 掌握线段中点的定义,并会用符号语言来解决简单的几何问题。
课内助学任务一:本节知识回顾任务二:基础训练一.选择题:1.下列叙述正确的有( )(1)棱柱的底面不一定是四边形;(2)棱锥的侧面都是三角形;(3)柱体都是多面体;(4)锥体一定不是多面体A.1个B.2个C.3个D.4个2.在世界地图上,一个城市可以看作( )A.一个点B.一条直线C.一个面D.一个几何体3.将一个直角三角形绕它的最长边(斜边)旋转一周,得到的几何体是( )A .B .C .D .4.下列图形中属于棱柱的有( )A .1个 B.2个 C.3个 D.4个5.图中的立体图形是由哪个平面图形旋转后得到?请用线连起来。
基本的几何图形立体图形 1.构成立体图形的基本元素: ,点动 ,线动 ,面动 ,并请分别举例说明: , , 。
2.多面体: , 3.欧拉公式: 平面图形1.直线、射线、线段的表示方法: , ,2.直线的性质: ,3.线段的性质: 。
4.两点间的距离: ,5.线段中点的定义: 。
B A二.填空题:1、底面是三角形的棱柱有 个面, 个顶点, 条棱。
2.观察图中的立体图形,分别写出它们的名称._____3.下面三个图形中,图形 可以用平面截长方体得到,图形 可以用平面截圆锥得到,图形 可以用平面截圆柱得到。
4.若一个多面体的顶点数20,面数为12,则棱数为 。
三.解答题:1.如图,在运河(不记河的宽度)的两岸有A,B 两个村庄,现在上修建一座跨河的大桥,为方便交通要使桥到要在运河两个村庄的距离之和最短,应在运河的哪一点修建才能满足要求?2.在同一平面内的三条直线能把平面分成几部分?并画出相应的图形。
任务三:精讲例题:思考题:已知线段AB=16㎝,BC=6㎝,M ,N 分别是线段AB ,BC 的中点,(1)若点B 在线段AC 上,求MN ;(2)若点B 在直线AC 上,求MN ;(3)第3题体现了数学的什么思想?任务四:课堂小结本节课你有哪些收获?(1) (2) (3)课末测学(时间:8分钟,分数:20分)1.(4分)如图中是正方体的展开图的有( )个A 、2个B 、3个C 、42.(4分)下列说法正确的是( )①教科书是长方形②教科书是长方体,也是棱柱③教科书的表面是长方形A .①②B .①③C .②③D .①②③3.(4分)下列说法中:①直线是射线长度的2倍;②线段AB 是直线AB 的一部分;③延长射线OA 到B。



青岛版初一数学上册第1章基本的几何图形知识点1.1 我们身边的图形世界几何图形:从实物中抽象出来的各种图形,包括立体图形和平面图形。
立体图形:有些几何图形的各个部分不都在同一平面内,它们是立体图形。
详细知识点请点击gt;gt;gt;gt;gt;青岛版七年级数学我们身边的图形世界知识点1.2 几何图形第一类:柱体;包括:圆柱和棱柱,棱柱又可分为直棱柱和斜棱柱,棱柱体按底面边数的多少又可分为三棱柱、四棱柱、N棱柱;棱柱体积统一等于底面面积乘以高,即V=SH,第二类:锥体;包括:圆锥体和棱锥体,棱锥分为三棱锥、四棱锥以及N棱锥;棱锥体积统一为V=SH/3,详细知识点请点击gt;gt;gt;gt;gt;青岛版七年级数学上册几何图形知识点1.3 线段、射线和直线1.直线:一根拉得很紧的线,就给我们以直线的形象,直线是直的,并且是向两方无限延伸的。
一条直线可以用一个小写字母表示,如直线l;2.射线:直线上一点和它一旁的部分叫做射线。
这个点叫做射线的端点。
一条射线可以用端点和射线上另一点来表示,如射线l或射线OA;详细知识点请点击gt;gt;gt;gt;gt;青岛版七年级数学上册线段射线和直线知识点1.4 线段的比较与作法射线:1、射线的定义:直线上一点和它们的一旁的部分叫做射线。
2、射线的特征:“向一方无限延伸,它有一个端点。
”详细知识点请点击gt;gt;gt;gt;gt;青岛版七年级数学上册线段的比较与作法知识点基本的几何图形知识点的全部内容就是这些,更多的精彩内容请点击初一数学知识点栏目了解详情,预祝大家在新学期可以更好的学习。

教案 基本的几何图形一、 本节课复习目标1、通过实物和具体模型,了解从物体抽象出来的几何体、平面、直线和点等几何图形。
2、会比较线段的长短,理解线段的和、差,以及线段中点的意义,并能运用这些解决简单问题。
3、掌握基本事实:两点确定一条直线和两点之间线段最短,并能运用他们解释实际问题。
4、理解两点间距离的意义,并能度量两点间的距离。
5、经历对简单图形的观察、实验、猜想、推断等活动,发展合情推理、有条理的思考与表达能力。
在用符号表示点、线的过程中,感受符号在描述图形中的重要作用。
6、经历观察、测量、展开、折叠、模型制作等数学活动,积累数学活动经验,体验立体图形与平面图形的相互转化。
7、在探究好认识基本的几何图形的过程中,进一步发展空间观念,丰富数学学习的成功体验,激发对几何学习的好奇心和求知欲,树立积极参与数学活动、主动与同学合作交流的意识。
二、复习重点:1、认识点线面,知道立体图形与平面图形;掌握线段、直线、射线的有关概念、性质和表示方法,会比较线段的大小,理解线段的和差及中点的意义,会画出线段的和差倍分。
2、感受符号语言在描述图形中的作用三、复习难点了解平面图形与立体图形可以相互转化;对直线、射线、线段等有关概念和性质的理解及其文字语言和符号语言的表述;以及研究对象“有数到形”的过渡而带来的学习方式上的不适应。
四、教学过程课前预习预习任务一:几何图形请同学们先明确下列任务,然后通读课本4-12页,完成下列问题1、我们研究几何体,只研究他们的_______、_______和位置关系。
我们学过的几何体有_______、_______、_______、_______、_______、等。
2、_______、_______、_______、_______、以及他们是组合都是几何图形,我们学过的几何图形可以分为_______和_______两大类。
3、点动成_______,线动成_______,面动成_______。


第一章基本的几何图形1.1我们身边的图形世界1.体的概念如果对于我们看到的物体,只研究它们的形状、大小和位置关系,而不考虑颜色、质量、原料等其他性质时,就得到各种几何体,几何体简称体。
平面与曲面平面:平的面,(1)没有厚薄,(2)没有边界,(3)向四周无限延展。
曲面:曲的面2.几何体的分类常见的几何体通常分为三类:柱体,锥体和球体。
柱体包括圆柱和棱柱,结构特征是上下底面是两个平行且形状相同,大小相等的面,圆柱的底面是圆,棱柱的底面是多边形。
锥体包括圆锥和棱锥,圆锥的底面是圆,底面是多边形。
3.体与面的关系体是由面围成的。
包括只含有平面的几何体(如长方体,正方体等棱柱,棱锥)与只含有曲面的几何体(如球),既含有平面又含有曲面的几何体,(如圆柱,圆锥)习题:1.说出下列几何体的名称:(1)2.下列实物形状类似于哪种几何体?茶叶桶——(),蛋糕帽——(),足球——(),漏斗——()3.圆柱由几个面组成?有几个曲面?有几个平面?4.圆锥由几个面组成?有几个曲面?有几个平面?1.2几何图形1.几何图形:点、线、面、体以及它们的组合都是几何图形。
2.点:线与线的交接处是点,点是组成几何图形的基本元素。
在长方体或正方体中,棱与棱的公共点叫做长方体或正方体的顶点。
3.线:一般地,两个面的交接处是一条线,线可以是直的,也可以是曲的。
(1)长方体和正方体中,相邻两个面的交接处是一段直的线,叫做棱。
(2)圆柱和圆锥中,侧面与底面的交接处都是圆,圆是一条封闭的曲线。
4.在数学上,点无大小,线无粗细,面无厚薄。
5.点、线、面、体之间的关系:点动成线,线动成面,面动成体。
6.几何图形的分类:平面图形与立体图形(1)立体图形:如果一个几何图形上的点不都在同一平面内,那么这样的几何图形叫做立体图形(2)平面图形:如果一个几何图形上所有的点都在同一个正方体的表面展开图:11种(1)一四一型:中间四连方,两侧各一个共6种(2)二三一型:中间三连方,二一两侧放共3种(3)二二二型:中间二连方,台阶逐级上共1种(4)三三型:两排三连方,一日放光芒共1种8.正方体表面展开图折成正方体时,相对的面有以下规律:“隔一相对法”(1)若正方体中相对的两个面在展开图的同行或同列中,则它们中间一定隔着一个正方形;(2)若展开图中正方形A在同行或同列中隔正方形C 的位置是空白的,则与该空白位置相邻的正方形B与正方形A是相对面习题:1.正方体有几个面?几个顶点?几条棱?2.五棱柱有几个面?几个顶点?几条棱?3.流星划过夜空留下的痕迹可用什么定理解释?风扇旋转的过程运用什么定理解释?硬币在桌面快速旋转,形成一个球的印象,运用了什么定理?4.正方体的平面展开图都分几种类型?5.找出下列正方体平面展开图的对立面?1.3线段、射线和直线1.线段(1)特征:①有两个端点;②有长短(即可度量);③无方向(2)表示方法:①用表示线段端点的两个大写字母表示,如线段AB或线段BA(字母无序)②用一个小写字母表示,如线段a2.射线:将线段向一个方向无限延伸就得到射线(1)特征:①有一个端点;②无长短(即可度量);③有方向(只向一个方向无限延伸)(2)表示方法:①用两个大写字母表示,第一个字母表示射线的端点,第二个字母是射线上任意一点,与字母排序有关②用一个小写字母表示,如射线a3.直线:将线段向两个方向无限延伸就得到直线(1)特征:①无端点;②无长短(即可度量);③无方向(2)表示方法:①用直线上任意两个点的大写字母表示,与字母排序无关②用一个小写字母表示,如直线a4.直线、射线、与线段的关系:射线、线段都是直线的一部分,线段向一个方向无限延伸就得到射线,向两个方向无限延伸就得到直线5.点与直线的位置关系:(1)点在直线上(或直线经过点);(2)点在直线外(或直线不经过点)6.直线的确定:两点确定一条直线7.两条直线的关系:平面上的两条直线有相交(有一个交点)与不相交(无交点)两种位置关系如果两条直线经过同一个点,就称这两条直线相交。

第一章基本的几何图形1.2 几何图形一、几何图形现实生活中的物体我们只管它的形态、大小、位置而得到的图形,叫做几何图形。
1.基本元素:点、线、面、体。
⑪点动成线,线动成面,面动成体。
(体是由面围成的,很多立体图形是由一些平面图形围成的,将它们适当地剪开,就可以绽开成平面图形。
面有平面和曲面)(举例)笔写字、汽车在雨中行驶,雨刷器来回摇摆成面、硬币旋转会产生一个圆球。
⑫线与线相交(点)面与面相交(线)棱顶点(长方体,正方体)2. 分类长方体、正方体、球、圆柱、圆锥等都是立体图形。
此外棱柱、棱锥也是常见的立体图形。
长方形、正方形、三角形、圆等都是平面图形。
几何图形有平面图形和立体图形(两者之间的转化)几何体:①柱体(圆柱和棱柱)②锥体(圆锥和棱锥)③球④台体3.正方体的平面绽开图有“11种”(至少剪7条棱正方体展成平面图形)考点:1.识别常见的几何体1.在六角螺母、乒乓球、圆形烟囱、书本、热水瓶胆等物体中,形态类似于棱州钦丽美 爱我柱的有___1__个,球体有____1_个。
2.圆锥由__2__个面围成,其中__1____个平面,__1___个曲面.3.写出你所熟识的、由三个面围成的几何体的名称是 圆柱4.六棱柱由几个面围成( C )A.6个B.7个C.8个D.9个5.下列平面绽开图是由5个大小相同的正方形组成,其中沿正方形的边不能折成无盖小方盒的是(B )6.一个正方体的每个面都有一个汉字,其平面绽开图如图所示,则该正方体中与“美”字相对的面上的字是7.如图,各图中的阴影图形围着直线旋转360度,各能形成怎样的立体图形。
8.图甲能围成 圆锥 ;图乙能围成 三棱锥 ;图丙能围成 长方体 。
A B C D 丙甲乙1.3 线段、射线、直线线段有两个端点。
将线段向一个方向无限延长就得到射线,射线有一个端点。
将线段向两个方向无限延长就得到线段,线段有两个端点。
1.线段、射线、直线的区分和联系.留意:线段、射线、直线的表示方法,要会画图形。

城聊丽美爱我基本的几何图形复习目标:1、通过实物和具体模型,了解从物体抽象出来的几何体、平面、直线和点等几何图形。
2、进一步认识直线、射线、线段,能按要求画出直线、射线和线段,并能用符号表示它们。
理解点与直线的位置关系,掌握直线的基本性质。
3、掌握线段的基本性质,会比较线段的大小,理解线段的和、差以及线段的中点的意义,能用直尺和圆规作一条线段等于已知线段,能用刻度尺或直尺和圆规画出线段的和差、倍、分。
复习过程:一、知识网络体系:⎧⎪⎪⎪⎨⎪⎪⎪⎩点: 是组成图形的基本元素 概念:表示方法:(1) ( 2) 线段:大小比较:线段的性质:中点:线:概念:射线表示方法:(1) ( 2) 几何图形⎧⎪⎪⎪⎪⎪⎪⎪⎪⎧⎨⎨⎪⎩⎪⎪⎧⎪⎪⎪⎨⎪⎪⎩⎪⎪⎩概念:直线表示方法:(1) ( 2) 性质:曲线平面:平面图形定义: 面⎧⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎪⎧⎪⎨⎪⎩⎪⎧⎪⎨⎪⎩⎩曲面定义:体:立体图形正方体的展开图例2.(1)下列平面展开图是由5个大小相同的正方形组成,其中沿正方形的边不能折成无盖小方盒的是( )(2)一个正方体的每个面都有一个汉字,其平面展开图如图所示,则该正方体中与“美”字相对的面上的字是 知识点3:线段、射线、直线的有关知识例3 (1)下列说法正确的是;( )A 、经过一点有且只有一条直线B 、射线OA=3cm A BC Dba CB AC 、所有连接两点的线中,线段最短D 、延长线段AB 到C 使AC=BC(2)、两点A 、B 间的距离是( )A 、连接两点A 、B 间的线段 B 、连接两点A 、B 间的直线C 、线段AB 的长度D 、直线AB 的长度(3)下列图形中,能够相交的是( ).知识点4:用直尺和圆规作线段等于已知线段或已知线段的和、差、倍例4 如图,已知线段a 、b ,求作线段AB =2a+b 。
知识点5:线段中点的应用 例5 如图,AB=24cm ,C 、D 点在线段AB 上,且CD=10cm ,M 、N 分别是AC 、BD 的中点,求线段MN 的长.练习:在直线上顺次取A 、B 、C 三点,使得AB=9cm,BC=4cm,若点O 是线段AC 的中点,求线段OB 的长.三、课堂小结:通过本节课的学习,你有什么收获?四、课下练习:一、精心选一选1.下列说法错误的是( )A.若AP=BP,则点P 是线段的中点B.若点C 在线段AB 上,则AB=AC+BCC.若AC+BC>AB,则点C 一定在线段AB 外D.两点之间,线段最短2.开往A 市的特快列车途中停靠两个站点,如果任意两站间的票价都不同,不同的车票有( )种A.14B.20C.10D. 123.如图所示,图中共有几条线段( )A. 4B. 5C. 10D.15N M B C A4.已知线段AB=8cm ,在直线AB 上画线段BC ,使它等于3cm,则线段AC 等于( )A.5cmB. 11cmC. 5cm 或11cmD. 5cm 或12cm5.任意画三条直线,则交点可能是( )A.1个B.1个或3个C.1个或2个或3个D.0个或1个或2个或3个二、细心填一填6.直角三角形绕一条直角边旋转一周得到的几何体是7.已知点B 在线段AC 上,AB=6cm,BC=10cm,P 、Q 分别是AB 、BC 中点,则线段PQ= cm8.已知线段CD ,延长CD 到点B ,使DB =21CD ,再反向延长CD 到A ,使AC =CD ,若AB =10厘米,则CD =_________厘米。
基本的几何图形知识点回顾:知识点一:几何体的认识1.我们常见的几何体有:正方体、长方体、圆锥、圆柱、棱柱、棱台、棱锥、球,其中____________属于柱体, _________属于锥体。
2. 像棱台、棱锥的面都是______的,这样的几何体称多面体.同步测试:1.下列判断正确的有()①长方体是棱柱,正方体不是长方体②正方体是棱柱,长方体也是棱柱③正方体是柱体,圆柱也是柱体④正方体不是柱体,圆柱是柱体A.1个B.2个C.3个D.4个2.下列几何体不属于柱体的有()A.正方体B.长方体C.圆锥D.圆柱知识点二:几何体的展开与平面图形的折叠:1.数学上所说的平面没有边界,可以向四面八方无限_________.2.三角形、正方形、长方形、平行四边形、梯形、圆等都是__________. 同步测试:1.下列图形折叠后的几何体是五棱柱的是()2.下列图形不是四棱柱的展开图的是()知识点三:几何体的基本要素:点、线、面、体1. 天上一颗颗闪烁的星星给我们以“______”的形象;划过夜空的流星给我们以“_________”的形象;打开的折扇给我们以“__________”的形象;宾馆里旋转的大门给我们以“___________”的形象.几何图形是由_____、______、______、______组成的.2.一个正方体共有______个面,______条棱,______个顶点.同步测试:1.将三角形绕直线l旋转一周,可以得到图1所示的立体图形的是().A.B.C.2.五棱柱的棱数和侧面数分别是()A.5,5 B.15,5 C.10,7 D.5,7知识点四:线段、直线、射线1. “拔河时,拉直的绳子给我们以________的形象.”把线段向两方无限延伸,就得到________;将线段向一个方向无限延伸就形成了__________;射线有____个端点,线段有____个端点,而直线________端点.2. 线段、直线、射线都可以用两个大写的字母或一个小写的字母表示,而表示射线时表示端点的大写字母必须写在________.同步测试:1.下列说法中,错误的是().A.经过一点的直线可以有无数条 B.经过两点的直线只有一条C.一条直线只能用一个字母表示 D.线段CD和线段DC是同一条线段2.下列图形中,能够相交的是( ).知识点五:线段的基本性质,线段的度量与比较1.经过一点可以画______条直线,经过两点能且只能画_______条直线,也就是说_______确定一条直线.如果两条直线经过同一个点,那么这两条直线________,这个点叫做这两条直线的________.2.两点之间的所有连线中,_______最短;两点之间的线段的长度叫做这两点之间的________.3.如图2,如果点M把线段AB分成相等的两条线段AM与BM,那么点M叫做这条线段AB的________,记作AM = BM =21AB.同步测试:1. 线段AB的长为8cm,点C为线段AB上任意一点,若M为线段AC的中点,N为线段CB的中点,则线段MN的长是_________.2.已知点A、B、C都是直线l上的点,且AB=5cm,BC=3cm,那么点A与点C之间的距离是().A.8cm B.2cm C.8cm或2cm D.4cmA.B.C.D.图1。
初中上册单元复习一遍过Unit 1 of junior high school精品资源·备战中考第一单元《基本的几何图形》(知识梳理)【思维导图】【知识清单】知识点一:几何图形(一)基本元素:点、线、面、体。
点:线和线相交的地方是点,它是几何图形最基本的图形。
线:面和面相交的地方是线,分为直线和曲线。
面:包围着体的是面,分为平面和曲面。
体:几何体也简称体。
(二)分类几何图形有平面图形和立体图形1.立体图形概念:有些几何图形的各部分不都在同一个平面内。
2.常见的几何体:(1)柱体(圆柱和棱柱)(2)锥体(圆锥和棱锥)(3)球(4)台体……3.立方体图形平面展开图4.正方体的平面展开图有“11种”(至少剪7条棱正方体展成平面图形)(1)“一四一型”(2)“二三一型”(3)“三三型”(4)“二二二型”点拨:(1)正方体的表面展开图中,一条直线上的小正方形不会超过四个;(2)正方体的表面展开图中不能出现“田”字、“凹”字和“7”字;(3)相间的两个小正方形(中间隔着一个小正方形)是正方体的两个对面型两端处的小正方形是正方体的对面;(4)中间隔着两个小正方形或拐角型的三个面的正方体的邻面.5.平面图形概念:有些几何图形的各部分不都在同一个平面内。
常见的平面图形:线段、角、三角形、长方形、圆等6.立体图形和平面的区别(1)所含平面数量不同。
平面图形是存在于一个平面上的图形。
立体图形是由一个或者多个平面形成的图形,各部分不在同一平面内,且不同的立体图形所含的平面数量不一定相同。
(2)性质不同。
根据“点动成线,线动成面,面动成体”的原理可知,平面图形是由不同的点组成的,而立体图形是由不同的平面图形构成的。
由构成原理可知平面图形是构成立体图形的基础。
(3)观察角度不同。
平面图形只能从一个角度观察,而立体图形可从不同的角度观察,如左视图,正视图、俯视图等,且观察结果不同。
(4)具有属性不同。
平面图形只有长宽属性,没有高度;而立体图形具有长宽高的属性。