下载文档原格式
图的哈密顿路径与TSP问题图论是离散数学中的一个重要分支，研究的是图的性质和特征。
在图论中存在着一些重要的问题，其中包括哈密顿路径和旅行商问题（TSP）。
本文将介绍图的哈密顿路径和TSP问题，并探讨它们的联系和应用。
一、图的哈密顿路径1.1 图的定义与基本概念在图论中，图是由顶点和边组成的一种数学模型。
顶点用于表示不同的元素，边则表示这些元素之间的关系。
图可以分为有向图和无向图，有向图中的边具有方向性，而无向图中的边没有方向性。
1.2 哈密顿路径的定义对于一个图G，如果存在一条路径，使得该路径经过图中的每个顶点恰好一次，并且最后返回起点，则称这条路径为哈密顿路径。
1.3 哈密顿环的定义如果在哈密顿路径的定义中，该路径的起点和终点相同，则称这条路径为哈密顿环。
二、TSP问题2.1 TSP问题的定义旅行商问题（Traveling Salesman Problem，简称TSP）是一种著名的组合优化问题。
在TSP问题中，假设有n个城市，一个旅行商要从起点出发，经过每个城市一次，并最终回到起点。
求解TSP问题的目标是找到一条最短路径，使得旅行商的总旅行距离最短。
2.2 TSP问题的难解性TSP问题是一个NP难问题，即目前没有找到有效的解决方法，只能通过穷举法或近似算法来求解。
当城市数量较少时，可以通过穷举法找到最优解，但当城市数量增多时，穷举法的计算复杂度将呈指数级增长，因此需要采用启发式算法等近似求解方法。
三、TSP问题与哈密顿路径的联系3.1 TSP问题的哈密顿路径特性TSP问题可以看作是在一个完全图中寻找一个哈密顿路径，使得路径的总权重最小。
完全图是指图中的每两个顶点之间都有一条边。
因此，TSP问题是哈密顿路径的特殊情况。
3.2 TSP问题的解与哈密顿路径的关系在实际求解TSP问题时，常常通过构造图的哈密顿路径来逼近TSP 问题的最优解。
其中最著名的算法是Christofides算法，该算法通过构造最小生成树和欧拉回路的方式来逼近TSP问题的解。
最小生成树题目 最小生成树是图论中的一个重要概念，被广泛应用于路由算法、网络设计、电力传输等领域。
最小生成树问题可以简单描述为：给定一个连通图，选择一些边使得图中所有节点都能够连接，并且总边权之和最小。
最小生成树题目是在解决最小生成树问题时所遇到的具体情境。
以下通过分析两个不同的最小生成树题目，来理解最小生成树算法的应用。
题目1：某城市的道路规划 假设一个城市有多个地区，每个地区之间需要建立道路来连接。
已知每条道路的长度，在保证每个地区都能连通的情况下，设计一个道路规划方案，使得总道路长度最小。
解题思路： 1、首先，根据题目中给出的道路长度，建立一个无向带权图。
其中，每个地区对应图的节点，道路对应图的边，道路长度对应边的权值。
2、通过使用Kruskal或Prim算法，从这个带权图中构建最小生成树，即选取一些道路使得所有地区连通，并且这些道路的权值之和最小。
3、最小生成树即为最优的道路规划方案，输出最小生成树的边集合即可。
题目2：电力传输网络设计 某地区有多个居民点，需要建立电力传输网络来确保每个居民点都能接收到电力供应。
已知每个居民点之间建立电力线路的成本，在保证每个居民点都能接收到电力供应的情况下，设计一个电力传输网络，使得总成本最小。
解题思路： 1、根据题目给出的电力线路成本，建立一个带权完全图。
其中，每个居民点对应图的节点，电力线路对应图的边，电力线路成本对应边的权值。
2、通过使用Kruskal或Prim算法，从这个带权图中构建最小生成树，即选取一些电力线路使得所有居民点都能接收到电力供应，并且这些电力线路的成本之和最小。
3、最小生成树即为最优的电力传输网络设计方案，输出最小生成树的边集合即可。
最小生成树问题是一个经典的优化问题，通过构建最小生成树，我们可以找到图中连接所有节点的最优边集合。
在实际应用中，最小生成树算法可以帮助我们进行有效的资源分配、网络规划等决策。
总体来说，最小生成树题目涉及到图的建模和优化算法的运用。
榆林学院12届课程设计《最小生成树问题》课程设计说明书学生姓名：赵佳学号：1412210112院系：信息工程学院专业：计算机科学与技术班级：计14本1指导教师：答辩时间：年月日最小生成树问题一、问题陈述最小生成树问题设计要求：在n个城市之间建设网络，只需保证连通即可，求最经济的架设方法。
存储结构采用多种。
求解算法多种。
二、需求分析1.在n个城市之间建设网络，只需保证连通即可。
2.求城市之间最经济的架设方法。
3.采用多种存储结构，求解算法也采用多种。
三、概要设计1、功能模块图2、功能描述（1)CreateUDG()创建一个图：通过给用户信息提示，让用户将城市信息及城市之间的联系关系和连接权值写入程序，并根据写入的数据创建成一个图。
（2)Switch()功能选择：给用户提示信息，让用户选择相应功能。
（3)Adjacency_Matrix()建立邻接矩阵：将用户输入的数据整理成邻接矩阵并显现在屏幕上。
（4)Adjacency_List()建立邻接表：将用户输入的数据整理成临接表并显现在屏幕上。
（5)MiniSpanTree_KRSL()kruskal算法：利用kruskal算法求出图的最小生成树，即：城市之间最经济的连接方案。
（6)MiniSpanTree_PRIM()PRIM算法：利用PRIM算法求出图的最小生成树，即：城市之间最经济的连接方案。
四、详细设计本次课程设计采用两种存储结构以及两种求解算法。
1、两种存储结构的存储定义如下：typedef struct Arcell{double adj;}Arcell,AdjMatrix[MAX_VERTEX_NUM][MAX_VERTEX_NUM];typedef struct{char vexs[MAX_VERTEX_NUM]; //节点数组AdjMatrix arcs; //邻接矩阵int vexnum,arcnum; //图的当前节点数和弧数}MGraph;typedef struct Pnode //用于普利姆算法{ char adjvex; //节点double lowcost; //权值}Pnode,Closedge[MAX_VERTEX_NUM];//记录顶点集U到V-U的代价最小的边的辅助数组定义typedef struct Knode//用于克鲁斯卡尔算法中存储一条边及其对应的2个节点{char ch1; //节点1char ch2; //节点2double value;//权值}Knode,Dgevalue[MAX_VERTEX_NUM];2、求解算法采用Prim算法和Kruskal算法。
数据结构课程设计选题数据结构课程设计选题题⽬选题⼀：迷宫与栈问题【问题描述】以⼀个mXn的长⽅阵表⽰迷宫，0和1分别表⽰迷宫中的通路和障碍。
设计⼀个程序，对任意设定的迷宫，求出⼀条从⼊⼝到出⼝的通路，或得出没有通路的结论。
【任务要求】1)⾸先实现⼀个以链表作存储结构的栈类型，然后编写⼀个求解迷宫的⾮递归程序。
求得的通路以三元组（i，j，d）的形式输出。
其中：（i，j）指⽰迷宫中的⼀个坐标，d表⽰⾛到下⼀坐标的⽅向。
如，对于下列数据的迷宫，输出⼀条通路为：（1，1，1），（1，2，2），（2，2，2），（3，2，3），（3，1，2），…。
2)编写递归形式的算法，求得迷宫中所有可能的通路。
3)以⽅阵形式输出迷宫及其通路。
【测试数据】迷宫的测试数据如下：左上⾓（0，1）为⼊⼝，右下⾓（8，9）为出⼝。
出⼝出⼝选题⼆：算术表达式与⼆叉树【问题描述】⼀个表达式和⼀棵⼆叉树之间，存在着⾃然的对应关系。
写⼀个程序，实现基于⼆叉树表⽰的算术表达式的操作。
【任务要求】假设算术表达式Expression内可以含有变量（a～z）、常量（0～9）和⼆元运算符（+，-，*，/，^(乘幂)）。
实现以下操作：1)ReadExpre(E)—以字符序列的形式输⼊语法正确的前缀表达式并构造表达式E。
2)WriteExpre(E)—⽤带括弧的中缀表达式输出表达式E。
3)Assign(V,c)—实现对变量V的赋值（V=c），变量的初值为0。
4)Value(E)—对算术表达式E求值。
5)CompoundExpr（P，E1，E2）--构造⼀个新的复合表达式（E1）P（E2）【测试数据】1)分别输⼊0；a；-91；+a*bc；+*5^x2*8x；+++*3^x3*2^x2x6并输出。
2)每当输⼊⼀个表达式后，对其中的变量赋值，然后对表达式求值。
选题三：银⾏业务模拟与离散事件模拟【问题描述】假设某银⾏有4个窗⼝对外接待客户，从早晨银⾏开门（开门9：00am，关门5：00pm）起不断有客户进⼊银⾏。
摘要：最小生成树（Minimum Spanning Tree，MST）是图论中的一个基本概念，它在网络设计、数据结构、算法设计等领域有着广泛的应用。
本文将详细介绍最小生成树定理的定义、性质、算法以及在实际应用中的重要性。
一、引言在图论中，一个图由顶点和边组成。
如果这个图是一个连通图，那么它的任意两个顶点之间都存在一条路径。
最小生成树定理研究的是如何从一个连通无向图中选择一些边，使得这些边构成一个连通子图，并且所有边的权值之和最小。
二、定义1. 图：由顶点集合V和边集合E组成，记为G=(V,E)，其中V表示顶点集，E表示边集。
2. 连通图：对于图G中的任意两个顶点u、v，若存在一条路径连接u和v，则称图G是连通的。
3. 无向图：对于图G中的任意两个顶点u、v，若边(u,v)和边(v,u)同时存在，则称边(u,v)为无向边。
4. 权值：对于图G中的任意一条边(u,v)，可以赋予一个非负实数w(u,v)作为权值。
5. 最小生成树：对于图G的一个连通子图T，如果满足以下两个条件，则称T为G 的最小生成树：（1）T是连通的；（2）T中的边权值之和最小。
三、性质1. 存在性：对于任意一个连通无向图，都存在一个最小生成树。
2. 唯一性：对于任意一个连通无向图，其最小生成树是唯一的。
3. 极小性：对于任意一个连通无向图，它的最小生成树中的边权值之和最小。
4. 极大性：对于任意一个连通无向图，它的最小生成树中的边权值之和最大。
四、算法1. 克鲁斯卡尔算法（Kruskal's Algorithm）（1）将图G中的所有边按照权值从小到大排序；（2）初始化一个空的最小生成树T；（3）遍历排序后的边，对于每条边(u,v)：①检查边(u,v)是否与T中的任意一条边形成环；②若不形成环，则将边(u,v)加入T；（4）当T中的边数等于顶点数减1时，算法结束。
2. 普里姆算法（Prim's Algorithm）（1）从图G中选择一个顶点作为起始顶点v0；（2）初始化一个空的最小生成树T，并将v0加入T；（3）对于图G中的其他顶点v，初始化一个距离数组dist，其中dist[v]表示顶点v到T的距离，初始时dist[v]=∞（v≠v0）；（4）遍历T中的顶点，对于每个顶点v，更新其相邻顶点的距离；（5）从距离数组中选择距离最小的顶点u，将其加入T；（6）重复步骤（4）和（5），直到T中的边数等于顶点数减1。
最小生成树算法在城市规划中的应用城市规划是指针对城市的发展和布局进行系统设计和管理的过程。
在城市规划中，如何高效地建立城市的基础设施和交通网络是一个重要的问题。
最小生成树算法作为一种经典的图论算法，被广泛应用于城市规划中，用于优化城市的基础设施和交通布局。
一、最小生成树算法简介最小生成树算法是图论中的经典算法之一，用于找到一个连通图的最小生成树。
最小生成树是指包含图中所有顶点，并且边的总权重最小的树。
常见的最小生成树算法有Prim算法和Kruskal算法。
1. Prim算法Prim算法是一种贪心算法，主要思想是从一个初始节点开始，每次选择一个未被访问的节点和连接它的边中权重最小的边，并将该节点加入到树中，直到所有节点都被访问为止。
2. Kruskal算法Kruskal算法是一种基于边的排序算法，主要思想是按照边的权重递增的顺序依次选择边，当选择的边不会形成环时，将该边加入到树中，直到树中包含了所有的节点为止。
二、1. 基础设施规划最小生成树算法可以应用于基础设施规划中，例如道路、给排水系统、电力网络等。
通过将城市的基础设施抽象成一个图，节点代表不同的设施，边的权重代表建设设施所需的成本或者距离。
利用最小生成树算法，可以找到一种最优的布局方式，使得总的建设成本最小或者各设施之间的距离最小。
2. 交通网络规划最小生成树算法也可以应用于城市的交通网络规划中。
通过将城市的道路网抽象成一个图，节点代表交叉口或者重要的地点，边的权重代表道路的长度或者通行的成本。
利用最小生成树算法，可以找到一种最优的道路布局方式，使得整个城市的交通效率最高或者交通成本最低。
3. 公共设施规划另外，最小生成树算法还可以应用于城市的公共设施规划，例如学校、医院、公园等。
通过将城市不同区域的需求和供给抽象成一个图，节点代表不同的区域，边的权重代表区域之间的距离或者需求与供给的匹配度。
利用最小生成树算法，可以找到一种最佳的公共设施布局方式，使得城市的公共设施服务覆盖率最高或者供给与需求的匹配度最好。
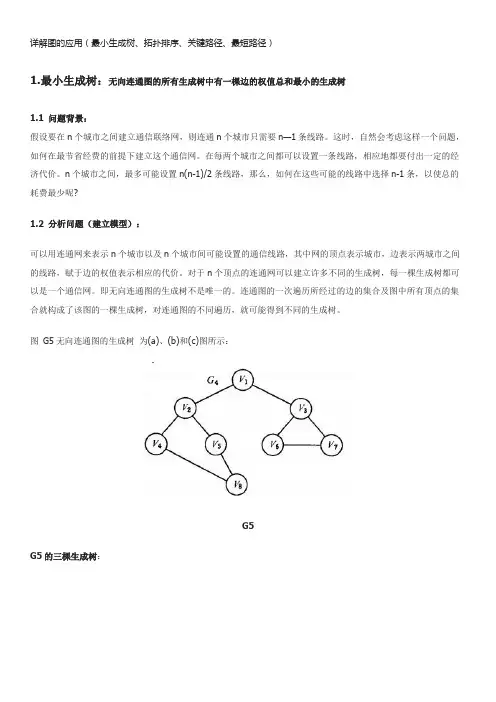
详解图的应用（最小生成树、拓扑排序、关键路径、最短路径）1.最小生成树：无向连通图的所有生成树中有一棵边的权值总和最小的生成树1.1 问题背景：假设要在n个城市之间建立通信联络网，则连通n个城市只需要n—1条线路。
这时，自然会考虑这样一个问题，如何在最节省经费的前提下建立这个通信网。
在每两个城市之间都可以设置一条线路，相应地都要付出一定的经济代价。
n个城市之间，最多可能设置n(n-1)/2条线路，那么，如何在这些可能的线路中选择n-1条，以使总的耗费最少呢?1.2 分析问题（建立模型）：可以用连通网来表示n个城市以及n个城市间可能设置的通信线路，其中网的顶点表示城市，边表示两城市之间的线路，赋于边的权值表示相应的代价。
对于n个顶点的连通网可以建立许多不同的生成树，每一棵生成树都可以是一个通信网。
即无向连通图的生成树不是唯一的。
连通图的一次遍历所经过的边的集合及图中所有顶点的集合就构成了该图的一棵生成树，对连通图的不同遍历，就可能得到不同的生成树。
图G5无向连通图的生成树为(a)、(b)和(c)图所示：G5G5的三棵生成树：可以证明，对于有n 个顶点的无向连通图，无论其生成树的形态如何，所有生成树中都有且仅有n－1 条边。
1.3最小生成树的定义：如果无向连通图是一个网，那么，它的所有生成树中必有一棵边的权值总和最小的生成树，我们称这棵生成树为最小生成树，简称为最小生成树。
最小生成树的性质：假设N=(V,{ E}) 是个连通网，U是顶点集合V的一个非空子集，若（u,v）是个一条具有最小权值(代价)的边，其中，则必存在一棵包含边（u,v）的最小生成树。
1.4 解决方案：两种常用的构造最小生成树的算法：普里姆（Prim）和克鲁斯卡尔（Kruskal）。
他们都利用了最小生成树的性质1.普里姆（Prim）算法：有线到点，适合边稠密。
时间复杂度O(N^2)假设G＝（V，E）为连通图，其中V 为网图中所有顶点的集合，E 为网图中所有带权边的集合。
数据结构课程设计说明书学院：信息科学与工程学院班级：计算机11-2完成人：姓名：学号：************ 姓名：学号：************ 指导教师：山东科技大学2012年12月13日课程设计任务书一、课程设计题目：构造可以使n个城市连接的最小生成树二、课程设计应解决的主要问题：（1）邻接矩阵的构造及其存储（2）判断是否能够生成最小生成树（3）克鲁斯算法的设计（4）利用克鲁斯算法构造最小生成树时是否产生回路的判断（5）界面的设计三、任务发出日期：2012-11-28 课程设计完成日期：2012-12-13小组分工说明小组编号 35 题目：构造可使n个城市连接的最小生成树小组分工情况：王露：算法设计，void Kruskal()函数，void set ()函数，void find()函数，void Union()函数王炜程：void creat()函数，void judge()函数，int main()函数；int menu()函数，void display()函数组长签字：年月日指导教师对课程设计的评价成绩：指导教师签字：年月日目录一、主要问题------------------------------------------------------------------5二、基本要求------------------------------------------------------------------5三、算法基本思想描述------------------------------------------------------5四、详细设计------------------------------------------------------------------51、数据结构的设计----------------------------------------- 5<1> 存储结构------------------------------------------------------- 5<2> 图的表示--------------------------------------------------------62、算法的设计---------------------------------------------6<1> 克鲁斯卡尔算法设计----------------------------------------------6<2> 防止不能构成最小生成树的图--------------------------------------6<3> 模块结构及功能-------------------------------------------------- 7<4> 主要模块算法描述------------------------------------------------ 7五、源程序清单-----------------------------------------------------------------9六、测试数据及测试结果-----------------------------------------------------91、开始画面--------------------------------------------------------- 92、输入信息--------------------------------------------------------- 103、数据处理---------------------------------------------------------10（1）判断能否构成最小生成树--------------------------------------- 10（2）遍历所有的最小生成树----------------------------------------- 10（3）退出--------------------------------------------------------- 11七、课程设计总结--------------------------------------------------------------11八、附录--------------------------------------------------------------------------------11 参考书目--------------------------------------------------------------------------15构造可以使n个城市连接的最小生成树一、主要问题给定一个地区的n个城市间的距离网，用Prim算法或Kruskal算法建立最小生成树，并计算得到的最小生成树的代价。
二、基本要求（1）城市间的距离网采用邻接矩阵表示，邻接矩阵的存储结构定义采用课本中给出的定义，若两个城市之间不存在道路，则将相应边的权值设为自己定义的无穷大值。
要求在屏幕上显示得到的最小生成树中包括了哪些城市间的道路，并显示得到的最小生成树的代价。
（2）表示城市间距离网的邻接矩阵（要求至少6个城市，10条边）（3）最小生成树中包括的边及其权值，并显示得到的最小生成树的代价。
三、算法基本思想描述Kruskal算法思想基本描述：假设连通图N=（V，{E}），则令最小生成树的初始状态为只有n 个顶点而无边的非连通图T=(V,{ })，图中每个顶点自成一个连通分量。
在E中选择代价最小的边，若该边依附的顶点落在T中不同的连通分量上，则将此边加入到T中，否则舍去此边而选择下一条代价最小的边。
以此类推，直至T中所有顶点都在同一个连通分量上为止。
四、详细设计1、数据结构的设计<1> 存储结构邻接矩阵存储方法（数组存储方法），利用两个数组来存储一个图，其构造原理比较简单。
对于具有n个顶点的图G=(V,E),定义一个具有n个元素的一维数组VERTEX[0..n-1]，将图中顶点的数据信息分别存入该数组的一个数组元素中。
另外，定义一个二维数组A[0..n-1][0..n-1],该二维数组通常被称为邻接矩阵。
若以顶点在VERTEX数组中的下标来代表一个顶点，则邻接矩阵中元素A[i][j]存放顶点i到顶点j之间的关系信息，有1当顶点i与顶点j之间有边时A[i][j] =0 当顶点i与顶点j之间无边时对于网络，有ij W 当顶点i 与顶点j 之间有边时，且边上的权值为ij W 时A[i][j] =当顶点i 与顶点j 之间无边时<2> 图的表示用n 表示城市的个数，st 表示起始城市，ed 表示终点城市，dis 表示两城市间的距离。
下面是构成该结构体的源代码：typedef struct node { int st ;/*起点*/ int ed;/*终点*/ int dis ;/*距离*/ }node; node p[]； /*p[]数组用来储存城市和城市间的信息*/ 2 、算法的设计 <1> 克鲁斯卡尔算法设计a. 设置计数器E ，初值为0，记录已选中的边数。
将所有边从小到大排序，存于p[ ]中。
b. 从p[ ]中选择一条权值最小的边，检查其加入到最小生成树中是否会构成回路，若是，则此边不加入生成树；否则，加入到生成树中，计数器E 累加1。
c. 从E 中删除此最小边，转b 继续执行，直到k=n-1, 算法结束d. 判断是否构成回路的方法：设置集合S ，其中存放已加入到生成树中的边所连接的顶点集合，当一条新的边要加入到生成树中时，检查此边所连接的两个顶点是否都已经在S 中，若是，则表示构成回路，否则，若有一个顶点不在S 中 或者两个顶点都不在S 中，则不够成回路。
<2> 防止不能构成最小生成树的图为避免输入的图构成的不是连通图，设计了judge ( ) 函数来判断输入数据构成的是否为连通图，此函数的主要算法是源于普里姆算法，经过改编，形成了新的函数。
<3> 模块结构及功能a)int main ( ) //主程序b)int menu ( ) //菜单函数c)void create ( ) //输入城市信息函数d)void judge ( ) //判断是否能够生成最小生成树函数e)void display( ) //打印输出f)void set ( ) //初始化pre[],rank[]函数g)void find（）//判断是否构成回路函数h)void Union ( ) //将能构成最小生成树的边添加到一个集合i)void Krushal( ) //克鲁斯算法求最小生成树<4> 主要模块算法描述Krushal算法描述：/*下面三个函数作用是检验当一条边添加进去，是否会产生回路*/ void set(int x)/*初始化*/{pre[x] = x;rank[x] = 0;}int find(int x)/*找到这个点的祖先*/{if(x != pre[x])pre[x] = find(pre[x]);return pre[x];}void Union(int x,int y)/*将这两个添加到一个集合里去*/{x = find(x);y = find(y);if(rank[x] >= rank[y]){pre[y] = x;rank[x] ++;}else pre[y] = x;}void Kruskal( ){int ans = 0,i,j,k = 0; /*ans用来记录生成最小树的权总值*/int index;int count = 0; /*记录打印边的条数*/for(i = 1;i <= n;i ++) /*初始化数组pre[x],rank[x]*/set(i);for(i = 1;i <= n;i ++){for(j = i + 1;j <= n;j ++){p[++k].st = i;p[k].ed = j;p[k].dis = a[i][j]; /*先把所有城市之间的路段看成一个边*/ }}for(i=1;i<=k;i++) /*把所有的边按从小到大进行排序*/{index=i;for(j=i+1;j<=k;j++) if(p[j].dis <p[index].dis) index=j;temp=p[index];p[index]=p[i];p[i]=temp;}for(i = 1;i <= k;i ++){if (find(p[i].st) != find(p[i].ed))/*如果这两点连接在一起不构成一个回路，则执行下面操作*/ {printf("\t 第%d 条路段为：%d--%d,权值为%d\n",++ count,p[i].st,p[i].ed,p[i].dis);/*将这条边的起点、终点打印出来*/ ans += p[i].dis; /*说明这条路段要用*/ Union(p[i].st,p[i].ed); } }printf("\t 遍历所有城市得到最小生成树的代价为: %d\n\n",ans); }五、源程序清单（详见附录）六、测试数据及测试结果以一个6个城市、10条边的网络图为例进行测试GE = ∞∞∞∞∞∞∞∞∞∞∞∞∞∞∞∞9591814618221914221120561116192016邻接矩阵1、开始画面2、输入信息设置两顶点之间无边时∞权值为10000003、数据处理(1)、判断能否构成最小生成树（2）、遍历所有城市生成最小生成数16 115618生成的最小生成树1 53 2 64（3）、退出七、课程设计总结通过最小生成树的学习，我学会了树的多种存储结构和遍历方法，最小生成树的设计可以应用于我们生活中。
