判别分析例题及SAS程序
- 格式:pdf
- 大小:392.67 KB
- 文档页数:5
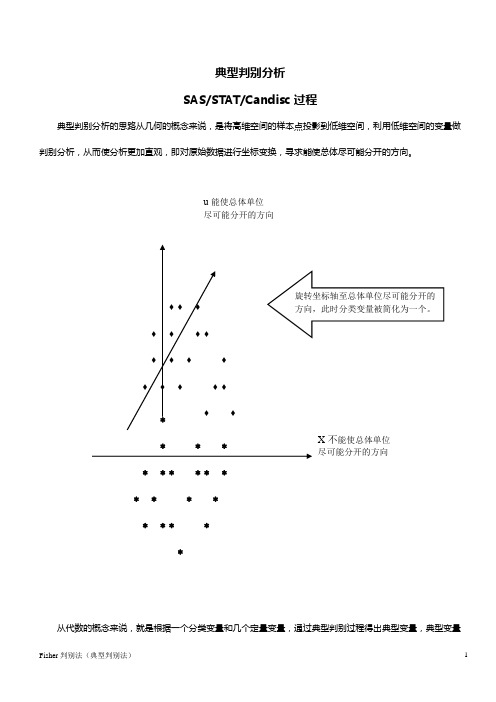
典型判别分析SAS/STAT/Candisc 过程典型判别分析的思路从几何的概念来说,是将高维空间的样本点投影到低维空间,利用低维空间的变量做判别分析,从而使分析更加直观,即对原始数据进行坐标变换,寻求能使总体尽可能分开的方向。
从代数的概念来说,就是根据一个分类变量和几个定量变量,通过典型判别过程得出典型变量,典型变量是定量变量的线性组合。
典型判别分析得出与组有最大可能多重相关的变量的线性组合,最大的多重相关叫做第一典型相关,其线性组合称为第一典型变量1u ,线性组合的相关系数称为典型系数,次大的叫做第二典型相关,其线性组合称为第二典型变量2u 。
Candisc 过程可使用的语句为:数据集选项:DATA=SAS-data-set (SAS 数据集):指定欲分析的数据集。
OUT=SAS-data-set (SAS 数据集):生成一个包含原始数据和典型变量得分的数据集。
OUTSTAT=SAS-data-set (SAS 数据集):生成一个type=corr 包含各种统计量的输出数据集。
典型变量选项:NCAN=n :指定将被计算的典型变量的个数。
n 的值必须小于或等于变量的个数。
u 能使总体单位打印选项:BCORR:类间相关系数。
PCORR:合并类内相关系数。
TCORR全样本相关系数。
WCORR每一类水平的类内相关系数。
BCOV:类间协方差。
PCOV:合并类内协方差。
TCOV:全样本协方差。
WCOV:每一类水平的类内协方差。
BSSCP:类间SSCP矩阵。
PSSCP:合并类内修正SSCP矩阵。
TSSCP:全样本修正SSCP矩阵。
WSSCP:每一类水平的类内修正SSCP矩阵。
ANOVA:检验总体中每一个变量类均值相等的假设的单变量统计量。
SIMPLE:全样本合类内的简单描述性统计量。
ALL:产生以上所有的打印选项。
NOPRINT:不打印。
一般语句By variables;By语句与Proc candisc一起使用可以对由BY变量分组的观测进行独立分析。

一、主成分分析1、数据引入PROC IMPORT OUT= WORK.shuruDA TAFILE= "E:\****\****\数据分析\试验\shouru.xls"DBMS=EXCEL2000 REPLACE;GETNAMES=YES;RUN;2、程序proc princomp data=shouru out=defen;var x1-x9;run;proc sort data=defen;by prin1 prin2;run;proc print data=defen;run;二、判别分析程序2.2方法1:先改变shuru 数据的结构,把待判的数据去掉,再引入数据data shouru1;input diqu $ x1-x9;cards;广东211.3 114 41.44 33.2 11.2 48.72 30.77 14.9 11.1西藏175.93 163.8 57.89 4.22 3.37 17.81 82.32 15.7 0;run;proc discrim data=shourutestdata=shouru1 method=normallist all crosslist testlist;class leixing;var x1-x9;run;方法2:原shuru数据不变,直接判别,但此法虽可判断待判的两省属于那类,但无法给出误判率;proc discrim data=shouruout=a1outstat=a2 outcross=a3method=normallist all crosslist testlist;class leixing;var x1-x9;run;程序2.3proc discrim data=shourutestdata=shouru1 method=normallist all crosslist crossvalidate testlist;class leixing;var x1-x9;priors prop;run;三、聚类分析程序proc cluster data=yjshr method=sin outtree=y1 ;/*最短距离法*/ var x1-x9;run;proc tree data=y1 nclusters=3 out=z1;run;proc print data=z1;run;proc cluster data=yjshr method=com outtree=y2 ;/*最长距离法*/ var x1-x9;run;proc tree data=y2 nclusters=3 out=z2;run;proc print data=z2;run;proc cluster data=yjshr method=ave outtree=y3 ;/*类平均距离法*/ var x1-x9;run;proc tree data=y3 nclusters=3 out=z3;run;proc print data=z3;run;proc fastclus data=yjshr out=a1maxc=3 cluster=c distance list; /*快速聚类分三类情况*/ proc plot;plot x2*x1=c;run;。
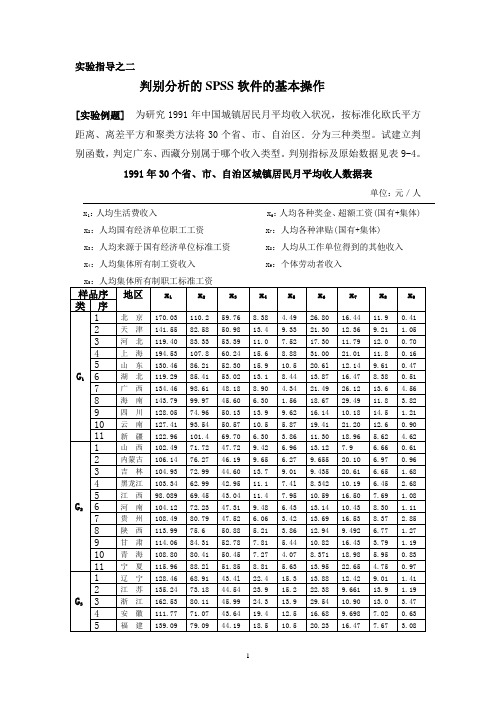
实验指导之二判别分析的SPSS软件的基本操作[实验例题]为研究1991年中国城镇居民月平均收入状况,按标准化欧氏平方距离、离差平方和聚类方法将30个省、市、自治区.分为三种类型。
试建立判别函数,判定广东、西藏分别属于哪个收入类型。
判别指标及原始数据见表9-4。
1991年30个省、市、自治区城镇居民月平均收人数据表单位:元/人 x1:人均生活费收入 x6:人均各种奖金、超额工资(国有+集体) x2:人均国有经济单位职工工资 x7:人均各种津贴(国有+集体)x3:人均来源于国有经济单位标准工资 x8:人均从工作单位得到的其他收入x4:人均集体所有制工资收入 x9:个体劳动者收入x5:人均集体所有制职工标准工资贝叶斯判别的SPSS操作方法:1. 建立数据文件2.单击Analyze→Classify→Discriminant,打开Discriminant Analysis判别分析对话框如图1所示:图1 Discriminant Analysis判别分析对话框3.从对话框左侧的变量列表中选中进行判别分析的有关变量x1~x9进入Independents 框,作为判别分析的基础数据变量。
从对话框左侧的变量列表中选分组变量Group进入Grouping Variable 框,并点击Define Range...钮,在打开的Discriminant Analysis: Define Range 对话框中,定义判别原始数据的类别数,由于原始数据分为3类,则在Minimum(最小值)处输入1,在Maximum(最大值)处输入3(见图2)。
选择后点击Continue按钮返回Discriminant Analysis主对话框。
图2 Define Range对话框4、选择分析方法✧Enter independent together 所有变量全部参与判别分析(系统默认)。
本例选择此项。
✧Use stepwise method 采用逐步判别法自动筛选变量。



距离判别和贝叶斯判别法SAS/STAT (DISCRIM )过程部分语句说明一、 D ISCRIM 过程语句SAS/STAT (DISCRIM )产生线性判别函数并进行分类,主要的语句如下:二、程序实例及解释例:某年为了研究某年全国各地农民家庭收支的分布情况,对全国28个地区进行了抽样调查。
食品1x ,衣着2x ,燃料3x ,住房4x ,生活用品及其他5x 和文化服务支出6x 。
data a;input type x1-x6;cards;数据行;run;data b;input x1-x6; cards;190.33 43.77 9.73 60.54 49.01 9.04 221.11 38.64 12.53 115.65 50.82 5.89 182.55 20.52 18.32 42.40 36.97 11.68 ;PROC DISCRIM DATA=a TESTDATA=b out=c crossvalidate method=normal TESTLIST testout=d; priors proportional; CLASS TYPE; VAR x3 x5 x6; proc print data=d; RUN;PROC DISCRIM DATA=a 指定对数据集a 中的数据进行判别分析; TESTDATA=b 指定欲分类观测的样品所在的数据集;crossvalidate 要求做交叉核实。
交叉核实的想法是,为了判断对观测i 的判别正确与否,用删除第method=normal 或npar 确定导出分类准则的方法,却上缺省值为method=normal 。
当指定method=normal 时,基于类内服从多员正态分布,并产生的判别函数是线性函数或二次判别函数; ALL 规定打印出所有的结果;TESTLIST 规定列出TESTDATA=b 中的全部的分类结果;testout=d 生成一个新的数据集,该数据集包括TESTDATA=b 中的所有数据,后验概率和每个样品被分的类。
SAS数据分析应用实例及相关程序正态性检验及T检验【例1】已知玉米单交种群105的平均穗重为300g。
喷药后,随机抽取9个果穗,其穗重分别为:308,305,311,298,315,300,321,294,320g。
问喷药后与喷药前的果穗平均重量之间的差别是否具有统计学意义?2.配对T检验【例2】对血小板活化模型大鼠以ASA进行实验性治疗,以血浆TXB2(ng/L)为指标,其结果如表2-1,试进行统计分析。
表2-1 2的变化(ng/L)3. 秩和检验【例3】探讨正己烷职业接触人群生化指标特征,用气相色谱法检测受检者尿液2,5-己二酮浓度(mg/L),为该人群的健康监护寻找动态观察依据。
正己烷职业接触组(A组)为广州市印刷行业彩印操作位作业人员64 人,其均在同一个大的车间轮班工作,工作强度相当;对照组(B组)选同厂其他车间工人53 人。
两组人员除接触正己烷因素不同外,生活水平、生活习惯、劳动强度、吸烟、饮酒情况基本相同。
问两组间尿液中2,5-己二酮浓度(mg/L)平均含量之间的差别是否有统计学意义?数据如下所示。
正己烷职业接触组:2.89、1.85、2.27、2.07、1.62、1.77、2.53、2.02、2.07、2.07、1.93、3.01、1.93、1.88、1.55、1.36、2.23、2.55、1.73、2.65、1.95、2.45、1.41、2.46、2.38、1.55、2.16、2.01、1.37、2.16、2.00、2.07、2.57、2.11、2.37、1.39、2.18、2.33、1.46、2.16、2.03、2.96、2.21、2.00、2.58、2.19、2.41、1.68、1.93、1.93、1.93、1.87、1.74、2.70、1.83、2.17、2.52、2.09、2.28、1.65、1.19、1.58、0.89、1.65对照组:0.27、0.36、0.26、0.16、0.49、0.58、0.16、0.45、0.22、0.25、0.66、0.05、0.31、0.12、0.51、0.30、0.37、0.14、0.28、0.33、0.36、0.51、0.37、0.36、0.47、0.34、0.72、0.39、0.55、0.17、0.27、0.33、0.30、0.26、0.50、0.17、0.22、0.18、0.17、0.62、0.27、0.26、0.34、0.17、0.61、0.42、0.39、0.28、0.36、0.43、0.24、0.15、0.194.两独立正态总体的检验【例4】一个小麦新品种经过6代选育,从第5代(A组)中抽出10株,株高为:66、65、66、68、62、65、63、66、68、62(cm),又从第6代(B组)中抽出10株,株高为:64、61、57、65、65、63、62、63、64、60(cm),问株高性状是否已经达到稳定?5.单因素K(K≥3)水平方差分析【例5】从津丰小麦4个品系中分别随机抽取10株,测量其株高(cm),数据如下所示,问不同品系津丰小麦的平均株高之间的差别是否具有统计学意义?品系0-3-1:63、65、64、65、61、68、65、65、63、64品系0-3-2:56、54、58、57、57、57、60、59、63、62品系0-3-3:61、61、67、62、62、60、67、66、63、65品系0-3-4:53、58、60、56、55、60、59、61、60、596. 双因素无重复试验的方差分析【例6】某医生欲研究回心草各单体成分对试验性心肌缺血血流动力学的影响,选取健康新西兰家兔若干只,体重(2.0±0.3)kg,雌雄不计,将其随机分成9组:胡椒碱高剂量组(100nmol/L)、胡椒碱中剂量组(10nmol/L)、胡椒碱低剂量组(1nmol/L)、胡椒酸甲酯高剂量组(100nmol/L)、胡椒酸甲酯中剂量组(10nmol/L)、胡椒酸甲酯低剂量组(1nmol/L)、咖啡酸甲酯高剂量组(100nmol/L)、咖啡酸甲酯中剂量组(10nmol/L)、咖啡酸甲酯低剂量组(1nmol/L)。
已知某研究对象分为三类,每个样品考察4项指标,各类的观测样品数分别为7,4,6;类外还有3个待判样品(所有观测数据见表2)。
假定样本均来自正态总体。
表2 判别分类的数据(1)试用马氏距离判别法进行判别分析,并对3个待判样品进行判别归类。
(2)使用其他的判别法进行判别分析,并对3个待判样品进行判别归类,然后比较之。
问题求解1判别分析及判别归类使用SAS软件中的DISCRIM过程进行判别归类,SAS程序及结果如下。
data d510;input x1-x4 group @@;cards;6 -11.5 19 90 1-11 -18.5 25 -36 390.2 -17 17 3 2-4 -15 13 54 10 -14 20 35 20.5 -11.5 19 37 3-10 -19 21 -42 30 -23 5 -35 120 -22 8 -20 3-100 -21.4 7 -15 1-100 -21.5 15 -40 213 -17.2 18 2 2-5 -18.5 15 18 110 -18 14 50 1-8 -14 16 56 10.6 -13 26 21 3-40 -20 22 -50 3-8 -14 16 56 .92.2 -17 18 3 .-14 -18.5 25 -36 .;proc print;run;proc discrim data=d510 simple pcov wsscp psscp wcovdistance list;class group;var x1-x4;run;从结果来看,样本2、3类之间的马氏距离为d 212=1.34,检验(2)(3)0:H μμ= 的F 统计量为0.63177,相应的p =0.651>0.10,故在显著性水平=0.10α时量总体2、3类的均值向量没有显著差异,即认为对讨论样本分为2、3类的判别问题是没有太大意义的。
此外,判别结果中两个样本被判错归类:1类中8号样本应属于2类,2类中9号样本应属于1类;且待判得三个样本分别属于1,2,3类。
一、实验目的及要求:1、目的用SPSS软件实现判别分析及其应用。
2、内容及要求用SPSS对实验数据利用Fisher判别法和贝叶斯判别法,建立判别函数并判定宿州、广安等13个地级市分别属于哪个管理水平类型。
二、仪器用具:三、实验方法与步骤:准备工作:把实验所用数据从Word文档复制到Excel,并进一步导入到SPSS 数据文件中,同时,由于只有当被解释变量是属性变量而解释变量是度量变量时,判别分析才适用,所以将城市管理的7个效率指数变量的变量类型改为“数值(N)”,度量标准改为“度量(S)”,以备接下来的分析。
四、实验结果与数据处理:表1 组均值的均等性的检验Wilks 的Lambda F df1 df2 Sig.综合效率标准指数.582 23.022 2 64 .000 经济效率标准指数.406 46.903 2 64 .000 结构效率标准指数.954 1.560 2 64 .218 社会效率标准指数.796 8.225 2 64 .001 人员效率标准指数.342 61.645 2 64 .000 发展效率标准指数.308 71.850 2 64 .000 环境效率标准指数.913 3.054 2 64 .054表1是对各组均值是否相等的检验,由该表可以看出,在0.05的显著性水平上我们不能拒绝结构效率标准指数和环境效率标准指数在三组的均值相等的假设,即认为除了结构效率标准指数和环境效率标准指数外,其余五个标准指数在三组的均值是有显著差异的。
表2 对数行列式group 秩对数行列式1 6 -33.4102 6 -33.1773 6 -40.584汇聚的组内 6 -32.308 打印的行列式的秩和自然对数是组协方差矩阵的秩和自然对数。
表3 检验结果箱的M 140.196F 近似。
2.498df1 42df2 1990.001Sig. .000 对相等总体协方差矩阵的零假设进行检验。
以上是对各组协方差矩阵是否相等的Box’M检验,表2反映协方差矩阵的秩和行列式的对数值。
实验报告实验项目名称聚类分析与判别分析所属课程名称统计分析及SAS实现实验类型验证性实验实验日期2016-12-19班级数学与应用数学学号姓名成绩图8.1 聚类谱系图图8.1为proc cluster过程不得出的谱系图,为更方便直观,我们利用proc tree过程步得出图8.2。
②利用proc tree过程步得出聚类谱系图。
过程步:proc tree data=Lmf.tree1 horizontal;id region;run;结果:The TREE ProcedureWard's Minimum Variance Cluster Analysis图8.2 聚类谱系图由表8.2、图8.2得出,分为三类较合适,第一类为北京、天津、上海,第二类为河北、山东、河南、内蒙、江苏、浙江、山西、湖北、四川、福建、江西、湖南、海南、广东、新疆、广西、吉林、黑龙江、辽宁、陕西,第三类为安徽、宁夏、贵州、云南、甘肃、青海、西藏。
【练习8-2】有6个铅弹头,用“中子活化”方法测得7种微量元素含量数据。
表 7种微量元素含量数据Num Ag Al Cu Ca Sb Bi Sn10.05798 5.515347.121.918586174261.6920.08441 3.97347.219.7179472000244030.07217 1.15354.85 3.05238601445949740.1501 1.702307.515.0312290146163805 5.744 2.854229.69.657809912661252060.2130.7058240.313.91898028204135①试用多种系统聚类分析方法对6个铅弹头和7种微量元素进行分类,并进行分类结果。
②试用VARCLUS过程对7中微量元素进行分类。
【解答】①通过比较⑴⑵⑶三种系统聚类的方法类平均法、ward离差平方和法、最长距离法,对6个铅弹头进行分类。
判别分析例题某医院眼科研究糖尿病患者的视网膜病变情况, 视网膜病变分轻、中、重三型。
研究者用年龄(age)、患糖尿病年数(time)、血糖水平(glucose)、视力(vision)、视网膜电图中的a波峰时(at)、a波振幅(av)、b波峰时(bt)、b波振幅(bv)、qp波峰时(qpt)及qp波振幅(qpv)等指标建立判别视网膜病变的分类函数, 以判断糖尿病患者的视网膜病变属于轻、中、重中哪一型。
为此观察131例糖尿病患者,要求其患眼无其他明显眼前段疾患, 眼底无明显其他视网膜疾病和视神经、葡萄膜等疾患,测定了他们的以上各指标值,并根据统一标准诊断其疾患类型,记分类指标名为group。
见表1 (表中仅列出前5例)。
试以此为训练样本, 仅取age,vision,at,bt和qpv 等指标, 求分类函数, 并根据王××的信息: 38岁, 视力1.0, 视网膜图at=14.25, bv=383.39, qpv=43.18判断其视网膜病变属于哪一型。
表1 131例糖尿病患者各指标实测记录(前5例)──────────────────────────────────例号年龄患病血糖视力a波a波b波b波qp波pq波视网膜年数峰时振幅峰时振幅峰时振幅病变程度──────────────────────────────────1 49 2.00 191 1.5 12.25 235.40 52.50 417.57 78.5 27.43 A12 49 2.00 191 1.2 13.50 225.15 52.00 391.20 78.5 46.69 A13 63 4.00 200 1.0 14.25 318.92 53.25 616.35 77.5 35.38 A14 63 4.00 200 0.6 14.00 361.90 55.00 723.30 77.0 47.01 A15 54 10.00 137 0.6 13.75 269.59 55.50 451.27 78.0 33.70 A2──────────────────────────────────解假定样本系从总体中随机抽取,则样本中三种疾患类型的样本量可近似地反映先验概率, 利用SAS的Discrim过程可得分类函数Y1=-181.447+0.473(age)+60.369(vision)+17.708(at)+0.048(bv)+0.364(qpv)Y2=-165.830+0.472(age)+49.782(vision)+17.658(at)+0.034(bv)+0.325(qpv)Y3=-189.228+0.178(age)+43.974(vision)+20.447(at)+0.040(bv)+0.265(qpv)以王××的观察值代入分类函数, 得Y1=-181.447+0.473×38+60.369×1.0+17.708×14.25+0.048×383.39+0.364×43.18 =183.36同样可算得:Y2=180.58, Y3=179.66其中最大者为Y1, 故判断为轻度病变。
由上例见, Y1, Y2, Y3的数值相差不多,单纯凭分类函数值的大小作决策有时易出偏差。
这时, 分别估计该个体属于各总体的概率却能客观地反映该个体的各种可能归属, 而避免武断。
令Y*=179, 从而有P(Y1|X1,X2,…,X5)=e(183.36-180)/(e(183.36-180)+e(180.58-180)+e(179.66-180))=e4.36/(e4.36+e1.58+e0.66)=0.9202类似地, 可得:P(Y2|X1,X2,…,X5)=0.0571 P(Y3|X1,X2,…,X5)=0.0227 由此可见王××为轻度病变的概率为0.9202,因此把他判断为轻度病变可靠性较大。
判别分析SAS程序(STEPDISC + DISCRIM)一.STEPDISC过程的使用1. 功能STEPDISC过程用于逐步判别分析中对变量的剔选。
本过程不能计算判别函数。
用剔选后得到的变量再调用DISCRIM过程计算判别函数等。
2. 语句PROC STEPDISC 选择项…;CLASS 变量;VAR 变量;BY 变量;FREQ 变量;WEIGHT 变量;3. 语句说明(1)PROC STEPDISC语句中的选择项如下:DATA=SAS数据集名指定用于分析的SAS数据集,即训练样本SLENTRY=P值指定选入方程的显著性水平,α选,默认值为0.15SLSTAY=P值指定剔出方程的显著性水平,α剔,默认值为0.15START=n值指定VAR语句中前n个变量先进入方程,然后再开始剔选INCLUDE=n值指定VAR语句中前n个变量必须包含在方程中SIMPLE 打印各变量总的及每一类内的简单描述性统计量(2)CLASS语句指定判别分析用的分类变量名,该变量可以是数字型, 也可以是字符型。
(3)VAR语句指定判别分析用的各指标的变量名。
二.DISCRIM过程的使用1. 功能DISCRIM过程用于判别分析,计算判别函数,进行组内,组外考核等,该过程不能剔选变量。
如欲剔选变量必须先调用STEPDISC过程。
2. 语句PROC DISCRIM 选择项…;CLASS 变量;VAR 变量…;PRIORS 选择项;TESTCLASS 变量;TESTFREQ 变量;3. 语句说明(1)PROC DISCRIM语句中的选择项如下:DATA=SAS数据集名指定用于训练样本的SAS数据集TESTDAT=SAS数据集名指定用于组外考核的SAS数据集SIMPLE 打印训练样本中各变量总的及各类别的简单描述性统计量THRESHOLD=P值指定判别分类时最小的可接受的事后概率P,默认值为0 LIST 对每个训练样品打印分类结果(即组内考核结果)LISTERR 仅对每个分类错误的训练样品打印分类结果CROSSLIST 对每个训练样品打印刀切法分类结果CROSSLISTERR 仅对分类错误的样品打印刀切法分类结果CROSSVALIDATE 要求进行刀切法考核TESTLIST 打印组外考核的每例分类结果TESTLISTERR 仅打印分类错误的组外考核结果DISTANCE 打印类间的平方距离其它选择项还有TCORR,BCORR,WCORR,PCORR,TCOV,BCOV,WCOV和PCOV等。
它们和STEPDISC过程中的选择项意义相同。
(2)CLASS,VAR,BY,FREQ和WEIGHT语句和STEPDISC过程中意义相同。
(3)PRIORS语句指定各类事先概率值,可有如下选择项。
EQVAL 各类事先概率值相等,这是默认值PROP 各类事先概率值取训练样本中各类所占比例类别变量的输出格式值1=P1,值2=P2,…(4)TESTCLASS语句指定组外考核数据集中分类变量的变量名。
当训练样本数据集和组外考核数据集的分类变量名相同时,此语句可省略。
(5)TESTFREQ语句指定组外考核数据集中的频数变量名。
当不需要频数变量或训练样本数据集和组外考核数据集的频数变量名相同时,此语句可省略。
对例1的资料进行逐步判别分析,剔选变量的P值均取0.05,进行组内考核和刀切法考核,并另取一组数据进行组外考核。
例1中的资料已存放在EYE1.XLS文件中,有131例11个变量,作为训练样本。
此外,还建立了一个有31例的组外考核样本存放在EYE2.XLS文件中。
首先进行变量的选择。
剔选变量的显著性水平均取0.05。
例题SAS程序如下程序1data eye1;infile 'eye1.xls';input age time glucose vision at av bt bv qpt qpv group $;proc stepdisc data=eye1 slentry=0.05 slstay=0.05;var age time glucose vision at av bt bv qpt qpv;class group;run;程序1说明:(1)先用数据步从外部数据文件“eye1.xls”中读入数据,建立SAS数据集“eye1”;其中有11个变量,input语句指定了这11个变量的变量名。
前10个为用于判别分析的指标,最后一个变量“group”是类别变量。
(2)用SAS的stepdisc过程进行逐步判别分析。
(3)选择项“DATA=SAS数据集名”指定用于分析的SAS数据集,即训练样本。
(4)选择项“SLENTRY=P值”指定选入方程的显著性水平,α选,默认值为0.15。
选择项“SLSTAY=P值”指定剔出方程的显著性水平,α剔,默认值为0.15。
这两个选择项也可分别简写为“SLE=P值”及“SLS=P值”。
(5)在“proc stepdisc”语句后可以用的其它常用选择项有:选择项“START=n值”指定VAR语句中前n个变量先进入方程,然后再开始剔选。
选择项“INCLUDE=n值”指定VAR语句中前n个变量必须包含在方程中。
选择项“SIMPLE”要求打印各变量总的及每一类内的简单描述性统计量(6)CLASS语句指定判别分析用的分类变量名,该变量可以是数字型, 也可以是字符型。
(7)VAR语句指定判别分析用的各指标的变量名。
程序2data eye2;infile 'eye2.xls';input age time glucose vision at av bt bv qpt qpv group $;proc discrim data=eye1 testdata=eye2 list crosslist testlist;class group;var age vision at bv qpv;run;程序2说明:(1)先用数据步从外部数据文件“eye2.xls”中读入数据,建立SAS数据集“eye2”;该数据集将用于组外考核。
(2)用SAS的“discrim”过程进行判别分析。
(3)选择项”data= SAS数据集名” 定义了训练样本数据集;选择项“testdata= SAS数据集名”定义了组外考核样本数据集。
(4)选择项“list”要求列出所有训练样品的回顾性考核结果。
(5)选择项“crosslist”要求列出所有训练样品的刀切法考核结果。
(6)选择项“testlist”要求列出所有组外考核样品的前瞻性考核结果。
(7)在“proc discrim”语句后可以用的其它常用选择项有:如果不需要列出所有样品的考核结果而只想列出考核错误的样品,则上述选择项“list”,“crosslist”和“testlist”可分别改为“listerr”,“crosslisterr”及“testlisterr”。