因子分析例题
- 格式:docx
- 大小:75.29 KB
- 文档页数:6


因子分析(Factor Analysis)是一种统计方法,用于发现数据集中潜在的模式或结构。
它可以帮助我们理解数据之间的关系,帮助我们简化数据集并找到隐藏的变量。
在市场分析中,因子分析可以帮助我们理解消费者行为和市场趋势,并为营销策略提供支持。
本文将通过几个实际的案例,介绍因子分析在市场分析中的应用。
案例1:消费者偏好分析一家汽车制造商希望了解消费者对汽车外观设计的偏好。
他们收集了一系列关于汽车外观设计的变量,例如车身长度、车窗玻璃面积、前脸设计等。
然后他们对这些变量进行了因子分析,发现这些变量可以归纳为几个潜在的因子,例如“动感性”、“奢华感”、“实用性”等。
通过这些因子,汽车制造商可以更好地了解消费者对汽车外观设计的偏好,从而设计出更符合市场需求的产品。
案例2:市场细分一家食品公司希望将他们的产品推向更多的消费者群体。
他们收集了消费者的购买数据,包括购买频率、购买金额、购买渠道等。
然后他们对这些数据进行因子分析,发现可以将消费者分为几个不同的群体,例如“高频购买者”、“高金额购买者”、“线上购买者”等。
通过这些不同的因子,食品公司可以更好地制定营销策略,针对不同的消费者群体进行定制推广。
案例3:品牌形象分析一家奢侈品牌希望了解消费者对他们品牌形象的认知。
他们收集了关于品牌形象的各种变量,例如品牌知名度、产品质量、价格水平等。
通过因子分析,他们发现这些变量可以归纳为几个潜在的因子,例如“高端形象”、“时尚形象”、“品质形象”等。
通过这些因子,奢侈品牌可以更好地把握消费者对他们品牌的认知,从而调整品牌形象和营销策略。
通过上面的案例可以看出,因子分析在市场分析中具有重要的应用价值。
它可以帮助我们理解消费者行为和市场趋势,为营销策略提供支持。
当然,在实际应用中,因子分析也面临一些挑战,比如如何选择合适的变量、如何解释因子等。
但是通过合理的数据收集和分析,因子分析可以成为市场分析工具中的重要一环。
总结起来,因子分析在市场分析中的应用案例丰富多样,从消费者偏好分析到市场细分再到品牌形象分析,都可以通过因子分析提供有力的支持。

因子分析因子分析(Factor Analysis )是主成分分析的推广,它也是从研究相关矩阵内部的依赖关系出发,把一些具有错综复杂关系的变量归结为少数几个综合变量的一种多变量统计分析方法。
第一节 因子分析的基本思想 首先我们看下面两个实际例子:例1. 例1. 某企业招聘人才,对每位应聘者进行外貌、申请书的形式、专业能力、讨人喜欢的能力、自信心、洞察力、诚实、推销本领、经验、积极性、抱负、理解能力、潜在能力、实际能力、适应性等15个方面的考核。
这15个方面可归结为应聘者的外露能力、讨人喜欢的能力、经验、专业能力4个方面,每一方面称之为一个公共因子。
企业可根据这4个公共因子的情况来衡量应聘者的综合水平。
例2. 例2. 在企业经济效益的评价中,有经济效益的指标体系。
通常这个指标体系有八项指标:固定资产利税率、资金利税率、销售收入利税率、资金利税率、固定资产产值率、流动资金周转天数、万元产值能耗、全员劳动生产率等。
这八项指标可概括为盈利能力、资金和人力利用、产值能耗三个方面。
这三个方面在企业的生产经营活动中为主要因子,起着支配作用,企业要提高经济效益就要在这三个公共因子方面下功夫。
因子分析的基本思想:是通过变量(或样品)的相关系数矩阵(对样品是相似系数矩阵)内部结构的研究,找出能控制所有变量(或样品)的少数几个随机变量去描述多个变量(或样品)之间的相关(相似)关系,但在这里,这少数几个随机变量是不可观测的,通常称为因子。
因子分析分为两类,即R 型因子分析(对变量作因子分析),Q 型因子分析(对样品作因子分析)。
第二节 第二节 因子分析的数学模型1. 1. 模型(R 型) 设),,,(21p x x x X =为观察到的随机向量,),,,(21m F F F F =是不可观测的向量。
有111111ε+++=m m F a F a x221212ε+++=m m F a F a xpm pm p p F a F a x ε+++= 11即ε+=AF X其中)',,(1p εεε =称作误差或特殊因子。

因子分析期末考试题及答案# 因子分析期末考试题及答案一、选择题(每题2分,共20分)1. 因子分析的主要目的是()A. 减少数据集的维度B. 增加数据集的维度C. 保持数据集的维度不变D. 以上都不是答案:A2. 以下哪个不是因子分析中的因子旋转方法?()A. 方差最大化B. 方差最小化C. 正交旋转D. 斜交旋转答案:B3. 在因子分析中,哪个指标用于衡量因子的解释能力?()A. 因子载荷B. 因子得分C. 因子方差D. 因子相关答案:A4. 以下哪个不是因子分析的前提条件?()A. 变量间存在一定的相关性B. 数据集必须是正态分布C. 变量间不存在多重共线性D. 变量间存在线性关系答案:B5. 因子分析中,如果一个变量的因子载荷小于0.3,通常意味着()A. 该变量与因子高度相关B. 该变量与因子低度相关C. 该变量是因子分析中的噪声变量D. 该变量是因子分析中的主因子答案:B...(此处省略剩余选择题及答案)二、简答题(每题10分,共20分)1. 简述因子分析与主成分分析的区别。
答案:因子分析与主成分分析都是降维技术,但它们在目的和方法上有所不同。
因子分析旨在发现隐藏在变量背后的潜在因子,这些因子解释了变量之间的相关性。
而主成分分析则旨在找到数据集中的主要成分,这些成分是原始变量的线性组合,并且是无序的。
因子分析通常用于社会科学领域,而主成分分析则更多用于自然科学领域。
2. 描述因子载荷矩阵在因子分析中的作用。
答案:因子载荷矩阵是因子分析中的核心,它显示了每个变量与每个因子之间的关系强度。
通过因子载荷矩阵,我们可以了解哪些变量与特定因子高度相关,哪些变量与因子关系较弱。
载荷矩阵有助于我们理解数据的结构,并在解释因子时提供依据。
三、计算题(每题15分,共30分)1. 假设有一个变量集,包含变量X1, X2, X3, X4,它们的相关矩阵如下所示:| | X1 | X2 | X3 | X4 ||-|-|-|-|-|| X1 | 1 | 0.5| 0.7| 0.6|| X2 | 0.5| 1 | 0.6| 0.5|| X3 | 0.7| 0.6| 1 | 0.8|| X4 | 0.6| 0.5| 0.8| 1 |请计算因子载荷,并确定因子的数量。

第四章因子分析一、填空题1.因子分析常用的两种类型为和。
2.因子分析是将具有错综复杂关系的变量(或样品)综合为数量较少的几个因子,以再现_____________与____________之间的相互关系。
3.因子分析就是通过寻找众多变量的来简化变量中存在的复杂关系的一种方法。
4.因子分析是把每个原始变量分解成两个部分即、。
5.变量共同度是指因子载荷矩阵中_______________________。
6.公共因子方差与特殊因子方差之和为_______。
7.求解因子载荷矩阵常用的方法有和。
8.常用的因子旋转方法有和。
9.Spss中因子分析采用命令过程。
10.变量X的方差由两部分组成,一部分为,另一部分为。
i二、判断题1.在因子分析中,因子载荷阵不是唯一的。
()2.因子载荷阵经过正交旋转后,各变量的共性方差和各个因子的贡献都发生了变化。
()3.因子分析和主成分分析的核心思想都是降维。
()4.因子分析有两大类,R型因子分析和Q型因子分析;其中R型因子分析是从变量的相似矩阵出发,而Q型因子分析是从样品的相关矩阵出发。
()5.特殊因子与公共因子之间是相互独立的。
()6.变量共同度是因子载荷矩阵列元素的平方和。
()7.公共因子的方差贡献是衡量公共因子相对重要性指标。
()8.对因子载荷阵进行旋转的目的是使结构简化。
()三、简答题1.因子分析的基本思想是什么,它与主成分分析有什么区别和联系?2.因子模型的矩阵形式ε+=X UF ,其中: ()()()u FF ij mp PmU F⨯='='=εεε,,,,11请解释式中F 、ε、U 的统计意义。
F l ,F 2,…,F m 叫做公共因子,它们是在各个变量中共同出现的因子。
εi (i=1,2,…,p )表示影响Xi 的独特因子。
u ij 做因子载荷,它是第i 个变量在第j 个主因子上的负荷,或者叫做第i 个变量在第j 个主因子上的权,它反映了第i 个变量在第j 主因子上的相对重要性。
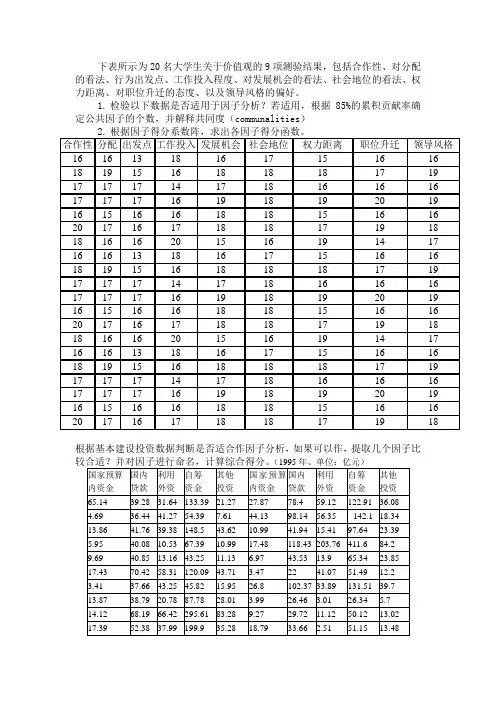
下表所示为20名大学生关于价值观的9项测验结果,包括合作性、对分配的看法、行为出发点、工作投入程度、对发展机会的看法、社会地位的看法、权力距离、对职位升迁的态度、以及领导风格的偏好。
1.检验以下数据是否适用于因子分析?若适用,根据85%的累积贡献率确定公共因子的个数,并解释共同度(communalities)
根据基本建设投资数据判断是否适合作因子分析,如果可以作,提取几个因子比
为研究全国各地区年人均收入的差异性和相似性,收集到1997年全国31个省市自治区各类经济单位包括国有经济单位、集体经济单位、联营经济单位、股份制经济单位、外商投资经济单位、港澳台经济单位和其他经济单位的年人均收入数据。
由于涉及的变量较多,直接进行地区间的比较分析较为繁琐,因此首先考虑。



《主成分分析与因子分析》训练题一、填空题a的统计意义是_____________。
1、在主成分分析中,因子负荷ij的统计意义是_____________。
2、在主成分分析中,参数ia的统计意义是__________________。
3、因子分析中因子载荷系数ijh是指因子载荷矩阵中______________________,其统计意义4、因子分析中变量的共同度2i是______________________。
g是指______________________。
5、因子分析中2j二、思考题1﹑因子分析与主成分分析有什么本质不同?2﹑因子分析的主要方法有那些?3﹑因子得分与主成分得分有什么关系?4﹑因子分析在SPSS中如何实现?三、验证题1、对全国31个省市自治区经济发展基本情况的八项指标作因子分析。
2、对31个省市自治区工业企业经济效益作作因子分析并作综合评价。
(以P136例4-4资料为例)3、对我国城市居民生活费支出作因子分析。
(以P139例4-5资料为例)四、计算题1、在一项对杨树的性状的研究中,测定了20株杨树树叶,每个叶片测定了四个变量,叶长(x1),2/3处宽(x2),1/3处宽(x3),1/2处宽(x4)。
这四个变量的相关系数矩阵的特征根和标准正交特征向量分别是:112.920,(0.1485,0.5735,0.5577,0.5814);U λ'==---221.024,(0.9544,0.0984,0.2695,0.0824);U λ'==---330.049,(0.2516,0.7733,0.5589,0.1624);U λ'==--440.007,(0.0612,0.2519,0.5513,0.7930)U λ'==--要求:(1)写出四个主成分的表达式;(2)计算每个主成分的方差贡献率,并按一般性原则选择主成分个数。
2、设变量123,,X X X 的相关阵为 1.000.650.450.65 1.000.350.450.35 1.00R ⎛⎫ ⎪= ⎪ ⎪⎝⎭,R 的特征根和标准标准正交化的特征向量分别为:111.96,(0.63,0.59,0.51);l λ'==220.68,(0.22,0.49,0.84);l λ'==--330.37,(0.75,0.64,0.18)l λ'==--要求:(1)取公共因子数为2,求因子载荷阵A 。

因子分析法案例因子分析法是一种用于确定变量之间潜在关联性的统计方法。
它可以帮助研究者发现多个变量背后的共同因素,从而简化数据分析和解释。
以下是一个关于市场调查数据的因子分析法案例。
假设一个市场研究机构要调查消费者对某个新产品的态度。
他们设计了一份调查问卷,包括多个问题,涉及到消费者对产品特性、价格、品牌知名度等方面的评价。
为了确定这些问题之间的潜在因素关联,研究机构采用了因子分析法。
首先,研究机构将问卷分发给一千名消费者,他们被要求根据自己的感觉和意见对每个问题进行评分。
得到的数据被整理成一个数据矩阵,每一行代表一个消费者,每一列代表一个问题,数值表示该消费者对该问题的评分。
接下来,研究机构使用因子分析法对数据进行分析。
他们通过计算相关系数矩阵来评估每两个问题之间的相关性。
然后,他们应用主成分分析法来确定主要因素。
主成分分析通过将原始变量进行线性组合来创建新的变量,这些新变量称为主成分或因子。
每个因子解释了原始变量方差的一部分。
通过设置解释方差的阈值,研究机构确定了主要因子的数量。
在这个案例中,研究机构决定保留三个主要因子,因为它们包括了大部分原始变量的方差。
这三个主要因子可以解释总方差的70%。
接下来,研究人员对这些因子进行命名和解释。
第一个因子被命名为“产品特性满意度”,它包括消费者对产品的外观、质量和性能的评价。
这个因子解释了总方差的35%。
第二个因子被命名为“价格敏感性”,它衡量了消费者对产品价格的反应。
这个因子解释了总方差的20%。
第三个因子被命名为“品牌认知度”,它反映了消费者对产品品牌知名度的评价。
这个因子解释了总方差的15%。
通过因子分析法,在这个案例中,研究机构可以简化数据分析,将多个问题归纳为较少的主要因素。
这样,他们可以更好地理解消费者对新产品的态度,并根据这些因素调整产品的设计,定价和品牌推广策略,从而满足消费者的需求并取得市场成功。

因子分析考试题及答案一、单项选择题1. 因子分析中,公共因子提取的目的是:A. 减少变量的数量B. 提高数据的解释性C. 降低数据的维度D. 增加变量的个数答案:C2. 在因子分析中,方差贡献率是指:A. 每个因子解释的总方差的比例B. 每个变量解释的总方差的比例C. 每个因子解释的方差占总方差的比例D. 每个变量解释的方差占总方差的比例答案:C3. 因子分析中,因子载荷矩阵中的值表示:A. 变量与因子之间的相关性B. 变量与因子之间的因果关系C. 变量与因子之间的回归系数D. 变量与因子之间的距离答案:A4. 因子分析中,因子旋转的目的是为了:A. 提高模型的稳定性B. 增加模型的解释性C. 减少模型的复杂性D. 增加模型的预测能力答案:B5. 因子分析中,Kaiser-Meyer-Olkin (KMO) 测试是用来评估的:A. 因子模型的适用性B. 变量的多变量正态性C. 变量之间的相关性D. 变量的独立性答案:A二、多项选择题6. 因子分析中,以下哪些指标可以用来确定因子的数量:A. 特征值大于1的规则B. 累积方差贡献率C. Scree图D. Bartlett球形度检验答案:A, B, C7. 因子分析中,以下哪些因素可能影响因子载荷的解释:A. 变量的测量误差B. 变量之间的相关性C. 样本大小D. 因子的旋转方式答案:A, B, D8. 在因子分析中,以下哪些方法可以用来进行因子旋转:A. 正交旋转B. 斜交旋转C. 最大似然估计D. 最小二乘法答案:A, B9. 因子分析中,以下哪些步骤是因子分析过程的一部分:A. 计算相关矩阵或协方差矩阵B. 提取公共因子C. 因子旋转D. 构建因子得分答案:A, B, C, D10. 因子分析中,以下哪些是因子载荷矩阵的属性:A. 矩阵是对称的B. 矩阵的对角线元素为1C. 矩阵的行表示变量D. 矩阵的列表示因子答案:C, D三、简答题11. 简述因子分析的基本步骤。
因子分析法案例因子分析法是一种统计技术,用于研究变量之间的内在关系,通过减少数据的维度来揭示数据背后的潜在结构。
这种方法在心理学、社会科学、市场研究等领域有着广泛的应用。
以下是一个因子分析法的案例分析。
在一项关于消费者购买行为的研究中,研究者希望了解影响消费者购买决策的潜在因素。
为了达到这个目的,研究者设计了一份问卷,包含了多个与购买行为相关的变量,如价格敏感度、品牌忠诚度、产品品质偏好等。
首先,研究者收集了一定数量的问卷数据,并进行了数据的预处理,包括数据清洗、缺失值处理和异常值检测。
在确保数据质量后,研究者使用因子分析法对数据进行分析。
在因子分析的第一步,研究者进行了Kaiser-Meyer-Olkin (KMO) 测试和Bartlett球形度测试,以检验数据是否适合进行因子分析。
结果显示,KMO值大于0.7,Bartlett检验的p值小于0.05,说明数据适合进行因子分析。
接下来,研究者选择了主成分分析法作为提取因子的方法,并通过特征值大于1的标准来确定因子的数量。
通过分析,研究者发现数据可以被简化为三个主要因子。
为了进一步理解这些因子,研究者进行了因子旋转,通常使用Varimax 旋转来最大化因子之间的差异。
旋转后的因子更容易解释,并且每个因子都对应了一组具有相似特征的变量。
最后,研究者对旋转后的因子进行了命名和解释。
第一个因子被命名为“价值导向”,它包括了价格敏感度和性价比等变量。
第二个因子被称为“品牌意识”,涵盖了品牌忠诚度和品牌影响力等变量。
第三个因子则被命名为“品质追求”,它关联了产品品质偏好和耐用性等变量。
通过这个案例,研究者能够识别出影响消费者购买行为的三个主要潜在因素,这有助于企业更好地理解消费者的需求,从而制定更有效的市场策略。
因子分析法为研究者提供了一种强有力的工具,以揭示数据背后的复杂关系,并对这些关系进行简化和解释。
SPSS因子分析练习题一、基础操作题1. 请在SPSS中打开一个数据集,并使用因子分析功能。
2. 对数据进行描述性统计分析,包括均值、标准差、最小值和最大值。
3. 对数据进行KMO和Bartlett's球形检验,判断数据是否适合进行因子分析。
二、因子提取题1. 使用主成分分析法提取因子。
2. 根据特征值大于1的原则,确定因子个数。
3. 计算各因子的方差贡献率和累积方差贡献率。
三、因子旋转题1. 使用正交旋转(Varimax)方法对因子进行旋转。
2. 根据旋转后的因子载荷,解释每个因子的含义。
3. 根据因子载荷,重新命名各个因子。
四、因子得分题1. 计算各样本的因子得分。
2. 使用因子得分进行回归分析,探讨因子与某个因变量的关系。
3. 根据因子得分,对样本进行聚类分析。
五、实际应用题1. 请选择一个实际研究领域,说明因子分析在该领域的应用价值。
2. 结合实际数据,进行因子分析,并提出研究建议。
3. 针对某一具体问题,利用因子分析结果进行解释和分析。
1. 对比主成分分析和因子分析的区别与联系。
2. 在进行因子分析时,如何判断因子个数的合理性?3. 请举例说明因子分析在心理学、教育学、市场营销等领域的应用。
七、拓展提高题1. 如何处理缺失值和异常值对因子分析的影响?2. 如何利用因子分析进行变量降维?3. 探讨因子分析与主成分分析在数据挖掘中的应用差异。
八、案例分析题1. 假设你有一份消费者满意度调查数据,请使用因子分析提取主要满意度维度。
2. 给出一组品牌形象调查的指标数据,使用因子分析确定品牌形象的主要构成因素。
3. 利用教育质量评价数据,通过因子分析识别影响教育质量的关键因素。
九、技能应用题1. 如何在SPSS中使用因子得分进行多元线性回归分析?2. 请描述如何通过因子分析来确定问卷的结构效度。
3. 如何利用因子分析结果对产品属性进行优先级排序?十、数据处理题1. 在进行因子分析前,如何对数据进行标准化处理?2. 如何判断因子分析中的交叉载荷问题,并如何解决?3. 请说明如何处理因子分析中的多重共线性问题。
第五部分 因子分析本部分内容:一、主成分分析二、因子分析三、SPSS 操作路径一、主成分分析(一)一个简化分析事例 1、坐标变换假定小学某班级学生的语文成绩(X 1)数学成绩(X 2)的相关系数r 12 = 0.6,且X 1和X 2都是标准化分数,其散点图如图1所示。
现通过旋转(X 1,X 2)变换出新坐标(Y 1,Y 2),使新坐标的Y 1轴对准散点分布方差最大的方向。
下面给出由原坐标系(X 1,X2)变换为新坐标系(Y 1,Y 2)的方法。
椭圆较长的直径的方差的65%,则可进行变量简化。
把变量标准化,λ即方差。
图1 图2记随机矢量X ′=(X 1,X 2)的协方差矩阵为∑,则∑=⎥⎥⎦⎤⎢⎢⎣⎡16.06.01设u 是以λ为特征值的特征矢量矩阵,把上述结果代入特征值矩阵方程(∑-λI )u = 0,得00016.06.0121=-⎥⎥⎦⎤⎢⎢⎣⎡⎪⎪⎪⎭⎫ ⎝⎛⎥⎥⎦⎤⎢⎢⎣⎡⎥⎥⎦⎤⎢⎢⎣⎡u u λλ,0)1(6.06.0)1(2121=-++-⎥⎥⎦⎤⎢⎢⎣⎡u u u u λλ。
036.0)1)(1(16.06.01=---=--λλλλ。
由此解得特征值的两个取值 λ1 = 1.6, λ2 = 0.4。
代入原方程组,取 特征矢量为单位矢量,即要求 求得对应的特征矢量 1u '=(u 11,u 21)=(22,22),2u '=(u 12,u 22)=(22,22-)。
最后求得新坐标系(Y 1,Y 2)与原坐标系(X 1,X 2)的关系为2112222X X Y +=X 1u '=,2122222X X Y -=X 2u '=。
结果显示,新坐标是通过原坐标逆时针旋转45°得到的。
如此求得的新坐标即可满足“Y 1轴对准散点分布方差最大的方向”这一要求。
2、特征值λi 与散点分布方差的关系 矢量Y 1和Y 2的方差的计算公式为Var (Y 1)= Var (1u 'X )= 11X X ∑'16.1222216.06.012222λ===⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡⎥⎥⎦⎤⎢⎢⎣⎡⎥⎥⎦⎤⎢⎢⎣⎡, 其中∑为协方差矩阵。
因⼦分析⽤因⼦分析法分析25名健康⼈的7项⽣化检验结果1.数据的采集和整理:本题提供了⼀张25名健康⼈的7项⽣化检验结果的表格。
2.数据的标准化处理由于不同变量之间存在着不同数量级的情况,需要对原指标数据进⾏标准化处理,吧不同指标数据之间转化成相同量纲的数据,使各指标数据具有可⽐性。
标准化处理⽤软件SPSS处理得,下图:3.判断是否适合因⼦分析:KMO检验和Bartlett球形检验KMO检验给出抽样充⾜量的测度,检验变量间的偏相关系数是否过⼩。
Bartlett球形检验检验相关系数矩阵是否是单位阵,如果是单位阵,则表明不适合采⽤因⼦模型。
根据Kaiser给出的是否做因⼦分析的KMO标准为:KMO>0.9,⾮常适合;0.9>KMO>0.8,适合;0.8>KMO>0.7,⼀般;0.7>KMO>0.6,不太适合;KMO<0.5不适合,故KMO检验通过。
同时,相伴概率为0.000,⼩于显著⽔平0.05,表明Bartlett球形检验通过,所以本⽂所选的变量适合做因⼦分析。
根据SPSS得出如下图:4.指标的相关性检验借助于多元分析软件SPSS,得到25名健康⼈的7项⽣化检验结果指标的相关系数矩阵,如下图:通过以上相关系数矩阵的分析可以看出,各个指标之间有较⼤的相关性,如果单纯以⼀个指标来评价市场绩效指标就会存在不够准确。
为了消除这种情况,简化计算,可以进⾏降维处理,把原来⽐较复杂的相关矩阵内部找出⼏个综合指标,使综合指标为原来变量的线性组合,利⽤相对较少的因⼦进⾏研究。
5.共同度分析根据变量共同度的统计意义,它刻画了全部公共因⼦对于原始变量的总⽅差所作的贡献,它说明了全部公共因⼦反映出原变量信息的百分⽐。
如下表2-4所⽰的变量共同度可知,除了1,2的共同度为0.796,0.773,其余变量的共同度都在80%以上,因此这两个公共因⼦对各变量的解释能⼒是⽐较强的。
采⽤因⼦分析的效果是⽐较好的。
评价指标的建立针对我国各省市综合发展情况做因子分析。
数据表中选取了六个指标分别是:人均GDP(元)X1,新增固定资产(亿元)X2,城镇居民人均年可支配收入(元)X3,农村居民机家庭纯收入(元)X4,高等学校数量(所)X5,卫生机构数量(所)X6。
见下表:考察数据是否适合做因子分析运用因子分析方法的前提是,变量之间存在线性的关系,这样才能够达到减少变量,方便分析的目的。
通过变量的相关矩阵可知,大多数变量的相关系数大于0.3,具有较强的相关性,同时,对上述变量进行了KMO测试度和Baetlett如果显著性水平为0.05,由于概率P小于显著性水平0.05,应拒绝零假设,认为相关矩阵与单位矩阵有显著差异。
同时,KMO值为0.635,较好的达到了标准,可以运用因子分析的方法。
提取因子根据原来变量的相关系数矩阵,采用主成分分析法提取因子并选取大于1的子分析最终解计算出的变量共同度。
可以看出,变量的绝大部分信息可被因子分析,信息丢失较少。
因子提取的总体效果比较好。
1.786. 它们一起解释了各省市综合发展情况的85.22%。
也就是说前2个因子集中体现了原始数据大部分的信息,因此,提取2个公共因子是合适的,能够比较全该图的横坐标为因子数目,纵坐标为特征根。
曲线迅速下降,然后下降变得平缓,从第3个因子开始变成近似一条直线,特征跟值小于1,解释原有的变量贡献小。
曲线变平开始的前一个点被认为是提取的最大因子数,即提取2个公因子。
第3个因子后面的这些散点像山脚下的碎石,可以舍去,不会损失太多信息。
因子的命名与解释计算输出因子载荷矩阵(component martix),是用标准化的公因子近似表示标准化原始变量的系数矩阵,见下表:人均GDP=0.831F1-0.490F2城镇居民人均年可支配收入=0.781F1-0.431F2新增固定资产=0.732F1-0.430F2高等学校数量=0.694F1-0.605F2F1在农村居民机家庭纯收入、人均GDP、城镇居民人均年可支配收入有较大的载荷,这三个指标是对城市整体经济发展情况的描述,因此,可称为经济因子;第二个因子F2在新增固定资产、高等学校数量、卫生机构数量有较大的载荷,这三个指标反映对社会建设情况的描述,因此可称为社会因子。
因子分析例题公司内部编号:(GOOD-TMMT-MMUT-UUPTY-UUYY-DTTI-因子分析因子分析(Factor Analysis )是主成分分析的推广,它也是从研究相关矩阵内部的依赖关系出发,把一些具有错综复杂关系的变量归结为少数几个综合变量的一种多变量统计分析方法。
第一节 因子分析的基本思想首先我们看下面两个实际例子:例1. 例1. 某企业招聘人才,对每位应聘者进行外貌、申请书的形式、专业能力、讨人喜欢的能力、自信心、洞察力、诚实、推销本领、经验、积极性、抱负、理解能力、潜在能力、实际能力、适应性等15个方面的考核。
这15个方面可归结为应聘者的外露能力、讨人喜欢的能力、经验、专业能力4个方面,每一方面称之为一个公共因子。
企业可根据这4个公共因子的情况来衡量应聘者的综合水平。
例2. 例2. 在企业经济效益的评价中,有经济效益的指标体系。
通常这个指标体系有八项指标:固定资产利税率、资金利税率、销售收入利税率、资金利税率、固定资产产值率、流动资金周转天数、万元产值能耗、全员劳动生产率等。
这八项指标可概括为盈利能力、资金和人力利用、产值能耗三个方面。
这三个方面在企业的生产经营活动中为主要因子,起着支配作用,企业要提高经济效益就要在这三个公共因子方面下功夫。
因子分析的基本思想:是通过变量(或样品)的相关系数矩阵(对样品是相似系数矩阵)内部结构的研究,找出能控制所有变量(或样品)的少数几个随机变量去描述多个变量(或样品)之间的相关(相似)关系,但在这里,这少数几个随机变量是不可观测的,通常称为因子。
因子分析分为两类,即R 型因子分析(对变量作因子分析),Q 型因子分析(对样品作因子分析)。
第二节 第二节 因子分析的数学模型1.1. 模型(R 型)设),,,(21p x x x X =为观察到的随机向量,),,,(21m F F F F =是不可观测的向量。
有即其中)',,(1p εεε =称作误差或特殊因子。
满足假设:1)p m ≤2)0),cov(=εF ,3)m I F =)var(,),,()var(221p diag σσε =。
称i F 为第i 个公共因子,ij a 为因子载荷。
因子分析与主成分的关系:联系:两者都可以看作逼近协方差矩阵∑。
差别:主成分分析的数学模型是一种变换,因子分析模型是描述X 的协方差∑的结构的一种模型。
其次,主成分中ij a 唯一确定,但因子分析中,每个因子的系数不是唯一的。
与多变量回归分析不同,此处的“自变量”F 是不可观测的。
2.公共因子:因子载荷和变量共同度的统计意义。
假定因子模型中,所有变量和因子都已标准化。
(1) (1) 因子载荷的统计意义设i m in i i F a F a x ε+++= 11 p i ,,1 =则ij F F m K ik j k m K ik j i a r a F F E a F x E j k ===∑∑==)(11)()( 由于k F ,j F 不相关,且1)(1=F F j r 即j i F x ij r a ,= 因子载荷ij a 是第i 个变量与第j 个公共因子的相关系数。
(2)变量共同度的统计意义:∑==m j ij i a h 122(p i ,,1 =)称作变量i x 的共同度:22212221)var()var()var()var(i i i m j ij i j ij mj i j ij i h a F a F a x σσσε+=+=+=+=∑∑∑== 即221i i h λ+= 即共同度是公共因子所占的i x 的方差,其共同度越大,说明公共因子包含的i x 的信息就越多。
(3)公共因子j F 的方差贡献的统计意义因子载荷矩阵中列的平方和。
称j s 为公共因子j F 对i x 的贡献,是衡量公共因子相对重要性的指标。
第三节 第三节 因子载荷的估计方法这是常用的主成分法,设随机向量)',(,1p x x X =的协方差为∑, ∑的特征值为021>≥≥≥p λλλ 其相应的特征向量为,,,21p e e e (标准正交基) 则:当公共因子i F 有P 个时,特殊因子为0,所以,AF X = A 为因子载荷阵。
因此,'')var()var()(AA A F A AF X D === 所以,'AA =∑, 因此,A 为(p p e e λλ,,11 ),所以,),,(11p p e e A λλ = 所以第j 列因子载荷为第j 个主成分j e 与j λ的乘积。
所以称为主成分法。
当最后m p -个特征根很小时,去掉p p m m e e λλ,,11 ++ 此时,),,(11m m e e A λλ =,方差ε∑+=∑'AA =),,(11m m e e λλ )'',,'(11m m e e λλ +diag ),,(221p σσ另外,当∑未知时,用样本协方差s 代替∑,或样本相关阵R 代替。
一般设p λλˆˆ1≥≥ 为样本相关阵R 的特征根,相应的标准正交化特征向量为p e e ˆ,,ˆ1 。
设p m ≤,则因子载荷阵的估计为)ˆ(ˆij a A =即)ˆˆ,,ˆˆ(11m m e e A λλ =第四节 第四节 因子旋转建立因子分析数学模型的目的不仅是为了找出公共因子,更重要的是要知道每个公共因子的意义,以便对实际问题进行分析。
如果每个公共因子的涵义不清,不便于对实际背景进行解释,这时根据因子载荷阵的不唯一性,可对因子载荷阵实行旋转,即用一个正交阵右乘使旋转后的因子载荷阵结构简化,便于对公共因子进行解释。
所谓结构简化就是使每个变量仅在一个公共因子上有较大的载荷,而在其余公共因子上的载荷比较小。
这种变换因子载荷的方法称为因子旋转。
因子旋转有方差最大正交旋转和斜交旋转,此处只介绍方差最大正交旋转。
先考虑两个因子的平面正交旋转,设因子载荷矩阵为:⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=2122211211p p a a a a a a A ,⎪⎪⎭⎫ ⎝⎛-=Γϕϕϕϕcos sin sin cosΓ 为正交矩阵。
记⎪⎪⎪⎭⎫ ⎝⎛=∆211211p p b b b b (*)这样做目的是希望所得结果能使载荷矩阵的每一列元素按其平方值说或者尽可能大或者尽可能小,即向1和0两极分化,或者说因子的贡献越分散越好。
这实际上是希望将变量p x x x ,,,21 分成两部分,一部分主要与第一因子有关,另一部分主要与第二因子有关,这也就是要求),,(),,,(2221221211p p b b b b 这两组数据的方差要尽可能地大,考虑各列的相对方差这里取2αi b 是为了消除符号不同的影响,除以2i h 是为了消除各个变量对公共因子依赖程度不同的影响。
现在要求总的方差达到最大,即要求使21V V G +=达到最大值,于是考虑G 对ϕ的导数,求出最大值。
如果公共因子多于2个,我们可以逐次对每2个进行上述的旋转,当公共因子数2>m 时,可以每次取2个,全部配对旋转,旋转时总是对A 阵中第α列、β列两列进行,此时公式(*)中只需将αj j a a −→−1, βj j a a −→−2就行了。
因此共需进行次旋转,但是旋转完毕后,并不能认为就已经达到目的,还可以重新开始,进行第二轮2m c 次配对旋转。
依次进行,可以是总的方差越来越大,直到收敛到某一极限。
例:考察我国各省市社会发展综合状况一、 一、运用方法:多元统计—因子分析因子分析的基本思想:通过变量的相关系数矩阵内部结构的研究,找出能够控制所有变量的少数几个随机变量的少数几个随机变量去描述多个变量之间的相关关系,但在这里,这少数.几个随机变量是不可观测的,通常称为因子。
然后根据相关性的大小把变量分组,只得同组内的变量之间相关性较高,但不同组的变量相关性较低。
二、二、因子分析方法的计算步骤:第一步:将原始数据标准化。
第二步:建立变量的相关系数R。
第三步:求R的特征根极其相应的单位特征向量。
第四步:对因子载荷阵施行最大正交旋转。
第五步:计算因子得分。
以下是我国各省市综合发展情况做因子分析。
数据表中选取了六个指标分别是:人均GDP(元)X1,新增固定资产(亿元)X2,城镇居民人均年可支配收入(元)X3,农村居民机家庭纯收入(元)X4,高等学校数量(所)X5,卫生机构数量(所)X6。
1、将原始数据标准化2、建立六个指标的相关系数阵R3、共因子方差4、总方差解建立因子载荷阵:5、建立因子载荷阵:由于前三个特征值的累计贡献率已达93.505%,所以取前三个特征值建立因子载荷阵如下:6、对因子载荷阵施行方差最大旋转,旋转后得正交因子表矩阵如下:由此有:X1=0.947F1+0.178F2-0.115F3X2=0.940F1+0.105F2+0.261F3X3=0.893F1-0.0747F2+0.404F3X4=0.0364F1+0.967F2+0.09455F3X5=0.212F1+0.830F2+0.345F3X6=0.222F1+0.493F2+0.806F37、输出因子成份得分系数矩阵最后,由上述表可见,每个因子只有少数几个指标的因子载荷较大,因此可根据。