控制系统CAD案例
- 格式:pdf
- 大小:1.41 MB
- 文档页数:42

控制系统CAD 案例2【例1】 已知单位反馈系统的被控对象的开环单位阶跃响应数据(存在随机扰动)在文件SourseData.mat 中,tout 是采样时间点,yout 是对应于采样时间点处的单位阶跃响应数据。
试设计串联补偿器,使得:① 在单位斜坡信号t t r )(的作用下,系统的速度误差系数K v ≥30sec -1;② 系统校正后的截止频率ωc ≥2.3sec -1;③ 系统校正后的相位稳定裕度P m ≥40°。
设计步骤:1 根据原始数据得到被控对象的单位阶跃响应 被控对象的开环单位阶跃响应数据在文件SourseData.mat 中。
在MATLAB 指令窗中键入:>> load SourseData>> plot(tout,yout)>> xlabel('tout')>> ylabel('yout')>> title('原始响应曲线')由所给数据可看出,仿真步长为0.05s,仿真时间为10s。
以时间tout为横坐标,输出yout为纵坐标,得到单位阶跃响应随时间的变化曲线如图1所示。
图1 被控对象的单位阶跃响应2系统模型的辨识由于被控对象模型结构未知,题中仅给出了被控对象的单位阶跃响应。
因此需要根据原始的数据分析得出原系统的基本结构。
至于结构以及参数的最终确定,将使用MATLAB 的系统辨识工具箱来实现。
(1) 预处理由图1可以看出被控对象模型中含积分环节,因此,对响应输出求导后进行辨识,即去积分。
再对辨识出的模型积分,即得被控对象模型。
对给定输出进行求导处理:tt y t t y t y ∆-∆+≈)()(d d 在MATLAB 指令窗中键入:>> dy=(yout(2:end,:)-yout(1:end-1,:))/0.05;% 差分代替导数>> t=tout(1:end-1,:);>> plot(t,dy)>> xlabel('t')>> ylabel('dy/dt')>> title('原始响应的导数曲线')以时间t 为横坐标,输出dy 为纵坐标,得到单位阶跃响应的导数随时间的变化曲线如图2所示。

【例1】已知单位反馈系统的被控对象为试设计串联校正器,使得:①在单位斜坡信号t t r )(的作用下,系统的速度误差系数Kv ≥30sec-1;②系统校正后的截止频率ωc≥2.3rad/sec ;③系统校正后的相位稳定裕度Pm>40°。
采用Bode 图设计方法。
(1)确定K 0 根据控制理论,给定被控对象为I 型系统,单位斜坡响应的速度误差系数Kv =K = K 0≥30sec-1,其中K 0是系统的开环增益。
取K 0=30sec -1,则被控对象的传递函数为(2)作原系统的Bode 图和阶跃响应曲线,检查是否满足要求编写M 脚本文件exam1_1.m 如下: % exam1_1cleark0=30; z=[]; p=[0;-10;-5]; sys0=zpk(z,p,k0*10*5);figure(1); margin(sys0) % 函数figure 用来创建图形窗口 figure(2); step(feedback(sys0,1)), grid运行exam1_1.m 后,得到如图1所示未校正系统的Bode 图和阶跃响应曲线。
(a) 未校正系统的Bode 图和频域性能(b) 未校正系统的单位阶跃响应图1 未校正系统的频域性能和时域响应根据计算可知未校正系统的频域性能指标为:对数幅值稳定裕度G m0=-6.02dB-180°穿越频率ωg0=7.07 rad/sec相位稳定裕度P m0=-17.2°截止频率ωc0=9.77 rad/sec由计算所得数据知:对数幅值稳定裕度和相位稳定裕度均为负值,这样的系统根本无法工作。
这一点也可从如图1(b)所示发散振荡的阶跃响应曲线看出,系统必须进行校正。
(3)求校正器的传递函数由于给定的开环截止频率ωc≥2.3rad/sec,远小于ωc0=9.77 rad/sec,可以通过压缩频带宽度来改善相位裕度,因此采用串联滞后校正是合理的。
实验一MATLAB的实验环境及基本命令一实验目的:1.学习了解MA TLAB的实验环境2.在MA TLAB系统命令窗口练习有关MA TLAB命令的使用。
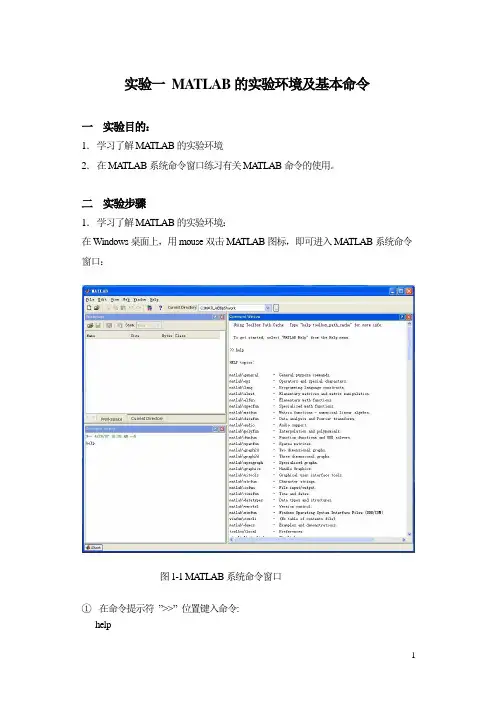
二实验步骤1.学习了解MA TLAB的实验环境:在Windows桌面上,用mouse双击MA TLAB图标,即可进入MA TLAB系统命令窗口:图1-1 MA TLAB系统命令窗口①在命令提示符”>>”位置键入命令:help此时显示MA T ALAB 的功能目录, 其中有“Matlab\general ”,“toolbox\control ”等;阅读目录的内容;② 键入命令:intro此时显示MA TLAB 语言的基本介绍,如矩阵输入、数值计算、曲线绘图等。
要求阅读命令平台上的注释内容,以尽快了解MA TLAB 语言的应用。
③ 键入命令:help help显示联机帮助查阅的功能,要求仔细阅读。
④ 键入命令:into显示工具箱中各种工具箱组件和开发商的联络信息。
⑤ 键入命令:demo显示MA TLAB 的各种功能演示。
2. 练习MA TLAB 系统命令的使用。
① 表达式MA TLAB 的表达式由变量、数值、函数及操作符构成。
实验前应掌握有关变量、数值、函数及操作符的有关内容及使用方法。
练习1-1: 计算下列表达式:要求计算完毕后,键入相应的变量名,查看并记录变量的值。
②.向量运算: )6sin(/250π=d 2/)101(+=a )sin(3.2-=e c i b 53+=n 维向量是由n 个成员组成的行或列数组。
在MA TLAB 中,由分号分隔的方括号中的元素产生一个列向量;由逗号或空号分隔的方括号中的元素产生一个列向量;同维的向量可进行加减运算,乘法须遵守特殊的原则。
练习1-2已知:X=[2 ;-4;8]求 :Y=R ';P=5*R ;E=X .*Y ;S=X '* Y练习1-3⑴产生每个元素为1的4维的行向量;⑵产生每个元素为0的4维的列向量;⑶产生一个从1到8的整数行向量,默认步长为1;⑷产生一个从π到0,间隔为π/3的行向量;③矩阵基本运算操作。



《控制系统仿真与CAD》实验课程报告一、实验教学目标与基本要求上机实验是本课程重要的实践教学环节。
实验的目的不仅仅是验证理论知识,更重要的是通过上机加强学生的实验手段与实践技能,掌握应用MATLAB/Simulink 求解控制问题的方法,培养学生分析问题、解决问题、应用知识的能力和创新精神,全面提高学生的综合素质。
通过对MATLAB/Simulink进行求解,基本掌握常见控制问题的求解方法与命令调用,更深入地认识和了解MATLAB语言的强大的计算功能与其在控制领域的应用优势。
上机实验最终以书面报告的形式提交,作为期末成绩的考核内容。
二、题目及解答第一部分:MATLAB 必备基础知识、控制系统模型与转换、线性控制系统的计算机辅助分析1.>>f=inline('[-x(2)-x(3);x(1)+a*x(2);b+(x(1)-c)*x(3)]','t','x','flag','a','b','c');[t,x]=ode45( f,[0,100],[0;0;0],[],0.2,0.2,5.7);plot3(x(:,1),x(:,2),x(:,3)),grid,figure,plot(x(:,1),x(:,2)), grid2.>>y=@(x)x(1)^2-2*x(1)+x(2);ff=optimset;rgeScale='off';ff.TolFun=1e-30;ff.Tol X=1e-15;ff.TolCon=1e-20;x0=[1;1;1];xm=[0;0;0];xM=[];A=[];B=[];Aeq=[];Beq=[];[ x,f,c,d]=fmincon(y,x0,A,B,Aeq,Beq,xm,xM,@wzhfc1,ff)Warning: Options LargeScale = 'off' and Algorithm ='trust-region-reflective' conflict.Ignoring Algorithm and running active-set algorithm. To runtrust-region-reflective, setLargeScale = 'on'. To run active-set without this warning, useAlgorithm = 'active-set'.> In fmincon at 456Local minimum possible. Constraints satisfied.fmincon stopped because the size of the current search direction is less thantwice the selected value of the step size tolerance and constraints aresatisfied to within the selected value of the constraint tolerance.<stopping criteria details>Active inequalities (to within options.TolCon = 1e-20):lower upper ineqlin ineqnonlin2x =1.00001.0000f =-1.0000c =4d =iterations: 5funcCount: 20lssteplength: 1stepsize: 3.9638e-26algorithm: 'medium-scale: SQP, Quasi-Newton, line-search'firstorderopt: 7.4506e-09constrviolation: 0message: [1x766 char]3.(a) >> s=tf('s');G=(s^3+4*s+2)/(s^3*(s^2+2)*((s^2+1)^3+2*s+5))G =s^3 + 4 s + 2------------------------------------------------------s^11 + 5 s^9 + 9 s^7 + 2 s^6 + 12 s^5 + 4 s^4 + 12 s^3Continuous-time transfer function.(b)>> z=tf('z',0.1);H=(z^2+0.568)/((z-1)*(z^2-0.2*z+0.99))H =z^2 + 0.568-----------------------------z^3 - 1.2 z^2 + 1.19 z - 0.99Sample time: 0.1 secondsDiscrete-time transfer function.4.>> A=[0 1 0;0 0 1;-15 -4 -13];B=[0 0 2]';C=[1 00];D=0;G=ss(A,B,C,D),Gs=tf(G),Gz=zpk(G)G =a =x1 x2 x3x1 0 1 0x2 0 0 1x3 -15 -4 -13b =u1x1 0x2 0x3 2c =x1 x2 x3y1 1 0 0d =u1y1 0Continuous-time state-space model.Gs =2-----------------------s^3 + 13 s^2 + 4 s + 15 Continuous-time transfer function.Gz =2---------------------------------(s+12.78) (s^2 + 0.2212s + 1.174) Continuous-time zero/pole/gain model.5.设采样周期为0.01s>> z=tf('z',0.01);H=(z+2)/(z^2+z+0.16) H =z + 2--------------z^2 + z + 0.16Sample time: 0.01 secondsDiscrete-time transfer function.6.>> syms J Kp Ki s;G=(s+1)/(J*s^2+2*s+5);Gc=(Kp*s+Ki)/s;GG=feedback(G*Gc,1) GG =((Ki + Kp*s)*(s + 1))/(J*s^3 + (Kp + 2)*s^2 + (Ki + Kp + 5)*s + Ki)7.(a)>>s=tf('s');G=(211.87*s+317.64)/((s+20)*(s+94.34)*(s+0.1684));Gc=(169.6*s+400)/(s*(s+4));H=1/(0.01*s+1);GG=feedback(G*Gc,H),Gd=ss(GG),Gz=zpk(GG)GG =359.3 s^3 + 3.732e04 s^2 + 1.399e05 s + 127056----------------------------------------------------------------0.01 s^6 + 2.185 s^5 + 142.1 s^4 + 2444 s^3 + 4.389e04 s^2 + 1.399e05 s + 127056Continuous-time transfer function.Gd =a =x1 x2 x3 x4 x5 x6x1 -218.5 -111.1 -29.83 -16.74 -6.671 -3.029x2 128 0 0 0 0 0x3 0 64 0 0 0 0x4 0 0 32 0 0 0x5 0 0 0 8 0 0x6 0 0 0 0 2 0b =u1x1 4x2 0x3 0x4 0x5 0x6 0c =x1 x2 x3 x4 x5 x6y1 0 0 1.097 3.559 1.668 0.7573d =u1y1 0Continuous-time state-space model.Gz =35933.152 (s+100) (s+2.358) (s+1.499)----------------------------------------------------------------------(s^2 + 3.667s + 3.501) (s^2 + 11.73s + 339.1) (s^2 + 203.1s + 1.07e04) Continuous-time zero/pole/gain model.(b)设采样周期为0.1s>>z=tf('z',0.1);G=(35786.7*z^2+108444*z^3)/((1+4*z)*(1+20*z)*(1+74.04*z));Gc= z/(1-z);H=z/(0.5-z);GG=feedback(G*Gc,H),Gd=ss(GG),Gz=zpk(GG)GG =-108444 z^5 + 1.844e04 z^4 + 1.789e04 z^3----------------------------------------------------------------1.144e05 z^5 +2.876e04 z^4 + 274.2 z^3 + 782.4 z^2 + 47.52 z + 0.5Sample time: 0.1 secondsDiscrete-time transfer function.Gd =a =x1 x2 x3 x4 x5 x1 -0.2515 -0.00959 -0.1095 -0.05318 -0.01791x2 0.25 0 0 0 0x3 0 0.25 0 0 0x4 0 0 0.125 0 0x5 0 0 0 0.03125 0b =u1x1 1x2 0x3 0x4 0x5 0c =x1 x2 x3 x4 x5y1 0.3996 0.6349 0.1038 0.05043 0.01698d =u1y1 -0.9482Sample time: 0.1 secondsDiscrete-time state-space model.Gz =-0.94821 z^3 (z-0.5) (z+0.33)----------------------------------------------------------(z+0.3035) (z+0.04438) (z+0.01355) (z^2 - 0.11z + 0.02396)Sample time: 0.1 secondsDiscrete-time zero/pole/gain model.8.>>s=tf('s');g1=1/(s+1);g2=s/(s^2+2);g3=1/s^2;g4=(4*s+2)/(s+1)^2;g5=50;g6=(s^2+2) /(s^3+14);G1=feedback(g1*g2,g4);G2=feedback(g3,g5);GG=3*feedback(G1*G2,g6) GG =3 s^6 + 6 s^5 + 3 s^4 + 42 s^3 + 84 s^2 + 42 s---------------------------------------------------------------------------s^10 + 3 s^9 + 55 s^8 + 175 s^7 + 300 s^6 + 1323 s^5 + 2656 s^4 + 3715 s^3 + 7732 s^2 + 5602 s + 1400Continuous-time transfer function.9.>>s=tf('s');T0=0.01;T1=0.1;T2=1;G=(s+1)^2*(s^2+2*s+400)/((s+5)^2*(s^2+3*s+100 )*(s^2+3*s+2500));Gd1=c2d(G,T0),Gd2=c2d(G,T1),Gd3=c2d(G,T2),step(G),figure,st ep(Gd1),figure,step(Gd2),figure,step(Gd3)Gd1 =4.716e-05 z^5 - 0.0001396 z^4 + 9.596e-05 z^3 + 8.18e-05 z^2 - 0.0001289 z + 4.355e-05----------------------------------------------------------------z^6 - 5.592 z^5 + 13.26 z^4 - 17.06 z^3 + 12.58 z^2 - 5.032 z + 0.8521Sample time: 0.01 secondsDiscrete-time transfer function.Gd2 =0.0003982 z^5 - 0.0003919 z^4 - 0.000336 z^3 + 0.0007842 z^2 - 0.000766 z + 0.0003214----------------------------------------------------------------z^6 - 2.644 z^5 + 4.044 z^4 - 3.94 z^3 + 2.549 z^2 - 1.056 z + 0.2019Sample time: 0.1 secondsDiscrete-time transfer function.Gd3 =8.625e-05 z^5 - 4.48e-05 z^4 + 6.545e-06 z^3 + 1.211e -05 z^2 - 3.299e-06 z + 1.011e-07---------------------------------------------------------------z^6 - 0.0419 z^5 - 0.07092 z^4 - 0.0004549 z^3 + 0.002495 z^2 - 3.347e-05 z + 1.125e-07Sample time: 1 secondsDiscrete-time transfer function.10.(a)>> G=tf(1,[1 2 1 2]);eig(G),pzmap(G) ans =-2.0000-0.0000 + 1.0000i-0.0000 - 1.0000i系统为临界稳定。

皮带输送机电气控制系统的设计一、设计目的通过对电气控制系统的设计,掌握电气控制系统设计的一般方法,能够设计出满足控制要求的电气原理图,能够设计电器元件布置图、接线图和控制箱,并能够根据负载选择主要电器元件的型号,具有电气控制系统工程设计的初步功能。
二、控制要求皮带输送机由三条皮带组成并由电动机控制。
1#、2#、3#皮带顺序运行。
电动机功率各3KW,其控制要求如下:1、按下系统启动按钮→1#电动机启动→延时2秒→2#电动机启动→延时5秒→3#电动机启动2、按下停机按钮→延时10秒→3#电动机停止→延时10秒→2#电动机停止→延时10秒→1#电动机停止3、1#电动机过载时,1#、2#、3#电动机全停,2#电动机过载时,2#、3#电动机停止,3#电动机停止时,顺序停机,并设有紧急停车按钮4、具有手动、自动工作方式5、各种指示及报警三、设计内容及要求根据控制要求,采用PLC为中心控制单元,设计出其控制系统的原理图(主电路和控制电路)、元件布置土、接线图以及元件明细表。
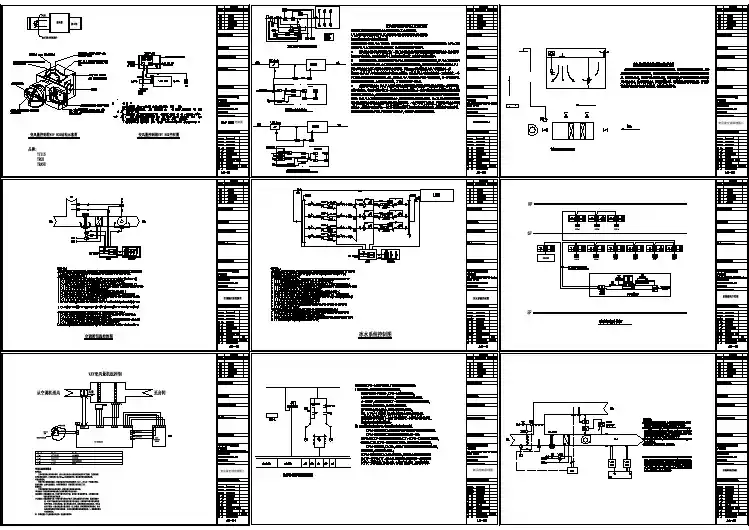
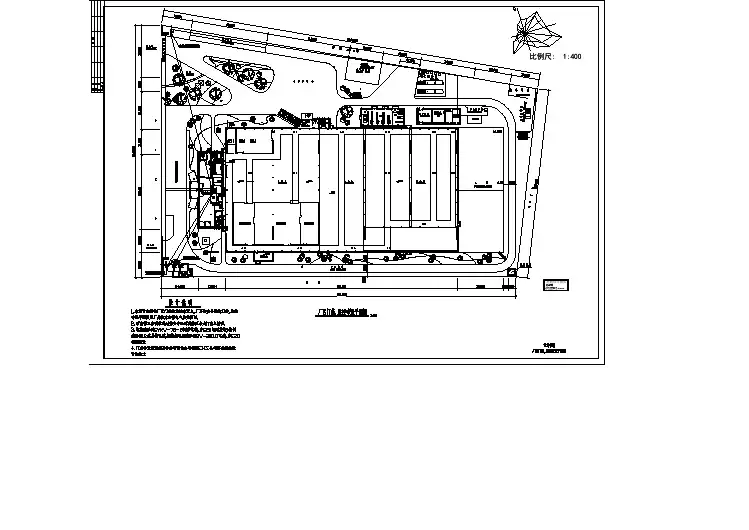
所完成的图纸资料包括:1、电气原理图:主电路、控制电路、梯形图、指令系统2、电气箱面板布置图,电气箱内部布置图3、接线图4、元件明细表5、控制箱尺寸6、系统工作原理说明及操作使用说明四、系统总体设计1、主电路的设计主电路线路如图1所示,图中的M1、M2、M3为输送带电动机,三台电动机都采用直接启动方式,各台电动机分别使用一个接触器控制,各电动机分别由FR1、FR2、FR3提供过载保护,各自通过自锁实现失压保护。
2、PLC的选择及I/O分配根据给定的控制要求,可统计出现场输入信号共14个,输出信号共8个,故选用OMRON C系列C28P,此型号具有16点输入和12点输出,满足要求。
(I/O分配如表2所示)。
3、PLC外部接线图的设计PLC根据表2的I/O分配关系和C28P的端子跑列位置进行相应的接线,PLC系统外部接线图在图1中,图中各接触器采用220V电源,信号指示及报警指示灯与接触器共用220V电源。
《控制系统CAD及仿真》实验指导书自动化学院自动化系实验一SIMULINK 基础与应用一、实验目的1、熟悉并掌握Simulink 系统的界面、菜单、工具栏按钮的操作方法;2、掌握查找Simulink 系统功能模块的分类及其用途,熟悉Simulink 系统功能模块的操作方法;3、掌握Simulink 常用模块的内部参数设置与修改的操作方法;4、掌握建立子系统和封装子系统的方法。
二、实验内容:1. 单位负反馈系统的开环传递函数为:1000()(0.11)(0.0011)G s s s s =++应用Simulink 仿真系统的阶跃响应曲线。
2.PID 控制器在工程应用中的数学模型为:1()(1)()d p i d T s U s K E s T s T s N=++ 其中采用了一阶环节来近似纯微分动作,为保证有良好的微分近似效果,一般选10N ≥。
试建立PID 控制器的Simulink 模型并建立子系统。
三、预习要求:利用所学知识,编写实验程序,并写在预习报告上。
实验二 控制系统分析一、 实验目的1、掌握如何使用Matlab 进行系统的时域分析2、掌握如何使用Matlab 进行系统的频域分析3、掌握如何使用Matlab 进行系统的根轨迹分析4、掌握如何使用Matlab 进行系统的稳定性分析5、掌握如何使用Matlab 进行系统的能观测性、能控性分析 二、 实验内容: 1、时域分析(1)根据下面传递函数模型:绘制其单位阶跃响应曲线并在图上读标注出峰值,求出系统的性能指标。
8106)65(5)(232+++++=s s s s s s G (2)已知两个线性定常连续系统的传递函数分别为1G (s)和2G (s),绘制它们的单位脉冲响应曲线。
451042)(2321+++++=s s s s s s G , 27223)(22+++=s s s s G (3)已知线性定常系统的状态空间模型和初始条件,绘制其零输入响应曲线。