12.3 恒定磁场的高斯定理

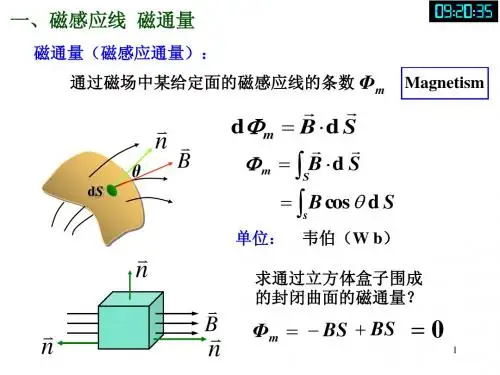
恒定磁场的高斯定理
高斯定理是伟大物理学家兼数学家高斯在1839年发表的著作《有关被称为数学分析的普洛斯特拉分支之一的制定法》中提出的定理，它是电磁学的重要基础。

根据它，电场的磁场是受磁场而产生的电流的积分，它可以用来解释恒定磁场的性质及其分布规律。

首先，高斯定理指出，如果把一个恒定磁场看成一个圆柱体，磁场沿着柱体的侧面改变，结果就像斜率在每一点中恒定，那么在这个柱体上，斜率最大，我们可以轻松求出磁场的分布规律。

尤其是，当磁场穿过两个柱体轴之间的沿着轴的定义域积分时，磁场结果就是沿着轴的定义域的累加的和，也就是磁场的平均值。

其次，通过高斯定理，可以利用距离类比的方法，确定定向性磁场的强度。

比如，可以把它看做一个受定向磁场影响的小铁球，这个铁球会受到磁场的拉力，从而可以从距离类比的角度来了解磁场的强度。

综上所述，高斯定理是一个非常重要的物理定理，它深刻地解释了恒定磁场的性质及分布规律，为我们了解定向性磁场提供了新的理解手段，为电磁学提供了重要依据，该定理有着重要的理论意义和应用价值，为日常生活提供了多项便利。

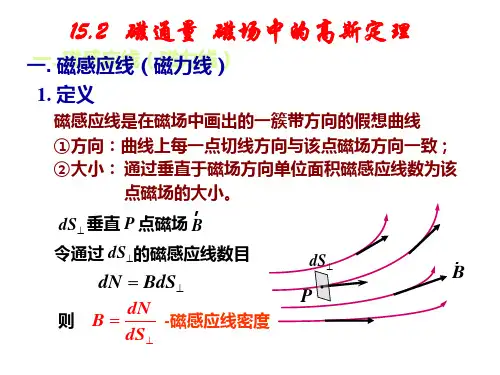
磁场高斯定理的内容
磁场高斯定理是电磁学中的一条重要定理，它描述了磁场的分布与其周围磁荷的关系。

磁场高斯定理可以表述为：闭合曲面上通过磁场力线的磁通量等于该曲面内部所有磁荷的代数和的倍数。

具体来说，磁场高斯定理可以表示为以下公式：
∮B·ds = μ₀∑qi
其中，∮B·ds 表示磁场B与曲面ds的点积在闭合曲面上的积
分（也称为磁通量），μ₀为真空中的磁导率（常数），∑qi
表示闭合曲面内部所有磁荷的代数和。

根据磁场高斯定理，当闭合曲面上没有内部磁荷时，磁场的总磁通量为零。

而当闭合曲面内有磁荷时，磁场的总磁通量与闭合曲面内的磁荷成正比，比例系数为磁导率。

磁场高斯定理可以用于计算磁场，尤其是当磁荷分布较复杂时。

通过选择合适的闭合曲面，可以简化磁场计算的过程，并得到准确的结果。

恒定磁场高斯定理公式
恒定磁场高斯定理：
1. 定义：恒定磁场高斯定理是物理学中一种物理学定理，其主要涉及
到磁场如何影响物体，及磁场是如何分布的。

2. 原理：恒定磁场高斯定理称为「磁产生定律」，这个定律表明：磁
场的强度、施加力的大小和物体的深度之间的关系是简单的高斯模型，即在空间上，磁场的强度衰减率满足高斯型模型，而不是简单的正弦
型模型。

3. 应用：恒定磁场高斯定理常用来描述磁场的强度分布，如果一个磁
场内没有任何外部质量或电流的影响，那么磁场的强度衰减率将满足
高斯型模型。

这一定律经常用于测量磁场的强度，以了解地磁场的强
度分布和磁场方位，以及估计电磁散射层的厚度。

4. 公式：恒定磁场高斯定理的数学公式表述为，若将物体的中心视为
原点，则磁场的强度B随着距离r的变化满足：
$$B(r)=\frac{B_0}{1+\left(\frac{2c}{r}\right)^2}$$
其中，B_0为物体中间磁力线的平均强度，而c是磁场到物体中心的距离。

5. 参考：E.W Jorry曾表明恒定磁场高斯定理，这个定律经常被用于研究地磁场和大气层。

6. 总结：测量磁场强度及分布与恒定磁场高斯定理有关，它给出了磁场强度衰减率满足高斯型模型的物理定律，广泛的应用于地磁方位、磁场强度分布和电磁散射层厚度估计等等方面。

磁场的高斯定理数学表达式
高斯定理数学公式是：∮F·dS=∫(▽·F)dV。

在静电学中，表明在闭合曲面内的电荷之和与产生的电场在该闭合曲面上的电通量积分之间的关系。

高斯定律（Gauss' law）表明在闭合曲面内的电荷分布与产生的电场之间的关系。

静电场与磁场：
两者有着本质上的区别。

在静电场中，由于自然界中存在着独立的电荷，所以电场线有起点和终点，只要闭合面内有净余的正（或负）电荷，穿过闭合面的电通量就不等于零，即静电场是有源场。

而在磁场中，由于自然界中没有磁单极子存在，N极和S极是不能分离的，磁感线都是无头无尾的闭合线，所以通过任何闭合面的磁通量必等于零。

磁场高斯定理磁场的高斯定理：对于任意磁场B(r)B(r)和任意闭合曲面，曲面上的磁通量为零。

∮B(r)⋅ds=0(1)(1)∮B(r)⋅ds=0也就是说空间任意一点的磁场散度为零。

适用高斯定理可以写成微分形式：∇⋅B=0(2)(2)∇⋅B=0接下来我们试着验证一下这一结论是否和我们之前的理论是一致的，也就是说我们能否直接从比奥萨伐尔定律所给出的磁场B(r)B(r)推出，首先我们考虑静磁场下，电流是恒定的，因此电流密度j j不会在某一个点聚集或者散开，因此有：∇⋅j=0(3)(3)∇⋅j=0结合比奥萨伐尔：B(r)=μ04π∫j(r′)×(r−r′)|r−r′|3dV′(4)(4)B(r)=μ04π∫j(r′)×(r−r′)|r−r′|3dV′利用矢量乘法的规则可得：∇⋅(j×(r−r′)|r−r′|3)=(r−r′)|r−r′|3⋅(∇×j)−j⋅(∇×(r−r′)|r−r′|3)(5)(5)∇⋅(j×(r−r′)|r−r′|3)=(r−r′)|r−r′|3⋅(∇×j)−j⋅(∇×(r−r′)|r−r′|3)由于∇×(r−r′)|r−r′|3=0∇×(r−r′)|r−r′|3=0：∇⋅B=0(6)(6)∇⋅B=0注意磁场高斯定律适用于经典电动力学的任何情况，而后者只适用于静态的情况。

磁场的高斯定律实际上是电场的高斯定律在磁学中的对应，它反映了自然界没有孤立的磁单极（或者我们还没找到）。

形象地看，任意一条磁感线都不会起始或终止于空间中的某一点，它要么是闭合的回路，要么从无穷远来延伸到无穷远去。

正因为磁场的这条性质，我们可以将磁感应强度B B写成某个矢量场A A的旋度，其中A A称为矢量势（矢势）。