下载文档原格式
第二章 一元線性回歸分析思考與練習參考答案2.1 一元線性回歸有哪些基本假定?答： 假設1、解釋變數X 是確定性變數，Y 是隨機變數；假設2、隨機誤差項ε具有零均值、同方差和不序列相關性： E(εi )=0 i=1,2, …,n Var (εi )=σ2 i=1,2, …,n Cov(εi, εj )=0 i≠j i,j= 1,2, …,n 假設3、隨機誤差項ε與解釋變數X 之間不相關： Cov(X i , εi )=0 i=1,2, …,n假設4、ε服從零均值、同方差、零協方差の正態分佈 εi ~N(0, σ2 ) i=1,2, …,n 2.2 考慮過原點の線性回歸模型 Y i =β1X i +εi i=1,2, …,n誤差εi （i=1,2, …,n ）仍滿足基本假定。
求β1の最小二乘估計 解： 得：2.3 證明（2.27式），∑e i =0 ，∑e i X i =0 。
證明：∑∑+-=-=nii i ni X Y Y Y Q 121021))ˆˆ(()ˆ(ββ其中：即： ∑e i =0 ，∑e i X i =021112)ˆ()ˆ(ini i ni i i e X Y Y Y Q β∑∑==-=-=01ˆˆˆˆi ii i iY X e Y Y ββ=+=-0100ˆˆQQββ∂∂==∂∂2.4回歸方程E （Y ）=β0+β1X の參數β0，β1の最小二乘估計與最大似然估計在什麼條件下等價?給出證明。
答：由於εi ~N(0, σ2 ) i=1,2, …,n所以Y i =β0 + β1X i + εi ~N （β0+β1X i , σ2 ) 最大似然函數：使得Ln （L ）最大の0ˆβ，1ˆβ就是β0，β1の最大似然估計值。
同時發現使得Ln （L ）最大就是使得下式最小，∑∑+-=-=nii i n i X Y Y Y Q 121021))ˆˆ(()ˆ(ββ上式恰好就是最小二乘估計の目標函數相同。
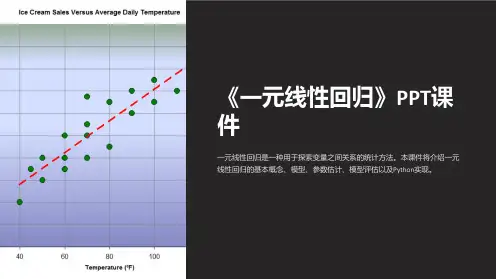
第二节一元线性回归方程的建立一元线性回归分析是处理两个变量之间关系的最简单模型，它所研究的对象是两个变量之间的线性相关关系。
通过对这个模型的讨论，我们不仅可以掌握有关一元线性回归的知识，而且可以从中了解回归分析方法的基本思想、方法和应用。
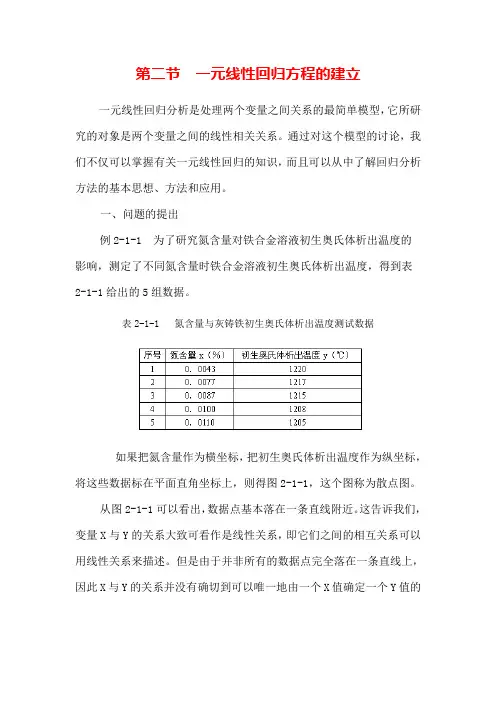
一、问题的提出例2-1-1 为了研究氮含量对铁合金溶液初生奥氏体析出温度的影响，测定了不同氮含量时铁合金溶液初生奥氏体析出温度，得到表2-1-1给出的5组数据。
表2-1-1 氮含量与灰铸铁初生奥氏体析出温度测试数据如果把氮含量作为横坐标，把初生奥氏体析出温度作为纵坐标，将这些数据标在平面直角坐标上，则得图2-1-1，这个图称为散点图。
从图2-1-1可以看出，数据点基本落在一条直线附近。
这告诉我们，变量X与Y的关系大致可看作是线性关系，即它们之间的相互关系可以用线性关系来描述。
但是由于并非所有的数据点完全落在一条直线上，因此X与Y的关系并没有确切到可以唯一地由一个X值确定一个Y值的程度。
其它因素，诸如其它微量元素的含量以及测试误差等都会影响Y 的测试结果。
如果我们要研究X与Y的关系，可以作线性拟合（2-1-1）我们称（2-1-1）式为回归方程，a与b是待定常数，称为回归系数。
从理论上讲，（2-1-1）式有无穷多组解，回归分析的任务是求出其最佳的线性拟合。
二、最小二乘法原理如果把用回归方程计算得到的i值(i=1,2,…n)称为回归值，那么实际测量值y i与回归值i之间存在着偏差，我们把这种偏差称为残差，记为e i(i=1,2,3,…,n)。
这样，我们就可以用残差平方和来度量测量值与回归直线的接近或偏差程度。
残差平方和定义为:(2-1-2) 所谓最小二乘法，就是选择a和b使Q(a,b)最小，即用最小二乘法得到的回归直线是在所有直线中与测量值残差平方和Q最小的一条。
由(2-1-2)式可知Q是关于a,b的二次函数，所以它的最小值总是存在的。
下面讨论的a和b的求法。
三、正规方程组根据微分中求极值的方法可知，Q(a,b)取得最小值应满足(2-1-3)由(2-1-2)式，并考虑上述条件，则(2-1-4)(2-1-4)式称为正规方程组。
回归分析法概念及原理一（一元线性回归）2009-12-14 14:27最近，在学一门统计学，有点意思。
问题一点一点出现，又一点一点被慢慢解决，慢慢消化~~做为初学者，搞不清的地方还真多。
今天刚好又看了有关相关分析和回归分析的学习资料，感觉不错，闲来与大家分享分享。
一、一元回归分析法，是在考虑预测对象发展变化本质基础上，分析因变量随一个自变量变化而变化的关联形态，借助回归分析建立它们因果关系的回归方程式，描述它们之间的平均变化数量关系，据此进行预测或控制。
1、基本原理假设预测目标因变量为Y，影响它变化的一个自变量为X，因变量随自变量的增（减）方向的变化。
一元线性回归分析就是要依据一定数量的观察样本（Xi,Yi）i=1，2…，n，找出回归直线方程Y=a+bX (1)对应于每一个Xi，根据回归直线方程可以计算出一个因变量估计值Yi。
回归方程估计值Yi 与实际观察值Yj之间的误差记作e-i=Yi-Yi。
显然，n个误差的总和越小，说明回归拟合的直线越能反映两变量间的平均变化线性关系。
据此，回归分析要使拟合所得直线的平均平方离差达到最小，简称最小二乘法将求出的a和b代入式（1）就得到回归直线Y-i =a+bXI 。
那么，只要给定Xi-值，就可以用作因变量Y i的预测值。
2、变量间的关系确定性关系或函数关系：研究的是确定性现象非随机变量间的关系。
统计依赖关系或相关关系：研究的是非确定性现象随机变量间的关系。
几点注意：–不线性相关并不意味着不相关；–有相关关系并不意味着一定有因果关系；–相关分析对称地对待任何（两个）变量，两个变量都被看作是随机的；回归分析对变量的处理方法存在不对称性，即区分因变量（被解释变量）和自变量（解释变量）：前者是随机变量，后者不是。
总体回归函数：•给定解释变量X的某个确定值X i，与之统计相关的被解释变量Y的总体均值（期望值）可以表示为：上式说明了被解释变量Y平均地说随解释变量X变化的规律，一般称为总体回归函数或总体回归方程（population regression function，PRF）；对应的曲线称为总体回归曲线（population regression curve），它可以是线性的或非线性的。
一元回归分析方法在节电管理中的应用设备能源工程处谭春艳一元回归分析在节电管理中的应用能源管理中用电计划的编制及耗电定额的确定是一项十分重要的工作，正确科学地编制用电计划和制定合理的产品耗电定额对于控制企业能源消耗，实现企业节支降耗目标具有重要的意义。
用电消耗，根据历年消耗的统计数据进行分析，是存在一定规律的，找出这种规律性，就可以比较准确的预测出新的年度耗电量。
回归分析所建立的熟悉模型，综合了企业历年耗电的各种“平均”影响因素，能够简便的预测出新的年度耗电量，从而为企业节能管理带来科学性和明显的节能效益。
回归分析方法是现代化科学管理方法预测和决策技术的一种回归分析所建立起的数学模型是一种统计模型，按其变量的多少，分为一元回归分析数学模型和多元回归分析数学模型，按因变量与自变量之间的函数关系，分析线性模型和非线性模型，实际应用中多为一元线性回归分析数学模型或多元线性分析数学模型，实践证明回归分析方法在企业管理中有比较强的适用性本文结合企业实际，讨论其在企业节能管理中的应用及取得的经济效益。
一、应用一元回归分析方法实例如果所选择的用电消耗数据是近似线性关系，则设数学模型为：Y=a+bx (1)利用最小二乘法求系数 a 、b 值：b=Lxy/Lxxa=Y-bx其中：Lxx=、xi 2-1/n( 、xi )2Lxy= ' XiYi -1/n(' Xi ) (' Yi )22Lyy=、Yi -1/n(、Yi )Y=1/n - Yi 是Yi 的平均数 X=1/n - Xi 是Xi 的平均数以公司2000〜2006年七年间的产品产量和耗电量统计 数据，建立一元回归分析数学模型，预测2007、2008的目标耗电量，以便确定成本费用指标，实施目标控制和管理。
表1、2000-2006 年我公司产品产量和耗电量统计数据以 y 表示耗电量、 x 表示产量设Xi 、丫i 分别表示第i 年的产量和耗电量，i=1、2、3…,n 为年份，统计n 年，则可以得到数据点（XiYi ）。
多项式回归研究一个因变量与一个或多个自变量间多项式的回归分析方法，称为多项式回归（Polynomial Regression ）。
如果自变量只有一个时，称为一元多项式回归；如果自变量有多个时，称为多元多项式回归。
一元m 次多项式回归方程为：2012ˆ m m yb b x b x b x =++++ 二元二次多项式回归方程为：22011223142512ˆ yb b x b x b x b x b x x =+++++ 在一元回归分析中，如果依变量y 与自变量x 的关系为非线性的，但是又找不到适当的函数曲线来拟合，则可以采用一元多项式回归。
多项式回归的最大优点就是可以通过增加x 的高次项对实测点进行逼近，直至满意为止。
事实上，多项式回归可以处理相当一类非线性问题，它在回归分析中占有重要的地位，因为任一函数都可以分段用多项式来逼近。
因此，在通常的实际问题中，不论依变量与其他自变量的关系如何，我们总可以用多项式回归来进行分析。
§9.5.1多项式回归分析的一般方法多项式回归问题可以通过变量转换化为多元线性回归问题来解决。
对于一元m 次多项式回归方程，令212,,,m m x x x x x x === ，则该一元m 次多项式就转化为m 元线性回归方程01122ˆm m yb b x b x b x =++++因此用多元线性函数的回归方法就可解决多项式回归问题。
需要指出的是，在多项式回归分析中，检验回归系数i b 是否显著，实质上就是判断自变量x 的i 次方项i x 对依变量y 的影响是否显著。
对于二元二次多项式回归方程，令2211223142512,,,,z x z x z x z x z x x =====则该二元二次多项式函数就转化为五元线性回归方程01122334455ˆyb b z b z b z b z b z =+++++ 但随着自变量个数的增加,多元多项式回归分析的计算量急剧增加。
南京工业大学 数值分析 试题（A ）答案2009--2010 学年第一学期学年第一学期 使用班级使用班级 信科0701应数0701 一、填空题 （每小题3分，共30分）1．已知974997.999995»，则»-9995100 0.025003126 具有 8 位有效数字。
2．对f(x)=2x 4+x+1,差商f[0,1,2,3,4]= 2 ;f[0,1,2,3,4,5]= 0 。
3．设方程x=j (x)有根x *,且设j (x)在含x *的区间(a,b)内可导，设x 0Î(a,b)则迭代格式x k+1=j (x k )收敛的充要条件为 1|)(|*<¢x j 。
4．÷÷øöççèæ=011001001001....A ,||A||µ= 2.01 ,cond(A)µ= 404.01 。
5．中矩形公式：)()2()(a b b a f dx x f ba-+=ò的代数精度为 2 。
6．在区间[1，2]上满足插值条件îíì==1)2(2)1(P P 的一次多项式P(x)= 3-x 。
7．设å==nk k k n x f A f I 0)()(是函数f(x)在区间[a,b]上的插值型型求积公式，则å=nk kA= a b - 。
8．梯形公式和改进的Euler 公式都是 2 阶的。
9．在区间[0，1]上，函数ax x +=)(1j与函数22)(x x =j 正交，则a= -0.75 。
10．求解线性方程组Ax=b 的迭代格式x (k+1)=Jx (k)+f 收敛的充要条件为1)(<J r 。
二、计算题 （每题8分，共48分）1．试用Gauss 消元法解下列方程组，计算过程按5位小数进行：÷÷÷øöçççèæ=÷÷÷øöçççèæ÷÷÷øöçççèæ---08.255.190.05.11.40.10.15.26.15.05.12.3321x x x （写出详细过程！）解：A=÷÷÷øöçççèæ--2524.01010.0001000.12500.12500.309000.05000.05000.12000.3 （4分）分） ÷÷÷øöçççèæ 2.5000 1.0000 0 0 1.3000 0 1.0000 0 0.5000 0 0 1.0000~ （3分）分） 所以方程组的解为：5.2,3000.1,5000.0321===x x x （1分）分） 2. 给出f(x)f(x)的函数表，的函数表，（1）在表中填上指定阶的差商；（2）写出f(x)f(x)的的2次牛顿插值多项式；（3）给出截断误差。
一元多项式回归模型
如果在回归分析中，只包括一个自变量和一个因变量，且二者的关系可用一条直线近似表示，这种回归分析称为一元线性回归分析。
常见的回归分析方法有以下6种：
1、线性回归方法：通常因变量和一个（或者多个）自变量之间拟合出来是一条直线（回归线），可以用一个普遍的公式来表示：Y （因变量）=a*X（自变量）+b+c，其中b表示截距，a表示直线的斜率，c是误差项；
2、逻辑回归方法：通常是用来计算“一个事件成功或者失败”的概率，此时的因变量一般是属于二元型的（1 或0，真或假，有或无等）变量。
以样本极大似然估计值来选取参数，而不采用最小化平方和误差来选择参数，所以通常要用log等对数函数去拟合；
3、多项式回归方法：通常指自变量的指数存在超过1的项，这时候最佳拟合的结果不再是一条直线而是一条曲线；
4、岭回归方法：通常用于自变量数据具有高度相关性的拟合中，这种回归方法可以在原来的偏差基础上再增加一个偏差度来减小总体的标准偏差；
5、套索回归方法：通常也是用来二次修正回归系数的大小，能够减小参量变化程度以提高线性回归模型的精度；
6、ElasticNet回归方法：是Lasso和Ridge回归方法的融合体，使用L1来训练，使用L2优先作为正则化矩阵。
当相关的特征有很多
个时，ElasticNet不同于Lasso，会选择两个。
一元线性回归分析和多元线性回归分析一元线性回归分析1.简单介绍当只有一个自变量时，称为一元回归分析（研究因变量y 和自变量x 之间的相关关系）；当自变量有两个或多个时，则称为多元回归分析（研究因变量y 和自变量1x ，2x ，…，n x 之间的相关关系）。
如果回归分析所得到的回归方程关于未知参数是线性的，则称为线性回归分析；否则，称为非线性回归分析。
在实际预测中，某些非线性关系也可以通过一定形式的变换转化为线性关系，所以，线性回归分析法成为最基本的、应用最广的方法。
这里讨论线性回归分析法。
2.回归分析法的基本步骤回归分析法的基本步骤如下： （1） 搜集数据。
根据研究课题的要求，系统搜集研究对象有关特征量的大量历史数据。
由于回归分析是建立在大量的数据基础之上的定量分析方法，历史数据的数量及其准确性都直接影响到回归分析的结果。
（2） 设定回归方程。
以大量的历史数据为基础，分析其间的关系，根据自变量与因变量之间所表现出来的规律，选择适当的数学模型，设定回归方程。
设定回归方程是回归分析法的关键，选择最优模型进行回归方程的设定是运用回归分析法进行预测的基础。
（3） 确定回归系数。
将已知数据代入设定的回归方程，并用最小二乘法原则计算出回归系数，确定回归方程。
这一步的工作量较大。
（4） 进行相关性检验。
相关性检验是指对已确定的回归方程能够代表自变量与因变量之间相关关系的可靠性进行检验。
一般有R 检验、t 检验和F 检验三种方法。
（5） 进行预测，并确定置信区间。
通过相关性检验后，我们就可以利用已确定的回归方程进行预测。
因为回归方程本质上是对实际数据的一种近似描述，所以在进行单点预测的同时，我们也需要给出该单点预测值的置信区间，使预测结果更加完善。
3. 一元线性回归分析的数学模型用一元线性回归方程来描述i x 和i y 之间的关系，即i i i x a a y ∆++=10 （i =1，2，…，n ）（2-1）式中，i x 和i y 分别是自变量x 和因变量y 的第i 观测值，0a 和1a 是回归系数，n 是观测点的个数，i ∆为对应于y 的第i 观测值i y 的随机误差。
