计量经济学自相关性检验报告分析(doc 7页)

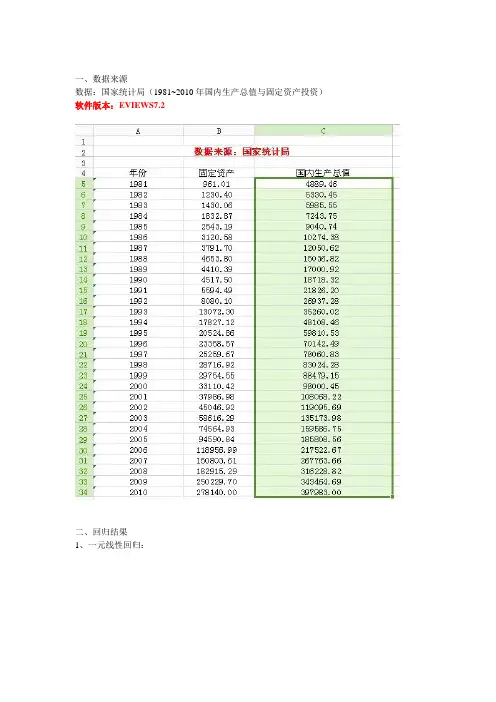
一、数据来源
数据：国家统计局（1981~2010年国内生产总值与固定资产投资）软件版本：EVIEWS7.2
二、回归结果
1、一元线性回归：
三、模型诊断与修正
DW检验：相关系数δ=0.8546，查表得，
1.35
1.49
L
U
d
d
=
=
经检验，DW<1.35,自变量呈一阶正自
相关
四、广义差分法修正后的结果
对E 进行滞后一期的自回归，可得回归方程：E=0.9337E(-1)
对原模型进行广义差分，输出结果为：
**ˆˆ6981.723 1.002749t t y x =+
由于使用广义差分数据，样本容量减少了1个，为29个。

查5%的显著性水平的DW
统计表可知， 1.341.48
L U d d ==，模型中的4-DU>DW>DU ，所以广义差分模型已无序列相关。

根据()1ˆˆ16981.723βρ-=，可得1
ˆ=105305.023β。

因此，原回归模型应为 105305.023 1.002749t t y x =+
采用普莱斯-文斯滕变换后第一个观测值变为211y δ-为1750.7019和211x δ-为344.1377，变换后普通最小二乘结果为**ˆˆ7555.503 1.0611t t y
x =+，根据()1ˆˆ17555.503βρ-=，得1
ˆ=113959.321β，由此，最终模型是 ˆ113959.321 1.0611t t y
x =+。

一、实验目的及要求：1、目的利用EVIEWS 实验软件，使学生在实验过程中全面了解和熟悉计量经济学的基本概念，熟悉一元线性回归模型估计的基本程序和基本方法。

2、内容及要求(1) 熟悉ＥＶＩＥＷＳ实验软件的基本操作程序和方法； (2) 掌握一元线性回归模型基本概念，了解其估计和检验原理 (3) 提交实验报告二、仪器用具：三、实验结果与数据处理：1下面是利用1970-1980年美国数据得到的回归结果。

其中Y 表示美国咖啡消费（杯/日.人），X 表示平均零售价格（美元/磅）。

注：262.2)9(2/=αt ，228.2)10(2/=αt6628.006.42)()1216.0(4795.06911.2ˆ2===-=R t se X Y tt）（值1. 写空白处的数值。

12. 对模型中的参数进行显著性检验。

3. 解释斜率系数1β的含义，并给出其95%的置信区间。

解：（1）1308.221216.06911.2)(00===ββse t0114.006.424795.0)(11-=-==tse ββ（2）用t 检验法分别对模型中的参数0β1β进行显著性水平检验： 在5%的显著性水平下，模型的自由度为11-2=9，且262.2)9(025.0=t 由于262.21308.220>=βt ，故该模型的截距项在统计上是显著的； 同理 262.206.421>=βt ，即斜率系数在统计上也是显著的。

（3）斜率系数4795.01-=β，小于0，在其他条件不变的情况下，咖啡的平均零售价格每增加一个单位，美国咖啡的日消费将平均减少0.4795个单位，说明咖啡的消费量与其平均零售价格呈负相关关系。

1β的95%的置信区间为：]4537.0,5053.0[)]ˆ(ˆ),ˆ(ˆ[12/112/1--+-即ββββααse t se t2美国各航空公司业绩的统计数据公布在《华尔街日报1999年年鉴》（The Wall Street Journal Almanac 1999）上。

一、实验背景随着经济全球化和信息技术的发展，计量经济学作为一门重要的应用经济学分支，在各个领域都得到了广泛的应用。

本实验旨在通过综合运用计量经济学方法，对某一经济问题进行实证分析，从而加深对计量经济学理论和方法的理解，提高实际操作能力。

二、实验目的1. 掌握计量经济学的基本理论和方法；2. 学会使用计量经济学软件（如EViews）进行数据处理和模型分析；3. 培养分析实际经济问题的能力；4. 提高论文写作和报告表达能力。

三、实验内容1. 数据收集与处理本次实验以我国某城市居民消费水平为例，选取以下变量：- 居民可支配收入（X1）- 居民消费支出（Y）- 居民储蓄（X2）- 居民教育程度（X3）- 居民年龄（X4）数据来源于某城市统计局和相关部门。

在收集数据后，对数据进行整理和清洗，确保数据质量和准确性。

2. 模型设定根据实际情况和理论依据，选择以下模型：Y = β0 + β1X1 + β2X2 + β3X3 + β4X4 + ε其中，Y为居民消费支出，X1为居民可支配收入，X2为居民储蓄，X3为居民教育程度，X4为居民年龄，β0为常数项，β1、β2、β3、β4分别为各变量的系数，ε为误差项。

3. 模型估计使用EViews软件对模型进行估计，得到以下结果：Y = 5.23 + 0.83X1 - 0.16X2 + 0.15X3 - 0.02X4 + ε4. 模型检验（1）残差分析：对残差进行检验，发现残差基本服从正态分布，不存在明显的异方差。

（2）自相关检验：对残差进行自相关检验，发现残差不存在自相关。

（3）拟合优度检验：计算R²值，得到R² = 0.89，说明模型拟合效果较好。

5. 模型解释根据模型结果，可以得出以下结论：（1）居民可支配收入对消费支出有显著的正向影响，即收入越高，消费支出越高。

（2）居民储蓄对消费支出有显著的负向影响，即储蓄越高，消费支出越低。

（3）居民教育程度对消费支出有显著的正向影响，即教育程度越高，消费支出越高。

摘要：本文利用我国1985年以来的统计数字建立了可以通过各种检验的居民消费价格的模型，对我国居民消费价格指数进行实证分析。

通过对该模型的经济含义分析得出各主要因素对我国居民消费价格指数的影响程度，并针对现状提出自己的一些建议。

关键词：居民消费价格指数城镇居民农村居民一、引言CPI是英文“Consumer Price Index”的缩写，直译为“消费者价格指数”，在我国通常被称为“居民消费价格指数”。

CPI的定义决定了其所包含的统计内容，那就是居民日常消费的全部商品和服务项目。

日常生活中，我国城乡居民消费的商品和服务项目种类繁多，小到针头线脑，大到彩电汽车，有数百万种之多，由于人力和财力的限制，不可能也没有必要采用普查方式调查全部商品和服务项目的价格，世界各国都采用抽样调查方法进行调查。

作为学经济的本科阶段的学生，我们所理解的并不彻底，我们所能涉及的范围也很小，所以借由国家统计数据做以下分析，促使我们更好的掌握专业知识，了解国情，提高我们实际操作水平和理论联系实际、发现问题、分析问题、解决问题的能力。

二、影响因素的分析居民消费价格指数是反映一定时期内居民消费价格变动趋势和变动程度的相对数。

居民消费价格指数分为食品、衣着、家庭设备及用品、医疗保健、交通和通讯、娱乐教育和文化用品、居住、服务项目等八个大类。

国家规定325种必报商品和服务项目，其中，一般商品273种，餐饮业食品16种，服务项目36种。

该指数是综合了城市居民消费价格指数和农民消费价格指数计算取得。

利用居民消费价格指数，可以观察和分析消费品的零售价格和服务人格变动对城乡居民实际生活费支出的影响程度。

下面主要介绍一下城镇居民消费价格指数、农村居民消费价格指数、城镇居民人均消费价格支出、农村居民人均消费支出的影响：1、城镇居民消费价格指数（y1）2、农村居民消费价格指数（y2）3、城镇居民人均消费支出（x1）4、农村居民人均消费支出（x2）5、其他因素（用随机变量u来处理）三、模型：1、本文模型数据样本从1985—2006年：Y居民消费价格指数Y1城镇居民消费价格指数Y2农村居民消费价格指数X1 城镇居民人均消费支出X2农村居民人均消费支出年份1985 109.3 111.9 107.6 765 3491986 106.5 107 106.1 872 3781987 107.3 108.8 106.2 998 421 1988 118.8 120.7 117.5 1311 509 1989 118 116.3 119.3 1466 549 1990 103.1 101.3 104.5 1596 560 1991 103.4 105.1 102.3 1840 602 1992 106.4 108.6 104.7 2262 688 1993 114.7 116.1 113.7 2924 805 1994 124.1 125 123.4 3852 1038 1995 117.1 116.8 117.5 4931 1313 1996 108.3 108.8 107.9 5532 1626 1997 102.8 103.1 102.5 5823 1722 1998 99.2 99.4 99 6109 1730 1999 98.6 98.7 98.5 6405 1766 2000 100.4 100.8 99.9 6850 1860 2001 100.7 100.7 100.8 7113 1969 2002 99.2 99 99.6 7387 2062 2003 101.2 100.9 101.6 7901 2103 2004 103.9 103.3 104.8 8679 2301 2005 101.8 101.6 102.2 9410 2560 2006 101.5 101.5 101.5 10359 28482、基于以上数据，建立一下模型：Y=β1+β2y1+β3y2+β4x1+β5x2+u ①检验各变量是否为y的格兰杰原因Y y1Pairwise Granger Causality Tests Date: 12/22/10 Time: 12:13 Sample: 1985 2006Lags: 2Null Hypothesis: Obs F-Statistic Prob.Y1 does not Granger Cause Y 20 4.56120 0.0283 Y does not Granger Cause Y1 3.37364 0.0617 P=0.0283<0.05 显著，y1是y的格兰杰原因Y y2Pairwise Granger Causality TestsDate: 12/22/10 Time: 12:13Sample: 1985 2006Lags: 2Null Hypothesis: Obs F-Statistic Prob.Y2 does not Granger Cause Y 20 3.86484 0.0443 Y does not Granger Cause Y2 5.07054 0.0208 P=0.0443<0.05 显著，y2是y的格兰杰原因Y x1Pairwise Granger Causality TestsDate: 12/22/10 Time: 12:13Sample: 1985 2006Lags: 2Null Hypothesis: Obs F-Statistic Prob.X1 does not Granger Cause Y 20 11.1781 0.0011 Y does not Granger Cause X1 2.80821 0.0921 P=0.0011<0.05 显著，x1是y的格兰杰原因Y x2Pairwise Granger Causality TestsDate: 12/22/10 Time: 12:13Sample: 1985 2006Lags: 2Null Hypothesis: Obs F-Statistic Prob.X2 does not Granger Cause Y 20 7.78739 0.0048Y does not Granger Cause X2 1.28602 0.3052P=0.0048<0.05 显著，x2是y的格兰杰原因经过格兰杰检验，4个解释变量均为y的格兰杰原因，可以作为解释变量②普通最小二乘法Dependent Variable: YMethod: Least SquaresDate: 12/22/10 Time: 12:25Sample: 1985 2006Included observations: 22Variable Coefficient Std. Error t-Statistic Prob.C -0.039682 0.405396 -0.097885 0.9232Y10.432584 0.010802 40.04835 0.0000 Y20.567086 0.010740 52.80087 0.0000 X1-9.56E-05 0.000104 -0.915566 0.3727X20.000357 0.000414 0.863621 0.3998R-squared 0.999884 Mean dependentvar 106.650AdjustedR-squared 0.999856 S.D. dependentvar 7.370388S.E. of regression 0.088378 Akaike infocriterion -1.817677Sum squaredresid 0.132781 Schwarz criterion -1.569713Log likelihood 24.99445 Hannan-Quinncriter. -1.759264F-statistic 36509.31 Durbin-Watsonstat 1.420561Prob(F-statistic) 0.000000由以上分析，初步建立模型为：Y=-0.039682+0.432584*y1+0.567086*y2-9.56*x1+0.000357 *x2R2的拟合程度为0.999884 F=36509.31③异方差的检验Ⅰ、white检验Heteroskedasticity Test: WhiteF-statistic 0.527426 Prob. F(14,7) 0.8540Obs*R-squared 11.29363 Prob.Chi-Square(14) 0.6628Scaled explainedSS 6.684989 Prob.Chi-Square(14) 0.9462Test Equation:Dependent Variable: RESID^2Method: Least Squares Date: 12/22/10 Time: 12:30 Sample: 1985 2006 Included observations: 22Variable Coefficient Std. Error t-Statistic Prob.C -0.793516 1.975576 -0.401663 0.6999Y1 0.010665 0.024387 0.437300 0.6751 Y1^2 0.000950 0.000831 1.144012 0.2902Y1*Y2 -0.001960 0.001686 -1.162006 0.2833Y1*X1 9.39E-06 1.67E-05 0.562184 0.5915Y1*X2 -3.22E-05 6.65E-05 -0.484229 0.6430Y2 -0.000172 0.035384 -0.004857 0.9963Y2^2 0.000972 0.000852 1.141293 0.2913Y2*X1 -4.95E-06 1.69E-05 -0.293341 0.7778Y2*X2 1.47E-05 6.91E-05 0.212909 0.8375X1 -0.000629 0.000692 -0.909063 0.3935X1^2 -4.47E-09 1.25E-07 -0.035782 0.9725X1*X2 1.39E-07 9.85E-07 0.141053 0.8918 X2 0.002533 0.002839 0.892048 0.4020X2^2 -4.71E-07 1.95E-06 -0.240981 0.8165R-squared 0.513347 Mean dependentvar 0.006035Adjusted R-squared -0.459959S.D. dependentvar 0.008698S.E. of regression 0.010510 Akaike infocriterion -6.054459 Sum squaredresid 0.000773 Schwarz criterion -5.310566Log likelihood 81.59905 Hannan-Quinncriter. -5.879220F-statistic 0.527426 Durbin-Watsonstat 3.341695Prob(F-statistic) 0.853973由于Obs*R-squared=11.29363>卡方0.05（5）=11.07，所以存在异方差，用加权最小二乘法消除异方差Ⅱ、加权最小二乘法消除异方差Dependent Variable: YMethod: Least SquaresDate: 12/22/10 Time: 12:37Sample: 1985 2006Included observations: 22Weighting series: WWeight type: Inverse standard deviation (EViews default scaling)Variable Coefficient Std. Error t-Statistic Prob.C -0.131244 0.136038 -0.964757 0.3482Y1 0.429947 0.002008 214.1169 0.0000 Y2 0.570375 0.002160 264.0622 0.0000X1 -0.000137 3.91E-05 -3.499721 0.0027X2 0.000517 0.000157 3.296181 0.0043 Weighted StatisticsR-squared 0.999989 Mean dependentvar 106.6536AdjustedR-squared 0.999986 S.D. dependentvar 129.1117S.E. of regression 0.027333 Akaike infocriterion -4.164758 Sum squaredresid 0.012700 Schwarz criterion -3.916794Log likelihood 50.81234 Hannan-Quinncriter. -4.106345F-statistic 384834.4 Durbin-Watsonstat 0.860182Prob(F-statistic) 0.000000 Weighted meandep. 106.0005 UnweightedStatisticsR-squared 0.999882 Mean dependentvar 106.6500AdjustedR-squared 0.999854 S.D. dependentvar 7.370388 S.E. of regression 0.089116 Sum squared resid 0.135010Durbin-Watsonstat 1.385850分析各变量是否存在相关性，并予以消除从上表（加权最小二乘法）的统计结果中可知，DW=0.860182 查表得DL=0.96 DU=1.80 0<DW<DL，所以，存在一介正自相关差分—消除Dependent Variable: DYMethod: Least SquaresDate: 12/22/10 Time: 12:50Sample (adjusted): 1986 2006Included observations: 21 after adjustmentsVariable Coefficient Std. Error t-Statistic Prob.C 0.004360 0.045369 0.096098 0.9246 DY10.425938 0.010577 40.27064 0.0000 DY20.572954 0.011062 51.79573 0.0000DX1-9.20E-05 0.000170 -0.540527 0.5963DX20.000367 0.000500 0.733528 0.4738 R-squared 0.999746 Mean dependent var -0.371429AdjustedR-squared 0.999683 S.D. dependent var 5.992507 S.E. of regression 0.106754 Akaike info criterion -1.432327 Sum squaredresid 0.182342 Schwarz criterion -1.183631 Log likelihood 20.03943 Hannan-Quinn criter. -1.378354F-statistic 15751.09 Durbin-Watson stat 2.05844 Prob(F-statistic) 0.000000由上表的统计结果可知：DW=2.05844，查表得DL=0.93 DU=1.81，DU<DW<4-DU，所以解释变量之间无自相关从上表中看得出：dx1的T统计结果是-0.540527，其绝对值小于T0.025（16）=2.120，且其系数符号与预期相反，这表明可能存在严重的多重共线性。

计量经济学实验报告
标题：基于地区人民收入与犯罪率的实证分析
摘要：
本实验报告旨在使用计量经济学方法对地区的人民收入与犯罪率之间的关系进行实证分析。

通过收集该地区多年的相关数据，并建立合适的计量模型，我们得出了以下结论：在控制其他因素的情况下，人民收入对犯罪率具有显著的负向影响。

这一研究结果对相关当局在制定犯罪预防政策时具有重要的指导意义。

1.引言
犯罪问题一直是社会关注的焦点。

了解犯罪率的影响因素对改善社会治安具有重要的意义。

本实验以地区为例，通过实证分析人民收入对犯罪率的影响，希望为相关当局提供制定犯罪预防政策的参考。

《 计量经济学 》课程实验第 3 次实验报告实验内容及基本要求：实验项目名称：运用Eviews 软件进行自相关模拟分析实验类型： 上机实验每组人数： 1实验内容及要求：1、总体要求：数据已经输入到eviews 中，数据文件为：自相关实验.wf1，其中的income 为家庭收入，consume 为家庭开支，以此数据建立以consume 为被解释变量的消费方程，用最小二乘法估计变量间的相关关系。

并检验数据中自相关性等特征，采用相应方法进行修正。

2、具体步骤：依次回答下列问题（得到回归结果是指给出回归方程，并做检验）： 1、建立消费方程，做回归，得到回归结果。

2、根据回归结果，边际消费倾向为多少？显著不为1吗，给出检验过程。

3、数据中存在自相关吗，给出检验过程。

4、用dw 值来估计ρ，据此ρ做广义差分来消除自相关性，给出结果 5、 假定为ar(1)，用科克兰内-奥克特法来消除自相关性，给出结果6、 假定为ar(2)，用科克兰内-奥克特法来消除自相关性，给出结果实验结果：一．模型设定假定被解释变量Y 与解释变量X 存在线性相关关系，则可设定为如下模型:t t t u X Y ++=21ββ其中Y 为家庭支出consume,X 为家庭收入income.Ut 为随机误差项。

二．参数估计——用最小二乘法估计Y 与X 之间的参数值1.数据输入由于之前数据已输入到“自相关实验.wf1”中，故在eviews 设定完Y 和X 之后直接把相对应的数据粘贴就可以了。

2.参数估计通过最小二乘法进行回归估计，结果如图所示：可知该模型为：t t X Y 7829.02336.81^+= SE=180.2928 0.032038T=0.4506 24.4377R 2=0.9552 F=597.1988 DW=1.23373.边际消费倾向分析根据该回归结果可知，边际消费倾向为2β=0.7829，对其显著性进行检验H0：2β=1 H1：2β≠1给定显著性水平α=0.05，查表得2/αt (n-2)=025.0t (28)=2.0487752.6032038.017829.0)(22=-=-=βββSE t可知2/αt （28）=2.048<t ，所以，拒绝H0，即边际消费倾向2β显著不为1.4.自相关检验由上面的回归结果可知，该模型的可决系数R 2，2R 很高，拟合程度较好，回归系数显著。

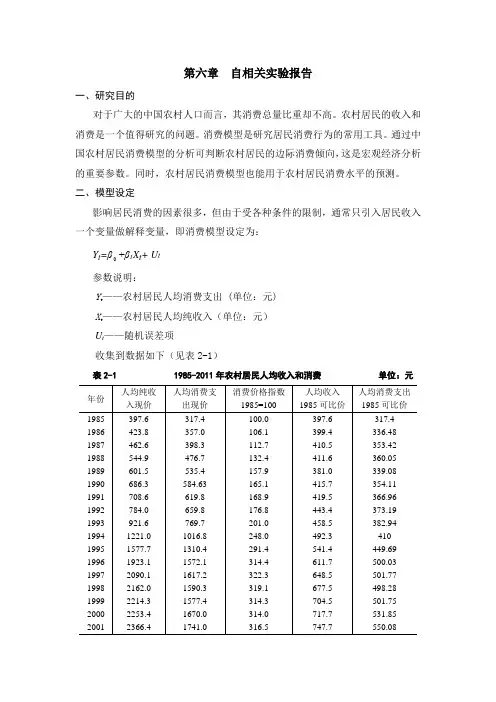
第六章自相关实验报告一、研究目的对于广大的中国农村人口而言，其消费总量比重却不高。

农村居民的收入和消费是一个值得研究的问题。

消费模型是研究居民消费行为的常用工具。

通过中国农村居民消费模型的分析可判断农村居民的边际消费倾向，这是宏观经济分析的重要参数。

同时，农村居民消费模型也能用于农村居民消费水平的预测。

二、模型设定影响居民消费的因素很多，但由于受各种条件的限制，通常只引入居民收入一个变量做解释变量，即消费模型设定为：+β1X t+ U tY t=β参数说明：Y——农村居民人均消费支出 (单位：元)tX——农村居民人均纯收入（单位：元）tU t——随机误差项收集到数据如下（见表2-1）表2-1 1985-2011年农村居民人均收入和消费单位：元注：资料来源于《中国统计年鉴》1986-2012。

为了消除价格变动因素对农村居民收入和消费支出的影响，不宜直接采用现价人均收入和现价人均消费支出的数据，而需要用经消费价格进行调整后的1985年可比价格及人均纯收入和人均消费支出的数据做回归分析。

根据表2-1中调整后的1985年可比价格计的人均纯收入和人均消费支出的数据，使用普通最小二乘法估计消费模型得如下结果。

表2-2 最小二乘估计结果Dependent Variable: YMethod: Least SquaresDate: 12/04/13 Time: 20:00Sample: 1985 2011Included observations: 27Coefficient Std. Error t-Statistic Prob.C 45.40225 10.30225 4.407025 0.0002X 0.718526 0.012526 57.36069 0.0000R-squared 0.992459 Mean dependent var 580.5296 Adjusted R-squared 0.992157 S.D. dependent var 256.4506 S.E. of regression 22.71079 Akaike info criterion 9.154744 Sum squared resid 12894.50 Schwarz criterion 9.250732 Log likelihood -121.5890 Hannan-Quinn criter. 9.183287 F-statistic 3290.249 Durbin-Watson stat 0.528075 Prob(F-statistic) 0.000000由以上结果得到以下方程:^Y t=45.4022545+0.718526X t（6.1）（10.30225）（0.012526）t = (4.407025) (57.36069)R2=0.992459--R2=0.992157 F=3290.249 DW=0.528075该回归方程可决系数较高，回归系数均显著。

计量经济学实验报告(多元线性回归自相关 )1. 背景计量经济学是一门关于经济现象的定量分析方法研究的学科。

它的发展使得我们可以对经济现象进行更加准确的分析和预测，并对社会发展提供有利的政策建议。

本文通过对多元线性回归模型和自相关模型的实验研究，来讨论模型的建立与评价。

2. 多元线性回归模型在多元线性回归模型中，我们可以通过各个自变量对因变量进行预测和解释。

例如，我们可以通过考虑家庭收入、年龄和教育程度等自变量，来预测某个家庭的消费水平。

多元线性回归模型的一般形式为：$y_i=\beta_0+\beta_1 x_{i1}+\beta_2 x_{i2}+...+\beta_k x_{ik}+\epsilon_i$在建立模型之前，我们需要对因变量和自变量进行观测和测算。

例如，我们可以通过调查一定数量的家庭，获得他们的收入、年龄、教育程度和消费水平等数据。

接下来，我们可以通过多元线性回归模型，对家庭消费水平进行预测和解释。

在实际的研究中，我们需要对多元线性回归模型进行评价。

其中一个重要的评价指标是 $R^2$ 值，它表示自变量对因变量的解释程度。

$R^2$ 值越高，说明多元线性回归模型的拟合程度越好。

3. 自相关模型在多元线性回归模型中，我们假设各个误差项之间相互独立，即不存在自相关性。

但实际上，各个误差项之间可能会互相影响，产生自相关性。

例如，在一个气温预测模型中，过去的温度对当前的温度有所影响，说明当前的误差项和过去的误差项之间存在相关性。

我们可以通过自相关函数来研究误差项之间的相关性。

自相关函数表示当前误差项和过去 $l$ 期的误差项之间的相关性。

其中，$l$ 称为阶数。

自相关函数的一般形式为：$\rho_l={\frac{\sum_{t=l+1}^{T}(y_t-\bar{y})(y_{t-l}-\bar{y})}{\sum_{t=1}^{T}(y_t-\bar{y})^2}}$在自相关模型中，我们通过对误差项进行差分或滞后变量，来消除误差项之间的自相关性。