浙江省义乌市2016届中考九年级5月调研考试数学试卷含答案
- 格式:pdf
- 大小:178.46 KB
- 文档页数:5

2016年义乌市初中毕业生调研考试(数学卷)试卷Ⅰ说明:本卷共有1大题,10小题,每小题4分,共40分.请用2B铅笔在“答题纸”上将你认为正确的选项对应的小方框涂黑、涂满.一、选择题(请选出各题中一个符合题意的正确选项,不选、多选、错选,均不给分)1、2016的倒数是A.2016 B.-2016 C.D.2. 某地区轨道交通3号线于2015年12月23日开工建设,预计2020年全线开通,3号线全长32.83千米, 32.83千米用科学计数法表示为A. 3.283×104米B. 32.83×104米C. 3.283×105米D. 3.283×103米3.下列运算中,正确的是A.xyyx532=+ B.aaa=-23C.bbaa-=--)( D.2)2)(1(2-+=+-aaaa4.在以下绿色食品、回收、节能、节水四个标志中,是轴对称图形的是A B C D5. 下列说法正确的是A.两名同学5次成绩的平均分相同,则方差较大的同学成绩更稳定.B.某班选出两名同学参加校演讲比赛,结果一定是一名男生和一名女生.C.学校气象小组预报明天下雨的概率为0.8,则明天下雨的可能性较大.D.为了解某市学校“阳光体育”活动开展情况,必须采用普查的方法.6.在市委市政府的领导下,经过全市人民的努力,义乌市获“全国文明城市”提名,为此小兵特制了一个正方体玩具,其展开图如图所示,正方体中与“全”字所在的面正对面上标的字是A.文 B.明 C.城 D.国7.如果一个正比例函数的图象经过不同象限的两点(2)A m,、()3B n,,那么一定有A.00m n>>, B.00m n><,C.00m n<<, D.00m n<>,8.如图,在平行四边形 ABCD中,AB=3cm,AD=6cm,∠ADC的角平分线DE交BC于点E,交AC于点F,CG⊥DE,垂足为G,DG=323cm,则EF的长为A.3cm B.2cm C.1cm D.332cm9.如图,用四个螺丝将四条不可弯曲的木条围成一个木框(形状不限),不2016120161-计螺丝大小,其中相邻两螺丝的距离依次为3、4、5、7,且相邻两木条的夹角均可调整.若调整木条的夹角时不破坏此木框,则任意两个螺丝间的距离的最大值为 A .6 B .7 C .8 D .910. 已知二次函数y =x 2-2x -3,点P 在该函数的图象上,点P 到x 轴、y 轴的距离分别为d 1、d 2.设d =d 1+d 2,下列结论中:①d 没有最大值;②d 没有最小值;③;-1<x <3时, d 随x 的增大而增大; ④满足d =5的点P 有四个. 其中正确结论的个数有 A .1个 B .2个 C .3个 D .4个试 卷 Ⅱ说明:本卷共有2大题,14小题,共110分. 答题请用0.5毫米及以上的黑色签字笔书写在“答题纸”的对应位置上. 二、填空题(本题有6小题,每小题5分,共30分)11.若根式1-x 有意义,则x 的取值范围是 ▲ .12.如图,一束平行太阳光照射到正五边形上,若∠1= 44°,则∠2= ▲ .13. 袋子中装有3个红球、5个黄球、2个白球,这些球的形状、大小、质地等完全相同,随机地从袋子中摸出一个红球的概率是 ▲ _.14.如图,在△ABC 中,AB =4,将△ABC 绕点B 按逆时针方向旋转30°后得到△A 1BC 1,则阴影部分的面积为 ▲ .15. 如图,点A 在双曲线xky =第一象限的图像上,AB ⊥y 轴于点B ,点C 在x 轴正半轴上,且OC =2AB ,点E 在线段AC 上,且AE =3EC ,点D 为OB 的中点,若△ADE 的面积为3,则 k 的值为 ▲ .16. 如图,点P (t,0)(t >0)是x 轴正半轴上的一点, 是以原点为圆心,半径为1的41圆,且A (-1,0),B (0,1),点M 是 上的一个动点,连结PM ,作直角△MP M 1,并使得∠MP M 1=90°,∠PMM 1=60°,我们称点M 1为点M 的对应点. (1)设点A 和点B 的对应点为A 1和B 1,当t =1时,求A 1的坐标 ▲ ;B 1的坐标 ▲ .(2当P 是x 轴正半轴上的任意一点时,点M 从点A 运动至点B ,求M 1的运动路径长 ▲ .三、解答题(本题有8小题,第17~19题每题8分,第20、21、22题每题10分,第23题每题12分,第24题14分,共80分)17. (1)计算:()11313216--⎛⎫-+ ⎪⎝⎭+-; (2)化简: ba ca b a c ab +-+++2. 18.(1)解方程:3121=-+-x x x (2)解不等式组:⎩⎨⎧-<-+<-x x x x 41525247 A B O PM M 1y x19. 如图,已知E、F分别是平行四边形ABCD的边BC、AD上的点,且BE=DF.(1)求证:四边形AECF是平行四边形;(2)若四边形AECF是菱形,且BC=10,∠BAC=90°,求BE的长.20. 义乌市某校在推进新课程改革的过程中,开设的体育选修课有:A﹣篮球,B﹣足球,C﹣排球,D﹣羽毛球,E﹣乒乓球,学生可根据自己的爱好选修一门,王老师对某班全班同学的选课情况进行调查统计,制成了两幅不完整的统计图(如图).(1)求出该班的总人数为▲,并补全频数分布直方图;(2)求出“足球”在扇形中的圆心角是多少度;(3)该班班委4人中,1人选修篮球,2人选修足球,1人选修排球,李老师要从这4人中人任选2人了解他们对体育选课的看法,请你用列表或画树状图的方法,求选出的2人恰好为1人选修篮球,1人选修足球的概率.21.图1是一个小朋友玩“滚铁环”的游戏,铁环是圆形的,铁环向前滚动时,铁环钩保持与铁环相切.将这个游戏抽象为数学问题,如图2.已知铁环的半径为25cm,设铁环中心为O,铁环钩与铁环相切点为M,铁环与地面接触点为A,∠MOA=α,且sinα=35.(1)求点M离地面AC的高度BM;(2)设人站立点C与点A的水平距离AC =55cm,求铁环钩MF的长度.22. 为进一步缓解城市交通压力,义乌市政府推出公共自行车,公共自行车在任何一个网店都能实现通租通还,某校学生小明统计了周六校门口停车网点各时段的借、还自行车数,以及停车点整点时刻的自行车总数(称为存量)情况,表格中x=1时的y的值表示8:00点时的存量,x=2时的y值表示9:00点时的存量……. 图1(第21题图)(1)m=__▲__,解释m的实际意义:__________▲___________;(2)求整点时刻的自行车存量y与x之间满足的二次函数关系式;(3)已知10:00-11:00这个时段的借车数比还车数的一半还要多2,求此时段的借车数.23. 如图1,新定义:直线l1、l、l2,相交于点O,长为m的线段AB在直线l2上,点P是直线l1上一点,点Q是直线l上一点.若∠AQB=2∠APB,则我们称点P是点Q的伴侣点;(1)如图1,直线l2、l的夹角为30°,线段AB在点O右侧,且OA=1,m=2,若要使得∠APB=45°且满足点P是点Q的伴侣点,则OQ=_________;(2)如图2,若直线l1、l2的夹角为60°,且m=3,若要使得∠APB=30°,线段AB在直线l2上左右移动.①当OA的长为多少时,符合条件的伴侣点P有且只有一个?请说明理由;②是否存在符合条件的伴侣点P有三个的情况?若存在,请直接写出OA长;若不存在,请说明理由.24. 如图1,点A,B分别是二次函数y=2x2的图象上的两个点,A、B的横坐标分别为a,b(a<0,b>0),点P(0,t)是抛物线对称轴上的任意一点.(1)当a+b=0时,探究是否存在t,使得△PAB是以AB为底的等腰三角形,若存在,请直接写出t、 a、b的其中一组值;若不存在,请说明理由;(2)当a+b≠0时,探究是否存在t,使得△PAB是以AB为底的等腰三角形,若存在,请写出t的取值范围,并用含t的代数式表示a2+b2的值;若不存在,请说明理由;(3)如图2作边长为4的正方形ACDE(A、C、D、E按逆时针排列),使得AC∥x轴,若边CD与二次函数的图象总有交点,求a的取值范围.2016年义乌市初中毕业生调研考试(评分标准)11. x ≥1(填x >1给1分) . 12. 28°(写28给4分) . 13. 103 . 14.4 . 15.316. 16.(1) A 1(1,32) B 1(1+3,3)(每空1分) (2)π23(3分). 三、解答题(本题有8小题,第17~19题每题8分,第20、21、22题每题10分,第23题每题12分,第24题14分,共80分)17. (1)解:原式=3-2+4-1……3分(算对1项1分、2项或者3项得2分,全对3分)=4 …………………………………………………………………………4分(2)解:原式=ba a ab ++2………………………………………………………………………2分=ba ab a ++)( ……………………………………………………………………3分=a ……………………………………………………………………………4分18.解:(1)化简:x +(-2)=3(x -1) ………………………………………………………… 1分∴2x =1 ………………………………………………………………… 2分∴x = 21………………………………………………………………… 3分 经检验:x =21是原方程的解………………………………………………………4分 (2)解:解不等式①:x >-3…………………………………………………………… 1分解不等式②:x <5………………………………………………………………… 2分 ∴不等式组的解是-3<x <5…………………………………………………… 4分19.(1)证明:在平行四边形ABCD 中,AD =BC ,AD ∥BC∵BE =DF ∴AF =CE …………………………………………………………………2分 ∵AD ∥BC ∴AF ∥CE …………………………………………………………… 3分 ∴四边形AECF 是平行四边形 ………………………………………………………………4分 (2)∵四边形AECF 是菱形 ∴∠EAC =∠ECA AE =CE∵∠BAC =90° ∴∠B =∠BAE …………………………………………………………6分 ∴AE =BE ∴BE =CE =5 ……………………………………………………………………8分20.(1) 50 ………………………………………………………………………………2分补全频数分布直方图略(A :14人 E :5人) ………………………………4分 (2)οο723605010=⨯ ……………………………………………………………………6分 (3)列表或树状图略………………………………………………………………………… 8分所求的概率为P =3162= ……………………………………………………10分 21.(1)过点M 作MD ⊥OA 交OA 于点D …………………………………………………1分 在RT △ODM 中,sin α=53=OM DM ∴DM =15cm ∴OD =20 cm ………………………………………3分 ∴AD =BM =5 cm ……………………………………………………5分(2) 延长DM 交CF 于点E ……………………………………………………………………6分 易得:∠FME =∠AOM =α…………………………………………………………………7分 ∵ME =AC -DM =55-15=40 cm …………………………………………………………………8分 ∴cos α=54=MF ME ∴MF =50 cm …………………………………………………………10分 22. (1)m = 13 ……………1分 m 的实际意义: 7:00时自行车的存量 ;…………2分 (2)由题意可得:n =16………………………………………………………………………4分设二次函数关系式为y =ax 2+bx +c 且二次函数图象过点(0,13)(1,15)(2,16)∴⎪⎩⎪⎨⎧=++=++=16241513c b a c b a c ∴132521==-=c b a∴二次函数关系式为1325212++-=x x y …………………………………………………6分 (3)设x =3,x =4时对应的函数值为y 3,y 4,还车数为x ,则由已知可得:)22(34+-=x y y 即)22(1615+-=x…………………………………………………8分∴ x =2 则322=+x……………………………………………………………………………………10分 答:10:00-11:00这个时段的借车数为3辆.23.(1)由题意可得:∠AQB =90°则点Q 在以AB 为直径的圆与直线l 的交点,此时圆与直线l 相切,OQ =3 ………3分(2)①如图1,当直线l 1与⊙C 相切于点P ,且A 在O 的右侧时,则∠APB =30°连接CP ,过A 作AD ⊥l 1于D则AD =CP =3,∴OA =ADsin60°= 23 ………………………………………5分 如图2,当直线l 1与⊙C 相切于点P ,且A 在O 的左侧时,则∠APB =30° 连结CP ,过B 作BE ⊥l 1于E 则BE =CP =3,∴OB =BEsin60°= 23 ∴OA = 23+3 ……………………7分 综上所述,当A 在O 的右侧,OA = 23 或A 在O 的左侧,OA = 23+3时符合条件的点P 有且只有一个②存在 …………………………………………………………………………………8分如图3,当直线l 1与⊙C 1相交于点P 1、P 2,与⊙C 2相切于点P 3时连结C 2P 3,过O 作OF ⊥BC 2于F ,则OF =C 2P 3=3,∴OB =BEsin60°= 2 3 ∴OA = 23-3 ………10分如图4,当直线l 1与⊙C 1相切于点P 1,与⊙C 2相交于点P 2、P 3时连接C 1P 1,过A 作AG ⊥l 1于G 则AG =C 1P 1=3,∴OA =AGsin60°= 23………………………………………………12分综上所述,当A 在O 的右侧,OA = 23-3或A 在O 的左侧,OA = 23 时,符合条件的点P 有三个(阅卷注意点:写出结论“存在”一分, OA = 23-3或OA = 23一个2分,只要写出OA = 23-图1图2图3图43或OA = 23不写结论“存在”,得3分或5分)24.(1)当 a +b =0时,显然PA =PB ∴只需满足t ≠2a 2即可……………………… 2分∴a =-1,b =1,t =3(答案不唯一) ………………………………………………3分(2)∵A (a ,2a 2), B (b ,2b 2) , P (0,t )由 PA =PB 可得 a 2+(t -2a 2)2=b 2+(t -2b 2)2………………………………………5分∴ a 2- b 2+(t -2a 2)2-(t -2b 2)2=0(a 2- b 2)[1-4(t -a 2-b 2)]=0………………………………………………………6分 ∵a 2- b 2≠0∴1-4(t -a 2-b 2)=0∴a 2+b 2=t -41……………………………………………………………………8分 ∴t -41>0 ∴t >41……………………………………………………………9分(3) A (a ,2a 2) ∴C(a+4,2a 2) D(a+4,2a 2+4) ………………………………11分设边CD 与二次函数图象交点为F (a+4,2(a+4)2)由题意可得:⎪⎩⎪⎨⎧+≥+≥+2222)4(2422)4(2a a aa∴⎪⎩⎪⎨⎧-≤-≥472a a∴472-≤≤-a ……………………………………………………………………14分初中数学试卷。
浙江省义乌市初中毕业生学业考试数学试题试 卷 Ⅰ一、选择题 1. -3的绝对值是A .3B .-3C .-13D .132.如图,DE 是△ABC 的中位线,若BC 的长是3cm ,则DE 的长是 A .2cm B .1.5cm C .1.2cm D .1cm 3.下列计算正确的是A .246x x x +=B .235x y xy +=C .632x x x ÷=D .326()x x =4.如图,下列水平放置的几何体中,主视图不是..长方形的是5.我市市场交易持续繁荣,市场成交额连续20年居全国各大专业市场榜首. 中国小商品城成交额首次突破450亿元关口.请将数据450亿元用科学记数法表示为(单位:元) A .4.50×102B .0.45×103C .4.50×1010D .0.45×10116.下列图形中,中心对称图形有A .4个B .3个C .2个D .1个7.不等式组⎩⎨⎧≥->+125523x x 的解在数轴上表示为8.如图,已知AB ∥CD ,∠A =60°,∠C =25°,则∠E 等于 A. 60° B. 25° C. 35° D. 45°9.某校安排三辆车,组织九年级学生团员去敬老院参加学雷锋活动,其中小王与小菲都可以从这三辆车中任选一辆搭乘,则小王与小菲同车的概率为 A .13 B .19 C .12 D .2310.如图,△ABC 和△ADE 都是等腰直角三角形,∠BAC =∠DAE =90°,四边形ACDE 是平行四边形,连结CE 交AD 于点F ,连结BD 交CE 于点G ,连结BE . 下列结论中:1 02 A .1 02 B .1 02 C .1 02 D . A .B .C .D .AB CDE60° E A BCD① CE =BD ; ② △ADC 是等腰直角三角形; ③ ∠ADB =∠AEB ; ④ CD ·AE =EF ·CG ; 一定正确的结论有 A .1个 B .2个C .3个D .4个试 卷 Ⅱ二、填空题(本题有6小题,每小题4分,共24分)11.一次函数y =2x -1的图象经过点(a ,3),则a = ▲ . 12.如果x 1与x 2的平均数是4,那么x 1+1与x 2+5的平均数是 ▲ .13.已知⊙O 1与⊙O 2的半径分别为3和5,且⊙O 1与⊙O 2相切,则O 1O 2等于 ▲ . 14.某校为了选拔学生参加我市无线电测向比赛中的装机比赛,教练对甲、乙两选手平时五次训练成绩进行统计,两选手五次训练的平均成绩均为30分钟,方差分别是251S =甲、212S =乙. 则甲、乙两选手成绩比较稳定的是 ▲ .15.右图是市民广场到解百地下通道的手扶电梯示意图.其中AB 、CD 分别表示地下通道、市民广场电梯口处地面的水平线,∠ABC =135°,BC 的长约是25m ,则乘电梯从点B 到点C 上升的高度h 是 ▲ m .16.如图,一次函数y =-2x 的图象与二次函数y =-x 2+3x 图象的对称轴交于点B .(1)写出点B 的坐标 ▲ ;(2)已知点P 是二次函数y =-x 2+3x 图象在y 轴右侧..部分上的一个动点,将直线y =-2x 沿y 轴向上平移,分别交x 轴、y 轴于C 、D 两点. 若以CD 为直角边的△PCD 与△OCD 相似,则点P 的坐标为 ▲ .三、解答题(本题有8小题,第17~19题每题6分,第20、21题每题8分,第22、23题每题10分,第24题12分,共66分)17.(1)计算: 45sin 2820110-+;(2)解分式方程:2323=-+x x . 18.如图,已知E 、F 是□ABCD 对角线AC 上的两点,且BE ⊥AC ,DF ⊥AC .(1)求证:△ABE ≌△CDF ;(2)请写出图中除△ABE ≌△CDF 外其余两对全等三角形(不再添加辅助线).19.商场某种商品平均每天可销售30件,每件盈利50元. 为了尽快减少库存,商场决定采取适当的降价措施. 经调查发现,每件商品每降价1元,商场平均每天可多售出 2件.设每件商品降价x 元. 据此规律,请回答:(1)商场日销售量增加 ▲ 件,每件商品盈利 ▲ 元(用含x 的代数式表示);A BCDEF G 135° ABCDhFEABCDOBC D(2)在上述条件不变、销售正常情况下,每件商品降价多少元时,商场日盈利可达到2100元? 20 . 为了解某市九年级学生学业考试体育成绩,现从中随机抽取部分学生的体育成绩进行分段(A :50分;B :49-45分;C :44-40分;D :39-30分;E :29-0分)统计如下:学业考试体育成绩(分数段)统计图 学业考试体育成绩(分数段)统计表根据上面提供的信息,回答下列问题:(1)在统计表中,a 的值为 ▲ ,b 的值为 ▲ ,并将统计图补充完整(温馨提示:作图时别忘了用0.5毫米及以上的黑色签字笔涂黑);(2)甲同学说:“我的体育成绩是此次抽样调查所得数据的中位数. ”请问:甲同学的体育成绩应在什么分数段内? ▲ (填相应分数段的字母)(3)如果把成绩在40分以上(含40分)定为优秀,那么该市今年10440名九年级学生中体育成绩为优秀的学生人数约有多少名?21.如图,已知⊙O 的直径AB 与弦CD 互相垂直,垂足为点E . ⊙O 的切线BF 与弦AD 的延长线相交于点F ,且AD =3,cos ∠BCD=34. (1)求证:CD ∥BF ; (2)求⊙O 的半径; (3)求弦CD 的长.22.如图,在直角坐标系中,O 为坐标原点. 已知反比例函数y=k xk>0)的图象经过点A (2,m ),过点A 作AB ⊥x 轴于点B ,且△AOB 的面积为12.(1)求k 和m 的值;(2)点C (x ,y )在反比例函数y=k x的图象上,求当1≤x ≤3时函数值y 的取值范围;(3)过原点O 的直线l 与反比例函数y=k x的图象交于P 、Q 两点,试根据图象直接写出线段PQ 长度的最小值.分数段 人数(人)频率 A 48 0.2 B a 0.25 C 84 0.35 D 36 b E120.0512243648607284人数分数段ABCDEBOA FMADOECO CB23.如图1,在等边△ABC 中,点D 是边AC 的中点,点P 是线段DC 上的动点(点P 与点C 不重合),连结BP . 将△ABP 绕点P 按顺时针方向旋转α角(0°<α<180°),得到△A 1B 1P ,连结AA 1,射线AA 1分别交射线PB 、射线B 1B 于点E 、F .(1) 如图1,当0°<α<60°时,在α角变化过程中,△BE F 与△AEP 始终存在 ▲ 关系(填“相似”或“全等”),并说明理由;(2)如图2,设∠ABP =β . 当60°<α<180°时,在α角变化过程中,是否存在△BEF 与△AEP全等?若存在,求出α与β之间的数量关系;若不存在,请说明理由;(3)如图3,当α=60°时,点E 、F 与点B 重合. 已知AB =4,设DP =x ,△A 1BB 1的面积为S ,求S 关于x 的函数关系式.24.已知二次函数的图象经过A (2,0)、C (0,12) 两点,且对称轴为直线x =4. 设顶点为点P ,与x 轴的另一交点为点B .(1)求二次函数的解析式及顶点P 的坐标;(2)如图1,在直线 y=2x 上是否存在点D ,使四边形OPBD 为等腰梯形?若存在,求出点D的坐标;若不存在,请说明理由;(3)如图2,点M 是线段OP 上的一个动点(O 、P 两点除外),以每秒2个单位长度的速度由点P 向点O 运动,过点M 作直线MN ∥N 沿直线MN 对折,得到△P 1MN. 在动点M 的运动过程中,设△P 1MN 与梯形OMNB 的重叠部分的面积为S ,运动时间为t 秒. 求S 关于t 的函数关系式.图1图2图3P B 1FM AD E C CBA 1PB 1FMADECCBA 1 PB 1AD CB A 1O PCBAxy图1图2MOAxPNCBy参考答案和评分细则一、选择题(本题有10小题,每小题3分,共30分)二、填空题(本题有6小题,每小题4分,共24分)11. 2 12. 7 13. 2或8(对一个得2分) 14. 乙 15. 5 16.(1))3-23(, (2分) (2)(2,2)、⎪⎭⎫⎝⎛4521,、⎪⎭⎫ ⎝⎛1611411,、⎪⎭⎫ ⎝⎛2526513, (注:共2分.对一个给0.5分,得2分的要全对,其余有错不倒扣分)三、解答题(本题有8小题,第17~19题每题6分,第20、21题每题8分,第22、23题每题10分,第24题12分,共66分)17. 解:(1)原式=1+22-2 (算对一项或两项给1分,全对2分) ……2分=1+2 …………………………………………………3分(2)2(x +3)=3 (x -2) …………………………………1分解得:x =12 ………………………………………………2分 经检验:x =12是原方程的根 ……………………………3分18. 解:(1)∵四边形ABCD 是平行四边形∴AB =CD AB ∥CD ∴∠BAE =∠FCD 又∵BE ⊥AC DF ⊥AC ∴∠AEB =∠CFD =90°∴△ABE ≌△CDF (AAS )…………………………4分(2)①△ABC ≌△CDA ②△BCE ≌△DAF (每个1分)………………6分19. 解:(1) 2x 50-x (每空1分)………………………2分(2)由题意得:(50-x )(30+2x )=2100 …………………………4分 化简得:x 2-35x +300=0解得:x 1=15, x 2=20……………………………………5分∵该商场为了尽快减少库存,则x =15不合题意,舍去. ∴x =20 答:每件商品降价20元,商场日盈利可达2100元. …………6分20.解:(1) 60 , 0.15 (图略) (每空1分,图1分) …………3分 (2) C ……………………………………………………5分(3)0.8×10440=8352(名)……………………………………7分 答:该市九年级考生中体育成绩为优秀的学生人数约有8352名.……8分21.解:(1)∵BF 是⊙O 的切线 ∴AB ⊥BF ………………………1分 ∵AB ⊥CD∴CD ∥BF ……………………………………………………2分(2)连结BD∵AB 是直径 ∴∠ADB =90°…………………………3分∵∠BCD =∠BAD cos ∠BCD =43…………………4分 ∴cos ∠BAD =43=AB AD 又∵AD =3 ∴AB =4∴⊙O 的半径为2 …………………………………5分(3)∵cos ∠DAE =43=AD AE AD =3∴AE =49 …………6分∴ED =47349322=⎪⎭⎫ ⎝⎛- ………………………7分∴CD =2ED =273 …………………………………8分 22.解:(1)∵A (2,m ) ∴OB =2 AB =m ∴S △AOB =21•OB •AB =21×2×m =21 ∴m =21…………………2分 ∴点A 的坐标为(2,21) 把A (2,21)代入y=x k ,得21=2k∴k =1 ………………………………………………………4分(2)∵当x =1时,y =1;当x =3时,y =31…………………6分 又 ∵反比例函数y =x1在x >0时,y 随x 的增大而减小……………7分 ∴当1≤x ≤3时,y 的取值范围为31≤y ≤1 ………………8分(3) 由图象可得,线段PQ 长度的最小值为22 …………………10分23.解: (1) 相似 …………………………………………………1分由题意得:∠APA 1=∠BPB 1=α AP = A 1P BP =B 1P则 ∠PAA 1 =∠PBB 1 =2902180αα-=- ……………………2分∵∠PBB 1 =∠EBF ∴∠PAE =∠EBF又∵∠BEF =∠AEP∴△BE F ∽△AEP ……………………………………3分 (2)存在,理由如下: ………………………………………4分易得:△BE F ∽△AEP若要使得△BEF ≌△AEP ,只需要满足BE =AE 即可……………5分 ∴∠BAE =∠ABE∵∠BAC =60° ∴∠BAE =30229060-=⎪⎭⎫ ⎝⎛--αα ∵∠ABE =β ∠BAE =∠ABE ………………………6分 ∴βα=- 302即α=2β+60° ……………………7分B(3)连结BD ,交A 1B 1于点G ,过点A 1作A 1H ⊥AC 于点H . ∵∠B 1 A 1P =∠A 1PA =60° ∴A 1B 1∥AC由题意得:AP= A 1 P ∠A =60° ∴△PAA 1是等边三角形∴A 1H=)2(23x + ……………………………8分在Rt △ABD 中,BD =32∴BG =x x 233)2(2332-=+-………………… 9分 ∴x x S BB A 33223342111-=⎪⎪⎭⎫⎝⎛-⨯⨯=∆ (0≤x <2)………10分24.解:(1)设二次函数的解析式为y =ax 2+bx +c由题意得⎪⎪⎩⎪⎪⎨⎧=++==-0241242c b a c a b 解得⎪⎩⎪⎨⎧=-==1281c b a∴二次函数的解析式为y = x 2-8x +12 …………2分 点P 的坐标为(4,-4) ……………………3分(2)存在点D ,使四边形OPBD 为等腰梯形. 理由如下:当y =0时,x 2-8x +12=0 ∴x 1=2 ,则⎩⎨⎧-=+=+4406m k m k 解得⎩⎨⎧-==122m k∴直线BP 的解析式为y =2x -12∴直线OD ∥BP ………………………4分xP 1 MAOBCPN yH DO xAOBCP yPB 1D B A 1H G∵顶点坐标P (4, -4) ∴ OP =42 设D (x ,2x ) 则BD 2=(2x )2+(6-x )2当BD =OP 时,(2x )2+(6-x )2=32解得:x 1=52,x 2=2…………………………6分 当x 2=2时,OD =BP =52,四边形OPBD 为平行四边形,舍去∴当x =52时四边形OPBD 为等腰梯形…………7分 ∴当D (52,54)时,四边形OPBD 为等腰梯形……8分(3)① 当0<t ≤2时,∵运动速度为每秒2个单位长度,运动时间为t 秒, 则MP =2t ∴PH =t ,MH =t ,HN =21t ∴MN =23t ∴S =23t ·t ·21=43t 2 ……………………10分② 当2<t <4时,P 1G =2t -4,P 1H =t ∵MN ∥OB ∴ EF P 1∆∽MN P 1∆∴211)(11H P G P S S MNP EF P =∆∆ ∴ 22)42(431t t t S EF P -=∆∴ EF P S 1∆=3t 2-12t +12∴S =43t 2-(3t 2-12t +12)= -49t 2+12t -12 ∴ 当0<t ≤2时,S=43t 2当2<t <4时,S =-49t 2+12t -12 ……12分xP 1 MA OBCPNG H E F y。

xx学校xx学年xx学期xx试卷姓名:_____________ 年级:____________ 学号:______________题型选择题填空题简答题xx 题xx题xx题总分得分一、xx题(每空xx分,共xx分)试题1:如果向东走记为,则向西走可记为( )A.B.C. D.试题2:绿水青山就是金山银山,为了创造良好的生态生活环境,浙江省2017年清理河湖库塘淤泥约方,数字用科学记数法可以表示为( )A. B. C. D.试题3:有6个相同的立方体搭成的几何体如图所示,则它的主视图是( )评卷人得分AB CD试题4:抛掷一枚质地均匀的立方体骰子一次,骰子的六个面上分别标有数字1,2,3,4,5,6,则朝上一面的数字为2的概率是( )A. B.C.试题5:下面是一位同学做的四道题:①;②;③;④.其中做对的一道题的序号是( )A.①B.② C.③ D.④试题6:如图,一个函数的图象由射线、线段、射线组成,其中点,,,,则此函数(A.当时,随的增大而增大B.当时,随的增大而减小C.当时,随的增大而减小D.当时,随的增大而减小试题7:学校门口的栏杆如图所示,栏杆从水平位置绕点旋转到位置,已知,,垂足分别为,,,,,则栏杆端应下降的垂直距离为( )A. B. C. D.试题8:利用如图1的二维码可以进行身份识别,某校建立了一个身份识别系统,图2是某个学生的识别图案,黑色小正方形表示1,白色小正方形表示0,将第一行数字从左到右依次记为,那么可以转换为该生所在班级序号,其序号为,如图2第一行数字从左到右依次为0,1,0,1,序号为,表示该生为5班学生,表示6班学生的识别图案是( )A BC D试题9:若抛物线与轴两个交点间的距离为2,称此抛物线为定弦抛物线,已知某定弦抛物线的对称轴为直线,将此抛物线向左平移2个单位,再向下平移3个单位,得到的抛物线过点( )A. B. C.D.试题10:某班要在一面墙上同时展示数张形状、大小均相同的矩形绘画作品,将这些作品排成一个矩形(作品不完全重合),现需要在每张作品的四个角落都钉上图钉,如果作品有角落相邻,那么相邻的角落共享一枚图钉(例如,用9枚图钉将4张作品钉在墙上,如图),若有34枚图钉可供选用,则最多可以展示绘画作品( )A.16张B.18张C.20张D.21张[试题11:因式分解:______________试题12:我国明代数字读本《算法统宗》一书中有这样一道题:一支竿子一条索,索比竿子长一托,对折索子来量竿,却比竿子短一托,如果1托为5尺,那么索长为________尺,竿子长为___________尺.试题13:如图,公园内有一个半径为20米的圆形草坪,,是圆上的点,为圆心,,从到只有路,一部分市民为走“捷径”,踩坏了花草,走出了一条小路.通过计算可知,这些市民其实仅仅少走了____________步(假设1步为米,结果保留整数).(参考数据:,取)试题14:.等腰三角形中,顶角为,点在以为圆心,长为半径的圆上,且,则的度数为______________.试题15:过双曲线上的动点作轴于点,是直线上的点,且满足,过点作轴的平行线交此双曲线于点.如果的面积为8,则的值是________________.试题16:实验室里有一个水平放置的长方体容器,从内部量得它的高是,底面的长是,宽是,容器内的水深为,现往容器内放入如图的长方体实心铁块(铁块一面平放在容器底面),过顶点的三条棱的长分别是、、(),当铁块的顶部高出水面时,满足的关系式是_____________.试题17:计算:.试题18:解方程:.试题19:为了解某地区机动车拥有量对道路通行的影响,学校九年级社会实践小组对2010年~2017年机动车拥有量、车辆经过人民路路口和学校门口的堵车次数进行调查统计,并绘制成下列统计图:根据统计图,回答下列问题:(1) 写出2016年机动车的拥有量,分别计算2010年~2017年在人民路路口和学校门口堵车次数的平均数;(2) 根据统计数据,结合生活实际,对机动车拥有量与人民路路口和学校门口堵车次数,说说你的看法.试题20:一辆汽车行驶时的耗油量为升/千米,如图是油箱剩余油量(升)关于加满油后已行驶的路程(千米)的函数图象(1)根据图象,直接写出汽车行驶400千米时,油箱内的剩余油量,并计算加满油时油箱的油量.(2)求关于的函数关系式,并计算该汽车在剩余油量5升时,已行驶的路程.试题21:学校拓展小组研制了绘图智能机器人(如图1),顺次输入点,,的坐标,机器人能根据图2,绘制图形.若图形是线段,求出线段的长度;若图形是抛物线,求出抛物线的解析式.请根据以下点的坐标,求出线段的长度或抛物线的函数关系式.(1),,;(2),,.试题22:.如图1,窗框和窗扇用“滑块铰链”连接,图3是图2中“滑块铰链”的平面示意图,滑轨安装在窗框上,托悬臂安装在窗扇上,交点处装有滑块,滑块可以左右滑动,支点,,始终在一直线上,延长交于点.已知,,.(1)窗扇完全打开,张角,求此时窗扇与窗框的夹角的度数.(2)窗扇部分打开,张角,求此时点,之间的距离(精确到).(参考数据:,)试题23:数学课上,张老师举了下面的例题:例1 等腰三角形中,,求的度数.(答案:)例2 等腰三角形中,,求的度数.(答案:或或)张老师启发同学们进行变式,小敏编了如下一题:变式等腰三角形中,,求的度数.(1) 请你解答以上的变式题(2) 解(1)后,小敏发现,的度数不同,得到的度数的个数也可能不同,如果在等腰三角形中,设,当有三个不同的度数时,请你探索的取值范围.试题24:小敏思考解决如下问题:原题:如图1,点,分别在菱形的边,上,,求证:.[来源~:中&*^@教网](1) 小敏进行探索,若将点,的位置特殊化,把绕点旋转得到,使,点分别在边上,如图2,此时她证明了.请你证明.(2) 受以上(1)的启发,在原题中,添加辅助线:如图3,作,,垂足分别为,请你继续完成原题的证明.(3) 如果在原题中添加条件:,,如图1,请你编制一个计算题(不标注新的字母),并直线给出答案.试题1答案:C试题2答案:B试题3答案:D试题4答案:A试题5答案:C试题6答案:A试题7答案:C试题8答案:B试题9答案:B试题10答案:B试题11答案:试题12答案:试题13答案:[试题14答案:试题15答案:或试题16答案:12或4试题17答案:或试题18答案:原式.试题19答案:,,.试题20答案:解:(1)万辆.人民路路口的堵车次数平均数为120(次).学校门口的堵车次数平均数为(次)(2)不唯一,如:2010年~2013年,随着机动车拥有量的增加,对道路的影响加大,年堵车次数也增加,尽管2017年机动车拥有量比2016年增加,由于进行了交通综合治理,人民路路口堵车次数反而降低.试题21答案:解:(1)汽车行驶400千米,剩余油量30升,加满油时,油量为70升.(2)设,把点,坐标分别代入得,,∴,当时,,即已行驶的路程为650千米.试题22答案:解:(1)∵,,,∴绘制线段,.(2)∵,,,.∴绘制抛物线,设,把点坐标代入得∴,即.试题23答案:解:(1)∵,,∴四边形是平行四边形,∴∴.(2)如图,过点作于点.∵,∴,,∵,,∴在中,,∴.试题24答案:解:(1)当为顶角,则,当为底角,若为顶角,则,若为底角,则.∴或或.(2)分两种情况:①当时,只能为顶角,∴的度数只有一个.②当时,若为顶角,则,若为底角,则或,当且,且,即时,有三个不同的度数.综上①②,当且时,有三个不同的度数. 23.解:(1)如图1,在菱形中,,,,∵,∴,∴,∵,∴,∴,,∴.∴.(2)如图2,由(1),∵,∴,∵,,∴,∵,∴,∴.(3)不唯一,举例如下:层次1:①求的度数,答案:.②分别求,的度数.答案:.③求菱形的周长.答案:16.④分别求的长.答案:.层次2:①求的值.答案:4.②求的值.答案:4.③求的值.答案:.层次3:①求四边形的面积.答案:.②求与的面积和.答案:.③求四边形的周长的最小值.答案:.④求中点运动的路径长.答案:.24.解:(1)第一班上行车到站用时小时.第一班下行车到站用时小时.(2)当时,.当时,.(3)由(2)知同时出发的一对上、下行车的位置关于中点对称,设乘客到达站总时间为分钟,[来源:中国*^&教育@#出版网]当时,往站用时30分钟,还需再等下行车5分钟,,不合题意当时,只能往站坐下行车,他离站千米,则离他右边最近的下行车离站也是千米,这辆下行车离千米.如果能乘上右侧第一辆下行车,,,∴,,∴符合题意.如果乘不上右侧第一辆下行车,只能乘右侧第二辆下行车,,,,∴,,∴符合题意.如果乘不上右侧第二辆下行车,只能乘右侧第三辆下行车,,,,∴,,不合题意.∴综上,得.当时,乘客需往站乘坐下行车,离他左边最近的下行车离站是千米,离他右边最近的下行车离站也是千米.如果乘上右侧第一辆下行车,,∴,不合题意.如果乘不上右侧第一辆下行车,只能乘右侧第二辆下行车,,,,∴,,∴符合题意.如果乘不上右侧第二辆下行车,只能乘右侧第三辆下行车,,,,,∴不合题意.∴综上,得.综上所述,,或.。

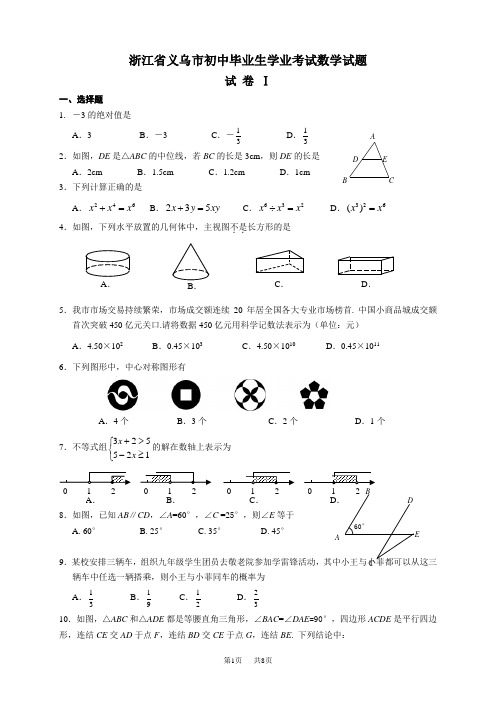
一、选择题(本题有10小题,每小题3分,共30分,请选出各题中一个符合题的正确选项)1.下列各组数中,互为相反数是( ▲ )A .3和31 B .3和-3 C .3和-13 D .-3和-13 【答案】B【解析】试题分析:只有符号不同的两个数,我们称这两个数互为相反数.考点:相反数的定义.2.如图,直线AB ∥CD ,∠A =70︒,∠C =40︒,则∠E 等于( )A.30°B. 40°C. 60°D. 70°【答案】A【解析】试题分析:根据平行线的性质可得:∠A=∠C+∠E ,则∠E=30°.考点:平行线的性质3.某市五月份连续五天的日最高气温分别为23、20、20、21、26(单位:°C ),这组数据的中位数和众数分别是( )A. 22°C ,26°CB. 22°C ,20°CC. 21°C ,26°CD. 21°C ,20°C【答案】D【解析】试题分析:根据这组数据可得中位数为21℃,众数为20℃.考点:(1)、中位数的求法;(2)、众数的求法4.不等式组⎩⎨⎧≥->+0101x x 的解集是( )A. 11≤<xB. 11≤<-xC. 1≥xD. 1->x【答案】C【解析】试题分析:首先求出每个不等式的解,然后得出不等式组的解.解不等式①得:x >-1,解不等式②得:x ≥1,则不等式组的解为x ≥1.考点:不等式组的解集.5.在水平的讲台上放置圆柱形水杯和长方体形粉笔盒(右图),则它的主视图是( )A .图①B .图②C .图③D .图④【答案】B【解析】试题分析:根据三视图的法则可得图②为主视图,图③为俯视图,图④为左视图.考点:三视图.6.若反比例函数(0)k y k x =≠的图象经过点(21)-,,则这个函数的图象一定经过点( ) A .122⎛⎫- ⎪⎝⎭,B .(12),C .112⎛⎫- ⎪⎝⎭,D .(12)-,【答案】D【解析】试题分析:根据反比例函数的性质可得:k=-2,则点D 一定在反比例函数图象上.考点:反比例函数的性质.7.一个圆形人工湖如图所示,弦AB 是湖上的一座桥.已知桥AB 长100m ,测得∠ACB=45°.则 这个人工湖的直径AD 为 ( )A .m B .m C .m D .m 图④图③图②图①实物图【答案】B【解析】试题分析:连接OB ,根据∠ACB=45°可得∠AOB=90°,则△AOB 为等腰直角三角形,根据AB=100m 可得:m ,则m.考点:圆的基本性质8.一把大遮阳伞,伞面撑开时可近似地看成是圆锥形,如图,它的母线长是2. 5米,底面半径为 2米,则做这把遮阳伞需用布料的面积是( )平方米(接缝不计)A.3πB.4πC.5πD.254p【答案】C【解析】试题分析:圆锥的侧面积=πrl=2×2.5π=5π.考点:圆锥的侧面积计算.9.如图是有关x 的代数式的方阵,若第10行第2项的值为1034,则此时x 的值为( )A. 10B. 1C. 5D. 2【答案】D【解析】试题分析:根据方阵可得第10行第2项的数为512x+10,则512x+10=1034,解得:x=2.第7题图考点:规律题.10.已知△ABC 中,D,E 分别是AC,AB 边上的中点,BD ⊥CE 与点F ,CE=2,BD=4,则△ABC 的面积为( ) A.163B .8C .4D .6【答案】A【解析】考点:三角形相似的应用.二、填空题(本题有6小题,每题4分,共24分)11.函数1-=x y 中自变量x 的取值范围是 .【答案】x ≥1【解析】试题分析:二次根式的被开方数为非负数,则x -1≥0,解得:x ≥1.考点:函数自变量的取值范围.12.分解因式:34x y xy -= .【答案】xy(x+2)(x -2)【解析】试题分析:首先提取公因式,然后利用平方差公式进行因式分解.原式=xy(2x -4)=xy(x+2)(x -2). 考点:因式分解13.如图,在ΔABC 中,M 、N 分别是AB 、AC 的中点,且∠A +∠B=136°,则∠ANM= °【答案】44°【解析】试题分析:根据中点可得:MN ∥BC ,则∠AMN=∠B ,∠ANM=∠C ,根据题意可得:∠C=44°,则∠ANM=44°. 考点:三角形中位线的性质14.除颜色外完全相同的五个球上分别标有1,2,3,4,5五个数字,装入一个不透明的口袋内搅匀.从口袋内任摸一球记下数字后放回.搅匀后再从中任摸一球,则摸到的两个球上数字和为5的概率是 【答案】425【解析】试题分析:首先根据题意得出所有可能出现的结果,然后根据概率的计算法则得出概率.考点:概率的计算.15.(2012扬州)如图,将矩形ABCD 沿CE 折叠,点B 恰好落在 边AD 的F 处.若23AB BC ,则tan ∠DCF 的值是_________.【解析】试题分析:设AB=CD=2x ,则BC=AD=3x ,根据折叠可得CF=BC=3x ,根据Rt △DCF 的勾股定理得出,则tan ∠DCF=DF DC . 考点:折叠图形的性质.16.(原创题)已知平面直角坐标系中,O 为坐标原点,点A 坐标为(0,8),点B 坐标为(4,0),点E 是直线y=x+4上的一个动点,若∠EAB=∠ABO ,则点E 的坐标为 。


2016年数学中考试题及答案【篇一:2016年全国中考数学模拟卷及答案】=txt>数学试卷一、选择题下面各题均有四个选项,其中只有一个是符合题意的。
..1.截止到2016年6月1日,北京市已建成39个地下调蓄设施,蓄水能力达到2 40 000立方平米。
将1240 000用科学记数法表示应为2.实数a,b,c,d在数轴上的对应点的位置如图所示,这四个数中,绝对值最大的是a.a b.bc.cd.d3.一个不透明的盒子中装有3个红球,2个黄球和1个绿球,这些球除了颜色外无其他差别,从中随机摸出一个小球,恰好是黄球的概率为 a. b. c. d.4.剪纸是我国传统的民间艺术,下列剪纸作品中,是轴对称图形的为6.如图,公路ac,bc互相垂直,公路ab的中点m与点c被湖隔开,若测得am的长为1.2km,则m,c两点间的距离为a.0.5km b.0.6km c.0.9km d.1.2km7.某市6月份日平均气温统计如图所示,则在日平均气温这组数据中,众数和中位数分别是 a.21,21 b.21,21.5 c.21,22 d.22,228.右图是利用平面直角坐标系画出的故宫博物院的主要建筑分布图。
若这个坐标系分别以正东、正北方向为x轴、y轴的正方向。
表示太和门的点坐标为(0,-1),表示九龙壁的点的坐标为(4,1),则表示下列宫殿的点的坐标正确的是a.景仁宫(4,2)b.养心殿(-2,3) c.保和殿(1,0) d.武英殿(-3.5,-4)9.一家游泳馆的游泳收费标准为30元/次,若购买会员年卡,可享受如下优惠:a.购买a类会员年卡b.购买b类会员年卡 c.购买c类会员年卡d.不购买会员年卡10.一个寻宝游戏的寻宝通道如图1所示,通道由在同一平面内的ab,bc,ca,oa,ob,oc组成。
为记录寻宝者的进行路线,在bc的中点m处放置了一台定位仪器,设寻宝者行进的时间为x,寻宝者与定位仪器之间的距离为y,若寻宝者匀速行进,且表示y与x的函数关系的图象大致如图2所示,则寻宝者的行进路线可能为a.a→o→bb.b→a→cc.b→o→c d.c→b→o 二、填空题11.分解因式:5x2-10x2=5x=_________.12.右图是由射线ab,bc,cd,de,组成的平面图形,则∠1+∠2+∠3+∠4+∠5=_____.13.《九章算术》是中国传统数学最重要的著作,奠定了中国传统数学的基本框架。
浙江省金华市义乌市中考数学试卷一、选择题(本大题共10小题,每小题4分,共40分)1.(4分)﹣5的相反数是()A .B.5 C .﹣D.﹣52.(4分)研究表明,可燃冰是一种替代石油的新型清洁能源,在我国某海域已探明的可燃冰存储量达150000000000立方米,其中数字150000000000用科学记数法可表示为()A.15×1010B.0.15×1012C.1.5×1011D.1.5×10123.(4分)如图的几何体由五个相同的小正方体搭成,它的主视图是()A .B .C .D .4.(4分)在一个不透明的袋子中装有4个红球和3个黑球,它们除颜色外其他均相同,从中任意摸出一个球,则摸出黑球的概率是()A .B .C .D .5.(4分)下表记录了甲、乙、丙、丁四名射击运动员最近几次选拔赛成绩的平均数和方差:根据表中数据,要从中选择一名成绩好且发挥稳定的运动员参加比赛,应选择()A.甲B.乙C.丙D.丁6.(4分)如图,小巷左右两侧是竖直的墙,一架梯子斜靠在左墙时,梯子底端到左墙角的距离为0.7米,顶端距离地面2.4米,如果保持梯子底端位置不动,将梯子斜靠在右墙时,顶端距离地面2米,则小巷的宽度为()A.0.7米B.1.5米C.2.2米D.2.4米7.(4分)均匀地向一个容器注水,最后把容器注满,在注水过程中,水面高度h随时间t的变化规律如图所示(图中OABC为折线),这个容器的形状可以是()A.B.C.D.8.(4分)在探索“尺规三等分角”这个数学名题的过程中,曾利用了如图.该图中,四边形ABCD是矩形,E是BA延长线上一点,F是CE上一点,∠ACF=∠AFC,∠FAE=∠FEA.若∠ACB=21°,则∠ECD的度数是()A.7°B.21°C.23°D.24°9.(4分)矩形ABCD的两条对称轴为坐标轴,点A的坐标为(2,1).一张透明纸上画有一个点和一条抛物线,平移透明纸,使这个点与点A重合,此时抛物线的函数表达式为y=x2,再次平移透明纸,使这个点与点C重合,则该抛物线的函数表达式变为()A.y=x2+8x+14 B.y=x2﹣8x+14 C.y=x2+4x+3 D.y=x2﹣4x+310.(4分)一块竹条编织物,先将其按如图所示绕直线MN翻转180°,再将它按逆时针方向旋转90°,所得的竹条编织物是()A.B.C.D.二、填空题(本大题共6小题,每小题5分,共30分)11.(5分)分解因式:x2y﹣y= .12.(5分)如图,一块含45°角的直角三角板,它的一个锐角顶点A在⊙O上,边AB,AC分别与⊙O交于点D,E,则∠DOE的度数为.13.(5分)如图,Rt△ABC的两个锐角顶点A,B在函数y=(x>0)的图象上,AC ∥x轴,AC=2,若点A的坐标为(2,2),则点B的坐标为.14.(5分)如图为某城市部分街道示意图,四边形ABCD为正方形,点G在对角线BD 上,GE⊥CD,GF⊥BC,AD=1500m,小敏行走的路线为B→A→G→E,小聪行走的路线为B→A→D→E→F.若小敏行走的路程为3100m,则小聪行走的路程为m.15.(5分)以Rt△ABC的锐角顶点A为圆心,适当长为半径作弧,与边AB,AC各相交于一点,再分别以这两个交点为圆心,适当长为半径作弧,过两弧的交点与点A作直线,与边BC交于点D.若∠ADB=60°,点D到AC的距离为2,则AB的长为.16.(5分)如图,∠AOB=45°,点M,N在边OA上,OM=x,ON=x+4,点P是边OB上的点,若使点P,M,N构成等腰三角形的点P恰好有三个,则x的值是.三、解答题(本大题共8小题,共80分)17.(8分)(1)计算:(2﹣π)0+|4﹣3|﹣.(2)解不等式:4x+5≤2(x+1)18.(8分)某市规定了每月用水18立方米以内(含18立方米)和用水18立方米以上两种不同的收费标准,该市的用户每月应交水费y(元)是用水量x(立方米)的函数,其图象如图所示.(1)若某月用水量为18立方米,则应交水费多少元?(2)求当x>18时,y关于x的函数表达式,若小敏家某月交水费81元,则这个月用水量为多少立方米?19.(8分)为了解本校七年级同学在双休日参加体育锻炼的时间,课题小组进行了问卷调查(问卷调查表如图所示),并用调查结果绘制了图1,图2两幅统计图(均不完整),请根据统计图解答以下问题:(1)本次接受问卷调查的同学有多少人?补全条形统计图.(2)本校有七年级同学800人,估计双休日参加体育锻炼时间在3小时以内(不含3小时)的人数.20.(8分)如图,学校的实验楼对面是一幢教学楼,小敏在实验楼的窗口C测得教学楼顶部D的仰角为18°,教学楼底部B的俯角为20°,量得实验楼与教学楼之间的距离AB=30m.(1)求∠BCD的度数.(2)求教学楼的高BD.(结果精确到0.1m,参考数据:tan20°≈0.36,tan18°≈0.32)21.(10分)某农场拟建一间矩形种牛饲养室,饲养室的一面靠现有墙(墙足够长),已知计划中的建筑材料可建围墙的总长为50m.设饲养室长为x(m),占地面积为y(m2).(1)如图1,问饲养室长x为多少时,占地面积y最大?(2)如图2,现要求在图中所示位置留2m宽的门,且仍使饲养室的占地面积最大,小敏说:“只要饲养室长比(1)中的长多2m就行了.”请你通过计算,判断小敏的说法是否正确.22.(12分)定义:有一组邻边相等,并且它们的夹角是直角的凸四边形叫做等腰直角四边形.(1)如图1,等腰直角四边形ABCD,AB=BC,∠ABC=90°,①若AB=CD=1,AB∥CD,求对角线BD的长.②若AC⊥BD,求证:AD=CD,(2)如图2,在矩形ABCD中,AB=5,BC=9,点P是对角线BD上一点,且BP=2PD,过点P作直线分别交边AD,BC于点E,F,使四边形ABFE是等腰直角四边形,求AE的长.23.(12分)已知△ABC,AB=AC,D为直线BC上一点,E为直线AC上一点,AD=AE,设∠BAD=α,∠CDE=β.(1)如图,若点D在线段BC上,点E在线段AC上.①如果∠ABC=60°,∠ADE=70°,那么α=°,β=°,②求α,β之间的关系式.(2)是否存在不同于以上②中的α,β之间的关系式?若存在,求出这个关系式(求出一个即可);若不存在,说明理由.24.(14分)如图1,已知▱ABCD,AB∥x轴,AB=6,点A的坐标为(1,﹣4),点D 的坐标为(﹣3,4),点B在第四象限,点P是▱ABCD边上的一个动点.(1)若点P在边BC上,PD=CD,求点P的坐标.(2)若点P在边AB,AD上,点P关于坐标轴对称的点Q落在直线y=x﹣1上,求点P的坐标.(3)若点P在边AB,AD,CD上,点G是AD与y轴的交点,如图2,过点P作y轴的平行线PM,过点G作x轴的平行线GM,它们相交于点M,将△PGM沿直线PG翻折,当点M的对应点落在坐标轴上时,求点P的坐标.(直接写出答案)浙江省金华市义乌市中考数学试卷参考答案与试题解析一、选择题(本大题共10小题,每小题4分,共40分)1.(4分)(•绍兴)﹣5的相反数是()A.B.5 C.﹣D.﹣5【解答】解:﹣5的相反数是5,故选:B.2.(4分)(•绍兴)研究表明,可燃冰是一种替代石油的新型清洁能源,在我国某海域已探明的可燃冰存储量达150000000000立方米,其中数字150000000000用科学记数法可表示为()A.15×1010B.0.15×1012C.1.5×1011D.1.5×1012【解答】解:150000000000=1.5×1011,故选:C.3.(4分)(•绍兴)如图的几何体由五个相同的小正方体搭成,它的主视图是()A.B.C.D.【解答】解:从正面看第一层是三个小正方形,第二层左边一个小正方形,故选:A.4.(4分)(•绍兴)在一个不透明的袋子中装有4个红球和3个黑球,它们除颜色外其他均相同,从中任意摸出一个球,则摸出黑球的概率是()A.B.C.D.【解答】解:∵在一个不透明的袋子中装有除颜色外其他均相同的4个红球和3个黑球,∴从中任意摸出一个球,则摸出黑球的概率是.故选B.5.(4分)(•绍兴)下表记录了甲、乙、丙、丁四名射击运动员最近几次选拔赛成绩的平均数和方差:根据表中数据,要从中选择一名成绩好且发挥稳定的运动员参加比赛,应选择()A.甲B.乙C.丙D.丁【解答】解:丁的平均数最大,方差最小,成绩最稳当,所以选丁运动员参加比赛.故选D.6.(4分)(•绍兴)如图,小巷左右两侧是竖直的墙,一架梯子斜靠在左墙时,梯子底端到左墙角的距离为0.7米,顶端距离地面2.4米,如果保持梯子底端位置不动,将梯子斜靠在右墙时,顶端距离地面2米,则小巷的宽度为()A.0.7米B.1.5米C.2.2米D.2.4米【解答】解:在Rt△ACB中,∵∠ACB=90°,BC=0.7米,AC=2.4米,∴AB2=0.72+2.42=6.25.在Rt△A′BD中,∵∠A′DB=90°,A′D=2米,BD2+A′D2=A′B′2,∴BD2+22=6.25,∴BD2=2.25,∵BD>0,∴BD=1.5米,∴CD=BC+BD=0.7+1.5=2.2米.故选C.7.(4分)(•绍兴)均匀地向一个容器注水,最后把容器注满,在注水过程中,水面高度h随时间t的变化规律如图所示(图中OABC为折线),这个容器的形状可以是()A.B.C.D.【解答】解:注水量一定,函数图象的走势是稍陡,平,陡;那么速度就相应的变化,跟所给容器的粗细有关.则相应的排列顺序就为D.故选:D.8.(4分)(•绍兴)在探索“尺规三等分角”这个数学名题的过程中,曾利用了如图.该图中,四边形ABCD是矩形,E是BA延长线上一点,F是CE上一点,∠ACF=∠AFC,∠FAE=∠FEA.若∠ACB=21°,则∠ECD的度数是()A.7°B.21°C.23°D.24°【解答】解:∵四边形ABCD是矩形,∴∠D=90°,AB∥CD,AD∥BC,∴∠FEA=∠ECD,∠DAC=∠ACB=21°,∵∠ACF=∠AFC,∠FAE=∠FEA,∴∠ACF=2∠FEA,设∠ECD=x,则∠ACF=2x,∴∠ACD=3x,在Rt△ACD中,3x+21°=90°,解得:x=23°;故选:C.9.(4分)(•绍兴)矩形ABCD的两条对称轴为坐标轴,点A的坐标为(2,1).一张透明纸上画有一个点和一条抛物线,平移透明纸,使这个点与点A重合,此时抛物线的函数表达式为y=x2,再次平移透明纸,使这个点与点C重合,则该抛物线的函数表达式变为()A.y=x2+8x+14 B.y=x2﹣8x+14 C.y=x2+4x+3 D.y=x2﹣4x+3【解答】解:∵矩形ABCD的两条对称轴为坐标轴,∴矩形ABCD关于坐标原点对称,∵A点C点是对角线上的两个点,∴A点、C点关于坐标原点对称,∴C点坐标为(﹣2,﹣1);∴抛物线由A点平移至C点,向左平移了4个单位,向下平移了2个单位;∵抛物线经过A点时,函数表达式为y=x2,∴抛物线经过C点时,函数表达式为y=(x+4)2﹣2=x2+8x+14,故选A.10.(4分)(•绍兴)一块竹条编织物,先将其按如图所示绕直线MN翻转180°,再将它按逆时针方向旋转90°,所得的竹条编织物是()A.B.C.D.【解答】解:先将其按如图所示绕直线MN翻转180°,再将它按逆时针方向旋转90°,所得的竹条编织物是B,故选B.二、填空题(本大题共6小题,每小题5分,共30分)11.(5分)(•绍兴)分解因式:x2y﹣y= y(x+1)(x﹣1).【解答】解:x2y﹣y,=y(x2﹣1),=y(x+1)(x﹣1),故答案为:y(x+1)(x﹣1).12.(5分)(•绍兴)如图,一块含45°角的直角三角板,它的一个锐角顶点A在⊙O 上,边AB,AC分别与⊙O交于点D,E,则∠DOE的度数为90°.【解答】解:∵∠A=45°,∴∠DOE=2∠A=90°.故答案为:90°.13.(5分)(•绍兴)如图,Rt△ABC的两个锐角顶点A,B在函数y=(x>0)的图象上,AC∥x轴,AC=2,若点A的坐标为(2,2),则点B的坐标为(4,1).【解答】解:∵点A(2,2)在函数y=(x>0)的图象上,∴2=,得k=4,∵在Rt△ABC中,AC∥x轴,AC=2,∴点B的横坐标是4,∴y==1,∴点B的坐标为(4,1),故答案为:(4,1).14.(5分)(•绍兴)如图为某城市部分街道示意图,四边形ABCD为正方形,点G在对角线BD上,GE⊥CD,GF⊥BC,AD=1500m,小敏行走的路线为B→A→G→E,小聪行走的路线为B→A→D→E→F.若小敏行走的路程为3100m,则小聪行走的路程为4600 m.【解答】解:连接GC,∵四边形ABCD为正方形,所以AD=DC,∠ADB=∠CDB=45°,∵∠CDB=45°,GE⊥DC,∴△DEG是等腰直角三角形,∴DE=GE.在△AGD和△GDC中,∴△AGD≌△GDC∴AG=CG在矩形GECF中,EF=CG,∴EF=AG.∵BA+AD+DE+EF﹣BA﹣AG﹣GE=AD=1500m.∵小敏共走了3100m,∴小聪行走的路程为3100+1500=4600(m)故答案为:460015.(5分)(•绍兴)以Rt△ABC的锐角顶点A为圆心,适当长为半径作弧,与边AB,AC各相交于一点,再分别以这两个交点为圆心,适当长为半径作弧,过两弧的交点与点A 作直线,与边BC交于点D.若∠ADB=60°,点D到AC的距离为2,则AB的长为2.【解答】解:如图,作DE⊥AC于E.由题意AD平分∠BAC,∵DB⊥AB,DE⊥AC,∴DB=DE=2,在Rt△ADB中,∵∠B=90°,∠BDA=60°,BD=2,∴AB=BD•tan60°=2,故答案为216.(5分)(•绍兴)如图,∠AOB=45°,点M,N在边OA上,OM=x,ON=x+4,点P 是边OB上的点,若使点P,M,N构成等腰三角形的点P恰好有三个,则x的值是x=0或x=4﹣4或4<x<4.【解答】解:分三种情况:①如图1,当M与O重合时,即x=0时,点P恰好有三个;②如图2,以M为圆心,以4为半径画圆,当⊙M与OB相切时,设切点为C,⊙M与OA交于D,∴MC⊥OB,∵∠AOB=45°,∴△MCO是等腰直角三角形,∴MC=OC=4,∴OM=4,当M与D重合时,即x=OM﹣DM=4﹣4时,同理可知:点P恰好有三个;③如图3,取OM=4,以M为圆心,以OM为半径画圆,则⊙M与OB除了O外只有一个交点,此时x=4,即以∠PMN为顶角,MN为腰,符合条件的点P有一个,以N圆心,以MN为半径画圆,与直线OB相离,说明此时以∠PNM为顶角,以MN为腰,符合条件的点P不存在,还有一个是以NM为底边的符合条件的点P;点M沿OA运动,到M1时,发现⊙M1与直线OB有一个交点;∴当4<x<4时,圆M在移动过程中,则会与OB除了O外有两个交点,满足点P 恰好有三个;综上所述,若使点P,M,N构成等腰三角形的点P恰好有三个,则x的值是:x=0或x=4﹣4或4.故答案为:x=0或x=4﹣4或4.三、解答题(本大题共8小题,共80分)17.(8分)(•绍兴)(1)计算:(2﹣π)0+|4﹣3|﹣.(2)解不等式:4x+5≤2(x+1)【解答】解:(1)原式=1=﹣3;(2)去括号,得4x+5≤2x+2移项合并同类项得,2x≤﹣3解得x.18.(8分)(•绍兴)某市规定了每月用水18立方米以内(含18立方米)和用水18立方米以上两种不同的收费标准,该市的用户每月应交水费y(元)是用水量x(立方米)的函数,其图象如图所示.(1)若某月用水量为18立方米,则应交水费多少元?(2)求当x>18时,y关于x的函数表达式,若小敏家某月交水费81元,则这个月用水量为多少立方米?【解答】解:(1)由纵坐标看出,某月用水量为18立方米,则应交水费18元;(2)由81元>45元,得用水量超过18立方米,设函数解析式为y=kx+b (x≥18),∵直线经过点(18,45)(28,75),∴,解得,∴函数的解析式为y=3x﹣9 (x≥18),当y=81时,3x﹣9=81,解得x=30,答:这个月用水量为30立方米.19.(8分)(•绍兴)为了解本校七年级同学在双休日参加体育锻炼的时间,课题小组进行了问卷调查(问卷调查表如图所示),并用调查结果绘制了图1,图2两幅统计图(均不完整),请根据统计图解答以下问题:(1)本次接受问卷调查的同学有多少人?补全条形统计图.(2)本校有七年级同学800人,估计双休日参加体育锻炼时间在3小时以内(不含3小时)的人数.【解答】解:(1)40÷25%=160(人)答:本次接受问卷调查的同学有160人;D组人数为:160×18.75%=30(人)统计图补全如图:(2)800×=600(人)答:估计双休日参加体育锻炼时间在3小时以内(不含3小时)的人数为600人.20.(8分)(•绍兴)如图,学校的实验楼对面是一幢教学楼,小敏在实验楼的窗口C 测得教学楼顶部D的仰角为18°,教学楼底部B的俯角为20°,量得实验楼与教学楼之间的距离AB=30m.(1)求∠BCD的度数.(2)求教学楼的高BD.(结果精确到0.1m,参考数据:tan20°≈0.36,tan18°≈0.32)【解答】解:(1)过点C作CE⊥BD,则有∠DCE=18°,∠BCE=20°,∴∠BCD=∠DCE+∠BCE=18°+20°=38°;(2)由题意得:CE=AB=30m,在Rt△CBE中,BE=CE•tan20°≈10.80m,在Rt△CDE中,DE=CD•tan18°≈9.60m,∴教学楼的高BD=BE+DE=10.80+9.60≈20.4m,则教学楼的高约为20.4m.21.(10分)(•绍兴)某农场拟建一间矩形种牛饲养室,饲养室的一面靠现有墙(墙足够长),已知计划中的建筑材料可建围墙的总长为50m.设饲养室长为x(m),占地面积为y(m2).(1)如图1,问饲养室长x为多少时,占地面积y最大?(2)如图2,现要求在图中所示位置留2m宽的门,且仍使饲养室的占地面积最大,小敏说:“只要饲养室长比(1)中的长多2m就行了.”请你通过计算,判断小敏的说法是否正确.【解答】解:(1)∵y=x•=﹣(x﹣25)2+,∴当x=25时,占地面积最大,即饲养室长x为25m时,占地面积y最大;(2)∵y=x•=﹣(x﹣26)2+338,∴当x=26时,占地面积最大,即饲养室长x为26m时,占地面积y最大;∵26﹣25=1≠2,∴小敏的说法不正确.22.(12分)(•绍兴)定义:有一组邻边相等,并且它们的夹角是直角的凸四边形叫做等腰直角四边形.(1)如图1,等腰直角四边形ABCD,AB=BC,∠ABC=90°,①若AB=CD=1,AB∥CD,求对角线BD的长.②若AC⊥BD,求证:AD=CD,(2)如图2,在矩形ABCD中,AB=5,BC=9,点P是对角线BD上一点,且BP=2PD,过点P作直线分别交边AD,BC于点E,F,使四边形ABFE是等腰直角四边形,求AE的长.【解答】解:(1)①∵AB=AC=1,AB∥CD,∴S四边形ABCD是平行四边形,∵AB=BC,∴四边形ABCD是菱形,∵∠ABC=90°,∴四边形ABCD是正方形,∴BD=AC==.(2)如图1中,连接AC、BD.∵AB=BC,AC⊥BD,∴∠ABD=∠CBD,∵BD=BD,∴△ABD≌△CBD,∴AD=CD.(2)若EF⊥BC,则AE≠EF,BF≠EF,∴四边形ABFE表示等腰直角四边形,不符合条件.若EF与BC不垂直,①当AE=AB时,如图2中,此时四边形ABFE是等腰直角四边形,∴AE=AB=5.②当BF=AB时,如图3中,此时四边形ABFE是等腰直角四边形,∴BF=AB=5,∵DE∥BF,∴DE:BF=PD:PB=1:2,∴DE=2.5,∴AE=9﹣2.5=6.5,综上所述,满足条件的AE的长为5或6.5.23.(12分)(•绍兴)已知△ABC,AB=AC,D为直线BC上一点,E为直线AC上一点,AD=AE,设∠BAD=α,∠CDE=β.(1)如图,若点D在线段BC上,点E在线段AC上.①如果∠ABC=60°,∠ADE=70°,那么α=20 °,β=10 °,②求α,β之间的关系式.(2)是否存在不同于以上②中的α,β之间的关系式?若存在,求出这个关系式(求出一个即可);若不存在,说明理由.【解答】解:(1)①∵AB=AC,∠ABC=60°,∴∠BAC=60°,∵AD=AE,∠ADE=70°,∴∠DAE=180°﹣2∠ADE=40°,∴α=∠BAD=60°﹣40°=20°,∴∠ADC=∠BAD+∠ABD=60°+20°=80°,∴β=∠CDE=∠ADC﹣∠ADE=10°,故答案为:20,10;②设∠ABC=x,∠AED=y,∴∠ACB=x,∠AED=y,在△DEC中,y=β+x,在△ABD中,α+x=y+β=β+x+β,∴α=2β;(2)①当点E在CA的延长线上,点D在线段BC上,如图1设∠ABC=x,∠ADE=y,∴∠ACB=x,∠AED=y,在△ABD中,x+α=β﹣y,在△DEC中,x+y+β=180°,∴α=2β﹣180°,②当点E在CA的延长线上,点D在CB的延长线上,如图2,同①的方法可得α=180°﹣2β.24.(14分)(•绍兴)如图1,已知▱ABCD,AB∥x轴,AB=6,点A的坐标为(1,﹣4),点D的坐标为(﹣3,4),点B在第四象限,点P是▱ABCD边上的一个动点.(1)若点P在边BC上,PD=CD,求点P的坐标.(2)若点P在边AB,AD上,点P关于坐标轴对称的点Q落在直线y=x﹣1上,求点P的坐标.(3)若点P在边AB,AD,CD上,点G是AD与y轴的交点,如图2,过点P作y轴的平行线PM,过点G作x轴的平行线GM,它们相交于点M,将△PGM沿直线PG翻折,当点M的对应点落在坐标轴上时,求点P的坐标.(直接写出答案)【解答】解:(1)∵CD=6,∴点P与点C重合,∴点P坐标为(3,4).(2)①当点P在边AD上时,∵直线AD的解析式为y=﹣2x﹣2,设P(a,﹣2a﹣2),且﹣3≤a≤1,(a,2a+2)在直线y=x﹣1上,若点P关于x轴的对称点Q1∴2a+2=a﹣1,解得a=﹣3,此时P(﹣3.4).(﹣a,﹣2a﹣2)在直线y=x﹣1上时,若点P关于y轴的对称点Q3∴﹣2a﹣2=﹣a﹣1,解得a=﹣1,此时P(﹣1,0)②当点P在边AB上时,设P(a,﹣4)且1≤a≤7,(a,4)在直线y=x﹣1上,若等P关于x轴的对称点Q2∴4=a﹣1,解得a=5,此时P(5,﹣4),(﹣a,﹣4)在直线y=x﹣1上,若点P关于y轴的对称点Q4∴﹣4=﹣a﹣1,解得a=3,此时P(3,﹣4),综上所述,点P的坐标为(﹣3,4)或(﹣1,0)或(5,﹣4)或(3,﹣4).(3)①如图1中,当点P在线段CD上时,设P(m,4).在Rt△PNM′中,∵PM=PM′=6,PN=4,∴NM′==2,在Rt△OGM′中,∵OG2+OM′2=GM′2,∴22+(2+m)2=m2,解得m=﹣,∴P(﹣,4)根据对称性可知,P(,4)也满足条件.②如图2中,当点P在AB上时,易知四边形PMGM′是正方形,边长为2,此时P(2,﹣4).③如图3中,当点P在线段AD上时,设AD交x轴于R.易证∠M′RG=∠M′GR,推出M′R=M′G=GM,设M′R=M′G=GM=x.∵直线AD的解析式为y=﹣2x﹣2,∴R(﹣1,0),在Rt△OGM′中,有x2=22+(x﹣1)2,解得x=,∴P(﹣,3).点P坐标为(2,﹣4)或(﹣,3)或(﹣,4)或(,4).。
xx学校xx学年xx学期xx试卷姓名:_____________ 年级:____________ 学号:______________题型选择题填空题简答题xx题xx题xx题总分得分一、xx题(每空xx 分,共xx分)试题1:计算的结果是A. -3B. -2C. 2D. 3试题2:据报道,2015年第一季度,义乌电商实现交易额约为26 000 000 000元,同比增长22%,将26 000 000 000用科学计数法表示为A. 2.6×1010B. 2.6×1011C. 26×1010D. 0.26×1011试题3:有6个相同的立方体搭成的几何体如图所示,则它的主视图是试题4:下面是一位同学做的四道题:①;②;③;④,其中做对的一道题的序号是A. ①B. ②C. ③D. ④试题5:在一个不透明的袋子中装有除颜色外其它均相同的3个红球和2个白球,从中任意摸出一个球,则摸出白球的概率是评卷人得分A. B. C. D.试题6:化简的结果是A. B. C. D.试题7:如图,小敏做了一个角平分仪ABCD,其中AB=AD,BC=DC,将仪器上的点A与∠PRQ的顶点R重合,调整AB和AD,使它们分别落在角的两边上,过点A,C画一条射线AE,AE就是∠PRQ的平分线。
此角平分仪的画图原理是:根据仪器结构,可得△ABC≌△ADC,这样就有∠QAE=∠PAE。
则说明这两个三角形全等的依据是A. SASB. ASAC. AASD. SSS试题8:如图,四边形ABCD是⊙O的内接四边形,⊙O的半径为2,∠B=135°,则的长A. B. C. D.试题9:如果一种变换是将抛物线向右平移2个单位或向上平移1个单位,我们把这种变换称为抛物线的简单变换。
已知抛物线经过两次简单变换后的一条抛物线是,则原抛物线的解析式不可能的是A. B.C. D.试题10:挑游戏棒是一种好玩的游戏,游戏规则:当一根棒条没有被其它棒条压着时,就可以把它往上拿走。
(第9题)(第4题图)浙江省义乌市绣湖中学2016届九年级数学第二学期期中教学质量检测试题参考公式:二次函数2y ax bx c =++图像的顶点坐标是24,24b ac b aa ⎛⎫-- ⎪⎝⎭一、选择题(本题有10小题,每小题4分,共40分)1.在直角坐标系中,点(2,1)在( ▲ )A .第一象限B .第二象限C .第三象限D .第四象限 2.四边形的内角和为 ( ▲ )A .90°B .180°C .360°D .720°3.下列计算正确的是 ( ▲ )A. 32x x x =⋅B.2x x x =+C. 532)(x x =D. 236x x x =÷ 4.如图几何体由单位立方体搭成,则它的俯视图的面积是( ▲ ) A .7 B .6 C .5 D .45.函数y =中,自变量x 的取值范围是( ▲ )A .2x >B .2x ≠C .2x <D .2x ≤6.“义新欧”铁路的建设和开通,义乌市经济保持平稳增长.据统计,截止到今年3月初,我市金融机构存款余额约为1193亿元,用科学记数法应记为( ▲ )A .101.19310⨯元 B .111.19310⨯元 C .121.19310⨯元 D .131.19310⨯元 7.如果圆柱的母线长为5cm ,底面半径为2cm ,那么这个圆柱的侧面积是( ▲ ) A .102cm B .102πcm C .202cm D .202πcm8.小茜课间活动中,上午大课间活动时可以先从跳绳、乒乓球、健美操中随机选择一项运动, 下午课外活动再从篮球、武术、太极拳中随机选择一项运动.则小茜上、下午都选中球类运动的概率是( ▲ )A .19B .13C .23D .299.如图,已知AD 为△ABC 的角平分线,DE ∥AB 交AC 于E , 如果AE EC =23,那么ABAC =( ▲ ) A .13 B .23 C .25 D .3510.如图,在△ABC 中,AD 是中线,DE ⊥BC 交AB 于E ,AH ∥DE 交BC 于H ,且∠DAH =∠CAH ,连接CE 交AD 于F ,交AH 于G .下列结论:①△AEF ∽△CEA ;②FH ∥AC ;③若CE ⊥AB ,则tan ∠BAC =2;④若四边形AEDG 是菱形,则∠ACB =60°.其中正确的是( ) A .①②③ B .②③④ C .①② D.①②③④第10题(15题)二、填空题 (本题有6小题,每小题5分,共30分) 11.=16 ▲ .12. 分解因式:2x xy += ▲ .13.化简nnm n m +÷+11(的结果是 ▲ .14.如图,︒=∠=∠90E C ,3=AC ,4=BC ,2=AE ,则=AD ▲ .15.如图,已知点A ,C 在反比例函数)0(>=a xay 的 图象上,点B ,D 在反比例函数)0(<=b xby 的图象上, AB ∥CD ∥y 轴,AB ,CD 在y 轴的同侧,AB =3,CD =2, AB 与CD 的距离为1,则b a -的值是 ▲ 16.如图:在平面直角坐标系中,直线y =x +3与x 轴、y 轴分别交于A , B 两点,直线y =kx +8与直线AB 相交于点D ,与x 轴相交于点C ,过D 作DE ⊥x 轴于点E (1,0),点P (t ,0)为x 轴上一动点.若点T 为直线DE 上一动点,当以O,B, T 为顶点的三角形与以O,B, P 为顶点的三角形相似时,则相应的点P (t <0)的坐标为 ▲ .三、解答题(本大题共8小题, 第17、18,19题各8分, 第20,21,22题各10分, 第23题12分,24题14分)17.(本题8分)032(π2012)4sin 45(1)--+-°.18.(本题8分)(1)解不等式:3x -2>x +4; (2)解方程:1x x ++1x x-=219.(本题8分)如图,在□ABCD 中,已知点E 在AB 上,点F 在CD 上且AE =CF . (1)求证:DE =BF ;(2)连结BD ,并写出图中所有的全等三角形.(不要求证明) 20.(本题10分)位于义乌市江滨路和香山路交叉十字路口的“施粥摊”,每天早晨向群众免费施粥,某天早上7:30时亭前已经排起了180人长的队伍,预计从7:30开始到8:30每分钟有8位群众过来喝粥,8:30后过来喝粥人逐渐减少,现在施粥摊上有志愿工作人员3人,每人每分钟能服务3名群众喝粥,设从7:30开始x 分钟后队伍人数为y 人。