SPC常用公式和参数

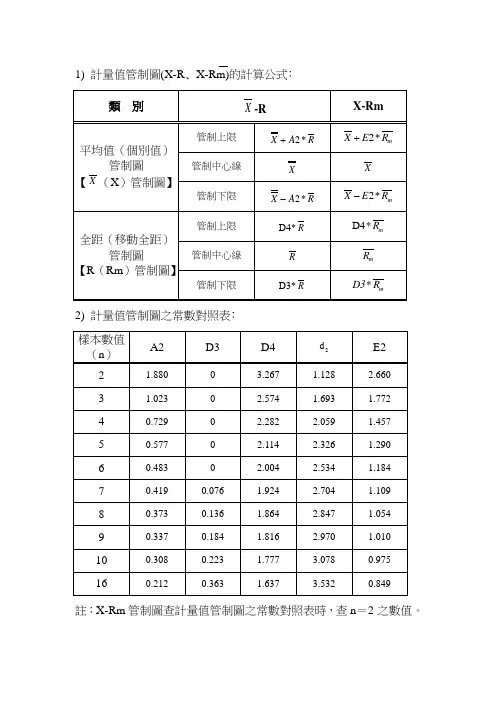
R X -一、 管制图公式说明1. 计量值公式管制图 1.1X 管制图：n 为组内样本量，m 为抽样组数；标准偏差 nσσ=2m i nm a x X X R -=估计标准偏差 2^d R=σ 全距平均值 m R m R R R R mi im ∑==+++=121...... 管制上限 → R A X R nd X U C L 22)3(+=+= 中心线 → X CL = 管制下限 → R A X R nd X L C L 22)3(-=-=其中 nd A 223=R 管制图： R 的标准偏差 )(23d R d R =σ 管制上限 → R D d Rd R R U C L R 423)(33=+=+=σ中心线 → R CL =管制下限 → R D d Rd R R U C L R 323)(33=-=-=σ 其中 23331d d D -= ， 23431d dD +=mx nx x x x mi in∑=++++==++=1m ....32121 m x x x x x ......X 管制图：第i 组之标准偏差1)(12--=∑=n x xS ni ii∑==mi i S m S 11估计标准偏差 4C S =σ 管制上限 →S A X S nC X U C L 34)3(+=+=中心线 → X CL = 管制下限 → S A X S nC X L C L 34)3(-=-=其中nC A 433=S 管制图： 管制上限 → S B U C L s4= 中心线 → S C L s= 管制下限 → S B L C L s 3=1.3 X-Rm 管制图Rm 管制图：移动全距 1--=i i i x x MR nMRMR ni i∑==1管制上限 → MR D UCL 4=中心线 → MR CL =管制下限 → MR D LCL 3=(当n=2时，3D 和4D 以样本数为2来查表)个别管制图管制上限 → 23d MRx UCL +=中心线 → x CL =管制下限 → 23d MRx LCL -= (当n=2时，2d 以样本数为2来查表)**中位数随着计算机技术的发展，计算已经不是困难，逐步被淘汰**2. 计数值公式2.1不良率管制图 ( P Chart )当每组之样本数均相同时：中心线 → ∑==Ki i P K P 11管制上限 → ) 1 , )1(3min(n P P P UCL -+= 管制下限 → ) 0 , )1(3max(nP P P LCL --=当各组之样本数不相同时：中心线 → ∑==Ni i i P n N P 11 ， 其中 k n n n N +++= (21)各组管制上下限分别为 管制上限 → ) 1 , )1(3min(i n P P P UCL -+= 管制下限 → ) 0 , )1(3max(in P P P LCL --=n 管制上限 → )1(3P P P U C L n n -+=管制下限 → )1(3P P P L C L n n --= 其中 n P 为各组之不合格数。

SPC常用公式和全参数
SPC（Statistical Process Control）即统计过程控制，是一种可以检测和预防生产过程中发生的未预期变异的统计技术，涉及概率统计学、质量控制、过程设计等多个领域。

它被广泛用于制造业、服务业以及其他行业，可以有效识别与控制过程中发生的质量问题，从而提高工作效率和质量。

1、X-R图（X-R chart）：X-R 图是 SPC 中最常用的一种图表，它用于检测和控制过程中发生的质量变异情况。

X-R 图可以通过样本数据来分析过程变异，并用线性直线限制上下限的范围，从而确定是否存在质量问题。

2、np图（np chart）：np 图是用于检测和控制质量问题的一种统计图表，可以用于检测和控制多个样本中每一个样本的变异情况。

np 图中的上下限被用于确定质量问题是否存在，可以根据上下限的范围来判断多个样本的变异程度。

3、C图（C chart）：C 图用于检测和控制过程中同一种类样本的变异情况，它将质量变异的概率分布密度函数作为观测变量，可以用来检测和控制样本数据之间的偏差。

4、P图（P chart）：P 图用于检测和控制过程中发生的质量变异情况，并使用概率分布函数来分析样本数据之间的差异，可以用来检测和控制不同样本的变异程度。

SPC常用公式和参数SPC（Statistical Process Control，统计过程控制）是一种质量管理方法，通过使用统计方法来监控生产过程中的变异性，以及使过程保持在可控状态，确保产品质量的稳定性。

在SPC中，常用的公式和参数用于描述、分析和控制过程的变异性，以及进行质量指标的计算和分析。

下面是SPC中常用的公式和参数：1. 均值（Mean）：均值是一组数据的平均值，用于描述数据的集中趋势。

均值可以表示为：Mean = (x1 + x2 + ... + xn) / n其中，x1 ~ xn表示一组数据，n表示数据的个数。

2. 范围（Range）：范围用于描述一组数据的离散程度，即最大值与最小值之间的差异。

范围可以表示为：Range = xmax - xmin其中，xmax表示一组数据的最大值，xmin表示最小值。

3. 标准差（Standard Deviation）：标准差是一组数据的离散程度的度量，用于衡量数据的波动性。

标准差可以表示为：Standard Deviation = sqrt[((x1 - mean)^2 + (x2 - mean)^2+ ... + (xn - mean)^2) / n]其中，x1 ~ xn表示一组数据，mean表示数据的均值，n表示数据的个数。

4. 方差（Variance）：方差是标准差的平方，也是一组数据的离散程度的度量。

Variance = (Standard Deviation)^25. 控制图（Control Chart）：控制图是SPC中最常用的工具，它用于监控过程的变异性，并确定过程是否处于可控状态。

在控制图中，常用的参数有：- 中心线（Center Line）：控制图的中心线表示过程的平均值或目标值。

- 控制限（Control Limit）：控制限是确定过程的可控状态的界限。

常用的控制图有三个控制限：- 上控制限（Upper Control Limit，UCL）：表示过程变异性在正常范围内的上限，超过该限制则表明过程存在特殊原因。

SPC各值计算公式SPC（统计过程控制）是一种统计方法，用于检测和控制过程的稳定性和变异性。

SPC各值计算公式包括控制图参数和过程能力指数等。

以下是常见的SPC各值计算公式及其解释：1.控制图参数：a.X̄控制图上的中心线是过程的平均值的估计量。

计算公式为：X̄=ΣX/n，其中X是测量值的总和，n是样本大小。

b. R 控制图上的极差线是过程的极差的估计量。

计算公式为：R = Xmax - Xmin，其中Xmax和Xmin是样本中最大值和最小值。

c.S控制图上的标准偏差线是过程的标准偏差的估计量。

计算公式为：S=√(Σ(X-X̄)²/(n-1))，其中Σ(X-X̄)²是样本值与平均值的差的平方的总和。

d.UCL控制图上的上限控制限是过程的可接受上限。

计算公式为：UCL=X̄+3S，其中3是标准差的倍数，用于确定上限控制限。

e.LCL控制图上的下限控制限是过程的可接受下限。

计算公式为：LCL=X̄-3S，其中3是标准差的倍数，用于确定下限控制限。

2.过程能力指数：a.Cp过程能力指数是衡量过程发生误差在可接受范围内的能力。

计算公式为：Cp=(USL-LSL)/(6σ)，其中USL和LSL是规范上限和下限，σ是标准偏差的估计量。

b. Cpk 过程能力指数是衡量过程发生误差在可接受范围内的能力，同时考虑了过程的中心线偏移。

计算公式为：Cpk = min((USL - X̄) /(3σ), (X̄ - LSL) / (3σ))，其中USL和LSL是规范上限和下限，X̄是过程的平均值的估计量，σ是标准偏差的估计量。

c. Cpm 过程能力指数是衡量过程发生误差在可接受范围内的能力，同时考虑了过程的中心线偏移和过程的极差。

计算公式为：Cpm = (USL - LSL) / (6√((ΣR/n)² + σ²))，其中USL和LSL是规范上限和下限，ΣR/n是极差均值的估计量，σ是标准偏差的估计量。

SPC所有公式详细解释及分析SPC（统计过程控制）是一种通过统计方法对产品或过程的变化进行控制的质量管理工具。

它以数据为基础，通过收集、分析和解释数据，帮助确定过程是否稳定、符合规范，并提供改进措施。

在SPC中，有一些重要的公式用于计算和分析数据，下面将介绍其中一些常用的公式及其详细解释和分析。

1. 平均值（Mean）：平均值是统计数据的中心点，通过计算数据的总和除以数据的个数得到。

平均值用于评估过程的中心位置，并对过程的稳定性进行评估。

2. 中位数（Median）：中位数是将数据按照大小顺序排列后，排在中间位置的数值，它能够反映数据的集中趋势。

与平均值相比，中位数对异常值的影响较小，更适用于非正态分布的数据。

3. 标准差（Standard Deviation）：标准差是数据分布离散程度的度量，用于描述数据的波动性。

标准差越大，表示数据越分散；标准差越小，表示数据越集中。

标准差可以帮助确定过程是否稳定，是否存在特殊因素影响。

4. 变异系数（Coefficient of Variation）：变异系数是标准差除以平均值的比值，用于比较不同数据集的离散性。

较小的变异系数表示数据越稳定，较大的变异系数表示数据集的离散性较大。

5. 极差（Range）：极差是数据的最大值和最小值之间的差别，用于评估数据的波动范围。

较大的极差表示数据集的波动性较大，较小的极差表示数据集的波动性较小。

6. 四分位数（Quartiles）：四分位数是将数据按大小顺序排列后，将数据分为四等份的数值。

第一四分位数是中位数的前一半数据的中位数，第二四分位数即中位数，第三四分位数是中位数之后的一半数据的中位数。

四分位数可以帮助了解数据的分布情况。

7. 直方图（Histogram）：直方图使用柱状图形象地展示数据的分布情况。

通过将数据按照一定的区间划分，并统计每个区间内的数据个数，可以直观地了解数据的分布情况。

8. 管理图（Control Chart）：管理图是SPC最重要的工具之一，它通过将数据的统计量（如平均值、标准差等）绘制在图表上，并与控制限进行比较，用于监控过程的稳定性。

SPC常用公式和参数SPC（Statistical Process Control，统计过程控制）是一种通过收集和分析数据，对过程进行统计学监控的方法。

它可以帮助企业实时监控生产过程的稳定性和一致性，并通过识别和纠正异常，改善产品质量和生产效率。

SPC常用的公式和参数包括：1. 均值（Mean）：均值是一组数据的平均值，用于描述数据的中心趋势。

计算公式为：均值= Σ数据值 / 数据个数。

2. 范围（Range）：范围是一组数据的最大值与最小值之间的差异，用于描述数据的离散程度。

计算公式为：范围 = 最大值 - 最小值。

3. 方差（Variance）：方差是一组数据与其均值之间的差异的平方和的平均数，用于描述数据的波动程度。

计算公式为：方差= Σ(数据值- 均值)² / 数据个数。

4. 标准差（Standard Deviation）：标准差是方差的算术平方根，用于描述数据的离散程度。

计算公式为：标准差= √方差。

5.Cp指数：Cp指数是过程能力指数，用于评估过程的稳定性，即过程的变异范围是否在产品规格范围内。

计算公式为：Cp=(规格上限-规格下限)/(6*标准差)。

6. Cpk指数：Cpk指数是过程能力指数的修正值，考虑了过程中离规格上下限最远的数据点，用于评估过程的能力。

计算公式为：Cpk =min[(规格上限 - 均值) / (3 * 标准差), (均值 - 规格下限) / (3 * 标准差)]。

7. 控制限（Control Limits）：控制限是一组上限和下限，用于判断过程数据是否正常。

常用的控制限包括平均数控制限（X控制限）和范围控制限（R控制限），计算公式为：X控制限 = 均值± 3 * 标准差，R控制限 = D4 * 范围平均数。

8. 过程能力指数（Process Capability Index）：过程能力指数用于评估过程的能力是否满足产品规格要求，常用的指数包括Cp、Cpk和Cpm。

SPC计算公式和判定准则SPC（Statistical Process Control，统计过程控制）是一种通过统计方法对过程进行监控和控制来确保产品质量的方法。

SPC包含了一系列的计算公式和判定准则，用于对过程数据进行分析和判断。

本文将介绍SPC的常用计算公式和判定准则。

一、计算公式1. 平均值（X－bar）和范围（R）控制图的计算公式：平均值控制图：X-bar = (X1 + X2 + ... +Xn)/n范围控制图：R = Xmax - Xmin2.方差（S）控制图的计算公式：方差控制图：S = √((∑(xi - x̄)²)/(n-1))其中，xi为单个数据点，x̄为平均数，n为样本个数。

3.标准差（σ）控制图的计算公式：标准差控制图：σ = √((∑(xi - x̄)²)/n)其中，xi为单个数据点，x̄为平均数，n为样本个数。

4. 标准分数（Z-score）的计算公式：标准分数：Z=(X-μ)/σ其中，X为观测值，μ为总体平均值，σ为总体标准差。

5.概率（P）的计算公式：概率：P=1-Z其中，Z为标准分数。

二、判定准则SPC通过控制图上的控制限来进行判定，一般包括控制线和规范线。

常用的判定准则有以下几种：1.控制线：控制线用于界定过程是否处于统计控制状态。

一般有上限控制线（UCL）和下限控制线（LCL）。

当数据点超过控制线时，表明过程处于非随机状态，可能存在特殊原因。

2.规范线：规范线用于界定过程是否处于规范状态。

一般有上限规范线（USL）和下限规范线（LSL）。

当数据点超过规范线时，表明产品或过程不符合规格要求。

3.判定准则：SPC根据运行趋势和控制限来进行判定，常见判定准则包括：-单点超出控制限：当单个数据点超出控制限时，可能存在特殊原因，需要进行调查和纠正。

-一组连续点趋势逐渐上升或下降：当连续的数据点呈增加或减少的趋势时，表明过程可能不稳定，需要进行调查和纠正。

SPC所有公式详细解释及分析SPC（统计过程控制）是一种用于监控和控制过程变异的统计方法。

在SPC中，有许多公式用于计算统计量和确定控制界限，以帮助检测异常和评估过程的稳定性。

本文将详细解释和分析一些常见的SPC公式。

1. 平均值（Mean）：平均值是样本数据的算术平均值。

计算平均值的公式是将所有观测值相加，然后除以观测值的个数。

平均值可以用来了解过程的中心位置。

2. 范围（Range）：范围表示样本数据的最大值和最小值之间的差异。

计算范围的公式是将样本数据的最大值减去最小值。

范围主要用于检测过程变异的大小。

3. 方差（Variance）：方差用于测量样本数据的离散程度。

计算方差的公式是将每个观测值与平均值的差异平方后相加，并除以观测值的个数减1、方差越大，表示过程的波动性越大。

4. 标准差（Standard Deviation）：标准差是方差的平方根，用于衡量过程数据的离散程度。

标准差可以用来判断过程的稳定性和控制界限的设定。

标准差越大，表示过程的变异性越大。

5. 控制图界限（Control Limits）：控制图界限是用来判断过程是否处于统计控制的范围内。

常用的控制图包括X-bar图和R图。

在X-bar图中，控制界限由平均值加减3倍标准差计算得到。

在R图中，控制界限由平均范围的加减2.66倍平均范围的标准差计算得到。

如果一个点超出了控制界限，则表示该点可能是异常值或过程发生了变化。

6. 过程能力指数（Process Capability Index）：过程能力指数用来衡量过程在规格限制内产生产品的能力。

常用的过程能力指数包括Cp、Cpk、Pp和Ppk。

Cp和Pp表示过程的潜在能力，只考虑过程的平均值和规格限制的距离；Cpk和Ppk表示过程的实际能力，同时考虑过程的变异性。

7. 规格上限与规格下限（Specification Limits）：规格上限和规格下限是产品或过程的设计要求。

当产品或过程的测量值超出规格限制时，表示产品或过程不符合设计要求，可能需要调整或改进。

SPC计算公式和判定准则SPC（Statistical Process Control，统计过程控制）是一种用于监测和控制过程稳定性的方法，通过对过程进行统计分析和监测，可以及时发现过程中的变异，从而采取相应的控制措施，提高过程的稳定性和可控性。

本文将介绍SPC的计算公式和判定准则，以帮助读者了解如何应用SPC进行过程监控和控制。

1. SPC计算公式SPC计算公式是用于计算各种统计指标和控制图的数学公式，下面是常用的SPC计算公式。

1.1 均值（Mean）均值是一组数据的平均值，用于表示过程的中心位置。

计算均值的公式如下：均值公式均值公式其中，mu 表示均值，n 表示数据的数量，x_i 表示第i 个数据。

1.2 极差（Range）极差是一组数据的最大值和最小值之差，用于表示过程的变异程度。

计算极差的公式如下：极差公式极差公式其中，R 表示极差，x_{\text{max}} 表示数据的最大值，x_{\text{min}} 表示数据的最小值。

1.3 标准偏差（Standard Deviation）标准偏差是一组数据的离均差平方和的平均值的平方根，用于表示过程的稳定性。

计算标准偏差的公式如下：标准偏差公式标准偏差公式其中，sigma 表示标准偏差，n 表示数据的数量，x_i 表示第i 个数据，\bar{x} 表示数据的均值。

2. SPC判定准则SPC判定准则用于判断一个过程是否处于稳定状态，常用的判定准则有以下几种。

2.1 均值控制图（Mean Control Chart）均值控制图用于监测过程均值是否稳定。

常用的均值控制图有Xbar-R 控制图和 Xbar-S 控制图。

•Xbar-R 控制图：对应的是过程均值和极差的统计指标。

当连续 n 个点全部落在中心线（均值线）的上方或下方时，表示过程中有特殊原因的变异，需要采取相应措施进行调整。

•Xbar-S 控制图：对应的是过程均值和标准偏差的统计指标。

当连续 n 个点全部落在中心线（均值线）的上方或下方时，表示过程中有特殊原因的变异，需要采取相应措施进行调整。

SPC计算公式范文SPC（Statistical Process Control）是一种统计过程控制方法，用于监控和控制工业过程的质量。

它通过收集数据、分析数据并提供即时反馈，帮助确定过程是否正常运行，并识别异常情况。

SPC计算公式是用来计算过程的控制图中的上限、下限、中心线以及其他统计参数的公式。

在SPC中，常用的计算公式包括平均值（mean）、标准差（standard deviation）、上限（upper control limit）、下限（lower control limit）和中心线（center line）等。

1. 平均值（mean）：计算数据的平均值用于确定中心线。

平均值的计算公式为：Mean = ΣX / n其中，X是样本数据的总和，n是样本个数。

2. 标准差（standard deviation）：衡量数据的离散程度。

标准差的计算公式为：Standard Deviation = sqrt(Σ(X - Mean)^2 / n)其中，Σ(X - Mean)^2表示每个数据与平均值的差的平方和，n是样本个数，sqrt表示开方。

3. 上限（upper control limit）和下限（lower control limit）：用于识别过程异常情况。

上限和下限的计算公式为：Upper Control Limit = Mean + k * Standard DeviationLower Control Limit = Mean - k * Standard Deviation其中，k是控制图的参数，可以根据过程的要求进行设定，通常为2或34. 中心线（center line）：表示过程的目标值。

中心线的位置通常与平均值相等。

除了上述基本参数外，SPC还可以计算其他统计参数，如极差（range）、方差（variance）、过程能力指数（process capability index）等。

SPC中所涉及到的所有统计量和相关的公式~！1、Mean (平均值)2、Max (最大值)3、Min (最小值)4、Range (Max－Min最大跨距)5、StdDev 标准差6、Cp (过程能力指数)7、Cr (过程能力比值)8、k (偏移系数)9、Cpu (上限过程能力指数)10、Cpl (下限过程能力指数)11、Cpk (过程能力指数)12、Cpm (目标能力指数)13、Zu(Cap) (规格上限SIGMA水平)14、Zl(Cap) (规格下限SIGMA水平)15、Fpu(Cap) (超出规格上限机率)16、Fpl(Cap) (超出规格下限机率)17、Fp(Cap) (超出规格限的机率)18、Pp (过程性能指数)19、Pr (过程性能比值)20、Ppu (上限过程性能指数)21、Ppl (下限过程性能指数)22、Ppk (过程性能指数)23、Ppm (目标过程性能指数)24、Zu(Perf) (规格上限SIGMA水平)25、Zl(Perf) (规格上限SIGMA水平)26、Fpu(Perf) (超出规格上限机率)27、Fpl(Perf) (超出规格下限机率)28、Fp(Perf) (超出规格界线的机率)29、Skewness (偏度)30、Kurtosis (峰度)2011-10-13 08:38 上传下载附件(29.39 KB)2011-10-13 08:38 上传下载附件(33.58 KB)2011-10-13 08:38 上传下载附件(41.15 KB)2011-10-13 08:38 上传下载附件(46.14 KB)2011-10-13 08:38 上传下载附件(46.81 KB)2011-10-13 08:38 上传下载附件(30.94 KB)2011-10-13 08:38 上传下载附件(30.97 KB)2011-10-13 08:38 上传下载附件(31.33 KB)2011-10-13 08:38 上传下载附件(28.83 KB)2011-10-13 08:38 上传下载附件(28.42 KB)2011-10-13 08:38 上传下载附件(31.83 KB)2011-10-13 08:38 上传下载附件(11.58 KB)2011-10-13 08:38 上传下载附件(19.16 KB)2011-10-13 08:38 上传下载附件(21.2 KB)2011-10-13 08:38 上传下载附件(23.23 KB)2011-10-13 08:38 上传下载附件(16.33 KB)。

SPC计算公式及参数SPC（统计过程控制）是用于过程监控和质量管理的一种方法。

它使用统计技术来分析过程数据，以确定是否存在特殊原因的变异，并采取适当的措施来改善过程。

SPC基于一些核心原则，包括过程稳定性、常见原因和特殊原因的变异性、数据分布的正态性以及过程改进的周期性。

1.过程稳定性的指标- 均值（Mean）：过程数据的平均值，用于衡量过程的中心性。

计算公式为所有数据之和除以数据点的数量。

- 极差（Range）：最大值和最小值之间的差异，用于衡量过程的变异性。

计算公式为最大值减去最小值。

- 标准偏差（Standard Deviation）：用于衡量过程数据的偏离程度。

计算公式有多种方法，常见的是样本标准偏差，即每个数据点与平均值偏离的平方和的平均值的平方根。

2.控制图参数- 控制上限（Upper Control Limit，UCL）和控制下限（Lower Control Limit，LCL）：用于确定过程数据在控制图上的控制限。

这些限制是根据过程稳定性和特殊原因变异性的统计性质确定的。

常见的计算方法包括基于过程数据的标准偏差和均值的控制限。

- 中心线（Center Line）：过程数据中心线，它通常与过程数据的均值相一致。

3.过程能力指数- 过程能力指数（Process Capability Index，Cpk）：用于衡量过程产生的变异性与允许变异性之间的关系。

计算公式为最小特殊规格上限和最大特殊规格下限之间的距离与过程的6标准偏差之间的较小值。

以上只是SPC计算公式和参数中的一部分，根据具体的应用和数据类型，可能需要使用其他的公式和参数。

在进行SPC分析时，还需要注意以下几点：-数据采集要准确和可靠，避免人为误差和其他偏差。

-样本选择和样本大小要合理，以提高数据的代表性和统计稳定性。

-控制图的维护和更新，及时反映过程的变化和改进。

-异常点的处理，及时发现特殊原因的变异并采取措施进行改进。

-统计技术和工具的正确应用，以确保分析的准确性和可靠性。

SPC计算公式跟判定准则SPC（Statistical Process Control，统计过程控制）是一种用统计学方法来监控和控制工业过程的方法。

它基于对过程进行统计分析，以确定该过程是否稳定，并且是否产生了超出规定范围的偏差。

SPC可以帮助企业实时监控过程，及时发现和纠正偏差，从而提高产品质量和生产效率。

在SPC中，有两个重要的概念：过程的中心线（Center Line，CL）和过程的控制限（Control Limits，CLs）。

中心线代表过程的平均水平，通过对样本数据进行测量和计算得出。

控制限则是在中心线周围设定的上下限，用于判断过程是否处于统计控制之中。

1.过程平均值计算公式：过程平均值（X̄）= (x1 + x2 + x3 + ... + xn) / n其中，x1、x2、x3...xn表示各个样本数据的值，n表示样本的数量。

2.样本标准差计算公式：样本标准差（S）= sqrt(((x1 - X̄)^2 + (x2 - X̄)^2 + (x3 -X̄)^2 + ... + (xn - X̄)^2) / (n-1))其中，sqrt表示平方根。

判定准则：SPC的判定准则主要是基于正态分布的特性，对数据进行判断和控制。

常见的判定准则包括：1.样本数据是否处于过程控制限内：如果样本数据的值都处于过程的控制限范围内，表示过程处于统计控制之中。

2.过程是否稳定：通过监控过程的均值和标准差的变化，判断过程是否稳定。

如果均值和标准差变化较小，则表示过程稳定。

3.是否存在特殊因素：当样本数据出现连续的、显著的趋势变化或者超出控制限，可能表示过程受到了特殊因素的影响，需要进行进一步的调查和改进。

4.是否存在异常点：如果样本数据中存在偏离正态分布的异常值，可能表示过程存在异常情况，需要进行分析和处理。

总结：SPC通过计算和分析过程的平均值和标准差，来判断过程是否处于统计控制之中，并识别可能存在的问题。

通过对过程进行持续监控和改进，可以提高产品的质量和生产的效率。

SPC各值计算公式SPC（统计过程控制）是一种用于监控和改进过程稳定性的方法。

它使用统计分析和控制图来识别过程中的变异性，并采取措施来减少非随机变异。

SPC中使用的一些关键参数和计算公式如下：1.平均值（X̄）：平均值是一组数据的总和除以数据个数。

它用于衡量过程的中心位置。

平均值的计算公式如下：X̄=(X1+X2+X3+...+Xn)/n2.极差（R）：极差是一组数据中最大值和最小值之间的差异。

它用于衡量过程的不稳定性。

极差的计算公式如下：R = Xmax - Xmin3.标准差（S）：标准差是一组数据与其平均值之间的离散程度。

它用于衡量过程的变异性。

标准差的计算公式如下：S=√[(Σ(Xi-X̄)²)/(n-1)]4.各类控制限：控制限用于判断过程是否处于统计控制之内。

常见的控制限有上限（UCL）和下限（LCL）。

根据数据的分布情况，控制限可以分为以下几种类型：-3σ控制限（常用控制限）：UCL=X̄+3SLCL=X̄-3S-2σ控制限：UCL=X̄+2SLCL=X̄-2S-1σ控制限：UCL=X̄+SLCL=X̄-S-S控制限：UCL=X̄+A2RLCL=X̄-A2RA2为常数，需要查找A2值表。

5.控制图中的数据点标记：控制图中的数据点通常使用特殊的标记，用于表示超出控制限的点。

常见的标记有以下几种：-O：超出3σ控制限-X：超出2σ控制限-*：超出1σ控制限以上是SPC中常用的一些计算公式和参数。

使用这些公式可以计算过程的平均值、极差、标准差以及相关的控制限，从而进行过程的监控和改进。

掌握这些公式可以帮助人们有效地进行SPC的应用和分析。